
龟壳演化算法(TSEA)
内容
1. 概述
乌龟是自然界中最古老且最令人惊叹的物种之一。它背负着龟壳——这是坚韧、保护和生存的象征。这个威严的盾牌,在乌龟的一生中逐渐形成,不仅实现了物理上的保护,还体现了它不断的发展和克服障碍的能力。
龟壳的设计是其独特发展轨迹的见证,象征着时间与生物体本身的和谐统一。 龟壳从一个被称为“脐带”的中心点开始生长。新层会在现有的壳上不断叠加,从而形成不同的图案。图案的每一部分都代表着乌龟成长的不同年份或季节。年复一年,层层叠加,龟壳随着乌龟一同成长成熟。它呈现出新的图案,形成独特的集群,这些集群反映了乌龟的生命经历和成长过程。
乌龟的壳主要由两部分组成:上部称为 背甲(carapace),下部称为腹甲(plastron)。乌龟壳的生长是蜕变(metamorphosis)的结果。龟壳上的图案是多种因素复杂相互作用的结果,包括遗传、环境和壳本身的生长。
乌龟壳由生物组织和碳酸盐物质(如钙和镁)组成。壳的碳酸盐结构为其提供了强度,并保护了乌龟的内部器官。幼龟的壳由柔软的软骨板组成,这些软骨板会随着时间的推移变硬并转化为骨骼。壳的生长是由于在乌龟皮肤下定期沉积新的骨组织层。这个过程使得壳能够随着乌龟的生长而增大,并可能出现新的图案,或是现有的图案随时间发生变化。
乌龟壳上的图案并非随机分布。它们是由特定的生物过程形成的,并可以根据其形状、颜色和位置被归类为不同的组或“集群”。例如,一些乌龟有星形图案,而其他乌龟的图案则类似于豹皮。随着龟壳的生长,其壳上的图案可能会发生变化和演化。这可能会导致图案所属的集群发生变化。例如,原本被归类为“星形”的图案可能会随着时间的推移变得更加复杂。
值得注意的是,每只乌龟的壳上都有独特的图案,这些图案有助于它们适应环境,并具有诸如伪装或吸引配偶繁殖等重要功能。
龟壳上的图案启发了我,让我创造了一种原创的优化算法,而龟壳的演化则成为了数据合并和聚类过程的隐喻,并促使我创造了一种新的工具,该工具可以根据经验和知识进行适应和演化。
2. 算法实现
龟壳演化算法背后的理念是,通过皮肤上新角化区域的逐渐形成来模拟壳的生长,这些区域代表着优化问题的解决方案。在这个模型中,最佳解决方案会变得坚硬,并位于更靠近外表面的位置,而不太理想的解决方案则仍然较软,并位于内部。
在这个背景下,壳被划分为多个集群,这些集群在其表面形成图案,而其层次则通过垂直划分为集群来模拟。在算法中模拟壳的生长过程包括向上(向外)和向下(向内)的移动,以及扩展。这种优化算法的一个独特之处在于它保留了不太理想的解决方案,这体现在壳向内生长的过程中。壳的内层是唯一一个在两个方向上扩展的层,而其他层只向外扩展,这样一来最差的解决方案就会被新的解决方案所替代。每个垂直集群(层)对解决方案的容纳能力是有限的;如果没有达到最大数量,就简单地添加解决方案,否则就根据所描述的原则替换解决方案。
图1清晰地展示了根据解决方案的质量和它们之间的距离进行的集群。为了更好地理解,这里使用了一个一维解决方案空间的假设示例。这个图表使我们能够清楚地看到,集群是如何根据解决方案的质量和相互之间的接近程度来形成的。
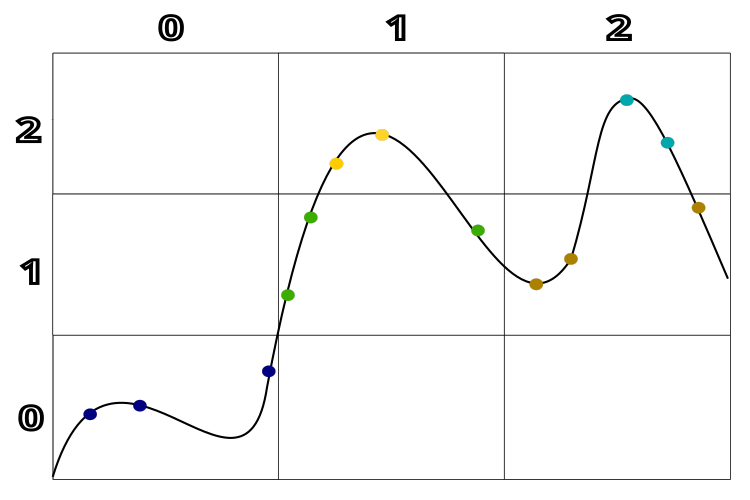
图例 1. 在TSEA算法中,聚类效果通常依据解决方案的质量以及解决方案之间的距离
让我们为TSEA算法编写一个伪代码:
1. 为群体生成随机个体。
2. 计算 FF。
3. 初始化垂直种群集群。
4. 初始化水平K-Means种群集群。
5. 将种群限制在壳中。
6. 根据壳中的数据生成新的群体:
6.1. 概率为0.8时:
垂直选择一个集群。
选择单元格内的最优智能体,或者以0.5的概率随机选择单元格内的任意一个智能体。
使用所选单元格内的智能体,或者以0.6的概率使用全局最优解决方案。
根据权限分配创建一个新的智能体坐标。
6.2 或者:
垂直选择一个集群。
垂直选择两个集群,并随机从这两个集群中选择一个智能体。
创建一个新坐标,该坐标为所选智能体坐标的平均值。
7. 计算FF。
8. 垂直种群聚类。
9. 在K-NN(K-Nearest Neighbors,K-最近邻)方法中,定义智能体属于K-NN壳的集群。
10. 对壳进行每50个训练周期一次的垂直集群。
11. 将种群限制在壳中。
12. 从p.开始重复。
根据二次定律 (见图 2) 进行垂直集群选择,该定律决定了列表中最后一个(即最优)集群相较于第一个(即最差)集群具有更高的被选中概率。
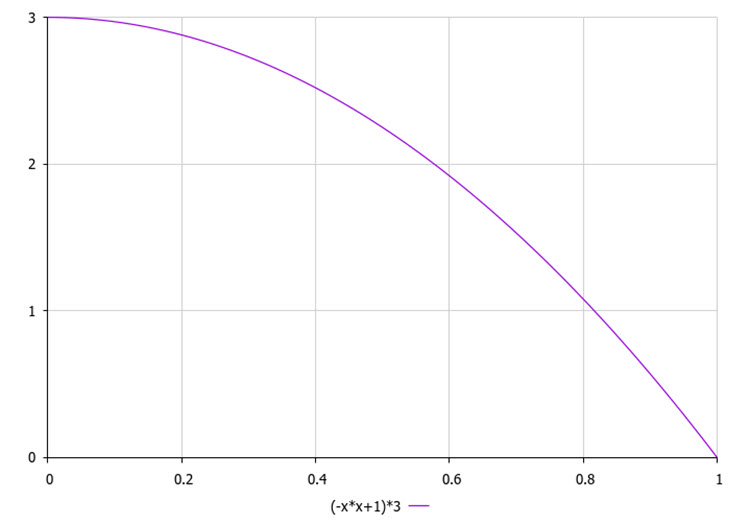
图例 2. 选择垂直集群的概率法则(按质量),其中3是集群的数量
因此,创建壳的新图案(智能体-优化问题的解决方案)的逻辑如下:
- 选择壳层(垂直集群)。选择上层(更硬层)的概率高于下层(较软层)。
- 从选定层的水平集群中选择硬壳部分。
- “融合”所选部分。
上层“融合”(硬化)的概率高于下层:
既然我们已经有了伪代码以及父代群体中选择智能体的法则,那么任务已经基本完成。当然,任务并未完成。我们仍然需要编写实际的代码。
通过TSEA算法中的S_TSEA_Agent结构实现智能体优化。在垂直和水平方向上,我们都需要对聚类进行标记。
1. 该结构包含以下字段:
- c[] - 用于存储智能体坐标的数组。
- f - 用于存储智能体得分(适应度)的变量。
- label - 集群成员标签
- labelClustV - 垂直集群
- minDist - 到最近质心的最小距离
2. Init 方法是 S_TSEA_Agent 结构体的一个组成部分,其主要功能是初始化结构体的各个字段。此方法接收一个名为"coords" 的整型参数,该参数被用于通过 ArrayResize 函数调整 "c"数组的大小。
3. f = -DBL_MAX - 将“f”变量的初始值设置为双精度数的最小可能值,即负无穷大。
4. label = -1 and labelClustV = -1 - 初始化集群成员标签为-1。
5. minDist = DBL_MAX - 将 " minDist" 变量的初始值设定为双精度数的最小可能值。
上述代码段定义了 TSEA 优化算法中代理的基本数据结构,并在创建新智能体时对其字段进行初始化。这样的设计帮助智能体存储有关其当前状态的信息,并在算法执行的过程中对这些信息进行更新。
//—————————————————————————————————————————————————————————————————————————————— struct S_TSEA_Agent { double c []; //coordinates double f; //fitness int label; //cluster membership label int labelClustV; //clusters vertically double minDist; //minimum distance to the nearest centroid void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; label = -1; labelClustV = -1; minDist = DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
我们需要清晰地描述龟壳(一个二维数组)及其包含的垂直适应度集群和水平位置集群。在这个二维数组的每一个单元格中,都存储着一个介于0到算法外部参数所指定的最大值之间的数值。
使用S_TSEA_horizontal结构描述水平集群,这个结构包含以下字段:
- indBest - 单元格中的最优智能体
- agent[] - 用于存储智能体的S_TSEA_Agent结构数组
在描述垂直集群时,我们可以使用包含以下字段的 S_TSEA_horizontal结构:
- cell[] - S_TSEA_horizontal结构数组。
代码赋予了我们通过二维数组的两个方面来描述龟壳的能力。我们可以在数组的每个单元格中存储优化智能体。实质上,龟壳是一个特别构建的父代种群,在创建子代智能体时方便我们访问。
//—————————————————————————————————————————————————————————————————————————————— struct S_TSEA_horizontal { int indBest; S_TSEA_Agent agent []; }; struct S_TSEA_vertical { S_TSEA_horizontal cell []; }; //——————————————————————————————————————————————————————————————————————————————
为了执行聚类,根据给定的伪代码,TSEA算法采用了两种聚类方法:K-Means和K-NN。在关于BSO算法的文章中,我们已将K-Means方法纳入考虑之中。让我们回顾一下聚类结构的样式:
- centroid[] - 用于存储单元格质心坐标的数组
- f - 用于存储质心得分(适应度)的变量
- count - 集群中的智能体数量
- agentList[] - 集群中的智能体清单
- Init - 使用S_Cluster结构方法初始化结构字段
//—————————————————————————————————————————————————————————————————————————————— struct S_Cluster { double centroid []; //cluster centroid double f; //centroid fitness int count; //number of points in the cluster void Init (int coords) { ArrayResize (centroid, coords); f = -DBL_MAX; count = 0; ArrayResize (ideasList, 0, 100); } }; //——————————————————————————————————————————————————————————————————————————————
为了确定子代理所属的相应集群,我们将使用K-NN方法(即k-最近邻方法)。
除了K-Means方法外,C_TSEA_clusters类还包含以下方法:
1. VectorDistance 方法:
- 该方法用于计算由'双精度'类型数字数组表示向量“v1”和“v2”之间的欧几里得距离。
- 它使用了欧几里得距离公式:
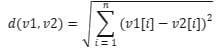 .
. - 返回计算出的距离。
2. DistanceIndex 结构:
- 该结构表示了一对数值:“距离”和“索引”。
- 该结构用于存储从一个点到其他点的距离及其索引。
3. BubbleSort 方法:
- 该方法使用冒泡排序方法按距离升序对DistanceIndex类型的对象数组进行排序。
- 使用临时“temp”变量交换数组元素。
4. KNN方法实现了k近邻算法,用于对“point”进行分类:
- 它计算“点”到“数据”数组中所有点的距离,并对这些距离进行排序,根据k的最近邻来确定该点是否属于n_clusters集群中的某一个。
- 使用“votes”数组计算每个集群的投票数。
- 返回投票数最高的集群索引。
//—————————————————————————————————————————————————————————————————————————————— class C_TSEA_clusters { public: double VectorDistance (double &v1 [], double &v2 []) { double distance = 0.0; for (int i = 0; i < ArraySize (v1); i++) { distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]); } return MathSqrt (distance); } struct DistanceIndex { double distance; int index; }; void BubbleSort (DistanceIndex &arr [], int start, int end) { for (int i = start; i < end; i++) { for (int j = start; j < end - i; j++) { if (arr [j].distance > arr [j + 1].distance) { DistanceIndex temp = arr [j]; arr [j] = arr [j + 1]; arr [j + 1] = temp; } } } } int KNN (S_TSEA_Agent &data [], S_TSEA_Agent &point, int k_neighbors, int n_clusters) { int n = ArraySize (data); DistanceIndex distances_indices []; // Calculate the distances from a point to all other points for (int i = 0; i < n; i++) { DistanceIndex dist; dist.distance = VectorDistance (point.c, data [i].c); dist.index = i; ArrayResize (distances_indices, n); distances_indices [i] = dist; } // Sort the distances BubbleSort (distances_indices, 0, n - 1); // Define the cluster for the point int votes []; ArrayResize (votes, n_clusters); ArrayInitialize (votes, 0); for (int j = 0; j < k_neighbors; j++) { int label = data [distances_indices [j].index].label; if (label != -1 && label < n_clusters) { votes [label]++; } } int max_votes = 0; int max_votes_cluster = -1; for (int j = 0; j < n_clusters; j++) { if (votes [j] > max_votes) { max_votes = votes [j]; max_votes_cluster = j; } } return max_votes_cluster; } }; //——————————————————————————————————————————————————————————————————————————————
让我们继续描述从C_AO基类衍生出的C_AO_TSEA类。该类实现了“龟壳演化算法”(TSEA)算法。类的字段和方法:
1. C_AO_TSEA-构造函数初始化类字段。它设置了算法的名称、描述和关于该算法的文章链接。它还设置了算法参数,如:种群大小、垂直和水平集群的数量、最近邻的数量和单元格中智能体的最大数量。
2. SetParams - 该方法根据“params”数组的值设置算法参数。
3. Init - 算法初始化方法。它接受最小和最大搜索范围、搜索步长和迭代次数。
4. Moving和Revision - 该方法是TSEA算法的主要方法,负责实现其基本逻辑。
5. vCluster、hCluster、neighbNumb和maxAgentsInCell - 这些字段是在构造函数中设置的算法参数,可以使用SetParams方法对它们进行更改。
6.The agent, cell and clusters - 该算法中使用的数据结构。它们分别包含有关智能体、单元格和簇的信息。
7. 使用C_TSA_clusters类的“km”对象执行聚类操作。
8. 私有字段minFval、stepF、epochs和epochsNow是内部变量。它们不能通过类的外部访问到。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_TSEA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_TSEA () { } C_AO_TSEA () { ao_name = "TSEA"; ao_desc = "Turtle Shell Evolution Algorithm"; ao_link = "https://www.mql5.com/ru/articles/14789"; popSize = 100; //population size vClusters = 3; //number of vertical clusters hClusters = 10; //number of horizontal clusters neighbNumb = 5; //number of nearest neighbors maxAgentsInCell = 3; //max agents in cell ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "vClusters"; params [1].val = vClusters; params [2].name = "hClusters"; params [2].val = hClusters; params [3].name = "neighbNumb"; params [3].val = neighbNumb; params [4].name = "maxAgentsInCell"; params [4].val = maxAgentsInCell; } void SetParams () { popSize = (int)params [0].val; vClusters = (int)params [1].val; hClusters = (int)params [2].val; neighbNumb = (int)params [3].val; maxAgentsInCell = (int)params [4].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- int vClusters; //number of vertical clusters int hClusters; //number of horizontal clusters int neighbNumb; //number of nearest neighbors int maxAgentsInCell; S_TSEA_Agent agent []; S_TSEA_vertical cell []; S_Cluster clusters []; C_TSEA_clusters km; private: //------------------------------------------------------------------- double minFval; double stepF; int epochs; int epochsNow; }; //——————————————————————————————————————————————————————————————————————————————
使用C_AO_TSEA类的Init方法初始化TSEA算法。该方法的具体描述如下:
1. StandardInit (rangeMinP, rangeMaxP, rangeStepP) - 该方法用于算法的标准初始化流程。它接受最小和最大搜索范围和搜索步长。若初始化失败,该方法会返回 false 值。
2. ArrayResize (agent, popSize) - 将“agent”数组调整为“popSize”种群规模。然后,每个智能体都会调用Init(coords)方法进行初始化操作。
3. ArrayResize(clusters, hClusters) - 该方法会根据水平集群的数量来重新调整“clusters”数组的大小。接下来,每个集群都会调用Init(coords)方法进行初始化。
4. ArrayResize (cell, vClusters) - 将“单元格”数组的大小调整为vClusters垂直集群的数量。对于每个单元格,初始化[i].cell数组和智能体数组。
5. "minFval = DBL_MAX", "stepF = 0.0", "epochs = epochsP", "epochsNow = 0" - 初始化算法内部变量。
最后,该方法返回“true”,表示初始化成功。
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSEA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (clusters, hClusters); for (int i = 0; i < hClusters; i++) clusters [i].Init (coords); ArrayResize (cell, vClusters); for (int i = 0; i < vClusters; i++) { ArrayResize (cell [i].cell, hClusters); for (int c = 0; c < hClusters; c++) ArrayResize (cell [i].cell [c].agent, 0, maxAgentsInCell); } minFval = DBL_MAX; stepF = 0.0; epochs = epochsP; epochsNow = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
C_AO_TSEA类的Moving方法实现了TSEA算法中智能体移动的基本逻辑。其主要步骤概述如下:
1. 种群初始化:
- 如果这是第一次迭代(即revision为false),则会在种群中随机生成个体。
- 否则,种群将根据现有决策进行更新。
2. 更新种群:
- 对于每个集群(垂直集群与水平集群),都能找到其最优解决方案。
- 形成新解决方案的方式如下:
- 以0.5的概率,从带有一定偏好的随机集群中复制最优解决方案。
- 以0.2的概率,通过取两个来自不同集群的随机解决方案的平均值来形成新的解决方案。
- 为了尽可能接近最优解决方案,会使用幂律分布来生成新解决方案的坐标。
3. 更新种群中的智能体(个体)
该方法实现了龟壳演化的基本思想,其中最优解决方案变得“更坚硬”并位于更接近外表面的位置,而不太理想的解决方案则保持“更柔软”并位于内部。解决方案的聚类和对不太理想变异体的保留,确保了算法的灵活性和适应性。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSEA::Moving () { epochsNow++; //---------------------------------------------------------------------------- //1. Generate random individuals for the population if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } return; } //---------------------------------------------------------------------------- int vPos = 0; int hPos = 0; int pos = 0; int size = 0; double val = 0.0; double rnd = 0.0; double min = 0.0; double max = 0.0; for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { size = ArraySize (cell [v].cell [h].agent); if (size > 0) { max = -DBL_MAX; pos = -1; for (int c = 0; c < size; c++) { if (cell [v].cell [h].agent [c].f > max) { max = cell [v].cell [h].agent [c].f; pos = c; cell [v].cell [h].indBest = c; } } } } } for (int i = 0; i < popSize; i++) { if (u.RNDprobab () < 0.8) { while (true) { rnd = u.RNDprobab (); rnd = (-rnd * rnd + 1.0) * vClusters; vPos = (int)rnd; if (vPos > vClusters - 1) vPos = vClusters - 1; hPos = u.RNDminusOne (hClusters); size = ArraySize (cell [vPos].cell [hPos].agent); if (size > 0) break; } pos = u.RNDminusOne (size); if (u.RNDprobab () < 0.5) pos = cell [vPos].cell [hPos].indBest; for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.6) val = cell [vPos].cell [hPos].agent [pos].c [c]; else val = cB [c]; double dist = (rangeMax [c] - rangeMin [c]) * 0.1; min = val - dist; if (min < rangeMin [c]) min = rangeMin [c]; max = val + dist; if (max > rangeMax [c]) max = rangeMax [c]; val = u.PowerDistribution (val, min, max, 30); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } else { int size2 = 0; int hPos2 = 0; int pos2 = 0; while (true) { rnd = u.RNDprobab (); rnd = (-rnd * rnd + 1.0) * vClusters; vPos = (int)rnd; if (vPos > vClusters - 1) vPos = vClusters - 1; hPos = u.RNDminusOne (hClusters); size = ArraySize (cell [vPos].cell [hPos].agent); hPos2 = u.RNDminusOne (hClusters); size2 = ArraySize (cell [vPos].cell [hPos2].agent); if (size > 0 && size2 > 0) break; } pos = u.RNDminusOne (size); pos2 = u.RNDminusOne (size2); for (int c = 0; c < coords; c++) { val = (cell [vPos].cell [hPos ].agent [pos ].c [c] + cell [vPos].cell [hPos2].agent [pos2].c [c]) * 0.5; a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } } } //——————————————————————————————————————————————————————————————————————————————在TSEA中,C_AO_TSEA类的Revision方法主要负责龟壳部分(即解的一部分)重新分配的阶段。
它负责修改(更新)智能体群体并更新最优全局解决方案。
这部分算法的主要步骤如下:
2. 根据适应度将智能体标记为垂直“labelClustV”集群。
3. 如果这是第一次迭代(revision为false),则使用K-Means算法初始化智能体集群。
4. 如果这不是第一次迭代,则执行以下操作:
- 将所有智能体收集到单个“data”数组中。
- 对于种群中的每个智能体,使用K-最近邻算法确定其水平“label”集群。
- 每50个周期更新一次存储智能体集群的“cell”结构。
5. 将每个智能体放置在适当的单元格中。如果单元格已满,则该智能体将替换单元格中适应度最低(如果单元格处于底层,则可能是适应度最高)的智能体。
此阶段的主要思想是保持壳体的结构,其中最优解决方案位于更接近外表面的位置,而不太理想的解决方案则位于内部。智能体的集群以及壳体结构的动态更新确保了算法的灵活性和适应性。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSEA::Revision () { //get fitness-------------------------------------------------- int pos = -1; for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; if (a [i].f > fB) { fB = a [i].f; pos = i; } if (a [i].f < minFval) minFval = a [i].f; } if (pos != -1) ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY); stepF = (fB - minFval) / vClusters; //Vertical layout of the child population----------------------------------- for (int i = 0; i < popSize; i++) { if (agent [i].f == fB) agent [i].labelClustV = vClusters - 1; else { agent [i].labelClustV = int((agent [i].f - minFval) / stepF); if (agent [i].labelClustV > vClusters - 1) agent [i].labelClustV = vClusters - 1; } } //---------------------------------------------------------------------------- if (!revision) { km.KMeansPlusPlusInit (agent, popSize, clusters); km.KMeans (agent, popSize, clusters); revision = true; } //---------------------------------------------------------------------------- else { static S_TSEA_Agent data []; ArrayResize (data, 0, 1000); int size = 0; for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { for (int c = 0; c < ArraySize (cell [v].cell [h].agent); c++) { size++; ArrayResize (data, size); data [size - 1] = cell [v].cell [h].agent [c]; } } } for (int i = 0; i < popSize; i++) { agent [i].label = km.KNN (data, agent [i], neighbNumb, hClusters); } if (epochsNow % 50 == 0) { for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { ArrayResize (cell [v].cell [h].agent, 0); } } for (int i = 0; i < ArraySize (data); i++) { if (data [i].f == fB) data [i].labelClustV = vClusters - 1; else { data [i].labelClustV = int((data [i].f - minFval) / stepF); if (data [i].labelClustV > vClusters - 1) data [i].labelClustV = vClusters - 1; } int v = data [i].labelClustV; int h = data [i].label; int size = ArraySize (cell [v].cell [h].agent) + 1; ArrayResize (cell [v].cell [h].agent, size); cell [v].cell [h].agent [size - 1] = data [i]; } } } //Place the population in the shell------------------------------------ for (int i = 0; i < popSize; i++) { int v = agent [i].labelClustV; int h = agent [i].label; int size = ArraySize (cell [v].cell [h].agent); int pos = 0; int posMin = 0; int posMax = 0; if (size >= maxAgentsInCell) { double minF = DBL_MAX; double maxF = -DBL_MAX; for (int c = 0; c < maxAgentsInCell; c++) { if (cell [v].cell [h].agent [c].f < minF) { minF = cell [v].cell [h].agent [c].f; posMin = c; } if (cell [v].cell [h].agent [c].f > maxF) { maxF = cell [v].cell [h].agent [c].f; posMax = c; } } if (v == 0) { if (agent [i].f < minF) { pos = posMin; } else { pos = posMax; } } else pos = posMin; } else { ArrayResize (cell [v].cell [h].agent, size + 1); pos = size; } cell [v].cell [h].agent [pos] = agent [i]; } } //——————————————————————————————————————————————————————————————————————————————
3. 测试结果
TSEA结果:
TSEA|Turtle Shell Evolution Algorithm|100.0|3.0|10.0|5.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.811921100517765
25 Hilly's; Func runs: 10000; result: 0.5537631430428238
500 Hilly's; Func runs: 10000; result: 0.2813575513298344
=============================
5 Forest's; Func runs: 10000; result: 0.9564485273109922
25 Forest's; Func runs: 10000; result: 0.481362270824773
500 Forest's; Func runs: 10000; result: 0.181400891410298
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.3633846153846153
500 Megacity's; Func runs: 10000; result: 0.11670769230769343
=============================
总分: 4.41404 (49.04%)
所有测试函数的总得分为4.41404,这相当于理论上最优解的49.04%。
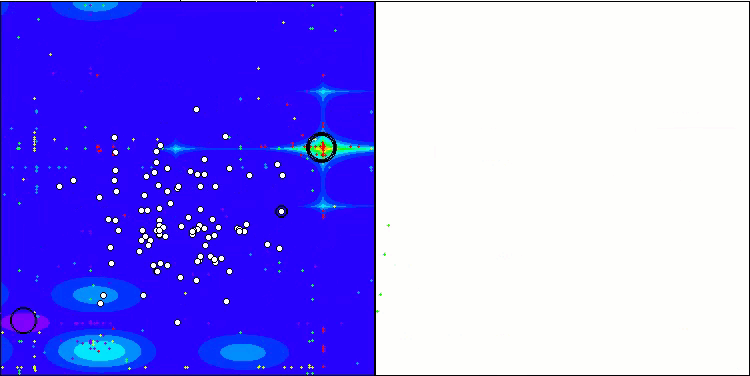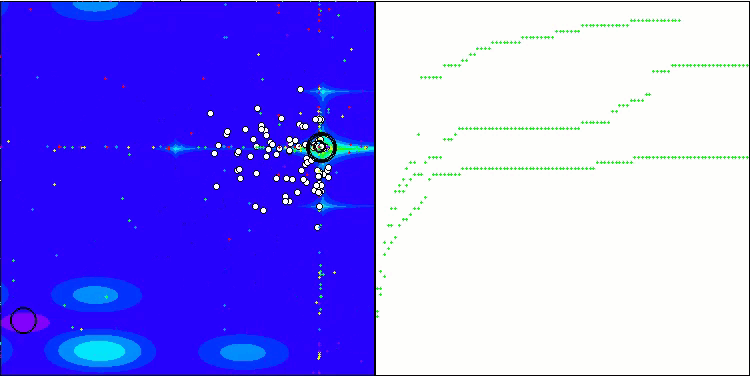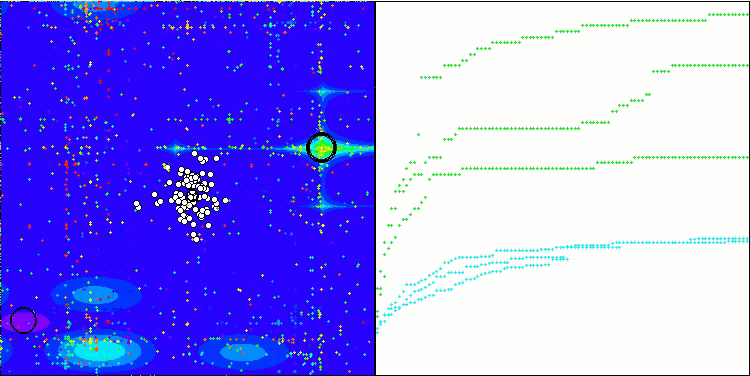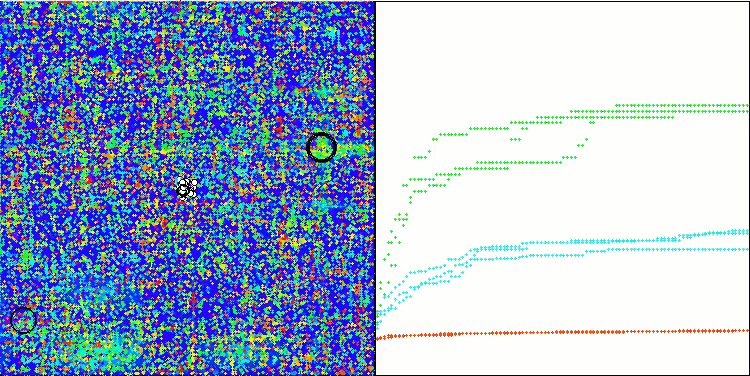
在测试平台的可视化运行结果展示了该算法良好的收敛性。对于所有测试函数,在收敛图上均存在着轨迹的分散现象。然而,随着自由度的增加,这种分散现象会减少。算法中聚类方法的使用,以及保持每个单元格中智能体数量的恒定,使得算法能够有效地遍历适应度函数的重要区域。
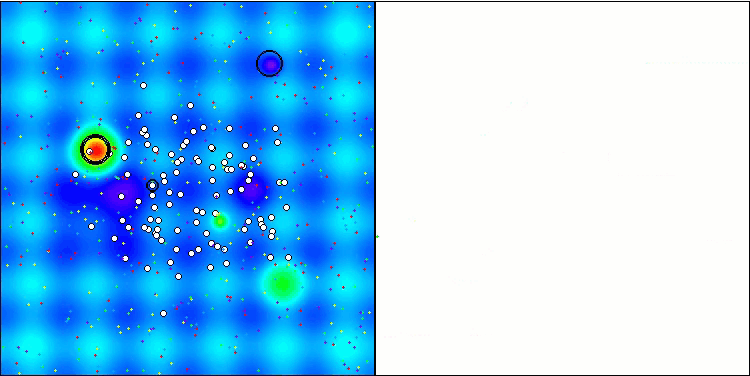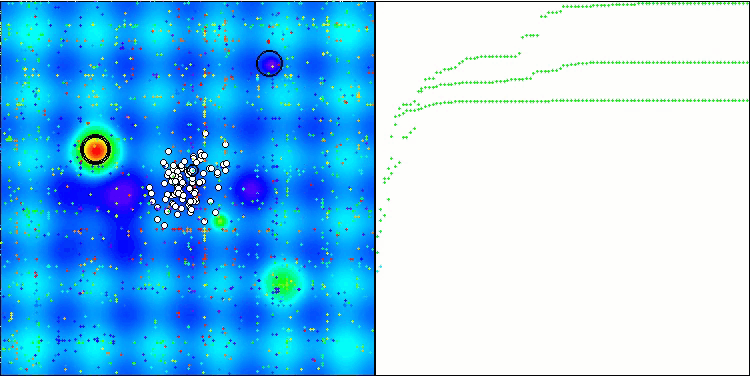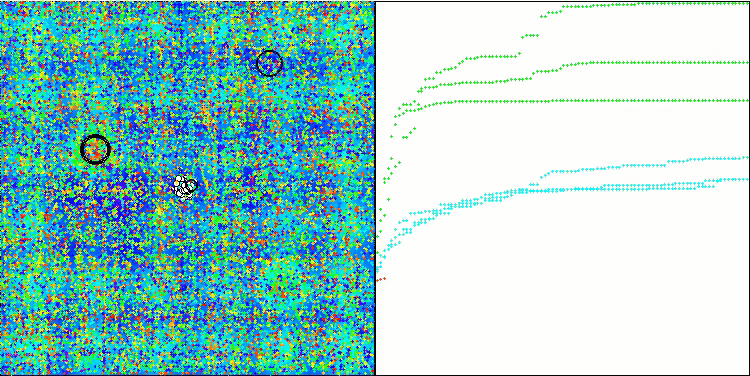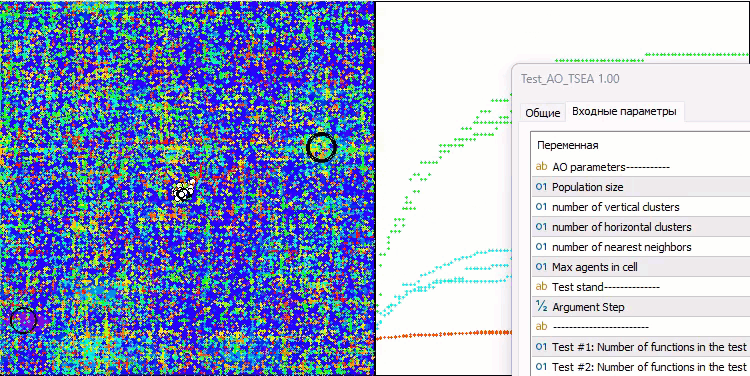
TSEA在 Hilly测试函数上
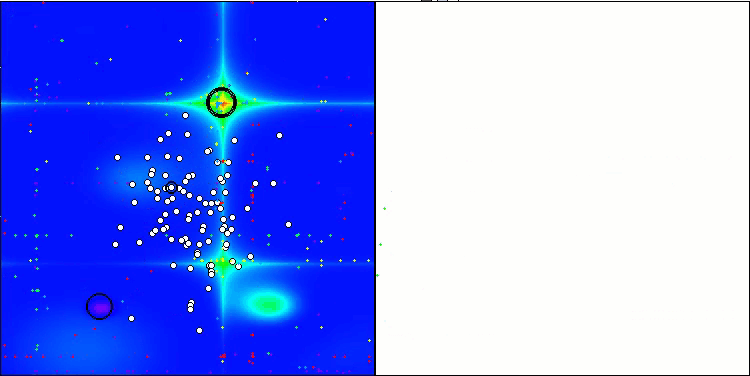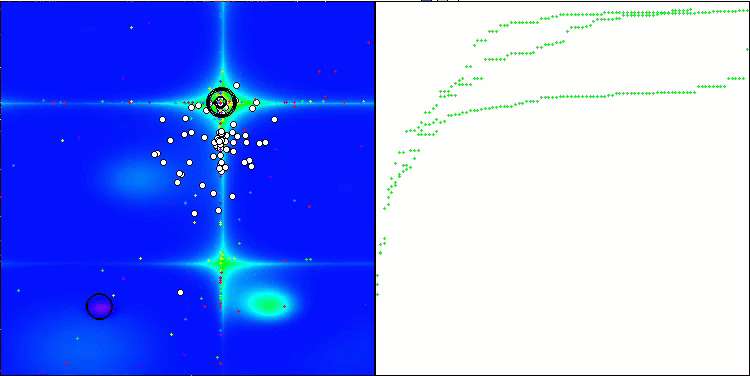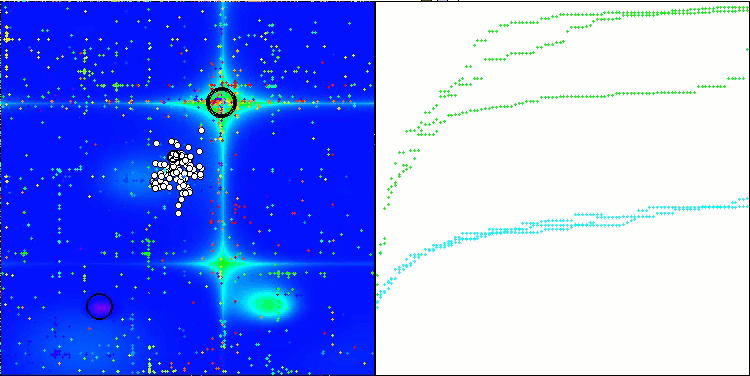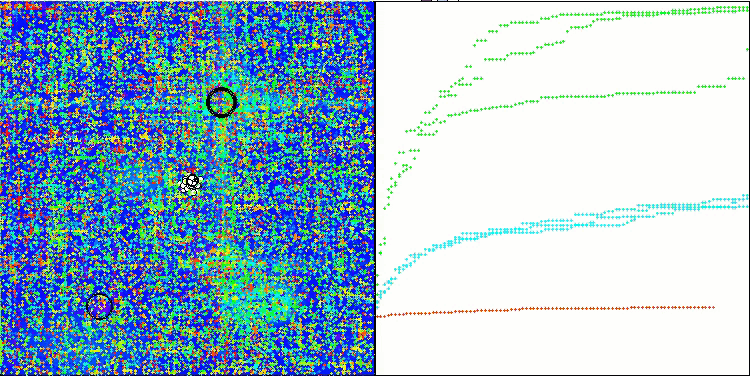
TSEA在 Forest测试函数上
TSEA在Megacity测试函数上
在通过测试函数检验后,该算法在最终评分表中排名第六。
# | AO | 说明 | Hilly值 | Hilly最终值 | Forest值 | Forest最终值 | Megacity (离散) | Megacity最终值 | 最终结果 | 最大百分比 | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | 二进制遗传算法 | 0.99992 | 0.99484 | 0.50483 | 2.49959 | 1.00000 | 0.99975 | 0.32054 | 2.32029 | 0.90667 | 0.96400 | 0.23035 | 2.10102 | 6.921 | 76.90 |
| 2 | (P+O)ES | (P+O) 进化策略 | 0.99934 | 0.91895 | 0.56297 | 2.48127 | 1.00000 | 0.93522 | 0.39179 | 2.32701 | 0.83167 | 0.64433 | 0.21155 | 1.68755 | 6.496 | 72.18 |
| 3 | SDSm | 随机扩散搜索 M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 4 | ESG | 社会群体的进化 | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 5 | SIA | 模拟退火算法 | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 6 | TSEA | 龟壳演化算法 | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 7 | DE | 差分进化 | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 8 | BSA | 鸟群算法 | 0.90857 | 0.73661 | 0.25767 | 1.90285 | 0.90437 | 0.81619 | 0.16401 | 1.88457 | 0.61692 | 0.54154 | 0.10951 | 1.26797 | 5.055 | 56.17 |
| 9 | HS | 和声搜索 | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 10 | SSG | 树苗播种和生长 | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 11 | (PO)ES | (PO) 进化策略 | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 12 | BSO | 头脑风暴优化 | 0.91301 | 0.56222 | 0.30047 | 1.77570 | 0.97162 | 0.57162 | 0.23449 | 1,77772 | 0.60462 | 0.27138 | 0.12011 | 0.99611 | 4.550 | 50.55 |
| 13 | WOAm | 鲸鱼优化算法M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 14 | ACOm | 蚁群优化 M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 15 | BFO-GA | 细菌觅食优化 - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 16 | MEC | 思维进化计算 | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 17 | IWO | 入侵杂草优化 | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 18 | Micro-AIS | 微型人工免疫系统 | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 19 | COAm | 布谷鸟优化算法 M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 20 | SDOm | 螺旋动力学优化 M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 21 | NMm | Nelder-Mead方法 M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 22 | FAm | 萤火虫算法 M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 23 | GSA | 引力搜索算法 | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 24 | BFO | 细菌觅食优化 | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 25 | ABC | 人工蜂群 | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 26 | BA | 蝙蝠算法 | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 27 | SA | 模拟退火 | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 28 | IWDm | 智能水滴 M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 29 | PSO | 粒子群优化 | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 30 | Boids算法 | 虚拟生物算法 | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 31 | MA | 猴群算法 | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 32 | SFL | 混合蛙跳算法 | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 33 | FSS | 鱼群搜索 | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 34 | RND | 随机 | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 35 | GWO | 灰狼优化算法 | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 36 | CSS | 人工电场算法 | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 37 | EM | 类电磁算法 | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
总结
基于乌龟壳生长原理提出优化算法,这一想法非常有趣。即使是行动如此缓慢的动物,也能成为大自然众多生物中的灵感来源和“技术”方案的解决范例。通过对TSEA(龟壳演化算法)的测试,我们成功定义了该算法的主要特征。
保留不太理想的解决方案是该算法的一个独特特点。这一点从不太理想的变异体被保留在壳的内层就可以看出。这种方法有助于保持种群的多样性,并防止过早收敛到局部最优解。重要的一点是要记住,看似最糟糕的局部最小值有可能接近全局最优解,因此继续遍历其附近区域是有意义的。尽管相比于更有潜力的区域,该算法可能会低频次地遍历这些区域,但它们仍然是关注的重点。
将解决方案分为垂直集群,模拟壳的层次,以及水平集群,模拟壳表面的特征图案,使我们能够相当有效地隔离解决方案空间中的区域并分别研究它们。同时,壳上的图案保持可移动性,能够改变并符合适应度函数。
壳的分层使用允许在每个层内形成新的解决方案。坚硬的上层不与柔软的下层相互作用,反之亦然。这与活体乌龟壳的生长过程相似,但不同之处在于,由于定期的重新聚类,下层中的坚硬部分可以移动到上层。这可以与蜕去旧壳并形成更硬更好的新壳过程相比较。
该算法在处理不同维度数量(可扩展性)的问题时表现出良好的性能,这显示了其灵活性。
总体而言,TSEA是一种有趣的方法,它结合了进化算法和聚类机制。然而,我坚信该算法仍有无限的潜力。到目前为止,从之前在文章中讨论过的众多创建新解决方案的方法中,我们只使用了其中少数几种。该算法仍然是我的研究重点,并且有待进一步改进。也许,它将为一些新的改进提供基础,就像粒子群优化算法(PSO)和其他知名算法所经历的发展过程一样。
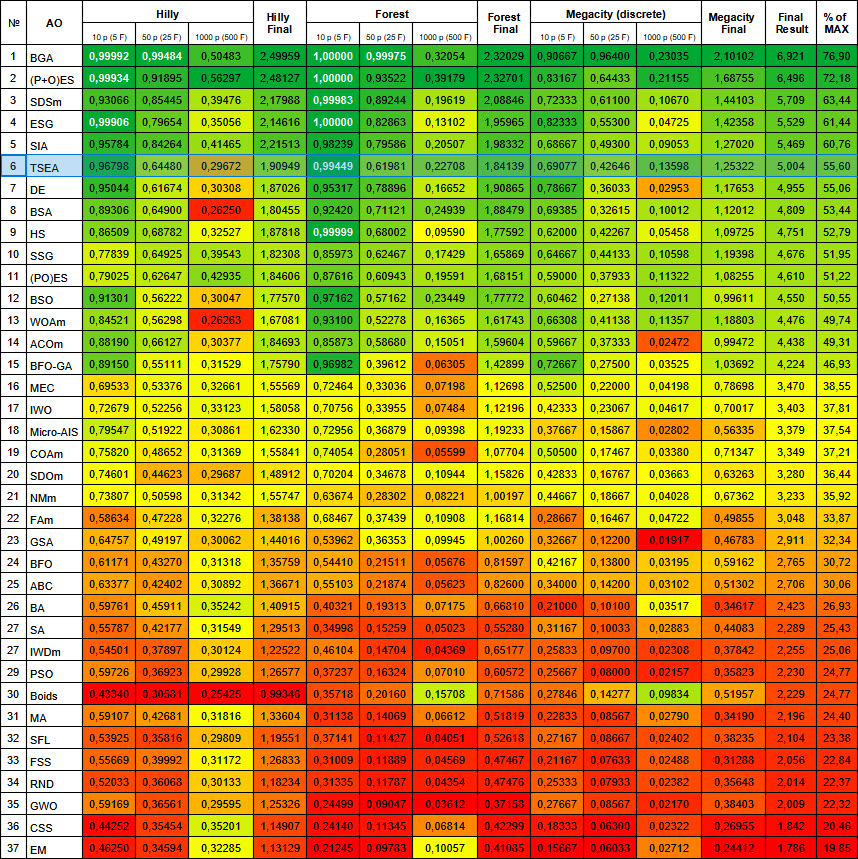
图例 3. 根据相关测试,将算法的颜色等级大于或等于0.99的结果以白色突出显示
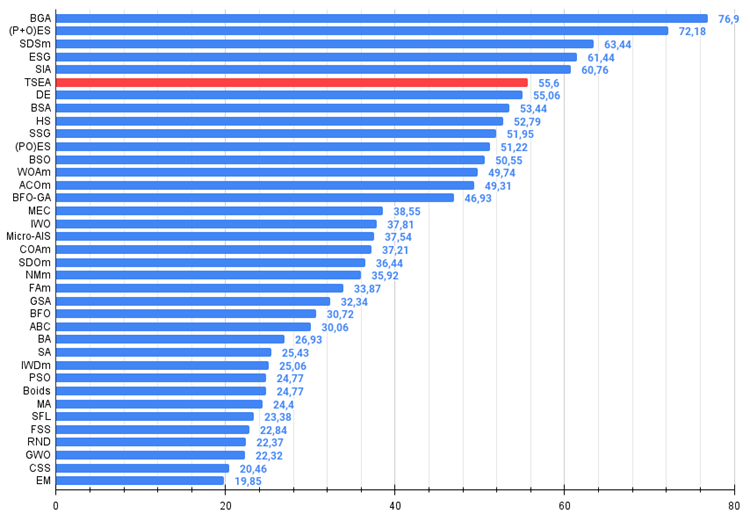
图例 4. 算法测试结果的直方图(标尺从 0 到 100,数字越大结果越好,
其中 100 是理论上的最大可能结果,将计算评级表格的脚本存档)。
TSEA算法的优缺点:
优势:
- 在各种类型的函数上具有良好的收敛性
- 外部参数数量少
缺点:
- 在低维函数上表现出的高离散性结果
- 对计算资源的高负载
文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力,已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。
github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
CodeBase: https://www.mql5.com/ru/code/49355
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/14789
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 构建一个K线图趋势约束模型(第二部分):融合原生指标
构建一个K线图趋势约束模型(第二部分):融合原生指标
 神经网络变得简单(第 76 部分):配合多未来变换器探索不同的交互形态
神经网络变得简单(第 76 部分):配合多未来变换器探索不同的交互形态
 两样本Kolmogorov-Smirnov检验作为时间序列非平稳性的指标
两样本Kolmogorov-Smirnov检验作为时间序列非平稳性的指标