用于预测金融时间序列的生物神经元

现代交易正在经历一场革命。神经网络、遗传算法、深度学习 —— 所有这些工具都能产生令人印象深刻的结果，但往往有一个显著的缺点：它们太“机械化”，无法捕捉市场波动的微妙本质，而市场波动本质上是活生生的市场参与者集体行为的结果。

在这种情况下，使用生物学上合理的神经模型变得尤为重要。我们没有创造抽象的数学结构，而是转向宇宙可观测部分中最先进的计算机 —— 人类大脑。我们的研究小组开发了一个基于霍奇金-赫胥黎模型的独特系统，该系统不仅模拟了神经过程的功能，还模拟了其物理性质。

诺贝尔奖获得者霍奇金-赫胥黎模型描述了细胞水平上神经冲动的产生和传播机制。但为什么这种特殊的模型可能是理解金融市场的关键呢？答案在于大脑中神经冲动的传播与市场中信息的传播之间的惊人类比。正如神经元通过突触连接交换电信号一样，市场参与者也通过交易交换信息。

我们方法的创新之处在于在经典模型中添加了类似等离子体的组件。我们将神经网络视为一个沉浸在市场信息“等离子体”中的动态系统，其中每个神经元不仅可以通过直接连接，还可以通过它产生的电磁场影响其他神经元的行为。这使得系统能够捕捉到传统算法未注意到的微妙相关性和关系。

本文将详细介绍系统架构、工作原理以及在各种金融工具上的实际应用结果。我们将展示生物启发的方法如何为金融时间序列预测问题提供新的视角，并在算法交易领域开辟新的视野。

霍奇金-赫胥黎模型：当生物学与金融相遇

想象一个神经元 —— 一个能够通过电脉冲处理和传输信息的神奇细胞。艾伦·霍奇金和安德鲁·赫胥黎在他们的开创性工作中描述了大脑的这个基本单位，他们后来因此获得了诺贝尔奖。他们的模型是神经科学的真正突破，现在想象一下，这个模型可以帮助我们理解和预测金融市场的走势。

该模型的核心是对神经元如何产生电脉冲的数学描述。正如交易者对传入的市场信息做出反应一样，神经元也会通过创建自己独特的活动模式来对传入的信号做出反应。让我们来看看描述这个惊人过程的代码：

class HodgkinHuxleyNeuron:
    def __init__(self):
        self.V = -65.0  # Initial resting potential
        self.m = 0.05   # Activation of sodium channels
        self.h = 0.6    # Inactivation of sodium channels
        self.n = 0.32   # Activation of potassium channels
        self.last_spike_time = float('-inf')

离子舞：神经元如何做出决定

霍奇金-赫胥黎模型最引人注目的地方是它对离子如何在神经元膜上“跳舞”的描述。钠和钾是这场分子芭蕾中的两个关键角色，它们通过特殊的通道移动，产生电势。这与订单流如何在市场中产生价格变动非常相似。在我们的交易系统中，我们通过将市场数据转换为离子电流来使用这个类比：

def ion_currents(self, V):
    I_Na = self.g_Na * (self.m ** 3) * self.h * (V - self.E_Na)  # Sodium current
    I_K = self.g_K * (self.n ** 4) * (V - self.E_K)             # Potassium current
    I_L = self.g_L * (V - self.E_L)                             # Leakage current
    return I_Na, I_K, I_L

等离子影响：神经网络的新视角

我们超越了经典模型，增加了类等离子体环境的概念。想象一下，神经元不仅仅是通过突触连接的，而是沉浸在市场的“信息等离子体”中。每个神经元尖峰都会产生一股影响力，随着时间的推移而减弱，就像市场上的一条新闻逐渐失去对价格的影响一样：

def plasma_influence(self, current_time):
    time_since_spike = current_time - self.last_spike_time
    influence = self.plasma_strength * np.exp(-time_since_spike / self.plasma_decay)
    return influence * self.get_market_correlation()

通过时间学习：STDP 机制

也许我们系统中最令人兴奋的部分是基于神经元尖峰之间的时间依赖性（STDP）的学习机制。正如交易者从经验中学习一样，我们的神经元会根据预测市场走势的成功程度来调整连接强度：

def update_synaptic_weights(self, pre_spike, post_spike, weight):
    delta_t = post_spike - pre_spike
    if delta_t > 0:
        return weight * (1 + self.A_plus * np.exp(-delta_t / self.tau_plus))
    else:
        return weight * (1 - self.A_minus * np.exp(delta_t / self.tau_minus))

这种受生物启发的架构使我们的系统不仅能够处理市场数据，还能像经验丰富的交易者一样“感受”市场。每个神经元都成为其自身市场动态方面的小专家，它们的集体工作创造了非常准确的预测。

系统架构：从生物学到交易决策

想象一下，一个交易者分析市场的大脑。数千个神经元处理有关价格、交易量、指标和新闻的信息。正是这种自然结构，我们在我们的系统中重新创建了它，为其添加了等离子体和电磁相互作用的独特特性。

系统之眼：输入数据结构

正如人脑通过感官接收信息一样，我们的系统也会收集和处理大量的市场信号。每一次报价、每一次价格变动都会转化为神经脉冲。我们来看看数据预处理代码：

class MarketFeatures:
    def __init__(self, window_size=20):
        self.window_size = window_size
        self.scaler = StandardScaler()
        
    def add_price(self, price: float, ohlc_data: pd.DataFrame) -> Dict[str, float]:
        features = {}
        
        # Technical indicators
        features['sma_10'] = self._calculate_sma(ohlc_data['close'], window=10)
        features['ema_20'] = self._calculate_ema(ohlc_data['close'], window=20)
        features['rsi'] = self._calculate_rsi(ohlc_data['close'], window=14)
        
        # Volumetric characteristics
        features['volume_sma'] = self._calculate_sma(ohlc_data['tick_volume'], window=10)
        
        # Temporal patterns
        features['hour'] = ohlc_data.index[-1].hour
        features['day_of_week'] = ohlc_data.index[-1].dayofweek
        
        return self.scaler.fit_transform(np.array(list(features.values())).reshape(1, -1))

神经网络：生物学和数学之间的桥梁

我们系统的核心是一个混合架构，它将经典神经网络与生物学上合理的霍奇金-赫胥黎模型相结合。这里的每个神经元不仅仅是一个数学函数，而是一个小的生命系统：

class BioTradingModel(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(BioTradingModel, self).__init__()
        self.layers = nn.ModuleList([
            nn.Linear(input_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, output_size)
        ])
        
        # Biological neurons
        self.bio_neurons = [HodgkinHuxleyNeuron() for _ in range(hidden_size)]
        self.plasma_field = PlasmaField(hidden_size)

等离子场：神经相互作用的新维度

我们系统的独特之处在于神经元所处的等离子体样环境。正如电磁场渗透到空间中一样，我们的等离子体在神经元之间产生了额外的相互作用：

class PlasmaField:
    def __init__(self, size):
        self.field_strength = np.zeros(size)
        self.decay_rate = 0.95
        
    def update(self, neuron_activities):
        # Update the field based on neuron activity
        self.field_strength = self.field_strength * self.decay_rate
        self.field_strength += neuron_activities
        
    def get_influence(self, neuron_index):
        # Calculate the influence of a field on a specific neuron
        return np.sum(self.field_strength * np.exp(-self.distance_matrix[neuron_index]))

学习机制：神经元和等离子体的舞蹈

在我们的系统中，训练同时在多个层面进行。经典梯度下降与生物 STDP 和等离子体动力学相结合：

def train_step(self, inputs, target):
    # Straight pass
    predictions = self.forward(inputs)
    loss = self.criterion(predictions, target)
    
    # Backpropagation
    self.optimizer.zero_grad()
    loss.backward()
    
    # Biological education
    for i, neuron in enumerate(self.bio_neurons):
        # STDP update
        neuron.update_weights(self.last_spike_times)
        
        # Plasma modulation
        plasma_influence = self.plasma_field.get_influence(i)
        neuron.modulate_weights(plasma_influence)
    
    self.optimizer.step()
    return loss.item()

这种多层架构使系统不仅可以捕获数据中明显的模式，还可以捕获市场动态不同方面之间微妙的、几乎不可察觉的关系。该系统的每个组件都发挥着自己独特的作用，它们的协同作用创造出比各部分总和更强大的东西 —— 一个用于分析金融市场的真正的人工大脑。

技术指标：我们系统的数字感官

如果我们把我们的神经系统想象成交易者的人工大脑，那么技术指标就是它的感觉器官。正如人类使用视觉、听觉和触觉来感知世界一样，我们的系统也使用各种指标来“感知”市场的所有表现形式。

基本指标：系统视觉

让我们从最基本的指标 —— 移动平均线开始。它们就像我们系统的视觉，使其能够通过市场噪音辨别潜在趋势：

def calculate_moving_averages(self, prices):
    def sma(window):
        return np.convolve(prices, np.ones(window)/window, mode='valid')
    
    def ema(window):
        alpha = 2 / (window + 1)
        kernel = alpha * (1 - alpha)**np.arange(window)
        return np.convolve(prices, kernel[::-1], mode='valid')
    
    return {
        'sma_fast': sma(10),  # Fast SMA for short-term trends 
        'sma_slow': sma(20),  # Slow SMA for long-term trends
        'ema_fast': ema(10),  # Exponential MA for fast response
        'ema_slow': ema(20)   # Slow EMA for sorting out noise
    }

振荡器：感知市场动态

RSI、动量和随机震荡指标是我们系统的触觉感受器。它们让我们“感受到”价格变动的强度和潜在的反转点：

def calculate_oscillators(self, data):
    def rsi(prices, period=14):
        delta = np.diff(prices)
        gain = np.where(delta > 0, delta, 0)
        loss = np.where(delta < 0, -delta, 0)
        
        avg_gain = np.mean(gain[:period])
        avg_loss = np.mean(loss[:period])
        
        for i in range(period, len(gain)):
            avg_gain = (avg_gain * 13 + gain[i]) / 14
            avg_loss = (avg_loss * 13 + loss[i]) / 14
            
        rs = avg_gain / avg_loss
        return 100 - (100 / (1 + rs))
    
    return {
        'rsi': rsi(data['close']),
        'momentum': data['close'] - np.roll(data['close'], 10),
        'stoch_k': self._calculate_stochastic_k(data)
    }

波动性和交易量：系统听觉

波动性和成交量指标就像我们系统的耳朵 —— 它们可以捕捉市场“噪音”和运动的强度。布林带和 ATR 有助于评估波动幅度，而成交量指标则有助于评估其重要性：

def measure_market_dynamics(self, data):
    def bollinger_bands(prices, window=20):
        sma = np.mean(prices[-window:])
        std = np.std(prices[-window:])
        return {
            'upper': sma + 2 * std,
            'lower': sma - 2 * std,
            'width': 4 * std / sma  # Normalized strip width
        }
    
    def volume_profile(volumes, prices):
        return {
            'volume_ma': np.mean(volumes[-10:]),
            'volume_trend': np.corrcoef(volumes[-20:], prices[-20:])[0,1],
            'volume_oscillator': (np.mean(volumes[-5:]) / np.mean(volumes[-20:]) - 1) * 100
        }
    
    volatility = bollinger_bands(data['close'])
    volume = volume_profile(data['volume'], data['close'])
    return {**volatility, **volume}

正常化：调整灵敏度

正如人脑使其感官对环境条件的敏感性适应一样，我们的系统也会动态调整输入数据的规模。这对于神经网络的稳定运行至关重要：

def normalize_features(self, features: dict) -> dict:
    class AdaptiveNormalizer:
        def __init__(self, window=100):
            self.window = window
            self.history = {}
            
        def update(self, feature_name, value):
            if feature_name not in self.history:
                self.history[feature_name] = []
            
            self.history[feature_name].append(value)
            if len(self.history[feature_name]) > self.window:
                self.history[feature_name].pop(0)
            
            mean = np.mean(self.history[feature_name])
            std = np.std(self.history[feature_name])
            return (value - mean) / (std + 1e-8)  # Avoid zero divide
    
    normalizer = AdaptiveNormalizer()
    return {name: normalizer.update(name, value) 
            for name, value in features.items()}

所有这些指标和特征紧密结合，形成了市场现实的多维图景。正如人脑整合所有感官的信息一样，我们的系统将所有指标的数据合成为市场状况的单一表示。这使得它不仅可以跟随趋势或对单个信号做出反应，还可以对市场动态形成全面的理解。

实验结果

测试方法

在研究过程中，我们对 EURUSD 货币对的历史数据进行了全面的系统测试。使用每日时间周期 D1，时间范围为 5 年。遵循传统的机器学习原理，我们按照 80/20 的比例将数据分成训练集和测试集。结果，1659 个数据点用于训练，415 个数据点用于测试。该模型经过了 20 次不同权重初始化的训练迭代，以找到最佳配置。

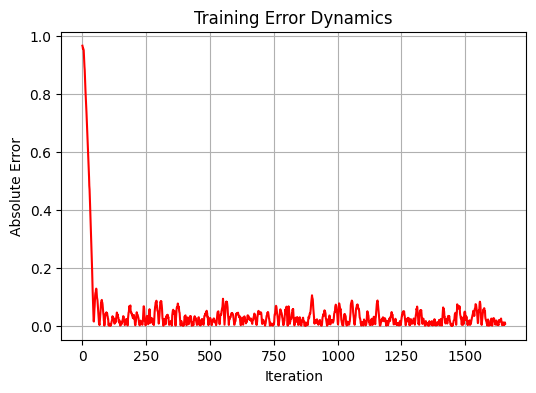
性能分析

在分析结果时，我们发现了模型的一个有趣特征。该系统似乎旨在确定货币对的某种“公平”价格，而不是试图预测短期价格走势。训练样本上相当高的相关性证实了这一观察结果，达到了 0.583 的值，标准误差相对较低，为 0.012346。但在测试样本上，模型的性能下降明显：相关性下降为负值（-0.108），MSE 增加90多倍，达到 1.156584。

与传统方法的比较

与经典技术指标和标准神经网络相比，我们的生物启发模型表现出明显不同的行为。事实证明，其预测的波动性要大得多。 

以下是对测试样本的测试，预测范围为 15 个柱：

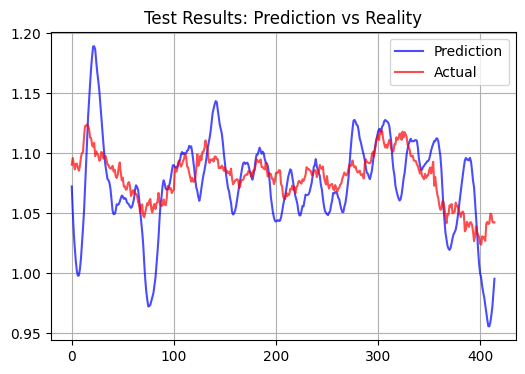
统计性能指标

模型性能最显著的结果是测试样本的判定率（R²）极低，约为 0.01。有趣的是，该模型在训练样本上显示出相当高的相关性，这表明它能够捕捉数据中的长期模式。此外，模型预测通常包含明显可见的尖峰。这些尖峰是否对应于最小的价格变动以及是否适合剥头皮交易还有待观察。

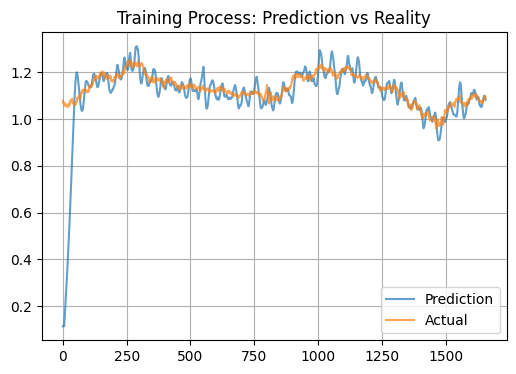
特点及实际应用

模型的观察行为可以用其生物学性质来解释。类等离子体神经系统似乎起到了强大的过滤器的作用，显著放大了市场信号，该模型产生了夸大的增量预测。理论上，STDP（尖峰时间依赖塑性）机制应导致稳定激活模式的形成，从而导致预测的平均化，因此，我们应该对测试和实际状态有不同的了解。另一个因素可能是大量以技术指标形式输入，从而产生过度正则化效应。

从实用的角度来看，该模型可用于确定货币对的短期公允价值水平。 

结论

我们对预测金融市场的生物启发神经系统的研究产生了意想不到但有趣的结果。正如人类大脑能够直观地感知资产的“公平”价值一样，我们的模型基于活神经元的工作原理，在识别基本合理的价格水平方面表现出了非凡的能力。

在神经网络架构中引入类似等离子体的环境创造了一种“集体智能”，其中每个神经元不仅通过直接连接，还通过长距离电磁相互作用影响系统的运行。事实证明，这种机制在整理市场噪音和识别长期趋势方面特别有效。 

也许这其中有更深层次的含义。正如生物系统为了长期生存而进化一样，我们建立在它们的图像中的神经网络也在努力识别稳定、基本健全的模式。

读到最后的人的福利

我还根据这个模型创建了一个指标。该指标将系统的其余部分作为一个模块加载，并在一个简单的窗口中打开，如下所示：

我没有在真实环境中尝试过，但考虑到所有其他系统通常都预测相同的方向，该指标可能会正常工作。