MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
人工电场算法（AEFA）

人工电场算法（AEFA）

MetaTrader 5 — 示例 |
612 0
Andrey Dik
Andrey Dik
内容
  1. 引言
  2. 算法的实现
  3. 测试结果


引言

人工电场算法是一项令人惊叹的创造，它体现了技术与自然的和谐统一。受库仑静电力定律启发，该算法因其独特的模拟电学现象以解决复杂优化问题的能力而备受瞩目。在之前与自然法则相关的文章中已经描述过的算法，如电荷系统搜索（CSS）、 电磁类算法（ЕМ）、引力搜索算法（GSA）等背景下，人工电场算法是一项激动人心的创新，它将不会让任何研究人员无动于衷。

人工电场算法受库仑定律启发，该定律表明，两个带电粒子之间的静电力（吸引力或排斥力）与它们的电荷量的乘积成正比，与它们之间距离的平方成反比。在所提出的算法中，智能体被视为带电粒子，其强度由电荷量来衡量。所有这些粒子都可以通过静电力相互吸引或排斥，并且由于这种力的作用，物体在搜索空间中移动。因此，电荷通过静电力作为直接通信形式，而电荷的位置对应于问题的解。电荷是根据候选解的适应度和种群的适应度函数来定义的。在所提出的算法中，我们仅考虑静电力的吸引作用，即电荷量最高的带电粒子（即“最优”个体）吸引所有电荷量较低的粒子，并在搜索空间中缓慢移动。

因此，人工电场算法（AEFA）可以视为一个孤立的电荷系统，这些电荷遵循库仑静电学的第一定律（即静电力的定律，同种电荷相互排斥，异种电荷相互吸引）和运动定律，以及库仑静电学的第二定律（即异种电荷之间的吸引力或同种电荷之间的排斥力与它们的电荷量的乘积成正比，与电荷中心之间的距离的平方成反比），还有运动定律（任何电荷的当前速度等于其先前速度与速度变化量之和的分数）。任何电荷的速度变化或加速度等于作用在系统上的力除以粒子的质量。

AEFA（人工电场算法）由以下人员开发：

1. 阿尼塔（Anita）——就职于印度斯利那加乌塔拉坎德邦国立技术学院科学与人文系。
2. 阿努潘·亚达夫（Anupam Yadav）——就职于印度贾朗达尔的Dr. B.R. 安贝德卡国立技术学院数学系。

人工电场算法（AEFA）于2019年被提出，并发表在《群体智能与进化计算》杂志上。文章的作者指出，电场和带电粒子的概念为我们提供了一个强有力的理论，用以解释两个带电粒子之间的吸引力或排斥力是如何作用的。因此，人工电场算法利用静电力的原理来开发了一种群体优化算法。


算法的实现

AEFA蕴含了丰富的方程，在深入探讨这些方程之前，让我们先总结其关键点：

  • 该算法的主体（决策）被表示为在静电力作用下移动的带电粒子。
  • 粒子的电荷量取决于其个人最佳结果以及种群中的当前最佳和最差结果（这里的最佳和最差结果是指种群中当前的结果，而非优化过程中取得的最佳结果）。
  • 作用于粒子上的力取决于粒子的电荷量以及它们之间的距离。
  • 库仑常数K(t)随着迭代次数的增加而减小，从而控制全局搜索与局部优化之间的平衡。

接下来，让我们转向算法的正式表述，并更详细地探讨其中所使用的方程。

设第i个粒子在d维搜索空间中的位置表示为X_i = (x_1, x_2, ..., x_d)，其中i = 1, 2, ..., N，而N表示种群大小。
第i个粒子找到的最佳位置表示为P_i，而全局最佳位置表示为P_best。

1. 库仑静电力方程：F_ij = K * Q_i * Q_j / R^2，其中：

  • F_ij - 两个带电物体第i个和第j个之间的静电力大小
  • K - 库仑常数
  • Q_i和Q_j - 分别表示第i个和第j个物体的电荷量
  • R - 两个电荷Q_i和Q_j之间的距离

2. 电荷Q_i周围的电场方程：E_i = F_ij / Q_i，其中：

  • E_i - Q_i电荷周围的电场
  • F_ij - 作用在Q_i电荷上的力

3. 根据牛顿第二定律的粒子加速度方程：a_i = F_ij / M，其中：

  • a_i - 第i个粒子的加速度
  • F_ij - 作用在粒子上的力
  • M - 粒子质量

4. 通过电场计算粒子加速度的方程：a_i = E_i * Q_i / M，其中：

  • a_i - 第i个粒子的加速度
  • E_i - 粒子周围的电场
  • Q_i - 粒子电荷量
  • M - 粒子质量

5. 更新最佳粒子位置的方程：p_di (t+1) = {p_di (t)且 X_i (t+1) = X_i (t)}，如果 f (X_i (t+1)) > f (X_i (t))，其中：

  • p_di (t) - 在给定时刻t时，第i个粒子的适应度
  • p_di (t+1) - 在给定时刻t+1时，第i个粒子的适应度
  • X_i (t) - 在给定时刻t时，第i个粒子的位置
  • X_i (t+1) - 在给定时刻(t+1)时，第i个粒子的新位置
  • f(X_i (t)) - 在给定时刻t时，第i个粒子在之前位置上的目标函数
  • f(X_i (t+1)) - 在给定时刻(t+1)时，第i个粒子在新位置上的目标函数值

6. 自第j个粒子作用于第i个粒子的力的方程：F_dij (t) = K (t) * (Q_i (t) * Q_j (t) * (p_dj (t) - X_di (t))) / (R_ij (t)^2 + ε)，其中：

  • F_dij (t) - 在给定时刻t时，第i个粒子受到第j个粒子的作用力
  • K (t) - 在时刻t的库仑常数
  • Q_i (t)和Q_j (t) - 在给定时刻t时，第i个和第j个粒子的电荷量
  • p_dj (t) - 在时刻t时，第j个粒子的最佳位置
  • X_di (t) - 在给定时刻t时，第i个粒子的位置
  • R_ij (t) - 在给定时刻t时，第i个和第j个粒子之间的欧几里得距离
  • ε - 用于防止除以0的小正常数。

7. 第i个和第j个粒子之间的欧几里得距离公式：R_ij (t) = (X_i (t) - X_j (t))^2

8. 库仑常数方程：K(t) = K_0 * exp(-α * t / maxiter)，其中：

  • K_0 - 库仑常数的初始值
  • α - 外部参数
  • t - 当前时刻（迭代次数）
  • maxiter - 最大迭代次数

9. 作用于第i个粒子的总力方程：F_di(t) = Σ(rand() * F_dij(t))，j=(从1到N)，j≠i，其中：

  • F_di(t) - 在时刻t作用于第i个粒子的总力
  • rand() - [0, 1]区间内的随机数
  • N - 搜索空间中的粒子数

10. 作用于第i个粒子的电场方程：E_di(t) = F_di(t) / Q_i(t)，其中：

  • E_di(t) - 在时刻t作用于第i个粒子的电场
  • F_di(t) - 作用于第i个粒子的总力
  • Q_i(t) - 在时刻t第i个粒子的电荷

11. 更新粒子i在时刻t+1的速度方程：V_i(t+1) = rand() * V_i(t) + a_i(t)，其中：

  • V_i(t) - 之前的速度
  • a_i(t) - 影响粒子的加速度
  • rand() - [0, 1]区间内的随机数

12. 更新粒子i在时刻<b1>t+1</b1>的位置方程：X_i(t+1) = X_i(t) + V_i(t+1)，其中：

  • V_i(t+1) - 新的速度

13. 方程规定种群中所有粒子的电荷相同，且对于所有i, j = 1, 2,..., N，Q_i(t) = Q_j(t)

14. 计算每个粒子i在时刻t的相对电荷q_i(t)的方程：q_i(t) = exp((fit_p_i(t) - worst(t)) / (best(t) - worst(t)))，其中：

  • fit_p_i(t) - 粒子个人最佳位置的适应度值
  • fit_best(t) - 全局最佳位置的适应度值
  • fit_worst(t) - 种群中适应度值最差的粒子的适应度值

15. 方程：Q_i(t) = q_i(t) / Σ_j=1...N q_j(t).
该方程将所有粒子的相对电荷q_i(t)进行归一化，使它们的总和等于1。通过这种方式，为每个粒子获得归一化电荷Q_i(t)。

16. 方程：best(t) = max(fit_j(t)) for j = 1, 2,..., N
该方程计算当前时刻t种群中的最佳适应度值——即所有粒子适应度值的最大值作为best(t)值。

17. 方程：worst(t) = min(fit_j(t)) for j = 1, 2,..., N
该方程计算当前时刻t种群中的最差适应度值worst(t)，即所有粒子适应度值的最小值。

现在我们已经了解了算法中粒子运动规律的方程，接下来我们可以创建一个伪代码，这将有助于我们在未来用MQL5编写AEFA算法代码。


AEFA 伪代码：

步骤1：初始化

- 随机初始化粒子位置。
- 计算每个粒子的目标函数值。
- 设置当前迭代次数 t = 0。

步骤2：更新粒子位置，直到满足停止条件：  

1. 根据方程(8)计算K(t)库仑常数。
2. 在当前迭代次数下，计算目标函数的最佳fit_best(t)和最劣fit_worst(t)值。
3. 对于每个粒子i = 1, 2, ..., N：
   a. 根据方程(14)计算粒子Q_i(t)的电荷。
   b. 根据方程(6)计算粒子i从粒子j受到的力。
   c. 使用方程(9)计算作用在粒子i上的总力。
   d. 使用方程(4)计算粒子i的加速度。
   e. 使用方程(11)更新速度，并使用方程(12)更新粒子i的位置。
4. 迭代计数器增加 t = t + 1
。

步骤3：停止条件。 检查停止条件（例如达到最大迭代次数）。如果条件不满足，则返回步骤2。

K0

图例 1. 根据库仑公式，静电力与α比率（外部参数）的关系。

好吧，最后我们弄清楚了算法的描述、方程和伪代码。现在我们需要继续生成代码。

让我们实现S_AEFA_Agent结构，用于描述算法中的代理。该结构包含以下字段：

  • best_fitness - 表示代理的最佳适应度。
  • best_position[] - 代理在搜索空间中最佳位置的坐标数组。
  • velocity[] - 表示粒子速度向量的数组。
  • charge - 代理的电荷。
  • relative_charge - 粒子的相对电荷。

该结构还定义了Init函数，用于初始化粒子（代理）。它接受coords参数，表示代理坐标的数量，并分别更改best_position和velocity数组的大小。之后，将best_fitness设置为最小可能的双精度值-DBL_MAX，而charge和relative_charge设置为0。

该代码为描述人工电场算法中的代理提供了基础，并为它们在此上下文中进一步工作做好了准备。

//——————————————————————————————————————————————————————————————————————————————
struct S_AEFA_Agent
{
    double best_fitness;
    double best_position [];
    double velocity      [];
    double charge;
    double relative_charge;

    void Init (int coords)
    {
      ArrayResize (best_position, coords);
      ArrayResize (velocity,      coords);

      best_fitness    = -DBL_MAX;
      charge          = 0;
      relative_charge = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们描述从C_AO类继承的C_AO_AEFA类。该类中定义了以下方法和变量：

  • C_AO_AEFA - 构造函数，用于设置变量和参数的值。
  • SetParams - 方法根据存储在params数组中的值设置参数。
  • Init - 方法接受一组值并进行初始化。
  • Moving和Revision - 这两个方法执行算法的主要逻辑。
  • 几个double类型的变量，如K0、alpha、particleMass、epsilon，以及agent数组和其他私有变量。
  • CalculateK、UpdateCharges、CalculateForces、CalculateDistance和UpdateVelocityAndPosition这几个私有方法执行在搜索空间中移动粒子的操作。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEFA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEFA () { }
  C_AO_AEFA ()
  {
    ao_name = "AEFA";
    ao_desc = "Artificial Electric Field Algorithm";
    ao_link = ""; //"https://www.mql5.com/en/articles/15162";

    popSize      = 50;
    K0           = 500.0;
    alpha        = 20.0;
    particleMass = 1.0;

    ArrayResize (params, 4);

    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "K0";            params [1].val = K0;
    params [2].name = "alpha";         params [2].val = alpha;
    params [3].name = "particleMass";  params [3].val = particleMass;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    K0           = params      [1].val;
    alpha        = params      [2].val;
    particleMass = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double K0;
  double alpha;
  double particleMass;
  double epsilon;

  S_AEFA_Agent agent [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  double K;
  double CalculateK                (int t);
  void   UpdateCharges             (double best, double worst);
  void   CalculateForces           ();
  double CalculateDistance         (const double &x1 [], const double &x2 []);
  void   UpdateVelocityAndPosition (int i);
};
//——————————————————————————————————————————————————————————————————————————————

接下来，我们将实现C_AO_AEFA类的Init方法。该方法使用给定的参数初始化AEFA算法。

Init方法的输入：

  • rangeMinP - 最小范围边界值的数组。
  • rangeMaxP - 最大范围限制值的数组。
  • rangeStepP - 范围步长值的数组。
  • epochsP - 迭代次数（默认为0）。

Init方法执行的操作：

1. 调用StandardInit方法。它接收rangeMinP、rangeMaxP和rangeStepP数组。如果StandardInit方法返回false，则Init方法返回false。
2. 将epochs和epochNow变量分别设置为epochsP和0。
3. 将agent数组的大小调整为popSize。
4. 在循环中，通过调用Init方法并将coords数组传递给它来初始化agent数组的每个元素。
5. 将epsilon变量设置为1e-10。
6. 方法返回true。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEFA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  epsilon = 1e-10;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

接下来，我们讨论C_AO_AEFA类中的Moving()方法。在此方法中，会更新优化算法中的粒子位置。以下是该方法的主要流程概述：

1. epochNow变量的值会递增。
2. 如果revision变量等于false，则会初始化粒子的初始位置。每个粒子的坐标会在给定范围内设置为一个随机值，然后根据给定的步长对这个值进行变换。
3. 如果revision等于true，则会计算K值，以及每个粒子的最佳和最差函数估计值。接下来会计算力，并更新每个粒子的速度、位置以及电荷。

该方法的总体思路是利用计算粒子运动定律方程的特殊方法来更新优化算法中粒子的位置。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  K            = CalculateK (epochNow);
  double best  = -DBL_MAX;
  double worst =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > best)  best  = a [i].f;
    if (a [i].f < worst) worst = a [i].f;
  }

  UpdateCharges   (best, worst);
  CalculateForces ();

  for (int i = 0; i < popSize; i++)
  {
    UpdateVelocityAndPosition (i);
  }
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_AEFA类的CalculateK()方法中，根据当前迭代索引t以及其他参数K0、alpha和epochs来计算K参数。以下是该方法的工作流程：

1. 该方法接收参数t作为输入，该参数代表算法中当前迭代的索引。
2. 然后计算K的值。
3. 根据公式计算的结果作为方法的返回值。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AEFA::CalculateK (int t)
{
  return K0 * MathExp (-alpha * t / epochs);
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_AEFA类的UpdateCharges()方法中，根据最佳和最差适应度值来更新粒子的电荷。该方法中操作的简要说明：

1. 创建sum_q变量并将其设置为0。
2. 然后，通过一个从0到popSize的循环遍历所有粒子。
3. 在循环内部，使用公式计算每个粒子的相对电荷。
4. 将相对电荷值添加到sum_q变量中。
5. 然后，对所有粒子进行第二次循环，为每个粒子分配一个电荷值，该值等于相对电荷除以sum_q。

因此，该方法根据粒子的适应度来更新它们的电荷，以便它们能够反映出与最佳和最差适应度值相比的相对质量。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::UpdateCharges (double best, double worst)
{
  double sum_q = 0;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].relative_charge = MathExp ((a [i].f - worst) / (best - worst));
    sum_q += agent [i].relative_charge;
  }
  for (int i = 0; i < popSize; i++)
  {
    agent [i].charge = agent [i].relative_charge / sum_q;
  }
}
//——————————————————————————————————————————————————————————————————————————————

以下是C_AO_AEFA类中CalculateDistance()和CalculateForces()方法的描述。

CalculateDistance()方法接受两个数组x1[]和x2[]作为输入，它们分别代表两个粒子的坐标，并计算它们之间的空间距离。为此，该方法遍历数组的所有坐标，对于每个坐标，计算数组对应元素之差的平方，然后将这些平方值相加。接着，提取所得和的平方根，并将该值作为两点在空间中的距离（欧几里得距离）返回。

CalculateForces()方法计算作用于每个粒子的力。对于每个粒子，相对于所有其他粒子计算其力向量。对于每对粒子（除了相同的粒子(i != j)），使用CalculateDistance()方法计算它们之间的距离。然后，对于空间中的每个坐标，使用包含粒子电荷、位置和它们之间距离的方程来计算作用于粒子的力。对每个坐标的结果进行求和，然后将所得力除以粒子电荷，以考虑它们对粒子速度的影响。

因此，这些方法分别用于计算算法中粒子之间的作用力以及它们在空间中的距离。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::CalculateForces ()
{
  double force [];
  ArrayResize (force, coords);

  for (int i = 0; i < popSize; i++)
  {
    ArrayInitialize (force, 0);

    for (int j = 0; j < popSize; j++)
    {
      if (i != j)
      {
        double R = CalculateDistance (a [i].c, a [j].c);

        for (int d = 0; d < coords; d++)
        {
          force [d] += u.RNDprobab () * K *
                       (agent [i].charge * agent [j].charge * (agent [j].best_position [d] - a [i].c [d])) /
                       (R * R + epsilon);
        }
      }
    }

    for (int d = 0; d < coords; d++)
    {
      agent [i].velocity [d] = force [d] / agent [i].charge;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AEFA::CalculateDistance (const double &x1 [], const double &x2 [])
{
  double sum = 0;
  for (int d = 0; d < coords; d++)
  {
    sum += (x1 [d] - x2 [d]) * (x1 [d] - x2 [d]);
  }
  return MathSqrt (sum);
}
//——————————————————————————————————————————————————————————————————————————————

接下来是C_AO_AEFA类中的UpdateVelocityAndPosition()方法。此方法更新索引为i的粒子的速度和位置。对于粒子在空间中的每个坐标，会发生以下情况：

1. 计算加速度，它取决于粒子的电荷、当前速度和粒子质量。
2. 通过添加当前速度与加速度相乘的随机分量来更新粒子速度。
3. 通过将新速度加到当前位置上来更新粒子位置。然后，使用u.SeInDiSp()方法将新位置限制在每个坐标指定的最小值和最大值之间。

因此，UpdateVelocityAndPosition()方法在考虑加速度、随机因素以及粒子在空间中的位置约束的情况下，更新优化算法中的粒子速度和位置。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::UpdateVelocityAndPosition (int i)
{
  for (int d = 0; d < coords; d++)
  {
    double acceleration = (agent [i].charge * agent [i].velocity [d]) / particleMass;

    agent [i].velocity [d] = (u.RNDfromCI (0, 1)) * agent [i].velocity [d] + acceleration;

    a [i].c [d] += agent [i].velocity [d];
    a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

最后，我们来看C_AO_AEFA类中的Revision()方法。在此方法中，会更新有关粒子最佳位置及其最佳适应度值的信息，以及fB表示的最佳全局解决方案。该方法执行以下操作：

1. 创建一个名为ind的变量，作为最佳解决方案数组中位置的标志和索引，并将其设置为-1。
2. 然后，通过一个从0到popSize的循环遍历所有粒子。
3. 在循环内部，检查粒子的适应度函数值是否超过fB（当前最佳全局适应度值）。如果是，则更新fB的值，并将ind变量设置为当前粒子的索引i。
4. 接着检查粒子的适应度是否大于该粒子在所有迭代周期中的最佳适应度（存储在agent[i].best_fitness中）。如果是，则更新该粒子的最佳分数和位置。
5. 最后，如果ind不等于-1，则通过复制索引为ind的粒子的位置来更新cB（可能表示当前最佳粒子位置）。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f > agent [i].best_fitness)
    {
      agent [i].best_fitness = a [i].f;
      ArrayCopy (agent [i].best_position, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————


3. 测试结果

AEFA标准测试结果：

AEFA|Artificial Electric Field Algorithm|20.0|1000.0|10.0|100.0|
=============================
5 Hilly's；函数运行次数：10000；结果：0.8769988087850553
25 Hilly's；函数运行次数：10000；结果：0.617530930198765
500 Hilly's；函数运行次数：10000；结果：0.2523539056281608
=============================
5 Forest's；函数运行次数：10000；结果：0.927287032866128
25 Forest's；函数运行次数：10000；结果：0.7269761843712702
500 Forest's；函数运行次数：10000；结果：0.18063577020760296
=============================
5 Megacity's；函数运行次数：10000；结果：0.6661538461538462
25 Megacity's；函数运行次数：10000；结果：0.11630769230769236
500 Megacity's；函数运行次数：10000；结果：0.0950769230769239
=============================
全部得分：4.45932 (49.55%)

我们可以看到，不同测试的结果之间存在显著的差异。此外，该算法在处理高维函数时表现出了非常弱的搜索能力，这一点从其结果中也得到了证实。在处理离散函数时，已经发现了一些特殊问题。

Hilly

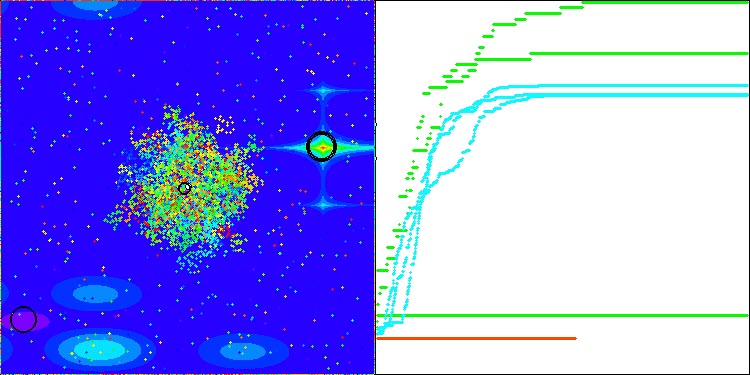
  AEFA在Hilly测试函数上的表现

Forest

  AEFA在 Forest测试函数上表现

  AEFA在Megacity测试函数上的表现

我想强调AEFA算法的一个重要方面。在进行了10,000次适应度函数的标准测试后，我决定增加测试次数至100,000次，进行额外的实验，而实验结果超出了我的预期。在许多参数较少的函数上，随着适应度函数运行次数的增加，该算法实现了100%的收敛。重要的是要注意，排名表中的算法，即使是占据前列的算法，也并非都能通过增加运行次数实现100%的收敛，因为它们可能会陷入局部极值。在这种情况下，该算法展现出了避免陷入局部极值的抗性。然而，该算法在多维空间搜索时，尤其是处理离散函数时，同样面临着困难。

AEFA测试台在100,000次测试函数运行下的结果：

SDSm|Stochastic Diffusion Search M|100.0|100.0|0.05|
=============================
5 Hilly's；函数运行次数：10000；结果：0.9874670077970368
25 Hilly's；函数运行次数：10000；结果： 0.9355482229513405
500 Hilly's；函数运行次数：10000；结果：0.5943074120378588
=============================
5 Forest's；函数运行次数：10000；结果：0.994126703499673
25 Forest's；函数运行次数：10000；结果：0.9627011069578397
500 Forest's；函数运行次数：10000；结果：0.5628894538341265
=============================
5 Megacity's；函数运行次数：10000；结果：0.9015384615384615
25 Megacity's；函数运行次数：10000；结果：0.7264615384615385
500 Megacity's；函数运行次数：10000；结果：0.37464615384615396
=============================
全部得分：7.03969 (78.22%)

您可以从下面的图片中注意到该算法的收敛特性。

MrunsHilly

MrunsForest

MrunsMegacity

种群优化算法评级表：

# 算法 说明 Hilly Hilly final Forest Forest final Megacity (离散) Megacity final 最终结果 最大 %
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA 二进制遗传算法 0.99989 0.99518 0.42835 2.42341 0.96153 0.96181 0.32027 2.24360 0.91385 0.95908 0.24220 2.11512 6.782 75.36
2 ANS 交叉邻近搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
3 CLA 密码锁算法 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 ESG 社会群体的演化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
8 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
9 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
10 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
11 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
12 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
13 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
14 HS 和声搜索算法 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
15 SSG 树苗播种和生长算法 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
16 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
17 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
18 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
19 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
20 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
21 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
22 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
23 IWO 入侵性杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
24 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
25 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
26 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
27 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
28 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
29 GSA 重力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
30 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
31 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
32 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
33 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
34 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
35 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
36 Boids boids算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
37 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
38 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
39 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
40 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
41 GWO 灰狼优化器 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
42 CSS 电荷系统搜索算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
43 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


总结

基于人工电场算法（AEFA）在不同维度测试函数上的结果，可以得出以下结论：

1. AEFA在各种测试函数上，包括Hilly、Forest和Megacity，均表现出令人满意的结果。然而，在离散Megacity函数上的结果相较于其他函数较差。
2. 当进行大量函数运行（100,000次）时，该算法展现出良好的性能，这使其在小维度上能够将收敛精度提高到100%。
3. AEFA的总体得分为4.45932（49.55%），在评级表中排名第19位，处于中游水平。

尽管在我们的标准测试中，AEFA算法在不同维度的测试函数上并未展现出最佳结果，但它具有一个额外优势：随着适应度函数运行次数的增加，它取得了令人印象深刻的总体结果7.03969（78.22%），这使其在涉及小维度，尤其是那些具有平滑表面的任务中非常有用。

TAB

图例 2. 根据相关测试结果，算法的颜色渐变中，结果大于等于0.99的将以白色高亮显示。

图表

图例 3. 算法测试结果的直方图（标尺从 0 到 100，越多越好，

其中100是理论上的最大可能结果，附件提供了一个计算评级表格的脚本）


AEFA的优势和劣势：

优势：

  1. 在具有足够多适应度函数运行次数的情况下，对低维平滑函数具有出色的收敛性。
  2. 外部参数相对较少。

缺点：

  1. 在我们标准测试中所使用的函数上，结果范围较大。
  2. 在离散函数上表现不佳。
  3. 可扩展性极低。
  4. 实现复杂。

本文附带了一个文档，其中包含了算法代码的当前版本。文章作者不对典型算法描述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/15162

附加的文件 |
下载ZIP
AEFA.zip (26.78 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论
化学反应优化 (CRO) 算法（第二部分）：汇编和结果 化学反应优化 (CRO) 算法（第二部分）：汇编和结果
在第二部分中，我们将把化学运算符整合到一个算法中，并对其结果进行详细分析。让我们来看看化学反应优化 (CRO) 方法是如何解决测试函数的复杂问题的。
您应当知道的 MQL5 向导技术（第 17 部分）：多币种交易 您应当知道的 MQL5 向导技术（第 17 部分）：多币种交易
当经由向导组装一款智能系统时，默认情况下，跨多币种交易不可用。我们研究了 2 种可能采取的技巧，可令交易者在同一时间据多个品种测试他们的思路。
开发回放系统（第 54 部分）：第一个模块的诞生 开发回放系统（第 54 部分）：第一个模块的诞生
在本文中，我们将探讨如何将多个真正功能模块中的第一个组合在一起，用于回放/模拟器系统，这些模块也将用于其他用途。我们现在说的是鼠标模块。
化学反应优化（CRO）算法（第一部分）：在优化中处理化学 化学反应优化（CRO）算法（第一部分）：在优化中处理化学
在本文的第一部分中，我们将深入化学反应的世界并发现一种新的优化方法！化学反应优化 (CRO，Chemical reaction optimization) 利用热力学定律得出的原理来实现有效的结果。我们将揭示分解、合成和其他化学过程的秘密，这些秘密成为了这种创新方法的基础。