MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
种群优化算法：杜鹃优化算法（COA）

种群优化算法：杜鹃优化算法（COA）

MetaTrader 5 — 示例 | 18 四月 2023, 12:31
1 274 0
Andrey Dik
Andrey Dik

内容

1. 概述
2. 算法描述、决策树和 Levy 飞行
3. COA 代码
4. 测试结果


1. 概述

杜鹃是一种迷人的鸟类，不仅因为它会唱歌，还因为它激进的繁殖策略，其中包括将蛋产入其它鸟类的巢穴之中。 因此，这种鸟完全将其应承担的父母责任转移到其它物种身上。 每种杜鹃都会产下某种颜色和大小的蛋，以便更好地匹配各种养父母的蛋。 扔进其它鸟巢的杜鹃雏鸟通常比鸟巢主人自己的雏鸟更大、更强壮，所以杜鹃需要更多的食物。 在发育过程中，霍奇森（Hodgson）的杜鹃雏鸟在翅膀上以开放喙的形式发展出一种特殊的图案，这令它们能够从养父母那里获得更多的食物。 杜鹃并不是唯一表现出这种特征的鸟类。 在至少 80 种鸟类中都发现了筑巢寄生。 此外，这种现象在某些种群的社会性昆虫中很普遍 — 大黄蜂、蜜蜂、和蚂蚁，它们的雌性渗透到另一个繁殖地，杀死原本的女王并产卵。 一些鱼类也存在巢穴寄生，例如来自非洲坦噶尼喀湖（Lake Tanganyika）的鲶鱼，它们将卵扔给其它在嘴里孵化鱼卵的鱼类。


杜鹃搜索是杨（Yang）和 Deb 于 2009 年开发的最新型自然启发式算法之一。 它基于一些杜鹃物种的寄生。 该算法已由所谓的 Levy 飞行进一步改进，远超简单的各向同性随机游走方法。


2. 算法说明

杜鹃优化算法（COA）用于连续非线性优化。 COA 的灵感来自这种鸟的生活方式。 优化算法基于物种产蛋繁殖的特点。 像其它进化方法一样，COA 从初始种群开始。 该算法的基础是争夺生存权。 在竞争生存的同时，一些鸟类会死亡。 幸存的杜鹃会搬到更好的地方，开始繁殖和产蛋。 最后，幸存的杜鹃会收敛这样的方式，如此杜鹃社会获得了相似的适应度。
这种方法的主要优点是它的简单性：杜鹃搜索只需要四个可理解的参数，因此调优变得不费吹灰之力。

在杜鹃搜索算法中，鸟巢中原来的蛋被解释为优化问题的可能解，杜鹃蛋代表新的解。 该方法的终极目标是使用这些新的（并且可能更好）寄生杜鹃蛋解决方案来取代当前的鸟巢蛋解。 这种替换，迭代进行，最终导出最佳解。

杨教授和 Deb 教授为该算法提出了以下三组理想状态：
1. 每只杜鹃产一枚蛋，并将其放入随机选择的鸟巢当中。
2. 拥有优质鸟蛋的最佳巢穴将传给下一代。
3. 可用的鸟巢数量是固定的，且鸟巢具有检测出外来鸟蛋的 “pa” 概率。 在这种情况下，宿主鸟可以扔掉鸟蛋，或离开巢穴，鸟蛋就会死亡。
出于简单起见，第三个假设可以用 n 个鸟巢的 pa 分数来近似。 对于最大化问题，解的品质或适当性也许只是与目标函数成正比。 然而，也可以定义适应度函数的其它（更复杂的）表达式。

对于每次迭代 g，随机选择一枚杜鹃鸟蛋 i，并采用 Levy 飞行生成新的解 xi(g + 1)，这是一种随机游走，其中步数由具有一定概率分布的步长范围内判定，且步长的方向是各向同性和随机的。 根据该方法的原建者的说法，采用 Levy 飞行策略比其它简单的随机游走更可取，因为它会产生更好的整体性能。 一般的 Levy 飞行方程如下所示：

xi(g + 1) = xi(g) + α ⊕ levy(λ),

其中 g 表示当前生成的数量，而 α > 0 表示步长，这应该与正在研究的特定问题的规模有关。 ⊕ 符号则表示逐元素乘法。 请注意，这本质上是一个马尔可夫（Markov）链，因为第 g + 1 代的下一个位置仅取决于 g 代的当前位置，以及分别由第一项和第二项给出的转移概率。 该转移概率由 Levy 分布调制为：

levy(λ) ∼ g−λ, (1 < λ ≤ 3),

其具有无限均值的无限方差。 实践表明，在固定的 2.0 度下，可以达到最好的结果。 此处，这些步骤基本上形成了一个随机游走过程，具有幂律重尾步长分布。 从计算的角度来看，利用 Levy 飞行生成随机数包括两个阶段：首先，根据均匀分布选择随机方向，然后根据所选的 Levy 分布生成步骤。 然后，该算法评估新解的适用度，并将其与当前解进行比较。 如果新解提供了更好的适用度，则它将取代当前解。 另一方面，一些鸟巢被遗弃（鸟巢的宿主扔掉杜鹃蛋，或离开巢穴，故鸟蛋坏死了），以便提升针对搜索空间的探索，从而寻找更有希望的解。 替换率由 pa 概率判定，模型参数需要调整以便提高性能。 该算法应用迭代方式，直到满足停止条件。 常见的终止准则是，已找到满足较低阈值的解、已达到固定的更新换代数量、或者连续迭代不再产生更好的结果。

我们来更详细地讨论杜鹃产蛋的过程。 从所有鸟巢中，随机选择一个预备产蛋的鸟巢。 由于鸟蛋是一个解，因此可以用鸟蛋的质量来表示。 如果杜鹃蛋的质量高于宿主蛋，那么它将被替换。 否则，宿主蛋将留在鸟巢中。 事实上，随后的进化将自幸存的雏鸟继续。 这意味着，如果宿主蛋的雏鸟幸存下来，那么进化将从同一个地方继续。 进而只有当杜鹃蛋变得更强势，并且从新的地方继续寻找解时，才有可能进一步发展。 示意性决策树如图例 1 所示。


决策树

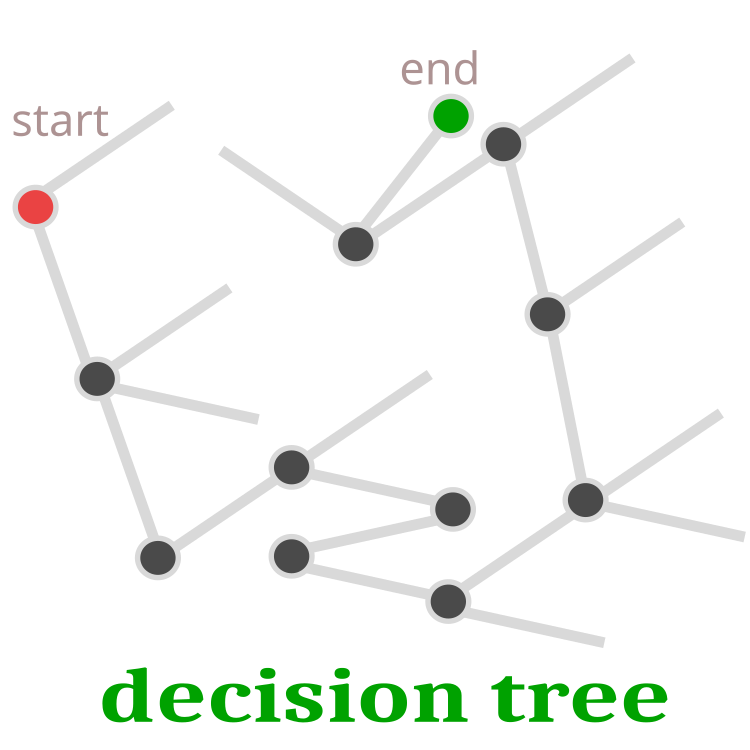
图例 1. 决策树。 红点是开始，绿点是最终决策


决策树之后算法基础的第二个组成部分是 Levy 飞行。 Levy 飞行是一种随机游走（马尔可夫统计过程），其中跳跃的长度以步为单位变化，跳跃的方向随机变化，概率分布是帕累托（Pareto）分布的特例，其特征是重尾。 它被定义为空间中的跳跃，并且跳跃在随机方向上是各向同性的。 Levy 飞行是描述异常随机过程的工具。 分散是无限的（长距跳跃也有可能），跳跃的长度在所有级别上都是自相似的（短跳穿插着长途飞行）。 术语 Levy 飞行有时会扩展为包括发生在离散网格，而不仅是连续空间中的随机游走。

如果我们考虑一个参数的优化问题，可以想象 Levy 飞行在布谷鸟算法中的明确应用。 我们以一个假设的函数（图例 2 中的黑线）为例，它在其大部分定义域，即水平线（y=x）上不会改变。 仅在很小的区域内，该函数会发生变化，并且有一个最大值。 如果我们从图例 2 中的橙点开始搜索最大值，然后得到一个带有 Levy 分布的随机值 x，我们将远离起点，同时在函数里不再得到变化。 然而，随着在分布尾部的强烈跳跃，我们得到一个绿点，这是一个比原始橙色更好的解，然后只从绿点我们能改善结果，同时接近函数的最大值。 在此示例中，Levy 飞行极大地提高了算法的搜索能力。

Levy 飞行

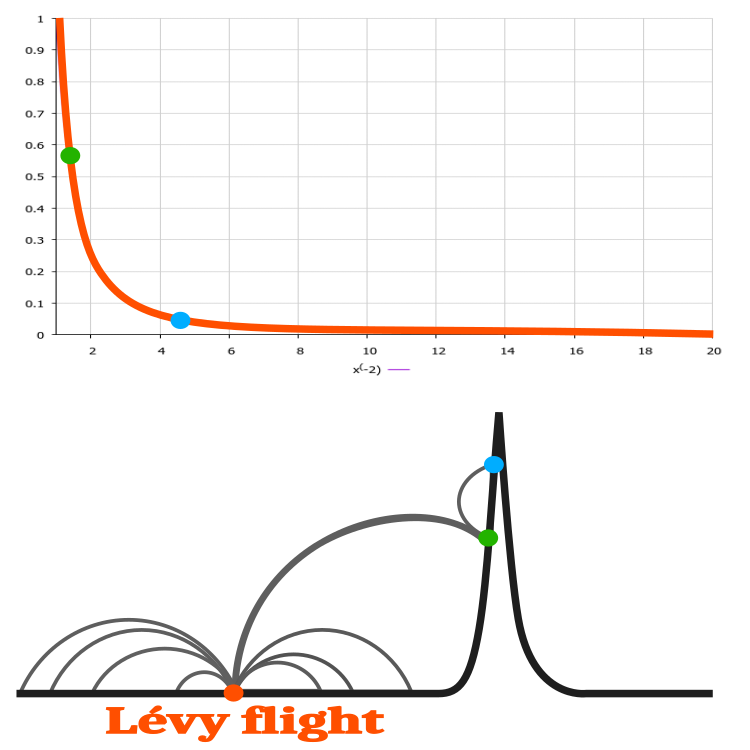
图例 2. 利用 Levy 飞行查找假设一维函数解的示例

Levy 飞行的概念用于混沌理论，用于模拟随机或伪随机自然现象（例如，信天翁的飞行，结合长短轨迹）。 示例包括地震数据分析、金融数学、密码学、信号分析、湍流运动，以及天文学、生物学和物理学中的许多应用。

COA 算法伪代码（图例 3）:

1. 初始杜鹃是随机值。
2. 定义适应度。
3. 在随机鸟巢中产蛋。
4. 以给定的概率清空鸟巢。
5. 从当前位置将杜鹃发送到 Levi 飞行距离内的随机方向。
6. 定义适应度。
7. 在随机鸟巢中产蛋。
8. 以给定的概率清空鸟巢。
9. 重复 第 5 步，直到满足停止准则。

示意图

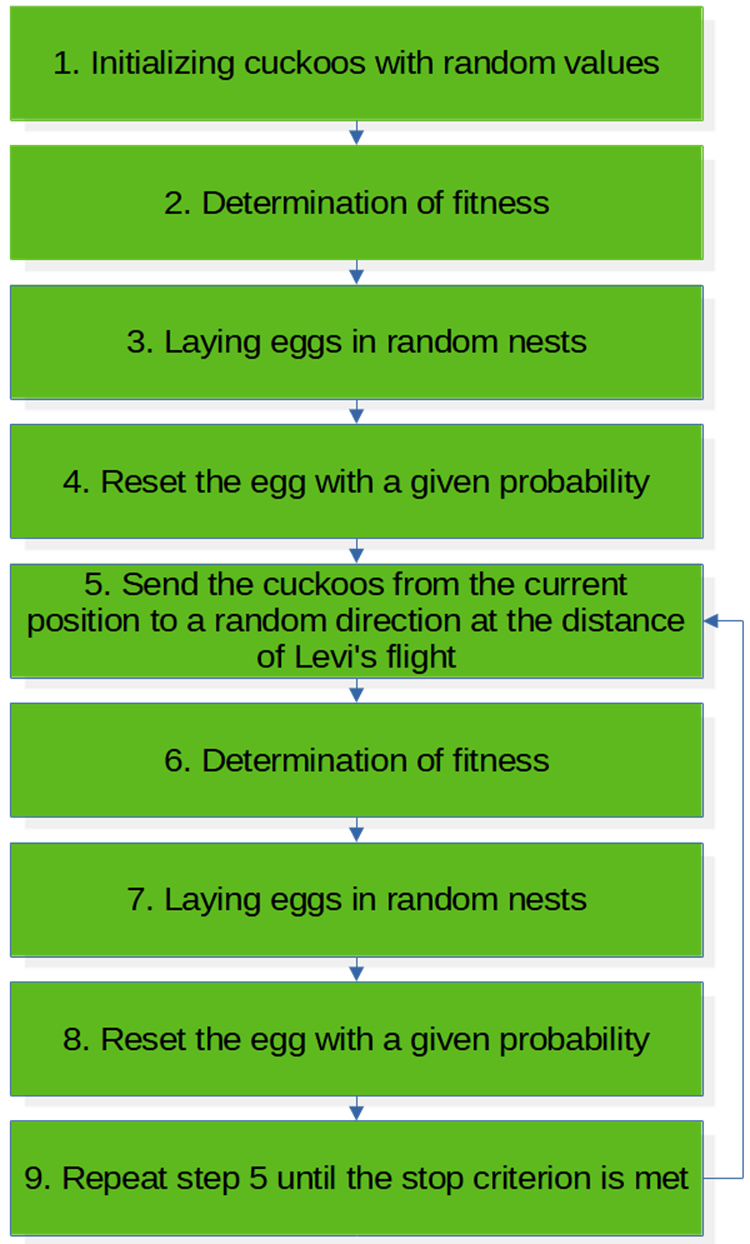
图例 3. COA 算法框图 


3. COA 代码

我们开始研究算法的代码。 解是杜鹃，也是鸟蛋。 这是一个简单的结构，包括搜索空间中的坐标和适应度函数的值（鸟蛋质量）。 

//——————————————————————————————————————————————————————————————————————————————
struct S_Cuckoo
{
  double c []; //coordinates (egg parameters)
  double e;    //egg quality 
};
//——————————————————————————————————————————————————————————————————————————————

我们以结构的形式讲述鸟巢。 此处，就像在鸟蛋的结构中一样，空间中有坐标和适应度函数的值。 “在鸟巢中产蛋”本质上意味着将鸟蛋的结构复制到鸟巢的结构之中。 当采用 pa 概率参数时，当从 0.0 到 pa 的随机数落在 [0.0;1.0] 范围内，且 e 值设置为 -DBL_MAX 时，鸟蛋则会从鸟巢中抛出。

//——————————————————————————————————————————————————————————————————————————————
struct S_Nest
{
  void Init (int coordinates)
  {
    ArrayResize (c, coordinates);
    e = -DBL_MAX;
  }
  double c []; //coordinates (egg parameters)
  double e;    //egg quality
};
//——————————————————————————————————————————————————————————————————————————————

算法类。 这里声明了公开的初始化方法、在用户程序中调用的两个主要方法，优化问题参数的值范围，以及执行服务函数的其它私密方法。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_COA
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Cuckoo cuckoos []; //all the cuckoos
  public: double cB        []; //best coordinates (egg parameters)
  public: double eB;           //best eggs quality

  public: void Init (const int    coordinatesP, //number of opt. parameters
                     const int    cuckoosP,     //number of cuckoos
                     const int    nestsP,       //number of cuckoo nests
                     const double koef_paP,     //probability of detection of cuckoo eggs
                     const double koef_alphaP); //step control value

  public: void CuckooFlight ();
  public: void LayEggs      ();


  //============================================================================
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: S_Nest nests [];      //nests
  private: int    cuckoosNumber; //number of cuckoos
  private: int    nestsNumber;   //number of cuckoo nests
  private: double koef_pa;       //probability of detection of cuckoo eggs
  private: double koef_alpha;    //step control value
  private: double v     [];
  private: int    coordinates;   //coordinates number
  private: bool   clutchEggs;    //clutch of eggs
};
//——————————————————————————————————————————————————————————————————————————————

Init() 公开方法。 在此，变量的值被重置，并给数组分配内存。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::Init (const int    coordinatesP,  //number of opt. parameters
                     const int    cuckoosP,     //number of cuckoos
                     const int    nestsP,       //number of cuckoo nests
                     const double koef_paP,     //probability of detection of cuckoo eggs
                     const double koef_alphaP)  //step control value
{
  MathSrand (GetTickCount ());
  clutchEggs = false;
  eB         = -DBL_MAX;

  coordinates   = coordinatesP;
  cuckoosNumber = cuckoosP;
  nestsNumber   = nestsP;
  koef_pa       = koef_paP;
  koef_alpha    = koef_alphaP;

  ArrayResize (nests, nestsNumber);
  for (int i = 0; i < nestsNumber; i++)
  {
    nests  [i].Init (coordinates);
  }

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (v, coordinates);

  ArrayResize (cuckoos, cuckoosNumber);
  for (int i = 0; i < cuckoosNumber; i++)
  {
    ArrayResize (cuckoos [i].c, coordinates);
  }
}
//——————————————————————————————————————————————————————————————————————————————

第一个公开方法在每次“杜鹃飞行”迭代时都会调用。 如果 clutchEgg 标志关闭，那么我们将杜鹃发送到一个随机方向，在相应坐标范围内生成随机数。 如果启用该标志，则根据 Levy 飞行在 v 向量范围内的分布分派杜鹃的实际飞行。 v 向量是在 Init() 中针对每个坐标分别预先计算得出的，因为每个坐标可能具有不同的数值范围。

表达式 cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0)；意即我们要加上 offset r1 * v [c] * pow (r2, -2.0)，其中 r1 是 -1 或 1，它决定了偏移从原始位置的方向，V 是位移向量，R2 是从 0.0 到 20.0 范围内提高到 -2.0 的随机数。 将随机数升幂是 Levy 飞行函数。 其图形如图例 2 所示。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::CuckooFlight ()
{
  //----------------------------------------------------------------------------
  if (!clutchEggs)
  {
    for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha;

    for (int i = 0; i < cuckoosNumber; i++)
    {
      for (int c = 0; c < coordinates; c++)
      {
        cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    clutchEggs = true;
  }
  else
  {
    double r1 = 0.0;
    double r2 = 0.0;

    for (int i = 0; i < cuckoosNumber; i++)
    {
      for (int c = 0; c < coordinates; c++)
      {
        r1 = RNDfromCI (0.0, 1.0);
        r1 = r1 > 0.5 ? 1.0 : -1.0;
        r2 = RNDfromCI (1.0, 20.0);

        cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0);
        cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

每次迭代调用的第二个公开方法是“产蛋”。 在这个方法中，通过算法再现了在鸟巢中产下杜鹃蛋的模拟。 这是通过从所有现有鸟巢中随机选择一个巢穴而实现的。 之后，将杜鹃蛋的质量与已经在鸟巢中的宿主鸟蛋的质量进行比较。 如果杜鹃蛋更好，则进行替换。 该方法算法的一个有趣特征是，即使杜鹃蛋更合适，产蛋后也会检查鸟蛋是否会死亡的概率。 这意味着任何鸟蛋都可能死亡 koef_pa，无论蛋下在哪里，就像在自然界中一样。 如果鸟蛋死亡或被扔出鸟巢，这实际上是一回事，那么鸟巢则允许产下任何新的健康鸟蛋，甚至降低一点，算法会探索新的地方。

这就是自然进化的途径之一，诸如鸟巢寄生，可以用几行代码来描述。 许多作者在他们的出版物中建议，鸟蛋被剔除后，取新的随机值重新初始化鸟巢，而这意味着从头开始搜索。 在大多数情况下，在提高算法的探索能力方面，这样做不会得到预期的结果。 我自己的研究表明，简单地让鸟巢空置更方便，其中一只杜鹃会在里面产蛋，且不管鸟蛋的质量如何。 这比随机值要好。 在研究时，可变性是通过从当前坐标往随机方向随机跳跃提供的。 结果就是，在寻找最佳解时，我们需要更少的迭代，从而提高算法的整体收敛率。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::LayEggs ()
{
  int ind = 0;

  //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  for (int i = 0; i < cuckoosNumber; i++)
  {
    ind = (int)round (RNDfromCI (0.0, nestsNumber - 1));

    if (cuckoos [i].e > nests [ind].e)
    {
      nests [ind].e = cuckoos [i].e;
      ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY);

      if (cuckoos [i].e > eB)
      {
        eB = cuckoos [i].e;
        ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY);
      }
    }
    else
    {
      ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }
  //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv

  for (int n = 0; n < nestsNumber; n++)
  {
    if (RNDfromCI (0.0, 1.0) < koef_pa)
    {
      nests [ind].e = -DBL_MAX;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


4. 测试结果

此为测试结果:

2022.11.30 11:31:54.490    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:31:54.507    Test_AO_COA_fast (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.918379100238852
2022.11.30 11:31:54.507    Test_AO_COA_fast (EURUSD,M1)    Score: 1.00000
2022.11.30 11:31:54.854    Test_AO_COA_fast (EURUSD,M1)    20 Skin's; Func runs 10000 result: 4.257477577760983
2022.11.30 11:31:54.854    Test_AO_COA_fast (EURUSD,M1)    Score: 0.84220
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.3521208312080903
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    Score: 0.14849
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:02.368    Test_AO_COA_fast (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.7600394018343262
2022.11.30 11:32:02.368    Test_AO_COA_fast (EURUSD,M1)    Score: 0.99557
2022.11.30 11:32:02.775    Test_AO_COA_fast (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.4968964923017033
2022.11.30 11:32:02.775    Test_AO_COA_fast (EURUSD,M1)    Score: 0.28107
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.07638950254648778
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    Score: 0.04321
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:13.148    Test_AO_COA_fast (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 12.0
2022.11.30 11:32:13.148    Test_AO_COA_fast (EURUSD,M1)    Score: 1.00000
2022.11.30 11:32:13.584    Test_AO_COA_fast (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 2.69
2022.11.30 11:32:13.584    Test_AO_COA_fast (EURUSD,M1)    Score: 0.22417
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.40800000000000003
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    Score: 0.03400
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    All score for C_AO_COA: 0.507633670637353

Levy 飞行杜鹃搜索算法显示出令人印象深刻的结果。 在大多数测试中，它的性能优于其它优化算法。 特别是，该算法在具有两个变量的平滑 Skin 函数，和具有两个变量的离散 Megacity 函数上显示出 100% 收敛。 更令人惊讶的是，它在离散函数上表现出优异的可扩展性。 在其它测试中，它仅略逊于蚁群算法。 目前，它在我们的评级表上是一个毫无疑问的领先者。

我想澄清一下，所有算法都有优调参数，这些参数会在某种程度上影响最终结果，因此这些算法中很可能具有更优化的参数，如此会令评级表看起来不同。 我只是展示了测试结果，以及我可以找到的参数，以确保获得最佳结果。 如果您设法找到了更多最佳参数，并获得更好的结果，那么我可以根据它们修正评级表。 有一种假设是，蚂蚁算法可以成功地与当前的领先者竞争，因为在某些指标上它领先于杜鹃鸟搜索算法，且在最终指标方面仅落后于它。 GWO 仍然是具有 1000 个变量的 Skin 函数的领先者。 无论如何，那些考虑解决优化问题时在项目中选取算法的人，可以浏览表格，并选择满足其特定需求的算法。


Skin

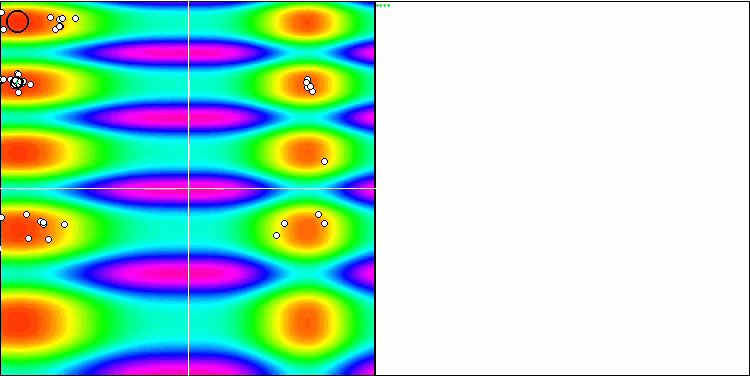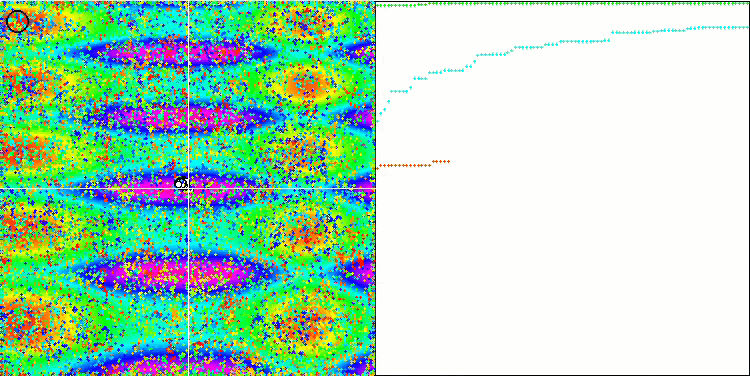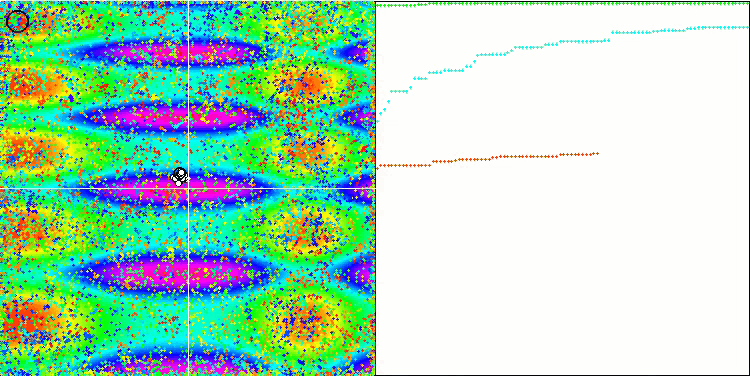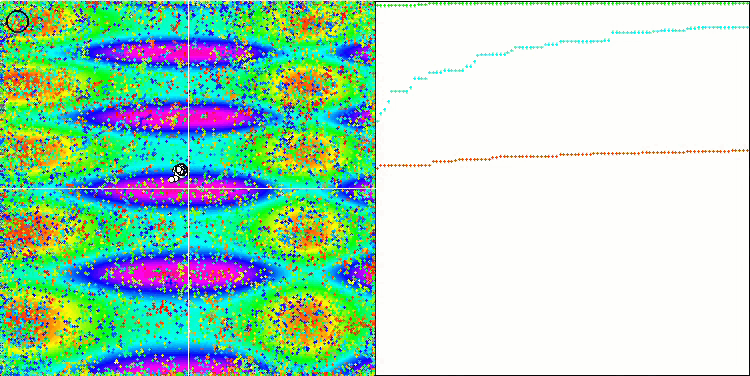
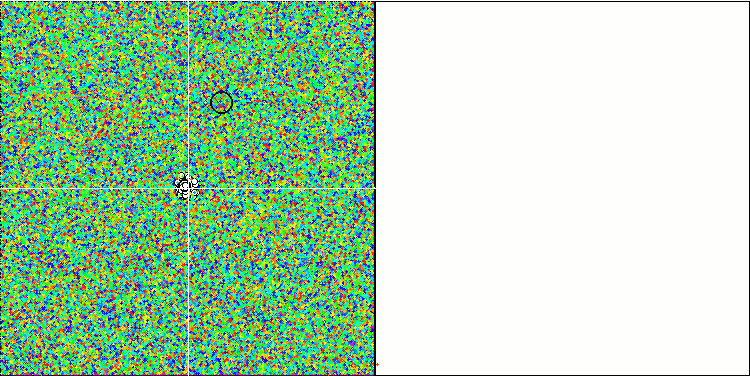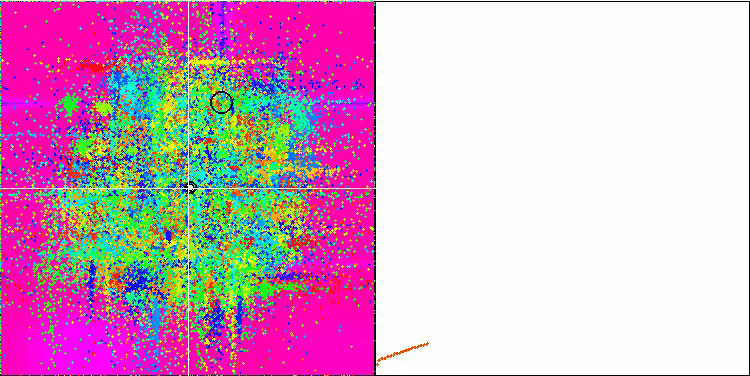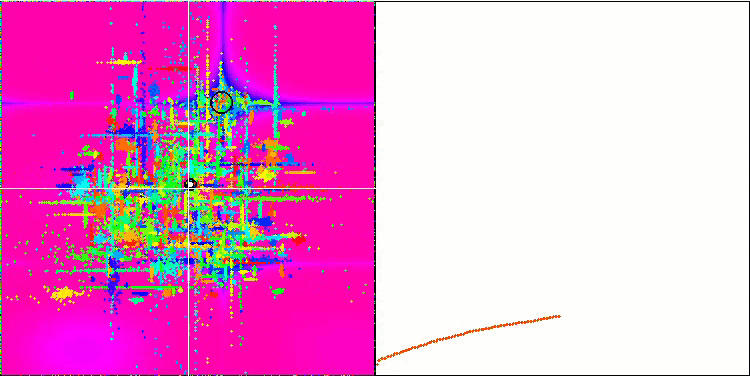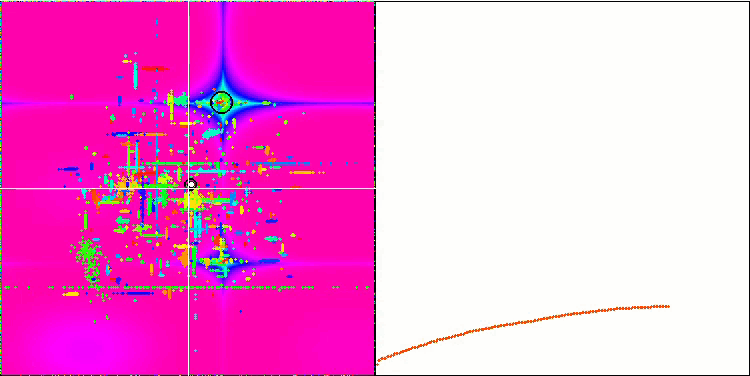
Skin 测试函数上的 COA。

Forest

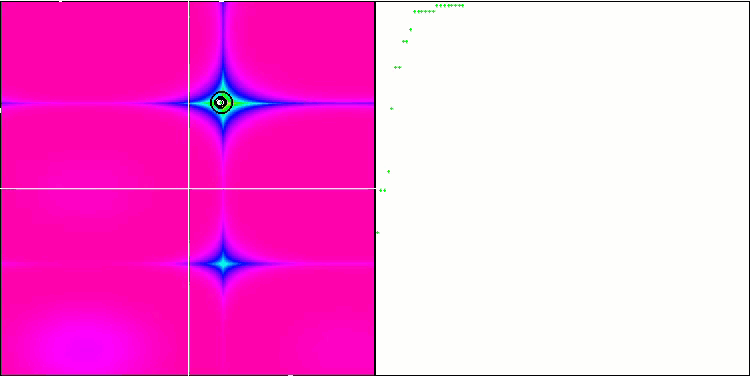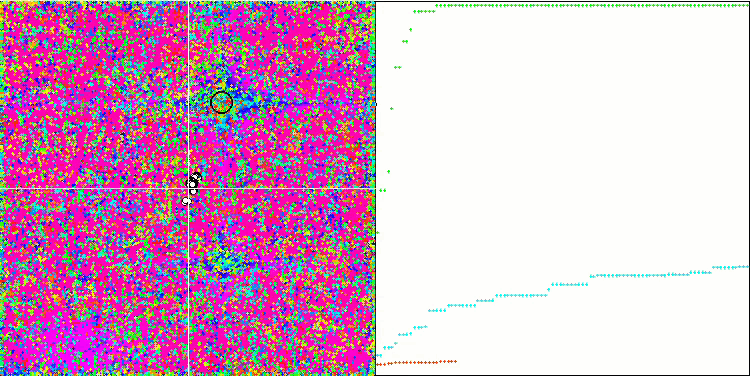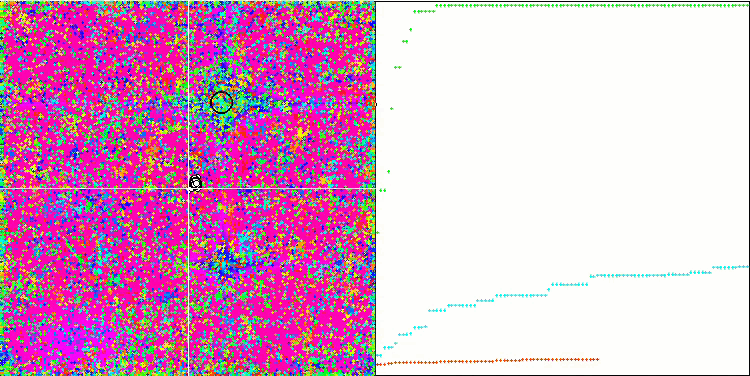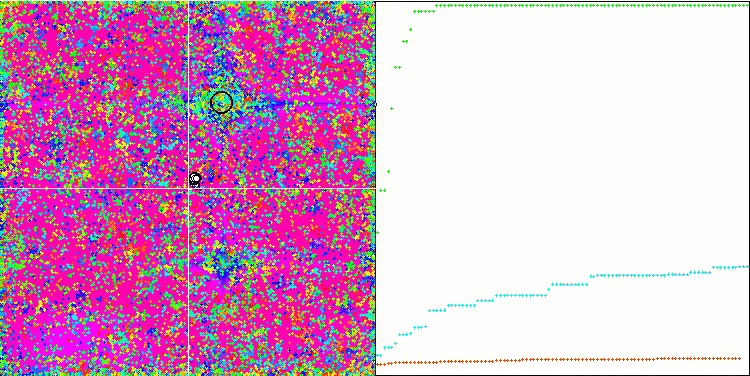
  Forest 测试函数上的 COA。

Megacity

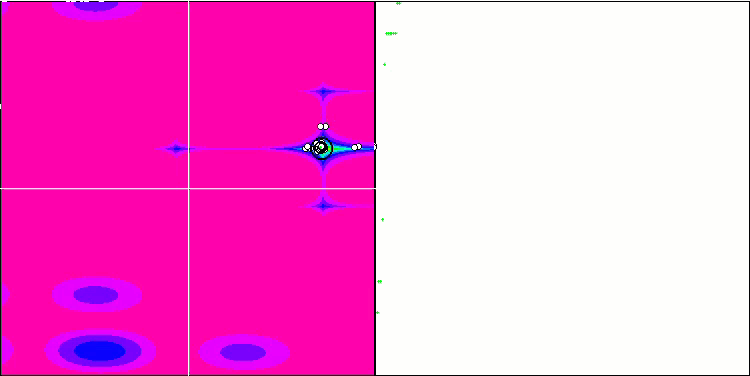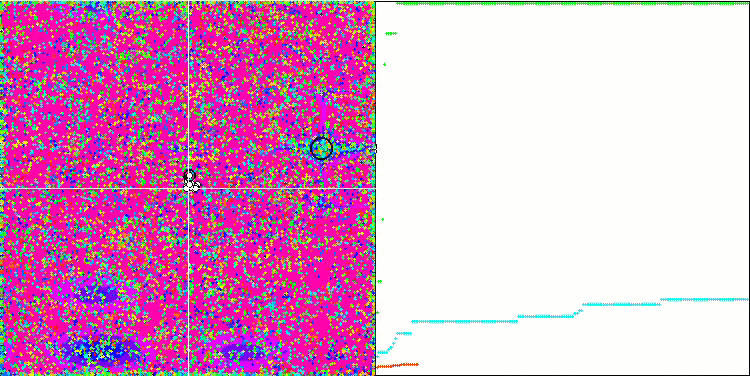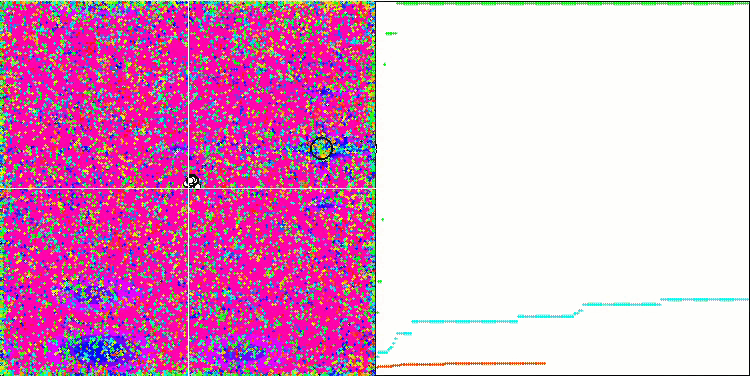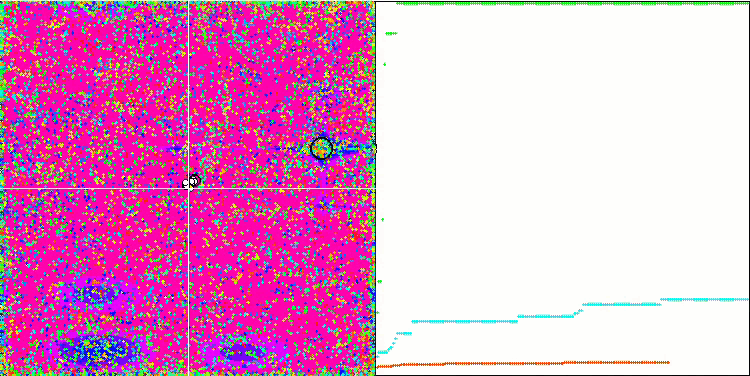
  Megacity 测试函数上的 COA。

在测试台的可视化中，算法的行为与之前研究的行有所为不同，但有一些特征是将任务分解为研究区域的算法的特征，例如蜂群算法。 这表征了算法不专注于单个极值的能力，而是探索几个潜在的有前途的领域，为算法提供防止陷入局部极值的阻力。 有关于此，可以通过对鸟巢进行分类，并由杜鹃鸟根据鸟巢质量按比例选择来改进算法。 这意味着杜鹃会选择鸟巢，而不是像算法的常规版本那样，将鸟蛋放入随机选择的鸟巢当中。 然而，这并没有改善展现随机选择鸟巢的现实结果。 也许这与自然界中发生的事情相呼应。 在更聪明的宿主情况下更换鸟蛋更加困难，故导致随机和统计不合理。

该算法的另一个特点是它的行为类似于对多变量函数的随机游走。 从视觉上，它看起来像白噪声或旧电视屏幕。 只有在迭代结束时，局部极值位置的坐标集中度才很明显。 我更愿意提供更清晰的参数“晶化”，就像蚁群算法一样。 故此，我们遇到了所有优化算法的常见问题，它没有通用的解。 许多经典和新颖算法的作者都试图解决这个问题。

问题的本质如下：不确定所研究函数的哪个优化参数具有优先级或强度，不知道每个参数在多大程度上，以及如何影响结果。 例如，有若干参数，算法已经找到了正确的参数，但究竟是哪个起决定作用则是未知的。 该算法将继续尝试更改所有这些，尽管仅更改几个就足以达到全局极值。 当涉及到具有数以万计，和数千个变量的函数时，问题会加剧。 变量越多，问题就越严重。 从视觉上，这看起来像屏幕上的白噪声。 

我已尝试至少部分解决这个问题。 如果事先不知道所研究函数的哪些参数应该改变，哪些应该保持不变，我们可以尝试以概率方式解决这个问题。 我们假设只需要更改所有参数的一部分，而不是同时更改所有参数。 PSO 算法的行为方式具有特征性。 随着优化函数的参数的增加，它的行为就像没有集中能力的云朵。 为此，我为算法引入了一个新参数，该参数设置坐标更改的概率，否则坐标将保持不变。

结果是... 有效！！！ 测试结果有所改善。 我想要达成的“晶化”出现在多变量函数上。

测试台结果如下所示：

2022.12.03 16:01:26.256    Test_AO_COAm (EURUSD,M1)    =============================
2022.12.03 16:01:27.511    Test_AO_COAm (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.918367945334852
2022.12.03 16:01:27.511    Test_AO_COAm (EURUSD,M1)    Score: 1.00000
2022.12.03 16:01:30.291    Test_AO_COAm (EURUSD,M1)    20 Skin's; Func runs 10000 result: 4.328327964103814
2022.12.03 16:01:30.291    Test_AO_COAm (EURUSD,M1)    Score: 0.85911
2022.12.03 16:01:59.306    Test_AO_COAm (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.3297901702583084
2022.12.03 16:01:59.306    Test_AO_COAm (EURUSD,M1)    Score: 0.14316
2022.12.03 16:01:59.306    Test_AO_COAm (EURUSD,M1)    =============================
2022.12.03 16:02:00.511    Test_AO_COAm (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.755200932219688
2022.12.03 16:02:00.511    Test_AO_COAm (EURUSD,M1)    Score: 0.99283
2022.12.03 16:02:03.566    Test_AO_COAm (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.5089243656052672
2022.12.03 16:02:03.566    Test_AO_COAm (EURUSD,M1)    Score: 0.28787
2022.12.03 16:02:35.468    Test_AO_COAm (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.08044934398920801
2022.12.03 16:02:35.468    Test_AO_COAm (EURUSD,M1)    Score: 0.04551
2022.12.03 16:02:35.468    Test_AO_COAm (EURUSD,M1)    =============================
2022.12.03 16:02:36.628    Test_AO_COAm (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 12.0
2022.12.03 16:02:36.628    Test_AO_COAm (EURUSD,M1)    Score: 1.00000
2022.12.03 16:02:39.628    Test_AO_COAm (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 2.9899999999999998
2022.12.03 16:02:39.628    Test_AO_COAm (EURUSD,M1)    Score: 0.24917
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.4244
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)    Score: 0.03537
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)    =============================
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)    All score for C_AO_COAm: 0.5125572342985216

我们能在可视化中清楚地看到“晶化”。 起初看起来像白噪声的屏幕被清除，坐标开始集中，集中中心变得移动：

结晶

Megacity 测试函数上的 COAm。 “晶化”的效果更加明显。

一方面，存在可变性，即动态搜索新区域的能力；而另一方面，已达到的极端坐标的澄清能力。 下面是带有明显“晶化”的蚁群算法动画，以便进行比较：

cristACO

  Forest 测试函数上的 ACOm。

测试结果

算法

说明

Skin

Forest

Megacity (离散)

最终结果

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

COAm

杜鹃优化算法

1.00000

0.85911

0.14316

0.99283

0.28787

0.04551

1.00000

0.24917

0.03537

0.51255778

ACOm

蚁群优化

0.98229

0.79108

0.12602

1.00000

0.62077

0.11521

0.38333

0.44000

0.02377

0.49805222

ABCm

人工蜂群 M

1.00000

0.63922

0.08076

0.99908

0.20112

0.03785

1.00000

0.16333

0.02823

0.46106556

ABC

人工蜂群

0.99339

0.73381

0.11118

0.99934

0.21437

0.04215

0.85000

0.16833

0.03130

0.46043000

GWO

灰狼优化器

0.99900

0.48033

0.18924

0.83844

0.08755

0.02555

1.00000

0.10000

0.02187

0.41577556

PSO

粒子群优化

0.99627

0.38080

0.05089

0.93772

0.14540

0.04856

1.00000

0.09333

0.02233

0.40836667

RND

随机

0.99932

0.44276

0.06827

0.83126

0.11524

0.03048

0.83333

0.09000

0.02403

0.38163222


杜鹃鸟搜索算法的一个优点是它的全局搜索采用飞行或 Levy 过程，而非标准的随机游走。 由于 Levy 飞行具有无限均值和方差，因此 COA 可以比标准高斯过程算法更有效地探索搜索空间。 Levy 飞行：一种随机游走过程，其特征是从具有幂律尾部的概率密度函数中选择的一系列瞬时跳跃。

目前，该算法在单个测试中明显优于其它算法，并且在其它“学科”中也不遑多让。 具有 1000 个参数的 Megacity 离散函数具有出色的结果，这令杜鹃鸟搜索成为交易者任务的绝佳工具（在大多数情况下是离散的）。 具有 1000 个参数的 Skin 函数的优秀（但不是最佳）结果，令我们有理由断言该算法特别适合训练神经网络和一般机器学习。

优点:
1. 高速。
2. 多功能性。 该算法适用于各种优化问题。 3. 不光死盯局部极值的能力。
4. 平滑和离散函数的高度收敛性。
5. 可扩展。

缺点:
1. 多种设置。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11786

附加的文件 |
下载ZIP
26_The_world_of_AO_8COAn.zip (57.59 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
MQL5 酷宝书 — 服务 MQL5 酷宝书 — 服务
本文讲述了服务的多功能性 — 不需要绑定图的 MQL5 程序。 我还会重点介绍服务与其它 MQL5 程序的区别，并强调开发人员使用服务的细微差别。 作为示例，为读者提供了各种任务，涵盖了可以作为服务实现的各种功能。
DoEasy. 控件 (第 28 部分): 进度条控件中的柱线样式 DoEasy. 控件 (第 28 部分): 进度条控件中的柱线样式
在本文中，我将开发进度条控件的柱线显示样式和说明文本。
神经网络变得轻松（第三十五部分）：内在好奇心模块 神经网络变得轻松（第三十五部分）：内在好奇心模块
我们继续研究强化学习算法。 到目前为止，我们所研究的所有算法都需要创建一个奖励政策，从而令代理者能够每次从一个系统状态过渡到另一个系统状态的转换中估算其每个动作。 然而，这种方式人为因素相当大。 在实践中，动作和奖励之间存在一些时间滞后。 在本文中，我们将领略一种模型训练算法，该算法可以操控从动作到奖励的各种时间延迟。
构建自动运行的 EA（第 08 部分）：OnTradeTransaction 构建自动运行的 EA（第 08 部分）：OnTradeTransaction
在本文中，我们将目睹如何利用事件处理系统快速有效地处理与订单系统相关的问题。 配合这个系统，EA 就能更快地工作，如此它就不必持续不断地搜索所需的数据。