MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
人工协作搜索算法 (ACS)

人工协作搜索算法 (ACS)

MetaTrader 5 — 示例 | 3 十二月 2024, 08:59
202 0
Andrey Dik
Andrey Dik

内容

1. 概述
2. 算法实现
3.测试结果


1. 引言

自然界是科学家和工程师寻求创新解决方案的无穷灵感源泉。其中一个引人注目的现象是互利共生——不同物种之间的一种互利互惠的生物性的相互作用。参与互利共生关系的生物体致力于从这种相互作用中获得相互益处，旨在促进种群的发展和多样性。为了理解这一点，我将举出几个生物体之间互利共生（共生）关系的例子，在这些关系中，它们相互受益：

1. 开花植物与传粉者：

  • 植物产生花蜜和其他奖励来吸引如昆虫、鸟类和蝙蝠等传粉者。
  • 反过来，传粉者将花粉从一朵花传到另一朵花上，从而促进植物的繁殖。

2. 真菌与植物根系（菌根）：

  • 真菌侵入植物根系并从中获取有机化合物（光合作用的产物）。 
  • 反过来，真菌扩大了根系的吸收面积，增加了植物对水分和矿物质的获取。

3. 白蚁与共生细菌：

  • 白蚁肠道内含有共生细菌，这些细菌帮助它们消化纤维素，即木材的主要成分。
  • 细菌从白蚁那里获取营养，而白蚁则获得了消化纤维的能力。

这些例子展示了生物体如何相互作用以获得互利并增加其生存机会。

ACS算法也从共享共同环境的真社会性超生物体的迁徙行为中汲取灵感。以下是一些此类真社会性超生物体迁徙行为的例子：

1. 蚁群：

  • 在群体迁徙期间，蚂蚁携带幼虫、蛹和其他巢穴的重要元素一同迁徙。

2. 蜂群：

  • 在蜂群聚集时，蜂群可能会暂时从蜂巢迁出，以在别处建立新的蜂群。
  • 在蜂群迁徙期间，蜜蜂携带蜂王、幼虫和必要的蜂蜜供应以建立新巢穴。

这些例子的共同特征是，如蚂蚁、白蚁、蜜蜂和黄蜂等真社会性超生物体能够集体迁移其群体以应对环境变化或资源枯竭这种迁徙能力使它们能够适应不断变化的环境条件，并确保整个群体的生存。生活在同一环境中的两个完全群居的生物体，互利共生和合作的生物特性为ACS算法提供了灵感。在该算法中，栖息地的概念对应于与相应优化问题相关的搜索空间的概念。

从概念上讲，ACS算法将相应问题的随机解视为迁移到更肥沃觅食区域的人工超生物体。两个主要超生物体，称为α 和 β，包含与种群大小相等的人工子超生物体。种群大小对应于这些子超生物体中的个体数量。在协同进化过程中， α 和 β 超生物体作为捕食者和猎物相互作用，使用两个动态种群来高效地探索搜索空间并找到数值优化问题的全局最优解。

ACS算法由Pinar Civicioglu于2013年提出。它首先使用两个包含置信区域内候选解的基种群。然后，该算法通过使用随机步骤和二进制矩阵从初始α 和 β种群中映射值来创建两个新种群，即捕食者和猎物。此外，还根据捕食者和猎物种群中的值计算第五个种群。该过程涉及在指定次数的迭代中更新初始种群，并从这两个种群中选取最佳解。

两个在生物上相互作用的人工超生物体的迁徙和进化，以达到目标函数的全局极值，以及与自然中合作行为类似的过程，是ACS在数值优化问题中高性能的关键。这种在种群之间生物激励相互作用的独特方法使ACS算法能够实现令人印象深刻的收敛速度和高解精度。由于其能够快速准确地找到最优解，ACS已被证明是解决广泛数值优化问题的强大工具。

在本文中，我将详细描述ACS算法背后的概念，并展示其卓越的能力。读者将深入了解如何将来自生物界的灵感成功地应用于能够高效解决复杂问题的高级优化算法中。

2. 算法实现

人工写作搜索算法（ACS）的工作原理如下：

1. 初始化。设定了种群大小“popSize”、变量数量“N”、变量下界“XLow”和上界“XHi”，以及生物交互概率“Probab”。接着生成初始的“A”和“B”种群位置，并计算它们的“YA”和“YB”适应度值。

2. 循环迭代。在每次迭代中执行以下步骤：

  • 选择。在当前迭代中，会确定是从A种群还是B种群中选择一组个体作为“捕食者”。
  • 打乱“猎物”位置。将选定集合中的个体位置进行打乱。
  • 变异。使用随机生成的R缩放因子来更新个体位置。“捕食者”利用“猎物”决策向量的信息进行变异。
  • 填充二进制矩阵M。创建了M二进制矩阵，用于确定在当前迭代中哪些变量将被更新。
  • 更新智能体位置。智能体位置会根据M矩阵中的值进行更新。如果M中的值为1，则更新对应的变量。
  • 边界控制。如果更新后的位置在指定边界之外，则对其进行调整。
  • 更新选择。在此阶段，最佳解决方案被保存以供下一次算法迭代使用。
  • 全局最佳解决方案更新。如果发现更好的解决方案，则将其保存。

3. 返回结果。在算法结束时，返回全局最佳解决方案及其对应的值。

该算法包含一些独特的运算符，如“猎物”洗牌运算符和变异运算符，这些运算符涉及使用M二进制矩阵。

M矩阵是一个二维数组，具有“popSize”行（种群中的候选者数量）和“N”列（每个候选者的变量数量）。矩阵的每个元素可以是0或1。M矩阵用于确定哪些候选者将被选中以在种群中进一步更新。矩阵中的0和1值表示基于随机Rand值和Probab交互概率，对应的候选者是否会被选中进行更新。
M矩阵有助于调节种群中候选者的更新选择。因此，M矩阵在种群进化和ACS中寻找最优解决方案中发挥着关键作用。

让我们以伪代码的形式详细审视ACS算法的每一步：

1. 初始化：
   - 设置以下参数：
       - popSize - 种群大小
       - N - 变量数量
       - MaxIter - 最大迭代次数
       - XLow - 变量的下边界
       - XHi - 变量上边界
       - Probab - 生物间相互作用的概率
   - Rand - 返回在(0, 1)范围内均匀分布数字的函数
   - GlobMax 被负DBL_MAX初始化

2. 主循环：
- 对于种群的每个元素（I = 1到popSize）：
- 对于每个变量（J = 1到N）：
- 在范围[XLow(J), XHi(J)]内计算初始值A(I,J)和B(I,J)
- 计算目标函数的初始值YA(I) = Fx(A(I,:))和YB(I) = Fx(B(I,:))
- 开始主循环，迭代次数为(Iter = 1到MaxIter)

3. 选择：
- 我们随机选择A或B作为捕食者：
- 如果Rand < 0.5，则Predator=A，Ypred=YA，Key=1
- 否则，Predator=B，Ypred=YB，Key=2
- 我们随机选择A或B作为猎物：
- 如果Rand < 0.5，则Prey=A
- 否则，Prey=B
- 对猎物进行随机洗牌
- 计算R参数：
- 如果Rand < 0.5，则R = 4 * Rand * (1 - Rand) - 否则，R = 1/exp(4 * Rand)
- 创建一个popSize x N的M二进制矩阵，初始值全为1
- 以Probab概率随机将M矩阵的某些元素设置为0
- 如果Rand < Probab，随机将M矩阵的某些元素设置为0或1
- 对于M矩阵的每一行，如果元素之和为N，则随机选择一个元素并将其设置为0

4. 变异：
- 计算新值 X = Predator + R * (Prey - Predator)
- 对于种群的每个元素（I = 1到popSize）和每个变量（J = 1到N）：
- 如果M矩阵的对应元素大于0，则X(I,J) = Predator(I,J)
- 如果X(I,J)不在范围[XLow(J), XHi(J)]内，则X(I,J)被设置为该范围内的随机值

5. 更新选择：
- 对于种群的每个元素（I = 1到popSize）：
- 如果Fx(X(I,:)) < Ypred(I)，则Predator(I,:) = X(I,:)且Ypred(I) = Fx(X(I,:))
- 如果Key = 1，则A = Predator且YA = Ypred，否则B = Predator且YB = Ypred
- Ybest = min(Ypred)
- Ibest = 与Ybest对应的Predator行索引
- 如果Ybest > GlobMax，则GlobMax = Ybest且GlobMax的值设置为Predator(Ibest,:)

6. 返回结果：
- 返回GlobMax 和 GlobMaxX向量

接下来，我们转向ACS算法实现的描述。我们将使用最简单的结构“S_D ”来描述种群（算法中有五个这样的结构）：

  • c [] 是一个用于存储坐标（任务的优化参数）的数组
  • Init (int coords) - 方法使用ArrayResize函数将c数组的大小更改为coords中指定的大小（坐标的数量）

一般来说，这个结构用于创建一个包含实数数组的对象。Init方法用于调整数组的大小。

//——————————————————————————————————————————————————————————————————————————————
struct S_D
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    double c [];
};
//——————————————————————————————————————————————————————————————————————————————

为了描述M矩阵，我们创建了与S_D字段类型结构不同的S_C结构：

  • c[] - 用于存储矩阵符号“0”和“1”的数组
  • Init (int coords) - 方法使用ArrayResize函数将c数组的大小更改为coords中指定的大小
//——————————————————————————————————————————————————————————————————————————————
struct S_C
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    char c [];
};
//——————————————————————————————————————————————————————————————————————————————

该算法将被描述为从C_AO基类派生的C_AO_ACS类 ，并包含以下字段：

  •  ~C_AO_ACS () { } - 类析构函数，在删除类对象时被调用。在这种情况下，析构函数是空的。
  • C_AO_ACS () - 类构造函数，用于初始化类的数据成员，调整params数组的大小，并为算法参数分配默认值。
  • SetParams () - 方法根据params数组中的值设置popSize（种群大小）和bioProbab（生物交互概率）。
  • Init () - 方法接受多个参数并返回一个布尔值。 
  • Moving ()和Revision ()是包含算法主要逻辑的方法。
  • bioProbab - 数据成员，用于存储生物交互的概率。
  • S_D A [], S_D B [], S_D Predator [], S_D Prey [], S_C M [], double YA [], double YB [], double Ypred [], int Key, int phase - 类的私有数据成员。
  • ArrayShuffle () - 私有方法，用于打乱数组元素。 
//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACS () { }
  C_AO_ACS ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search";
    ao_link = "https://www.mql5.com/ru/articles/15004";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_D A              [];
  S_D B              [];
  S_D Predator       [];
  S_D Prey           [];

  S_C M              [];

  double YA          [];
  double YB          [];
  double Ypred       [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

接下来，展示C_AO_ACS类的Init方法。该方法用于初始化类对象：

  • Init () - 方法声明。它接受四个参数：最小搜索范围"rangeMinP"，最大搜索范围"rangeMaxP"，搜索步长"rangeStepP"，以及默认值为0的迭代次数"epochsP"。
  • if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - 调用StandardInit函数，该函数执行基类的标准初始化。如果StandardInit 返回false，则Init方法立即终止并返回false。
  • 在循环for (int i = 0; i < popSize; i++)中，使用Init方法初始化A、B、Predator、Prey和M数组的每个元素。
  • ArrayResize (YA, popSize)等类似行将YA、YB和Ypred数组的大小更改为popSize。
  • ArrayInitialize (YA, -DBL_MAX)等类似行使用-DBL_MAX值初始化YA、YB和Ypred数组的所有元素。
  • 在嵌套的for循环中，使用给定范围内的随机值初始化A和B数组中每个对象的每个c元素。
  • phase = 0将'phase'设置为0。

原始算法并没有将逻辑划分为不同的阶段。为了同我所有种群算法所采用的风格保持一致，我不得不分阶段来实现这个算法。这是必要的，因为ACS需要使用预先计算的适应度来评估А和B种群中的个体。为了在方法中按顺序执行这些操作，为此我进行了分段。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACS::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,         popSize);
  ArrayResize (B,         popSize);
  ArrayResize (Predator,  popSize);
  ArrayResize (Prey,      popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A         [i].Init (coords);
    B         [i].Init (coords);
    Predator  [i].Init (coords);
    Prey      [i].Init (coords);

    M         [i].Init (coords);
  }

  ArrayResize (YA,    popSize);
  ArrayResize (YB,    popSize);
  ArrayResize (Ypred, popSize);

  ArrayInitialize (YA,    -DBL_MAX);
  ArrayInitialize (YB,    -DBL_MAX);
  ArrayInitialize (Ypred, -DBL_MAX);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
    }
  }

  phase = 0;
 
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACS类的Moving方法实现了算法中个体移动的基本逻辑。该方法执行多个操作，包括数组复制、选择、排列、变异和交叉。

  • if (phase == 0) - 在此阶段，复制A种群中的个体。
  • if (phase == 1) - 在此阶段，返回А种群中个体的适应度，并复制B种群中的个体。
  • if (phase == 2) - 在此阶段，返回B种群中个体的适应度，并在之后执行整个算法的后续逻辑。 
  • Selection - 该代码块执行选择操作。根据随机数，将A或B数组复制到Predator数组，同时将相应的值复制到Ypred数组。
  • Prey Permutation - 在此处执行Prey数组元素的排列。
  • R - 声明了一个变量，该变量随后根据随机数被初始化为两个可能值中的一个。
  • 用1填充二进制矩阵M - 在这里，M二进制矩阵被填充为全1。
  • 对矩阵M的额外操作 - 该代码块对M矩阵执行额外操作，包括根据随机数和生物相互作用概率bioProbab将其中的一些元素更改为0或1。
  • 变异 - 该代码块执行变异操作，其中a数组的元素根据Predator（捕食者）和Prey（猎物）数组的元素以及R值进行改变。
  • 交叉 - 该代码块执行交叉操作，其中a数组的一些元素被Predator数组的元素替换。
  • 边界控制 - 该代码块执行边界控制，其中a数组中超出指定优化参数范围的元素被替换为该范围内的随机值。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) YA [i] = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) YB [i] = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, A [i].c);
    }

    ArrayCopy (Ypred, YA);
    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, B [i].c);
    }

    ArrayCopy (Ypred, YB);
    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, A [i].c);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, B [i].c);
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
      else
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }
 
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACS类的Revision方法。该方法执行一系列操作：数组的排序和反向复制，以及更新全局最优解的最佳值。

  • if (phase < 3) return - 在准备种群以进行进一步交互的所有三个阶段完成之前，不执行该方法的基本逻辑。
  • 选择更新 - 该代码块更新个体的选择。对于每个a数组中的个体，我们检查其f适应度值是否超过Ypred数组中相应的值。
  • if (Key == 1)和else - 在这些代码块中，根据Key的值，Predator数组的元素从A或B数组复制，同时相应的Ypred值从YA或YB数组复制。
  • ArraySort(Ypred);ArrayReverse(Ypred, 0, WHOLE_ARRAY) - 包含适应度值的Ypred数组进行排序，然后反转，以便值按降序排列。
  • Ybest = Ypred[0]; int Ibest = ArrayMaximum(Ypred) - 在这里，Ybest是Ypred中的最大值，而Ibest是该最大值的索引。
  • if (Ybest > fB) - 如果Ybest超过当前的fB，则更新fB，同时从Predator数组复制相应的a和cB数组元素。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Ypred [i])
    {
      ArrayCopy (Predator [i].c, a [i].c);
      Ypred [i] = d;
    }
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (A [i].c, Predator [i].c);
    }

    ArrayCopy (YA, Ypred);
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (B [i].c, Predator [i].c);
    }

    ArrayCopy (YB, Ypred);
  }

  ArraySort (Ypred);
  ArrayReverse (Ypred, 0, WHOLE_ARRAY);
  double Ybest = Ypred [0];
  int Ibest = ArrayMaximum (Ypred);

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACS类的ArrayShuffle方法用于对数组中的元素进行随机洗牌。

  • for (int i = n - 1; i > 0; i--) - 该循环以逆序遍历arr数组，从最后一个元素开始。
  • j = MathRand() % (i + 1) - 在这里，j是一个从0 到i的随机数（包括0和i）。
  • tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp - 这几行代码执行arr[i]和arr[j]元素的交换。

结果，arr数组的元素被随机洗牌。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 测试结果

该算法的独特性已经通过所进行的测试得到验证。此算法在种群数量减少时仍能获得优异结果的能力是独一无二的。随着迭代次数的增加，该算法在单个测试函数上可以达到100%的收敛率，这一特点使其与其他算法区分开来，因为对于其他算法来说，无论适应度函数运行次数如何增加，都仍然无法获得收敛的机会。此特征表现为该算法具有避免陷入局部“陷阱”的能力。

让我们看看算法结果如何随着种群大小的变化而变化。我通常在种群中使用平均50个个体。然而，在测试过程中，该算法在种群数量较低时就开始表现出不错的结果。

在种群中有10个个体且适应度函数运行次数保持在10,000次的情况下，该算法达到了49.97%的结果。

ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8213829114300768
25 Hilly's; Func runs: 10000; result: 0.5418951009344799
500 Hilly's; Func runs: 10000; result: 0.2811381329747021
=============================
5 Forest's; Func runs: 10000; result: 0.9750514085798038
25 Forest's; Func runs: 10000; result: 0.5078176955906151
500 Forest's; Func runs: 10000; result: 0.20112458337102135
=============================
5 Megacity's; Func runs: 10000; result: 0.736923076923077
25 Megacity's; Func runs: 10000; result: 0.31446153846153846
500 Megacity's; Func runs: 10000; result: 0.11721538461538572
=============================
All score: 4.49701 (49.97%)

在种群中有3个个体且适应度函数运行次数保持在10,000次的情况下，该算法达到了55.23%的结果。

ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8275253778390631
25 Hilly's; Func runs: 10000; result: 0.6349216357701294
500 Hilly's; Func runs: 10000; result: 0.29382093872076825
=============================
5 Forest's; Func runs: 10000; result: 0.9998874875962974
25 Forest's; Func runs: 10000; result: 0.6985911632646721
500 Forest's; Func runs: 10000; result: 0.2132502183011688
=============================
5 Megacity's; Func runs: 10000; result: 0.7507692307692307
25 Megacity's; Func runs: 10000; result: 0.4270769230769231
500 Megacity's; Func runs: 10000; result: 0.1252615384615397
=============================
All score: 4.97110 (55.23%)

在种群中有1个个体且适应度函数运行次数保持在10,000次的情况下，该算法达到了58.06%的结果。

ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7554725186591347
25 Hilly's; Func runs: 10000; result: 0.7474431551529281
500 Hilly's; Func runs: 10000; result: 0.3040669213089683
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999993218
25 Forest's; Func runs: 10000; result: 0.888607840003743
500 Forest's; Func runs: 10000; result: 0.2241289484506152
=============================
5 Megacity's; Func runs: 10000; result: 0.6907692307692308
25 Megacity's; Func runs: 10000; result: 0.4818461538461539
500 Megacity's; Func runs: 10000; result: 0.1332153846153859
=============================
All score: 5.22555 (58.06%)

您可能会问，在只有一个个体的种群中如何进行交互。但您可能还记得，该算法使用了五个种群，并且这些种群中的个体之间会发生交互。尽管个体数量非常少，但该算法仍然能够保持种群的多样性，并且不会出现“瓶颈”效应。

在可视化图像中，我们可以看到没有任何聚类效应，并且这些智能体似乎表现出混乱的行为。智能体会进入搜索空间的区域，即使那里没有明确的搜索方向。在“Forest”和“Megacity”这两个特征中，这一点尤为明显，因为这些特征包含大片平坦且变化很小的区域。

Hilly

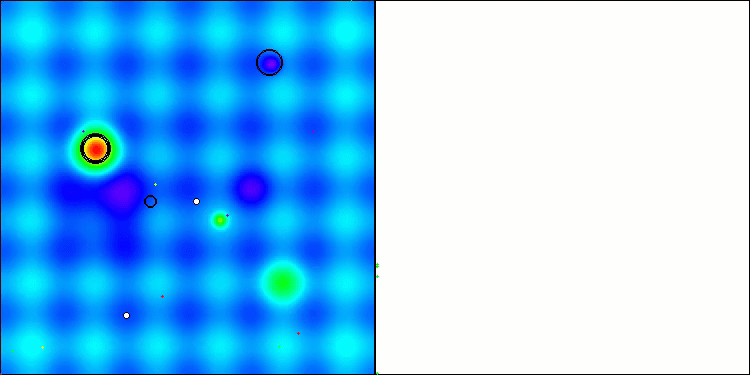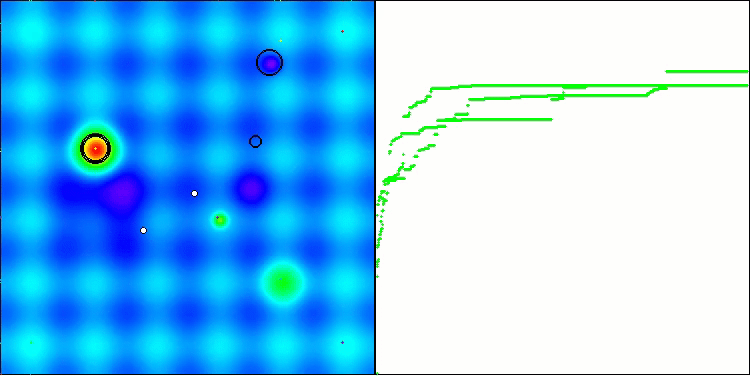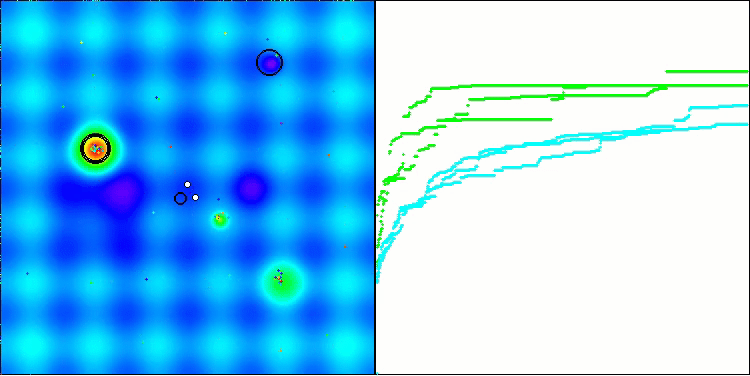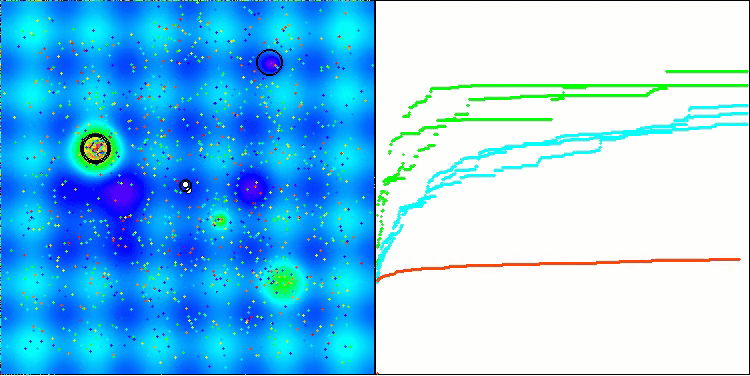
  在Hilly测试函数上的ACS

Forest

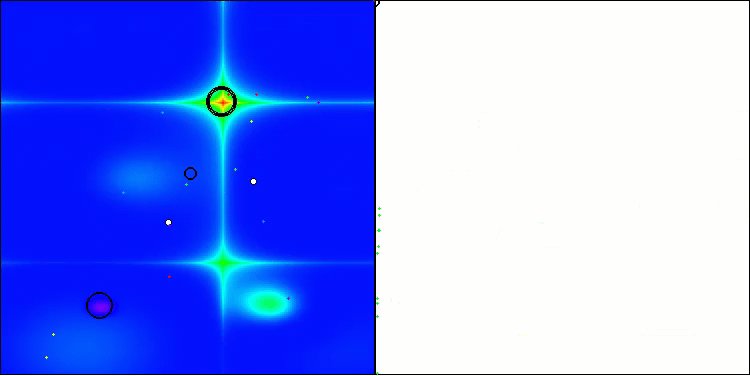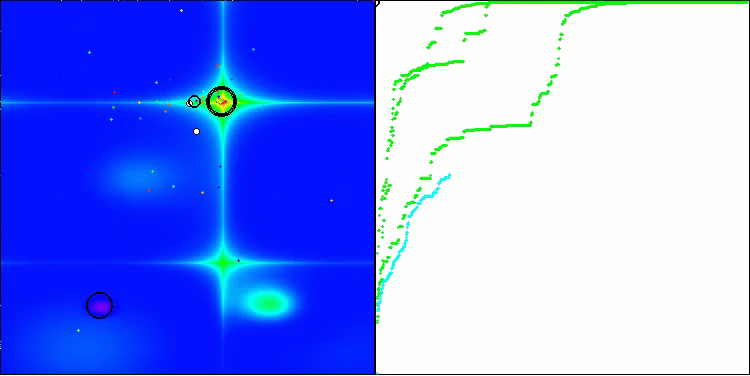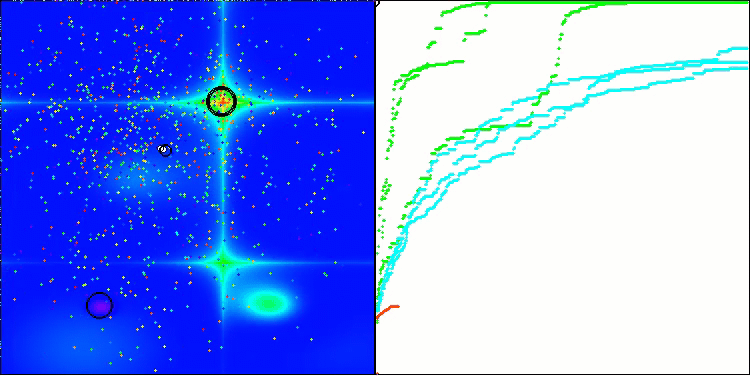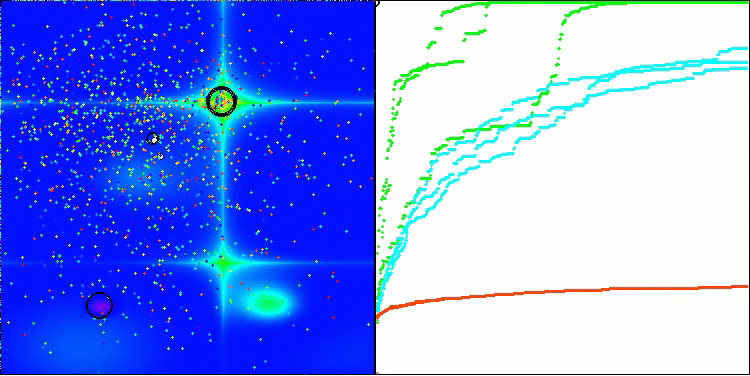
  在 Forest测试函数上的ACS

Megacity

  在Megacity测试函数上的ACS

基于测试结果，这一算法排名第八。ACS在Forest和Megacity这两个函数上表现尤为出色。

#
AO
说明
Hilly
Hilly 最终
Forest
Forest 最终
Megacity (离散)
Megacity 最终
最终结果
最大 %
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA 二进制遗传算法 0.99989 0.99518 0.42835 2.42341 0.96153 0.96181 0.32027 2.24360 0.91385 0.95908 0.24220 2.11512 6.782 75.36
2 CLA 密码锁算法 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
4 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
5 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
6 ESG 社会群体的演化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
7 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
8 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
9 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
10 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
11 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
12 HS 和声搜索算法 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
13 SSG 树苗播种和生长算法 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
14 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
15 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
16 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
17 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
18 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
19 MEC 维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
20 IWO 入侵性杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
21 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
22 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
23 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
24 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
25 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
26 GSA 重力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
27 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
28 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
29 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
30 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
31 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
32 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
33 Boids boids算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
34 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
35 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
36 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
37 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
38 GWO 灰狼优化器 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
39 CSS 电荷系统搜索算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
40 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


总结

人工协同搜索（ACS）算法已被证明是一种有趣的优化方法，这体现在它使用多个智能体种群相互交互，从而提供多样性并避免陷入局部最优解；同时，它还使用特殊算子，如“猎物”的洗牌操作和基于二进制矩阵的变异。后者赋予了算法独特性和在种群规模非常小（每个种群中只有一个个体，总共五个种群）的情况下仍能实现高成果的能力。这种原创的方法和能够处理小种群的能力（这强调了其抗种群退化性）使得ACS成为一种真正有前景的优化算法。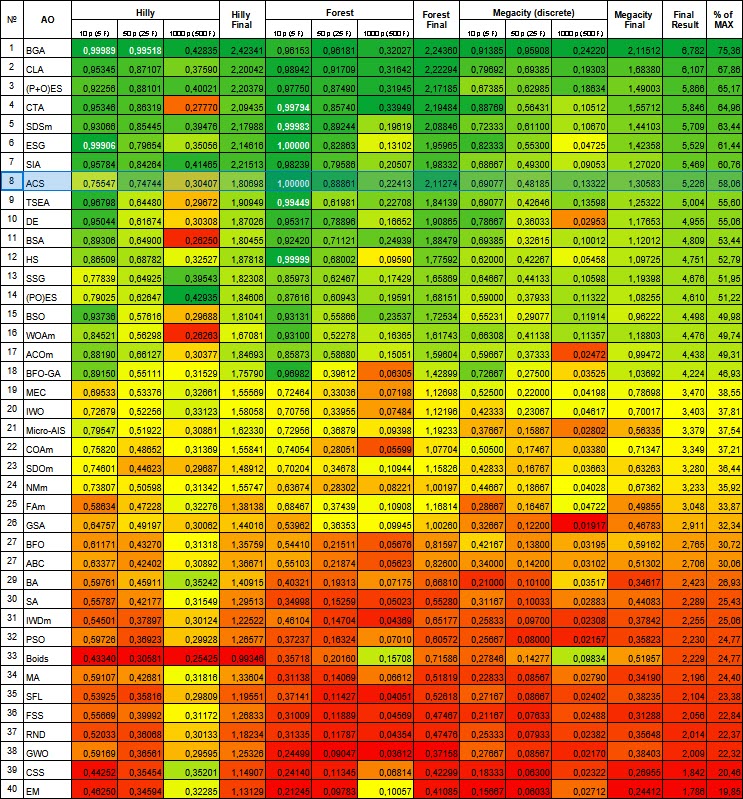

tab

图例 1. 根据相关测试结果，算法的颜色渐变中，结果大于等于0.99的将以白色高亮显示。

图表

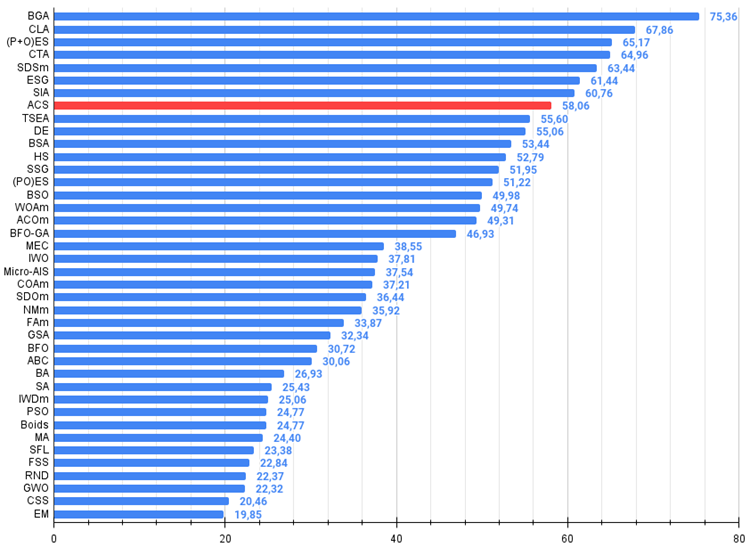
图例 2. 算法测试结果的直方图（标尺从 0 到 100，越多越好，

其中 100 是理论上的最大可能结果，附件提供了一个计算评级表格的脚本）。


ACS算法优缺点：

优势：

  1. 外部参数少（仅有一个）。
  2. 在各种类型的函数上都能表现出良好的收敛性。

缺点：

  1. 在低维函数上，算法的结果呈现出较大的离散性或分散性。

本文附带了一个文档，其中包含了算法代码的当前版本。文章作者不对典型算法描述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/15004

附加的文件 |
下载ZIP
ACS.zip (26.11 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
开发多币种 EA 交易（第 8 部分）：负载测试和处理新柱 开发多币种 EA 交易（第 8 部分）：负载测试和处理新柱
随着我们的进步，我们在一个 EA 中使用了越来越多的同时运行的交易策略实例。让我们试着弄清楚在遇到资源限制之前，我们可以得到多少实例。
使用图表可视化交易（第一部分）：选择分析时段 使用图表可视化交易（第一部分）：选择分析时段
在这里，我们将从头开始编写一个脚本，以简化卸载交易截图用于分析交易入场点的过程。能够方便地将所有关于单个交易的必要信息展示在一个图表上，并且该图表可以根据不同时间周期绘制。
最负盛名的人工协作搜索算法的改进版本（AXSm） 最负盛名的人工协作搜索算法的改进版本（AXSm）
在这里，我们将探讨 ACS 算法的演变：三种修改旨在改善收敛特性和算法效率。对最领先的优化算法之一进行修订改版。从数据矩阵修改到种群形成的革命性方法。
开发回放系统（第 46 部分）：Chart Trade 项目（五） 开发回放系统（第 46 部分）：Chart Trade 项目（五）
厌倦了浪费时间搜索应用程序工作所需的文件吗？在可执行文件中包含所有内容如何？这样，你就不用再去找东西了。我知道很多人都使用这种分发和存储形式，但还有一种更合适的方式。至少在可执行文件的分发和存储方面是这样。这里将介绍的方法非常有用，因为您可以将 MetaTrader 5 本身用作优秀的助手，也可以使用 MQL5。此外，它并不难理解。