MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
人工喷淋算法（ASHA）

人工喷淋算法（ASHA）

MetaTrader 5 — 测试者 |
170 0
Andrey Dik
Andrey Dik

目录

  1. 概述
  2. 算法的实现
  3. 测试结果


概述

随着当今世界数据量的快速增长，任务变得越来越复杂和能源密集，对有效优化方法的需求比以往任何时候都更加迫切。具有高收敛性和处理速度的元启发式算法为解决从金融市场到科学研究等各个领域的各种问题开辟了新的视野。

数据处理的速度和由此产生的解决方案的质量在项目的成功实施中起着关键作用。在严格的时间限制条件下，每个时刻都可能至关重要，元启发式算法允许实现以前似乎无法实现的结果。与传统的数值方法相比，它们不仅可以快速处理大量信息，还有助于找到更好的解决方案。

节约资源是优化时需要考虑的另一个重要方面。在计算能力有限的情况下，这种算法需要更少的时间和内存，这在云计算中尤其有价值。算法对不断变化的条件的适应性和快速响应新数据的能力使其几乎成为动态系统的理想选择。这使我们能够保持解决方案的相关性，并提高在实际情况下解决问题的效率。

通过比较不同算法的特性，如收敛速度、解质量和抗陷入局部极值，可以选择质量最高的算法，这反过来又促进了创新和全新方法的发展，这些方法往往受到大自然的启发，是优化领域的重要一步。

人工淋浴算法（ASHA）是一种为解决一般优化问题而开发的新型元启发式方法。该算法基于对理想场地上人为控制设备分配的水的流动和积聚进行建模。ASHA 模拟田野上的水分布（淋浴），其中水代表资源单位，田野是搜索空间。该算法使用流和累积原理来找到无约束问题的最优解。人工淋浴算法（ASHA）是由一组作者开发的：Ali J.、M. Saeed，NAChaudhry、M. Luqman 和 MFTabassum 并于 2015 年出版。


算法的实现

该方法基于以下原则：

  1. 理想的区域。搜索空间是一个理想区域，其中水流动时没有阻力，并且渗透只发生在最低点。
  2. 没有外界因素。没有蒸发，没有降雨，也没有水流。
  3. 喷雾器的可用性。搜索空间的每个部分都在现场上方喷雾器的范围内。
  4. 恒定量的水。有多余的水，在整个迭代过程中，封闭系统中的水量保持不变。
  5. 水的运动。每个单位的水都有下坡的概率趋势。

ASHA（人工淋浴算法）的逐步描述。

算法参数：

  • f — 要最小化的目标函数
  • R*n — n 维搜索空间
  • K — 迭代计数器中的当前位置
  • m — 水单元数量（搜索代理）
  • F — 水流量
  • δ — 抵抗水平（渗透阈值）
  • ρ₀ — 初始概率
  • β — 概率变化率
  • M — 最大迭代次数

 算法步骤：

1.初始化：

    设置初始值 ρ = ρ₀
    创建 m 个单位的水并将它们随机放置在 R*n 搜索空间中

2. 景观评估：对于每单位水，我们计算 f 目标函数在其当前位置的值

3.主循环（重复 m 次）：对于每单位水 i（1 ≤ i ≤ m）：

   a）选择一个随机数 r_i∈（0,1）
   b) 如果 r_i < ρ：
       选择当前位置下方的随机 x_lower 位置
       生成一个随机向量 s ∈ (0, 1)*n
       计算新位置：
          x_new = x_old + F × (s ∘ (x_lower x_old))
          其中 ∘ 表示元素乘法
       如果 x_new 的级别低于 x_old：
          接受新位置
       否则：
          生成一个随机数 r ∈ (0, 1)
          找到所有水体单元中最低的位置 x_lowest
          计算新位置：
             x_new = x_old + F × r × (x_lowest x_old)
   c) 检查渗透情况：
      如果一单位水克服了 δ 的阻力水平：
       在随机位置创建一个新的水单元
   d) 与最低位置的比较：
       找到目标函数值最低的水单元
       如果当前水单元的值较低，则交换它们
   e) 更新概率 ρ = max((M - K) / (β × M), ρ₀)

4.完成：

    找到目标函数值最小的水单元
    我们将其位置返回作为找到的最佳解决方案

算法解释：

1.该算法模拟了田野喷淋的过程，其中每个单位的水代表一个搜索代理。
2.搜索空间被视为景观区域，其中目标函数的较低值对应于地形的较低点。
3.水单元倾向于“流向”景观的较低点，这对应于对目标函数最小值的搜索。
4.参数 ρ 控制空间探索（较大的 ρ 值）和找到的解决方案的利用（较小的 ρ 值）之间的平衡。
5.渗透机制通过在随机位置创建新的水单元来避免陷入局部最小值。
6.与最低位置的比较和交换可确保保留找到的最佳解决方案。
7.动态更新 ρ 允许算法随着迭代次数的增加逐渐从探索转向开发。

该算法使用水流类比进行优化，其中水（搜索代理）寻求找到景观中的最低点（目标函数的最小值）。

据作者介绍，该算法的主要优点是：

  1. 由于水的随机运动，能够探索较大的解空间。
  2. 使用渗透机制避免局部最小值的能力。
  3. 由于 ρ 概率的动态变化而产生的自适应行为。

让我们详细考虑该算法使用的所有方程。

1.在概率满足 “ρ” 的情况下更新位置的方程式： x_new = x_old + F × (s ∘ (x_lower - x_old)) ，其中：

  • x_new — 水单元的新位置
  • x_old — 水单元的当前位置
  • F — 水流量（算法参数）
  • s — 范围内的随机向量（0，1）
  • x_lower — 随机选择当前位置下方的位置
  • ∘ — 元素乘法运算符

该方程模拟了水沿斜坡向下的运动。随机向量 s 为运动添加了随机性元素，而 F 控制步长。

2.替代公式，在 ρ 概率失败的情况下，位置更新： x_new = x_old + F × r × (x_lowest - x_old) ，其中：

  • r — 范围内的随机数（0，1）
  • x_lowest — 目标函数值最低的位置

当基本公式不能带来改进时，使用该方程。它将水单元导向全局最小值。

从这些方程式可以看出，水总是倾向于向低于其当前位置的位置移动。如果算法只实现到这一步，它将不可避免地陷入局部极值。

3.概率更新方程， ρ = max ((M - K) / (β × M), ρ₀) ，其中：

  • ρ — 当前水运动的概率
  • M — 最大迭代次数
  • K — 当前迭代次数
  • β — 概率变化率
  • ρ₀ — 初始概率

该方程逐渐降低了水向随机选择的较低位置移动的概率，并增加了向全局最小值移动的概率。这使得算法能够从探索空间转向完善找到的解决方案。

4.渗透条件，如果 f (x_current) < δ ，则创建一个新的水单元，其中： 

  • f (x_current) — 当前位置的目标函数值
  • δ — 抵抗水平（渗透阈值）

当当前水单元找到足够低的点时，这种情况允许在随机位置创建新的水单元。这是为了避免陷入局部最小值。

5.比较位置如果 f (x_i) < f (x_lowest) ，则交换 x_i 和 x_lowest ，其中：

  • f (x_i) — 第 i 个水单元的目标函数值
  • f (x_lowest) — 目标函数的最小找到值

上述方程构成了 ASHA 算法的基础。

  1. 位置更新方程模拟了水沿斜坡向下的运动。随机元素（s 或 r）允许探索解决方案空间的不同区域，从而增加了搜索的多样性。
  2. 随着每次新迭代的增加，使用概率增加的替代位置更新方程，以确保全局解的细化程度在所有迭代中都会增加。
  3. ρ 概率更新方程在探索和利用之间提供了平衡。在算法开始时，向景观中随机选择的较低位置移动的概率很高，这鼓励了对空间的广泛探索。随着迭代的进行，概率会降低，从而对有前景的领域进行更彻底的探索。
  4. 当找到足够好的解决方案时，渗透条件允许算法从新的随机位置“重新开始”搜索。这有助于避免陷入局部最小值。
  5. 比较位置可确保算法始终“记住”找到的最佳解决方案，并使用它来指导进一步的搜索。

因此，该算法首先试图通过向随机底部点移动来找到更好的位置。如果失败，它会尝试向找到的全局最佳位置移动。这在局部搜索和解决方案空间的全局探索之间提供了平衡。

ASHA 算法中的渗透原理可能乍一看并不明显。让我们一起来仔细看看吧：

  1. 我们有 δ （delta）参数，它被称为抵抗水平或渗透阈值。
  2. 在每次迭代中，对于每个单位的水，我们都会检查它是否变得“太好”，也就是说，它是否已经低于 δ 的水平。
  3. 如果给定单位水的目标函数值小于 δ，则认为水已“泄漏”或“渗透”到地下。
  4. 在这种情况下，我们通过将水放置在搜索空间中的随机位置来“创建”一个新的水单元。

形式上可以写成如下形式：如果 f (x_i) < δ，则 x_i = random_position () ，其中 f (x_i) 是第 i 个区域单元的目标函数值， x_i — 第 i 个水单元的位置。

该机制背后的想法是避免所有水单元陷入单一局部最小值；即使找到好的解决方案后也要尝试继续探索搜索空间；并有可能在未探索的区域找到更好的解决方案。

选择正确的 δ 值很重要。如果 δ 太小，渗透可能根本不会发生；如果 δ 太大，算法可能会不断“重新启动”，而没有时间找到最优解。此外，确定 δ 的适当值可能并非一项简单的任务，尤其是当我们事先不知道目标函数的值范围并且无法将此参数设置为外部参数时。因此，我为每一滴引入了一个尝试“泄漏”的计数器，在外部参数中，有必要设置其最大值。每次尝试后，“泄漏”的概率都会按照二次定律（即加速度）增加。这样，就不会有水滴在一个地方停留太久，这将有助于避免陷入局部极值。

公式

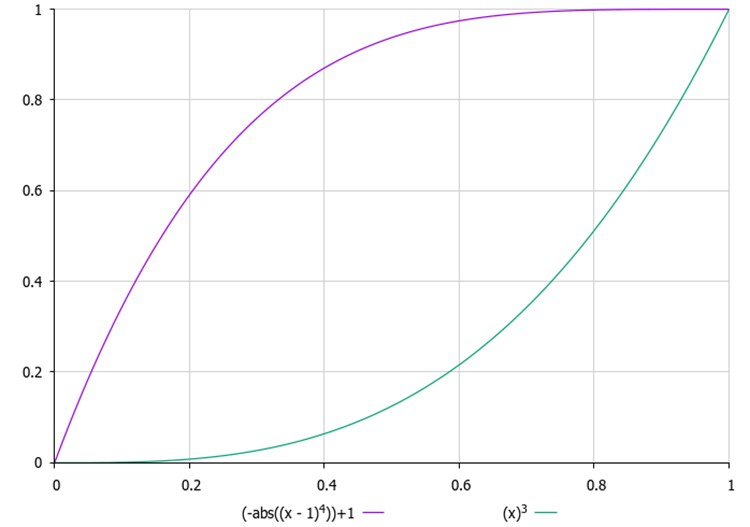
图 1.渗透概率随尝试次数变化的示例

当涉及到使用最低点的坐标时，通常使用以下方法：

  1. 找到目标函数值最小的水单位（我们称之为 x_lowest ）。
  2. 更新位置时，使用此最低点的所有坐标： x_new = x_old + F × r × (x_lowest - x_old) 。这里， x_new 、 x_old 和 x_lowest 是包含所有坐标的向量。
  3. 这个矢量方程同时适用于所有坐标。也就是说，新位置被“吸引”到搜索空间所有维度的最低点。

这种方法使我们能够同时考虑所有维度，将搜索定向到解决方案空间中最有前景的区域。

对于此算法（以及可能在必要时用于后续算法），有必要扩展标准结构以存储有关优化代理的其他信息。新输入的字段以绿色突出显示。

让我们回顾一下用户程序访问的优化代理的 S_AO_Agent 标准结构是什么样的。加上附加内容后，它看起来是这样的：

1.结构字段：

  • c [] — 代理在搜索空间中的当前坐标数组。
  • cP [] — 前一个代理坐标的数组。 
  • cB [] — 代理一直以来找到的最佳坐标数组。
  • f — 当前代理坐标的适应度函数值，用于评估代理应对任务的程度。
  • fP — 先前坐标的适应度函数值，用于跟踪代理性能的变化。
  • fB — 最佳坐标的适应度函数值，保留代理所取得的最佳结果。
  • cnt — 用于跟踪迭代次数的计数器。

2.Init（） — 初始化方法获取代理所需的坐标数量并执行以下操作：

  • 将 c 数组大小更改为 coords ，分配内存来存储当前坐标。
  • 类似地，改变 cP 数组的大小以存储先前的坐标，并改变 cB 数组的大小以存储最佳坐标。
  • 将适应度函数的当前值初始化为最小可能值，允许代理在第一次评估时更新它。
  • 以类似的方式初始化适应度函数的先前值和最佳值。
  • 将计数器值初始化为 0。

因此， S_AO_Agent 结构允许存储有关代理的当前状态、其性能和变化历史的信息。对结构所做的更改不会影响已经在其基础上编写的优化算法，但会简化未来新算法的构建。

//——————————————————————————————————————————————————————————————————————————————
struct S_AO_Agent
{
    double c  []; //coordinates
    double cP []; //previous coordinates
    double cB []; //best coordinates

    double f;     //fitness
    double fP;    //previous fitness
    double fB;    //best fitness

    int    cnt;   //counter

    void Init (int coords)
    {
      ArrayResize (c,  coords);
      ArrayResize (cP, coords);
      ArrayResize (cB, coords);

      f  = -DBL_MAX;
      fP = -DBL_MAX;
      fB = -DBL_MAX;

      cnt = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASHA 类继承自 C_AO 基类，是 ASHA 优化算法的实现。我们来分析一下它的结构和功能：

  • F 、 δ 、 β 和 ρ0 — 前面描述的特定参数决定了其行为。
  • params — 结构数组存储算法参数。每个数组元素包含参数的名称及其值。

SetParams() 方法用于从 params 数组中设置算法参数的值。

Init () 方法通过将最小和最大搜索边界、搜索步长和时期数作为输入来初始化算法。 

Moving () 和 Revision () 方法负责在搜索空间中移动代理，并根据优化标准审查和更新代理的状态及其位置。

私有字段：

  • S_AO_Agent aT [] — 用于对种群进行排序的临时种群数组。
  • epochs — 优化中使用的总世代数。
  • epochNow — 算法所在的当前世代。

C_AO_ASHA 类包括控制优化过程和代理交互所需的参数、方法和结构。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASHA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASHA () { }
  C_AO_ASHA ()
  {
    ao_name = "ASHA";
    ao_desc = "Artificial Showering Algorithm";
    ao_link = "https://www.mql5.com/en/articles/15980";

    popSize       = 100;  //population size

    F             = 0.3;  //water flow velocity
    δ             = 2;    //resistance level(infiltration threshold)
    β             = 0.8;  //parameter that controls the rate of change in probability
    ρ0            = 0.1;  //initial probability

    ArrayResize (params, 5);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "F";       params [1].val = F;
    params [2].name = "δ";       params [2].val = δ;
    params [3].name = "β";       params [3].val = β;
    params [4].name = "ρ0";      params [4].val = ρ0;

  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    F       = params      [1].val;
    δ       = (int)params [2].val;
    β       = params      [3].val;
    ρ0      = params      [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double F;  //water flow velocity
  int    δ;  //resistance level(infiltration threshold)
  double β;  //parameter that controls the rate of change in probability
  double ρ0; //initial probability

  private: //-------------------------------------------------------------------
  S_AO_Agent aT [];
  int  epochs;
  int  epochNow;
};
//——————————————————————————————————————————————————————————————————————————————

Init 方法负责初始化优化算法。方法逻辑：

1.标准初始化检查：该方法调用 StandardInit ，执行基本检查和参数初始化。 

2.计数器安装：

  • epochs 设置为等于通过的 epochsP 值（算法应执行的总迭代次数）。
  • epochNow 初始化为零，算法刚刚开始执行，尚未执行一个 epoch。

3.为临时代理种群保留内存。

4.如果所有初始化步骤都成功，该方法返回 true ，表示算法初始化成功。

Init 是准备算法工作的关键。它检查输入的有效性，设置控制优化过程所需的值，并为代理分配内存。成功的初始化允许算法继续执行进一步的操作，例如移动和修改代理。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASHA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Moving 方法实现了 ASHA 算法中在搜索空间中移动代理的逻辑。我们来一步步分析一下：

1.该方法会增加当前时期计数器，使我们能够跟踪执行的迭代次数。

2.初始初始化（如果不需要修改）：对于每个 i 代理和 c 坐标

  • 该方法使用 u.RNDfromCI 为给定范围内的所有代理生成初始位置并应用离散化。
  • 之后，将 revision 设置为 true ，该方法完成执行。

3.代理运动的主循环，对于每一个 i 代理，执行以下操作：

  • inf — 使用 u.Scale 计算的概率，以获得取决于 cnt 代理计数器的值。然后将该值提升至四次方以增加影响力。
  • 生成一个随机数 rnd 用于决策。

4.循环遍历坐标，对于每个 c 坐标执行以下操作：

  • 生成 ind 索引以选择搜索空间中位置较低的另一个代理，该代理将用于更新坐标。
  • 如果 i < 1 ，则：如果 rnd < inf ，则使用 u.GaussDistribution 围绕最佳坐标 cB 的正态分布来更新当前代理的坐标。
  • 如果 i >= 1 ，则：如果 rnd < inf ，则当前代理的坐标相对于另一个代理 a[ind].cB 的坐标进行类似更新。
  • 否则： xOld 旧值保持不变。如果生成的随机数小于 ρ ：
  • xNew 根据另一个代理 xLower 的最佳值进行更新。
  • 否则： xNew 根据 xLowest 全局最佳值进行更新。
  • 然后将新值 xNew 分配给当前代理。

5.坐标调整：最后，使用 u.SeInDiSp 调整每个新的坐标值，以使其适合指定的范围和步骤。

Moving 方法既提供了代理位置的初始化，也提供了基于代理当前状态和与其他代理的交互在优化过程中更新代理位置的功能。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASHA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double xOld    = 0.0;
  double xNew    = 0.0;
  double xLower  = 0.0;
  double xLowest = 0.0;
  double ρ       = MathMax (β * (epochs - epochNow) / epochs, ρ0);
  double inf     = 0.0;
  int    ind     = 0;
  double rnd     = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    inf = u.Scale (a [i].cnt, 0, δ, 0, 1);
    inf = inf * inf * inf * inf;

    rnd = u.RNDprobab ();

    for (int c = 0; c < coords; c++)
    {
      ind = (int)u.RNDintInRange (0, i - 1);
      
      if (i < 1)
      {
        if (rnd < inf)
        {
          a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
        }
      }
      else
      {
        if (rnd < inf)
        {
          a [i].c [c] = u.GaussDistribution (a [ind].cB [c], rangeMin [c], rangeMax [c], 8);
        }
        else
        {
          xOld = a [i].c [c];

          if (u.RNDprobab () < ρ)
          {
            xLower = a [ind].cB [c];

            xNew = xOld + F * (u.RNDprobab () * (xLower - xOld));
          }
          else
          {
            xLowest = cB [c];

            xNew = xOld + F * (u.RNDprobab () * (xLowest - xOld));
          }

          a [i].c [c] = xNew;
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision 方法负责更新有关群体中最佳解决方案（代理）的信息，以及跟踪其适应度。步骤描述如下：

1.ind 变量初始化为 -1 。它将用于存储具有最佳适应度函数值 f 的代理的索引。

2.循环代理：该方法循环遍历 popSize 种群中的所有代理：

  • 如果当前代理的 f 适应度函数值超过其当前最佳值 fB ，则更新 fB 并将代理索引保存在 ind 变量中。
  • 如果当前代理的适应度函数 f 的值超过其局部最佳值 fB ，则代理的 fB 的局部最佳值也会更新。
  • 代理的 c 坐标被复制到 cB ，这是其最为人所知的坐标。
  • cnt 计数器重置为 0 。否则，如果适应度函数值没有改善，则 cnt 计数器会增加。

3.复制最佳坐标：如果找到了具有最佳功能值（ ind 不等于 -1 ）的代理，则将其坐标复制到 cB 的全局变量中。

4.对代理进行排序：最后，调用 u.Sorting_fB 根据代理的 fB 局部最佳值对代理进行排序。

Revision 方法在算法中起着核心作用，监控代理的性能并更新其已知的最佳解决方案。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASHA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
      a [i].cnt = 0;
    }
    else
    {
      a [i].cnt++;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————


测试结果

ASHA 算法测试结果表现平均：
ASHA|Artificial Showering Algorithm|100.0|0.3|2.0|0.8|0.1|
=============================
5 Hilly's; Func runs:10000; result：0.8968571984324711
25 Hilly's；Func runs：10000; result：0.40433437407600525
500 Hilly's；Func runs：10000; result：0.25617375427148387
=============================
5 Forest's; Func runs：10000; result：0.8036024134603961
25 Forest's; Func runs：10000; result：0.35525531625936474
500 Forest's; Func runs：10000; result：0.1916000538491299
=============================
5 Megacity's; Func runs:10000; result：0.4769230769230769
25 Megacity's; Func runs:10000; result：0.1812307692307692
500 Megacity's；Func runs：10000; result：0.09773846153846236
=============================
All score:3.66372（40.71%）

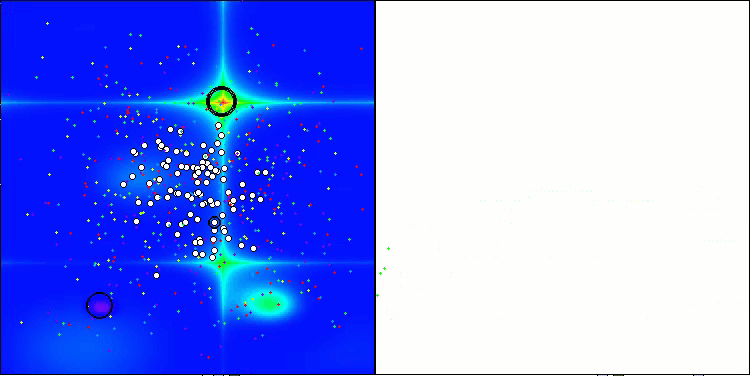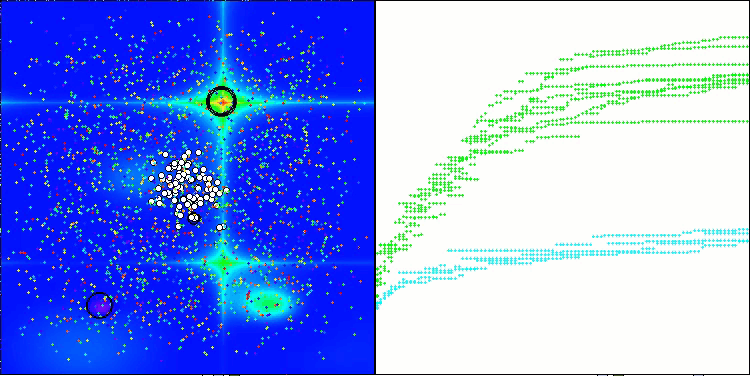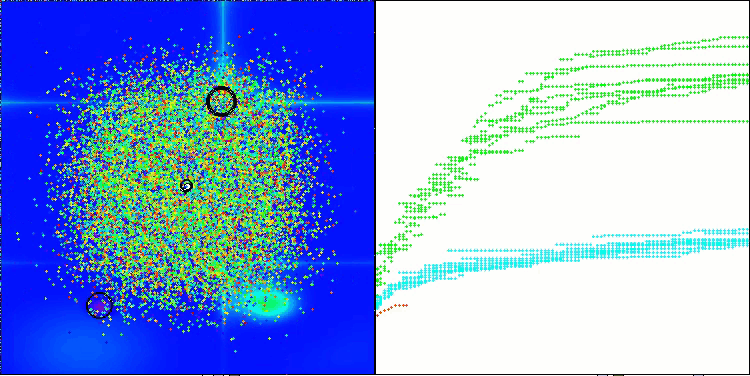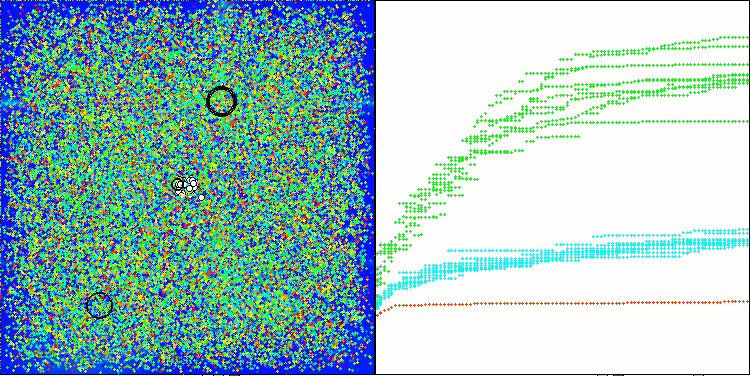
在测试期间观察 ASHA 的工作时，很难识别该算法的任何特征。没有发现对搜索空间有前景的领域的孤立研究。

Hilly

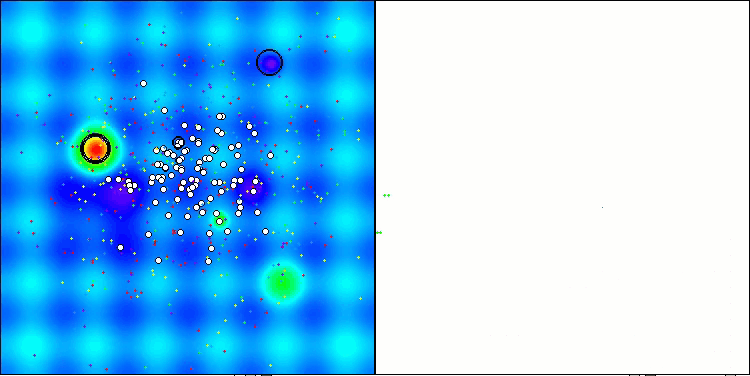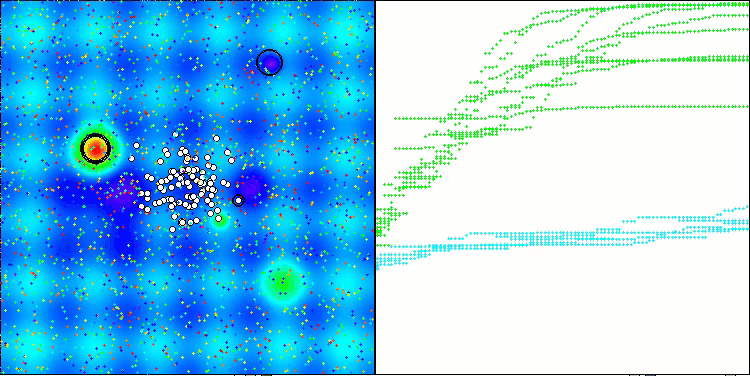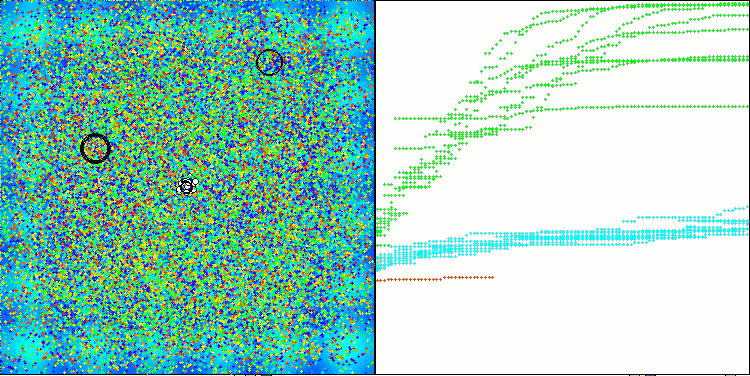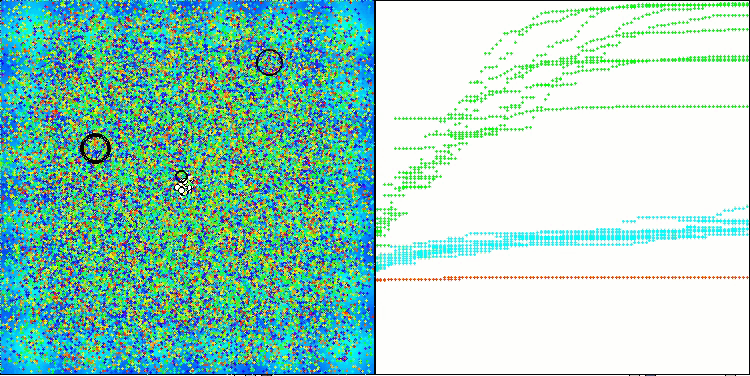
ASHA 在 Hilly 测试函数上

Forest

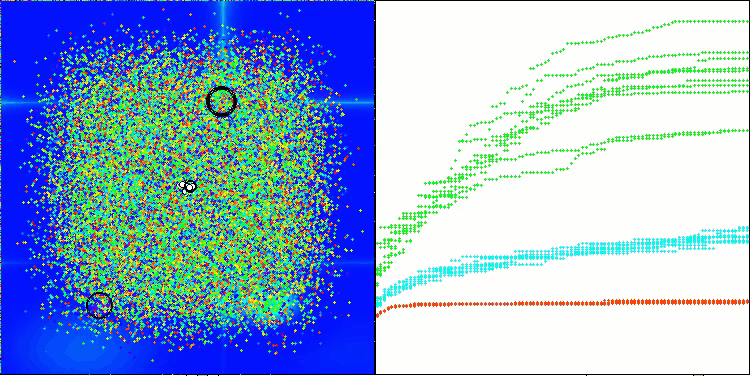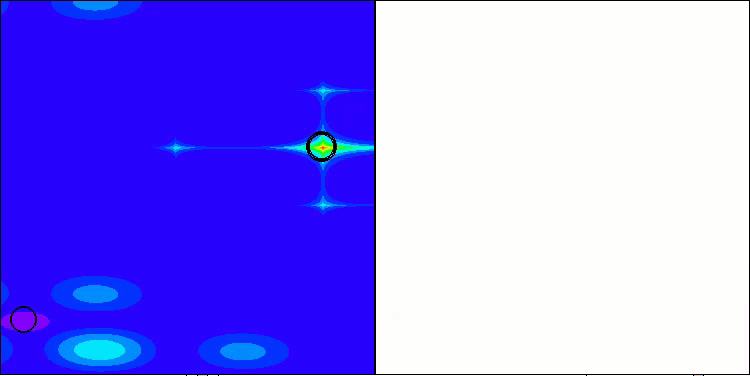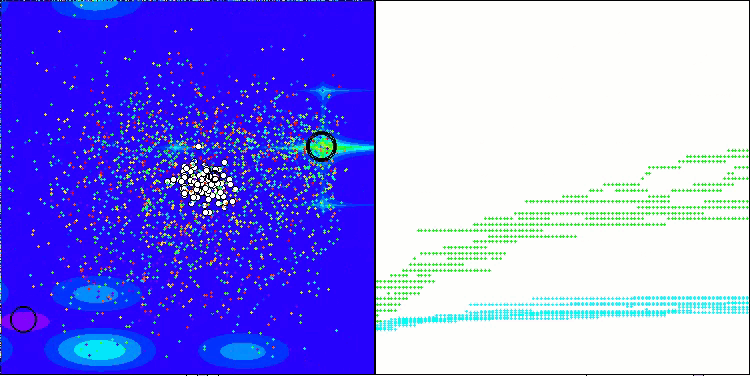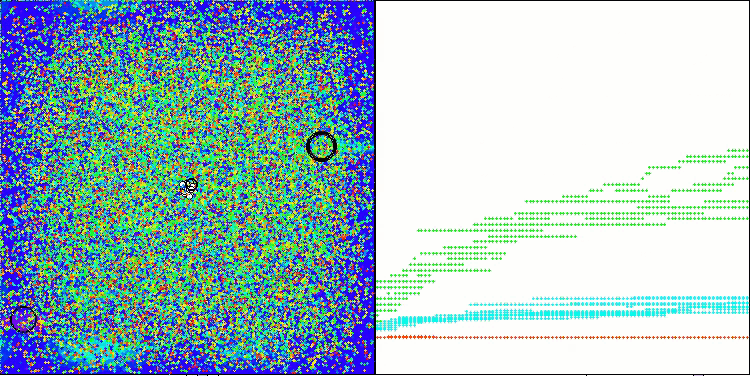
ASHA 在 Forest 测试函数上

Megacity

ASHA 在 Megacity 测试函数上

根据测试结果，ASHA 算法在评级表中排名第28位。

# AO 描述 Hilly Hilly 最终 Forest Forest 最终 Megacity (discrete) Megacity 最终 最终结果 最大值的百分比
10 p（5 F） 50 p（25 F） 1000 p（500 F） 10 p（5 F） 50 p（25 F） 1000 p（500 F） 10 p（5 F） 50 p（25 F） 1000 p（500 F）
1 ANS 跨邻里搜索（across neighbourhood search） 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA 代码锁定算法（code lock algorithm） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 动物迁徙优化 M（animal migration optimization M） 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O) 演进战略（(P+O) evolution strategies） 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾算法（comet tail algorithm） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 随机扩散搜索 M（stochastic diffusion search M） 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm 射箭算法 M（archery algorithm M） 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会群体演变（evolution of social groups） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 模拟各向同性退火（simulated isotropic annealing） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工协同搜索（artificial cooperative search） 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 无政府社会优化（anarchy society optimization） 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA 龟甲进化算法（turtle shell evolution algorithm） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差分进化（differential evolution） 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反应优化（chemical reaction optimization） 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鸟群算法（bird swarm algorithm） 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS 和声搜索（harmony search） 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 树苗播种和生长（saplings sowing and growing） 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 细菌趋化性优化 M（bacterial chemotaxis optimization M） 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 (PO)ES (PO) 进化策略（(PO) evolution strategies） 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
20 TSm 禁忌搜索 M（tabu search M） 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
21 BSO 头脑风暴优化（brain storm optimization） 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
22 WOAm Wale 优化算法 M（wale optimization algorithm M） 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
23 AEFA 人工电场算法（artificial electric field algorithm） 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
24 ACOm 蚁群优化M（ant colony optimization M） 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
25 BFO-GA 细菌觅食优化 - ga（bacterial foraging optimization - ga） 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
26 ABHA 人工蜂巢算法（artificial bee hive algorithm） 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
27 ACMO 大气云模型优化（atmospheric cloud model optimization） 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
28 ASHA 人工喷淋算法（artificial showering algorithm） 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
29 ASBO 适应性社会行为优化（adaptive social behavior optimization） 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
30 MEC 思维进化计算（mind evolutionary computation） 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
31 IWO 入侵性杂草优化（invasive weed optimization） 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
32 Micro-AIS 微型人工免疫系统（micro artificial immune system） 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
33 COAm 布谷鸟优化算法 M（cuckoo optimization algorithm M） 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
34 SDOm 螺旋动力学优化 M（spiral dynamics optimization M） 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
35 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
36 FAm 萤火虫算法 M（firefly algorithm M） 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
37 GSA 重力搜索算法（gravitational search algorithm） 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
38 BFO 细菌觅食优化（bacterial foraging optimization） 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
39 ABC 人工蜂群（artificial bee colony） 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
40 BA 蝙蝠算法（bat algorithm） 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
41 AAA 藻类自适应算法（algae adaptive algorithm） 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
42 SA 模拟退火（simulated annealing） 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
43 IWDm 智能水滴 M（intelligent water drops M） 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
44 PSO 粒子群优化（particle swarm optimisation） 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
45 Boids Boids 算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77



总结

我喜欢这个算法的想法，但在实现和测试过程中，我觉得这个算法缺少了一些东西。该算法不是最弱的，但远非最好的。这为研究人员创造了继续使用它的机会，特别是由于它的简单性，因为在我看来，这个想法本身非常有前景。此外，作者没有对渗透比提供更详细的解释，这使得它可以以不同的方式进行解释，仅受研究人员想象力的限制。

从这篇文章中可以得出的主要结论是，并非每个简单的想法都像更复杂的想法一样有效。优化算法的效率是一个复杂的问题，涉及权衡。我希望这个算法将成为关于寻找最佳解决方案的艺术的微妙之处和技巧的知识大书中的另一页。

表格

图 2.根据相关测试对算法进行颜色分级 结果大于或等于 0.99 以白色突出显示

图表

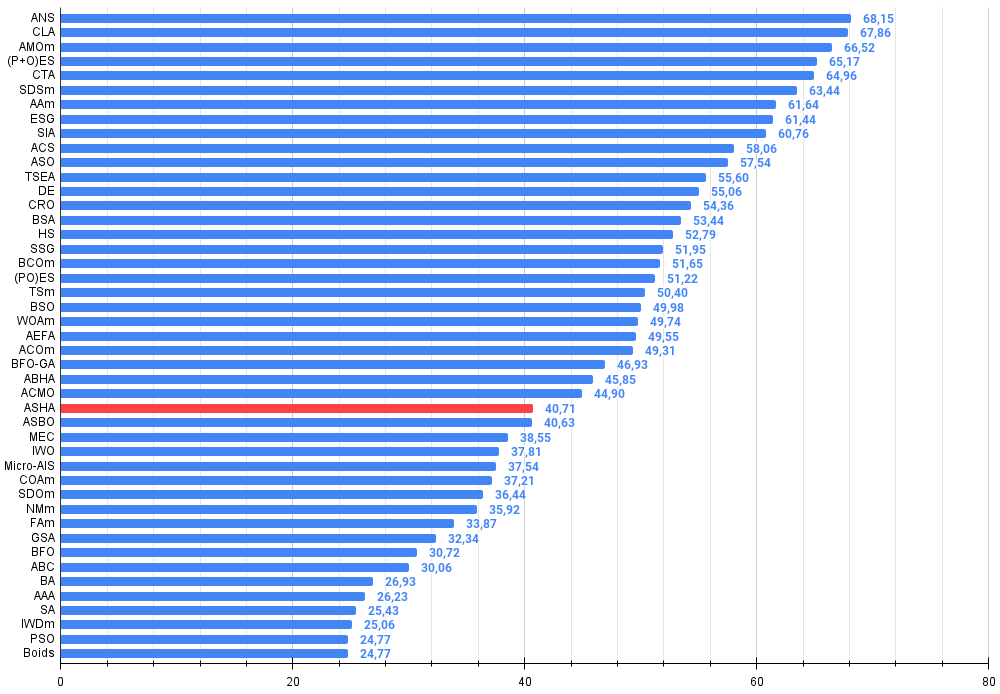
图 3.算法测试结果的直方图（范围从 0 到 100，越多越好，

其中 100 是可能的最大理论结果，档案库包含一个用于计算评级表的脚本）


ASHA 的优缺点：

优点：

  1. 快速。
  2. 实现简单。

缺点：

  1. 收敛精度低。

这篇文章附有一个归档，其中包含当前版本的算法代码。文章作者不对规范算法描述的绝对准确性负责。为提高搜索能力，已对其中多项功能进行了修改。文章中提出的结论和判断都是基于实验结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/15980

附加的文件 |
下载ZIP
ASHA.zip (35.93 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
创建一个基于布林带PIRANHA策略的MQL5 EA 创建一个基于布林带PIRANHA策略的MQL5 EA
在本文中，我们将创建一个MQL5 EA，它基于PIRANHA策略，并使用布林带来提升交易表现。我们会系统梳理该策略的核心原理、代码实现细节，以及测试与优化方法。并助您轻松将 EA 部署到实际的交易环境中。
交易中的神经网络：对比形态变换器 交易中的神经网络：对比形态变换器
对比变换器在设计上基于单根烛条水平和整个形态来分析行情。这有助于提升行情趋势建模的品质。甚至，运用对比学习来统调烛条和形态的表示、促进自我调节，并提升预测的准确性。
名义变量的序数编码 名义变量的序数编码
在本文中，我们将讨论并演示如何使用Python和MQL5将名义预测变量转换为适合机器学习算法的数值格式。
使用经典机器学习方法预测汇率：逻辑回归（logit）模型和概率回归（probit）模型 使用经典机器学习方法预测汇率：逻辑回归（logit）模型和概率回归（probit）模型
本文尝试构建一款用于预测汇率报价的EA。该算法以经典分类模型——逻辑回归与概率回归为基础。并利用似然比检验作为交易信号的筛选器。