头脑风暴优化算法（第一部分）：聚类

内容

1. 概述
2. 算法描述
3. K-Means

1. 概述

头脑风暴优化算法（Brain Storm Optimization ，即BSO），是一种受自然现象——头脑风暴启发而诞生的、令人兴奋且富有创新性的群体优化算法。该优化方法利用集体智慧和集体行为准则，是解决复杂问题的一种有效途径。BSO模拟了新观点和解决方案的产生过程，这与小组讨论中的情况类似，这使得它成为在各个领域寻找最优解决方案的一种独特且前景广阔的工具。在本文中，我们将探讨BSO的基本原理、优点以及应用领域。

基于种群的方法是解决复杂优化问题的重要工具。然而，在需要找到多个最优解的多模式问题下，现有方法仍具有局限性。本文提出了一种新的优化方法，称为头脑风暴优化方法。

现有方法，如小生境技术和聚类方法，通常将种群划分为子种群以搜索多个解。然而，这些方法需要预先确定子种群的数量，这可能存在不确定性，尤其是当最优解的数量事先未知时。头脑风暴优化（BSO）方法通过将目标空间转换为个体，根据坐标进行聚类和更新的空间，来弥补这一不足。与现有方法致力于寻找一个全局最优解不同，BSO方法将搜索过程指向多个“有意义”的解。

让我们更深入地了解一下头BSO方法及其在多模式优化问题中的应用。BSO算法由Shi等人于2015年开发。它受到人们聚在一起产生和分享想法以解决问题的自然过程的启发。

该算法还存在几个变形体算法，例如基于假设方差（或子方差）而非高斯方差来估计目标函数的假设方差头脑风暴优化（Hypo Variance Brain Storm Optimization）。此外还有其他变形体，如全局最优头脑风暴优化（Global-best Brain Storm Optimization），其中全局最优包括一个由当前种群状态触发的重新初始化方案，该方案将基于变量的更新和基于适应度的分组相结合。

在BSO算法中，每个个体不仅代表待优化问题的一个解，还代表揭示问题特征的一个数据点。可以将集体智慧与数据分析技术相结合，以获得超越单一方法所能达到的效果。

2. 算法

通过模拟这一过程来实现BSO算法，其中候选解（称为“个体”或“观点”）的种群经过迭代更新达到收敛从而获得最优解。该算法主要包括以下几个主要阶段：

1.初始化：

- 算法首先生成一个初始个体种群，其中每个个体代表优化问题的一个潜在解。
- 每个个体由一组定义解特性的解变量来表示。

2. 集思广益：

- 在这一阶段，算法模拟了头脑风暴的过程，其中个体通过组合和修改自己的观点以及其他个体的观点来生成新的观点（即新的候选解）。
- 头脑风暴由一组决定如何产生新想法的规则来指导。这些规则受到人类头脑风暴的启发，其中包括：

• 随机生成新想法
• 结合不同个体的想法
• 修改现有的想法

3. 评级：

- 使用优化问题的目标函数评估新产生的观点（即新的候选解）。
- 通过目标函数衡量每个候选解的质量或适应度，该算法旨在找到使该函数最小化（或最大化）的解。

4. 选择：

- 在评估步骤之后，该算法从种群中选择最佳个体以保留到下一轮迭代中。
- 基于个体的适应度值做出选择，适应度高的个体被选中的概率也高。

5. 完成：

- 在BSO中，算法会不断地迭代头脑风暴、评估和选择这三个阶段，直到满足终止条件，如达到最大迭代次数或目标解的质量。

下面列出一些BSO方法和算法的特征，将其与其他种群优化方法区分开来：

1. 聚类。个体根据其在搜索空间中的位置相似性被划分为不同的簇。这是通过使用K-means聚类算法来实现的。
2. 收敛。在这一阶段，每个簇内的个体都围绕簇质心进行分组。这模拟了头脑风暴阶段，即参与者聚在一起讨论观点的过程。
3. 发散。在这个阶段，生成了新的个体。新个体的生成是基于集群中的一个或两个个体。这个过程模仿了头脑风暴阶段，参与者开始跳出思维定势，提出新想法。
4. 选择。生成新个体后，将其放入主父组，然后对组进行排序。这模拟了头脑风暴阶段，即参与者聚在一起讨论想法的过程。
5. 变异。在整合观点并给出新思路后，所有的新思路都会发生变异，为群体增加额外的多样性，防止过早收敛。

我们将BSO算法的逻辑用伪代码表示：

1. 初始化参数与生成初始种群
2. 计算种群中每个个体的适应度
3. 直到满足停止条件为止
    4. 计算种群中每个个体的适应度
    5. 确定种群中的最优个体
    6. 将种群划分为多个簇，并将簇中的最优解设置为簇中心
    7. 对于种群中的每个新个体：
        |7.1. 如果满足pReplace概率：
        |    |为随机选择的簇生成新的移动中心（簇中心被移动）
        |7.2. 如果满足pOne概率：
        |    |随机选择一个簇
        |    |如果满足pOne_center概率：
        |    |    |7.2.a 选择集群中心
        |    |其他情况：
        |         |7.2.b从集群中随机选择一个个体
       |7.3 其他情况：
        |         |选择两个簇
        |         |如果满足pTwo_center概率：
        |             |7.3.a 合并 两个簇中心形成一个新个体
        |         |其他情况：
        |             |7.3.b 通过合并 每个集群中选定两个个体的位置来创建新个体（集群应该不同）
        |7.4 变异： 将随机高斯偏差添加到新个体的位置中
        |7.5 如果新个体落在搜索空间之外，则将其映射回搜索空间内
    8. 用新个体更新当前数量
    9. 返回步骤4，直到满足停止标准
10. 将人群中最好的个体作为解决方案
11. BSO操作结束

让我们看一下伪代码步骤7中的操作。

7.1的开始步骤，实际上并不创建新个体，而是移动簇的中心，以便在该算法的其他操作步骤中可以基于该中心创建新个体。对于每个坐标，位移是随机的，且遵循正态分布，其距离由外部参数中指定的原始位置决定。

7.2步骤选择簇中心或选定簇中的某个个体，该个体将在7.4步骤中发生变异，以创建新个体。

7.3步骤旨在通过合并两个随机选择的簇的中心或这两个选定簇中的两个个体来创建新个体。簇本应是不同的，但如果只有一个非空簇（簇可能是空的），则会在唯一的非空簇中选择两个个体执行合并操作。此操作旨在实现簇之间的观点交流。

合并操作如下：

其中：
Xf - 合并后的新个体，
v - 从0到1的随机数，
X1 and X2 - 用于合并的两个随机个体（或两个聚类中心）。

合并方程的含义是，在两种不同观点之间的随机位置新增一种观点。

变异操作可以用以下方程式来描述：

其中：
Xm - 变异后的新个体，
Xs - 选择要变异的个体，
n(µ, σ) - 具有均值µ和方差σ的高斯随机数，
ξ - 用数学式表示的变异率。

变异率使用以下方程式计算：:

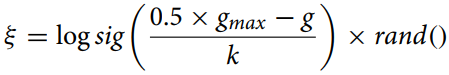
其中：
gmax - 最大迭代次数，
g - 当前迭代次数，
k - 正确率。

这个等式（变异率）用于计算优化算法中个体之间的收缩距离，以实现变异参数的自适应变化。"logsig()"函数呈现了一个平滑的非线性值的减小过程，与"rand"相乘则引入了一个随机元素，这有助于避免过早收敛并维持种群的多样性。

在脑风暴优化（BSO）算法中，在控制“ξ”比率随时间变化的速度方面，“k”校正比率起着重要作用。“k”的取值可能因具体问题和数据分布而不同，通常是通过经验计算或使用超参数调优方法来确定的。

通常来说，在算法中，参数"k" 的选择对于在探索（exploration）和利用（exploitation）之间取得平衡至关重要。如果"k" 值太大, "ξ" 值的变化就会非常缓慢， 这可能会导致算法过早收敛。如果"k" 值太小, "ξ" 值的变化就会非常显著，这可能会导致搜索空间的探索过度和收敛缓慢。

对数S型函数（logistic function），也被称为逻辑函数（logistic function），通常表示为σ(x)（σ(x)）或sig(x)（sig(x)）。它是通过以下公式计算的：

其中：
exp(-x) - 表示-x的指数幂。
1 / (1 + exp(-x)) 提供从0到1范围内的输出值。

下图显示了sigmoid函数的图形。允许在早期迭代中探索减少不均匀函数，并在后期迭代中进行细化。

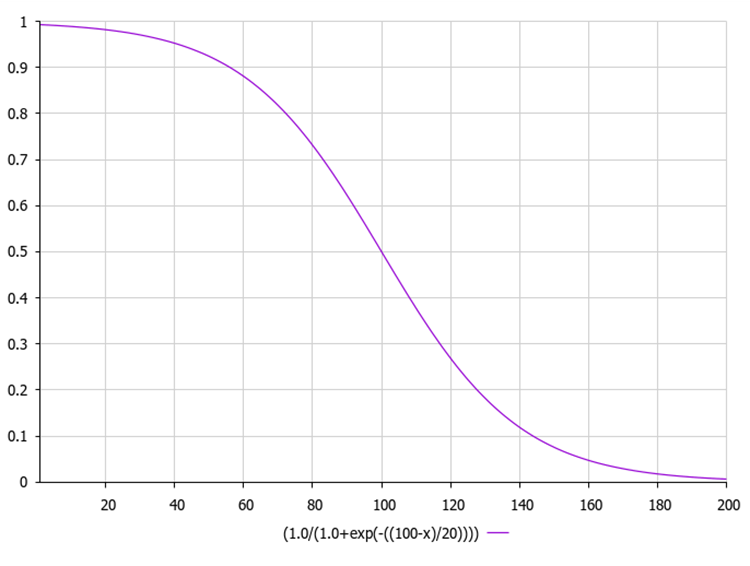
下面是一个示例代码，用于计算变异率以及使用指数的sigmoid函数。

在这段代码中，函数“sigmoid”用于计算输入数字“x”的sigmoid值，而函数“xi”则根据上面的方程计算“ξ”的值。在这里，“gmax”表示最大迭代次数，“g”表示当前迭代次数，而“k”表示校正比率。MathRand函数生成一个介于0和32767之间的随机数，所以我们将其除以32767.0，得到一个介于0和1之间的随机数。然后，我们计算这个随机数的sigmoid值。由“xi”函数返回该值。

double sigmoid(double x) 
{
    return 1.0 / (1.0 + MathExp(-x));
}

double xi(int gmax, int g, double k) 
{
    double randNum = MathRand() / 32767.0; // Generate a random number from 0 to 1
    return sigmoid (0.5 * (gmax - g) / k) * randNum;
}

3. k-均值聚类法

BSO算法使用K-means聚类分析将观点分成不同的组。为了模拟小组讨论中参与者的行为并提高搜索效率，当前用于迭代的“n”个解决方案集合被分成“m”个类别。

我们将使用S_Cluster结构来描述一个单独的聚类，该结构实现了K-means算法，这是一种流行的聚类方法。

让我们来看一下结构：

• centroid[] - 表示簇质心的数组。
• f - 质心适应度值。
• count - 集群中的点数。
• ideasList[] - 观点列表。

Init函数通过调整“质心”和“ideasList”数组的大小并设置“f”的初始值来初始化结构。

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster
    int    ideasList []; //list of ideas

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f = -DBL_MAX;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_BSO_KMeans类是通过BSO优化算法中作为聚类代理的K-means算法来实现的。以下是每种方法的作用：

1. KMeansInit - 通过从数据中随机选择代理来初始化簇质心。对于每个集群，选择一个随机代理，并将其坐标复制到集群质心。
2. VectorDistance - 计算两个向量之间的欧几里德距离。它将两个向量作为参数，并返回它们的欧几里德距离。
3. KMeans - 实现数据聚类的k-means算法的基本逻辑。它将数据和集群数组作为参数。

K-means方法在运行过程中执行以下步骤：

• 将数据点分配给最近的质心。
• 根据分配给每个聚类的点的均值更新质心。
• 重复这两个步骤，直到质心不再变化或达到最大迭代次数。

在K-means算法中，质心是聚类的中心指示点。在K-means方法中，质心是属于给定聚类的所有数据点的算术平均值。
在K-means算法的每次迭代中，都会重新计算质心，然后根据选定的度量标准，将数据点再次分组到距离新质心更近的聚类中。
因此，质心在K-means方法中扮演着关键角色，决定了聚类的形状和位置。

这个类代表了BSO算法的关键部分，通过为代理提供聚类功能来改进搜索过程。K-means算法迭代地将点分配给聚类并重新计算质心，直到不再发生变化或达到最大迭代次数为止。

//——————————————————————————————————————————————————————————————————————————————
class C_BSO_KMeans
{
  public: //--------------------------------------------------------------------

  void KMeansInit (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    for (int i = 0; i < ArraySize (clust); i++)
    {
      int ind = MathRand () % dataSizeClust;
      ArrayCopy (clust [i].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    bool changed   = true;
    int  nClusters = ArraySize (clust);
    int  cnt       = 0;

    while (changed && cnt < 100)
    {
      cnt++;
      changed = false;

      //Assigning data points to the nearest centroid
      for (int d = 0; d < dataSizeClust; d++)
      {
        int    closest_centroid = -1;
        double closest_distance = DBL_MAX;

        if (data [d].f != -DBL_MAX)
        {
          for (int cl = 0; cl < nClusters; cl++)
          {
            double distance = VectorDistance (data [d].c, clust [cl].centroid);

            if (distance < closest_distance)
            {
              closest_distance = distance;
              closest_centroid = cl;
            }
          }

          if (data [d].label != closest_centroid)
          {
            data [d].label = closest_centroid;
            changed = true;
          }
        }
        else
        {
          data [d].label = -1;
        }
      }


      //Updating centroids
      double sum_c [];
      ArrayResize (sum_c, ArraySize (data [0].c));

      for (int cl = 0; cl < nClusters; cl++)
      {
        ArrayInitialize (sum_c, 0.0);

        clust [cl].count = 0;
        ArrayResize (clust [cl].ideasList, 0);

        for (int d = 0; d < dataSizeClust; d++)
        {
          if (data [d].label == cl)
          {
            for (int k = 0; k < ArraySize (data [d].c); k++)
            {
              sum_c [k] += data [d].c [k];
            }

            clust [cl].count++;
            ArrayResize (clust [cl].ideasList, clust [cl].count);
            clust [cl].ideasList [clust [cl].count - 1] = d;
          }
        }

        if (clust [cl].count > 0)
        {
          for (int k = 0; k < ArraySize (sum_c); k++)
          {
            clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
          }
        }
      }
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

在BSO算法中，个体的适应度被定义为它所代表的解决方案的质量。在优化问题中，适应度可以等于正在被优化的函数的值。

具体的聚类方法可能会有所不同。一种常见的方法是使用k-means方法，其中聚类质心被随机初始化，然后通过迭代更新来最小化每个点到其聚类质心的平方距离之和。

尽管适应度在聚类中起着关键作用，但它并不是影响聚类形成的唯一因素。其他方面，如决策空间中个体之间的距离，也可能发挥着重要作用。从算法角度，这样有助于保持种群的多样性，并防止过早收敛到不合适的解决方案。

K-means算法收敛所需的迭代次数在很大程度上取决于各种因素，如质心的初始状态、数据的分布以及聚类的数量。然而，通常来说，K-means算法基本在几十到几百次迭代内收敛。

值得注意的是，K-means算法通过最小化点到其最近质心的平方距离之和来进行聚类，但这并不总是最优的，聚类取决于特定任务和数据中簇的形状。在某些情况下，其他聚类算法可能更为合适。

K-means++是David Arthur和Sergei Vassilvitskii在2007年提出的一种K-means算法的改进版本。K-means++与标准K-means的主要区别在于质心的初始化方式。K-means++不是随机选择初始质心，而是以最大化它们之间的距离的方式来选择初始质心。这有助于提高聚类的质量并加速算法的收敛。

K-means++的初始化步骤主要包括以下几点：

1. 从数据点中随机选择一个点作为第一个质心。
2. 对于每个数据点，计算其到最近的一个已选质心的距离。
3. 从数据点中选择下一个质心，选取某个点作为质心的概率与其到最近已选质心的距离成正比（即距离最近质心最远的点最有可能被选为下一个质心）。
4. 重复步骤2和3，直到选择了k个质心。

初始化质心之后，K-means++算法后续的操作与标准K-means算法相同。这种初始化方法有助于提高聚类的质量并加速算法的收敛。然而，这种方法计算成本较高。

如果每个点有1000个坐标，那么这将给K-means++算法带来额外的计算量，因为它需要在高维空间中计算距离。然而，K-means++仍然可能是有效的（需要通过实验来证实这一假设），因为它通常能实现更快的收敛速度和更好的聚类质量。

在处理高维数据（如1000个坐标）时，可能会遇到与“维数限制”相关的附加问题。这可能会降低两点之间距离数据的重要性，从而使聚类变得困难。这种情况下，在应用K-means或K-means++之前，使用降维方法（如主成分分析PCA）可能是有用的。这有助于降低数据的维数，并使聚类更加高效。

数据降维是数据处理中的一个重要步骤，尤其是在处理大量坐标或特征时。这有助于简化数据，降低计算成本，并提高聚类算法的性能。以下是聚类中常用的几种降维方法：

1. 主成分分析(PCA)。这种方法将包含大量变量的数据集转换为变量较少的数据集，同时保留尽可能多的信息。
2. 多维尺度分析（MDS)。该方法试图找到一个低维结构，该结构能够像在原始高维空间中一样保留点之间的距离。
3. t分布随机邻域嵌入（t-SNE）。它是一种非线性降维方法，特别适用于高维数据的可视化。
4. 自编码器（Autoencoders）。用于降低数据维度的神经网络。其工作原理是将输入数据编译成紧凑代码的形式，然后将该表示形式解码回原始数据。
5. 独立成分分析（ICA）。这是一种统计方法，它将数据集转换为独立成分，这些成分可能比原始数据更具有信息量。这些成分可能更好地反映数据的结构或重要方面，例如，它们可能使一些隐藏因素变得可见，或者在分类问题中更好地归类。
6. 线性判别分析（LDA）。该方法用于寻找能够更好地分离两个或多个类别的特征线性组合。

因此，尽管K-means++在初始化步骤中可能计算成本更高，特别是对于高维数据，但在某些情况下它仍然是有价值的。但是，可以尝试和比较不同的方法来确定哪种方法最适合您的特定问题和数据集。

如果您想进一步尝试K-means++方法，下面是该算法的初始化方法（其余代码与传统K-means代码没有区别）。

下述代码实现了K-means++算法的初始化过程。该函数接受一个由S_BSO_Agent结构体表示的数据点数组、一个判断数据大小（dataSizeClust）数组以及一个由S_Cluster结构体表示的聚类数组。该方法会随机从数据点中初始化第一个质心。然后，对于每个后续的质心，算法会计算每个数据点到最近质心的距离，并根据距离的比例概率选择下一个质心。这是通过生成一个介于0和所有距离总和之间的随机数“r”来实现的，然后遍历所有数据点，通过减去每个点的距离来减小“r”，直到“r”小于或等于当前点的距离。在这种情况下，当前点被选为下一个质心。此过程会重复进行，直到所有质心都完成初始化。

综合以上部分，已经实现了K-Means++初始化，它是标准K-Means算法中初始化步骤的改进版本。质心的选择旨在最小化质心与数据点之间潜在距离的平方和，从而实现更高效、更稳定的聚类。

void KMeansPlusPlusInit (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [])
{
  // Choose the first centroid randomly
  int ind = MathRand () % dataSizeClust;
  ArrayCopy (clust [0].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);

  for (int i = 1; i < ArraySize (clust); i++)
  {
    double sum = 0;
      
    // Compute the distance from each data point to the nearest centroid
    for (int j = 0; j < dataSizeClust; j++)
    {
      double minDist = DBL_MAX;
       
      for (int k = 0; k < i; k++)
      {
        double dist = VectorDistance (data [j].c, clust [k].centroid);
          
        if (dist < minDist)
        {
            minDist = dist;
        }
      }
        
      data [j].minDist = minDist;
      sum += minDist;
    }

    // Choose the next centroid with a probability proportional to the distance
    double r = MathRand () * sum;
      
    for (int j = 0; j < dataSizeClust; j++)
    {
      if (r <= data [j].minDist)
      {
        ArrayCopy (clust [i].centroid, data [j].c, 0, 0, WHOLE_ARRAY);
        break;
      }
      r -= data [j].minDist;
    }
  }
}

继续...

在本文中，我们研究了BSO算法的逻辑结构，以及聚类方法和降低优化问题维度的途径。在下一篇文章中，我们将完成对BSO算法的研究，并总结其性能表现。