射箭算法（Archery Algorithm, AA）

MetaTrader 5 — 测试者 | 30 四月 2025, 09:14

759

Andrey Dik

内容

概述

在任务复杂度日益攀升、资源愈发紧缺的当下，优化举措不仅已成为一种必然需求，更在现代社会中演变成一门实实在在的算法艺术。如何在众多可能的解决方案中找到最佳的一个？如何降低成本、提高效率并实现最大利润？这些问题涉及众多领域的专家——从经济学到工程学，从社会系统到生态学。在解决优化问题之前，重要的是通过识别关键变量和数学关系来正确建模问题，从而真实地反映现实情况。优化在金融和交易中被广泛应用，它不仅有助于开发新的投资策略，还可以改进现有的策略。然而，尽管优化方法具有普遍性，但它们却被有条件地分为两类：确定性方法和随机方法。

像梯度下降这样的确定性方法通过使用数学导数来寻找最优解，提供严谨且可预测的解决方案，能够有效地模拟不同场景。然而，一旦问题变得非线性或多变量，它们的有效性可能会急剧下降。在此情况下，随机方法可以派上用场，它们依赖于随机过程，在复杂条件下能够找出可接受的解决方案，这在波动的市场中特别有效。

确定性方法和随机方法的结合在现代优化方法中发挥着关键作用。通过结合这两种方法，分析师可以创建更灵活且适应性强的模型，这些模型既能考虑稳定条件，也能应对变化条件。这不仅能够提高预测的质量，还能最小化风险，这对于成功的投资管理至关重要。

在本文中，我将介绍一种新的解决优化问题的方法——射箭算法（简称AA）。该算法由Fatemeh Ahmadi Zeidabadi及其同事开发，并于2022年2月发表。这种受射箭启发的方法通过基于随机选择的元素更新搜索空间中群体成员的位置，生成准最优解。我们将对标准目标函数进行测试，以评估AA的效率，并将获得的结果与我们已知的其他算法进行比较。通过深入细节，我们将揭示这种创新方法如何改变我们对优化的思维方式，并为解决复杂问题开辟新的视野。

算法实现

射箭算法（AA）是一种全新的随机优化方法，旨在寻找优化问题的最优解，其灵感来源于射箭者瞄准目标的行为。AA模拟了向目标射箭的过程。群体中的每个成员代表优化问题的一个潜在解，它们在搜索空间中的位置会根据随机选择的“目标”成员的表现进行更新，这类似于射箭者根据他们想要击中的位置调整瞄准方向。

群体以矩阵的形式表示，其中每一行对应一个成员（解），每一列对应问题的一个维度。这样可以根据目标函数值对决策进行结构化的评估和更新。每个成员的表现通过目标函数进行评估，该函数量化了找到的解的质量。结果存储在一个向量中，这使得算法可以比较不同解的效率。

目标被划分为若干区域，其宽度对应种群成员的生产力。计算概率函数以根据目标函数值确定每个成员被选中的概率，表现更优的“射箭者”被选中的概率更高。基于累积概率随机选择群体中的一个成员，模拟射箭者选择目标的过程。这一选择会影响其他成员位置的更新方式。该算法使用特定的方程在搜索空间中更新每个“射箭者”的位置。更新取决于所选“射箭者”的目标函数值是否优于当前值。这一过程涉及随机性，以探索搜索空间。AA以迭代的方式工作，直到达到停止条件（最大迭代次数）为止。在此过程中，算法会跟踪找到的最优解。

上述AA算法的原始版本将矩阵描述为群体，向量描述为群体的成员。然而，文本中并未指出对矩阵进行操作的具体动作。实际上，该算法包括了与大多数先前讨论的算法中类似的对搜索智能体的标准操作。

值得注意的是，“目标被划分为若干区域，其宽度对应于群体成员的生产力”这句话暗示了使用轮盘赌法进行选择。在此情况下，选择一个区域的概率与其宽度成正比。

通过这种方式，可以用更简单描述的解释许多复杂的概念，从而简化想法的实现。

因此，射箭算法是一种基于群体的优化方法，它使用射箭原理来指导寻找最优解的过程。它将随机性与正态分布相结合，以探索和利用搜索空间。算法的关键组成部分：

1. 群体成员（射箭者）
2. 概率向量和累积概率向量
3. 遗传机制（原始版本中不存在）
4. 位置更新机制
5. 训练强度参数（I）

首先，让我们展示该算法的伪代码：

初始化：
创建一个包含popSize个智能体的群体
对于每个智能体：
在搜索范围内随机初始化一个位置
初始化前一个位置和适应度

主循环：
直到达到停止条件：
对于群体中的每个i智能体：
计算概率向量P和累积概率向量C

对于每个c坐标：
使用累积概率选择k射箭者

                If (random_number < inheritance_probability):
                    new_position [c] = k_archer_position [c]
                Otherwise:
                    I = rounding (1 + random_number_from_0_to_1) // Training intensity parameter
                    random_gaussian = generate_gaussian_number (mean = 0, min =-1, max = 1)

                    If (k_archer_fitness > i_agent_fitness):
                        new_position [c] = previous_position [c] + random_gaussian * (k_archer_position [c] - I * previous_position [c])
                    Otherwise:
                        new_position [c] = previous_position [c] + random_gaussian * (previous_position [c] - I * k_archer_position [c])

将new_position[c]限制在搜索范围内

更新i智能体的位置

评估所有智能体的适应度
更新全局最优解
对于每个智能体：
如果新的适应度优于之前的适应度：
更新前一个位置和适应度

返回找到的最优解

代码的实现特征：

1. 算法采用概率方法选择学习对象（射箭者）。
2. 遗传机制允许智能体以一定的概率直接复制成功射箭者的位置。
3. 在更新位置时，使用高斯分布为射箭者的“学习过程”引入随机性。
4. 算法存储智能体之前的最优位置，使其能够“记住”良好的决策。
5. 实现中将包含一个机制，以确保新位置在允许的搜索范围内。
6. 所描述的训练强度参数（I）将用于调节当前位置对新位置的影响程度。

参数I （训练强度）是一个随机变量，可以取值1或2。其定义如下：I = 将（1 + 0到1之间随机生成的数字）四舍五入到最接近的整数。这意味着I有一半的概率等于1，也有一半的概率等于2。参数I在算法中的作用：

1. 当I = 1时，算法进行较小的位置调整。
2. 当I = 2时，算法可以对位置进行更大幅度的调整。

让我们继续讨论算法代码。描述“射箭者”结构——S_AA_Agent。它代表优化算法中的一个智能体，包含了解空间中的一组坐标，并包含有关其适应度函数效率的信息。

cPrev [] — 该数组存储智能体的前一个坐标。
fPrev — 该变量存储智能体的前一个适应度值。

Init 方法允许我们通过设置其坐标的初始值和适应度来准备智能体以进行工作。接下来，将fPrev的值设置为“double”类型的最小可能值，因为适应度尚未计算。

//——————————————————————————————————————————————————————————————————————————————
struct S_AA_Agent
{
    double cPrev []; // previous coordinates
    double fPrev;    // previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们来看看实现算法本身的C_AO_AAm类，它继承自C_AO类。

popSize - 种群大小。
inhProbab - 从其他射箭者继承特征的概率。

然后，初始化参数值为2的params数组，该数组存储了算法的参数：种群大小和继承概率。

SetParams - 该方法根据存储在params数组中的值设置参数。它提取popSize和inhProbab的值，并将它们转换为适当的数据类型。
Init - 该方法通过接受最小和最大搜索边界、搜索步长以及迭代次数来初始化算法。
Moving 和 Revision - 这两个方法负责智能体在解空间中的移动逻辑以及它们的修订（更新）。

S_AA_Agent agent [] - 用于执行优化的智能体数组。

C_AO_AAm类实现优化算法，而SetParams、Init、Moving和Revision则负责在算法运行期间管理其配置和行为。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AAm () { }
  C_AO_AAm ()
  {
    ao_name = "AAm";
    ao_desc = "Archery Algorithm M";
    ao_link = "https://www.mql5.com/en/articles/15782";

    popSize   = 50;    // population size
    inhProbab = 0.3;

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "inhProbab"; params [1].val = inhProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    inhProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // step search
             const int     epochsP = 0);  // number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double  inhProbab; //probability of inheritance

  S_AA_Agent agent [];

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

Init 方法在 C_AO_AAm 类中负责初始化优化算法。它接受四个参数：最小和最大搜索边界的数组、搜索步长以及默认值为0的迭代次数。

如果标准初始化成功，该方法会调整 agent 数组的大小，使其与指定的 popSize 种群大小相匹配。这使我们能够创建所需数量的智能体，将其用于算法中。
在 for 循环中，使用 Init方法初始化数组中的每个智能体，该方法为每个智能体指定初始坐标。

最后，该方法返回 true，表示算法初始化成功完成。因此，Init方法通过设置必要的参数并创建将参与优化的智能体，确保算法为运行做好了准备。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAm::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Moving方法在C_AO_AAm类中负责根据智能体的当前位置和它们正在优化的函数值，在解空间中移动智能体。让我们将其分解为几个部分：

如果该方法是首次调用（revision等于false），则在指定的rangeMin和rangeMax边界内，为每个智能体的各个坐标初始化一个随机值。
然后，使用SeInDiSp方法调整该值，以确保其符合指定的步长。

之后，将revision标识设置为true，并完成该方法。

接下来创建两个数组：P用于存储概率，C用于存储累积概率。
找到智能体适应度函数值中最差的 F_worst值，以对适应度函数值进行归一化。
然后计算每个智能体的概率，并对其进行归一化，使其总和为1。
根据P概率计算C累积概率。
对于每个智能体的各个坐标，基于累积概率选择一个伙伴射箭者（即另一个智能体）。
如果随机值小于指定的inhProbab继承概率，则智能体接受所选智能体的坐标（以给定的概率确保特征的继承）。
否则，智能体根据一个方程更新其位置，该方程考虑了当前位置、随机值以及伙伴射箭者的位置。
最后，使用SeInDiSp方法调整新的坐标值。

Moving方法实现了智能体在解空间中的移动，考虑了它们的当前位置和函数值，并使用概率方法选择移动方向和更新位置。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        // Update position using Eq. (5) and (6)
        double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);

        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

在C_AO_AAm类中，Revision方法负责更新种群中表现最优个体的相关信息。该方法执行以下操作：

将ind变量初始化为-1。它将用于存储具有最佳函数值的智能体的索引。
for循环遍历popSize种群中的所有智能体，如果当前智能体的函数值 a [i].f超过了当前最佳函数值fB：

则fB更新为新的更好的值a [i].f。
并将该智能体的索引存储在变量ind中。

循环完成后，如果ind不等于-1，则调用ArrayCopy函数。它将最佳智能体的坐标从数组a复制到数组 cB。第二个for循环也会遍历种群中的所有智能体：

如果当前智能体的函数值a [i].f超过了其之前的适应度函数值agent [i].fPrev：

则更新智能体的fPrev的前一个值。
并使用ArrayCopy将智能体的当前坐标复制到cPrev数组。

Revision方法的作用是更新有关全局最优解的信息，以及更新智能体的最佳位置。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

测试结果

我对算法进行了些许修改。原始算法并不提供射箭者之间的直接信息交换。信息交换是通过正态分布间接地通过坐标交互发生的，因此我认为有必要添加这种信息的交换。为此，我增加了一个附加的inhProbab算法，以给定的概率实现这种交换。

if (u.RNDbool () < inhProbab)
{
  x = a [k].c [c];
}

以下呈现的结果对应于作者最初设想算法的原始版本。

AA|Archery Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6699547926310098
25 Hilly's; Func runs: 10000; result: 0.37356238340164605
500 Hilly's; Func runs: 10000; result: 0.257542163368952
=============================
5 Forest's; Func runs: 10000; result: 0.38166669771790607
25 Forest's; Func runs: 10000; result: 0.199300365268835
500 Forest's; Func runs: 10000; result: 0.15337954055780398
=============================
5 Megacity's; Func runs: 10000; result: 0.4076923076923077
25 Megacity's; Func runs: 10000; result: 0.17907692307692308
500 Megacity's; Func runs: 10000; result: 0.10004615384615476
=============================
总分: 2.72222 (30.25%)

该算法在测试中的得分占比为30.25%，但经过我的修改后，算法的性能提高了超过13%。以下是修改版本的结果：

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9353194829441194
25 Hilly's; Func runs: 10000; result: 0.6798262991897616
500 Hilly's; Func runs: 10000; result: 0.2596620178276653
=============================
5 Forest's; Func runs: 10000; result: 0.5735062785421186
25 Forest's; Func runs: 10000; result: 0.22007188891556378
500 Forest's; Func runs: 10000; result: 0.1486980566819649
=============================
5 Megacity's; Func runs: 10000; result: 0.6307692307692309
25 Megacity's; Func runs: 10000; result: 0.344
500 Megacity's; Func runs: 10000; result: 0.10193846153846249
=============================
总分: 3.89379 (43.26%)

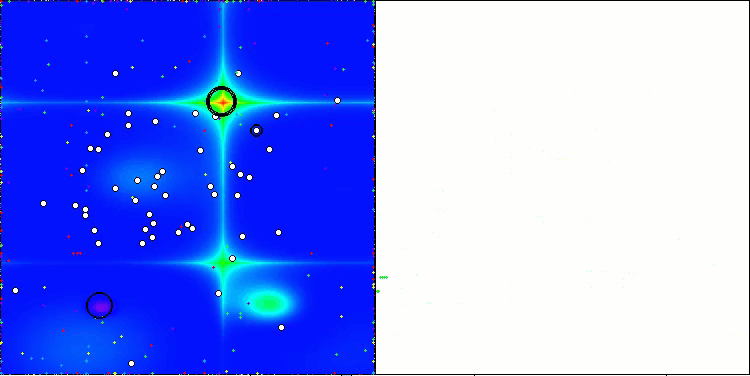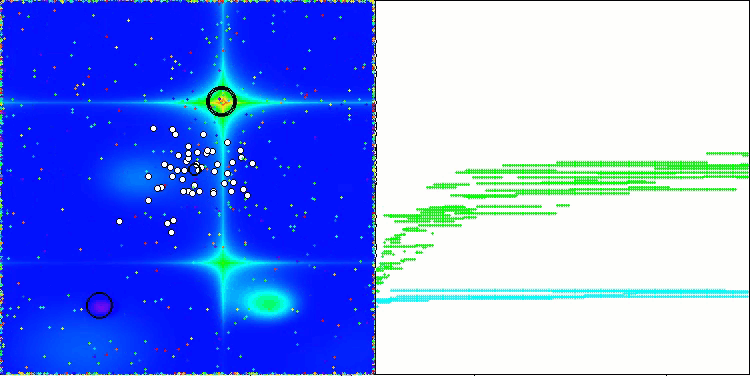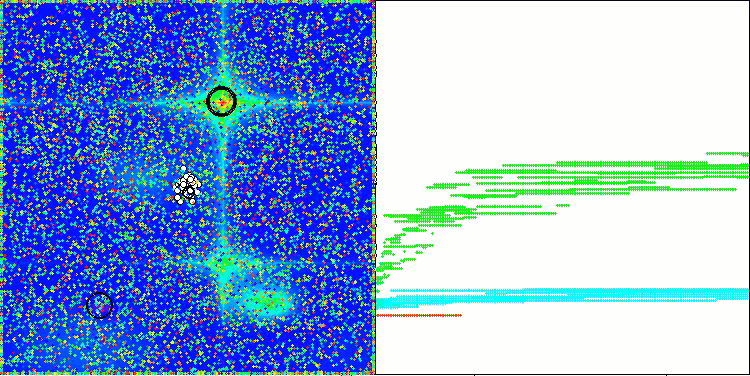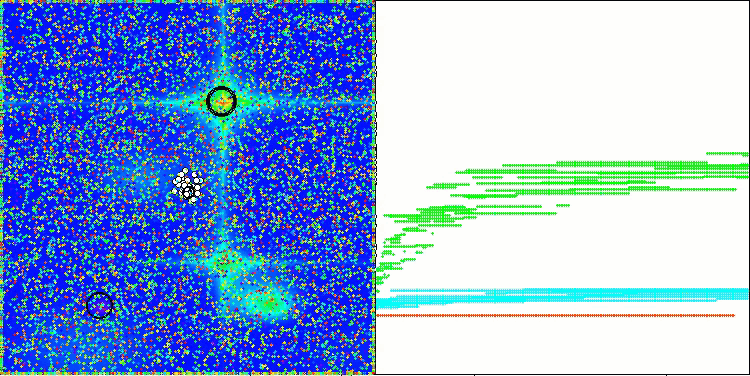
因此，我选择了经过修改的算法，并将其添加到了排名表中。算法的可视化结果如下。我认为它相当不错。当然，结果存在一定的分散性，不但不重要，而且仅仅出现在坐标数量较少的函数中。

Hilly值

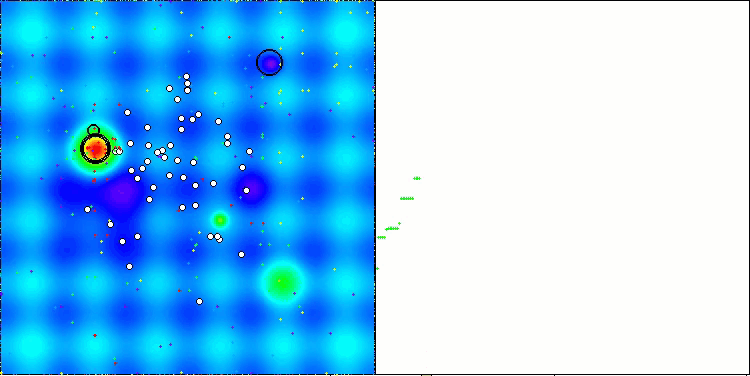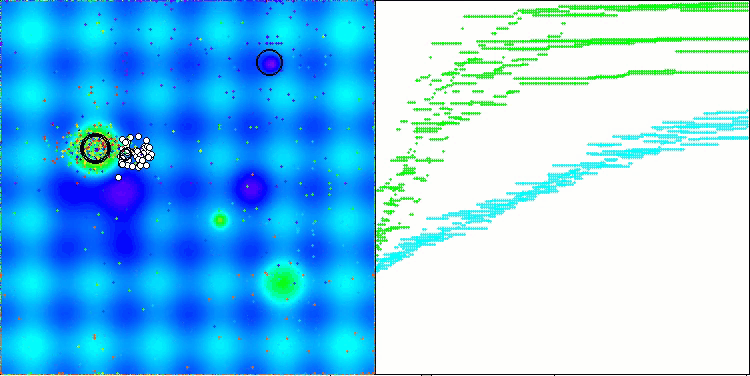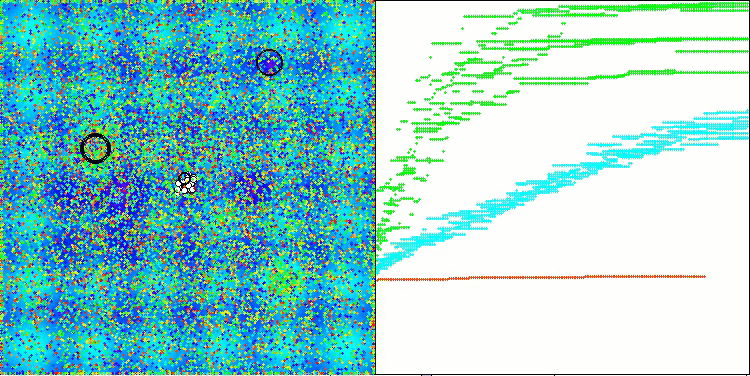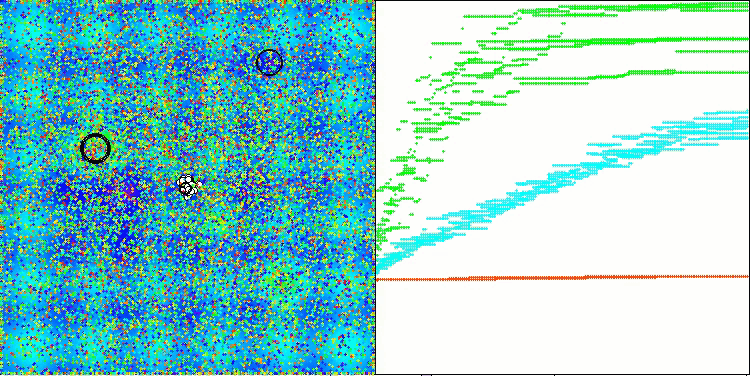
AAm在Hilly测试函数上

Forest值

AAm在Forest测试函数上

Megacity

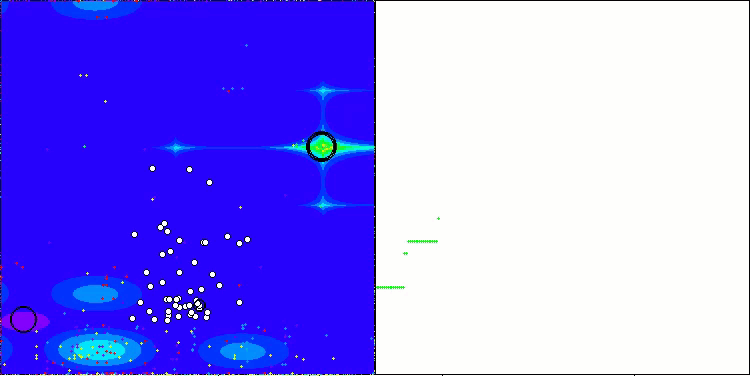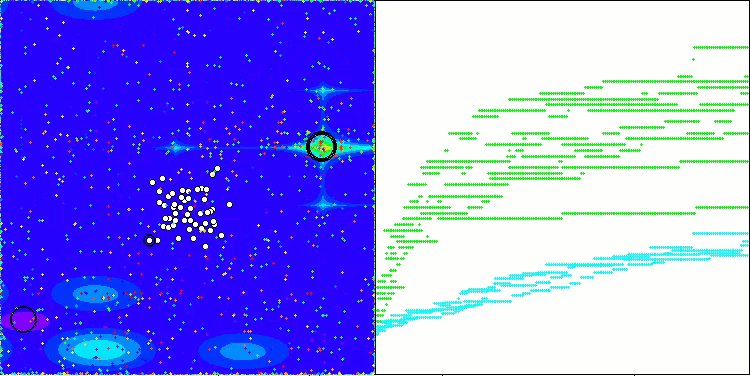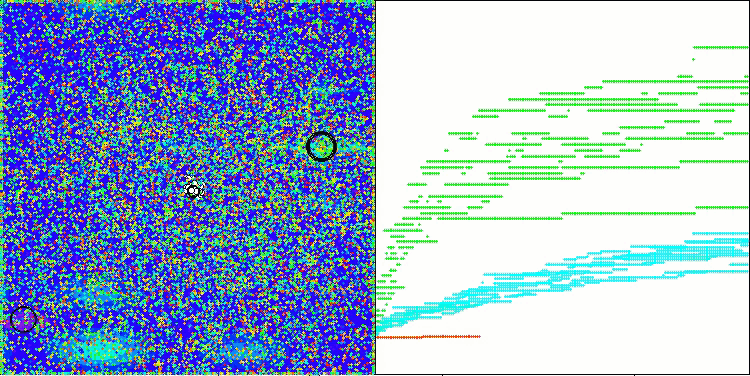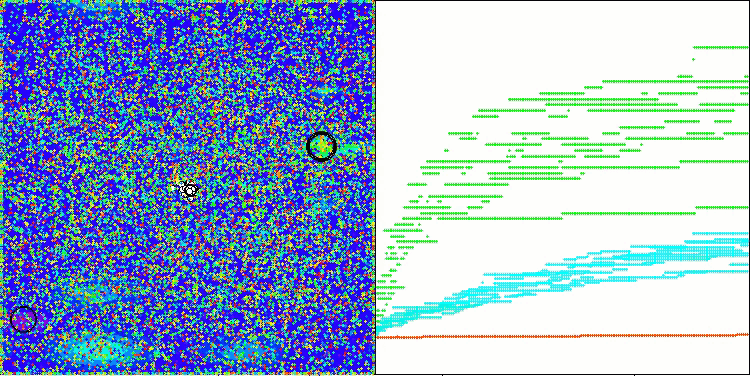
AAm在Megacity测试函数上

根据运行结果，经过修改的算法版本排名第26位。

#	AO	说明	Hilly值			Hilly最终值	Forest值			Forest最终值	Megacity (离散)			Megacity最终值	最终结果	最大百分比
#	AO	说明	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最终值	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最终值	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最终值	最终结果	最大百分比
1	ANS	跨邻域搜索	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	密码锁算法	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	动物迁徙优化M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) 进化策略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星尾算法	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	社会群体的进化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	模拟各向同性退火	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	人工协同搜索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	无序社会优化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	龟壳演化算法	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	差分进化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	化学反应优化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	鸟群算法	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	BCOm	细菌趋化性优化算法M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
18	(PO)ES	(PO) 进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
19	TSm	禁忌搜索M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
20	BSO	头脑风暴优化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
21	WOAm	鲸鱼优化算法M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
22	AEFA	人工电场算法	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
23	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
24	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
25	ABHA	人工蜂巢算法	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
26	AAm	射箭算法M	0.93532	0.67983	0.25966	1.87481	0.57351	0.22007	0.14870	0.94228	0.63077	0.34400	0.10194	1.07671	3.894	43.26
27	ASBO	适应性社会行为优化	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
28	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
29	IWO	入侵杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
30	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
31	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
32	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
33	NMm	Nelder-Mead方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
34	FAm	萤火虫算法 M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
35	GSA	引力搜索算法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
36	BFO	细菌觅食优化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
37	ABC	人工蜂群	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
38	BA	蝙蝠算法	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
39	AAA	人工藻类算法	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
40	SA	模拟退火	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
41	IWDm	智能水滴 M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
42	PSO	粒子群优化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
43	Boids算法	虚拟生物算法	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
44	MA	猴群算法	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
45	SFL	混合蛙跳算法	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38

总结

我呈现了算法的两个版本：原始版本和经过修改的版本，后者只进行了微小的改动，但却显著提高了性能。本文清楚地表明，即使是算法逻辑的微小调整，也能在各种任务中显著提高效率。同时，这也表明复杂的描述可能会让人难以理解算法的工作原理，从而阻碍其改进。相反，用简单的语言表达复杂的概念，可以为更高效的解决方案铺平道路。

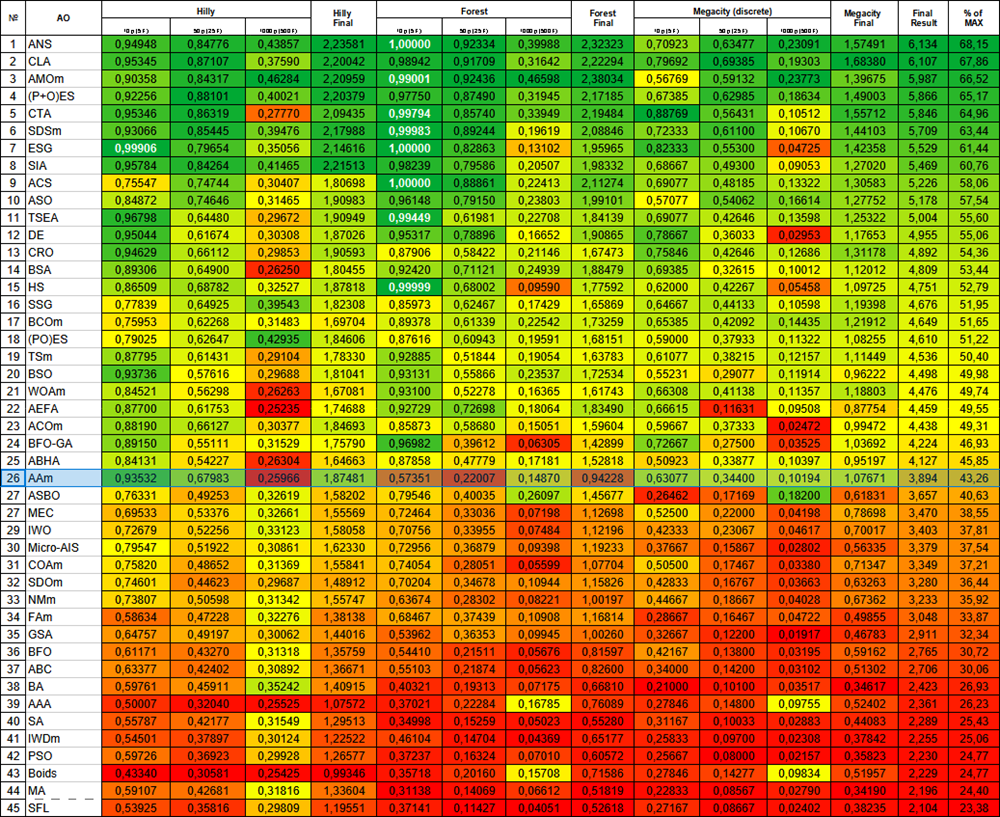
图1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

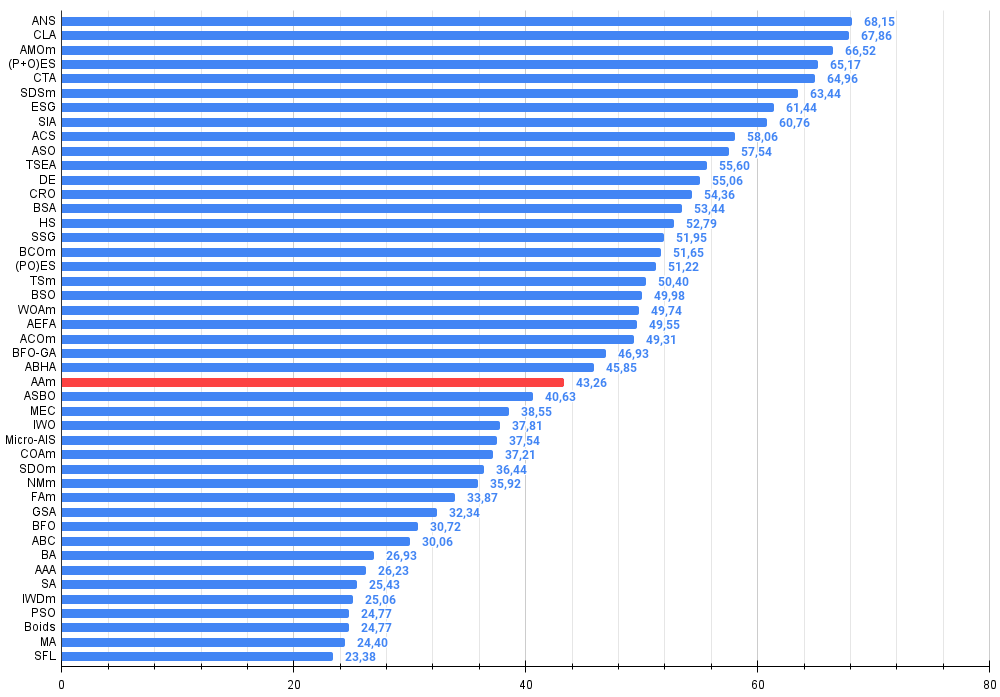
图例2. 算法测试结果的直方图（评分范围为0到100，越高越好，其中100为理论上的最高可能得分，档案中附有计算排名表的脚本）

文章即将完成并准备发表时，我突然有了一个想法，决定进行测试。如果按照作者关于目标和射箭者使用“轮盘赌”方法进行选择的逻辑，我们是否可以将目标本身的大小与找到的解决方案的质量成反比地调整呢？如果解决方案质量较高，那么应该对其进行细化，并探索其周围区域。反之，如果结果并不显著，则需要扩大搜索范围，以识别新的、潜在的有希望的区域。

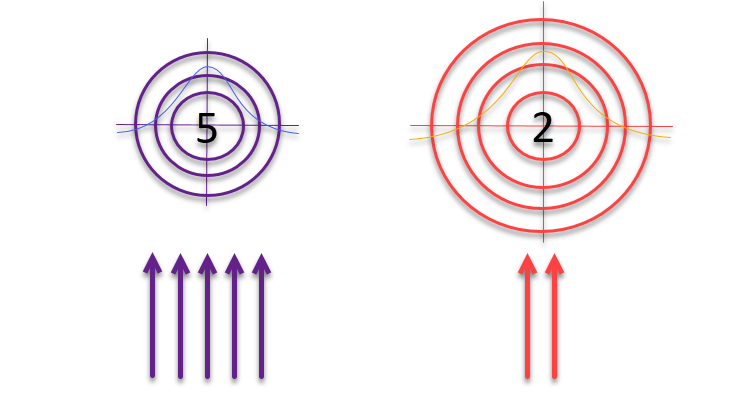
图例3. 射中目标的箭矢数量与目标本身的质量成正比，而目标的大小与它们的质量成反比

让我们看一下这段代码，其增加了目标大小与质量成反比的思路。

void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX; // a[ArrayMaximum(a, WHOLE_ARRAY, 0, popSize)].f;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst; ////F_worst - a[i].f;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;
  
  double maxFF = fB;
  double minFF = DBL_MAX;
  double prob1;
  double prob2;
  
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < minFF) minFF = a [i].f;
  } 

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        
        // Update position using Eq. (5) and (6)
        //double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);
        /*
        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
        */
        
        prob1 = u.Scale (a [i].f, minFF, maxFF, 0, 1);
        prob2 = u.Scale (a [k].f, minFF, maxFF, 0, 1);
        
        x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2);  
        
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//—

1. 原始版本中被注释的部分使用了if-else条件结构来确定如何更新智能体的位置。此逻辑已经被移除，并替换为一种新的计算方式。

2. 三条新的代码行：

prob1 = u.Scale(a[i].f, minFF, maxFF, 0, 1);
prob2 = u.Scale(a[k].f, minFF, maxFF, 0, 1);

x = agent[i].cPrev[c] + rnd * (a[k].c[c] - agent[i].cPrev[c]) * (1 - prob1 - prob2);

由此引入了一种计算更新位置的新方法：

a) 通过Scale函数计算出两个概率值（prob1和prob2），该函数根据最小适应度值minFF和最大适应度值maxFF，将智能体i和k的适应度值归一化到0到1的范围内。

b) 然后使用这些概率计算新的x位置。其使用了agent [i].cPrev [c]智能体的i前一个位置、a [k].c [c]所选射箭者k的位置以及rnd随机因子。

c) 当前的移动行为受到两个智能体适应度值之和与1的差值影响。作为一个缩放因子，允许目标根据所选射箭者的适应度成反比地扩展或收缩。射箭者越不熟练，箭的分布就越广，但击中目标的概率分布仍然遵循正态分布。

现在我们来看一下结果：

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9174358826544864
25 Hilly's; Func runs: 10000; result: 0.7087620527831496
500 Hilly's; Func runs: 10000; result: 0.42160091427958263
=============================
5 Forest's; Func runs: 10000; result: 0.9252690259821034
25 Forest's; Func runs: 10000; result: 0.7580206359203926
500 Forest's; Func runs: 10000; result: 0.353277934084795
=============================
5 Megacity's; Func runs: 10000; result: 0.6738461538461538
25 Megacity's; Func runs: 10000; result: 0.552
500 Megacity's; Func runs: 10000; result: 0.23738461538461658
=============================
总分: 5.54760 (61.64%)

算法的性能显著提升。在以下可视化结果中，我们可以看到算法的稳定收敛以及对函数曲面重要区域的识别。

Hilly2

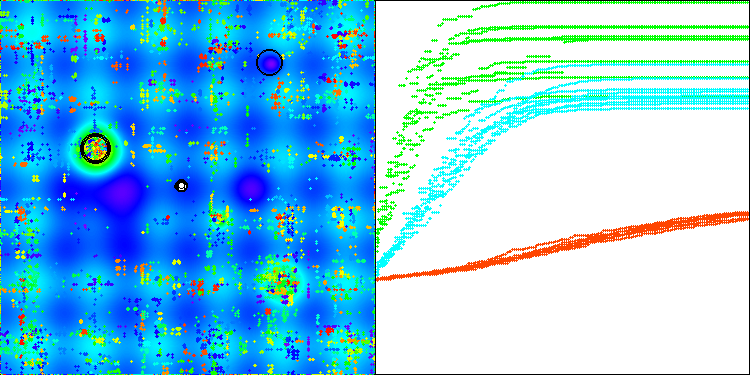
AAm在Hilly测试函数上

让我们再做一个小实验。上面的结果是从1中减去射箭者概率之和从而得到的。

//x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2); 
 x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (2 - prob1 - prob2);

主要的变化是从2中减去概率之和，而不是从1中减去。让我们看看这样一个简单的操作如何影响算法的行为：

在之前的版本中，如果两个射箭者的适应度都很高，这个操作结果可能是负数，从而在新射箭者的坐标中产生“突变”效应。
在新版本中，乘数将是一个介于0到2之间的值。

这一变化使得智能体在移动时加大幅度，更积极地探索解空间，因为智能体在每次位置更新时会迈出更大的步伐。

因此，正如算法结果的打印输出所示，这一改变在中等维度的函数上提高了算法的收敛性，但也导致了在高维函数（用黄色标记）上的性能下降，尽管总体上算法得到了更高的最终得分。

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9053229410164233
25 Hilly's; Func runs: 10000; result: 0.8259118221071665
500 Hilly's; Func runs: 10000; result: 0.2631661675236262
=============================
5 Forest's; Func runs: 10000; result: 0.9714247249319152
25 Forest's; Func runs: 10000; result: 0.9091052022399436
500 Forest's; Func runs: 10000; result: 0.2847632249786224
=============================
5 Megacity's; Func runs: 10000; result: 0.7169230769230768
25 Megacity's; Func runs: 10000; result: 0.6378461538461538
500 Megacity's; Func runs: 10000; result: 0.10473846153846252
=============================
总分: 5.61920 (62.44%)

之前的版本看起来更实用，将其保留作为AAm算法修改版的主要版本。我将再次展示带有热力分级的排名表。AAm现在占据了当之无愧的第7位。该算法可以被描述为非常平衡（在不同维度的函数上收敛良好），可以推荐其用于解决不同的问题。

Tab2

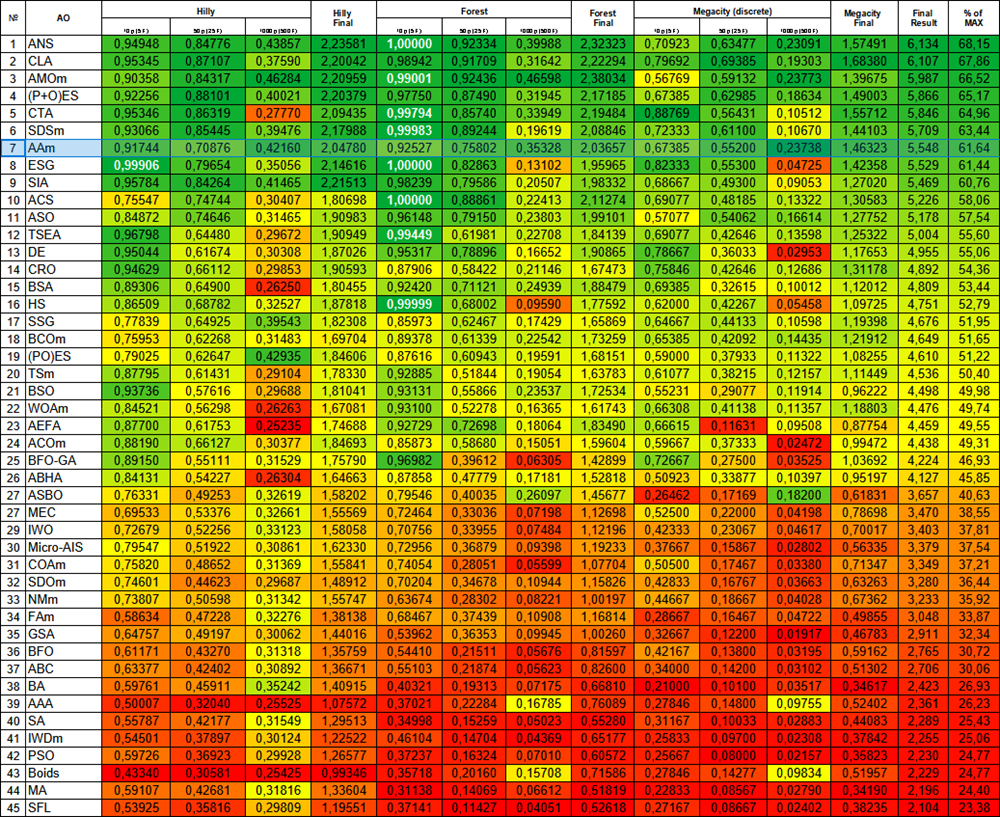
图例 4. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

AAm的优缺点：

优点：

速度相当快。
自适应性。
只有一个外部参数。
良好的收敛性。
良好的扩展性。
实现简单（尽管作者的描述较复杂）。

缺点：

在低维函数上易陷入局部最优。

进一步在评分表中新增算法会导致表格的可读性下降。因此，我决定将参与评分的算法数量限制为45种，并将竞赛改为“淘汰制”模式。为便于读者以直观且流畅的方式访问所有相关文章，我制作了一份HTML文件，其中包含按评分排序的已评审算法列表。该文件已在文章中存档了一段时间，首次打开它的读者还会发现一个小彩蛋。”

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/15782

附加的文件 |

下载ZIP

AAm.zip (35.89 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

最近评论 | 前往讨论 (2)

Ilya Melamed | 13 9月 2024 在 18:11

感谢您的研究。但作为 mql5 上 Expert Advisors 的一名普通程序员（我不是数学家），我有一个非常简单的问题。这个问题对您来说可能很愚蠢，我在此先向您道歉。但是，您的研究对优化 EA 有什么帮助？您能举个例子吗？比方说，我们有一个新的 EA，我们想优化它，....？谢谢。

Andrey Dik | 14 9月 2024 在 18:23

Ilya Melamed 优化 EA 有什么帮助？您能举个例子吗？比方说，我们有一个新的 EA，我们想优化它，....？谢谢。

感谢您对我工作的关注和提出的好问题。

应用优化算法的场景有很多，只要您想在可能的解决方案中获得最佳方案。

例如，您可以将其应用于 EA 的自我优化，如此处所述。

或者可以将其作为内部测试人员优化管理的一部分，如此处所述。

量化风险管理方法：应用 VaR 模型优化多货币投资组合（使用 Python 和 MetaTrader 5）

本文探讨了价值风险（VaR）模型在多货币投资组合优化中的潜力。借助 Python 的强大功能和 MetaTrader 5 的功能，我们展示了如何实施 VaR 分析，以实现高效的资金分配和头寸管理。从理论基础到实际实施，文章涵盖了将 VaR——这一最稳健的风险计算系统之一——应用于算法交易的方方面面。

高效处理指标的便捷方法

在本文中，我将介绍如何制作一个简单的面板，以便直接从图表中更改指标设置，以及需要对指标进行哪些更改以连接该面板。本文面向 MQL5 的新手用户。

在Python和MQL5中应用局部特征选择

本文探讨了Narges Armanfard等人在论文《数据分类的局部特征选择》中介绍的一种特征选择算法。该算法使用Python实现，用于构建二元分类器模型，这些模型可以与MetaTrader 5应用程序集成以进行推理。

开发回放系统（第 61 部分）：玩转服务（二）

在本文中，我们将研究使回放/模拟系统更高效、更安全地运行的修改。我也不会对那些想要充分利用这些类的人置之不理。此外，我们将探讨 MQL5 中的一个特定问题，即在使用类时降低代码性能，并解释如何解决它。