种群优化算法：鲸鱼优化算法（WOA）

内容

1. 概述
2. 算法
3. 测试结果

1. 概述

座头鲸是雄伟的海洋巨兽，也是海洋的主宰。当座头鲸开始它们的狩猎之舞时，时间仿佛静止了，每一个动作都充满了优雅与精准。这些气泡网大师会发射出一串串气泡形成的水幕，将猎物限制并聚集在圆环的中心。这种独特的觅食方式凸显了它们在狩猎过程中的智慧和战略思维。

它们与其他个体，甚至是陌生个体之间的动作同步，展现了深刻的相互理解和团结，证明了它们无论在任何情况下都具备集体工作和协调的能力。

它们每天能消耗多达1.4公吨食物的能力，凸显了它们在海洋生态系统中作为最强大的消费者之一的地位。它们的生活节奏，从丰富的狩猎期到平静禁食期的交替，向我们讲述了它们所统治的海洋的伟大与不可预测性。在冬季，座头鲸几乎不进食，这证明了它们惊人的生存能力。它们依靠在食物丰富时积累的脂肪储备，在食物稀缺时维持生存。这提醒我们，大自然是如何教会动物们节约地和明智地使用资源的。

座头鲸是生存与适应的活生生的编年史，是智慧的象征，是海洋力量和美丽的化身，也是我们取之不尽的灵感源泉。

鲸鱼优化算法（WOA）是由Mirjalili和Lewis于2016年提出的一种元启发式优化算法。该算法的灵感来源于鲸鱼的狩猎行为。

鲸鱼采用多种狩猎策略，包括“气泡网”（bubble net）和“螺旋穿透”（spiral penetration）。在“气泡网”策略中，鲸鱼通过制造一个气泡“网”来包围猎物，使猎物迷惑和害怕。而在“螺旋穿透”策略中，鲸鱼以螺旋运动从海洋深处上升，以捕获猎物。

这些狩猎策略在WOA算法中被抽象地建模。在WOA算法中，“鲸鱼”代表优化问题的解决方案，而“狩猎”则代表寻找最优解的过程。

2. 算法

WOA算法首先通过随机位置初始化一群鲸鱼。然后选择一个领导者——即目标函数值最优的鲸鱼（实际上是全局最优解）。其余鲸鱼的位置会根据领导者的位置进行更新。这发生在两种模式下：探索模式和利用模式。在探索模式下，鲸鱼会围绕当前全局最优解进行随机搜索，以更新其位置。在开发模式下，鲸鱼会向其当前的最优解靠近，以更新其位置。

WOA算法已成功解决了许多优化问题，并取得了良好的效果。然而，与其他优化算法一样，它也有其优缺点。例如，它可能容易陷入局部最优解，并且收敛速度相对较慢。

以下是关于如何将座头鲸的有趣事实与鲸鱼优化算法（WOA）原理相关联的说明：

• 合作与协调。座头鲸经常群体狩猎，相互合作以实现共同的成功。这与鲸鱼优化算法的原理相呼应，在该算法中，各个智能体（如鲸鱼）协同工作，交换信息并协调行动，以找到最优解。

• 智能策略。座头鲸采用多种智能狩猎策略，如气泡网捕食法和群体协作法。鲸鱼优化算法（WOA）同样基于智能优化策略，包括寻找最优解和适应不断变化的环境。

• 适应性和效率。座头鲸在狩猎过程中展现出适应性和效率，根据具体情况改变对策。鲸鱼优化算法也通过应用各种优化策略和改变其行为来追求适应性和效率，以获得更好的结果。

因此，鲸鱼优化算法从座头鲸独特的狩猎策略和行为中汲取灵感，这有助于它高效且智能地解决各种领域的优化问题。

经过改进的鲸鱼优化算法（WOAm）包括以下几个主要阶段：

1. 向全局最优解移动：
- 在算法的初始阶段，每个“鲸鱼”（即每个解决方案）都向全局最优解移动。这有助于探索解空间，并找到通向最优解的大致方向。

2. 改善自身位置：
    - 每只鲸鱼都试图改进其当前位置，以接近一个更好的解决方案。个体鲸鱼可以改变其参数或策略，以实现更好的性能。

3. 螺旋运动：
- 此阶段是鲸鱼优化算法（WOA）中的一个重要机制。鲸鱼可以围绕最佳解决方案进行螺旋运动，这有助于它们更有效地探索搜索空间区域，并逐步接近最优解。

4. 迁移：
    - 此步骤涉及随机改变个体的位置，以增加多样性并防止算法陷入局部最优解。迁移有助于避免算法过早收敛从而获得非最优解决方案。

这些步骤共同协作，在优化问题的解空间中高效地搜索得到最优解。我添加的第四阶段——迁移，提高了该算法的抗卡滞性。当先前的食物来源耗尽时，模拟鲸鱼在野外迁移到新领地继续寻找食物的过程是必要的。这一增加赋予了算法额外的灵活性，并帮助它更有效地探索解空间，这反映了自然界中的生存和适应策略。

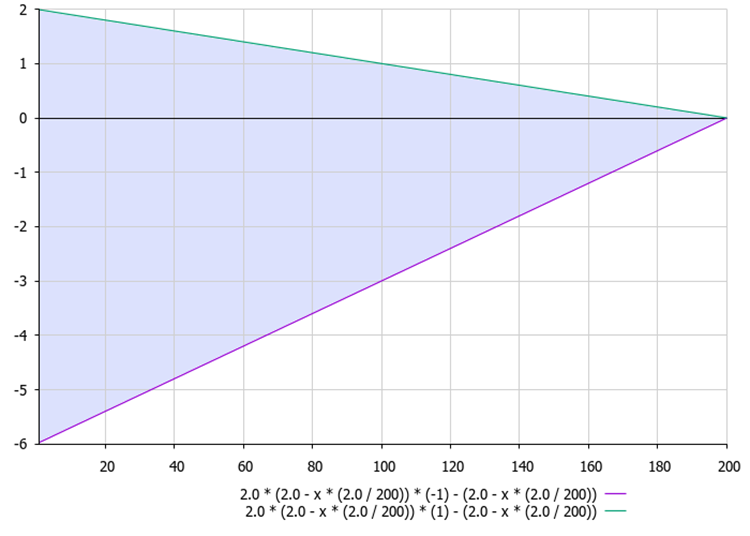
Figure 1. 方程A=2.0*aKo*r-aKo中A比值的范围取决于当前阶段

鲸鱼优化算法（WOAm）的伪代码：

1. 使用随机定位初始化种群。
2. 计算体能。
3. 计算aKo比率：aKo = 2.0 - epochNow * (2.0 / epochs)。
4. 从-1到1的均匀分布中生成随机数“r”。
5. 计算变量A和C：
   - A = 2.0 * aKo * r - aKo (figure 1)
   - C = 2.0 * r
6. 设置“spiralCoeff”值、均匀分布中的随机数“l”和随机概率“p”值。
7. 如果"p"小于"refProb"：
   - 如果A的绝对值大于1.0：X = Xbest - A * |Xbest - Xprev|
   - 否则，选择从0到“popSize”的随机索引“leaderInd”，且X = Xlead - A * |Xlead - Xprev|
8. 除此之外，如果随机概率小于spiralProb：X = Xprev + | Xprev - X| * exp (b * l) * cos (2 * M_PI * l)
9. 除此之外：X = PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30)
10. 计算体能。
11. 更新全局解。
12. 从步骤 3 开始重复，直到满足停止规则。

Figure 2. “气泡”捕鲸法——启发WOA的灵感来源

让我们继续编写WOAm算法的代码。

定义结构“S_WOA_Agent”用于描述每头鲸鱼。让我们来看看当前的进展：

1. 该结构包含以下字段：
    - cPrev[] - 用于存储先前智能体坐标的数组。
    - fPrev - 用于存储先前评估智能体（适合性）的变量。

2. Init - "S_WOA_Agent" 结构方法，初始化结构字段。它接受“coords”整数参数，使用ArrayResize函数调整“cPrev”数组的大小。

3. fPrev = -DBL_MAX - 将“fPrev”变量的初始值设置为双精度类型的最小可能值。

该代码表示WOAm优化算法中智能体的基本数据结构，并在新建智能体时完成字段的初始化。

//——————————————————————————————————————————————————————————————————————————————
struct S_WOA_Agent
{
    double cPrev []; //previous coordinates
    double fPrev;    //previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们来定义WOAm算法的“C_AO_WOAm”类，它是“C_AO”种群算法基类的继承者，其包含以下字段和方法：

1. 公共字段:

• <b0>ao_name </b0>- 优化算法名称。
• <b0>ao_desc </b0>- 优化算法描述。
• <b0>popSize </b0>- 种群规模。
• <b0>params </b0>- 算法参数数组。
• refProb - 优化概率。
• spiralCoeff - 螺旋比。
• spiralProb - 螺旋概率。
• agent - 智能体载体。

2. 可用的选项有：

• C_AO_WOAm - 初始化类字段的类构造函数。
• <b0>SetParams </b0>- 算法参数设置方法。
• <b0>Init </b0>- 算法初始化方法。该方法需要最小和最大搜索范围、搜索步长和迭代次数。
• <b0>Moving </b0>- 智能体移动方法。
• <b0>Revision </b0>- 智能体修改方法。

3. 私有字段：

• epochs - 迭代次数。
• epochNow - 当前迭代数。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_WOAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_WOAm () { }
  C_AO_WOAm ()
  {
    ao_name = "WOAm";
    ao_desc = "Whale Optimization Algorithm M";

    popSize = 100;   //population size


    ArrayResize (params, 4);

    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "refProb";     params [1].val = refProb;
    params [2].name = "spiralCoeff"; params [2].val = spiralCoeff;
    params [3].name = "spiralProb";  params [3].val = spiralProb;
  }

  void SetParams ()
  {
    popSize     = (int)params [0].val;
    refProb     = params      [1].val;
    spiralCoeff = params      [2].val;
    spiralProb  = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double refProb;     //refinement probability
  double spiralCoeff; //spiral coefficient
  double spiralProb;  //spiral probability


  S_WOA_Agent agent []; //vector

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
};
//——————————————————————————————————————————————————————————————————————————————

根据传递的参数使用“C_AO_WOAm”类的Init方法初始化类变量。该方法使用 StandardInit 方法执行标准初始化，需要输入最小搜索范围、最大搜索范围以及搜索步长作为参数。

如果标准初始化成功，该方法将继续初始化“epochs”（迭代次数）和“epochNow”（当前迭代数）这两个变量。设置“epochs”的值为传入的参数“epochsP”，而“epochNow”则被初始化为0。

该方法将“agent”（智能体）数组的大小调整为“popSize”的大小。对于“agent”（智能体）中的每个元素，都会调用 Init 方法，并传入一个名为 "coords" 的参数。

如果初始化成功，该方法返回“true”，否则返回“false”。

该方法使用给定的参数对WOAm优化算法进行初始化设置，并且准备好在给定的迭代次数内执行优化。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_WOAm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

使用“C_AO_WOAm”类的Moving方法在优化过程中移动智能体。该方法执行以下操作：

"epochNow++" - 当前迭代值增加。

"if (!revision)" - 检查"revision"是否为"false"。

如果 "revision"是"false"，接下来：

• 使用指定范围内的随机值初始化智能体的坐标“a[i].c[c]”。
• 设置"revision" 标识为"true"。
• 用该方法完成工作。

如果"revision" 标识为"false"，接下来：

• 对于每个智能体，使用特定的方程和概率计算新的坐标。
• 通过各种数学计算、随机数和概率确定智能体的新坐标。
• 新的“x”坐标是根据条件和概率计算得出的。
• 使用SeInDiSp方法设置新坐标“a[i].c[c]”，该方法根据搜索范围和步长调整取值。

该方法负责根据当前迭代次数、随机值和概率，更新WOAm算法中智能体的坐标。让我们用颜色高亮代码中描述鲸鱼不同行为模式的部分：

优化全局解： 随着每次更新迭代，鲸鱼根据线性规律和计算出的A比率更仔细地在已发现的全局解附近探索，试图更接近全局最优解。

在种群“领导者”附近探索：考虑到A比率，鲸鱼在种群“领导者”附近区域探索，该“领导者”是根据均匀分布规律随机选择得到的。之后，研究继续进行，涵盖鲸鱼在种群中出现过的所有区域。

螺旋运动和“气泡”网络： 鲸鱼以螺旋模式移动，同时考虑其最优个体位置和当前位置，这确保了鱼类被聚集在密集的云团中，食物也集中在同一地点。

鲸鱼迁徙： 通过直接远离全局最佳解来模拟鲸鱼迁徙。此过程决定了处于全局解附近的个体概率高，以及远离全局解的个体概率虽然很小但也非零。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double aKo = 2.0 - epochNow * (2.0 / epochs);
      double r = u.RNDfromCI (-1, 1);
      double A = 2.0 * aKo * r - aKo;
      double C = 2.0 * r;
      double b = spiralCoeff;
      double l = u.RNDfromCI (-1, 1);
      double p = u.RNDprobab ();
      double x;

      if (p < refProb)
      {
        if (MathAbs (A) > 1.0)
        {
          x = cB [c] - A * MathAbs (cB [c] - agent [i].cPrev [c]);                                                      //Xbest - A * |Xbest - X|
        }
        else
        {
          int leaderInd = u.RNDminusOne (popSize);
          x = agent [leaderInd].cPrev [c] - A * MathAbs (agent [leaderInd].cPrev [c] - agent [i].cPrev [c]);            //Xlid - A * |Xlid - X|;
        }
      }
      else
      {
        if (u.RNDprobab () < spiralProb)
        {
          x = agent [i].cPrev [c] + MathAbs (agent [i].cPrev [c] - a [i].c [c]) * MathExp (b * l) * cos (2 * M_PI * l); //XbestPrev + |XbestPrev - X| * MathExp (b * l) * cos (2 * M_PI * l)
        }
        else
        {
          x = u.PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

使用“C_AO_WOAm”类的修订方法更新最优全局解决方案，并更新鲸鱼本身的最佳位置。该方法执行以下操作：

1. 更新全局解。在“for”循环中，该方法会遍历所有个体。如果当前个体的适应度函数值超过了当前最佳适应度值，那么就会更新这个最佳值，并将当前个体的坐标数组复制到最佳解决方案的坐标数组中。

2. 更新之前的适应度函数值和智能体坐标。在“for”循环中，该方法会遍历所有个体。如果当前个体的适应度函数值超过了之前的适应度函数值，那么就会更新该函数值，并将当前个体的坐标数组复制到之前的智能体坐标数组中。

“Revision”方法负责根据特征值更新最优智能体，同时也作为WOAm优化算法的一部分，更新之前的特征值和智能体坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

遗憾的是，作者所提出的算法基础版本仍有诸多不足之处，所展示的结果相对较弱，具体如下。

WOA|鲸鱼优化算法|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.45323929163422483
25 Hilly's; Func runs: 10000; result: 0.3158990997230676
500 Hilly's; Func runs: 10000; result: 0.25544320870775555
=============================
5 Forest's; Func runs: 10000; result: 0.43485195446891795
25 Forest's; Func runs: 10000; result: 0.2454326019188397
500 Forest's; Func runs: 10000; result: 0.1557433572339264
=============================
5 Megacity's; Func runs: 10000; result: 0.3400000000000001
25 Megacity's; Func runs: 10000; result: 0.18800000000000003
500 Megacity's; Func runs: 10000; result: 0.10146153846153938
=============================
总分: 2.49007 (27.67%)

然而，通过努力和创造力，已经取得了显著的进步，其中包括迁移和幂律分布等要素。另外，我们现在不再使用鲸鱼的当前位置作为计算下一个位置的起点，而是使用之前鲸鱼的最佳位置。这些改进使算法焕然一新，赋予了它新的特性，并显著提高了改进版本的效果。因此，该算法变得更加高效，在解决指定问题时能够取得更好的效果。

以下是WOAm改进版本的结果，其中改进幅度超过22%（其中0%表示可能的最差结果，100%表示可实现的最佳理论结果）。

WOAm|鲸鱼优化算法|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8452089588169466
25 Hilly's; Func runs: 10000; result: 0.562977678943021
500 Hilly's; Func runs: 10000; result: 0.262626056156147
=============================
5 Forest's; Func runs: 10000; result: 0.9310009723200832
25 Forest's; Func runs: 10000; result: 0.5227806126625986
500 Forest's; Func runs: 10000; result: 0.1636489301696601
=============================
5 Megacity's; Func runs: 10000; result: 0.6630769230769229
25 Megacity's; Func runs: 10000; result: 0.41138461538461535
500 Megacity's; Func runs: 10000; result: 0.11356923076923182
=============================
总分:4.47627 (49.74%)

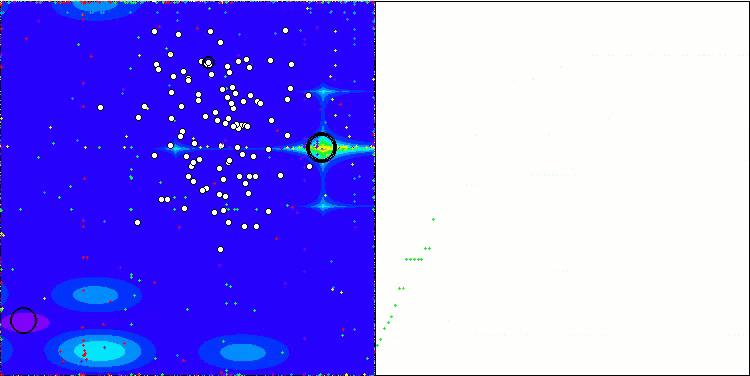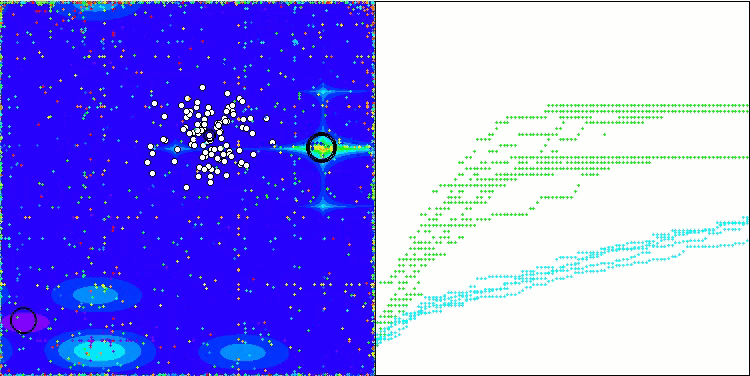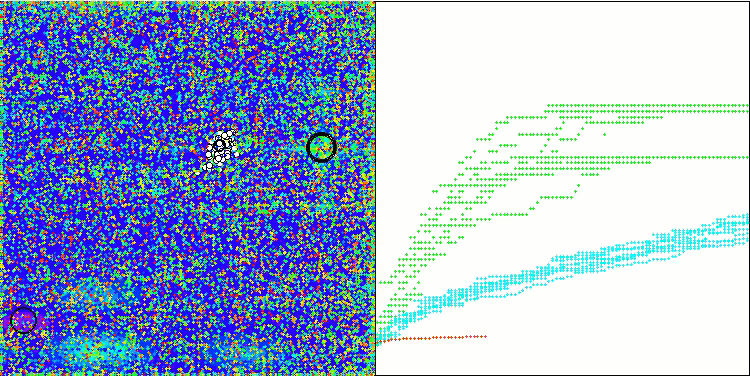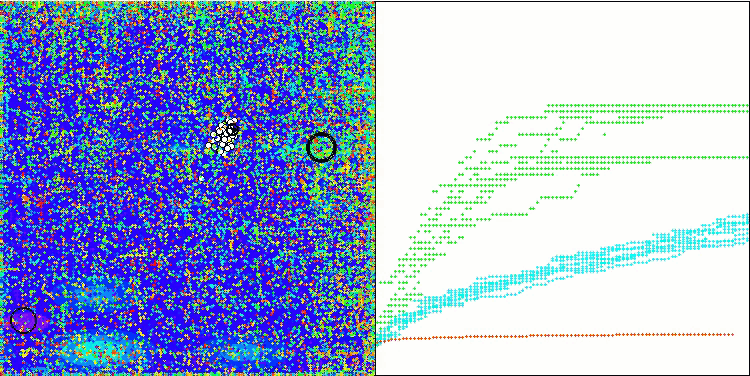
在改进版本的可视化操作中，我们可以看到Hilly函数的结果分布较为分散，而离散Megacity函数的结果分布则相对集中。值得注意的是，通常对于大多数算法来说，Megacity函数更为复杂，结果分布也更为分散。因此，WOAm算法在这个函数上表现出非常稳定和良好的结果，令人十分惊讶。

该算法成功探索了搜索空间内各区域的表面，从而找出有前景的区域。这得益于将种群的整体群居行为划分为个体动物的阶段行为，旨在分别改善每只鲸鱼的情况。

这种方法使算法能够有效地探索搜索空间以找到最优解，同时专注于改善群体中个体智能体的位置。这有助于更精确且深入地探索潜在的有前景的区域，进而提高了算法的整体性能。

该可视化中未显示基础版本。另外，提供了算法在Ackley测试函数上操作的可视化。请注意，该函数不参与评分表的计算排名。

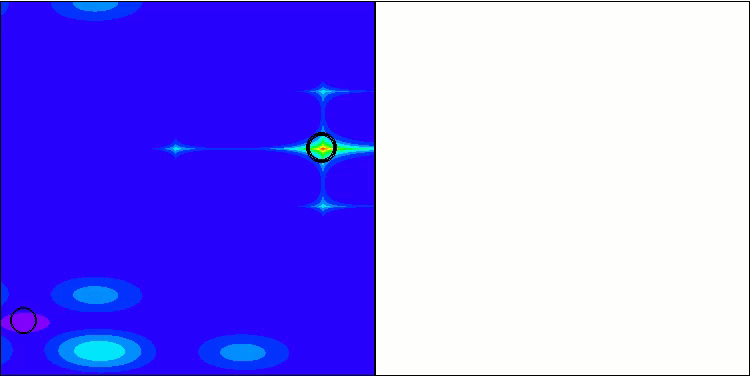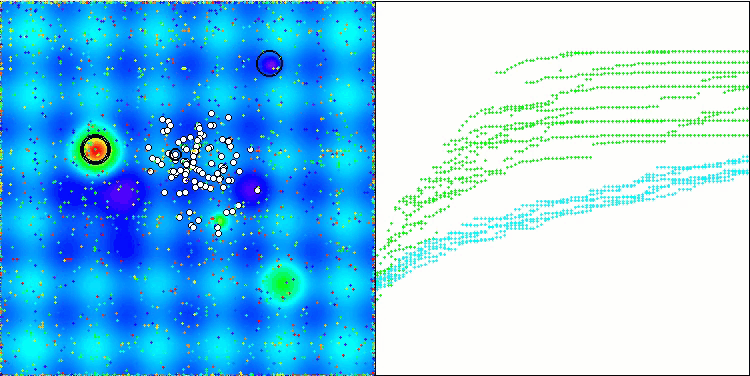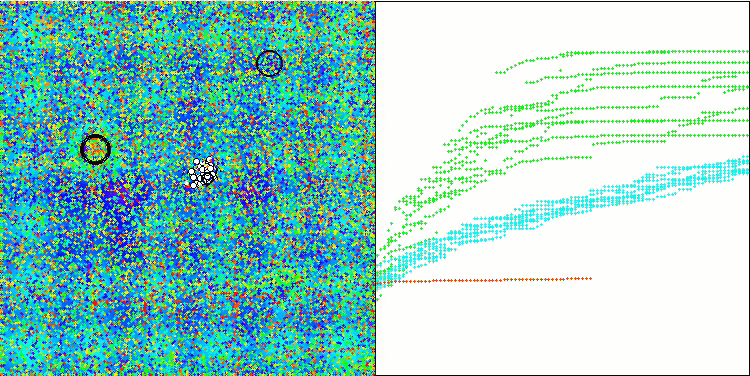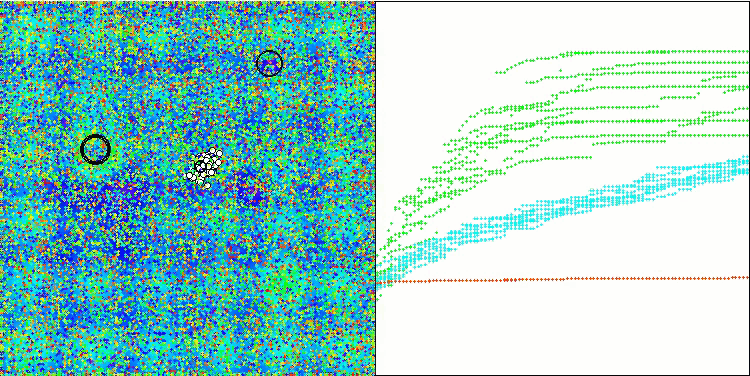
  WOAm在 Hilly 测试函数上

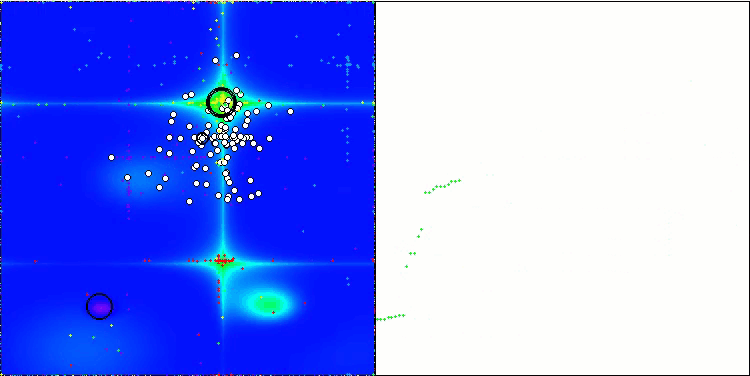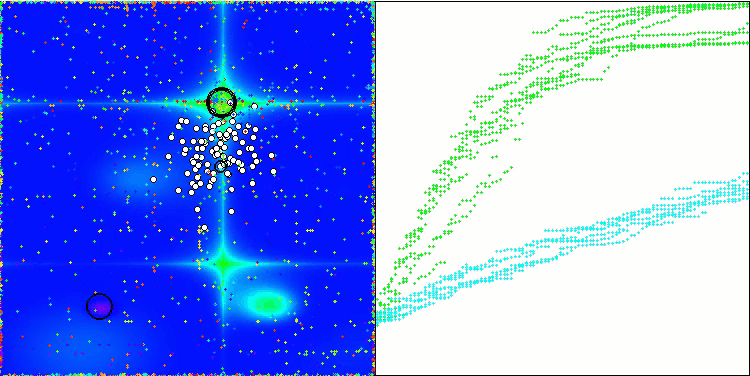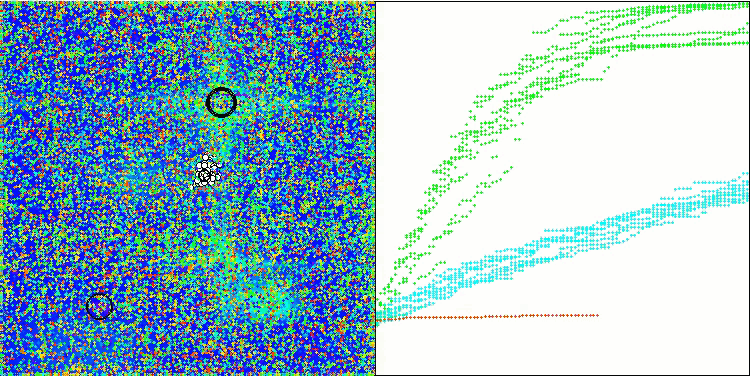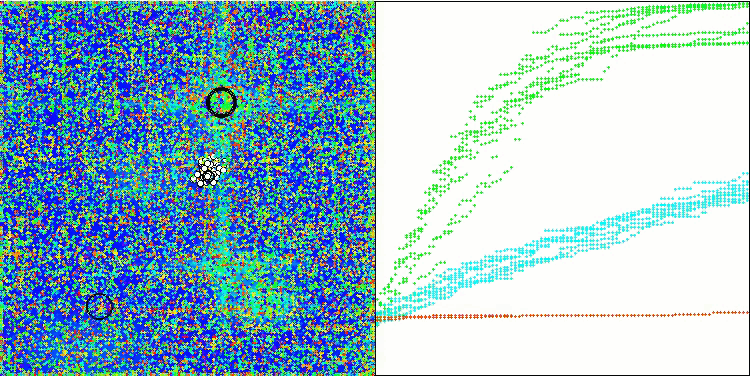
  WOAm在 Forest 测试函数上

  WOAm在 Megacity 测试函数上

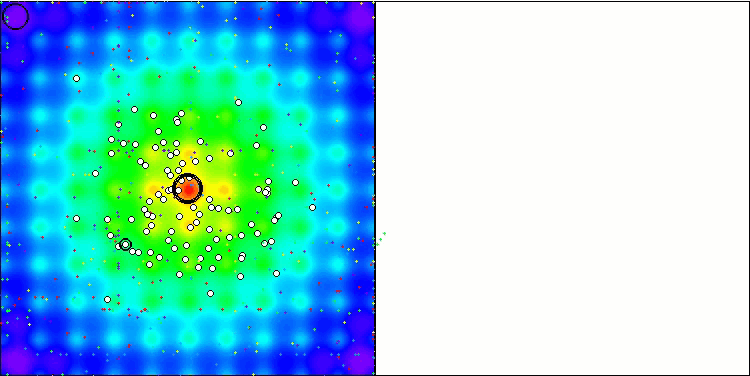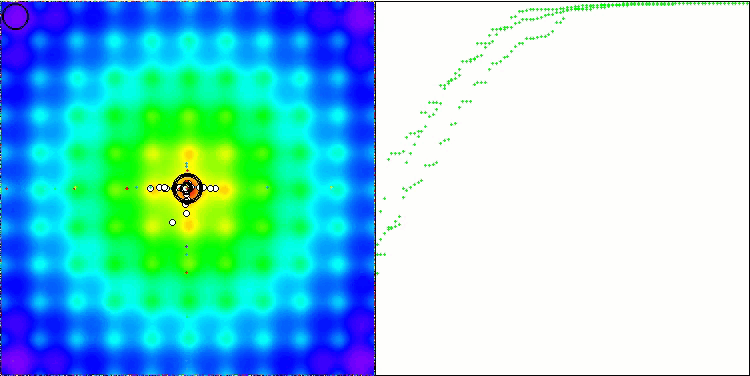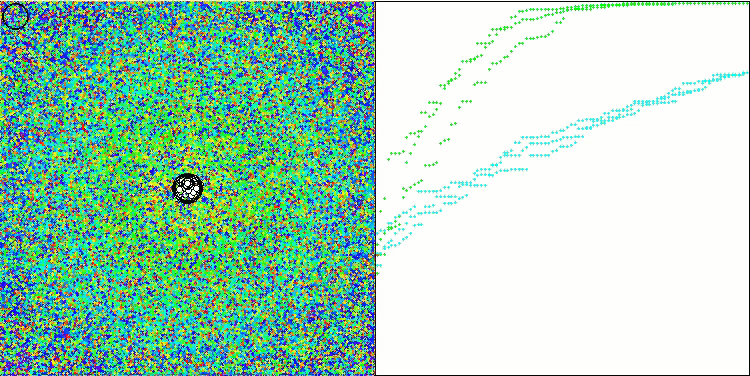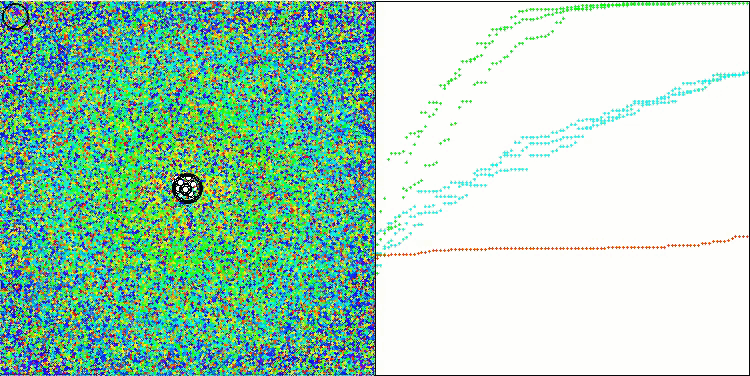
  WOAm在 Ackley 测试函数上

改进后的WOAm算法在表格上半部排名第十，整体结果良好且稳定。 

#	AO	说明	Hilly值			Hilly最终值	Forest值			Forest最终值	Megacity (离散)			Megacity最终值	最终结果	最大百分比
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	二进制遗传算法	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O) 进化策略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	社会群体的进化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	模拟退火算法	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	DE	差分进化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
7	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
8	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
9	(PO)ES	(PO) 进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
10	WOAm	鲸鱼优化算法M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
11	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
12	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
13	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
14	IWO	入侵杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
15	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
16	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
17	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
18	NMm	Nelder-Mead方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
19	FAm	萤火虫算法 M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
20	GSA	引力搜索算法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
21	BFO	细菌觅食优化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
22	ABC	人工蜂群	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
23	BA	蝙蝠算法	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
24	SA	模拟退火	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
25	IWDm	智能水滴 M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
26	PSO	粒子群优化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
27	MA	猴群算法	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
28	SFL	混合蛙跳算法	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
29	FSS	鱼群搜索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
30	RND	随机	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
31	GWO	灰狼优化算法	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
32	CSS	人工电场算法	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
33	EM	类电磁算法	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

总结

总体而言，我对本文所述的对该算法所做的改进感到满意。然而，对于这一版本的修订还有待更深入地研究，很适合对这一主题充满兴趣并渴望做进一步实验的人。深入研究这些技术可以开辟新的视野，并为给定的算法激发更好的解决方案。

以下是几种可以帮助改进鲸鱼优化算法（WOA）并降低陷入局部极值可能性的策略：

1. 种群多样化种群多样性有助于避免陷入局部最优。考虑维持种群多样性的方法，如变异机制、交叉机制或解邻域研究。

2.精英策略。此策略涉及从一代到另一代维持一定数量的几种不同的最佳解决方案（精英），从而避免种群多样性的降低。

3. 多策略机制. 该方法涉及同时使用多种搜索策略，这可以帮助算法更好地探索解空间并避免局部陷阱。

4. 与其他算法杂交。将WOA与其他优化算法进行杂交也可以提高其性能。例如，我们可以使用差分进化或粒子群算法来改进WOA算法的探索阶段。

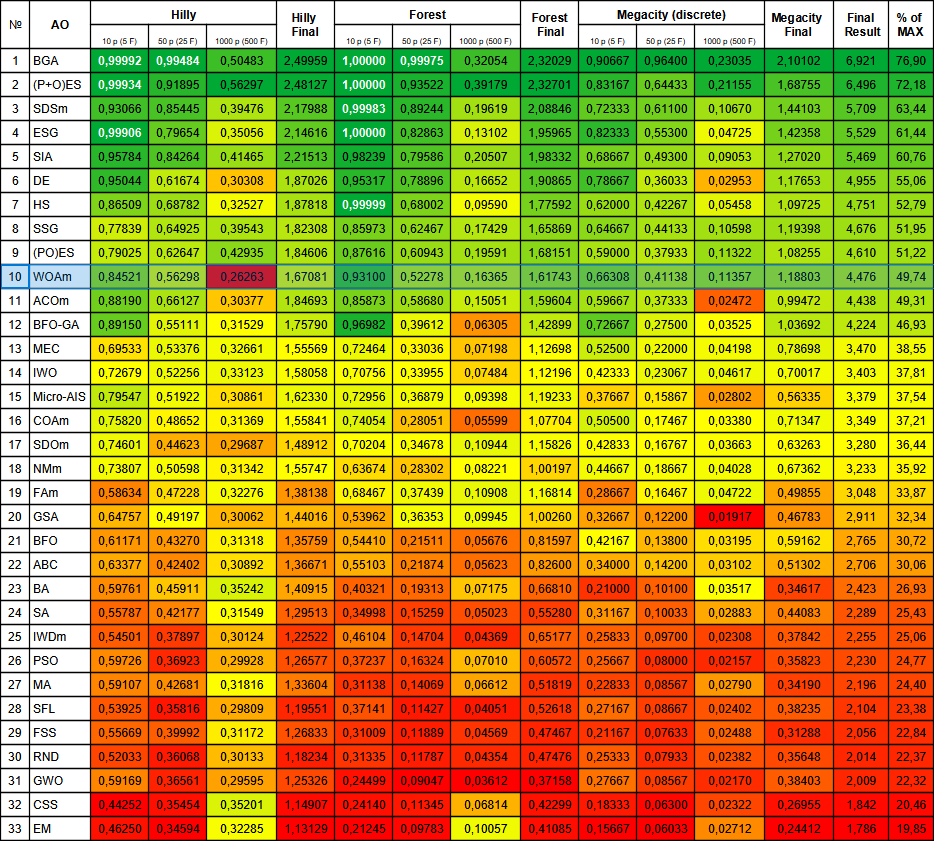
Figure 3. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

在具有1000个变量的平滑Hilly函数上，数值单元格的颜色值得注意，表明该结果在表格里所有列出的算法中表现最差。此外，我还想指出，对于具有五个变量的Forest函数，其性能指标很高，并且Forest和Megacity函数的整体性能也普遍良好。

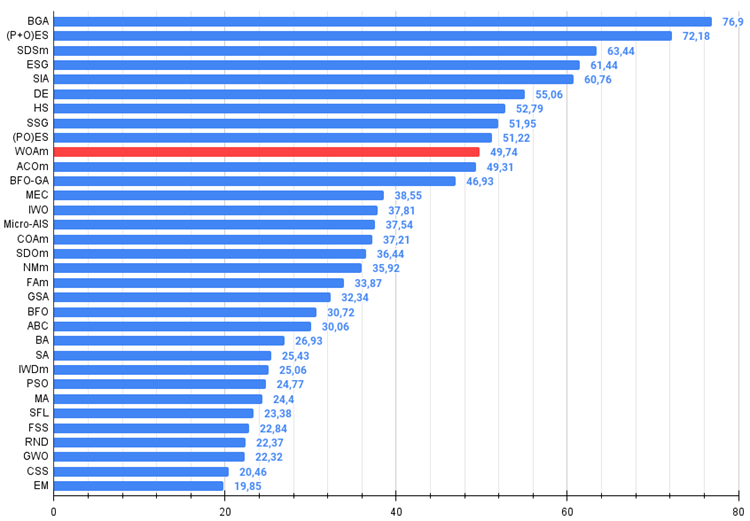
Figure 4. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）。

WOAm算法优缺点：

优势：

1. 简单的架构和实现。
   
2. 在陡峭的Forest函数和离散Megacity上取得了稳定且良好的结果。
3. 对计算资源要求不高。

缺点：

1. 低收敛性（无法接近100%的结果）。
2. 在诸如Hilly等平滑函数上，可扩展性低（高维任务存在问题）。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。