群体优化算法：差分进化（DE）

MetaTrader 5 — 示例 | 8 七月 2024, 10:57

715

Andrey Dik

1.概述

元启发式优化方法是一类使用启发式方法解决复杂优化问题的算法。它们与数值优化方法不同，后者通常基于数学分析，需要了解目标函数的梯度或导数。元启发式方法的主要区别在于，即使函数具有许多局部最优或不连续可微，它们也能探索大的搜索空间并找到全局最优。元启发式方法的优势在于可以处理 "黑盒子" - 一种没有分析解决方案的函数。它们基于随机概率原理，提供了良好的解决方案质量。

进化算法（Evolutionary algorithms，EA）是一类独立的元启发式优化方法，它模拟自然进化过程来解决复杂的优化问题。它们基于遗传、变异、交叉和自然选择的原理。进化算法中的进化过程模拟了自然选择，即最合适的解决方案更有可能存活下来，并将其特性传递给下一代。因此，群体会逐渐向最优解靠拢。最著名的进化算法包括：遗传算法 (GA)、进化编程 (EP)、进化策略 (ES) 和遗传编程 (GP)。这些算法各有特点，并被广泛应用于各个领域。

一般来说，进化算法是解决复杂优化问题的强大工具，尤其是在无法获得分析函数表达式或梯度的情况下。它们允许探索搜索空间，并通过结合来自不同单个解决方案的信息找到最佳解决方案。

差分进化（DE）是元启发式优化方法之一。它与其他方法的不同之处在于简单和高效。DE 使用变异和杂交的载体群体来创造新的解决方案。它不需要梯度知识，能够找到全局最优值。

差分进化算法由 Storn 和 Price 于上世纪 90 年代开发（发表于《差分进化 - 连续空间全局优化的简单高效启发式》），自此成为最流行的优化方法之一，它使用参数向量群来寻找最优解。

2.算法

差分进化的理念是简单和高效的结合。差分进化算法使用代表潜在解决方案的向量群，每个矢量由代表优化问题变量值的分量组成。

在 DE 中，向量扮演搜索代理的角色。该算法首先创建一个随机向量群，然后会出现一个迭代过程，在这个过程中，每个向量都会发生变异，并与种群中的其他向量交叉。突变是通过将从群体中随机选择的两个向量的差值加到第三个向量上实现的。这样就创建了一个新的向量，它代表问题的潜在解决方案。

变异后，变异的向量与原始向量交叉，交叉可以将两个向量的信息结合起来，创造出新的解决方案。将得到的结果与当前群体中的最佳解决方案进行比较，如果新向量更好，它就会取代旧向量，成为种群的一部分。突变允许探索搜索空间，而交叉则允许组合来自不同向量的信息并创建新的解决方案。

突变、交叉和替换在多次迭代中重复进行，直到达到停止条件，如给定的迭代次数或达到要求的求解精度（在我们的例子中，是适应度函数运行达到 10,000 次）。

DE 是广泛用于解决优化问题的进化算法之一。差分算法使用差分算子在当前群体的基础上创建新的候选者。以下是差分算法中使用的基本公式：

1.创建新候选者的公式（差分）：

r = r1 + F * (r2 - r3)

其中：

r - 新的向量
r1、r2 和 r3 - 随机选择的向量（群体中的单个解）
F - 差分比，用于控制解决方案的可变性（所得值的分散性），默认范围为 (0.0;1.0] 。

2.交叉公式：

u = crossover (x, v)

公式描述了当前解决方案 x 和新候选方案 v 之间的交叉。交叉算子决定从新的候选方案中提取解决方案的哪些成分。这是使用新向量分量的概率，否则这个部分就不会改变。使用数值范围是 (0.0;1.0]。

让我们来写一个 DE 算法的伪代码，由于算法本身简单易懂（事实上，代码会比其伪代码更复杂一些）：

创建随机向量群
计算适应度函数
更新最佳解决方案
更新群体（用更好的突变体替换向量）
创建一个突变向量或保留原有向量，这取决于哪个更好
重复第 2 步。

为了在 DE 算法中描述一个向量，我们将编写一个结构，并将其称为 S_Vector，它是 n 维空间中的一个向量。该结构包含以下字段：

Init（int coords）：该函数初始化指定长度为 "coords" 的向量。它会创建两个数组 - "c" 和 "cPrev"，分别代表矢量的坐标和前一个坐标。此外，f 和 fPrev 的初始值也设置为 -DBL_MAX。
c[]：包含向量坐标的数组
cPrev[]：包含上一次迭代时向量坐标的数组
f：当前向量的适应度函数值
fPrev：上一次迭代的向量适应度函数值

//——————————————————————————————————————————————————————————————————————————————
struct S_Vector
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

像 DE 这样的基本算法的类描述也非常简单。让我们声明 C_AO_DE 类。C_AO_DE 类的字段包含有关算法当前状态及其参数的信息，而方法则执行与优化函数相关的各种操作。

该类有以下字段和方法：

cB[]：包含算法找到的最佳坐标的数组
fB：最佳坐标的适应度函数值
v[]：表示向量群的 S_Vector 结构数组
rangeMax[]：数组，存储每个向量坐标的最大值
rangeMin[]：数组包含每个向量坐标的最小值
rangeStep[]：包含每个向量坐标步长值的数组
Init（int coordsP、int popSizeP、double diffWeightP、double crossProbabP）：初始化算法参数的函数。它的参数是 "coordsP" 坐标数、"popSizeP" 群体大小、"diffWeightP" 差分权重和 "crossProbabP"交叉概率。
Moving（）：该函数执行差分进化算法的一个步骤
Revision（）：该函数对向量群进行修订
SeInDiSp（double In，double InMin，double InMax，double Step）：该方法以给定的步长计算给定范围内的新坐标值
RNDfromCI（双 min，双 max）：该函数在 [min, max] 范围内生成一个随机数

//——————————————————————————————————————————————————————————————————————————————
class C_AO_DE
{
  //----------------------------------------------------------------------------
  public: double cB  []; //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Vector v []; //vector

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,       //coordinates number
                     const int    popSizeP,      //population size
                     const double diffWeightP,   //differential weight
                     const double crossProbabP); //crossover robability

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double diffWeight;   //differential weight
  private: double crossProbab;  //crossover robability

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_DE 类的 Init 方法用于初始化差分进化算法的参数。该方法需要四个参数：

coordsP - 坐标数；
popSizeP - 群体大小；
diffWeightP - 差分权重；
crossProbabP - 交叉概率。

一开始，该方法使用 MathSrand 函数重置随机数生成器。这确保每次启动算法时，都会使用新的随机数序列。

接下来，该方法将初始化 "fB" 和 "revision" 变量。"fB" 变量包含算法找到的最佳适应度函数值。最初，它被设置为"-DBL_MAX"，即一个很小的数字。"revision" 变量设置为 "false"，这意味着向量群尚未修订。

然后，该方法使用作为参数传递的值初始化 "coords"、"popSize"、"diffWeight" 和 "crossProbab"变量。

然后，该方法会创建一个大小为 "popSize" 的数组 "v"，其中包含一个向量群。

接下来，该方法会创建三个数组："rangeMax"、"rangeMin" 和 "rangeStep"，每个数组都有 "coords" 大小（坐标数）。

最后，该方法会创建大小为 "coords" 的 "cB" 数组，其中包含算法找到的最佳坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Init  (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double diffWeightP,  //differential weight
                     const double crossProbabP) //crossover robability
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordsP;
  popSize = popSizeP;

  diffWeight  = diffWeightP;
  crossProbab = crossProbabP;

  ArrayResize (v, popSize);
  for (int i = 0; i < popSize; i++) v [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

为了改变搜索空间中的解向量，我们将编写 C_AO_DE 类的 Moving 方法。该方法应用变异和交叉算子生成新的候选向量，并根据适应度函数选择最佳解决方案。

以 "if (!revision)" 条件开头的第一个代码块只有在首次运行 "Moving" 方法或调用 Init 方法后才会被执行。它使用给定范围内的随机值和 "rangeStep" 数组中指定的步长初始化初始向量群。

然后，该方法使用 "for" 循环更新群体中的每个向量。对于每个向量，该方法会从群体中选择三个与当前向量（i）不相同的随机向量（r1、r2、r3），并应用变异和交叉算子来获得新的候选向量。变异运算符会计算向量 "r2 "和 "r3 "之间的差值乘以差值权重 "diffWeight"，然后将结果添加到 "r1" 向量中。交叉算子会选择一个向量坐标，并以 crossProbab 概率将其替换为一个新候选向量的相应坐标。如果交叉概率不成立，则当前向量坐标保持不变。

如果你对下面的代码进行解析，就会发现改变向量的 Moving 方法并不提供在空间中创建坐标的功能，除了那些可以从现有坐标中获得的坐标。因此，算法的随机性仅在于选择交叉向量，而不在于创建新的原始向量。这一特点将产生深远的影响，我们将在下文中讨论。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        v [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;
  int    r   = 0;
  int    r1  = 0;
  int    r2  = 0;
  int    r3  = 0;

  for (int i = 0; i < popSize; i++)
  {
    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r1 = r;
    }
    while (r1 == i);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r2 = r;
    }
    while (r2 == i || r2 == r1);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r3 = r;
    }
    while (r3 == i || r3 == r1 || r3 == r2);

    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (0, 1.0);

      if (rnd < crossProbab)
      {
        v [i].c [c] = v [r1].cPrev [c] + diffWeight * (v [r2].cPrev [c] - v [r3].cPrev [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        v [i].c [c] = v [i].cPrev [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

最后，我们需要使用 C_AO_DE 类的 Revision 方法，它可以更新群体中的最优解，并保存之前的适应度函数值和向量坐标。

首先，该方法将 "ind" 变量初始化为"-1"。然后，它使用 "for" 循环遍历种群中的所有向量。如果当前向量的适应度函数大于 "fB"（迄今发现的最佳适应度函数），它就会在 "ind" 变量中存储该向量的索引。

如果 "ind "不等于"-1"，那么该方法会将 "fB" 的值更新为 "ind" 索引的向量的适应度函数值，并将其坐标存储到 "cB" 数组中。

然后，该方法使用另一个 "for" 循环遍历群体中的所有向量。如果当前向量的适应度函数大于其之前的值，那么该方法就会在相应的 v[i].fPrev 和 v[i].cPrev 字段中存储适应度函数的当前值和向量坐标。

通过这种方法，C_AO_DE 类可以存储群体中的最优解以及适应度函数和向量坐标的先前值，以便以后优化适应度函数时使用。

我们可以看到，在找到比原始（父）版本更好的向量之前，群体不会在搜索空间中继续移动。这一点是对上述内容的补充。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = v [ind].f;
    ArrayCopy (cB, v [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > v [i].fPrev)
    {
      v [i].fPrev = v [i].f;
      ArrayCopy (v [i].cPrev, v [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.测试结果

DE 试验台结果：

C_AO_DE:50;0.2;0.8
=============================
5 Rastrigin's; Func runs 10000 result:80.30183306326985
Score:0.99498
25 Rastrigin's; Func runs 10000 result:76.15178282331799
Score:0.94356
500 Rastrigin's; Func runs 10000 result:52.17316317703311
Score:0.64645
=============================
5 Forest's; Func runs 10000 result:1.7348423083855402
Score:0.98131
25 Forest's; Func runs 10000 result:1.28572746338484
Score:0.72727
500 Forest's; Func runs 10000 result:0.20833645141168078
Score:0.11785
=============================
5 Megacity's; Func runs 10000 result:9.640000000000002
Score:0.80333
25 Megacity's; Func runs 10000 result:3.9199999999999995
Score:0.32667
500 Megacity's; Func runs 10000 result:0.3548
Score:0.02957
=============================
All score:5.57100

根据算法的输出值，我们可以看到出色的测试结果。

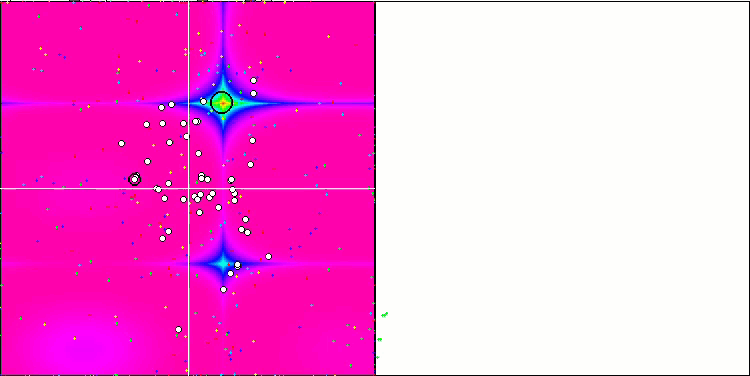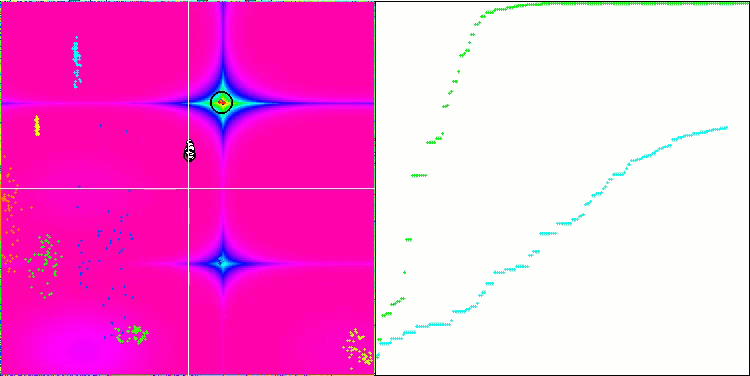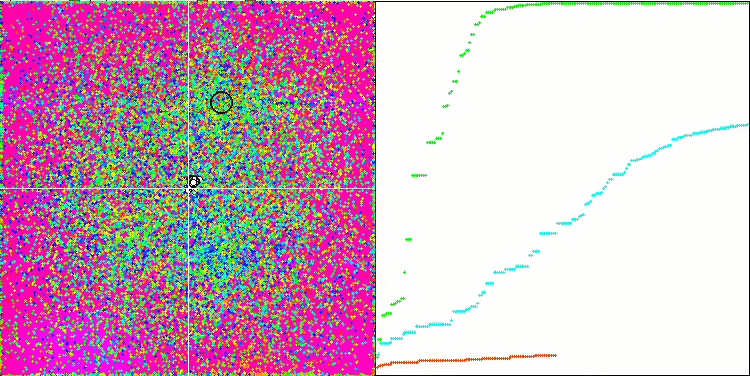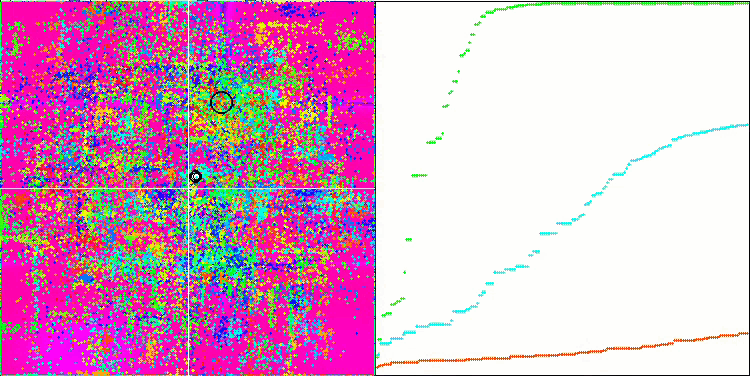
我们可以看到算法的惊人收敛性，但我们也可以注意到上文在描述Moving 和 Revision 方法时提到的特征。在创建可视化时，经过多次尝试，我特别选择了最成功的几种。事实上，结果并不总是那么突出。这可以用种群退化来解释，即整个种群，即每一个单一的向量，都会趋近于一个单一的极值。但这可能根本不是全局的最佳状态。如上所述，该算法没有继续探索搜索空间、创建新的独特向量的机制。DE 算法不会创建新的向量，只会从现有向量中生成组合。这就是完全退化的原因。没有 "新鲜血液"来丰富人口的"基因库"。

rastrigin

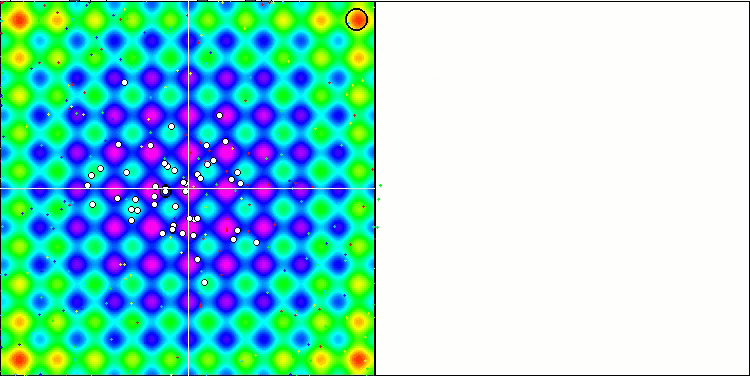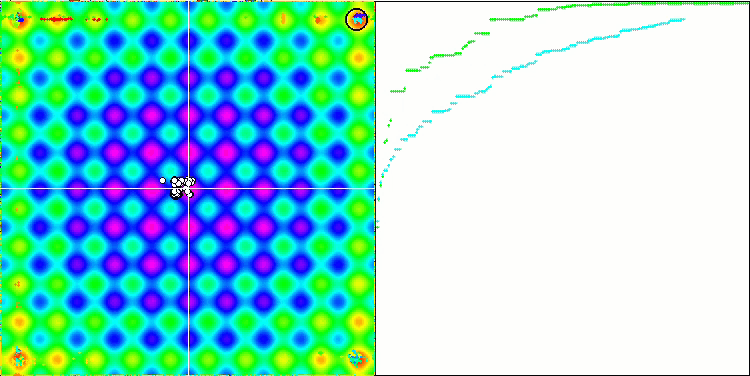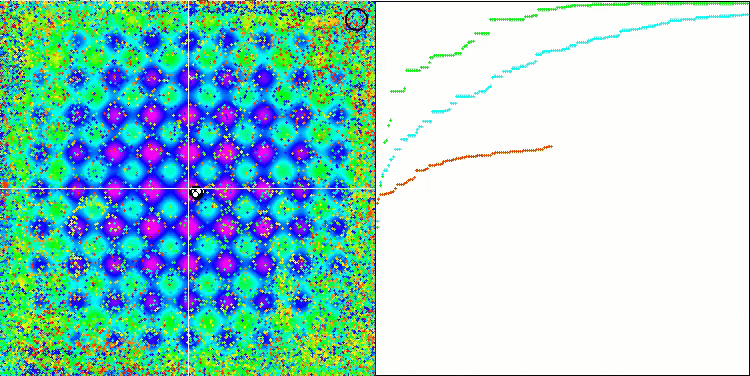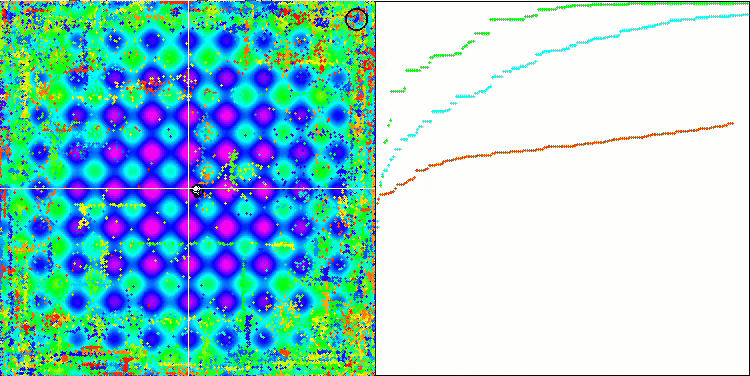
Rastrigin 测试函数上的 DE。

forest

Forest 测试函数上的 DE

megacity

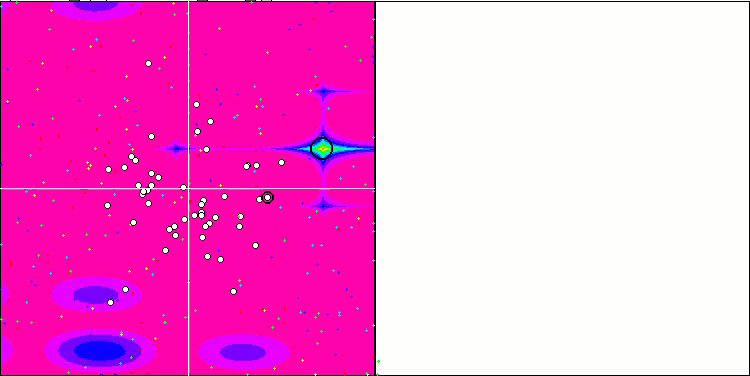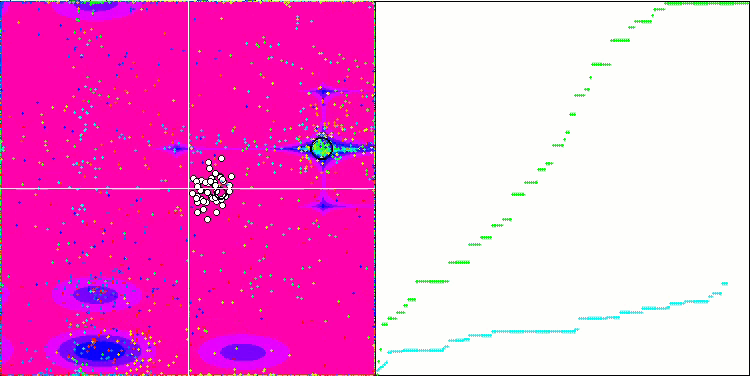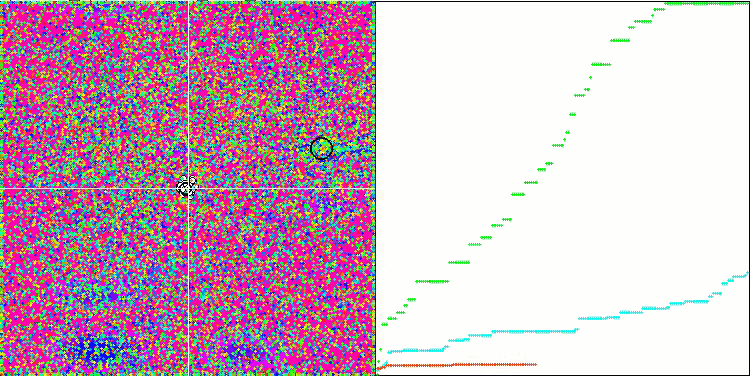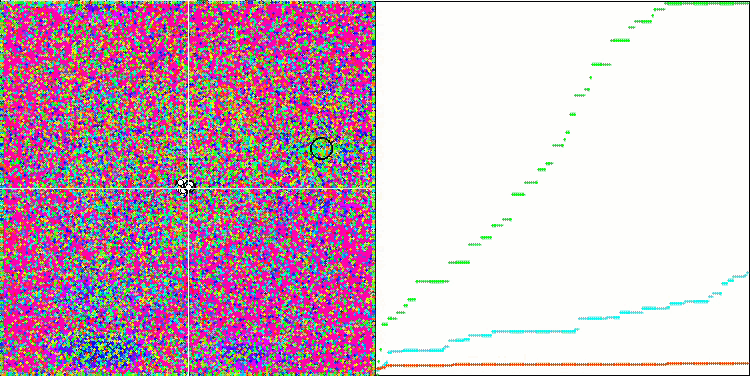
Megacity 测试函数上的 DE 。

differences

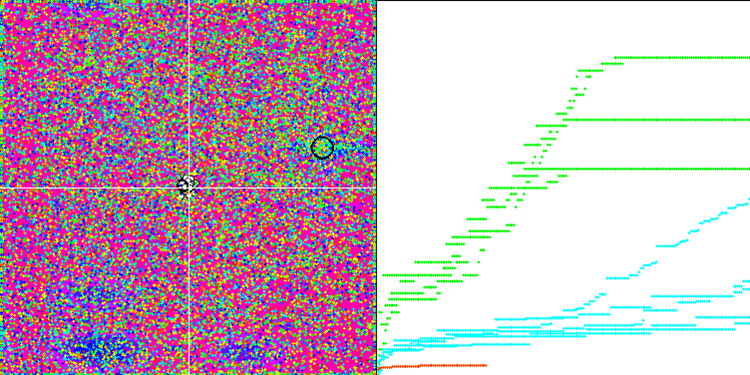
巨大的趋同扩散，在 Forest 和 Megacity 函数中尤为明显

让我们来看看新参与者 DE 的最终评分表。在包含 10 个变量的 Forest 测试中，该算法从目前的领先者 SDSm 手中夺得了第一名。其他测试的结果也非常好，DE 仅次于 SSG，排名第四。值得注意的是，由于 Forest 和 Megacity 函数的结果非常分散，我不得不对每个测试函数进行 10 倍测试，而不是通常的 5 倍测试。在平滑的 Rastrigin 函数中，结果的分散性不那么明显。

#	AO	描述	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (discrete)			Megacity 最终	最终结果
#	AO	描述	10 p（5 F）	50 p（25 F）	1000 p（500 F）	Rastrigin 最终	10 p（5 F）	50 p（25 F）	1000 p（500 F）	Forest 最终	10 p（5 F）	50 p（25 F）	1000 p（500 F）	Megacity 最终	最终结果
1	SDSm	随机扩散搜索 M（stochastic diffusion search M）	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SDS	随机扩散搜索（stochastic diffusion search）	0.99737	0.97322	0.58904	2.55963	0,96067	0.93572	0.79649	2.69288	0.78696	0.93815	0.71804	2.44315	88.201
3	SSG	树苗播种和生长（saplings sowing and growing）	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
4	DE	差分进化（differential evolution）	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
5	HS	和声搜索（harmony search）	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
6	IWO	入侵性杂草优化（invasive weed optimization）	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
7	ACOm	蚁群优化M（ant colony optimization M）	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
8	MEC	思维进化计算（mind evolutionary computation）	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
9	SDOm	螺旋动力学优化 M（spiral dynamics optimization M）	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
10	COAm	布谷鸟优化算法 M（cuckoo optimization algorithm M）	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	萤火虫算法 M（firefly algorithm M）	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	人工蜂群（artificial bee colony）	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	蝙蝠算法（bat algorithm）	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	带电系统搜索（charged system search）	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	重力搜索算法（gravitational search algorithm）	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	细菌觅食优化（bacterial foraging optimization）	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	类电磁算法（electroMagnetism-like algorithm）	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	混合蛙跳（shuffled frog-leaping）	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	MA	猴子算法（monkey algorithm）	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
20	FSS	鱼群搜索（fish school search）	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
21	IWDm	智能水滴 M（intelligent water drops M）	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
22	PSO	粒子群优化（particle swarm optimisation）	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
23	RND	随机（random）	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
24	GWO	灰狼优化器（grey wolf optimizer）	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

总结

差分进化算法能够非常迅速地找到全局最优值，而且收敛性极佳，而单个测试的结果却非常一般。DE 广泛应用于各个领域，如模型参数优化、神经网络调整、物理和经济学中的函数优化等。我建议使用这种算法进行多次优化运行，因为结果非常依赖于第一次迭代的初始种群。在增加迭代次数的同时，增加群体数量可能是有益的。

尽管差分进化算法操作简单、运行速度快，但它也有明显的缺点，比如种群退化，因此会陷入局部极值。在为优化问题选择 DE 时，有必要考虑到这一点。

本文讨论的 DE 算法是一种模板，可以用于创建若干修改版。我对改进差分进化（DE）算法的建议如下：

1.使用自适应参数控制方法DE 有几个参数需要调整，因为它们对结果有重大影响。

作者推荐的差分权重参数为 "0.2"。该值是我在 DE 测试脚本中采用的默认值。这一参数对群体的多样性有重大影响。如果我们选择一个小于 "0.2" 的值，算法的收敛性会更好，但同时结果也会更加分散。相反，如果我们增加该参数的值，那么算法就能抵御种群退化和陷入局部极值的情况，但与此同时，收敛质量会在测试限制的迭代次数内迅速下降，相应地，搜索时间也会不可避免地增加。

交叉概率也会影响优化质量。作者推荐的数值为 "0.9"。不过，我的实验表明，"0.8" 更合适。

综上所述，使用自适应方法来控制和动态改变参数似乎是明智之举，这样算法就能根据任务自动调整。

2.使用不同的变异和交叉策略。

3.使用混合方法：DE 可以与其他优化方法相结合，如遗传算法、基于梯度的优化方法、粒子群优化方法等。这可以提高算法的性能，有助于提高整个算法的效率。

4.提高收敛性：应用额外的随机向量生成来增加群体的多样性。

5.使用不同的策略选择突变个体：该算法采用完全随机的方法选择交叉个体。不过，也可以使用其他不同的策略来选择交叉/突变个体，如根据个体的适应度来选择个体的策略，从而补充或完全取代这种方法。这有助于提高群体的多样性，并大大提高算法的抗卡死能力。

总的来说，差分进化算法的性能给人留下了非常好的印象，但我们需要牢记这种有趣算法的特点，或者进行一些尝试，通过综合运用不同的策略和方法来改进差分进化算法。DE 已经自信地证明，算法可以非常高效，同时还可以非常简单和快速。在解决复杂的高维度优化问题时，可以推荐使用差分进化算法，因为当优化参数数量较多时，进化过程中多样性下降的影响并不明显。

评级表

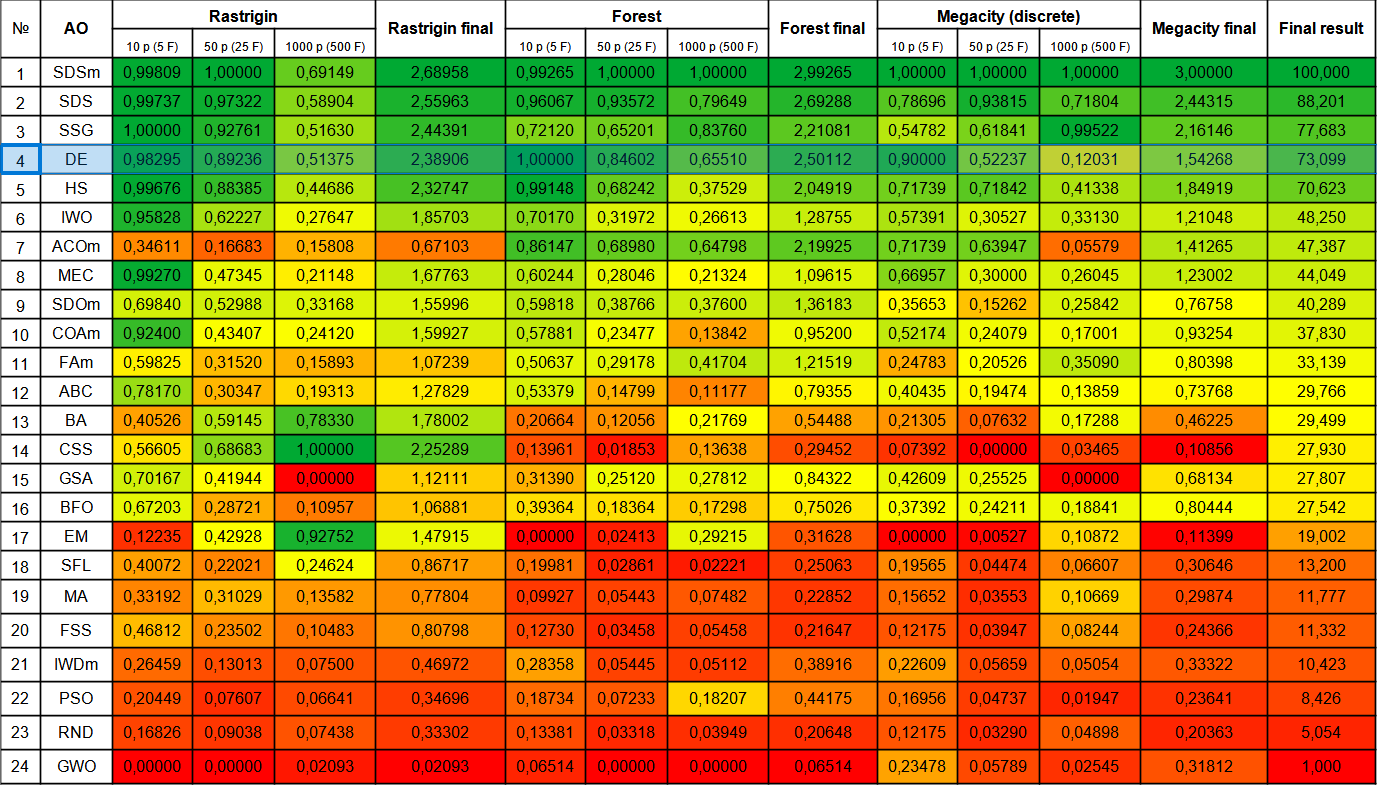
图 1.根据相关测试对算法进行颜色分级

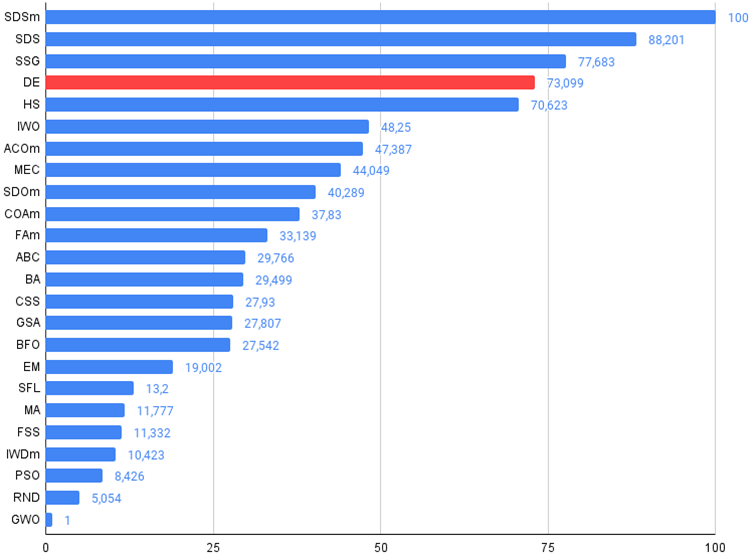
图 2.算法测试结果柱状图（从 0 到 100，越多越好、

存档中包含使用这篇文章中应用的方法计算评级表的脚本）。

差分进化算法的优缺点

优点：

外部参数数量少。
实现简单。
运行速度快。
良好的可扩展性。
在各类函数各方面表现出色（考虑到缺点）。

缺点：

结果高度分散。
容易陷入局部极值。

这篇文章还附有一个归档，其中包含前几篇文章中所述算法代码的最新版本。文章作者不对规范算法描述的绝对准确性负责。为提高搜索能力，已对其中多项功能进行了修改。文章中提出的结论和判断都是基于实验结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/13781

附加的文件 |

下载ZIP

23_The_world_of_AO_DE.zip (412.14 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论

开发回放系统（第 37 部分）：铺平道路 (一)

在这篇文章中，我们终于要开始做我们早就想做的事情了。之前，由于缺乏 "坚实的基础"，我没有信心公开介绍这部分内容。现在我有了这样做的基础。我建议您尽可能集中精力理解本文的内容。我指的不仅仅是阅读，我想强调的是，如果你不理解这篇文章，你可能就是完全放弃了理解以后文章内容的希望。

精通模型解释：从您的机器学习模型中获取深入见解

机器学习对于任何经验的人来说都是一个复杂而回报的领域。在本文中，我们将深入探讨为您所构建模型提供动力的内在机制，我们探索的错综复杂的世界，涵盖特征、预测和化解复杂性的有力决策，并牢牢把握模型解释。学习驾驭权衡、强化预测、特征重要性排位的艺术，同时确保做出稳健的决策。这篇基本读物可帮助您从机器学习模型中获得更高的性能，并为运用机器学习方法提取更多价值。

开发具有 RestAPI 集成的 MQL5 强化学习代理（第 2 部分）：用于与井字游戏 RestAPI 进行 HTTP 交互的 MQL5 函数

在本文中，我们将讨论 MQL5 如何与 Python 和 FastAPI 交互，使用 MQL5 中的 HTTP 调用与 Python 开发的井字游戏交互。这篇文章讨论了使用 FastAPI 为这种集成创建一个 API，并提供了一个 MQL5 测试脚本，突出了 MQL5 的多功能性、Python 的简易性以及 FastAPI 在连接不同技术以创建创新解决方案方面的效果。

群体优化算法：螺旋动态优化 (SDO) 算法

文章介绍了一种基于自然界螺旋轨迹构造模式（如软体动物贝壳）的优化算法 - 螺旋动力学优化算法（Spiral Dynamics Optimization，SDO）。我对作者提出的算法进行了彻底的修改和完善，本文将探讨这些修改的必要性。

目录

1.概述

2.算法

3.测试结果

总结

该作者的其他文章