种群优化算法：和弦搜索（HS）

内容：

1. 概述
2. 算法
3. 测试结果

1. 概述

音乐创作由若干个组成部分构成 — 节奏，旋律及和弦。 虽然节奏和旋律构成了音乐作品的单一整体，但和弦就是它的装饰。 没有和弦的戏剧或歌曲就像儿童读物中的一幅无色图画 — 它是画出来的，但没有颜色，没有亮度，没有表现力。 正确选择的和弦可以抚慰耳朵，令声音高贵，令我们能够充分享受钢琴、吉它或任何其它乐器的美妙声音。 旋律可以演唱，而和弦只能演奏。 音乐和弦是一组弦乐，没有它，任何一首歌或任何音乐都是不成熟和不完整的。

和弦恰好出现在我们连接两个声音的那个时刻 — 逐一或同时流动。 一个更宽泛的同义词是“组合”。 在一种声音与另一种声音连接后，我们得到了一个组合，其中层次结构已经尝试按自己的方式排列。 在音乐学校和学院中，有一个特殊的学科 — 和弦，在此学生会学习音乐理论中存在的所有和弦，学习在实践中应用它们，甚至解决和弦的问题。

在音乐即兴创作中，音乐家尝试调整乐器的音高，从而达到令人愉悦的和弦（最佳条件）。 在自然界中，和弦是由具有不同频率的若干种声波之间的特殊关系决定的。 即兴和弦的品质取决于审美评价。 为了提高审美鉴赏力，找到最佳的和弦，音乐家们经历了一次又一次的练习。 即兴创作和优化之间有相似之处。

和弦搜索（HS）方法是一种新兴的元启发式优化算法，在过去十年中已被用于解决许多复杂问题。 和弦搜索算法（HS）于 2001年由 Z. W. Geem 首次提出。 HS 方法的灵感来自音乐即兴创作和寻求音乐和弦的基本原则。 在多维优化问题中，声音的完美和弦组合与全局极值相匹配，而音乐即兴创作过程与极值搜索相匹配。

在即兴创作过程中，每位音乐家在一段音乐的任何尺度上（在其乐器的能力范围内）再现一种声音，以便管弦乐队所有音乐家的声音在这个尺度上形成一个和弦的载体。 形成“优美”和弦的声音组合会被每位音乐家记住，并可供他们用于在音乐作品的后续尺度中形成更好的和弦。

通常，在即兴创作过程中，音乐家满足以下三个要求之一：从可用的声音范围内形成绝对随机的声音；从和弦记忆中播放任何声音；播放来自同一记忆的相邻和弦向量。 HS 算法的主要特点是可以利用它来解决连续和离散优化问题。

HS 的显著特点是算法的简单性和搜索的效率。 有因于此，该算法引起了研究人员的极大关注，并且在理论和实践方面都在迅速推进。 HS 是一种元启发式技术，可在搜索过程中的勘探和发展阶段之间提供极高的稳定性。 HS 的灵感来自人类的创造力，针对给定问题找到完美解决方案的方式类似于音乐家尝试找到令人愉悦的和弦的方法。 获取适应度函数值的方法，与使用每种乐器获取音高参考相类似。

2. 算法

HS 逻辑的工作类似于音乐家在创造完美和弦方面的工作。 音乐家尝试改变各种音调，直到找到完美的和弦。 之后，把找到的和弦集合存储在记忆中。 在优化问题中，和弦会经历各种变化；如果变化的结果是有利的，那么就更新记忆，添加新的和弦，并删除不需要的元素... 所有这些也许听起来令人困惑。 那么什么是和弦呢？ 什么是音调？ 我们尝试用我们自己的术语来理解算法。

什么是一首音乐？ 当然，我不是音乐家（这很遗憾），而是一名程序员。 但为了算法检测，应用“音符”的概念就足够了。 一首音乐由音符（弦乐）组成。 图例 1 示意性地展示了构建一首音乐的“机制”。 音符的选择对应于一首音乐，即使没有受过音乐或声乐教育的耳朵也很容易判定。 那些愿意猜测的人也许会在下面发表评论。

优化 HS 算法包括将带有音符的绿色条移动到作品本身的蓝色条上。 绿色条的范围是一个八度，由单个音符组成。 作品（蓝色条）对应于其中一个优化解决方案。 绿色条上的音符是问题的相应优化参数。 音乐家的记忆里存储了作品的多个版本（蓝色条的几种变体），这就是算法群体。

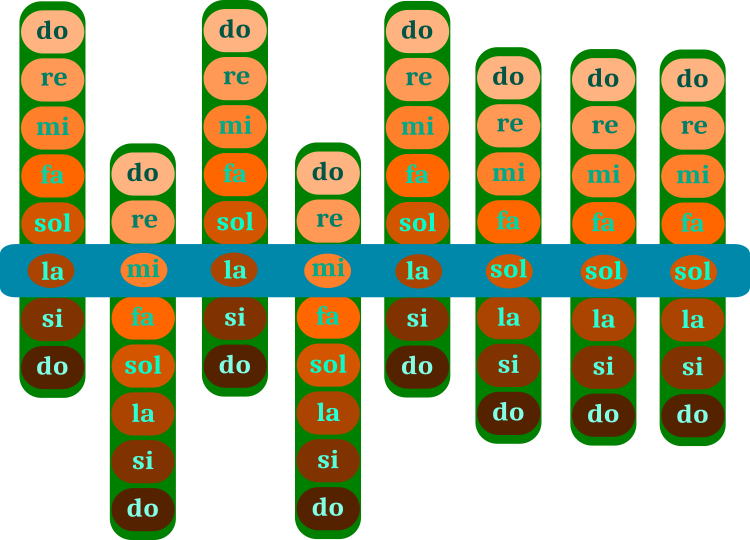
图例 1. 在一首音乐中选择音符（寻找和弦）。 蓝色条是一首。 绿色条是一组音符

图例 1 中的示例对应于离散问题的解，其参数中有八个音阶。 提供该示例是为了便于理解算法的操作。 但是，在任意任务中，可以有优化参数的任何音阶，并且还有过渡音符 — 半音阶。 解决问题的正确参数对应于作品中的正确音符。

因此，创作一首音乐的过程始于乐器的一组随机声音，这些声音位于乐器的可重复频率范围之内。 有必要创建一首曲子的多个变体，以便能够组合变体音符的各个部分。 下一步是更改这些变体中的音符。 我们可以通过三种可能的方式做到这一点：

1. 随机更改乐曲中乐器范围内的一个音符。
2. 我们可以从该作品的其它版本截取相应序号的音符。 3. 我们可以从该作品的另一个版本中提取，并稍微更改它，令其音调或高或低。

由此，在获得了音乐作品的一组新变体后，我们根据声音和弦评估每个变体，并将变体存储在记忆中的原始位置，前提是新版本要比以前的版本更好。 该算法的独特之处在于不需要对总体进行排序，在我们的例子中是作品集。 每个新的最佳选项都会替换同一位置旧的较差选项。 这个过程有点像遗传算法的操作，模仿进化过程的适者生存。 此外，还观察到染色体中基因组合的相似性。

基于前述，我们可以初步合成 HS 算法的伪代码：

1. 生成随机和弦。
2. 衡量和弦品质（适应度函数的计算）。
3. 使用随机选择的和弦，合成演奏弦乐，概率为 Eh。
3.1 如果弦乐是从 概率为 Ep 的某种和弦中选择的，则根据方程更改弦乐。
    3.1.1 保持所选弦乐不变。
  3.2 新弦乐遵照方程。
4. 衡量和弦品质（适应度函数的计算）。
5. 从第 3 步开始重复，直到满足停止准则。

好了，我们继续讲述算法的输入参数，这些参数很少且直观。

input int    Population_P = 50;    //Population size
input double Eh_P         = 0.9;   //random selection frequency
input double Ep_P         = 0.1;   //frequency of step-by-step adjustment
input double Range_P      = 0.2;   //range

• Population_P - 音乐家记忆中的作品变体数量（种群大小）;
• Eh_P - 从记忆中选择作品变体的频率，它会影响我们引用其它变体来借鉴音符的频率。 该值越高意味着算法的组合性质越高;
• Ep_P - 如果音符是从该作品的另一个版本中选择的，您需要将音符的音调调更高或调更低的频率；
• Range_P - 如果不是取自另一个版本，则音符范围处于某首作品的编辑版本。 例如，0.2 表示乐器音符范围的 20%。
• 
  

HS 算法操作依赖和弦（音乐合成），其可用 S_Harmony 结构来描述。 和弦由音符（弦乐）组成，它表示为一个需要优化的 c[] 参数数组。 一首作品的最佳和弦将存储在 cB [] 数组中。 审评过关的乐曲将发送到这个数组中，我们将从它们当中借鉴音符执行组合排列。 和弦的品质存储在 h 变量中，最佳和弦存储在 hB 变量中。

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

和弦结构数组用在 C_AO_HS 类当中。 类中的方法和成员声明是紧凑的，因为算法非常简洁，计算要求低。 于此，我们不会看到许多其它优化算法中使用的排序。 我们将需要数组来设置正在优化的参数的最大值、最小值和步长（它们扮演弦乐的范围和音阶的角色）、和常量变量，以便将算法的外部参数传递给它们。 我们继续讲述包含 HS 主逻辑的方法。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init() 公开方法初始化算法。 在此，我们设置数组的大小。 我们将最佳和弦的品质指标初始设置为双精度类型的最小可能值。 我们将对和弦结构数组的相应变量做同样的事情。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

第一个公开方法 Moving()，其需要在每次迭代时执行，具有 “iter” 输入 — 当前迭代。 在第一次迭代中，当 “revision” 标志为 “false” 时，需要用乐器范围内的随机值初始化和弦，这相当于音乐家随机演奏弦乐。 为了减少重复操作，我们将相应弦乐（优化参数）的声音频率范围存储在 frequency[] 数组之中。

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

在第二次和随后的迭代中，以即兴创作为主，那么弦乐及其组合的顺序发生变化。 记忆中有若干个和弦，我们将改变并组合它们。 对于每个新的和弦，我们将按顺序对弦乐进行排序。 对于每个弦乐，都有从记忆中随机选择和弦的概率，即和弦将被随机选择（等同于所有和弦）。 如果弦乐取自和弦的记忆，那么其变化的概率也按以下公式检查：

h [har].c [c] = h [har].c [c] + r * B * frequency [c];

其中:

r - 介于 -1 和 1 之间的随机数
frequency - 乐器的频率范围
B - 系数按公式计算：

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

其中:

maxIterations - 最大迭代次数
iter - 当前迭代
maxB - 最大系数限制
minB - 最小系数限制

图例 2 展示了系数 B 对算法调优参数和当前迭代的依赖性。

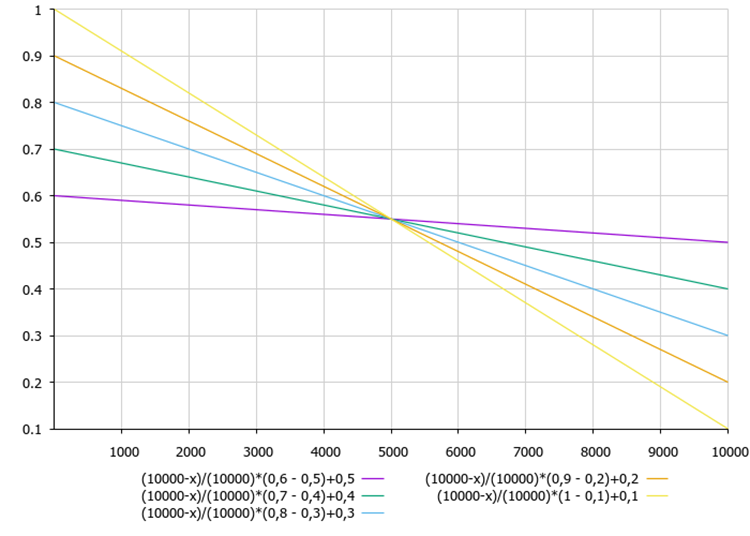
图例 2. B 系数对于 maxB、minB 算法调谐参数和当前迭代的依赖性

B 系数计算方程显示，B 系数随着每次迭代而减小。 故此，在优化结束时，发现的极值被优调。
如果尚未从和弦记忆中选择弦乐，则此刻已存在的将被更改。 弦乐变化与上一次变化的差异是声波值的固定范围。

更改弦乐的过程完成后，我们要检查生成的弦乐是否超出乐器的允许值。

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision () 是每次迭代时，继计算适应度函数后，调用的第二个公开方法。 其目的是更新找到的全局解。 如果和弦优于其最佳版本 h > hB，则更新此和弦的最佳版本。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

经过仔细研究代码后，我们发现和弦搜索算法中没有根本的新思路。 和弦搜索算法借鉴了以前使用的进化算法思想，包括全局均匀重组、均匀突变、高斯突变和替换每一代的最差个体。 一些来源表明需要用新的和弦替换记忆中最糟糕的和弦。 在我们的算法中，和弦只能由其最佳解取代。 这与经典版本略有不同，因为我的研究表明，算法这样实现将更有效率。

和弦搜索算法的贡献在于两个方面：这些思路在该算法中的结合是新颖的；和弦搜索算法的音乐动机是新的。 很少有关于和弦搜索的出版物讨论音乐主题或和弦搜索算法的扩展。 大多数出版物致力于和弦搜索算法与其它进化算法的混合，和弦搜索参数的调整或在特定问题上的应用。 如果可以将更多的音乐条件扩展应用于 HS 算法，那么这将有助于将其区分为单独的进化算法。 这样的研究需探索音乐理论，探索音乐创作和编曲的过程，探索音乐的教育理论，以及这些理论在和弦搜索算法中的创造性应用。

3. 测试结果

HS 试验台结果如下：

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Score: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's; Func runs 10000 result: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score: 0.05410

测试函数的超高数值令人震惊，给人以希望，总体测试得分极其出色。 HS 在可视化上的一个特征是，我们看不到任何坐标组形式的结构形成，就像以前的一些算法一样。 从视觉上看，代理者在搜索空间中的移动没有形态。 这类似于 RND 优化算法的行为，尽管收敛图形的行为非常自信，逐渐接近优化问题的解。 在局部极值的卡顿对于此算法来说并不典型。

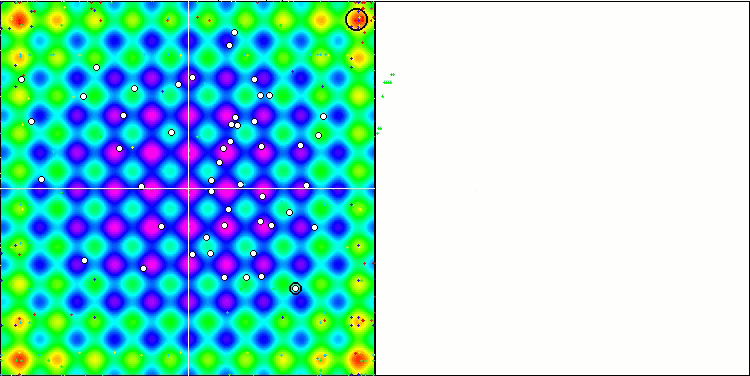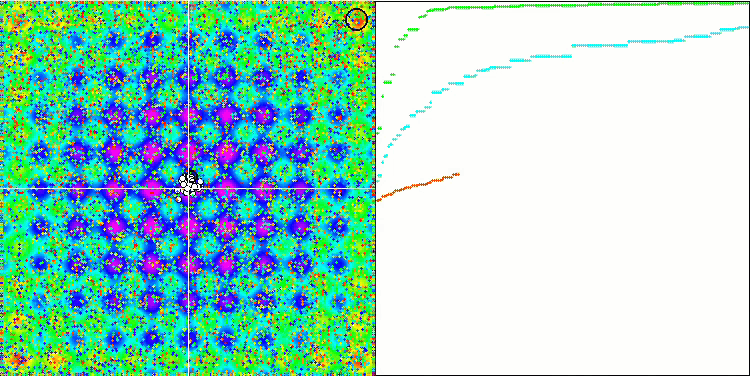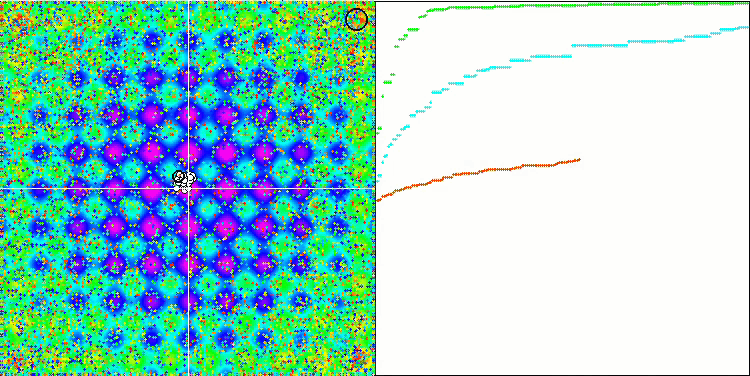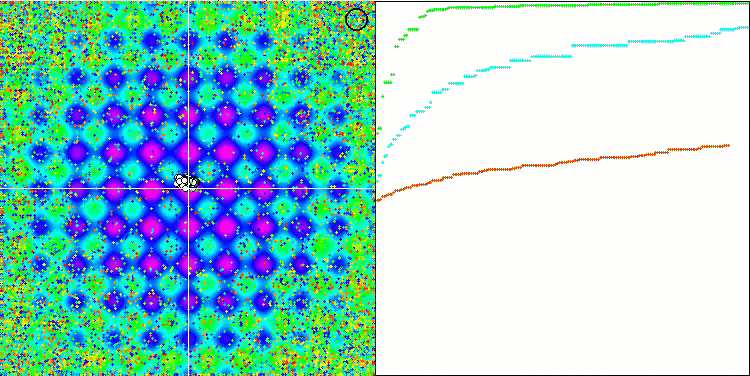
  基于 Rastrigin 测试函数上的 HS

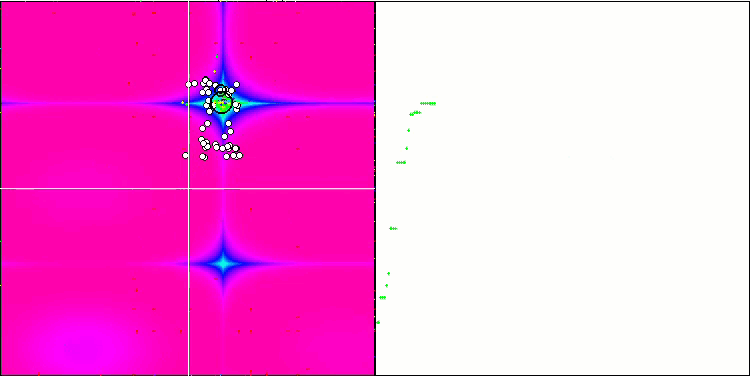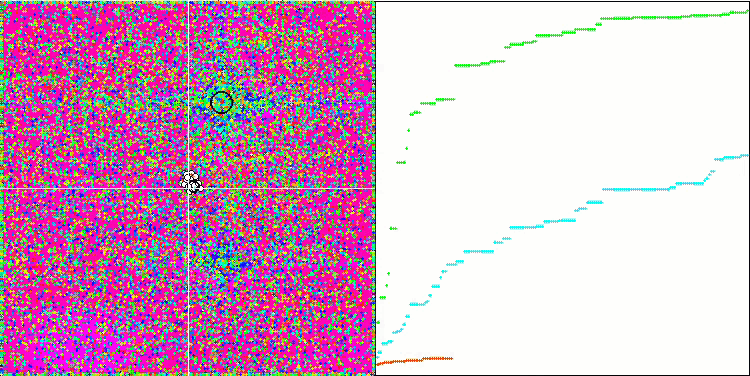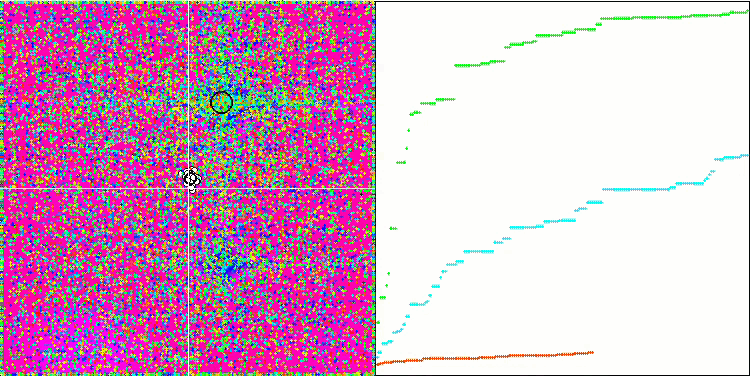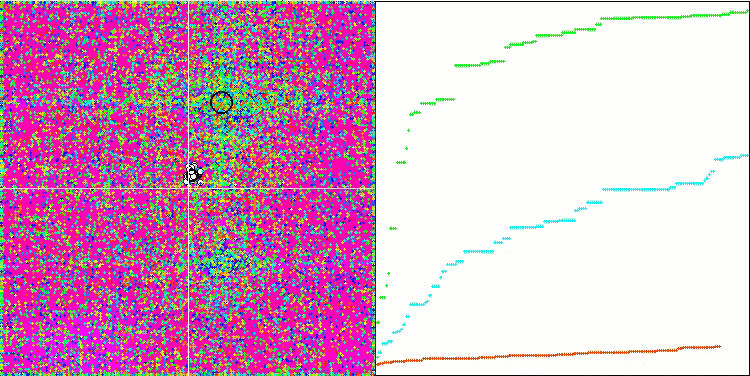
  基于 Forest 测试函数的 HS

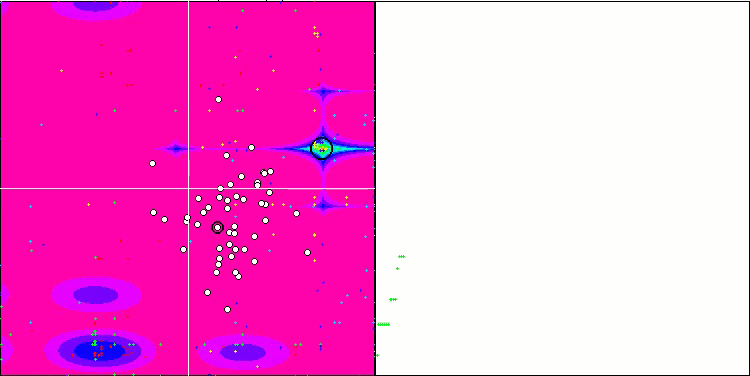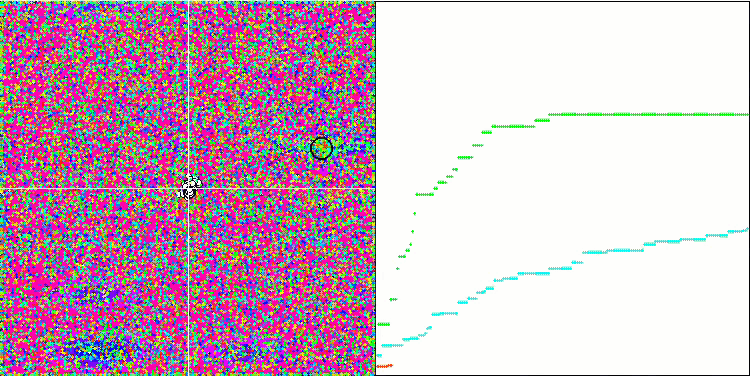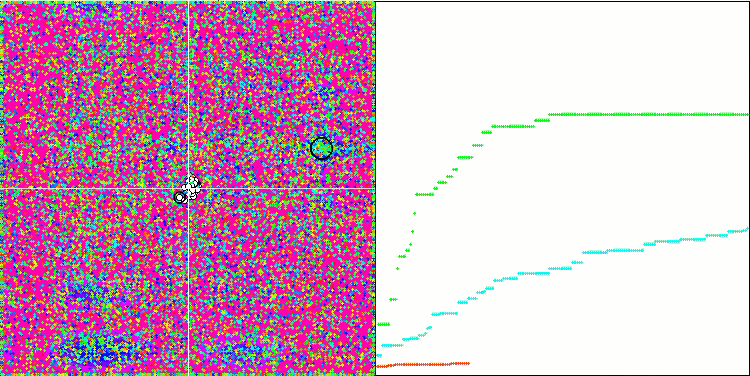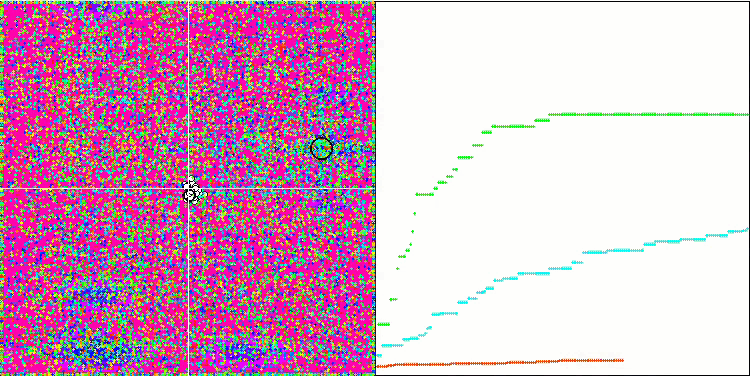
  基于 Megacity 测试函数上的 HS

是时候分析表中的结果，并回答文章标题中设置的问题了。 在之前的文章中，我层表示怀疑，我们是否能看到一种算法可以超过离散函数评级表中的领导者。 该算法在视觉上看起来像是随机算法，不仅能够在离散函数（在三个测试中最好）上成为领导者，而且在其它测试函数上也能够成为领导者，最终在 6 个测试中的 9 个中成为最佳。

算法	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)
HS	和弦搜索	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.00000
ACOm	蚁群优化 M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	入侵杂草优化	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	杜鹃优化算法 M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	萤火虫算法 M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	蝙蝠算法	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	人工蜂群	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	细菌觅食优化	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	引力搜索算法	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
FSS	鱼群搜索	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	粒子群优化	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	随机	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	灰狼优化器	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

我们总结一下。 在撰写本文时，HS 算法在测试结果直方图上占据领先地位，与其它优化算法相比具有巨大的领先优势，这表明该算法的强度和力度及其在解决不同复杂度问题的优化过程方面的潜力。

在我看来，能够在各种类型的测试函数（包括非常复杂的函数）上展示出令人印象深刻的结果的一个非常重要的因素，就是继承了其它优化算法中存在的一些方法（技术）： HS 没有求解结果池排序，每个解仅更新其本地决策 — 这是典型的杜鹃搜索优化算法， 只有当鸟蛋比巢中的蛋更好时，才会出现决策分支发育的新路径。 此外，HS 方法类似于遗传算法中所用的方法 —解元素的组合。
强大的 HS 优化算法具有极高的性能，可以安全地推荐用于解决拥有许多变量的各种复杂问题，无论是平滑缩放函数，还是复杂的离散组合问题。 HS 算法已经成功地应用于工程（优化结构拓扑和零件的最佳形状）、电子和物流的许多领域。
HS 算法的易于实现为研究提供了空间，令我们能够添加和组合各种优化策略。 这表明该算法的能力远未完全发挥。

算法测试结果的直方图如下。

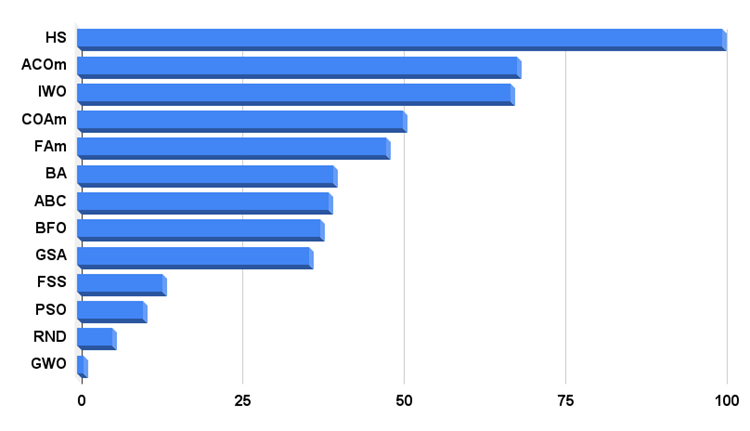
图例 3. 算法测试结果的直方图

HS 和弦搜索算法的优缺点：

优点:
1. 易于实现。
2. 在所有类型的函数上都具有出色的收敛性，无一例外。
3. 令人印象深刻的可扩展性。
4. 非常快速。
5. 外部参数较少。

缺点:
未发现。

每篇文章都提供一个存档，其中包含所有以前文章的算法代码的当前更新版本。 本文基于作者积累的经验，仅代表他的个人观点。 结论和判断基于实验。