种群优化算法:细菌觅食优化 — 遗传算法(BFO-GA)
内容
1. 概述
BFO-GA 混合型优化算法结合了两种不同的优化算法:觅食优化(BFO)算法和遗传算法(GA)。创建这种混合型算法是为了提高优化效率,并克服每种单独算法的一些缺点。
BFO(细菌觅食优化)是一种受到细菌觅食行为启发的优化算法。它是由 Rahul K. Kujur 于 2002 年提出的。BFO 使用三种主要机制对细菌运动进行建模:转移、扩散、和位置更新。算法中的每个细菌都代表优化问题的一个解,而食物对应于最优解。细菌在搜索空间中移动,从而找到最好的食物。
遗传算法(GA)是一种受自然选择和遗传学原理启发的优化算法。它由 John Holland 在 1970 年代开发。GA 工作于个体种群,代表优化问题的解。个体经历杂交(结合遗传信息)和突变(遗传信息的随机变化)操作,从而创造新的世代。经过若干世代,GA 努力寻找最优解。
混合型 BFO-GA 算法结合了两种算法的优点。BFO 具有良好的本地搜索和快速收敛能力,但也许难以进行全局搜索。另一方面,GA 具有良好的全局搜索能力,但收敛速度较慢,容易卡在局部最优状态。混合型 BFO-GA 算法试图通过使用 BFO 进行全局搜索,使用 GA 优化局部最优值来克服这些限制。
BFO-GA(细菌觅食优化 - 遗传算法)混合算法于 2007 年提出,代表人物 DH Kim、A. Abraham 和 JH Cho. 该算法将基于细菌群落行为的优化原则与选择、交叉和突变的遗传运算器相结合。
BFO-GA 使用细菌算法作为基础,但又扩展了遗传选择、交叉和突变运算器。该算法使用细菌群落来查找最优解。
BFO-GA 使用基于轮盘赌方法的算法作为选择运算器。该方法选择概率与其适应度成正比的亲本细菌。因此,更健康的细菌更有可能被选择进行杂交。
BFO-GA 算法中的交叉是使用算术交叉运算器实现的。它结合了两种亲本细菌的遗传信息,创造了具有新基因组合的新后代。
BFO-GA 中的突变是使用非均匀的 Mihaljevic 突变子进行的。这个突变子改变了细菌内部的遗传信息,做出随机变化。突变的不均匀性意味着突变的概率可能会因各种因素而异。
这些修订运算符是在完成细菌算法的趋化性和繁殖程序后进行的,然后该算法再执行消除和扩散程序。换言之,在细菌朝着最优解前进,并产生后代后,遗传运算器被应用于多样化和改进解。
2. 算法
BFO-GA 算法细菌群落行为建模来查找优化问题的最优解。它模拟细菌在参数空间中的运动,其中每个细菌代表一个问题的潜在解。细菌通过执行两种主要类型的运动来遍历参数空间:沿营养梯度方向的运动,以及沿随机方向的运动。
BFO-GA 算法使用以下步骤:
- 初始化:创建初始细菌群落,每个细菌群落都代表问题的潜在解。每种细菌都有自己的参数,可以在优化过程中更改这些参数。
- 营养梯度估算:计算群落中每种细菌的适应度函数值,然后比较最后两个值,其差值可判定每种细菌所代表解的品质。
- 沿梯度方向移动:每个细菌都沿食物梯度方向移动,这令它能够以恒定的位置变化向量,朝更理想的解移动。
- 沿随机方向移动:一些细菌还会进行随机运动,从而避免陷于局部最优状态。这种运动基于在先前不成功运动的情况下随机改变细菌参数。
- 遗传运算器:遗传运算器 — 针对细菌群落的选择、杂交和突变应用。这令我们能够创建新的参数组合,并提高解的品质。
- 重复步骤 2-5:重复沿梯度方向移动、沿随机方向移动,并应用遗传运算器的步骤,直至达到停止准则,例如达到最大迭代次数,或达到某个适应度函数值。
理论上,混合型 BFO-GA 算法拥有超越 BFO 的许多值得一提的优势:
- 探索和开采:由于细菌的随机运动,BFO-GA 具有探索参数空间的能力,以及由于沿食物梯度方向的运动而具有开采的能力。这允许算法通过避免陷于局部最优,并收敛到全局最优来找到最优解。
- 适应性: BFO-GA 能够适应不断变化的优化条件。在算法运作过程中,细菌的参数可能会发生变化,这令它们能够适应新的条件,并找到更理想的解。
- 无需参数调整:与任何优化算法一样,BFO-GA 也有一组参数,可以调整这些参数,从而获得更好的结果。这包括与细菌群落规模、沿梯度和随机运动方向的运动步骤、遗传运算器的概率等相关的参数。更改参数不会对结果产生重大影响。

图例 1. 子细菌对亲本“基因”的遗传
我们从理论基础转向实际实现。
首先,我放弃了采用轮盘赌方法进行选择(该方法曾用在人工蜂群算法)。使用来自亲本群落的简单随机抽样,实验在 BFO-GA 中产生了更好的结果。
其次,我决定把非均匀的 Mihaljevic 突变因子替换为幂律突变(在某些来源中,它被称为一种幂律突变因子)。事实上,这是具有幂律分布的随机数的生成,在关于 智能头足类 的文章中曾有所提及。
第三,算术交叉运算符会被来自根据均匀分布规律随机选择的不同亲本基因的简单随机遗传所取代。
为了描述细菌,我们将编写包含以下字段的 S_Bacteria 结构:
- c:细菌坐标数组,表示细菌在参数空间中的当前坐标。“c” 数组的大小取决于优化问题中的变量数量。
- cLast:细菌的先前坐标数组,计算细菌在参数空间中的新位置时,存储先前位置。
- v:细菌向量数组表示细菌在参数空间中的当前移动方向。“v” 数组的大小取决于优化问题中的变量数量。
- f:细菌健康(FITNESS)的当前值,判定细菌在参数空间中当前位置的品质。“f” 值越大越好。
- fLast:细菌的先前健康值,用于跟踪细菌位置的先前品质,并判定营养梯度。
- lifeCNT:细菌生存计数器,跟踪细菌在其当前位置花费的迭代次数。该字段用于限制细菌可以沿一个方向采取的步骤数。
//—————————————————————————————————————————————————————————————————————————————— struct S_Bacteria { double c []; //coordinates double cLast []; //coordinates double v []; //vector double f; //current health double fLast; //previous health double lifeCNT; //life counter }; //——————————————————————————————————————————————————————————————————————————————
声明 C_AO_BFO_GA 类,该类实现 BFO-GA 算法。我们看看每个字段和类方法:
类字段:
- b: 细菌数组。数组的每个元素都是一个 “S_Bacteria” 类型的对象,在算法中代表细菌。
- rangeMax:优化问题中每个变量的最大搜索范围值的数组。
- rangeMin:每个变量的最小搜索范围值的数组。
- rangeStep:每个变量的搜索步骤数组。
- cB:算法找到的最佳坐标数组。
- fB:最佳坐标的适应度函数值。
类方法:
- Init:初始化 BFO-GA 算法的参数,例如 “paramsP”(优化参数的数量)、“populationSizeP”(群落大小)、“lambda”(细菌移动长度)、“reproductionP”(繁殖概率)、“lifeCounterP”(生存计数器)— 在生存计数完成后,细菌进行滚翻,和 “powerMutP”(突变幂律)。
- Swimming:细菌在参数空间中运作的移动。
- Evaluation:群落修订和全局解更新。
私密类方法:
- NewVector:为指定的 “paramInd” 细菌参数生成新向量。
- PowerDistribution:在 In 输入端应用幂律分布,参数按指定的 “outMin”、“outMax” 和 “power”。
- Sorting:针对群落中的细菌,按其适应度函数值降序排序。
- SeInDiSp:按 “Step” 将 [InMin, InMax] 间隔中的 In 输入端常规化。
- RNDfromCI:在给定的 [min, max] 间隔内生成一个随机数。
- Scale:将 In 输入端从 [InMIN, InMAX] 间隔伸缩到 [OutMIN, OutMAX] 间隔。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BFO_GA { //---------------------------------------------------------------------------- public: S_Bacteria b []; //bacteria public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: void Init (const int paramsP, //number of opt. parameters const int populationSizeP, //population size const double lambdaP, //lambda const double reproductionP, //probability of reproduction const int lifeCounterP, //life counter const double powerMutP); //mutation power public: void Swimming (); public: void Evaluation (); //---------------------------------------------------------------------------- private: double NewVector (int paramInd); private: S_Bacteria bT []; //bacteria private: double v []; private: int ind []; private: double val []; private: int populationSize; //population size private: int parameters; //number of optimized parameters private: double lambda; //lambda private: double reproduction; //probability of reproduction private: int lifeCounter; //life counter private: double powerMut; //mutation power private: bool evaluation; private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power); private: void Sorting (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Init 方法用于初始化类。该方法初始化 BFO-GA 算法的参数。
方法输入:
- paramsP:所优化参数的数量。
- populationSizeP:群落大小。
- lambdaP:lambda 参数,判定细菌在每个步骤中移动的距离。
- reproductionP:繁殖概率。
- lifeCounterP:生存计数器。
- powerMutP:突变幂。
在该方法中,C_AO_BFO_GA 类的字段采用初始值进行初始化,并设置数组大小。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BFO_GA::Init (const int paramsP, //number of opt. parameters const int populationSizeP, //population size const double lambdaP, //lambda const double reproductionP, //probability of reproduction const int lifeCounterP, //life counter const double powerMutP) //mutation power { fB = -DBL_MAX; evaluation = false; parameters = paramsP; populationSize = populationSizeP; lambda = lambdaP; reproduction = reproductionP; lifeCounter = lifeCounterP; powerMut = powerMutP; ArrayResize (rangeMax, parameters); ArrayResize (rangeMin, parameters); ArrayResize (rangeStep, parameters); ArrayResize (v, parameters); ArrayResize (ind, populationSize); ArrayResize (val, populationSize); ArrayResize (b, populationSize); ArrayResize (bT, populationSize); for (int i = 0; i < populationSize; i++) { ArrayResize (b [i].c, parameters); ArrayResize (b [i].cLast, parameters); ArrayResize (b [i].v, parameters); b [i].f = -DBL_MAX; b [i].fLast = -DBL_MAX; ArrayResize (bT [i].c, parameters); ArrayResize (bT [i].cLast, parameters); ArrayResize (bT [i].v, parameters); } ArrayResize (cB, parameters); } //——————————————————————————————————————————————————————————————————————————————
编写 Swimming 方法来运作细菌的化学活性、它们的复制、选择、特征的遗传和突变:
void Swimming ()
{
} 在第一次迭代时,“evaluation” 标志等于 “false”。将细菌随机分布在整个搜索空间中,均匀分布。在该阶段,当前的健康状况(健康状况)和之前的健康状况都是未知的。我们将 DBL_MAX 值分配给相应的变量。此外,将随机运动向量添加到新创建的细菌之中。
检查细菌坐标是否超出边界,并应用更改优化参数的步骤。每种细菌的运动矢量令它们能够均匀地向前游动。
if (!evaluation) { fB = -DBL_MAX; for (int s = 0; s < populationSize; s++) { for (int k = 0; k < parameters; k++) { b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); v [k] = rangeMax [k] - rangeMin [k]; b [s].v [k] = NewVector (k); b [s].f = -DBL_MAX; b [s].fLast = -DBL_MAX; b [s].lifeCNT = 0; } } evaluation = true; return; }
首先在第二次和后续迭代中检查细菌繁殖(复制)的概率。如果满足繁殖的概率,则发生以下情况:
- “原始细菌”:整理过的细菌群落中最好的一半继续朝同一方向移动。为此,我们将每个细菌的单独运动向量添加到前一个位置的坐标中。
- “细菌克隆”:群落的另一半填充了从不同亲本细菌的“基因”(坐标)获得的子细菌。因此,它们继承了特征,并实现了算法的组合能力(见上面的图例 1)。
- 克隆细菌从不同亲本继承基因,也会继承亲本运动向量的一个组成部分,并且遗传基因会根据幂律分布突变。
因此,克隆细菌继承了不同亲本的特征。在这种情况下,基因在其附近发生变化的概率很高。概率随着与亲本基因值的距离增加而降低。这令我们能够结合亲本的成功特性,因为只有群落中最优秀的成员才能将基因传承给他们的继承人。此外,运动向量的遗传分量导致子细菌会在下一次迭代中按照亲本向量的最佳分量移动。
理想情况下,这应该类似于一群鱼的运动,但由于许多随机因素对细菌运动的影响,这种类比并不总能得到证实。这些因素包括适应度函数的景观、被更幸运的群落成员取代、以及由于生存数量的限制而不可避免地改变运动向量。
菌落较优部分的细菌生存计数器增加 1,而对于克隆的细菌,它会重置。
double r = RNDfromCI (0.0, 1.0); if (r < reproduction) { int st = populationSize / 2; //bacterium original-------------------------------------------------------- for (int s = 0; s < st; s++) { for (int k = 0; k < parameters; k++) { b [s].c [k] = b [s].cLast [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } b [s].lifeCNT++; } //bacterium clone----------------------------------------------------------- for (int s = st; s < populationSize; s++) { for (int k = 0; k < parameters; k++) { int i = (int)RNDfromCI (0, st); if (i >= st) i = st - 1; b [s].c [k] = b [i].cLast [k]; b [s].c [k] = PowerDistribution (b [s].c [k], rangeMin [k], rangeMax [k], powerMut); b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } b [s].lifeCNT = 0; } }
接下来,如果不满足繁殖的概率,则在整个群落的循环中:
for (int s = 0; s < populationSize; s++)
首先检查是否达到细菌生存极限。在达到生存极限后,细菌滚翻,并开始向新的方向移动,改变它们的运动向量。生存计数器被重置。
在检查细菌达到生存极限后,那些达到极限的细菌会发生变异,在下一次迭代中,它们开始向新的方向移动,改变它们的运动矢量。生存计数器被重置。
if (b [s].lifeCNT >= lifeCounter) { for (int k = 0; k < parameters; k++) { b [s].v [k] = NewVector (k); b [s].c [k] = PowerDistribution (b [s].cLast [k], rangeMin [k], rangeMax [k], powerMut); b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } b [s].lifeCNT = 0; }
如果细菌尚未达到其生存极限,我们检查积极趋化性,即细菌是否朝着提升食物梯度移动。如果前两次迭代中的适应度值相等,则认为细菌的运动是正确的。为什么完全相等?在下一阶段,在 Evaluation 方法中,我们检查细菌适应度状况的积极变化。如果变化为正值,则当前状态将分配给上一个状态。如果最近两次迭代中的适应度状态相同,则表明细菌为寻找更多食物而移动的方向是正确的。因此,细菌只能朝更多食物移动。否则,细菌开始在原地转圈。然而,这不是问题,因为卡住的细菌迟早会变异成新的状态,或者继承更幸运亲本的基因、及其运动向量。
朝着正确方向移动的细菌,其生命计数器递增。这意味着即使是成功的细菌迟早也会发生突变,如前面的代码模块中所述。
if (b [s].f == b [s].fLast) { for (int k = 0; k < parameters; k++) { b [s].c [k] = b [s].cLast [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } b [s].lifeCNT++; }
如果在细菌中没有观察到积极的趋化性,那么这种细菌会改变运动向量,做出翻滚。这种细菌的生存计数器也继续跳动。浮现这个思路是为了更密集地增加这种不成功细菌的生存计数器的数值,尽管我还没有测试过这个思路。
for (int k = 0; k < parameters; k++) { b [s].v [k] = NewVector (k); b [s].c [k] = b [s].cLast [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } b [s].lifeCNT++;
要执行翻滚(更改运动矢量),调用 NewVector 方法,其按 “paramInd” 索引执行优化参数:
- 调用 “RNDfromCI” 函数生成一个随机数 “r”,在 [-1.0, 1.0] 区间内均匀分布。
- 向量分量的新值是通过将优化参数的允许的 “v” 值范围乘以 “lambda” 比率和 “r” 随机数计算得出的。
//—————————————————————————————————————————————————————————————————————————————— double C_AO_BFO_GA::NewVector (int paramInd) { double r = RNDfromCI (-1.0, 1.0); return lambda * v [paramInd] * r; } //——————————————————————————————————————————————————————————————————————————————Evaluation 方法用于安排细菌之间的竞争,并更新全局解。
在方法开始处,测试群落中每种细菌的积极趋化性:如果适应度函数 “b[s].f” 的当前值大于先前值 “b[s].fLast”,则先前的适应度和坐标(细菌将从中移动)被更新。
然后,调用 Sorting 方法依据细菌的 fLast 值,并按适应度函数值的降序对群落排序。
此后,全局解将更新。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BFO_GA::Evaluation () { for (int s = 0; s < populationSize; s++) { if (b [s].f > b [s].fLast) { b [s].fLast = b [s].f; ArrayCopy (b [s].cLast, b [s].c, 0, 0, WHOLE_ARRAY); } } Sorting (); if (b [0].fLast > fB) { fB = b [0].fLast; ArrayCopy (cB, b [0].cLast, 0, 0, WHOLE_ARRAY); } } //——————————————————————————————————————————————————————————————————————————————
3. 测试结果
BFO-GA 测试台结果:
C_AO_BFO_GA:50;0.01;0.8;50;10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.8914957961234459
25 Hilly's; Func runs: 10000; result: 0.5511088047221568
500 Hilly's; Func runs: 10000; result: 0.31529201642392934
=============================
5 Forest's; Func runs: 10000; result: 0.9698155977381523
25 Forest's; Func runs: 10000; result: 0.39612322805995287
500 Forest's; Func runs: 10000; result: 0.06304955092899359
=============================
5 Megacity's; Func runs: 10000; result: 0.7266666666666667
25 Megacity's; Func runs: 10000; result: 0.275
500 Megacity's; Func runs: 10000; result: 0.035250000000000004
=============================
All score: 4.22380 (46.93%)
针对试验台操作的可视化分析表明,BFO-GA 算法可以快速检测全局极值的区域,而较少关注局部极值的研究,如果全局极值被证明是错误的,则有潜在导致卡顿的可能。通常,该算法能相当可靠地收敛,尽管收敛速度有些慢。观察到一些 “群落”,这是一个好兆头,但细菌之间完全没有交流,它们表现为独立的群落单位。
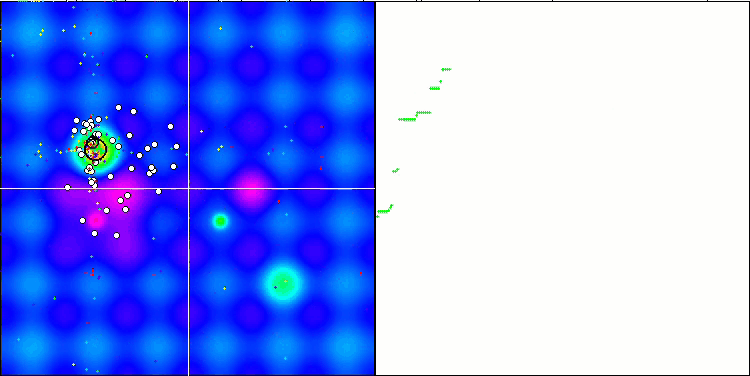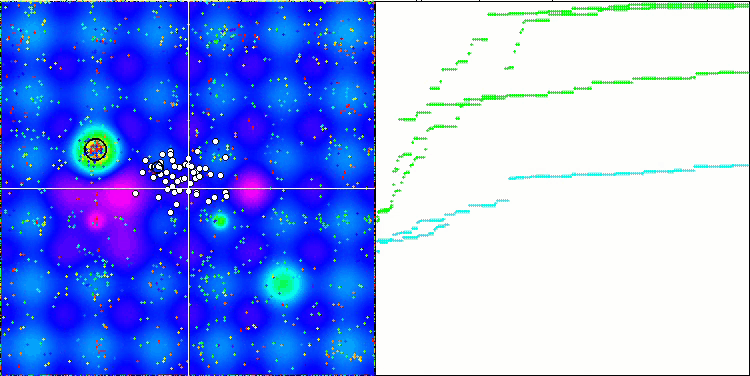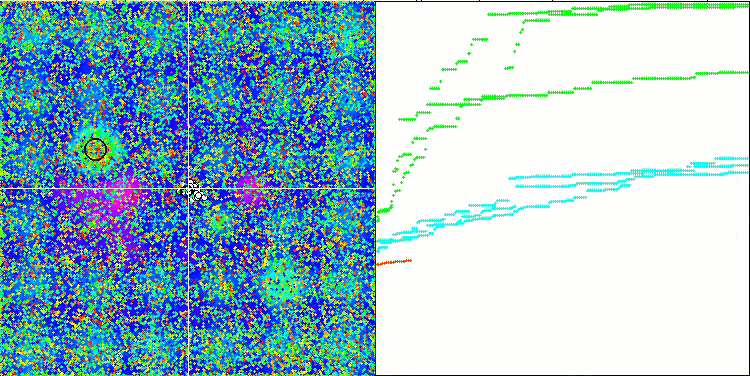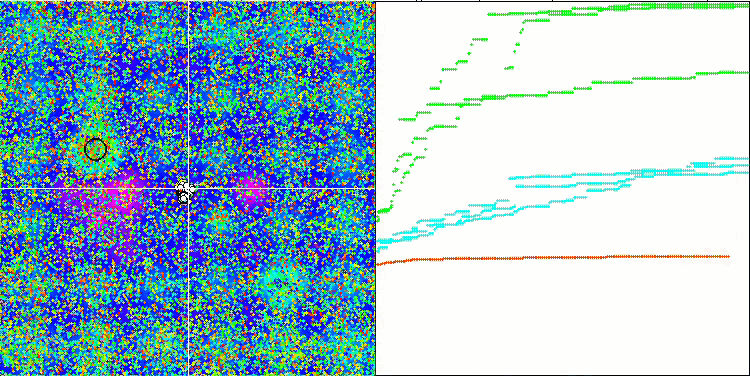
BFO-GA 依据 Hilly 测试函数
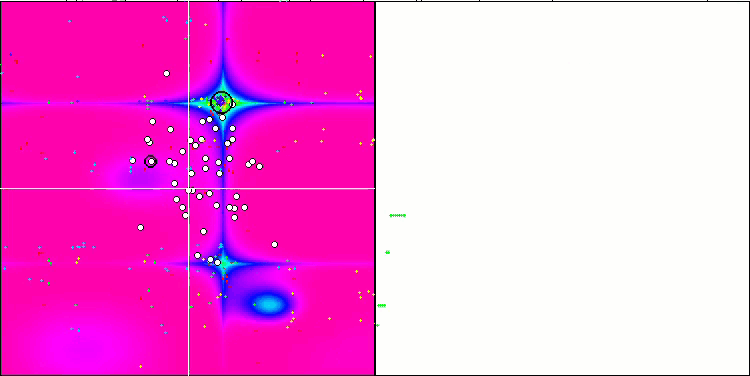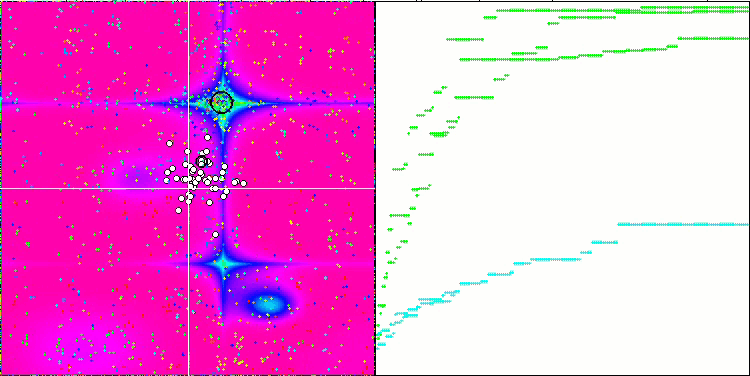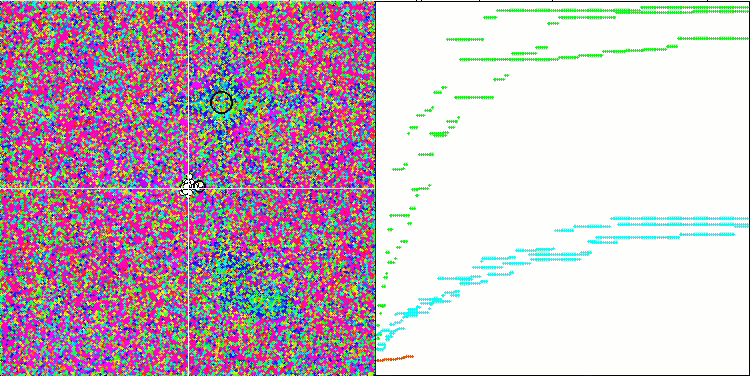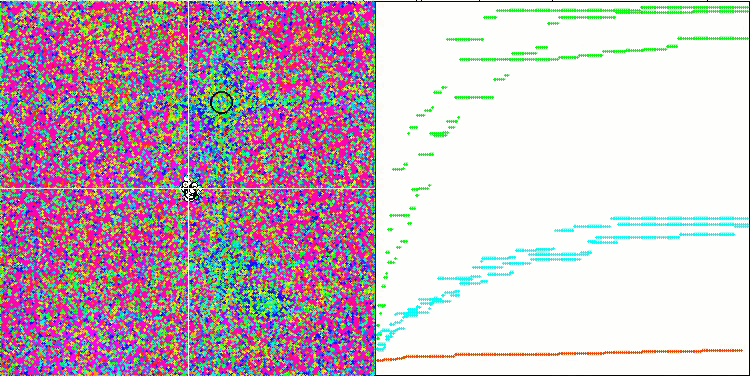
BFO-GA 依据 Forest 测试函数
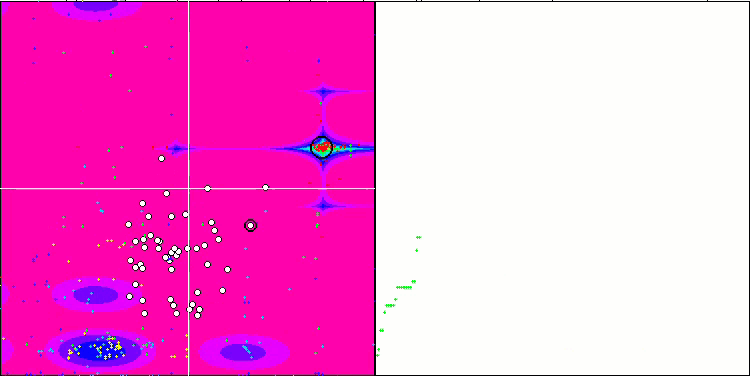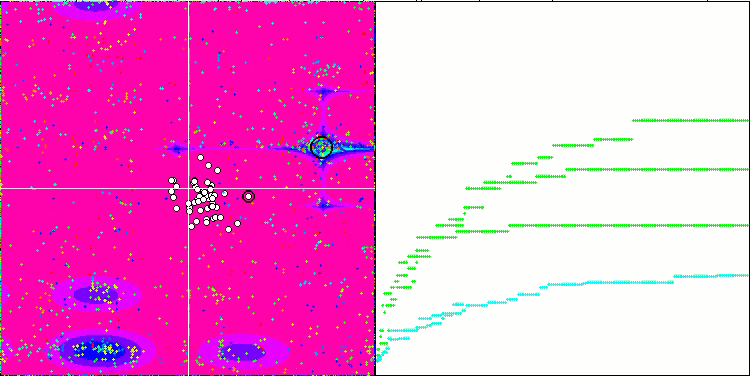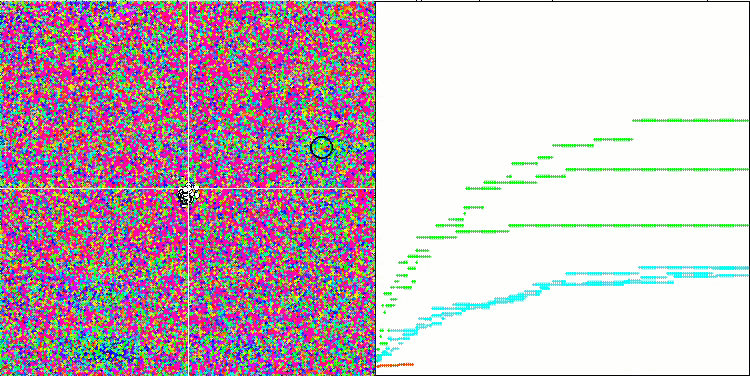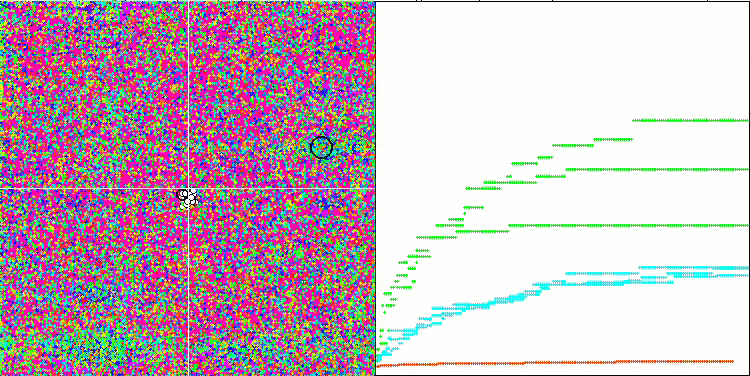
BFO-GA 依据 Megacity 测试函数
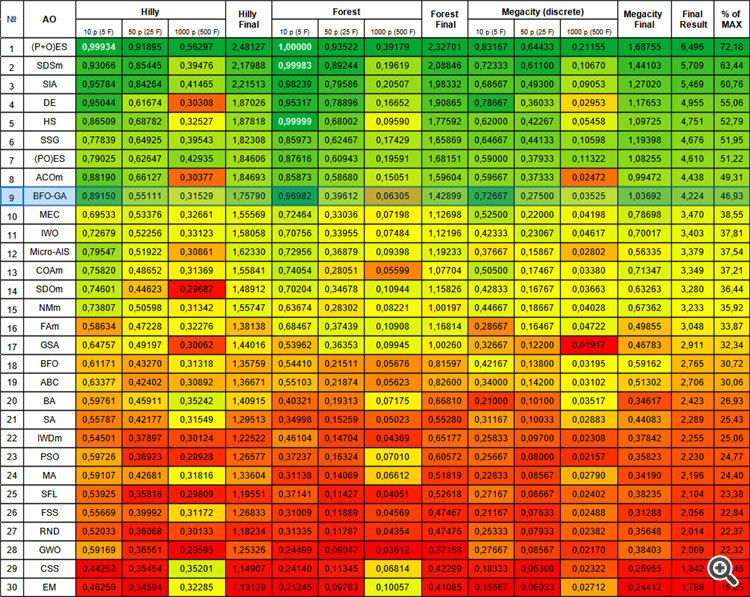
在总体评分表中,BFO-GA 算法排名第 9,这是一个相当高的结果。这表明在将遗传算法运算器添加到原始 BFO 算法时所做的转换并非徒劳,并导致了相应的结果。该算法主要在测试函数上展示了最佳结果,少数变量竟超过了大多数其它1算法。
| # | AO | 说明 | Hilly | Hilly 最终 | Forest | Forest 最终 | Megacity (离散) | Megacity 最终 | 最终结果 | 最大 % | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | (P+O)ES | (P+O) 进化策略 | 0.99934 | 0.91895 | 0.56297 | 2.48127 | 1.00000 | 0.93522 | 0.39179 | 2.32701 | 0.83167 | 0.64433 | 0.21155 | 1.68755 | 6.496 | 72.18 |
| 2 | SDSm | 随机扩散搜索 M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 3 | SIA | 模拟各向同性退火 | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 4 | DE | 差分进化 | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 5 | HS | 谐声搜索 | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 6 | SSG | 树苗播种和生长 | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 7 | (PO)ES | (PO) 进化策略 | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 8 | ACOm | 蚁群优化 M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 9 | BFO-GA | 细菌觅食优化 - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 10 | MEC | 心智进化计算 | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 11 | IWO | 入侵性杂草优化 | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 12 | Micro-AIS | 微型人工免疫系统 | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 13 | COAm | 布谷鸟优化算法 M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 14 | SDOm | 螺旋动力学优化 M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 15 | NMm | Nelder-Mead 方法 M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 16 | FAm | 萤火虫算法 M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 17 | GSA | 重力搜索算法 | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 18 | BFO | 细菌觅食优化 | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 19 | ABC | 人工蜂群 | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 20 | BA | 蝙蝠算法 | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 21 | SA | 模拟退火 | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 22 | IWDm | 智能水滴 M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 23 | PSO | 粒子群优化 | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 24 | MA | 猴子算法 | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 25 | SFL | 蛙跳 | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 26 | FSS | 鱼群搜索 | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 27 | RND | 随机 | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 28 | GWO | 灰狼优化器 | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 29 | CSS | 收费系统搜索 | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 30 | EM | 类电磁算法 | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
总结
与原始 BFO 算法相比,我们看到 BFO-GA 结果有了清晰的改进,这是由于使用了遗传算法运算器:选择、突变和遗传。BFO 以前没有退出局部极值的机制,现在这个问题不再存在。该算法为实验提供了巨大的机会,结合了细菌觅食策略的分量顺序和 GA 运算器。其中有许多我还未曾尝试。
在 BFO 算法中,我之前在计算细菌生存数时犯了一个错误,但这个错误已经被纠正了。BFO 的结果略有改善,比 ABC 高出一行。我想指出的是,在编写优化算法时,很难检测到搜索策略代码和逻辑中的错误。即使有错误,算法也几乎总是会继续搜索。错误并不总会影响结果。有时,结果会显著改善,“错误”反而成为了策略的一部分。始终值得记住的是,在优化算法中,逻辑的大幅变化并不总是会导致结果的显著改善,而微小的变化有时却会导致显著的改善。您可以在存档中找到修正后的 BFO 版本。
图例 2. 算法的颜色渐变是依据相关测试
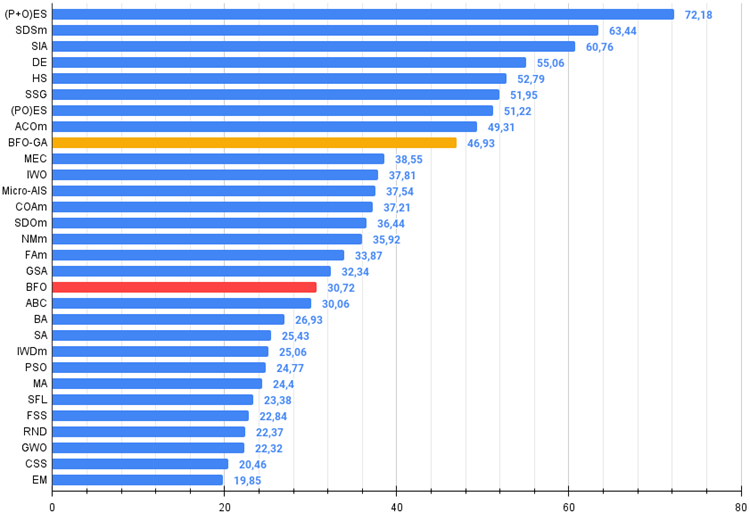
图例 3. 算法测试结果的直方图(标尺从 0 到 100,越多越好,
其中 100 是理论上的最大可能结果(存档提供了一个计算评级表格的脚本)。
BFO-GA 的优点和缺点:
- 算法运行速度快。
- 实现简单。
- 在参数量较少的函数上具有良好的收敛性。
- 搜索空间较大的任务收敛性低。
本文附有一个存档,其中包含前几篇文章中讲述的算法代码的当前更新版本。文章作者不对规范算法讲述的绝对准确性负责。它们当中进行了多处修改,从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/14011
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 种群优化算法:微人工免疫系统(Micro-AIS)
种群优化算法:微人工免疫系统(Micro-AIS)
 构建和测试肯特纳通道交易系统
构建和测试肯特纳通道交易系统


我建议添加速度估算对比图。
我建议添加一个速度估算对比图。
如果没有几个 "但是",这个建议是可以实现的:
1.图表可能会产生误导,因为这是算法本身的速度,而不是整个问题的解决方案。
2.算法代码的执行速度可以通过在测试台代码中插入相应的计数器来轻松测量。有些算法确实需要很长时间才能执行,而这种测试很难创造理想的条件,结果不会真正客观。
看着还可以啊