群体优化算法：随机扩散搜索（SDS）

目录

1. 概述
2. 算法
3. 测试结果

1. 概述

随机扩散搜索（Stochastic Diffusion Search，SDS）算法由 J.Bishop 于1989年提出，并由 Bishop 和 S.Nasuto 积极开发。与其他群体算法相比，该算法的一个显著特征是其深刻的数学合理性。SDS最初是为离散优化而开发的。2011年，提出了对其进行全局连续优化的修改。

有趣的事实：

1. 随机扩散搜索（SDS）是第一个群智能元启发式算法，属于群智能和自然搜索优化算法的家族。这种算法的其他例子是蚁群优化、粒子群优化和遗传算法。

2. 与基于柱头能量通信的蚁群优化不同，SDS使用代理之间的直接通信，类似于细齿蚁使用的串联呼叫机制。

SDS算法基于代理对假设（搜索问题的候选解决方案）的低成本部分评估。然后，代理通过直接的个体交流来交换关于假设的信息。通过扩散机制，可以从具有相同假设的代理集群中识别出高质量的解决方案。

为了更好地理解SDS算法的操作，我们可以使用一个简单的类比——餐厅游戏。

在餐厅游戏中，参与者扮演代理的角色，餐厅扮演假设的角色。每个代理根据自己的偏好和从其他代理那里收到的信息选择一家餐厅用餐。然后，代理交换关于他们的选择和偏好的信息。这一过程的结果是，选择了同一家餐厅的代理商形成了集群，可以被确定为潜在的好决定。

SDS算法有几个优点。首先，它允许代理进行廉价的部分假设估计，这降低了算法的计算复杂性。其次，它使用代理人之间的直接个人通信，这使得信息能够有效地传播。第三，SDS以数学为基础，使其更加可靠和可预测。

然而，SDS算法也有其局限性。首先，它只能在假设概念适用的某些类型的问题中有效。其次，它可能存在过早收敛的问题，即主体在没有探索其他可能性的情况下过于快速地收敛于一个假设。第三，该算法需要参数调整，这可能是一个复杂而耗时的过程。一些作者说明了这些限制，让我们检查一下它们是否合理。

总的来说，SDS是解决优化问题的一种有趣而有效的算法。它结合了群体算法和数学原理的优点，对各个领域的研究和应用具有吸引力。

2. 算法

让我们继续更详细地考虑SDS算法。

随机扩散搜索（SDS）是一种基于两种搜索策略思想的群体算法：

1. 解决方案的部分评估。
2. 向全体成员传播有希望的解决方案。

有两个规范的游戏可以简单地描述SDS的工作原理。
1. 餐厅游戏
2. 金矿游戏。

餐厅游戏

一群代表正在一个陌生的城市参加一个长会议，每天晚上，他们都面临着选择餐馆吃饭的问题。这座城市有许多餐馆，提供各种各样的菜肴。小组的目标是找到最好的一个，让每个代表都能享受一顿饭。然而，对所有可能的餐厅和菜肴组合进行详尽的搜索会花费太多时间。为了解决这个问题，代表们采用随机扩散搜索。

每位代表都充当一名代理人，对城市中最好的餐厅的选择进行猜测。每天晚上，代表们通过参观餐厅并从餐厅的菜肴中随机选择一种来测试他们的假设。第二天早上，在早餐时，每一位对前一晚的晚餐不满意的代表都会请他的一位同事分享他们对晚餐的印象。如果同事的印象是正面的，代表也会选择那家餐厅。否则，代表将从该城市的可用餐厅列表中随机选择另一个位置。

因此，得益于这一策略，大量代表迅速形成，聚集在城市中最好的餐厅周围。

这个游戏有几个有趣的特点。在完全没有外部控制和管理的情况下，一群代表进行沟通，以解决无法单独快速解决的问题。如果当前餐厅的服务或菜单显著下降或业务关闭，则代表有效地转到下一家最好的餐厅。主要要求是餐厅、菜单和个人菜肴的可比性。每个代理自己决定他们的体验是否良好。

在评估城市所有地点的所有菜肴之前，代表们将在一家高质量的餐厅度过许多晚上。
批评者指出，代表们可能有不同的食物偏好，因此一名代表可能会找到一家他们喜欢所有菜肴的餐厅，但这可能无法满足其他人的需求。如果只有一名或少数代表永久留在这样的餐厅，其余代表将继续照常行事，最终大多数代表仍会聚集在最好的餐厅。然而，在极端情况下，所有代理人可能会发现自己独自用餐。即使只有一家优秀的餐厅能让大多数代表满意，这家餐厅将永远找不到，因为所有代表都对他们目前的选择感到满意，不会寻找新的位置。

我们的实现对搜索策略的逻辑进行了微小的更改，这要归功于即使没有经验更好的代表，代表也会继续搜索餐厅，因此对餐厅的搜索不会停止，这与规范版本不同，在规范版本中，改变当前对餐厅的看法与前一个观点相比很重要。如果大多数代表的意见没有好转，那么他们将继续去同一家餐厅，这意味着陷入局部的极值。

金矿游戏

一群由经验丰富的矿工组成的朋友了解在山脉的山丘上开采黄金的可能性。然而，他们没有关于最富有的地方到底在哪里的信息。在他们的地图上，山脉被划分为几个单独的山丘，每个山丘都包含一组需要开采的地层。随着时间的推移，发现黄金的概率与其财富成正比。

为了最大限度地增加他们的集体财富，矿工们应该确定这座山上有最丰富的金矿层，以便最大数量的矿工能够在那里开采。但是，这些信息无法提前获得。为了解决这个问题，矿工们决定使用简单的随机扩散搜索。

采矿过程开始时，每个矿工被随机分配一座小山进行采矿（自定义小山假设）。每天，每个矿工都会随机选择他们山上的一个地层进行开采。

每天结束时，矿工感到高兴的概率与他或她发现的黄金量（适应度函数的值）成正比。
晚上，工作结束后，矿工们聚在一起。一个不开心的矿工随机选择另一个矿工与之交谈。如果被选中的矿工满意，他会很高兴地告诉他的同事他正在开采的山的名字。因此，两位矿工都支持山丘假说。如果被选中的矿工不高兴，他什么也不说，而原来的矿工再次被迫选择一个新的假设——随机确定他第二天要开采的山。

在SDS（自组织动态系统）的上下文中，代理充当矿工。活跃的代理人是“快乐的矿工”，而不活跃的代理人则是“不快乐的矿工“。每个代理人的假说代表了矿工的“山丘假说”。这一过程与SDS同构，允许矿工自然地自我组织，并迅速聚集在黄金浓度高的山脊上。

矿工的幸福感可以用概率来衡量，也可以用绝对布尔值来表示，假设每个矿工在每天结束时都是快乐或不快乐的。如果黄金被建模为一种随着时间的推移而减少的有限资源，那么搜索就会变得非常自适应，矿工会转移到黄金最多的地方。

尽管“快乐”一词是主观的，就像饮食习惯一样，但在这种情况下，它是在客观意义上使用的。所有矿工都使用相同的过程：当他们聚在一起可能分享他们正在开采的山丘的信息时，他们一天中发现的黄金数量决定了他们在一天结束时宣布自己“幸运”的可能性。

我们不会把矿工分为“快乐的”和“不快乐的”。与餐厅游戏概念的情况一样，这允许增加代理商搜索新的未经探索的地方的活动。

为了使算法形式化，我们将使用“候选者”的概念，它相当于餐馆游戏中的代表和金矿游戏中的矿工。候选人是一名搜索代理。为了更简单地理解餐馆或山丘的本质，我们可以想象一个有两个坐标的空间，尽管实际上可以使用无限数量的坐标来解决多维问题。在图1中，名称C1、C2、C3显示了存储餐厅编号的候选者（搜索字段中的相应空格）。在餐厅信息的扩散交换过程中，如果对话者的适应度函数值较高，候选人会从随机选择的会议参与者那里借用餐厅编号。每个优化参数（搜索空间坐标）的范围除以算法的外部参数中指定的餐厅数量。例如，如果在算法参数中指定了100家餐厅的数量，这意味着每个坐标的范围将被划分为100个部分。

每家餐厅的菜单上都有一份菜肴清单。每个菜单菜都是一个餐厅内搜索空间的特定坐标。该算法实现了一种方案，即候选人只品尝一道随机选择的餐厅菜肴。

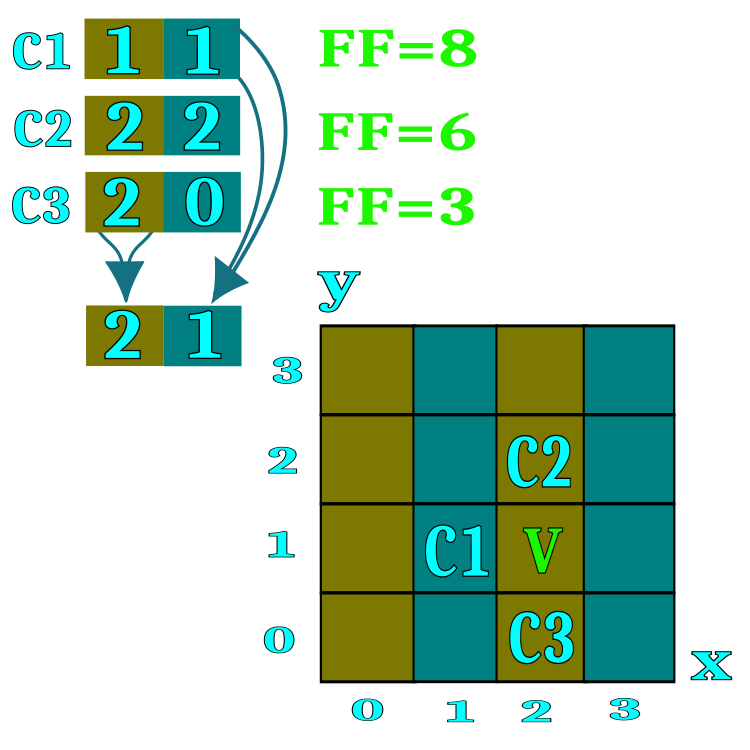
图1. 餐厅信息交换扩散原理的可视化表示

让我们以伪代码的形式来看看SDS算法的步骤。

1. 候选人的初始化（随机分配餐厅和菜肴）。

2.0. 假设检验和候选者之间的扩散交换。

2.1. 将候选人当前的经历与他或她以前的经历进行比较。

2.1.1. 如果体验更好，则指定餐厅地址作为下一次迭代的假设。

2.1.2. 如果体验更差，就询问随机选择的候选人的意见。

2.1.2.1. 如果对话者（候选人）的经验更好，那么记下（当前候选人）有前途的餐馆的地址。

2.1.2.2. 如果对话者——候选人——的经历更糟糕，那么在一定程度上，我们要么选择随机选择的餐厅的地址，要么保留当前的地址。

3.0. 从生成的餐厅列表中选择菜肴作为下一次迭代的假设。

假设检验的逻辑图如图2所示。大多数逻辑路线执行选择餐厅的任务，在餐厅选择完成后，随机选择一道菜。餐厅的选择是算法的主要任务，但菜肴的选择是完全随机的，与之前的迭代无关。

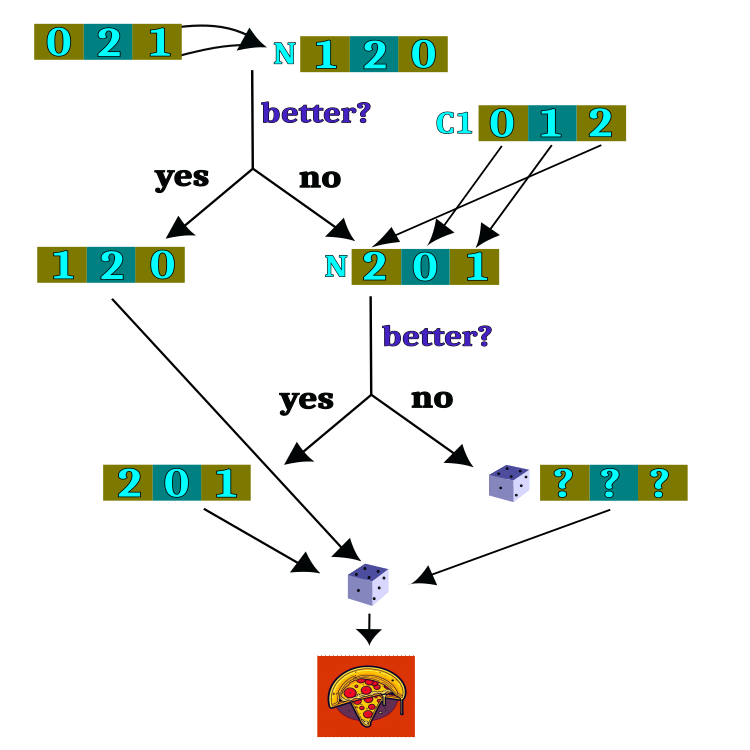
图 2检验假设的逻辑方案

现在是时候看看SDS（随机扩散搜索）代码，从算法的核心和灵魂开始了——代理，也就是候选，它可以用S_candidate结构来描述。它包含以下字段：

1. raddr: 包含餐厅地址的数组。每个数组元素表示一个餐厅的地址。
2. raddrPrev: 包含以前餐馆地址的数组。每个数组元素表示一个餐厅的地址。
3. c: 包含坐标（菜肴）的数组。数组的每个元素表示一个菜肴的坐标。
4. cPrev: 包含先前坐标（菜肴）的数组。数组的每个元素表示一个菜肴的坐标。
5. f: 代理当前状态的适应度函数值。
6. fPrev: 代理先前状态的适应度函数值。

S_Candidate 结构具有 Init 方法，该方法初始化所有“coords”大小的数组（坐标的数量-要优化的参数），并将f和fPrev的初始值设置为-DBL_MAX，因为在第一次迭代时没有也没有人可以比较候选者的经验。

//——————————————————————————————————————————————————————————————————————————————
struct S_Candidate
{
  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double c         []; //coordinates (dishes)
  double cPrev     []; //previous coordinates (dishes)
  double f;            //fitness
  double fPrev;        //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

声明包含以下内容的SDS算法类：

类字段：
- cB: 包含最佳坐标的数组
- fB: 最佳坐标的适应度函数值
- cands: 用于查找最佳坐标的候选数组
- rangeMax: 包含每个坐标的最大值的数组
- rangeMin: 包含每个坐标的最小值的数组
- rangeStep: 包含每个坐标的搜索步骤的数组

类方法：
- Init: 算法参数的初始化，如坐标数量、群体大小、餐厅数量和选择餐厅的概率
- Moving: 执行算法步骤，将候选者移动到新坐标
- Revision: 执行修订步骤，更新最佳坐标和适应度函数
- SeInDiSp: 用给定步骤计算给定范围内新坐标的方法
- RNDfromCI: 在给定区间内生成随机数的方法

其他类字段：
- coords: 坐标数
- populationSize: 群体大小
- restNumb: 餐厅数量
- probabRest: 选择餐馆的概率
- restSpace: 餐厅空间
- revision: 指示需要修订的标志

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDS
{
  //----------------------------------------------------------------------------
  public: double cB   [];       //best coordinates
  public: double fB;            //FF of the best coordinates
  public: S_Candidate cands []; //candidates

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search



  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP);         //probability restaurant choosing

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;            //coordinates number
  private: int    populationSize;    //population size

  private: int    restNumb;          //restaurants number
  private: double probabRest;        //probability restaurant choosing
  private: double restSpace [];      //restaurants space

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

SDS算法的初始化方法首先为一些变量和数组设置初始值。

该方法的输入参数为：
- coordinatesNumberP: 坐标数（搜索空间维度）
- populationSizeP: 群体大小（候选人数量）
- restaurantsNumberP: 餐馆数量
- probabRestP: 选择餐馆的概率

首先，使用MathSrand函数重置随机数生成器，并将当前值传递给它（以微秒为单位）。然后，fB 和 revision 变量分别初始化为初始值——DBL_MAX和“false”。
接下来，坐标NumberP和populationSizeP输入的值被分配给坐标和populationSize变量。
restNumb和probabRest变量是用restaurantsNumberP和probabRestP值初始化的。
“coords”大小的restSpace数组是使用ArrayResize函数创建的。
然后使用ArrayResize函数创建populationSize大小的“cands”数组。在循环中，通过使用“coords”参数调用Init方法来初始化“cands”数组的每个元素。
“coords”大小的rangeMax、rangeMin、rangeStep和cB数组也使用ArrayResize函数创建。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP)          //probability restaurant choosing
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  populationSize = populationSizeP;

  restNumb   = restaurantsNumberP;
  probabRest = probabRestP;
  ArrayResize (restSpace, coords);

  ArrayResize (cands, populationSize);
  for (int i = 0; i < populationSize; i++) cands [i].Init (coords);

  ArrayResize (rangeMax,       coords);
  ArrayResize (rangeMin,       coords);
  ArrayResize (rangeStep,      coords);
  ArrayResize (cB,             coords);
}
//——————————————————————————————————————————————————————————————————————————————

尽管每次迭代都会调用Moving（）方法，但该方法的主要逻辑只执行一次，由 revision 标志控制。

在函数开始时，会检查“revision”变量。如果为“false”，则初始化变量和数组。
然后，沿着空间中的点的坐标发生循环。

在这个循环中，计算restSpace[i]，这是每个坐标的间隔长度，定义为范围的最大值和最小值之间的差除以restNumb。

接下来，声明变量min和max，它们将用于确定特定餐厅空间的值范围。

然后初始化n和dish变量以用于确定所选餐厅范围内的随机值。

然后，通过populationSize大小的总体执行循环，其中在空间点的坐标上执行循环。在这个循环中，使用RNDfromCI（）函数生成一个随机数n，该函数用于确定restSpace数组中的索引。如果结果值n大于或等于restNumb，则将其赋值为restNumb-1，以确保随机变量的均匀分布。然后使用rangeMin、restSpace和n计算min和max。

我们使用RNDfromCI（）函数生成一个随机数“dish”，其范围从“min”到“max”（餐厅空间）。

然后使用SeInDiSp（）函数使用“dish”的值来计算c[i]的值，该函数使用rangeMin、rangeMax和rangeStep来确保优化参数的正确步长。

作为该算法的结果，空间中的每个点根据餐厅的空间接收每个坐标的随机值，模拟菜肴的随机选择。

“revision”变量设置为“true”，因此下次调用Moving（）函数时，变量和数组不会初始化。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Moving ()
{
  if (!revision)
  {
    for (int i = 0; i < coords; i++)
    {
      restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
    }

    double min = 0.0;
    double max = 0.0;

    int    n   = 0;
    double dish = 0.0;

    for (int i = 0; i < populationSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        n = (int)(RNDfromCI (0, restNumb));
        if (n >= restNumb) n = restNumb - 1;

        cands [i].raddr     [c] = n;
        cands [i].raddrPrev [c] = n;
        min = rangeMin [c] + restSpace [c] * n;
        max = min + restSpace [c];

        dish = RNDfromCI (min, max);

        cands [i].c [c] =  SeInDiSp (dish, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

SDS算法的 Revision 方法执行了选择餐馆和餐馆菜肴的基本逻辑。这对于前面讨论的算法来说并不典型，其中移动代理的主要逻辑位于Moving方法中，尽管调用算法方法的顺序保持不变，并且与本系列第一篇文章中选择的概念相对应。该算法由以下步骤组成：

1. 更新fB适应度函数的最佳发现值和相应的cB坐标集。对于总体中的每个候选i，进行比较，如果f的值（函数估计）大于fB的当前全局值，则更新fB并将其从i个候选复制到cB最佳全局坐标集。

2. 更新每位候选人之前的评分和餐馆设置。对于群体中的每个i个候选者，如果f的值大于fPrev的先前值，则更新fPrev，并且将来自i个候选者的餐馆c和raddr的集合复制到cPrevi和raddrPrevi的相应先前值。

3. 为每位候选人选择一套新的餐厅。对于群体中的每个i候选者和每个c坐标，选择从0到populationSize的随机数n。如果候选n的fPrv的值大于候选i的fPrve的值，则用n个候选的raddrPrevi值更新候选i的餐馆集合raddr。否则，生成在0.0到1.0的范围内的随机数rnd。如果rnd小于probabRest概率，则选择从0到restNumb范围内的n个随机数，并且用n的值更新i个候选餐厅的集合raddr。否则，候选人i的raddr餐厅集保持不变。

4. 为每个候选者生成一组新的坐标。基于相应坐标的rangeMin和restSpace，为总体中的每个i候选者和每个c坐标确定“min”和“max”最小值和最大值。然后，使用SeInDiSp函数生成“最小”到“最大”范围内的随机数，并将所得值分配给i个候选者的c集中的相应c坐标。

因此，SDS算法的Revision方法迭代整个候选群体，更新找到的最佳值和餐厅集，选择新的餐厅集，并为每个候选生成新的坐标集。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > fB)
    {
      fB = cands [i].f;
      ArrayCopy (cB, cands [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  double min = 0.0;
  double max = 0.0;
  double rnd = 0.0;
  int    n   = 0;

  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > cands [i].fPrev)
    {
      cands [i].fPrev = cands [i].f;
      ArrayCopy (cands [i].cPrev, cands [i].c, 0, 0, WHOLE_ARRAY);
      ArrayCopy (cands [i].raddrPrev, cands [i].raddr, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < populationSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, populationSize));
      if (n >= populationSize) n = populationSize - 1;

      if (cands [n].fPrev > cands [i].fPrev)
      {
        cands [i].raddr [c] = cands [n].raddrPrev [c];
      }
      else
      {
        rnd = RNDfromCI (0.0, 1.0);

        if (rnd < probabRest)
        {
          n = (int)(RNDfromCI (0, restNumb));
          if (n >= restNumb) n = restNumb - 1;
          cands [i].raddr [c] = n;
        }
        else
        {
          cands [i].raddr [c] = cands [i].raddrPrev [c];
        }
      }

      min = rangeMin [c] + restSpace [c] * cands [i].raddr [c];
      max = min + restSpace [c];

      cands [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

测试台上随机扩散搜索算法操作的打印输出：

C_AO_SDS:100;1000;0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.64253803557851
Score: 0.99921
25 Rastrigin's; Func runs 10000 result: 79.00996143538204
Score: 0.97898
500 Rastrigin's; Func runs 10000 result: 54.31544686388126
Score: 0.67300
=============================
5 Forest's; Func runs 10000 result: 1.677891584229713
Score: 0.94910
25 Forest's; Func runs 10000 result: 1.4089003503272384
Score: 0.79694
500 Forest's; Func runs 10000 result: 0.2437939668372883
Score: 0.13790
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.448
Score: 0.53733
500 Megacity's; Func runs 10000 result: 0.9551999999999999
Score: 0.07960
=============================
All score: 5.86873

立即查看打印的算法结果，我们可以注意到与其他算法相比，其结果高得令人难以置信。下表提供了详细的比较。

在可视化代理的移动时，请注意算法的非典型行为。代理的数量与适应度函数丘的高度成比例均匀分布，在局部极值处表现出高质量的聚类。看来算法不会遗漏任何一个山丘。我们还可以看到，在每次迭代时，算法的收敛性几乎无级增加，这表明陷入局部极值的趋势很低。即使在具有尖锐全局极值的最复杂的Forest函数上，也没有观察到逐步收敛。

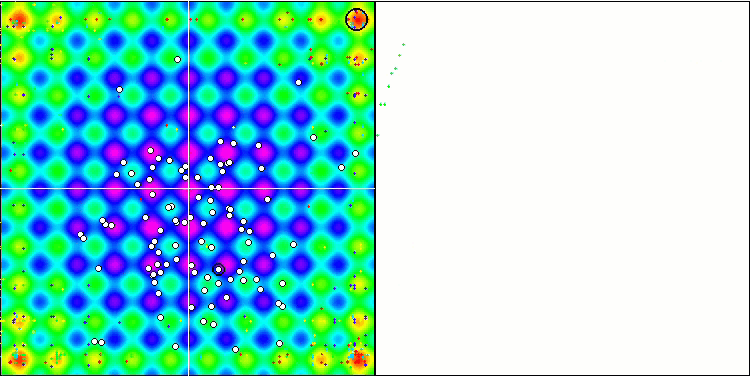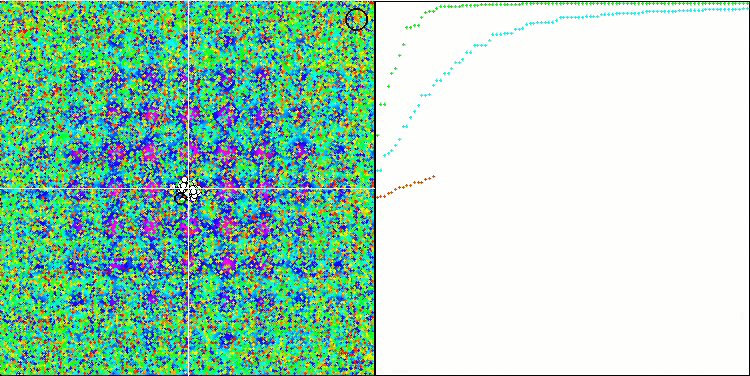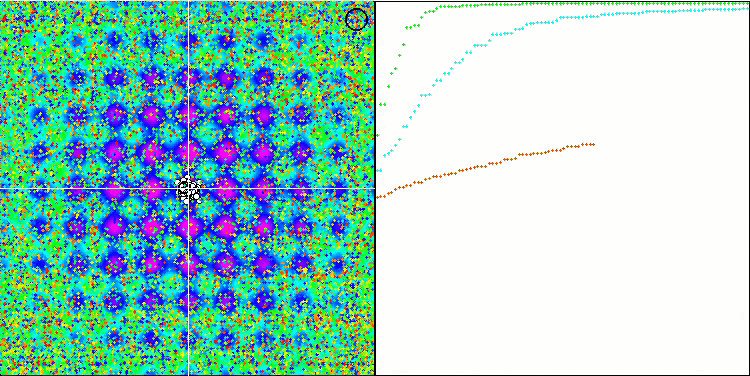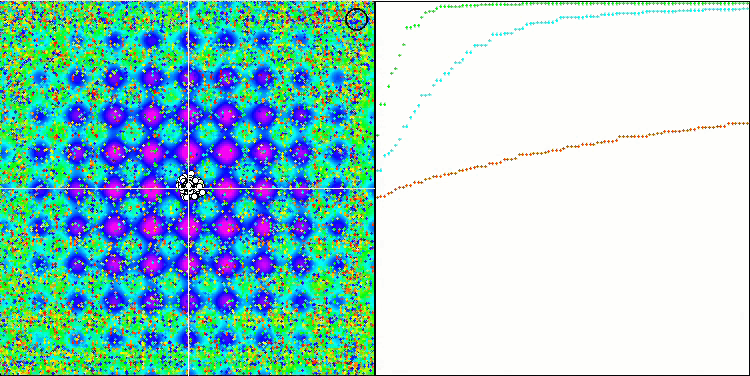
  Rastrigin测试函数上的SDS

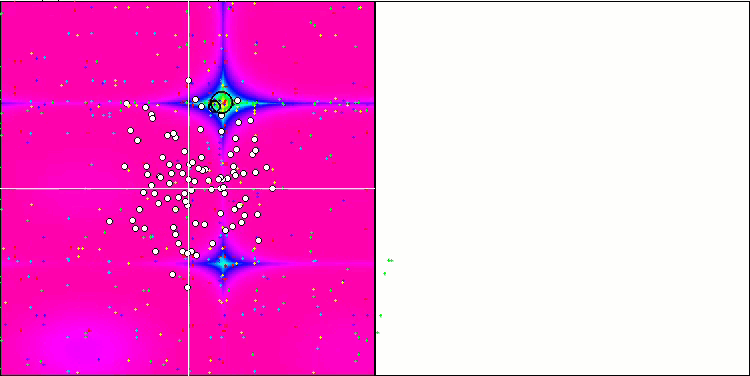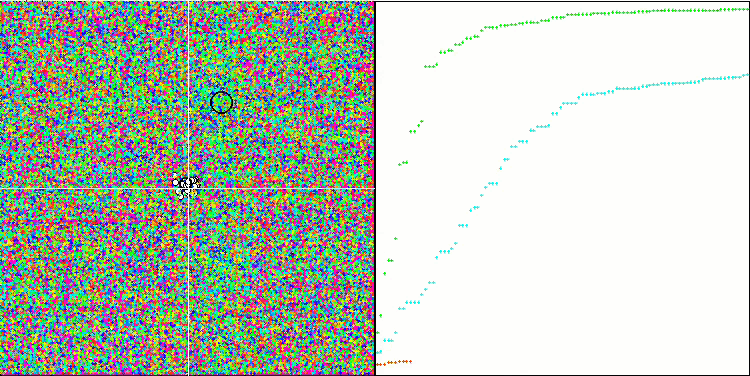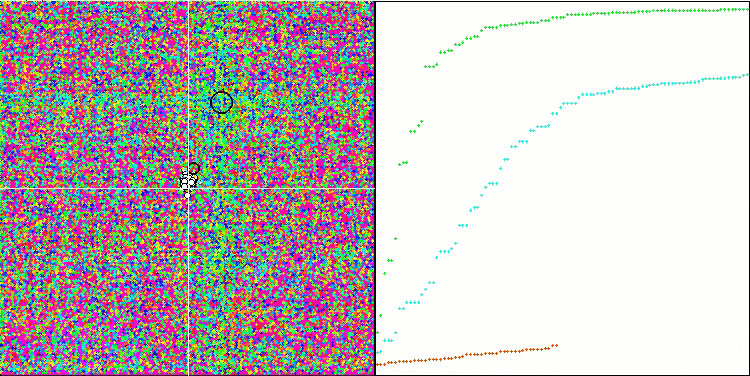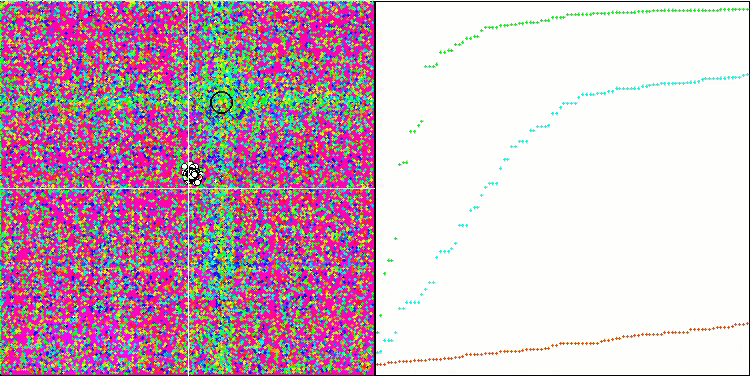
  Forest测试函数上的SDS

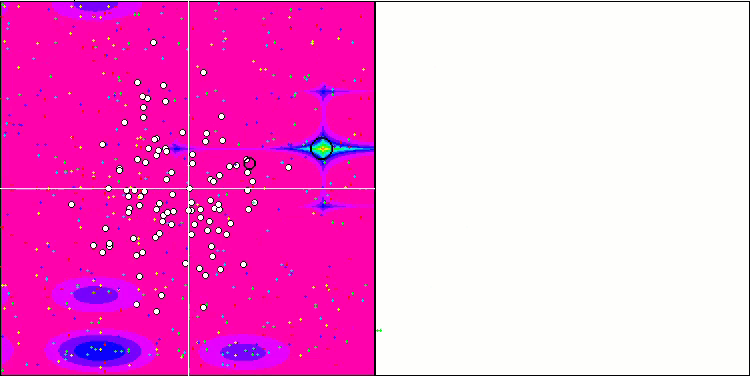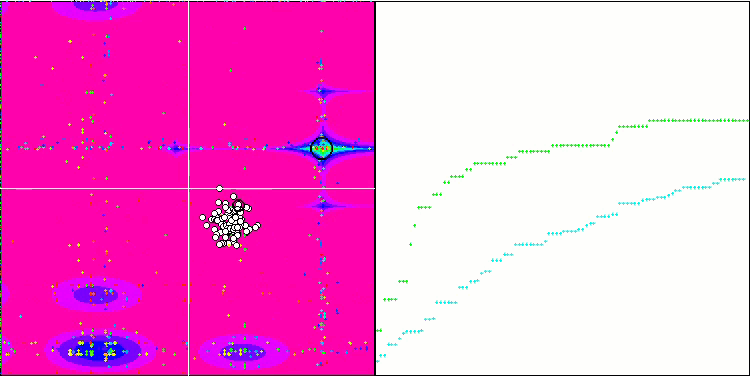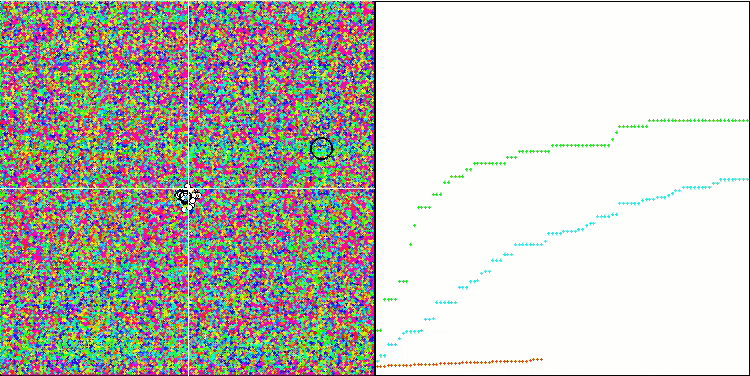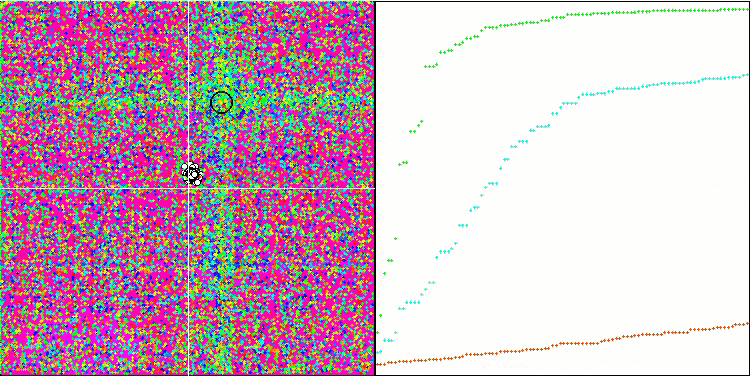
  Megacity测试函数上的SDS

我没想到这样一个基于纯随机游走的非常简单的算法会产生惊人的结果。SDS显著优于之前考虑的所有算法（几乎13%），在许多测试中显示出最佳结果（9个可能的测试中有4个排名第一）。唯一的例外是多变量Rastrigin函数，其中的领先者（EM算法）远远超过了所有其它算法。

即使在极其复杂的 Megacity 离散函数上，SDS算法也表现出色，几乎没有任何问题。在 Forest 和 Megacity 的1000个变量测试中，唯一一个击败SDS的是生长树（SSG）算法。 

#	AO	描述	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (discrete)			Megacity 最终	最终结果
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	随机扩散搜索（stochastic diffusion search）	0.99737	1.00000	0.63507	2.63244	0.96893	1.00000	0.95092	2.91985	1.00000	1.00000	0.72149	2.72149	100.000
2	SSG	树苗播种和生长（saplings sowing and growing）	1.00000	0.95313	0.55665	2.50978	0.72740	0.69680	1.00000	2.42421	0.69612	0.65726	1.00000	2.35338	87.489
3	HS	和声搜索（harmony search）	0.99676	0.90817	0.48178	2.38670	1.00000	0.72930	0.44806	2.17736	0.91159	0.76446	0.41537	2.09142	79.474
4	ACOm	蚁群优化M（ant colony optimization M）	0.34611	0.17142	0.17044	0.68797	0.86888	0.73719	0.77362	2.37968	0.91159	0.67983	0.05606	1.64749	54.863
5	IWO	入侵性杂草优化（invasive weed optimization）	0.95828	0.63939	0.29807	1.89575	0.70773	0.34168	0.31773	1.36714	0.72927	0.32158	0.33289	1.38375	53.994
6	MEC	思维进化计算（mind evolutionary computation）	0.99270	0.48648	0.22800	1.70718	0.60762	0.29973	0.25459	1.16194	0.85083	0.31594	0.26170	1.42847	49.567
7	COAm	布谷鸟优化算法M（COAm）	0.92400	0.44601	0.26004	1.63006	0.58378	0.25090	0.16526	0.99994	0.66298	0.25246	0.17083	1.08627	42.193
8	FAm	萤火虫算法M（firefly algorithm M）	0.59825	0.32387	0.17135	1.09348	0.51073	0.31182	0.49790	1.32045	0.31491	0.21438	0.35258	0.88188	36.860
9	ABC	人工蜂群（artificial bee colony）	0.78170	0.31182	0.20822	1.30174	0.53837	0.15816	0.13344	0.82998	0.51381	0.20311	0.13926	0.85617	32.954
10	BA	蝙蝠算法（bat algorithm）	0.40526	0.60773	0.84451	1.85750	0.20841	0.12884	0.25989	0.59714	0.27073	0.07616	0.17371	0.52060	32.794
11	GSA	重力搜索算法（gravitational search algorithm）	0.70167	0.43098	0.00000	1.13265	0.31660	0.26845	0.33204	0.91710	0.54144	0.26797	0.00000	0.80941	31.322
12	BFO	细菌觅食优化（bacterial foraging optimization）	0.67203	0.29511	0.11813	1.08528	0.39702	0.19626	0.20652	0.79980	0.47514	0.25388	0.18932	0.91834	30.615
13	EM	类电磁算法（electroMagnetism-like algorithm）	0.12235	0.44109	1.00000	1.56344	0.00000	0.02578	0.34880	0.37458	0.00000	0.00000	0.10924	0.10924	21.024
14	SFL	混合蛙跳（shuffled frog-leaping）	0.40072	0.22627	0.26548	0.89247	0.20153	0.03057	0.02652	0.25862	0.24862	0.04231	0.06639	0.35732	14.189
15	MA	猴子算法（monkey algorithm）	0.33192	0.31883	0.14644	0.79719	0.10012	0.05817	0.08932	0.24762	0.19889	0.03243	0.10720	0.33853	12.603
16	FSS	鱼群搜索（fish school search）	0.46812	0.24149	0.11302	0.82264	0.12840	0.03696	0.06516	0.23052	0.15471	0.03666	0.08283	0.27420	11.893
17	PSO	粒子群优化（particle swarm optimisation）	0.20449	0.07816	0.07160	0.35425	0.18895	0.07730	0.21738	0.48363	0.21547	0.04513	0.01957	0.28016	9.238
18	RND	随机（random）	0.16826	0.09287	0.08019	0.34132	0.13496	0.03546	0.04715	0.21757	0.15471	0.02962	0.04922	0.23354	5.108
19	GWO	灰狼优化器（grey wolf optimizer）	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.29834	0.05640	0.02557	0.38031	1.000

总结

随机搜索（SDS）算法是一种有效的优化方法，它使用随机样本来找到给定函数的全局最优值。
本文介绍了SDS算法运算的基本原理。它基于在分区搜索空间中随机选择点的思想。测试结果表明，SDS能够在具有大量局部极值的复杂函数中找到全局最优解，具有良好的收敛性。SDS算法的优点之一是其简单易实现。它不需要太多的计算，并且可以应用于各种类型的优化问题。

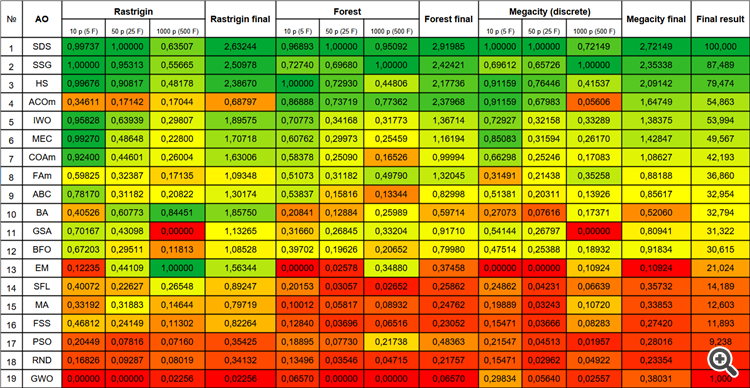
为了更直观地表示各个算法的优点和缺点，可以使用图3中的色标来表示上表。

图3. 根据相关测试的算法颜色等级

算法测试结果的直方图如下所示（从0到100，越多越好，在档案中有一个脚本，用于使用本文中描述的方法计算评级表）：

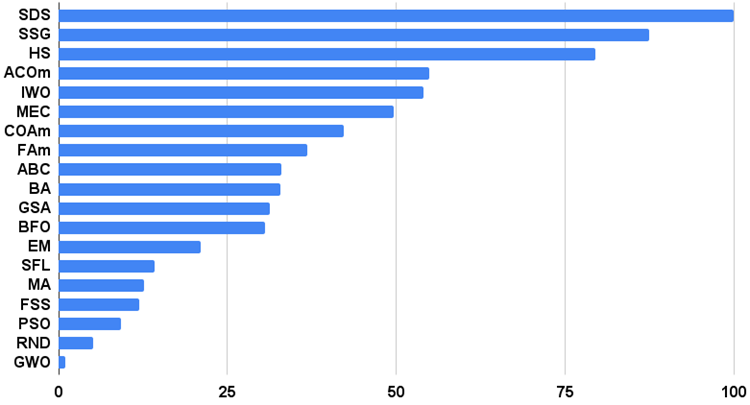
Figure 4. 测试算法最终结果的直方图

随机扩散搜索（SDS）算法的优点和缺点：

优点：
1. 最小数量的外部参数。
2. 高效解决各种问题。
3. 计算资源负载低。
4. 易于实施。
5. 抗粘连性。
6. 在光滑和复杂离散函数上都有希望的结果。
7. 高度收敛。

缺点：
1. 未发现。

每一篇文章都有一个归档，其中包含以前所有文章的算法代码的最新版本。然而，应该注意的是，我不对规范算法描述的绝对准确性负责。我经常根据自己的经验和个人意见添加自己的想法和改进。文章中给出的结论和判断是基于实验结果。