MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
彗星尾算法（CTA）

彗星尾算法（CTA）

MetaTrader 5 — 示例 | 22 十一月 2024, 10:50
739 0
Andrey Dik
Andrey Dik

内容

1. 概述
2. 算法实现
3. 测试结果


1. 概述

在天文学领域，彗星一直备受科学家和研究人员的特别关注。这些主要由冰、尘埃和气体构成的独特太空物体，是了解外太空变化过程的重要信息来源。彗星最令人瞩目和印象深刻的特点之一便是其尾部，当彗星接近太阳时便会形成。

太阳在彗星尾部的形成过程中起着关键作用。太阳的辐射和太阳风会导致彗星表面物质的受到蒸发和破坏。这一过程会形成彗星尾部— 一个由尘埃、气体和电离粒子组成的区域，太阳风和太阳引力将这些物质从彗星上分开。

在本文中，我们将探讨受这一独特天文现象启发的CTA。CTA利用彗星运动及其尾部的概念来寻找优化问题的最优解。我们将详细研究彗星及其尾部的运动，以及太阳在这些过程中的作用。我们还将讨论这些概念如何在CTA中得到应用，以便有效地找到最优解。

彗星是太阳系中的小天体，当它们接近太阳时会蒸发并释放气体。这个过程被称为升华。彗星通常具有高度椭圆的轨道，以及宽泛的轨道周期，从几年到可能数百万年不等。

彗星及其尾部的运动与太阳的影响密切相关。太阳的热量使彗星上的冰变成气体，导致彗发（围绕彗星核心的气体壳）膨胀。来自太阳辐射和高速太阳粒子（太阳风）的压力可以将彗发中的尘埃和气体吹离太阳，有时会形成一条长而明亮的尾部。此外，太阳辐射和太阳风还会使彗星尾部中的气体电离，从而使其发光。

在CTA的背景下，我们可以将每个解视为在解空间中移动的彗星尾粒子。彗星核心代表最佳解，而尾部的粒子是从核心发出的解的衍生物。这种表示允许算法“学习”解空间并适应其特征。


2. 算法实现

让我们更深入地了解一下彗星的运动及其尾部，这是该算法中的关键要素，同时我们也要探讨太阳在这些过程中所起的作用。

彗星运动：

  • 彗星围绕太阳沿椭圆轨道运动。
  • 当彗星接近太阳时，它开始释放气体和尘埃，形成彗星尾部。
  • 彗星的运动由太阳引力的吸引作用以及太阳风和太阳辐射的排斥作用共同决定。
  • 彗星沿着其轨道运动，其尾部始终指向与太阳相反的方向。

彗星尾部的运动：

  • 彗星的气体尾部由被太阳风“吹出”彗星核的离子化气体组成。
  • 太阳风是从太阳发出的带电粒子流。它“吹走”彗星的气体尾部，使其指向与太阳相反的方向。
  • 彗星的尘尾由较大的粒子组成，这些粒子因受到太阳辐射而从彗星核中被“抛出”。
  • 太阳辐射对尘粒施加压力，使它们略微偏离彗星的运动方向，从而形成弯曲的尘尾。

太阳的作用：

  • 太阳是彗星围绕其轨道运动的中心天体。
  • 太阳的引力决定了彗星沿椭圆轨道运动。
  • 太阳风和太阳辐射“塑造”了彗星的尾部，使其指向与太阳相反的方向。

    彗星

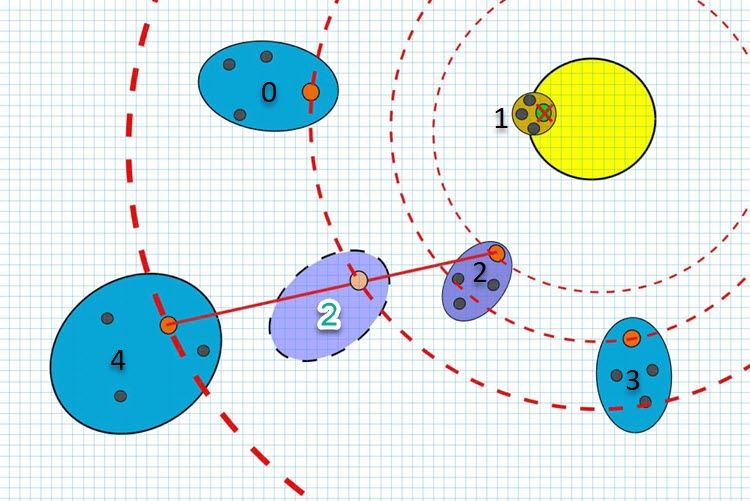
    图例1. CTA中的彗星形状和大小与恒星距离之间的函数关系（最优全局解决方案）

    图1展示的是算法中彗星的特性。每颗彗星都有其独特的编号，这个编号对应于它在数组中的索引。该图展示了彗星相对于恒星的运动轨迹。随着距离恒星越来越远，彗星的尾部变长，并呈现出接近球形的形状。同时，尾部粒子云相对于彗星核的位移变小。相反，彗星离恒星越近，尾巴的概率区域就越小，且形状越细长。


    彗星1离太阳过近导致蒸发。然而，在算法中，彗星的毁灭实际上并没有发生。相反，一个以恒星中心为中心的尾部云的形成过程仍在继续。这意味着尾部云越小，彗星所在区域的解的精细化程度越高。相反，尾部越大，搜索空间的探索频率就越高。在这种情况下，所有彗星的椭圆轴始终指向远离恒星的方向，即远离当前最优全局解的方向。
    算法的逻辑使我们能够调节彗星云的膨胀系数，既包括随距离恒星远近的膨胀方向，也包括减小的方向。我们还可以根据彗星轨道的半径来调整椭圆的扁平化程度。甚至，如果我们希望的话，还可以让彗星的尾部不朝着远离恒星的方向，而是指向恒星方向。
    图1还展示了彗星2有条件地迁移到新轨道的瞬间（圈有数字2之处）。这发生在两颗彗星核之间的物质交换过程中。在图中，彗星2从彗星4那里借取了物质。如果彗星间在进行物质交换的过程中找到了更好的解决方案，那么相应的彗星（当时正在形成物质的彗星）就会移动到新的轨道上。

    彗星尾部的大小以及它相对于彗星核的位移，可以根据距离恒星的远近，按照线性规律进行有效地计算。在这种情况下，最大距离等于1，对应于问题中相应优化坐标的最小值和最大值范围。这种方法使我们能够以简单明了的方式描述彗星尾部参数随距离恒星远近的变化规律。

    Graph

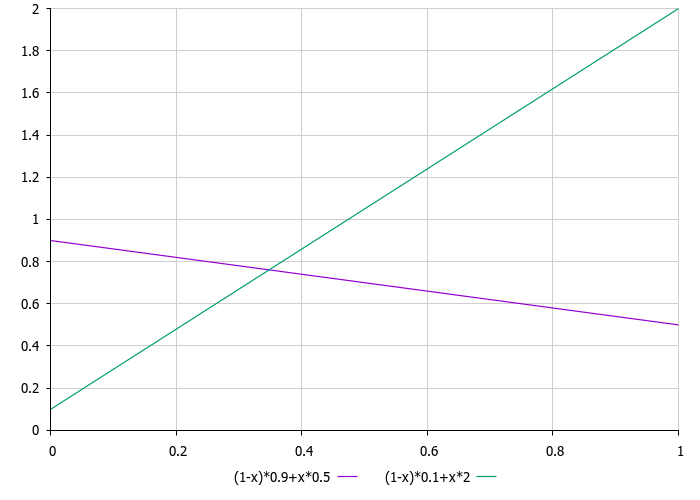
    图例2. 彗星尾迹位移比（紫色）和尾迹大小（绿色）与恒星距离的关系图

    我们已经为彗星粒子云的形状和大小变化制定了规律，因此我们可以总结出关于该算法可能具有的特性。考虑到彗星尾迹指向太阳（全局最优）的方向，并且在最优解和次优解上均进行搜索，受彗星尾迹启发的算法的主要特性如下所述：
    1. 解的蒸发与演化。该算法可以采用解的蒸发与演化过程，在此过程中，既可以探索最优解区域，也可以探索次优解区域。
    2. 多元性。该算法会尽可能生成多种反映不同优化程度的解选项，这与彗星尾迹中成分的多样性相似。
    3. 对外部因素的适应性。正如彗星会对太阳辐射作出反应一样，该算法也能够适应环境或目标函数的变化。
    4. 搜索全局最优。彗星尾迹远离太阳的方向可能代表了算法寻找全局最优解的目标，同时它也会考虑次优解，以避免过早收敛到局部最优。

    让我们用伪代码来简述该算法：

    1. 随机生成彗星核。
    2. 以彗星核为中心，创建其尾迹——即正态分布的粒子，其中彗星核位于中心。
    3. 计算彗星粒子的适应度。
    4. 更新全局解。
    5. 将对应彗星中表现最好的粒子作为其新的核。
    6. 对彗星粒子的每个坐标执行以下操作：
    以0.6的概率执行以下两种操作之一：
    以彗星核为中心，创建正态分布的粒子。
    或者： 使用两个随机选择的彗星核的坐标来创建一个新的彗星粒子。
    7. 更新全局解。
    8. 将对应彗星中表现最好的粒子作为其新的核。
    9. 从p开始重复。直到满足停止准则。

    我们无需为CTA编写特定的结构。用于算法与执行程序之间交换决策的代理的基本结构，已足够描述彗星及其粒子。让我们回顾一下这个结构是什么样的。

    S_AO_Agent结构包含两个字段：

    • c[] - 该数组用于存储智能体在解空间中的坐标。
    • f - - 智能体的适应度，用于评估解的质量。

    在CTA算法的上下文中，我们将使用这个结构来描述彗星本身以及它们尾部的粒子。

    //——————————————————————————————————————————————————————————————————————————————
struct S_AO_Agent
{
    double c []; //coordinates
    double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

    我们定义了一个C_AO_CTA类，它继承自C_AO类。

    • C_AO_CTA () - 构造函数使用预定义的值初始化类对象。它还设置了算法的一些参数，如种群大小（popSize）、彗星数量（cometsNumb）、尾长系数（tailLengthKo）、最大和最小移位系数（maxShiftCoef和minShiftCoef），以及最大和最小尺寸系数（maxSizeCoef和minSizeCoef）。
    • SetParams() - 根据params数组中的值设置算法参数。
    • Init() - 通过设置指定的搜索范围和迭代次数来初始化算法。
    • Moving()和Revision() - 该方法实现了算法的主要逻辑。

    comets[] - 代表一个S_AO_Agent类型对象的数组，它在算法中表示彗星。

    tailLength[]、maxSpaceDistance[]和partNumber - 私有变量用于算法的内部操作。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_CTA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CTA () { }

  C_AO_CTA ()
  {
    ao_name = "CTA";
    ao_desc = "Comet Tail Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14841";

    popSize      = 50;   //population size
    cometsNumb   = 5;    //number of comets
    tailLengthKo = 0.2;  //tail length coefficient
    maxShiftCoef = 0.9;
    minShiftCoef = 0.5;
    maxSizeCoef  = 0.1;
    minSizeCoef  = 1.5;

    ArrayResize (params, 7);

    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "cometsNumb";    params [1].val = cometsNumb;
    params [2].name = "tailLengthKo";  params [2].val = tailLengthKo;
    params [3].name = "maxShiftCoef";  params [3].val = maxShiftCoef;
    params [4].name = "minShiftCoef";  params [4].val = minShiftCoef;
    params [5].name = "maxSizeCoef";   params [5].val = maxSizeCoef;
    params [6].name = "minSizeCoef";   params [6].val = minSizeCoef;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    cometsNumb   = (int)params [1].val;
    tailLengthKo = params      [2].val;
    maxShiftCoef = params      [3].val;
    minShiftCoef = params      [4].val;
    maxSizeCoef  = params      [5].val;
    minSizeCoef  = params      [6].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    cometsNumb;    //number of comets
  double tailLengthKo;  //tail length coefficient
  double maxShiftCoef;  //maximum shift coefficient
  double minShiftCoef;  //minimum shift coefficient
  double maxSizeCoef;   //maximum size coefficient
  double minSizeCoef;   //minimum size coefficient

  S_AO_Agent comets [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  double tailLength       [];
  double maxSpaceDistance []; //maximum distance in space
  int    partNumber; //number of particles
};
//——————————————————————————————————————————————————————————————————————————————

    在C_AO_CTA类中定义Init方法。此方法使用给定的搜索范围和迭代次数来初始化算法。各步骤的描述如下：

    1. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - 该代码使用指定的搜索范围调用StandardInit 方法。如果StandardInit 返回'false'，则Init方法也立即返回'false'。

    2. ArrayResize (comets, cometsNumb); - 根据彗星的数量调整comets数组的大小。

    3. 在“for”循环中，初始化每个彗星的坐标和适应度函数值。

    4. ArrayResize (tailLength, coords); ArrayResize (maxSpaceDistance, coords); - 根据坐标的数量调整tailLength和maxSpaceDistance数组的大小。

    5. 在接下来的“for”循环中，为每个坐标计算空间中的最大距离和尾部长度。

    6. partNumber = popSize / cometsNumb; - 计算每个彗星尾部中的粒子数量。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CTA::Init (const double &rangeMinP [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (comets, cometsNumb);
  for (int i = 0; i < cometsNumb; i++)
  {
    ArrayResize (comets [i].c, coords);
    comets [i].f = -DBL_MAX;
  }

  ArrayResize (tailLength,       coords);
  ArrayResize (maxSpaceDistance, coords);

  for (int i = 0; i < coords; i++)
  {
    maxSpaceDistance [i] = rangeMax [i] - rangeMin [i];
    tailLength       [i] = maxSpaceDistance [i] * tailLengthKo;
  }

  partNumber = popSize / cometsNumb;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    在C_AO_CTA类的Moving()方法中，实现了彗星尾部粒子的形成过程。该方法的主要步骤如下：

    1. 该函数首先递增epochNow周期计数器，并初始化cnt、min和max局部变量。
    2. 如果revision为'false'，则在指定的rangeMin和rangeMax范围内初始化彗星的坐标。使用高斯分布在由 tailLength确定的范围内围绕每个彗星创建粒子（智能体）。
    3. 如果revision为'true'，则更新粒子（智能体）的位置。为每个粒子计算coefTail和coefSize。这些系数定义了彗星尾部相对于cB中心点距离的位移和大小。这些系数用于确定粒子在尾部限制范围内的新位置。
    4. 如果u.RNDprobab()的概率小于0.6，则使用高斯分布计算粒子的新位置。否则，粒子的新位置由两个随机选择的其他彗星核坐标的线性组合计算得到。
    5. 在所有情况下，粒子的新坐标都被限制在rangeMin和rangeMax范围内，并以rangeStep为步长进行离散化。

    该方法的总体思路是模拟CTA中彗星的运动和行为，其中粒子（智能体）代表彗星的尾部，它们的坐标和尾部大小取决于与全局最优解（太阳）的距离。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Moving ()
{
  epochNow++;
  int    cnt = 0;
  double min = 0.0;
  double max = 0.0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < cometsNumb; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        comets [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        comets [i].c [c] = u.SeInDiSp  (comets [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < cometsNumb; i++)
    {
      for (int p = 0; p < partNumber; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          min = comets [i].c [c] - tailLength [c] * 0.5; if (min < rangeMin [c]) min = rangeMin [c];
          max = comets [i].c [c] + tailLength [c] * 0.5; if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, 1);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  cnt             = 0;
  double coefTail = 0.0;
  double coefSize = 0.0;

  for (int i = 0; i < cometsNumb; i++)
  {
    for (int p = 0; p < partNumber; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < 0.6)
        {
          coefTail = fabs (comets [i].c [c] - cB [c]) / maxSpaceDistance [c];
          coefSize = coefTail;

          //(1-x)*0.9+x*0.5
          coefTail = (1 - coefTail) * maxShiftCoef + coefTail * minShiftCoef;

          //(1-x)*0.1+x*0.9
          coefSize = (1 - coefSize) * maxSizeCoef + coefSize * minSizeCoef;

          if (cB [c] * Dir > comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * coefTail         * coefSize;
            max = comets [i].c [c] + tailLength [c] * (1.0 - coefTail) * coefSize;
          }
          if (cB [c] * Dir < comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * (1.0 - coefTail) * coefSize;
            max = comets [i].c [c] + tailLength [c] * (coefTail)*coefSize;
          }
          if (cB [c] == comets [i].c [c])
          {
            min = comets [i].c [c] - tailLength [c] * 0.1;
            max = comets [i].c [c] + tailLength [c] * 0.1;
          }

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, Power);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
        else
        {
          int    r   = 0;
          int    r1  = 0;
          int    r2  = 0;

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r1 = r;
          }
          while (r1 == i);

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r2 = r;
          }
          while (r2 == i || r2 == r1);

          a [cnt].c [c] = comets [r1].c [c] + 0.1 * (comets [r2].c [c] - comets [i].c [c]) * u.RNDprobab();
          a [cnt].c [c] = u.SeInDiSp (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    接下来，实现C_AO_CTA类的Revision() 方法，该方法负责修改彗星尾算法（CTA）中彗星的位置。

    该方法的主要步骤如下：

    1. 在种群中寻找最优解决方案：

    • 该方法遍历popSize种群中的所有解决方案，并找到fB目标函数值的最优解决方案。
    • 如果找到了更好的解决方案，那么其a[ind].c位置将被复制到cB向量中，该向量负责存储已知的最优解决方案。

    2. 彗星位置更新：

    • 该方法遍历所有cometsNumb颗彗星，并在与partNumber每颗彗星相关联的粒子中搜索该彗星的最佳解决方案。
    • 如果为某颗彗星找到了最优解决方案，那么该彗星的comets[i].c位置将被更新为找到的最优解决方案a[ind].c的位置。

    此方法实现了CTA的一个重要步骤，即根据在彗星尾迹中找到的最优解决方案来修正彗星的位置。这使得搜索范围能够朝向目标函数值更高的区域进行。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //set a new kernel------------------------------------------------------------
  int cnt = 0;

  for (int i = 0; i < cometsNumb; i++)
  {
    ind = -1;

    for (int p = 0; p < partNumber;  p++)
    {
      if (a [cnt].f > comets [i].f)
      {
        comets [i].f = a [cnt].f;
        ind = cnt;
      }

      cnt++;
    }

    if (ind != -1) ArrayCopy (comets [i].c, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


    3. 测试结果

    CTA测试台结果

    CTA|Comet Tail Algorithm|80.0|40.0|4.0|-1.0|0.2|1.0|0.5|0.1|15.0|
    =============================
    5 Hilly's; Func runs: 10000; result: 0.9534613588697962
    25 Hilly's; Func runs: 10000; result: 0.863192334000326
    500 Hilly's; Func runs: 10000; result: 0.27769783965091077
    =============================
    5 Forest's; Func runs: 10000; result: 0.997942251272262
    25 Forest's; Func runs: 10000; result: 0.857403562283056
    500 Forest's; Func runs: 10000; result: 0.33949224947400775
    =============================
    5 Megacity's; Func runs: 10000; result: 0.8876923076923078
    25 Megacity's; Func runs: 10000; result: 0.5643076923076924
    500 Megacity's; Func runs: 10000; result: 0.10512307692307787
    =============================
    总分: 5.84631 (64.96%)

    根据测试，可以得出以下关于CTA操作的结论：

    该算法的整体得分为5.84631，相当于可能达到的最高得分的64.96%。这表明CTA的表现优异。

    Hilly值

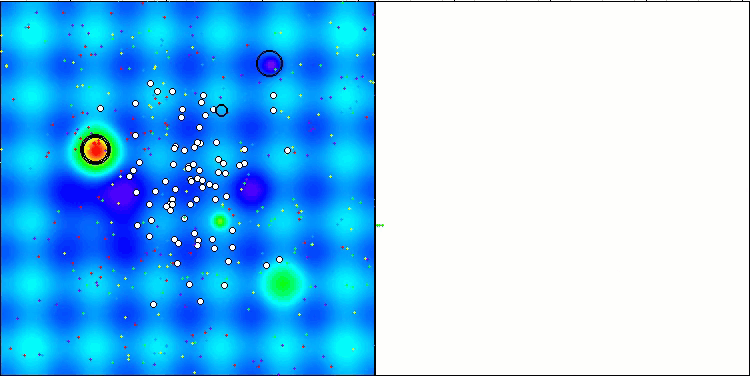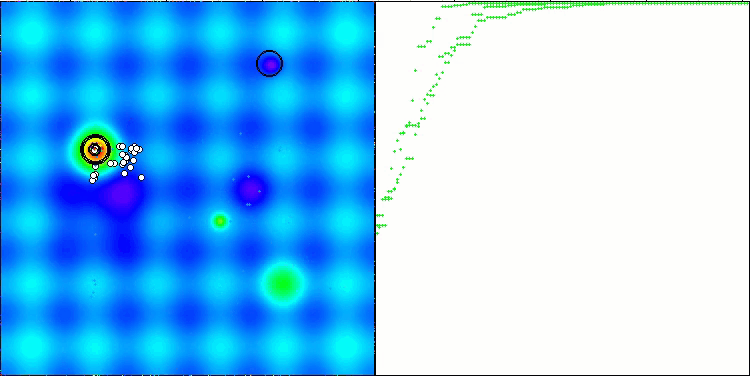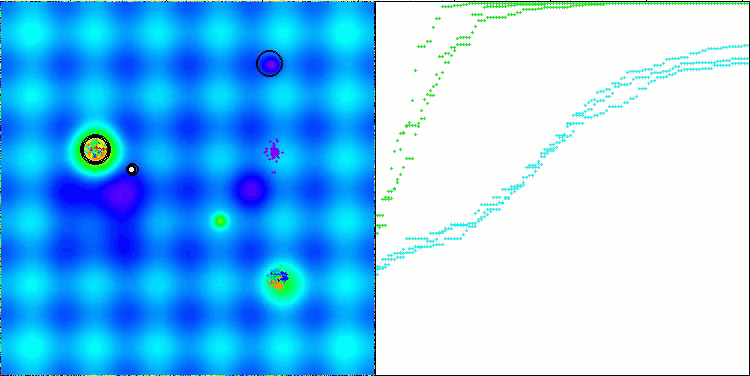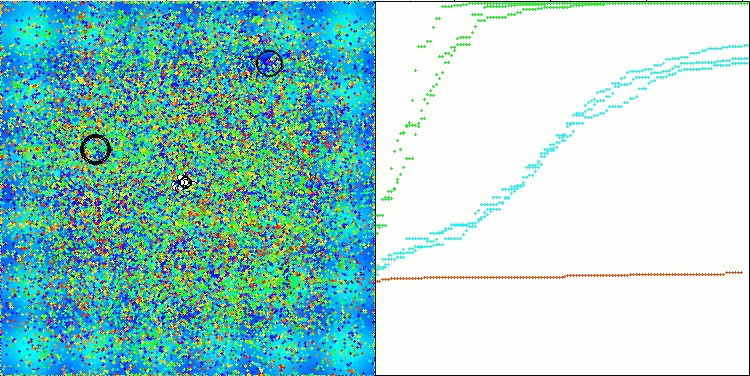
      CTA在Hilly测试函数上

    Forest值

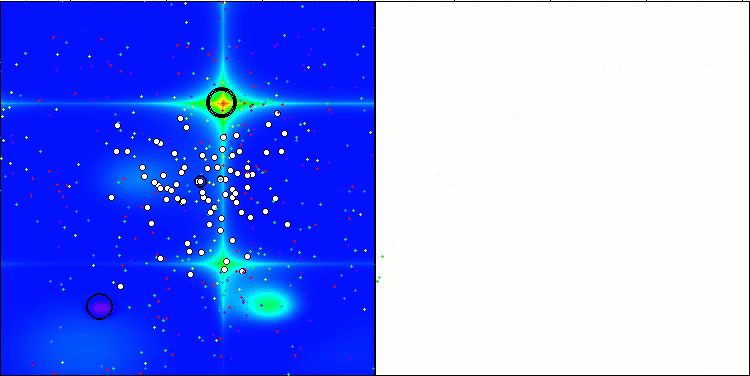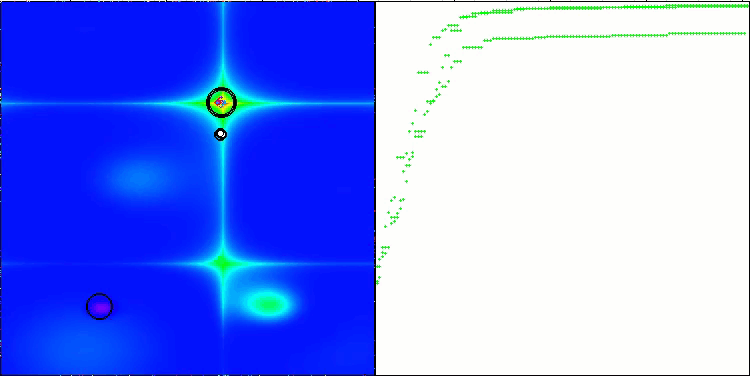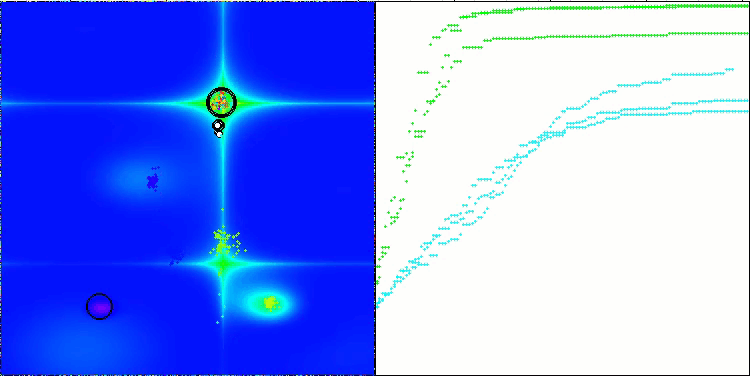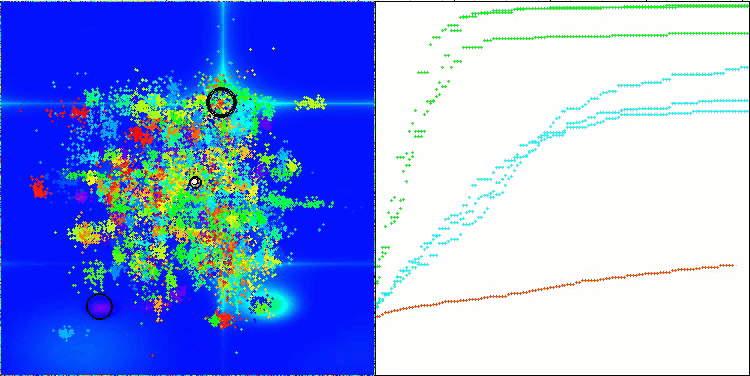
      CTA在Forest测试函数上

    Megacity

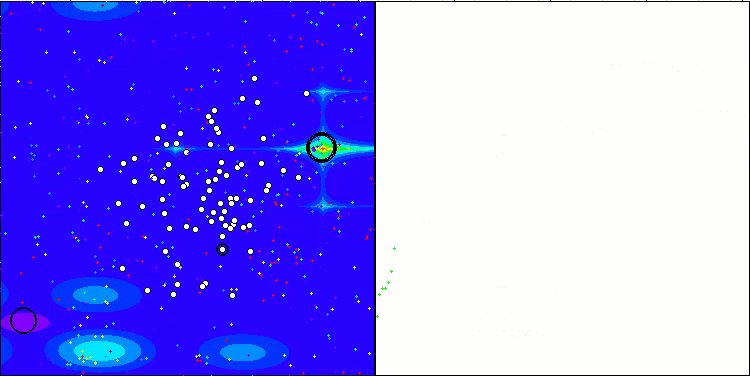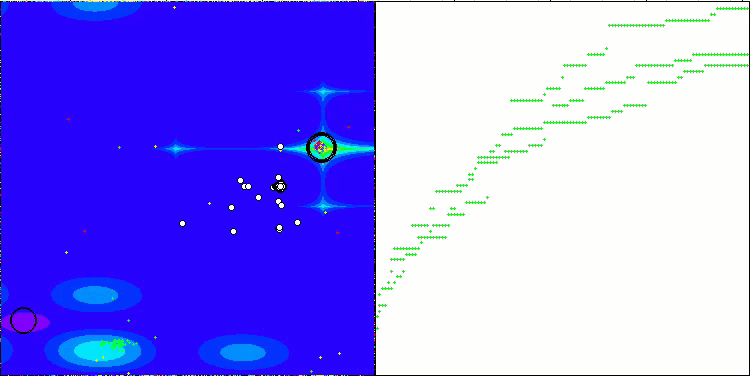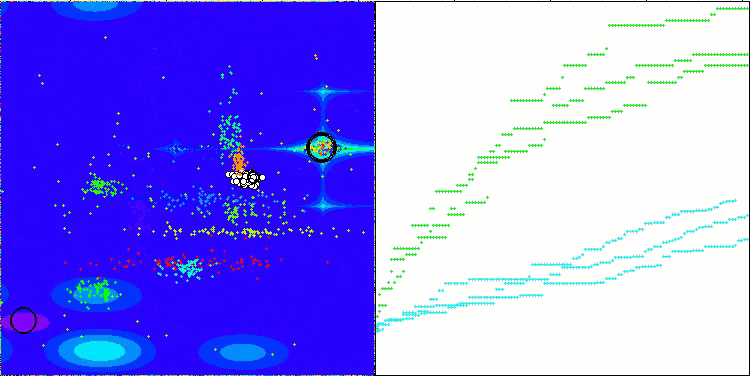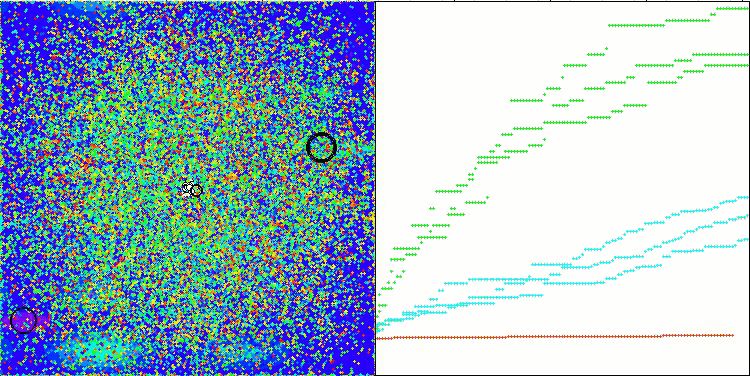
      CTA在Megacity测试函数上

    根据测试结果，CTA算法在评分表中排名第三。

    # AO 说明 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 BGA 二进制遗传算法 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
    2 (P+O)ES (P+O) 进化策略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
    3 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    4 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    5 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    6 SIA 模拟退火算法 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    7 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    8 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    9 BSA 鸟群算法 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
    10 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    11 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    12 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    13 BSO 头脑风暴优化 0.91301 0.56222 0.30047 1.77570 0.97162 0.57162 0.23449 1,77772 0.60462 0.27138 0.12011 0.99611 4.550 50.55
    14 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    15 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    16 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    17 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    18 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    19 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
    20 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
    21 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
    22 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
    23 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
    24 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
    25 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
    26 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
    27 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
    28 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
    29 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
    30 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
    31 Boids算法 虚拟生物算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
    32 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
    33 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
    34 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
    35 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
    36 GWO 灰狼优化算法 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
    37 CSS 人工电场算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
    38 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


    总结

    CTA（彗星尾算法）基于彗星运动的概念，并具有一些与物理定律和彗星演化相悖的特征。关于这些特征对算法最终结果的影响应更给出更详尽地考量。


    其中一个矛盾点涉及彗星尾部的方向。在CTA中，使用指向恒星（Dir_P = -1）尾部的方向通常会显著提高其性能。然而，使用恒星尾部的方向却能提高算法探索空间的能力。优化追求者可能会考虑根据当前迭代次数使用动态的尾部方向系数。值得注意的是，尾部远离恒星的方向在低维问题上提供了更好的收敛性，而指向恒星的方向在高维问题上更为有效。

    另一个争议点是彗星尾部的大小。在CTA中，研究发现动态改变尾部大小（随着与恒星距离的增加而增大尾部）可以提高算法的效率。这与物理定律相悖，因为在现实中，彗星尾部的大小会随着它接近太阳而增大。然而，这种尾部大小的动态变化，使我们能够在远离全局解的区域中，扩大围绕彗星核的解决方案空间的研究范围，从而增加发现有前景解的机会，并降低陷入局部极值的可能性。随着彗星接近恒星，其尾部减小，这增加了解决方案精细化的程度。
    CTA还涉及彗星之间的信息交换，类似于自然界中彗星捕获其他彗星留下的粒子的情况。这是算法探索解决方案空间的附加功能。我们已经尝试通过模拟恒星日冕物质抛射，以及通过借用其他彗星的坐标来拓展算法的组合性质，从而增加种群多样性的方法。

    CTA是一种利用彗星运动概念进行优化的新颖且有趣的方法。该算法在各类函数（包括平滑函数和离散函数）上都表现出良好的收敛性，实现起来非常简单（算法结构简单，简化软件实现过程），并且不需要大量的计算资源（因为它不使用解决方案的排序，也不计算所有解决方案之间的距离，这使得它应用广泛）。在处理离散函数时，该算法的结果分布较小（正如用于优化交易系统的大多数问题，其结果的稳定性和可重复性较好）。然而，该算法同时拥有许多外部参数（如彗星尾部的大小、尾部系数和方向偏移系数等）。在高维平滑函数上，该算法可能不会表现出最优结果。

    总的来说，CTA的特点在于它在探索解决方案空间和细化找到的全局最优解之间取得了动态平衡。

    因此，CTA采用了一些简化和假设，这些并不完全符合彗星运动的物理定律。然而，这些与现实的偏离使我们能够在保持实现简单性的同时，提高算法在解决优化问题时的效率。


    标签

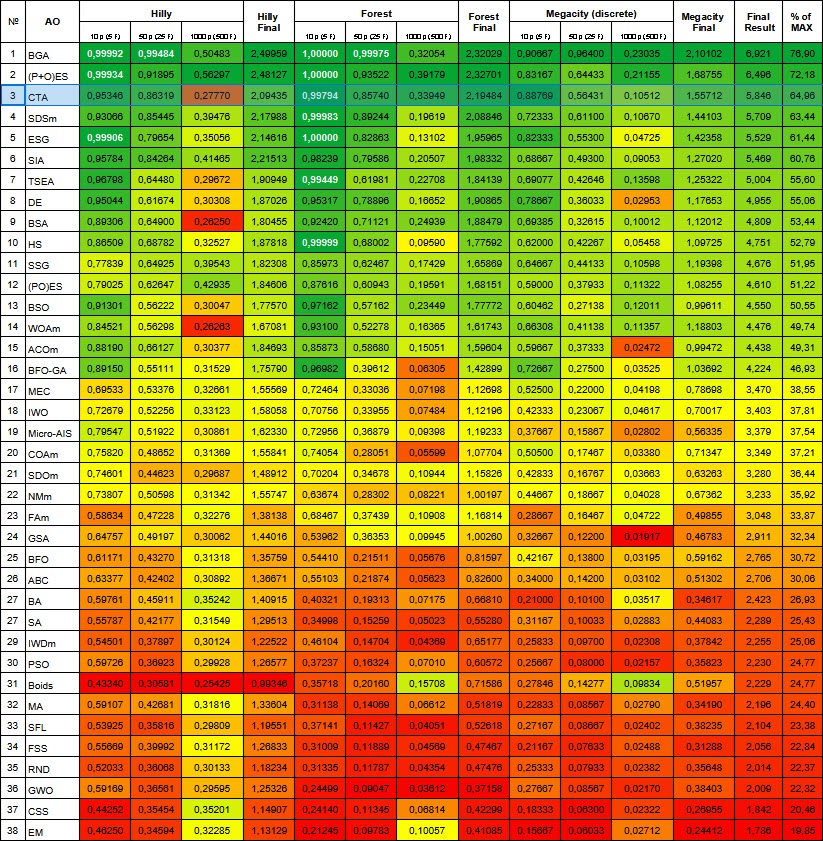
    图例 3. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

    图表

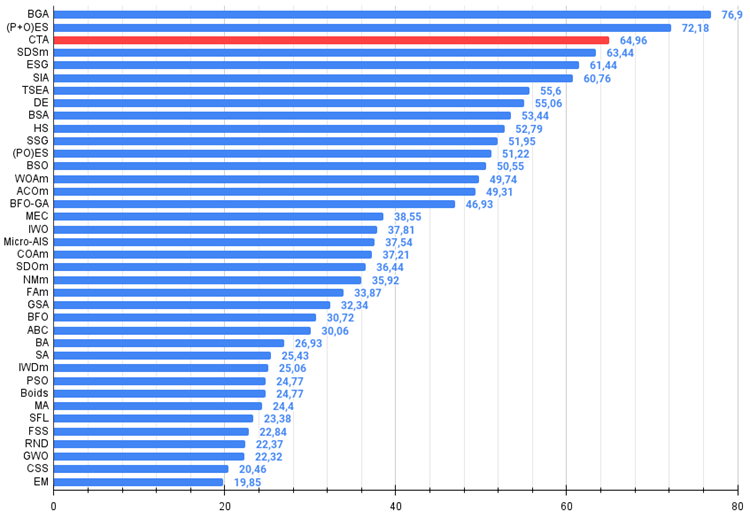
    图例 4. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

    其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）


    CTA的优缺点：

    优势：

    1. 在各种类型的函数上具有良好的收敛性。
    2. 实现简单。
    3. 对计算资源要求低。
    4. 离散函数结果分布较小。

    缺点：

    1. 许多外部参数。
    2. 在平滑高维函数上表现不佳。


    源代码

      文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

      本文由MetaQuotes Ltd译自俄文
      原文地址： https://www.mql5.com/ru/articles/14841

      附加的文件 |
      下载ZIP
      CTA.zip (25.65 KB)
      注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

      该作者的其他文章

      前往讨论
      矩阵分解：更实用的建模 矩阵分解：更实用的建模
      您可能没有注意到，矩阵建模有点奇怪，因为只指定了列，而不是行和列。在阅读执行矩阵分解的代码时，这看起来非常奇怪。如果您希望看到列出的行和列，那么在尝试分解时可能会感到困惑。此外，这种矩阵建模方法并不是最好的。这是因为当我们以这种方式对矩阵建模时，会遇到一些限制，迫使我们使用其他方法或函数，而如果以更合适的方式建模，这些方法或函数是不必要的。
      开发回放系统（第 45 部分）：Chart Trade 项目（四） 开发回放系统（第 45 部分）：Chart Trade 项目（四）
      本文的主要目的是介绍和解释 C_ChartFloatingRAD 类。我们有一个 Chart Trade 指标，它的工作方式非常有趣。您可能已经注意到了，图表上的对象数量仍然很少，但我们却获得了预期的功能。指标中的数值是可以编辑的。问题是，这怎么可能呢？这篇文章将使答案变得更加清晰。
      神经网络变得简单（第 79 部分）：在状态上下文中的特征聚合查询（FAQ） 神经网络变得简单（第 79 部分）：在状态上下文中的特征聚合查询（FAQ）
      在上一篇文章中，我们领略了一种从图像中检测对象的方法。不过，处理静态图像与处理动态时间序列（例如我们所分析的价格动态）有些不同。在本文中，我们将研究检测视频中对象的方法，其可在某种程度上更接近我们正在解决的问题。
      神经网络变得简单（第 78 部分）：带有变换器的无解码对象检测器（DFFT） 神经网络变得简单（第 78 部分）：带有变换器的无解码对象检测器（DFFT）
      在本文中，我提议从不同的角度看待构建交易策略的问题。我们不会预测未来的价格走势，但会尝试基于历史数据分析构建交易系统。