MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
种群优化算法：蚁群优化（ACO）

种群优化算法：蚁群优化（ACO）

MetaTrader 5 — 示例 | 14 二月 2023, 11:37
1 696 0
Andrey Dik
Andrey Dik

任何行为的最大秘诀是社会行为...

F. 巴特利特（Bartlett）

内容

1. 概述
2. 算法原理
3. 改编版
4. 测试结果


1. 概述

比利时研究人员马可·多里戈（Marco Dorigo）创建了一个数学模型，科学地描述了蚁群中集体智慧的过程。 他于 1992 年在他的博士论文中发表，并将其作为算法实现。

蚁群优化（ACO） 是一种基于种群的随机搜索方法，可解决各种组合优化问题。 ACO 的核心是信源动作（stigmergy）的概念。 1959年，皮埃尔-保罗·格拉塞特（Pierre-Paul Grasset）发明了信源动作 理论来解释白蚁筑巢的行为。 Stigmergy 由两个希腊词组成：stigma - 信源，和 ergon - 动作。

规范定义是一种间接互动类型，经与环境的相互作用，在种群成员之间，依时间扩展。 换言之，其中一个代理者留下了踪迹、或以某种方式修改了现场位置，如此其它代理者在进入其区域时会收到一些信息。 在蚂蚁的情况下，信源动作是信息素。 蚂蚁在觅食过程中的沟通就是一个示例：蚂蚁彼此相互间接交流，在地面上留下信息素踪迹，从而影响其它蚂蚁的决策过程。 个体蚂蚁之间的这种简单交流形式导致了整个蚁群的复杂行为和能力。

蚂蚁是群居昆虫，它们按领地生活。 蚂蚁的行为是由寻找食物的意图所控制。 在觅食时，它们在领地漫游。 蚂蚁反复从一个地方漫游到另一个地方寻找食物，当它爬动时，它会在地面上沉积一种叫做信息素的有机化合物。 因此，蚂蚁是利用信息素踪迹相互交流。

当一只蚂蚁发现了食物，它会携带尽可能多的食物。 返回时，它会沿途沉积信息素，具体取决于食物的数量和品质。 结果就是，其它蚂蚁可以遵循这条路线。 信息素水平越高，选择这条特定路径的概率就越高，通过特定路径的蚂蚁越多，这条路线上留下的信息素就越多。

我们来看下面的例子。 假设有两条途径可以从蚁群获取食物。 首先，地面上没有信息素。 如此，选择这两条路径的概率相等（50%）。 我们假设两只蚂蚁分别选择了这两条不同的觅食路径。 这两条路径的距离是不同的。 走较短路线的蚂蚁会先于另一只蚂蚁到达食物。 当它找到食物时，它会带走一些食物并返回蚁群。 为了追溯返回的路径，它会在地面上沉积信息素。 走较短路径的蚂蚁会更早到达蚁群。

当第三只蚂蚁想出去寻找食物时，它会根据地面上的信息素水平选择距离较短的路径。 因为较短的路径比较长的信息素较浓，所以第三只蚂蚁将遵循信息素较浓的路径。 当蚂蚁沿着更长的路径返回蚁群时，更多的蚂蚁已经迈上了信息素含量更高的路径。 然后，当另一只蚂蚁试图从蚁群到达目的地（食物）时，它会发现每条路径都有相同的信息素水平。 那么它会随机选择其中之一。 一遍遍地重复这个过程，一段时间后，较短的路径将比其它路径获得更多的信息素，且蚂蚁走这条路径的概率会更高。

ACO 算法是一种群体智能算法。 依据蚁群的觅食过程进行建模，利用蚁群的内部数据传输机制建立各种环境下的最短路径。 路径上残留的信息素浓度越高，蚂蚁选择这条路径的可能性就越大。 与此同时，信息素的浓度随着时间的推移而减弱。 因此，由于蚁群的行为，蚂蚁通过反馈机制不断学习和优化，从而判定最短的觅食路径。 ACO 算法广泛用于路径规划。


2. 算法原理

在 ACO 中，一组称为人工蚂蚁的软件代理者为给定的优化问题寻找良性解决方案。 为了应用 ACO，优化问题将转换为在加权图形上查找最佳路径的问题。 人工蚂蚁（以下简称蚂蚁）逐渐构建沿图形移动的解决方案。 构建解决方案的过程是随机的，并且取决于信息素模型 — 与图形组件（节点或边线）相关的一套参数，其值在执行过程中会由蚂蚁修改。

我们研究旅行推销员问题的算法。 我们有一组位置（城市）和它们之间的距离。 问题是找到一条最短长度的封闭路径，每个城市只访问一次。 一组相关联城市，再配合一组图形顶点而定义的图形称为构造图。 由于有可能从任意给定城市移动到任意其它城市，因此构造图是完全连接的，顶点数等于城市数。 我们将顶点之间的边线长度与其所代表城市之间的距离设定成正比，并将信息素值和启发式值与图形连线相关联。 信息素值在运行时发生变化，体现蚁群的累积经验，而启发式值是与问题相关的值。

蚂蚁按以下方式构造解决方案。 每只蚂蚁从一个随机选择的城市（构造图形顶点）开始。 然后，在每个构造步骤中，它沿着图形的边线移动。 每只蚂蚁保存其路径的记忆内存，并在后续步骤中不选择通往已访问过顶点的边线。 一旦蚂蚁在遍访了图形的所有顶点后，即构建了一个解决方案。 在每个构造步骤中，蚂蚁按概率选择下一个通向尚未访问顶点的边线。 概率规则基于信息素值和启发式信息：与边线相关的信息素和启发式值越高，蚂蚁选择该特定边线的概率就越高。 一旦所有的蚂蚁都完成了它们的旅程，随即就会更新边线的信息素。 每次信息素值的初值都会按一定百分比减少。 重复此过程，直到满足终止准则。

基于信息素的交流是自然界中广泛采用的最有效的沟通方式之一。 信息素由蜜蜂、蚂蚁和白蚁等社会性昆虫用于代理者之间的交流。 由于其可行性，人工信息素也已被应用于多机器人和群体机器人系统。

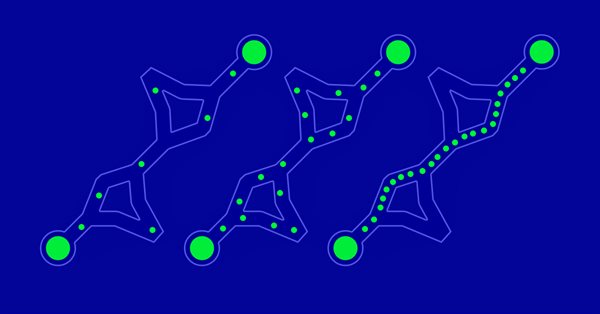
我们能如何理解我们的蚂蚁真的找到了最短路线呢？ 这是一个很棒的测试用例：所有点排列成一个圆圈。 对它们来说，最短的路径永远是一样的 — 圆圈。

首个 ACO 算法被称为蚂蚁系统，旨在解决旅行推销员问题，其目标是找到往返多个相连城市的最短路径。 普通算法相对简单，基于一组蚂蚁，每只蚂蚁完成绕所有城市的可能路径之一。 在每一步，蚂蚁都会根据一些规则选择一条从一个城市到另一个城市的路径：

  1. 它应该每个城市只访问一次；
  2. 选择遥远城市的可能性较小（可见性）；
  3. 在两个城市之间的边界上铺设的信息素踪迹越密集，选择这条边界的可能性就越大；
  4. 一条路径完成后，如果路径较短，蚂蚁会在经过的所有边线沉积更多的信息素；
  5. 每次迭代后，信息素踪迹蒸发。

城市

图例 1. 五个节点的可能路径示例

3. 修订版

已知的 ACO 算法的若干种最流行的变体。 我们来研究一下：

蚂蚁系统（AS）。
蚂蚁系统是第一个 ACO 算法。

蚁群系统（ACS）。
在蚁群系统算法中，原始的蚂蚁系统在三个方面进行了修改：
1. 边线选择偏向于因循沿袭（即有利于选择信息素较多的最短边线的概率）；
2. 在构建解决方案时，蚂蚁应用局部信息素更新规则来改变它们所选边线的信息素水平；
3. 在每次迭代结束时，只有最佳蚂蚁才能应用修改后的全局信息素更新规则来更新踪迹。

精英蚂蚁系统。
在这个算法中，全局最佳解决方案在每次迭代后（即使未曾重新访问该踪迹）将信息素与所有其它蚂蚁一起沉积在其踪迹上。 精英策略的目标是导引所有蚂蚁的搜索，从而构造包含当前最佳路线链接的解决方案。

最大最小蚂蚁系统（MMAS）。
此算法控制每个踪迹上信息素的最大和最小数量。 只有最好的全局旅途、或最好的重复旅途才能在它们的踪迹中加上信息素。 为了避免搜索算法陷入停滞，每条踪迹上可能的信息素量范围限定在 [τ max, τ min] 区间。 所有边线都用 τ max 初始化，以便加快解决方案的探索。 当接近停滞时，踪迹被重新初始化为 τ max。

基于排位的蚂蚁系统（Asrank）。
所有解决方案都根据其长度进行排位。 只有固定数量的最佳蚂蚁才能更新它们的挑战。 对于每种解决方案的信息素沉积量进行加权，如此拥有较短路径的解决方案比较长路径的解决方案沉积的信息素更多。

并行蚁群优化（PACO）。
具有交流策略的蚁群系统（ACS）。 人工蚂蚁被分为若干组。 提议七种交流方法，来更新处理旅行推销员问题的 ACS 群组之间的信息素水平。

连续正交蚁群（COAC）。
COAC 信息素沉积机制，令蚂蚁能够协调、有效地搜寻解决方案。 通过运用正交设计方法，允许区域内的蚂蚁可以快速、有效地探索其所选区域，并具有增强的全局搜索能力和准确性。 正交设计方法和自适应半径调整方法，也可以扩展到其它优化算法，为解决实际问题提供更广泛的优势。

蚁群的递归优化。
这是一种递归形式的蚁群，它将整个搜索区域划分为若干个子域，并解决这些子域中的问题。 比较所有子域的结果，取少量最佳子域进入下一个级别。 与所选结果相对应的子域被进一步细分，并重复该过程，直到获得所需的精度。 该方法已在矫正地球物理反演问题上进行了测试，证明了其有效性。

上面研究的蚁群算法最初是为解决图形的优化问题而开发的。 将问题集成到此类算法中，并将问题条件作为算法参数给出 — 图形节点的坐标。 因此，基于 ACO 原理的算法是高度专业化的。 此类算法不适用于我们的任务，因为我们未采用固定坐标。 我们也许有任意坐标，包括类似的坐标。 为了解决交易金融产品领域的各种优化问题，包括训练神经网络，我们需要开发一种新的通用算法，如此它能够通过我们的特殊测试，即它应该是一个全新的 ACO。

我们研究一下算法的基本概念。 就像在规范版本中一样，我们将拥有一个蚁群。 我们不用信息素标记已踏过的路径，它们可以去多维空间中的任何地方，记住和保存路线。 对于连续的步骤，这似乎不合适，因为沿着同一路线前进的概率趋于零。 此外，根本不需要记忆节点，因为没有重复的顺序通道问题 — 有必要将问题从算法中摘出。 那好，我们应该怎么做呢？ 在现阶段，完全不清楚这个概念的发展方向。

好吧，然后我们再次注意到将我们的新算法与规范算法区分开来的要点：

1. 空间中没有固定点。

2. 没有必要按一定的顺序通过路径。

3. 由于没有路径，因此无物需用信息素来标记。

然后，我们唤醒驻留脑海的蚁群的念头。 我们可以用信息素标记蚂蚁走过的点，而非它们走过的路径。 我们将适应度函数的值作为信息素数，设置到当前迭代中蚂蚁位置。 然后蚂蚁将不得不向信息素更多的坐标移动。 但当所有的蚂蚁都跑到一个点时，我们可能会遇到一个问题 — 该点的信息素肯定最多。 考虑到这些点都是优化函数的变量，故这不一定是问题的最佳解决方案。 我们还记得，在经典 ACO 中，节点路径的长度也很重要。 选择的路径越短越好。 故我们不得不计算从当前位置到蚂蚁前往地点的距离。 下一个地方是其它蚂蚁所在的地方，即我们接受蚂蚁以一定的随机性相互移动的概念。

我们可以为运动添加什么样的随机性？

  • 首先，在选择下一个位置 PheromoneEffect_P 时添加随机因子。
  • 其次，添加一个随机因子，同时考虑到到下一个位置的距离 PathLengthEffect_P（距离越小，选择越好）。

如此，我们有两个选择下一个位置的准则 — 蚂蚁所在的每个特定位置的信息素数量，以及所有这些成对点之间的距离。 然而，即使我们只用这两个选择准则，那么蚂蚁也会沿着假想边线在空间中移动，它们自己所在位置即是一个节点。 因此，在寻找更好的地方方面不会有任何进步。

在这种情况下，添加信息素的影响半径 PheromoneRadius_P（点之间的距离之比），蚂蚁可以在其内感知到它。 然后蚂蚁就能够溜过它前往的点。 这将为蚂蚁在多维空间中移动时提供额外的自由度。

为了能让蚂蚁探索新的区域，需要允许它们沿着任意坐标偏离方向矢量。 我们来引入 PathDeviation_P 比率，它将给出特定坐标处与增量的偏差。 由于我们有一个多维空间，按照位移矢量，一些坐标可以有一个正增量，而另一些坐标可以有一个负增量，并且增量可以有不同的模值。 这个比例会令所有想到的成为可能，并将为蚂蚁在觅食时提供一定程度的自由（函数的极值）。

那么什么是位移矢量，我们如何测量蚂蚁必须行进的距离呢？ 为了回答这些问题，利用公式计算三维空间中两点之间的距离：

VectorFormula

查看图例 2 可以获得位移矢量的直观表述。


矢量

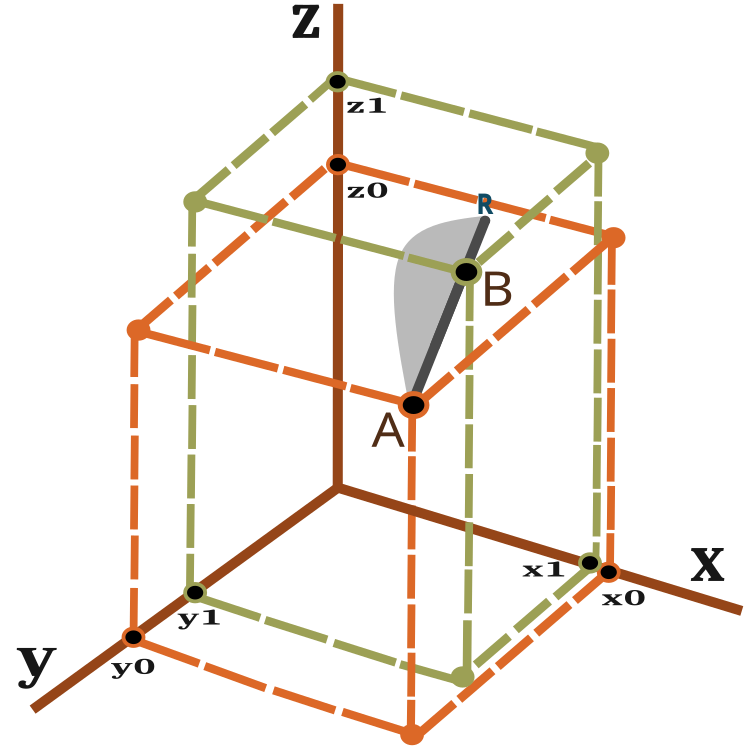
图例 2. 蚂蚁移动矢量

对于 n 维空间，计算类似。

一只蚂蚁在一次迭代（世代）中从 A 点移动到 B 点，并可能滑点到 R 点。从 B 点到 R 点的距离取决于 PheromoneRadius_P 比率，且可计算为 BR = AB x PheromoneRadius_P。

AR 线上新位置的概率在图例 2 中显示为灰色区域示意图（没有拉伸）。 因此，蚂蚁的新位置更有可能趋向于 B 点。概率偏移的原理在上一篇文章中曾经讨论过。

该算法在每次迭代时都包括以下步骤：

1) 蚂蚁在空间中的随机排列。
2) 判蚂蚁的信息素量（适应度函数）的值。
3) 计算从一只蚂蚁到另一只蚂蚁的距离。
4) 选择蚂蚁移动的首选点。
5) 计算 AR 矢量上一个点的概率。
6) 计算在 AR 矢量上获得的点的坐标。
7) 从步骤 2 开始重复，直到满足停止条件。

我们继续讲述算法代码。 首先，我们编写一个包含蚂蚁描述的结构，其中：

  • c [] - 蚂蚁坐标， 
  • cLast [] - 以前的坐标，
  • cB [] - 所有迭代的最佳坐标，
  • f - 当前信息素值，
  • fB - 在所有迭代中达到的最大信息素值。

在蚂蚁结构的构造函数中，我们可用 'double' 数据类型，表示初始化 f 和 fB 的最小可能值。

//——————————————————————————————————————————————————————————————————————————————
struct S_Ants
{
    double cLast  []; //last coordinates
    double c      []; //coordinates
    double cB     []; //best coordinates

    double f;     //pheromone of the current coordinates
    double fB;    //pheromone of the best coordinates

    S_Ants ()
    {
      f  = -DBL_MAX;
      fB = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

我们需要一个结构，其数组将允许我们存储所有成对蚂蚁之间的距离。

struct S_Paths
{
    double a [];
};

我将修改后的 ACO 算法编写为一个类，其中仍然只有三个公开方法，在构建优化算法的已开发概念框架内，这些是充分和必要的，在前面的文章中已讨论过 — InitAnts()、Preparation () 和 Dwelling()。 还有 GenerateRNDants() 和 AntsMovement() 私密方法，以及其它已经成为我们算法标配的私密方法。 ants [] 结构数组是蚁群。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACO
{
  public:
  //----------------------------------------------------------------------------
  S_Ants ants      []; //ants
  double rangeMax  []; //maximum search range
  double rangeMin  []; //manimum search range
  double rangeStep []; //step search
  double cB        []; //best coordinates
  double fB;           //pheromone of the best coordinates

  void InitAnts (const int    coordinatesP,       //number of opt. parameters
                 const int    antHillSizeP,
                 double       pheromoneEffectP,
                 double       pathLengthEffectP,
                 double       pheromoneRadiusP,
                 double       pathDeviationP);

  void Preparation ();
  void Dwelling ();

  private:
  //----------------------------------------------------------------------------
  S_Paths paths [];
  int coordinates;        //number of coordinates
  int antHillSize;        //ant hill size

  double goals     [];

  double pheromoneEffect;
  double pathLengthEffect;
  double pheromoneRadius;
  double pathDeviation;
  bool   dwelling;

  void   GenerateRNDants ();
  void   AntsMovement    ();

  double SeInDiSp             (double in, double inMin, double inMax, double step);
  double RNDfromCI            (double min, double max);
  double Scale                (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

在初始化方法中，分配变量初始值和数组大小。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::InitAnts (const int    coordinatesP,       //number of opt. parameters
                         const int    antHillSizeP,
                         double       pheromoneEffectP,
                         double       pathLengthEffectP,
                         double       pheromoneRadiusP,
                         double       pathDeviationP)
{
  fB = -DBL_MAX;

  coordinates      = coordinatesP;
  antHillSize      = antHillSizeP;
  pheromoneEffect  = pheromoneEffectP;
  pathLengthEffect = pathLengthEffectP;
  pheromoneRadius  = pheromoneRadiusP;
  pathDeviation    = pathDeviationP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);

  dwelling = false;

  ArrayResize (ants,  antHillSize);
  ArrayResize (paths, antHillSize);

  for (int i = 0; i < antHillSize; i++)
  {
    ArrayResize (ants  [i].c,      coordinates);
    ArrayResize (ants  [i].cLast,  coordinates);
    ArrayResize (ants  [i].cB,     coordinates);
    ArrayResize (paths [i].a,      antHillSize);
  }

  ArrayResize (cB,    coordinates);
  ArrayResize (goals, antHillSize);
}
//——————————————————————————————————————————————————————————————————————————————

每次迭代时首先调用 Preparation() 方法。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Preparation ()
{
  if (!dwelling)
  {
    fB = -DBL_MAX;
    GenerateRNDants ();
    dwelling = true;
  }
  else AntsMovement ();
}
//——————————————————————————————————————————————————————————————————————————————

GenerateRNDants() 方法负责创建一个随机蚁群。 蚂蚁坐标在给定的范围内随机分配。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::GenerateRNDants ()
{
  for (int s = 0; s < antHillSize; s++)
  {
    for (int k = 0; k < coordinates; k++)
    {
      ants [s].c     [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      ants [s].c     [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      ants [s].cLast [k] = ants [s].c [k];
      ants [s].cB    [k] = ants [s].c [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

在 Dwelling() 方法中记住蚂蚁的当前坐标，并更新当前迭代时获得的最大信息素值。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Dwelling ()
{
  for (int i = 0; i < antHillSize; i++)
  {
    ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY);

    //remember the best coordinates for the ant
    if (ants [i].f > ants [i].fB)
    {
      ants [i].fB = ants [i].f;
      ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }

    //remember the best coordinates for the anthill
    if (ants [i].f > fB)
    {
      fB = ants [i].f;
      ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

算法的主要方法是 AntsMovement ()。 它执行以下操作：计算从一只蚂蚁到另一只蚂蚁的距离，计算选择蚂蚁将移动的首选点，计算 AR 矢量上某个点的概率。 计算在 AR 矢量上得到的点坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::AntsMovement ()
{
  double rndPh;
  double rndPt;
  double summCoordinates = 0.0;
  double scores [];
  ArrayResize (scores, antHillSize);

  double maxPh = -DBL_MAX;
  double minPh =  DBL_MAX;
  double maxPt = -DBL_MAX;
  double minPt =  DBL_MAX;
  double goal;
  double goalBest = -DBL_MAX;
  int    goalInd  = 0;

  //measure the distance between all the ants-----------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    for (int k = 0; k < antHillSize; k++)
    {
      if (i == k)
      {
        paths [i].a [k] = DBL_MAX;
        continue;
      }
         
      for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0);

      paths [i].a [k] = pow (summCoordinates, 0.5);

      if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k];
      if (minPt > paths [i].a [k]) minPt = paths [i].a [k];
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    maxPh = -DBL_MAX;
    minPh =  DBL_MAX;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        if (maxPh < ants [k].f) maxPh = ants [k].f;
        if (minPh > ants [k].f) minPh = ants [k].f;
      }
    }

    goalBest = -DBL_MAX;
    goalInd  = 0;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        rndPh = RNDfromCI (0.0, pheromoneEffect);
        rndPt = RNDfromCI (0.0, pathLengthEffect);

        goal = Scale (ants  [k].f,     minPh, maxPh, 0.0, 1.0, false) * rndPh *
               Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true)  * rndPt;

        if (goalBest < goal)
        {
          goalBest = goal;
          goalInd  = k;
        }
      }
    }
    
    double wayToGoal      = paths [i].a [goalInd];
    double radiusNearGoal = wayToGoal * pheromoneRadius;
    double endWay         = wayToGoal + radiusNearGoal;

    double x = RNDfromCI (-1.0, 1.0);
    double y = x * x;
    
    if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay,    false);
    else         y = Scale (y, 0.0, 1.0, 0.0,       wayToGoal, true);

    for (int j = 0; j < coordinates; j++)
    {
      double incrementFactor = y / wayToGoal;
      double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j];
      
      ants [i].c [j] =  ants [i].cLast [j] + (coordDistance * incrementFactor);
      double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation;
      ants [i].c [j] += w;
      
      ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

值得关注的是将数字从一个范围拉伸到另一个范围的函数。 我在以前的文章中曾研究过。 这次我将扩展其功能。 revers 输入更改拉伸方向，如下图所示。

拉伸

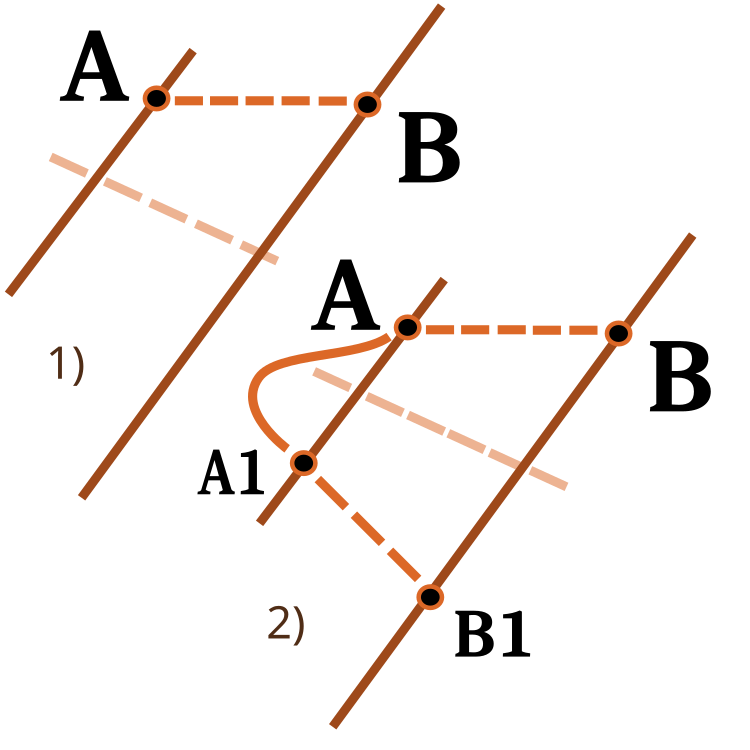
图例 3. 将数字从一个范围拉伸到另一个范围。

1) 直接拉伸；2) 逆向拉伸

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return revers ? OutMAX : OutMIN;
    if (In > InMAX) return revers ? OutMIN : OutMAX;

    double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);

    if (!revers) return res;
    else         return OutMAX - res;
  }
}
//——————————————————————————————————————————————————————————————————————————————

4. 测试结果

Func1

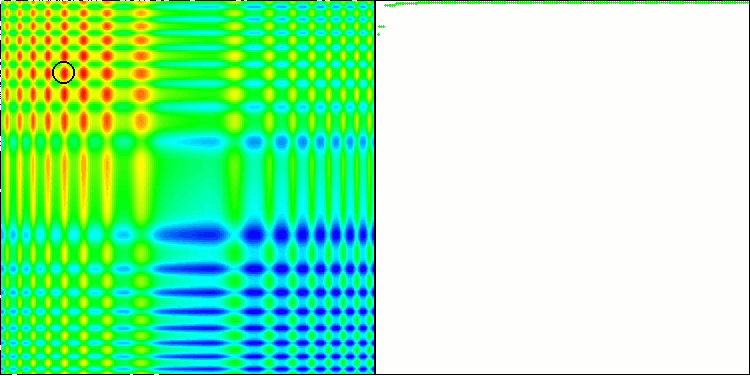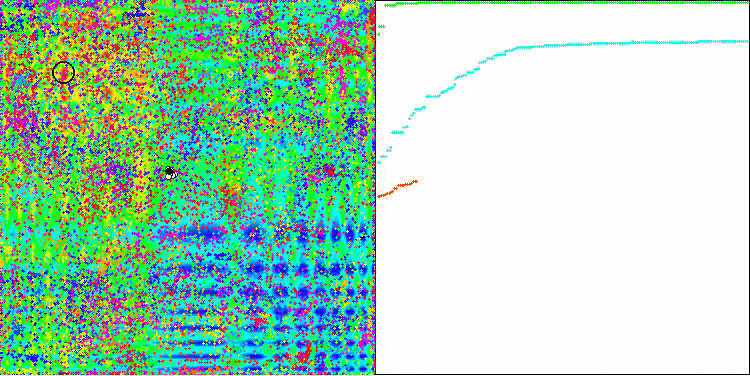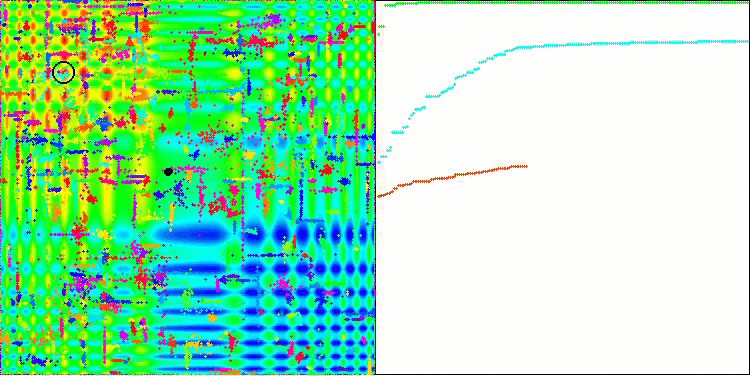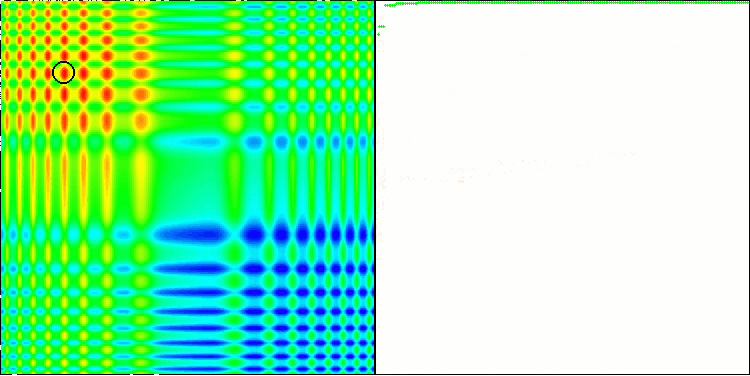
ACO 基于 Skin 测试函数

Func2

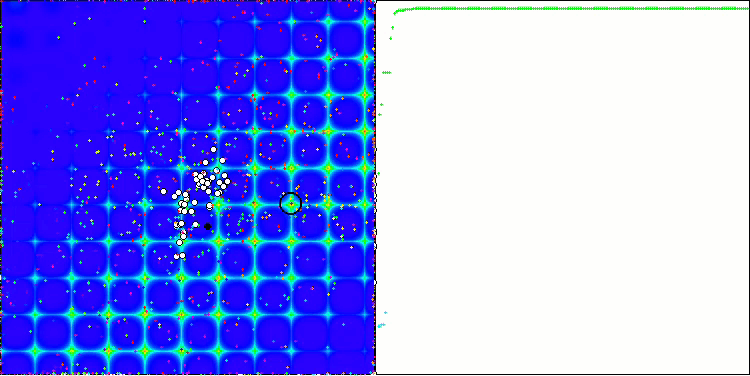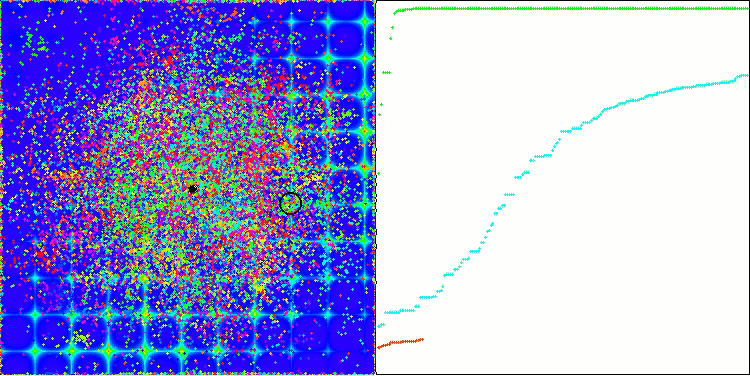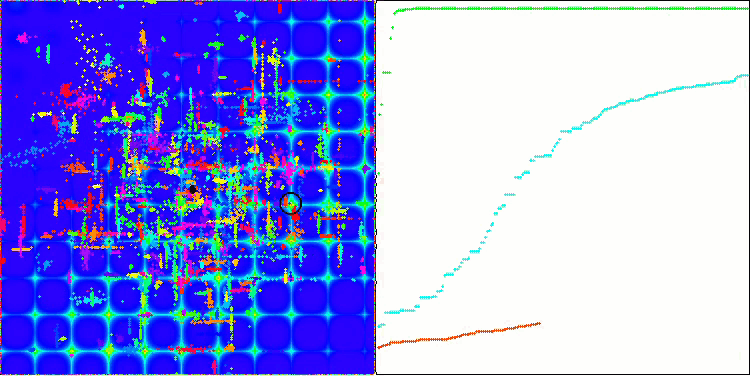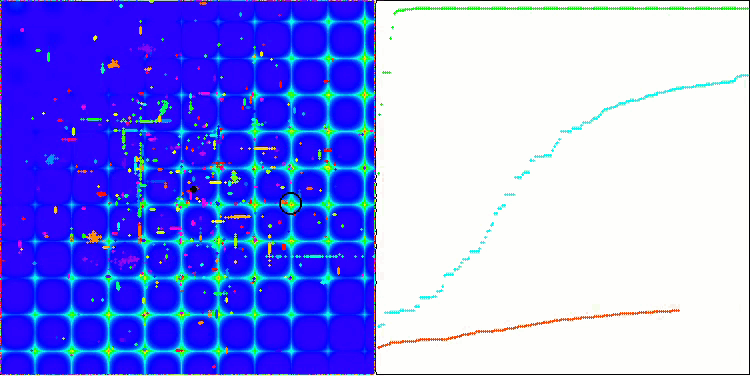
ACO 基于 Forest 测试函数

Func3

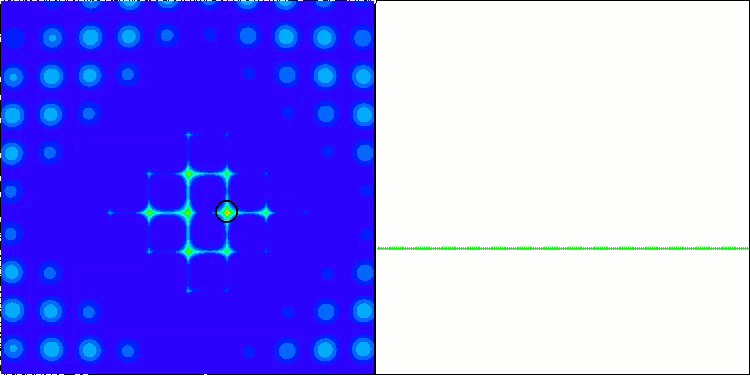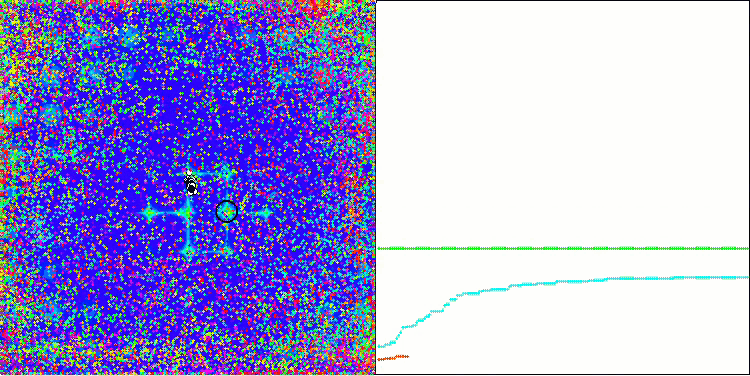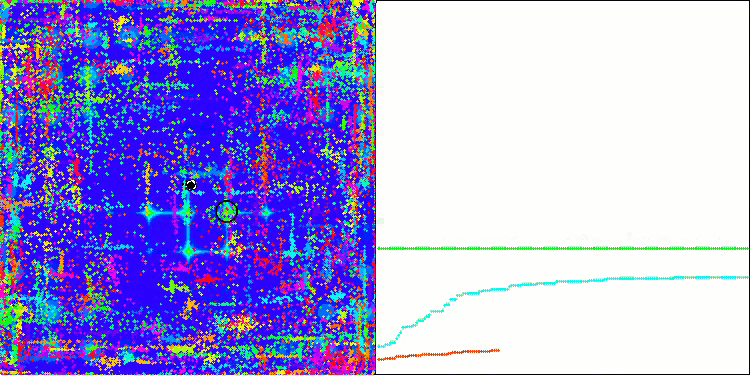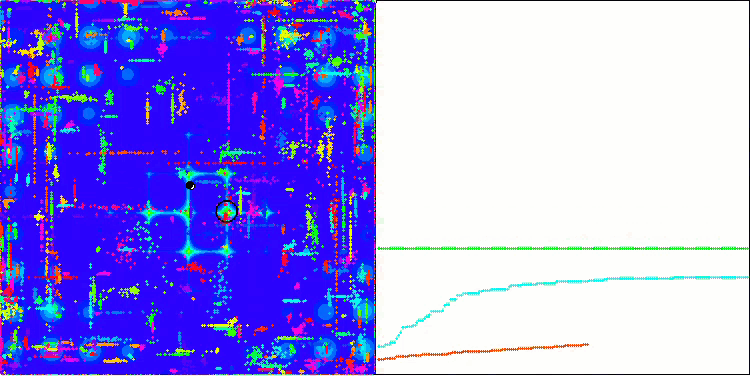
ACO 基于 Megacity 测试函数

好吧，到了得出结论的时候了。 一方面，传统的蚁群算法不适用于交易金融产品的优化问题。 然而，为了避免传统版本的局限性，我们见证了蚁群算法全新概念的出现，能够深入 ACO 的发展。 这样的算法已可应用在广泛的问题，包括旅行推销员问题。

此外，我们现在有了评价表的新领导者。 我们来详研结果。 首先，注意测试台的结果：

2022.10.27 16:46:28.678    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    Score1: 0.99502; Score2: 0.99599
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    Score1: 0.69826; Score2: 0.86403
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    Score1: 0.50498; Score2: 0.58800
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    Score1: 0.99087; Score2: 0.99302
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    Score1: 0.22374; Score2: 0.65571
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    Score1: 0.08408; Score2: 0.17442
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    Score1: 0.78667; Score2: 0.78667
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    Score1: 0.11667; Score2: 0.26133
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    Score1: 0.04224; Score2: 0.08208

2022.10.27 16:49:41.075    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    All score for C_AO_ACO: 0.5468768583006471

该算法在平滑 Skin 函数上表现良好，展现出完美的收敛性和良好的拉伸能力，尤其在 20 和 500 函数测试中遥遥领先。 在平滑 Forest 函数上，有急剧断裂，分离更加明显。 即使触及局部极值，该算法依然继续搜索。 在离散 Megacity 函数上，该算法仅在具有 500 个函数的问题上落后于随机 RND 算法。

算法

运行次数

Skin

Forest

Megacity (离散)

最终结果

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

ACOm

1000

0.99502

0.69826

0.50498

0.99087

0.22374

0.08408

0.78667

0.11667

0.04224

0.54688

10,000

0.99599

0.86403

0.58800

0.99302

0.65571

0.17442

0.78667

0.26133

0.08208

RND

1000

0.98744

0.61852

0.49408

0.89582

0.19645

0.14042

0.77333

0.19000

0.14283

0.51254

10,000

0.99977

0.69448

0.50188

0.98181

0.24433

0.14042

0.88000

0.20133

0.14283

PSO

1000

0.98436

0.72243

0.65483

0.71122

0.15603

0.08727

0.53333

0.08000

0.04085

0.47695

10,000

0.99836

0.72329

0.65483

0.97615

0.19640

0.09219

0.82667

0.10600

0.04085

PSOm

1000

0.96678

0.64727

0.57654

0.80616

0.13388

0.06800

0.53333

0.08067

0.04211

0.45144

10,000

0.99505

0.64986

0.57654

0.90401

0.18194

0.07104

0.74667

0.10400

0.04211


结束语

该算法有很多设置，如此能够得到更好的结果。 能够针对特定类型的任务进行自定义。 第一个参数 PheromoneEffect_P 直接影响收敛速率。 这对于平滑单调函数尤其优秀，例如抛物线。 收敛将是 100%，但如果设置得很大，这会同时导致在离散函数上陷入局部极值。

第二个参数 PathLengthEffect_P 代表蚂蚁的懒惰程度。 在参数值较高的情况下，则选择较近的目标前往。 有必要平衡此参数与第一个参数，从而获得最佳结果。 此参数旨在平衡蚂蚁前往有更多食物的地方的愿望，替代有时选择最近的目标，对小区域进行更详细的检查；这可能非常有用，例如在 Forest 函数示例中，翻牌后的最佳点也许非常接近。

最重要的成就是，我们已经设法摆脱了规范 ACO 的主要问题：仅解决离散组合问题的能力。 现在，蚁群算法可用于训练神经网络。

直观上，由于一定的聚类，测试台非常有趣，蚂蚁在多维函数的测量中集中，以某种方式突显出局部极值的特征群。 也许，这种效应可用于解决具体问题，但这需要额外的研究。

该算法有一个有趣的属性：当解决两个变量的问题时，陷于局部极值的概率略高于优化 40 个变量时的概率。 该算法继续搜索解决方案会涉及多个变量。 我假设这是用矢量作为链接搜索空间所有坐标的手段产生的效应。 例如，如果一只蚂蚁移动到一个新的更好的地方，那么所有的坐标在空间上都会变得更好，而不是只有一些坐标单独改变。

创建的算法是新的，未详细探索，因此如果有人共享算法设置，我将不胜感激，其中测试台将显示大于 0.6 的最终值，以便我可以更新表格的结果。 此请求也适用于以前研究的算法。

优点:
1. 算法非常快。
2. 多功能性。 该算法可用于各种优化问题。 3. 不只关注局部极值的能力。 4. 平滑和离散函数的收敛性都相当好。 5. 伸缩性。

缺点:
1. 也许，收敛需要比相同 PSO 更多的迭代才能实现平滑功能，但这部分被即使在 PSO 已经停止的情况下继续搜索的能力所抵消。
2. 算法参数对结果的影响很大。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11602

附加的文件 |
下载ZIP
q3_The_world_of_AO_7ACOg.zip (29.23 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
创建一个行情卷播面板：基本版 创建一个行情卷播面板：基本版
在此，我将展示如何创建价格播报屏幕，它通常在交易所滚动显示报价。 我会只用 MQL5 来做到这一点，无需复杂的外部编程。
帧分析器（Frames Analyzer）工具带来的时间片交易魔法 帧分析器（Frames Analyzer）工具带来的时间片交易魔法
什么是帧分析器（Frames Analyzer）？ 这是适用于任意智能系统的一个插件模块，在策略测试器中、以及测试器之外进行参数优化期间，该工具在参数优化完成后立即读取测试创建的 MQD 文件、或数据库，并分析优化帧数据。 您能够与拥有帧分析器工具的其他用户共享这些优化结果，从而共同讨论结果。
创建一个行情卷播面板：改进版 创建一个行情卷播面板：改进版
您如何看待复查我们的行情卷播面板基本版的主意？ 我们改进面板要做的第一件事就是能够添加图像，例如资产徽标或其它图像，从而用户可以迅速、轻松地识别所示品种。
DoEasy. 控件 (第 24 部分): 提示（Hint）辅助 WinForms 对象 DoEasy. 控件 (第 24 部分): 提示（Hint）辅助 WinForms 对象
在本文中，我将修改为所有 WinForms 函数库对象指定基准对象和主对象的逻辑，并开发一个新的提示（Hint）基准对象，及其若干个派生类，用以示意移动隔板的可能方向。