种群优化算法：Nelder-Mead（NM），或单纯形搜索方法

内容

1. 概述
2. 算法
3. 测试结果

1. 概述

Nelder-Mead 方法由 John Nelder 和 Roger Mead 于 1965 年开发。他们那时正在寻找一种优化方法，能配合没有导数、或没有导数解析方程的函数工作。他们还打算开发一种易于实现且高效的方法，从而在当时的计算机上使用。这项研究激发了他们使用单纯形的灵感 — 函数参数空间中的多面体。

该方法的创建历史始于约翰·内尔德（John Nelder）、及其同事在牛津计算实验室的工作。他们面对的问题是优化没有解析导数、或太复杂而无法计算的函数。传统的优化方法（如梯度方法）不适用于这种情况。代之，Nelder 和 Mead 提出了一种基于函数参数空间中迭代搜索最优解的新方法。

Nelder-Mead 方法被称为“单纯形法”，并于 1965 年发表在《计算机杂志》上的《函数最小化的单纯形方法》一文中。该方法已被科学界所接受，并已广泛应用于需要函数优化的各个领域。

单纯形是形成多面体的一组顶点，其中每个顶点都是需被优化的一组函数参数值。这个思路是在参数空间中改变和移动单纯形，从而找到函数的最优值。

Nelder-Mead 方法（Nelder-Mead 单纯形法）属于无条件优化算法类。它是一种判定性算法，不需要使用函数导数，并且可配合具有多个局部最小值的函数工作。

2. 算法

Nelder-Mead 方法不是群体方法，因为只用到了一个优化活体，代表单纯形，而单纯形又由搜索空间中的一组顶点构成，而搜索空间本身可被视为群体。不过，我们将使用多个智能体，每个活体都有自己的单纯形，因此该实现很可能被归类为群体算法。

故此，为了便于理解，假设有必要优化两个可变函数。换言之，空间的维度是 z = 2，那么单纯形将由 z + 1 = 3 个顶点组成。更改单纯形是针对这三者中最糟糕的一个点的操作。我们将这些点表示为“最好”、“好”、“最差”，其中“好”是“最差”之后的第二个点（如果维度大于 2，那么在已排序的顶点列表中“好”将始终是仅次于“最差”的第二个点）。

接下来，我们需要用到这三个顶点来计算和调整相对于其余顶点的最差值。我们相对于顶点的几何中心移动最差值，且排除其本身，即计算质心，并相对于质心移动最差值。

在 Nelder-Mead 方法的每次迭代中，我们执行以下步骤：

1. 根据目标函数的值对单纯形的顶点进行排序，即 

f(P0) ⩾ f(P1) ⩾ ... ⩾ f(P(n-1))

其中：

• P0, P1 ... P(n-1) - 单纯形顶点
• n - 单纯形顶点数量
  

2. 质心计算：计算单纯形所有顶点对应坐标上的平均值，最差顶点除外。设 Xo 向量将是除 X(n-1) 之外所有顶点的重心，那么： 

Xo = (X0 + X1 + ... + X(n-2)) / (n-1)

其中：

• X0, X1 ... X(n-2) - 除最差顶点外所有顶点坐标的对应向量

3. 反射：反射相对于质心的最差顶点。新反射顶点的 Xr 向量按以下方式计算：

Xr = Xo + α (Xo - Xw)

其中：

• Xw - 最差顶点向量，对应于顶点 P(n-1)
  
• α - 反射比率，通常等于 1
  

4. 新顶点的估测：计算该点目标函数的值。如果一个新顶点的目标函数值优于单纯形的最差顶点，那么它可以替换它，即反射替换原值。反射操作允许我们依据来自单纯形质心的反射，探索参数空间的新区域。

5. 扩张：当反射操作产生了比最佳值更好的顶点时进一步探索参数空间，假设反射方向上的深入能进一步改善其位置。扩张操作允许我们探索比反射操作更大的参数空间区域。它增加了质心和反射点之间的距离，这有助于找到目标函数的新局部最小值。Xe 扩张向量的计算公式如下：

Xe = Xo + γ(Xr - Xo)

其中：

• γ - 扩张比率，通常大于 1，默认为 2

5.1. 如果执行了扩张操作：计算 Xe 顶点的适应度函数。如果它优于 Xr 顶点，那么它可以替换最差的 Xw 单纯形顶点。完成扩张后，转到步骤 1。

请务必仔细选择 γ 扩张比率。如果碰巧它太大，也许就会导致单纯形扩散到参数空间大区域以外，而这会减慢收敛速度、或导致有关局部极值的信息丢失。如果反之它太小，它也许就无法充分探索参数空间的新区域。

6. 收缩：计算 Xc 顶点时，当反射操作产生的顶点差于或等于 Xb “好”点（最差点之后的第二位），即我们试图在单纯形内找到更好的位置。等式如下：

Xc = Xo + β(Xw - Xo)

其中：

• β - 收缩比率，通常在 0 到 1 之间，默认为 0.5

6.1. 如果执行了收缩：计算顶点的 Xc 目标函数的值。如果新顶点的目标函数值优于单纯形的最差顶点，则它可以替换最差顶点。完成扩张后，转到步骤 1。

收缩令我们能够将单纯形移近最差点，这有助于探索该点附近。与扩张一样，仔细选择 β 收缩比率很重要。如果碰巧它太大，则可能导致单纯形被压缩过多，从而导致有关局部最小值的信息丢失。如果反之它太小，则也许不足以收缩到探索最差点附近。

7. 缩窄：当前面的操作（反射、扩张、收缩）都没有导致目标函数值的提高时，执行 Nelder-Mead 方法中的最后一个操作。缩窄降低了单纯形的大小，从而减小搜索区域，并集中在最佳位置周围。

正如我们所见，作者针对单纯形进行了四个运算。为了开始优化，我们需要计算所有单纯形顶点的适应度函数。单纯形顶点的个数等于 “z+1”，其中 z 是搜索空间的维度。例如，如果我们的搜索维数为 1000，那么我们应该估算适应度函数 1001 次才能开始单纯形运算。尽管拥有 50 个活体的典型群体算法也许会运行 20 个轮次，该算法将只运行一个轮次，并且会消耗其有限迭代次数的大部分。

缩减涉及把所有点向最佳位置偏移。之后，需要计算 1000 遍适应度函数。换言之，缩减是极其资源密集型的。根据作者的思路，当算法卡住，且移动单纯形的最差点并不能改善数值解时，应该调用该操作。然而，我的实验表明，这种操作相对于计算资源来说非常昂贵，而且对优化算法来说毫无意义形同自杀，因为单纯形活体的所有点都收缩到一个局部极值将意味着卡住、并停止对搜索空间的探索。因此，我决定在实施算法实现时放弃缩减。

我们将针对单纯形使用前三个运算。为了更清晰起见，它们显示在图例 1：

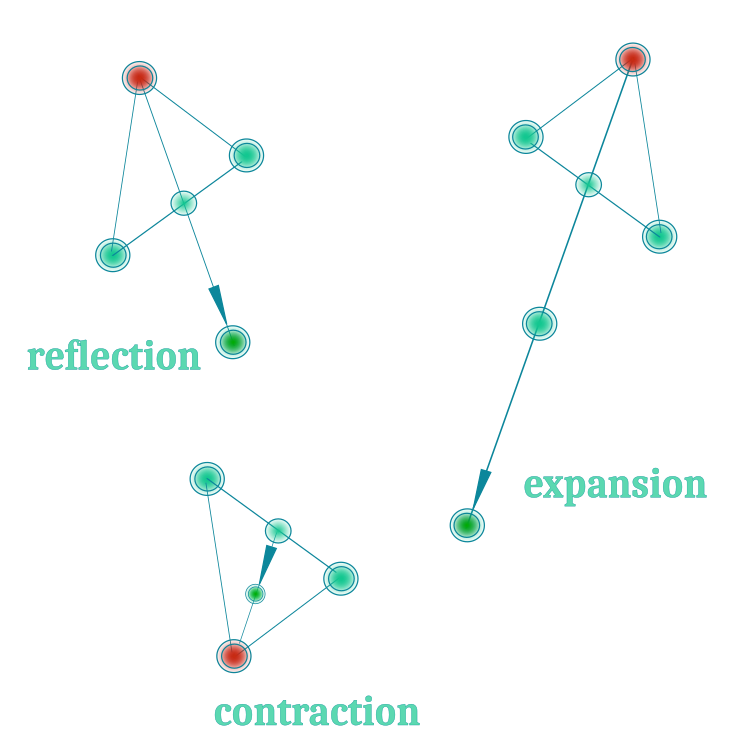
图例 1. Nelder-Mead 方法的三个主要操作

由于其不可抗性，单纯形搜索方法也许会遇到初始顶点选择不佳，故其优化结果也会不尽如人意。这种算法的实验只确认了人们的担忧：它的可接受工作范围仅在有限的坐标空间内。

由于收缩问题，单纯形的顶点只是移动了一个固定值。想象一下，站在高跷上，并尝试坐到长凳上。它对您来说太低了。变化的单纯形也会出现完全相同的状况。为了令算法运行完美，我们需要有很大的运气，以便单纯形的初始顶点最终位于正确的所在。这类似于高跷 — 为了安全坐下，我们需要一个高凳。该算法在光滑的单极值函数上收缩得相对较好，例如抛物线。然而，我们的实际问题要复杂得多，通常充满了局部的“陷阱”，尤其在交易问题当中，本质上是离散的。

那么问题浮现了。当单纯形“永远”卡在局部极值时该怎么办？Nelder-Mead 算法的逻辑没有提供摆脱这个“陷阱”的途径。每次操作后，无论是收缩还是扩张，算法都会返回反射，试图克服最坏的点。直觉上，这看起来像“闪烁”。为了解决这个问题，我尝试赋予单纯形离开局部“陷阱”的能力，并在新的空间区域继续搜索。为了达成这一目标，我使用了 Levy 航班，在某些情况下，它有助于“恢复”群体，如前几篇文章所述。然而，值得注意的是，“Levy 航班"并不总是有用的，它们的应用取决于优化算法的逻辑。在我们的案例中，这是一个实验，不能保证改善结果。

现在，我们转到最有趣的部分 — 编写代码。

每次迭代后，有必要知道在单纯形的最差顶点上执行了哪些操作。枚举器将派上用场。除了针对单纯形顶点的三个主要运算外，我还多加了一个 - “none”，以防我决定以某种方式补充算法。我们将枚举器称为 E_SimplexOperation。它具有以下字段：

• none：无操作
• reflection：反射
• expansion：扩张
• contraction：收缩
  

//——————————————————————————————————————————————————————————————————————————————
enum E_SimplexOperation
{
  none        = 0,
  reflection  = 1,
  expansion   = 2,
  contraction = 3
};
//——————————————————————————————————————————————————————————————————————————————

为了描述单纯形顶点，我们需要 S_Point 结构，它包含以下字段：

• Init(int coords): 点初始化，取 “coords” 参数
• c []: 多维空间中一个点的坐标数组，数组的大小在 Init 方法中判定
• f: 顶点适应度函数值
  

//——————————————————————————————————————————————————————————————————————————————
struct S_Point
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }
  double c [];
  double f;
};
//——————————————————————————————————————————————————————————————————————————————

对于单纯形，我们将使用 S_Simplex 结构，它是每个活体的单纯形，包含以下字段：

• Init(int coords)：单纯形初始化，取 “coords” 参数 - 坐标数量
• S_Point p []：单纯形顶点数组，数组大小在 Init 方法中判定
• c []：单纯形质心坐标的数组，数组的大小在 Init 方法中判定。
• S_Point Xr：反射点
• S_Point Xe：扩张点
• S_Point Xc：收缩点
• indG：单纯形中的好点索引
• indW：单纯形中最差点索引
• E_SimplexOperation：单纯形操作类型

//——————————————————————————————————————————————————————————————————————————————
struct S_Simplex
{
  void Init (int coords)
  {
    ArrayResize (p, coords + 1);

    for (int i = 0; i <= coords; i++)
    {
      p [i].Init (coords);
    }

    ArrayResize (c, coords);

    Xr.Init (coords);
    Xe.Init (coords);
    Xc.Init (coords);

    operation = none;
  }

  S_Point p [];
  double c  []; //centroid

  S_Point Xr;  //reflection point
  S_Point Xe;  //expansion point
  S_Point Xc;  //expansion point

  int indG;    //index of good point
  int indW;    //index of worst point

  E_SimplexOperation operation; //type of simplex operation
};
//——————————————————————————————————————————————————————————————————————————————

定义优化活体的 S_Agent 结构。该结构包含以下字段：

• Init(int coords)：活体初始化方法，取 “coords” 参数指定坐标数量。该方法调用 ArrayResize 函数将数组 “c” 的大小调整到 “coords” 的值。然后将 “f” 字段设置为 -DBL_MAX，这是活体估测函数的初始值。接下来，为 “s” 字段调用 Init 方法，该字段表示活体单纯形
• c []：与外部程序交换的活体多维空间坐标数组。数组大小是在 Init 方法中判定
• f：活体适应度函数值
• S：以 S_Simplex 结构表示的活体单纯形。通过调用 “s” 字段的 Init 方法来初始化单纯形

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;

    s.Init (coords);
  }

  double c  []; //coordinates
  double f;     //fitness
  S_Simplex s;  //agent simplex
};
//——————————————————————————————————————————————————————————————————————————————

定义单纯形搜索方法的算法类 C_AO_NMm，其中包含以下字段：

• cB []：最佳坐标数组
• fB：最佳坐标的适应度函数值
• a []：由 S_Agent 结构表示的活体数组
• rangeMax []：每个坐标的最大搜索范围值数组
• rangeMin []：每个坐标的最小搜索范围值数组
• rangeStep []：每个坐标的搜索步骤数组
• Init(const int coordsP, const int popSizeP, const double reflectionCoeffP, const double expansionCoeffP, const double contractionCoeffP)：算法初始化方法，取定义坐标数量、群体大小、反射、扩张和收缩操作比率的参数，该方法执行所有类字段的初始化
• Moving ()：该方法在算法中执行活体的移动
• Revision()：该方法在算法中执行活体的移动
• Sorting、CalcCentroid、Reflection、Expansion、Contraction、Flying：执行单纯形操作。这些 
• SeInDiSp、RNDfromCI 和 Scale 方法执行后，生成数值，并将其转换到给定步骤的有效范围
  

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NMm
{
  //----------------------------------------------------------------------------
  public: double cB [];  //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Agent a [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //Reflection coefficient
                     const double expansionCoeffP,    //Expansion coefficient
                     const double contractionCoeffP); //Contraction coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    simplexPoints; //simplex points


  private: double reflectionCoeff;  //Reflection coefficient
  private: double expansionCoeff;   //Expansion coefficient
  private: double contractionCoeff; //Contraction coefficient

  private: bool   revision;

  private: S_Point pTemp [];
  private: int     ind   [];
  private: double  val   [];

  private: void   Sorting      (S_Point &p []);
  private: void   CalcCentroid (S_Simplex &s, int indW);
  private: void   Reflection   (S_Agent &agent, int indW);
  private: void   Expansion    (S_Agent &agent);
  private: void   Contraction  (S_Agent &agent, int indW);
  private: void   Flying       (S_Agent &agent, int indW);

  private: double SeInDiSp     (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI    (double min, double max);
  private: double Scale        (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

若要初始化算法，调用 C_AO_NMm 类的 Init 方法，它初始化类的所有字段，并为优化算法的工作创建必要的数组。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //reflection coefficient
                     const double expansionCoeffP,    //expansion coefficient
                     const double contractionCoeffP)  //contraction coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  simplexPoints = coords + 1;

  reflectionCoeff  = reflectionCoeffP;
  expansionCoeff   = expansionCoeffP;
  contractionCoeff = contractionCoeffP;

  ArrayResize (pTemp, simplexPoints);
  ArrayResize (ind,   simplexPoints);
  ArrayResize (val,   simplexPoints);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++)
  {
    a [i].Init (coords);
  }

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

通常我们调用 Moving 方法在搜索空间中移动活体，但对于 NM 算法，我们将只保留在搜索空间中随机放置活体单纯形顶点的初始函数。为了创建单纯形的随机顶点，我们调用 RNDfromCI，并调用 SeInDiSp 方法按照所需步骤将其带到所需范围。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Moving ()
{
  if (!revision)
  {
    int cnt = 0;

    for (int i = 0; i < popSize; i++)
    {
      for (int p = 0; p < simplexPoints; p++)
      {
        cnt++;
        for (int c = 0; c < coords; c++)
        {
          a [i].s.p [p].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
          a [i].s.p [p].c [c] = SeInDiSp  (a [i].s.p [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

移动活体单纯形顶点的主要逻辑将在 Revision 方法中运作。

如果尚未执行修订 "if (!revision)"，则有必要对单纯形中的顶点进行排序，构造质心，并针对活体单纯形的最差顶点执行反射。针对顶点最先进行的操作，它始终是“反射”。此处，我们可以更新全局解，因为此刻我们已知晓每个顶点的适应度值。将 “revision” 变量的值设为 “true”，并退出该方法。

从下一次迭代开始，我们就知道适应度函数不再针对单纯形顶点，而是针对特定优化活体。根据针对单纯形执行的运算，我们把已知的活体的解分配给其对应的单纯形顶点。我们需要用活体的最佳适应度值更新全局解。

接下来，检查在上一次迭代中针对顶点执行了哪些运算。我们的意思是单纯形的顶点是向量。

如果执行的是“反射”：

• 将活体适应度值分配给 Xr 向量
• 比较 Xr 与 Xw 的向量适应度。如果该值更佳，则更新 Xw 向量
• 比较 Xr 与 Xb 的向量适应度。如果该值更佳，则执行“扩张”
• 比较 Xr 与 Xg（最差顶点后的第二位）的向量适应度，如果该值更差，则执行“收缩”
• 如果顶点有所改善，执行“反射”，对质心进行初步排序和构造。否则，执行 “飞行”
  

如果执行的是“扩张”：

• 将活体适应度值分配给 Xe 向量
• 比较 Xe 与 Xw 的向量适应度。如果该值更佳，则更新 Xw 向量
  
• 执行“反射”，对质心进行初步排序和构造
  

如果执行的是“收缩”：

• 将活体适应度值分配给 Xс 向量
  
• 比较 Xс 与 Xw 的向量适应度。如果该值更佳，则更新 Xw 向量。否则，执行“飞行”
• 如果顶点有所改善，则执行“反射”，对质心进行初步排序和构造。
  

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Revision ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    //sort agent simplex points by FF value and assign BGW
    for (int i = 0; i < popSize; i++)
    {
      Sorting (a [i].s.p);
    }

    //calculate the simplex centroid
    for (int i = 0; i < popSize; i++)
    {
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;

      CalcCentroid (a [i].s, a [i].s.indW);
    }

    //assign the next type of operation - reflection
    for (int i = 0; i < popSize; i++)
    {
      Reflection (a [i], a [i].s.indW);
      a [i].s.operation = reflection;
    }

    //save the best point of the agents’ simplexes as a global solution 
    for (int i = 0; i < popSize; i++)
    {
      if (a [i].s.p [0].f > fB)
      {
        fB = a [i].s.p [0].f;
        ArrayCopy (cB, a [i].s.p [0].c, 0, 0, WHOLE_ARRAY);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  if (revision)
  {
    int pos = -1;

    for (int i = 0; i < popSize; i++)
    {
      if (a [i].f > fB) pos = i;
    }

    if (pos != -1)
    {
      fB = a [pos].f;
      ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was reflection ++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == reflection)
    {
      a [i].s.Xr.f = a [i].f;
      bool needUpd = false;

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [a [i].s.indW].f)  //Xr > Xw                 |---w--Xr--g----------b---|
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xr;        //replace Xw with Xr
        needUpd = true;
      }
      
      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [0].f)             //if Xr > Xb            |---w----g----------b---Xr|
      {
        Expansion (a [i]);                            //perform expansion
        continue;
      }

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f <= a [i].s.p [a [i].s.indG].f) //if Xr < Xg            |---w---Xr--g----------b--|
      {
        Contraction (a [i], a [i].s.indG);            //perform contraction
        continue;
      }
      
      if (needUpd)
      {
        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was expansion +++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == expansion)
    {
      a [i].s.Xe.f = a [i].f;

      if (a [i].s.Xe.f > a [i].s.Xr.f) a [i].s.p [a [i].s.indW] = a [i].s.Xe;
      else                             a [i].s.p [a [i].s.indW] = a [i].s.Xr;

      Sorting (a [i].s.p);
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;
      CalcCentroid (a [i].s, a [i].s.indW);
      Reflection   (a [i],   a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was contraction +++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == contraction)
    {
      a [i].s.Xc.f = a [i].f;

      if (a [i].s.Xc.f > a [i].s.p [a [i].s.indW].f)
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xc;

        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

为了计算质心，我们将编写 CalcCentroid 方法。它计算给定单纯形 “s” 中坐标的平均值，直至指定的 indW 索引。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::CalcCentroid (S_Simplex &s, int indW)
{
  double summ = 0.0;

  for (int c = 0; c < coords; c++)
  {
    summ = 0.0;

    for (int p = 0; p < simplexPoints; p++)
    {
      if (p != indW) summ += s.p [p].c [c];
    }

    s.c [c] = summ / coords;
  }
}
//——————————————————————————————————————————————————————————————————————————————

“反射”运算将由 "agent" 单纯形 indW 索引处的顶点 Reflection 方法执行。

在循环内，使用等式 Xr = Xo + reflectionCoeff * (Xo - Xw) 计算反射值 Xr。此处的 reflectionCoeff 是一个反射比率，它判定反射顶点距初始顶点的偏差程度。
接下来，将 SeInDiSp 应用于 Xr，从而确保它在 rangeMin[c] 至 rangeMax[c] 的有效范围内，且步长为 rangeStep[c]。结果保存在 agent.s.Xr.c[c] 之中。
为 agent.s.operation 设置 "reflection" 操作，指明已对该活体执行了反射操作。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Reflection (S_Agent &agent, int indW)
{
  double Xo;
  double Xr;
  double Xw;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c [c];
    Xw = agent.s.p [indW].c [c];

    //Xr = Xo + RNDfromCI (0.0, reflectionCoeff) * (Xo - Xw);
    Xr = Xo + reflectionCoeff * (Xo - Xw);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

“扩张”操作将由 “agent” 的 Expansion 方法执行。

在循环内，使用等式 Xe = Xo + expansionCoeff * (Xr - Xo) 计算 Xe 的扩张值。此处，expansionCoeff 是扩张比率，它判定了扩张顶点距初始顶点的偏差增加程度。接下来，将 SeInDiSp 应用于 Xe，从而确保它在 rangeMin[c] 至 rangeMax[c] 的有效范围内，步长为 rangeStep[c]。结果保存在 agent.s.Xe.c[c] 之中。
为 agent.s.operation 设置 “expansion” 操作，指明已为该活体执行了“扩张”操作。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Expansion (S_Agent &agent)
{
  double Xo;
  double Xr;
  double Xe;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xr = agent.s.Xr.c [c];

    //Xe = Xo + RNDfromCI (0.0, expansionCoeff) * (Xr - Xo);
    Xe = Xo + expansionCoeff * (Xr - Xo);

    agent.s.Xe.c [c] = SeInDiSp  (Xe, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xe.c [c];
  }

  agent.s.operation = expansion;
}
//——————————————————————————————————————————————————————————————————————————————

“收缩”操作将由 “agent” 单纯形向量 indW 索引处的顶点 Contraction 方法执行。

在循环内，使用等式 Xc = Xo + contractionCoeff * (Xw - Xo) 计算 Xc 的收缩值。此处的 contractionCoeff 是收缩比率，它判定了收缩顶点距初始顶点的偏差减小程度。
接下来，将 SeInDiSp 应用于 Xc，从而确保它在 rangeMin[c] 至 rangeMax[c] 的有效范围内，步长为 rangeStep[c]。结果保存在 agent.s.Xc.c[c] 之中。
为 agent.s.operation 设置 “contraction” 操作，指明已为该活体执行了“收缩”操作。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Contraction (S_Agent &agent, int indW)
{
  double Xo;
  double Xw;
  double Xc;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xw = agent.s.p [indW].c [c];

    //Xc = Xo + RNDfromCI (0.0, contractionCoeff) * (Xw - Xo);
    Xc = Xo + contractionCoeff * (Xw - Xo);

    agent.s.Xc.c [c] = SeInDiSp  (Xc, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xc.c [c];
  }

  agent.s.operation = contraction;
}
//——————————————————————————————————————————————————————————————————————————————

对于 “Levy 航班”，我们应用了 Flying 方法，该方法针对 “agent” 执行飞行操作，目标是按照随机分布，将单纯形的顶点推进到搜索空间中的新位置，即概率集中在更接近最佳全局解的位置，概率递减至 0，朝向所研究空间的边界。

应用 Flying 方法后，为 agent.s.operation 设置 “reflection” 操作，如此在迭代中执行算法的后续逻辑，因已经执行了反射操作。
将 SeInDiSp 应用于 Xr，从而确保它在 rangeMin[c] 至 rangeMax[c] 的有效范围内，步长为 rangeStep[c]。结果保存在 agent.s.Xr.c[c] 之中。

因此，Flying 方法针对活体执行“飞行”操作，基于全局最佳解的当前坐标，和随机生成的值更改其坐标。这允许活体探索解空间的新区域，且具有发现更优解的潜力。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Flying (S_Agent &agent, int indW)
{
  for (int c = 0; c < coords; c++)
  {
    double r1 = RNDfromCI (-1.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);
    r2 = pow (r2, -2.0);

    if (r1 > 0.0) Xr = cB [c] + Scale (r2, 0.0, 1.0, 0.0, rangeMax [c] - cB [c], false);
    else          Xr = cB [c] - Scale (r2, 0.0, 1.0, 0.0, cB [c] - rangeMin [c], false);

    //Xr = RNDfromCI (rangeMin [c], rangeMax [c]);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

NM 测试台结果：

C_AO_NMm:5;1.0;2.0;0.5
=============================
5 Rastrigin's; Func runs 10000 result: 77.96849465506082
Score: 0.96607
25 Rastrigin's; Func runs 10000 result: 61.68192953373487
Score: 0.76427
500 Rastrigin's; Func runs 10000 result: 50.62713783555849
Score: 0.62730
=============================
5 Forest's; Func runs 10000 result: 0.9552378700292385
Score: 0.54033
25 Forest's; Func runs 10000 result: 0.45877475613538293
Score: 0.25951
500 Forest's; Func runs 10000 result: 0.09902427974784639
Score: 0.05601
=============================
5 Megacity's; Func runs 10000 result: 5.6
Score: 0.46667
25 Megacity's; Func runs 10000 result: 2.304
Score: 0.19200
500 Megacity's; Func runs 10000 result: 0.40280000000000005
Score: 0.03357
=============================
All score: 3.90573

基于算法结果，我们可以注意到在平滑的 Rastrigin 函数上取得了相当不错的结果。

可视化展现出群体退化和活体集中在一处的迹象。利用 “Levy 航班” 在一定程度上改善了这种状况。这在相应坐标的各个点上很明显。收缩图不形是很稳定。我仅可视化了每个函数的前两个测试，因为具有 1000 个变量的第三个测试运行时间太长，以至于无法在 GIF 中显示它。

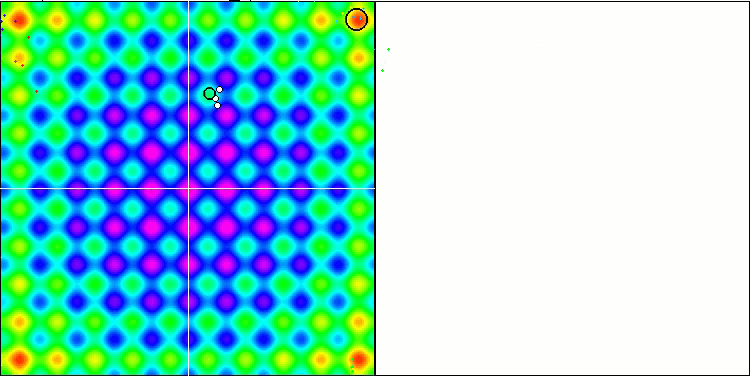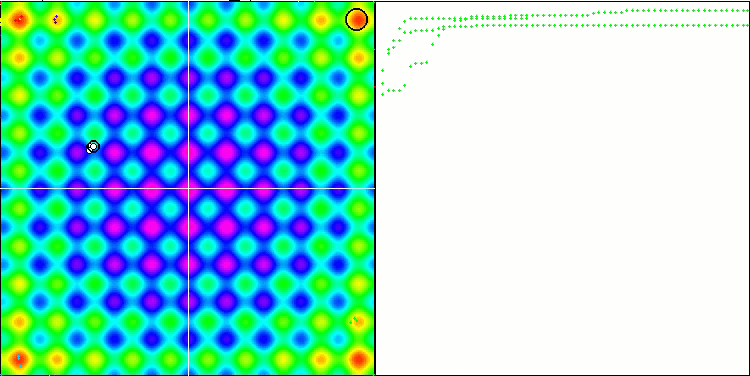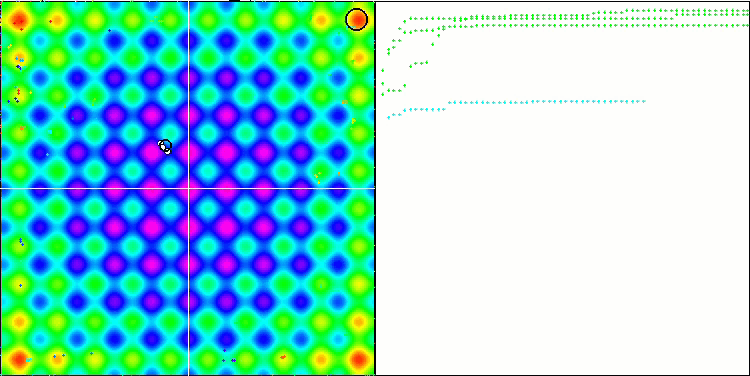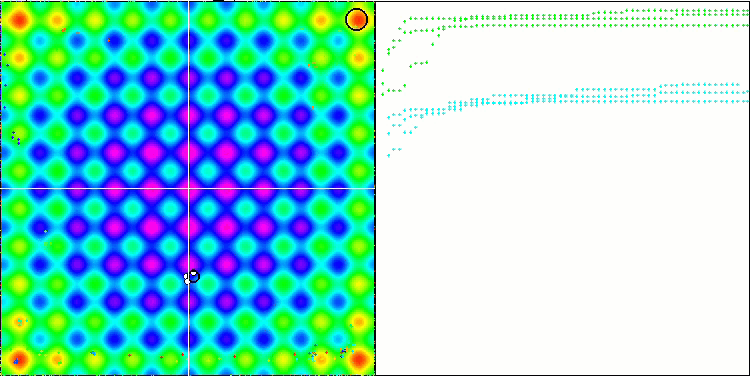
  NMm 基于 Rastrigin 测试函数。

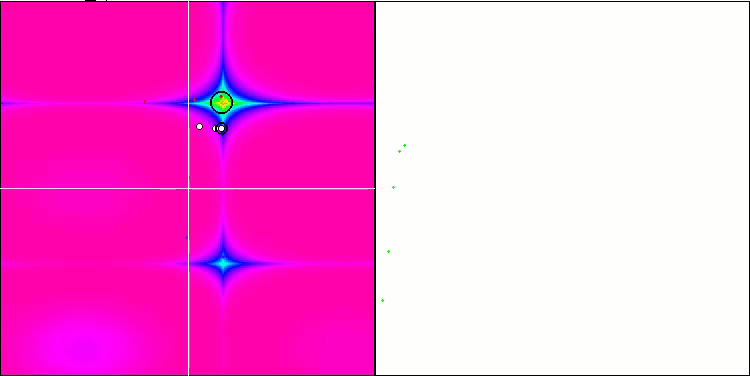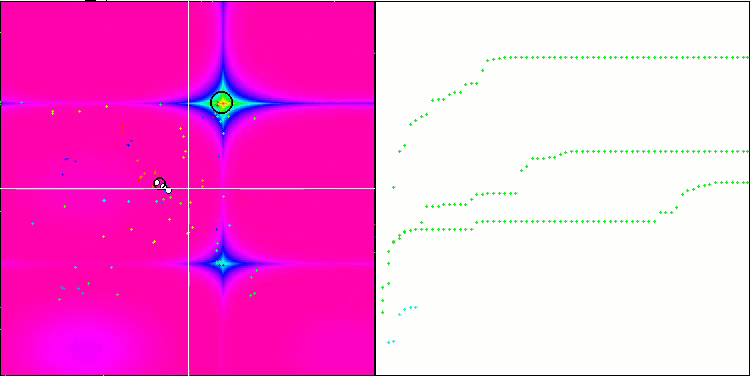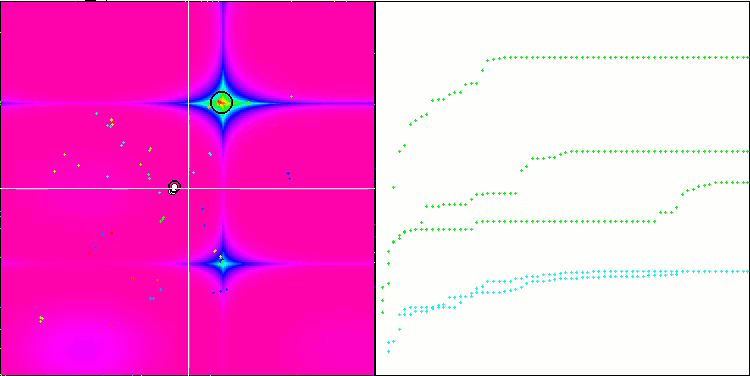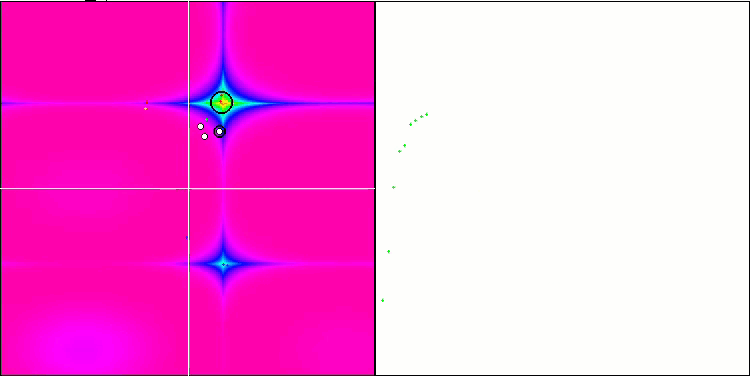
  NMm 基于 Forest 测试函数。

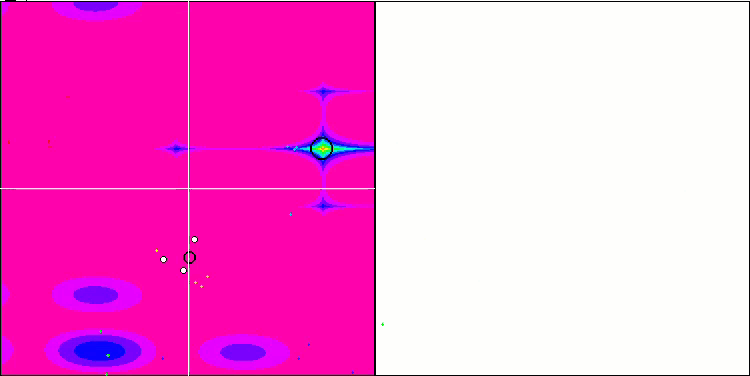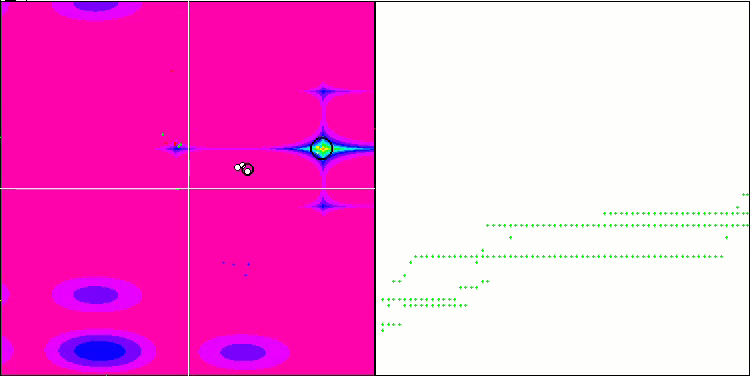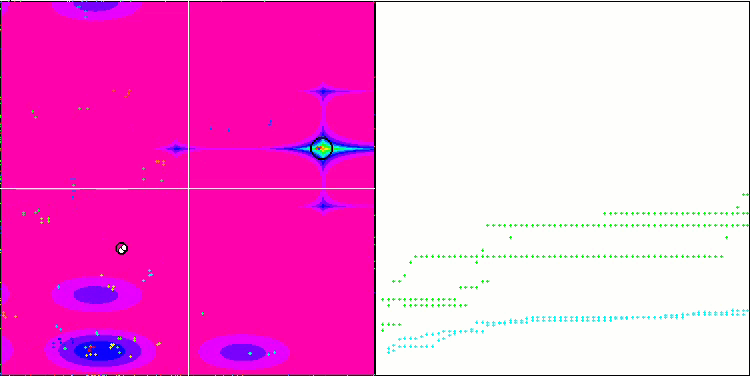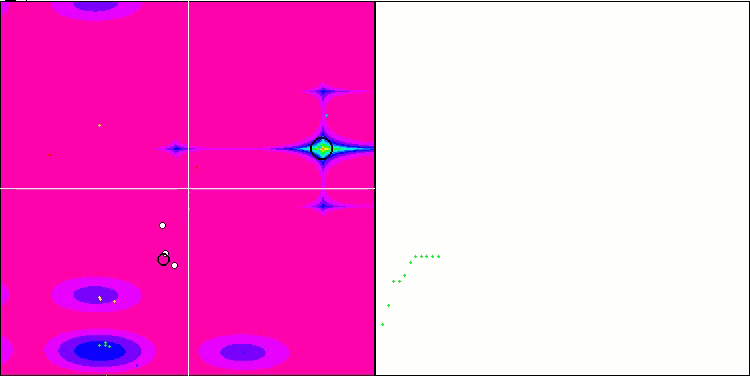
  NMm 基于 Megacity 测试函数。

尽管其有许多短处，但 Nelder-Mead 方法算法最终排在第 9 位。

#	AO	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	随机扩散搜索 M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SSG	树苗播种和生长	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
3	DE	差分进化	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
4	HS	谐声搜索	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
5	IWO	入侵性杂草优化	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
6	ACOm	蚁群优化 M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
7	MEC	心智进化计算	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
8	SDOm	螺旋动力学优化 M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
9	NMm	Nelder-Mead 方法 M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.21903	0.92437	0.46088	0.25658	0.16810	0.88555	39.660
10	COAm	布谷鸟优化算法 M	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	萤火虫算法 M	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	人工蜂群	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	蝙蝠算法	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	收费系统搜索	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	重力搜索算法	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	细菌觅食优化	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	类电磁算法	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	蛙跳	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	MA	猴子算法	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
20	FSS	鱼群搜索	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
21	IWDm	智能水滴 M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
22	PSO	粒子群优化	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
23	RND	随机	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
24	GWO	灰狼优化器	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

总结

Nelder-Mead 算法在当今重优化问题中用处不大，因为它需要在初始阶段计算单纯形每个顶点的适应度函数，这否定了它用于多维搜索空间的能力，故此不推荐使用该算法，尽管它的结果相对较好，及在评级表格中所处的位置。

SDS 算法已被从表格中删除，仅保留其修改版本。

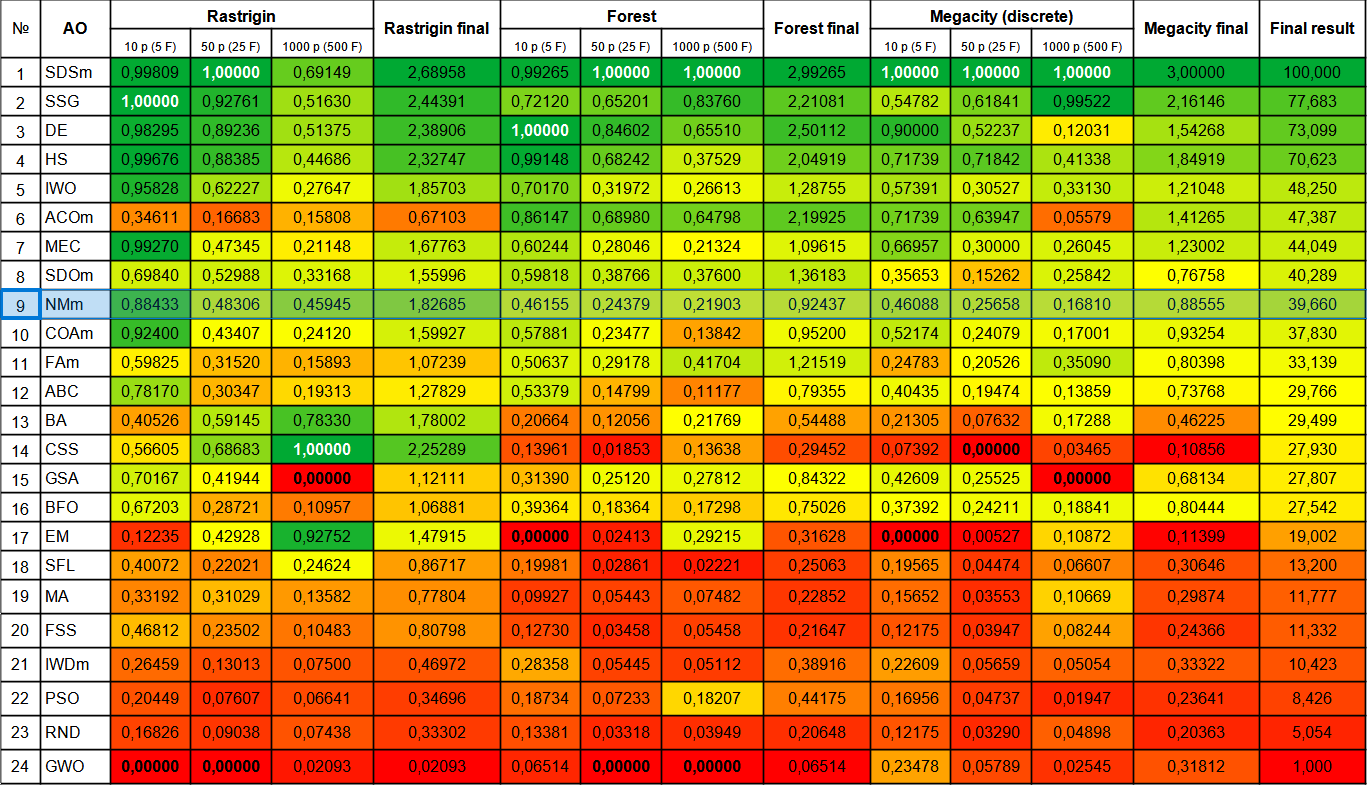
图例 2. 算法的颜色渐变是根据相关测试

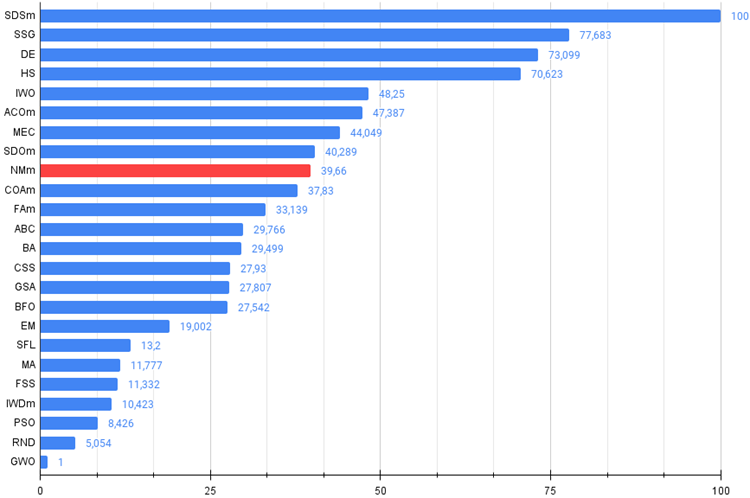
图例 3. 算法测试结果的直方图（标尺从 0 到 100，越多越好，

存档包含文章中应用的计算方法评级表格的脚本）。

改编的 Nelder-Mead（NMm）算法的优缺点：

优势：

1. 少量外部参数。
2. 在变量数量较少的平滑函数上取得良好的结果。
   

缺点：

1. 复杂的实现。
2. 由于需要预先计算所有单纯形顶点的适用度，因此难以与第三方应用程序一起使用。
3. 运算速度低。
4. 可伸缩性非常差。
5. 结果高度分散。
6. 有陷入局部极值的倾向。

请注意，优点和缺点与单纯形搜索的特定改编版本相关。由于结果太弱，因此在表格中包括常规 NM 版本没有意义。

本文附有一个存档，其中包含前几篇文章中讲述的算法代码的当前更新版本。文章作者不对规范算法讲述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中呈现的结论和论断是基于实验的结果。