接受者操作特征（ROC）曲线入门

MetaTrader 5 — 示例 | 3 十二月 2025, 15:50

432

Francis Dube

引言

接受者操作特征（ROC）图是一种基于性能来可视化、组织和选择分类器的方法。ROC 图源于信号检测理论，已被用于说明分类器的真正例率与假正例率之间的权衡。除了一般用作绘制性能图的工具外，ROC 曲线还展现出一些特性，使其在类别分布不均和分类错误成本差异显著的领域中尤其有价值。这对于应用于金融时间序列数据集的分类器来说，尤其具有相关性。

尽管 ROC 图的概念框架很直观，但实际应用中却揭示了值得仔细考虑的复杂性。此外，在它们的实际应用中，也存在一些常见的误解和潜在的误区。本文旨在提供关于 ROC 曲线的基础入门，并作为其在评估分类器性能方面的应用实践指南。

二元分类的表述

许多现实世界的应用都涉及二元分类问题，即实例属于两个互斥且穷尽的类别之一。这种场景的一个普遍实例是，当定义了一个单一的目标类别时，每个实例被归类为要么属于该类别，要么属于其补集。例如，考虑雷达信号分类，屏幕上检测到的轮廓被归类为坦克（目标类别）或非坦克物体。同样地，信用卡交易可以被归类为欺诈（目标类别）或合法。

是目标吗？

这种二元分类问题的特定表述，其特征是识别一个单一的目标类别，构成了后续分析的基础。这里采用的方法不是将实例明确分配到两个不同的类别之一，而是专注于确定一个实例是否属于指定的目标类别。虽然所使用的术语，即引用“目标”及其补集，可能让人联想到军事含义，但这个概念是广泛适用的。目标类别可以代表各种实体，例如恶性肿瘤、成功的金融交易，或者如前所述的欺诈性信用卡交易。其本质特征是主要关注的类别与所有其他可能性之间的二元性。

混淆矩阵

对于应用于测试数据集的给定分类器，有四种可能的结果。如果一个属于正类的实例被分类为正类，则它被指定为真正例（TP）。相反，如果它被分类为负类，则它被指定为假负例（FN）。类似地，如果一个属于负类的实例被分类为负类，则它被指定为真负例（TN）；如果被分类为正类，则它被指定为假正例（FP）。这四个值构成了一个 2x2 的混淆矩阵，也称为列联表。

混淆矩阵

该矩阵概括了实例在这四种结果中的分布，并作为许多常用性能指标的基础，其中一些指标包括：

命中率或灵敏度或召回率：被正确分类为目标的目标实例所占的比例，计算公式为 TP / (TP + FN)。

误报率（I 类错误率）：被错误分类为目标的非目标实例所占的比例，计算公式为 FP / (TN + FP)。

漏报率（II 类错误率）：被错误分类为非目标的目标实例所占的比例，计算公式为 FN / (TP + FN)。

特异度：被正确分类为非目标的非目标实例所占的比例，计算公式为 TN / (TN + FP)。

维基百科有一个有用的图表，其中显示了从混淆矩阵衍生出的广泛使用的性能指标列表。

混淆表

ROC 曲线

大多数二元分类模型的内部工作机制是，进行数值预测，然后将其与一个预定的阈值进行比较。如果预测值等于或超过此阈值，则该实例被分类为目标；否则，它被分类为非目标。很明显，阈值会影响所有上述的性能度量。将阈值设置在等于或低于最小可能预测值的位置，会导致所有实例都被分类为目标，从而产生完美的命中率，但同时也有相应糟糕的误报率。

决策机制

相反，将阈值设置在高于最大可能预测值的位置，会导致所有实例都被分类为非目标，从而导致零命中率和完美的零误报率。最佳的阈值值位于这两个极端之间。通过系统地改变阈值跨越其整个范围，命中率和误报率都会各自遍历从 0 到 1 的范围，其中一个指标的改善以牺牲另一个指标为代价。通过将这两个率相互对应绘制（阈值作为隐含参数）而生成的曲线，被称为受试者工作特征曲线。

ROC 曲线通常以误报率为横轴，命中率为纵轴来绘制。考虑一个分类模型，它产生随机的数值预测，与案例的真实类别不相关。

随机性能

在这种情况下，在所有阈值上，命中率和误报率平均而言将是等效的，从而产生一条近似于从图的左下角到右上角的对角线的 ROC 曲线。例如，如果一个分类器以 50% 的概率随机将一个实例分配到正类，那么它预计能正确分类 50% 的正类实例和 50% 的负类实例，从而在 ROC 空间中得到坐标点 (0.5, 0.5)。

类似地，如果分类器以 90% 的概率将一个实例分配到正类，那么预计它能正确分类 90% 的正类实例；然而，假正例率也会相应地增加到 90%，从而产生坐标点 (0.9, 0.9)。因此，一个随机分类器将产生一个沿着对角线移动的 ROC 点，其在图上的位置取决于它预测正类的频率。为了实现超越随机猜测的性能（表现为位于 ROC 空间上三角区域的位置），分类器必须利用数据中存在的、富含信息的模式。

完美性能

相反，一个完美的模型，其特征是存在一个阈值，能精确地将目标（预测值等于或超过阈值）与非目标（预测值低于阈值）分离开来，它展现出一条独特的 ROC 曲线。随着参数化阈值从其最小值过渡到最佳阈值，误报率从 1 降至 0，而命中率则始终保持为 1。随后，参数化阈值的增加导致命中率从 1 降至 0，而误报率保持为 0。这导致 ROC 曲线形成一条从右上角到左上角，然后再到左下角的路径。

中等性能

性能介于这两个极端之间的模型，其产生的 ROC 曲线将位于对角线和左上角之间。曲线偏离对角线、趋向左上角的程度，标志着模型的性能。一般来说，如果一个 ROC 图上的点具有更高的真正例率、更低的假正例率，或两者兼而有之，那么它就被认为优于另一个点。位于 ROC 图左侧、靠近横轴的分类器，可以被描述为保守的。

这些分类器表现出一种倾向，只有在面对实质性证据时才会做出正类分类，这导致了较低的假正例率，但常常伴随着较低的真正例率。相反，位于 ROC 图右上角的分类器，其特征是不那么保守，倾向于即使在证据最少的情况下也做出正类分类，这导致了较高的真正例率，但常常伴随着较高的假正例率。在许多负类实例占主导地位的现实世界领域中，分类器在 ROC 图左侧区域的性能变得愈发相关。

位于 ROC 空间右下三角区域的分类器，其性能劣于随机猜测。因此，在 ROC 图中，这个区域通常没有数据点。一个分类器的否定，被定义为将其对所有实例的分类决策反转，这会导致其真正例分类变为假负例错误，其假正例分类变为真负例分类。因此，任何在右下三角形内产生点的分类器，都可以通过否定，被转换以在左上三角形内产生一个对应的点。一个位于对角线上的分类器，可以被描述为不具备关于类别成员的可辨别信息。相反，一个位于对角线下方的分类器，可以被解释为拥有信息丰富的模式，只是以错误的方式应用了它们。

ROC 性能指标

虽然对 ROC 曲线图的目视检查可以提供初步的见解，但通过对相关性能指标的分析，可以更全面地理解模型性能。在进行详细分析之前，有必要阐明表征 ROC 曲线的数据结构。为了便于理解，这里提供了一个说明性示例。

下表展示了一个从分类模型中得出的假设性 ROC 性能指标样本。此示例使用了可通过 Sklearn Python 库访问的鸢尾花数据集。遵循目标/非目标范式，分类目标被限制为识别单一的鸢尾花变种。具体来说，如果将 setosa（山鸢尾）指定为目标，则所有其他变种都被归类为非目标。与传统的分类方法一致，该模型被训练为对非目标输出 0，对目标输出 1。样本标签也相应地进行了转换。值得注意的是，其他的标记方案也是可行的。

对于决策阈值范围内的每个阈值，都会生成一个混淆矩阵来计算真正例率和假正例率。这些计算利用了来自训练好的预测模型的输出概率或决策函数值，相应的阈值决定了类别归属。本文中呈现的表格是使用脚本 ROC_curves_table_demo.mq5 生成的。

KG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH
NF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195
DI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708
OI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556
GI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334
GH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221
RH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211
IK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935
CK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736
NK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715
EJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645
DJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552
HJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534
NM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417
GM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155
CL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943
LL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699
NL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593
KO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660
CN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489
OQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420
NQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619
GQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375
PP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087
OP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257
RP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124
RS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349
KS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523
JR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147
HE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841
QE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488
DE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058
MG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819
JG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744
EG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683
LF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635
CF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589
KF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494
NH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416
PH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347
LH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244
KK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238
HK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225
LK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213
PJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192
CJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189
EM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177
IM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157
HM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132
EL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127
DL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119
KL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104
DO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102
RO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085
DN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069
HN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062
HQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052
DQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048
FQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044
MP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028
LP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026
NS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015
ES      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012
MS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007
QR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004
CR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002

对表格化的 ROC 曲线数据的审视揭示了一个清晰的趋势：随着决策阈值的增加，TPR（真正例率）和 FPR（假正例率）都表现出从 1 到 0 的下降。鉴于模型固有的预测能力，FPR 的减少速度比 TPR 更快。值得注意的是，FPR 降至零时，TPR 仍保持为 1。因此，除非 I 类错误和 II 类错误的相对成本存在显著差异，否则最佳阈值预计将位于由这两个极值所定义的区间内。同样重要的是，观察到表格中包含了特异度，它等同于真负例率（TNR），并且是 FPR 的补数。

在许多情况下，可以通过直接检查真正例率和假正例率列来确定最佳阈值。通过包含目标和非目标的样本大小，增强了此过程的可解释性。当与 I 类和 II 类错误相关的成本大致相等时，平均误差可作为一个合适的标量性能指标。该指标在表中表示为 M_E，是误报率和漏报率的算术平均值。

然而，在这些错误类型的成本存在显著差异的场景中，平均误差指标的相关性就会降低。精确率尤其在不同应用中是一个关键的性能指标。通常，目标检测的精确率是主要关注点。在某些情况下，非目标识别的精确率也可能相关。对于准确目标检测这一目标，标记为 PREC 的列提供了相关信息。相反，标记为 NPREC 的列与非目标的精确识别相关。

该表格还提供了额外的性能指标，包括准确率（ACC）和平衡准确率（B_ACC）。准确率定义为在总数据集中，被正确分类的实例（包括真正例和真负例）所占的比例。平衡准确率，计算为灵敏度和特异度的算术平均值，用于减轻类别不平衡的影响，这是一种指目标和非目标类别的样本量存在显著差异的状况。在讨论 ROC 曲线下面积之前，有必要审视用于生成上述 ROC 指标表的计算过程。具体来说，将分析负责计算这些与 ROC 相关指标的代码。

相关的代码被封装在头文件 roc_curves.mqh 中，该文件定义了一系列函数和 conf_stats 数据结构。conf_stats 结构体作为一个容器，用于存储从混淆矩阵中导出的各种参数。

//+------------------------------------------------------------------+
//|  confusion matrix stats                                          |
//+------------------------------------------------------------------+
struct conf_stats
  {
   double              tn;                //true negatives
   double              tp;                //true positives
   double              fn;                //false negatives
   double              fp;                //false positives
   double              num_targets;       //number of actual positive labels(target)
   double              num_non_targets;   //number of acutal negative labels(non targets)
   double            tp_rate;             //true positives rate - hit rate -  recall - sensitivity
   double            fp_rate;             //false positives rate - fall out - type 1 error
   double            fn_rate;             //false negatives rate - miss rate - type 2 error
   double            tn_rate;             //true negatives rate - specificity
   double            precision;           //precision - positive predictve value
   double            null_precision;      //null precision - false discovery rate
   double            prevalence;          //prevalence
   double            lr_plus;             //positive likelihood ratio
   double            lr_neg;              //negative likelihood ratio
   double            for_rate;            //false omission rate
   double            npv;                 //negative predictive value
   double            acc;                 //accuracy
   double            b_acc;               //balanced accuracy
   double            f1_score;            //f1 score
   double            mean_error;          //mean error
  };

conf_stats 结构体作为 roc_stats() 函数中的主要参数，用于存储从混淆矩阵导出的评估结果。该评估在一个包含真实标签、相应预测值和指定阈值的数据集上进行。真实标签以向量形式提供，记为 targets，作为第二个参数。第三个参数 probas，代表了预测概率或决策变量的向量。

//+------------------------------------------------------------------+
//| defines                                                          |
//+------------------------------------------------------------------+
bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0)
  {
   vector all_labels = np::unique(targets);

   if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return false;
     }
//---
   cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0;
//---
   for(ulong i = 0; i<targets.Size(); i++)
     {
      if(probas[i]>=threshold && long(targets[i]) == target_label)
         cmat.tp++;
      else
         if(probas[i]>=threshold && long(targets[i]) == non_target_label)
            cmat.fp++;
         else
            if(probas[i]<threshold && long(targets[i]) == target_label)
               cmat.fn++;
            else
               cmat.tn++;
     }
//---
   cmat.num_targets = cmat.tp+cmat.fn;
   cmat.num_non_targets = cmat.fp+cmat.tn;
//---
   cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na");
   cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na");
   cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na");
   cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na");
   cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na");
   cmat.null_precision = 1.0 - cmat.precision;
   cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na");
   cmat.npv = 1.0 - cmat.for_rate;
   cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na");
   cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na");
   cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0);
   cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na");
   cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0);
//---
   return true;
//---
  }

threshold 参数定义了用于划分类别成员身份的临界值。最后两个参数分别用于显式指定目标和非目标的标签。该函数返回一个布尔值，true 表示成功执行，false 表示发生错误。

//+------------------------------------------------------------------+
//| roc table                                                        |
//+------------------------------------------------------------------+
matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0)
  {
   matrix roctable(probas.Rows(),10);

   conf_stats mts;

   vector probs = probas.Col(target_probs_col);

   if(!np::quickSort(probs,false,0,probs.Size()-1))
      return matrix::Zeros(1,1);

   for(ulong i = 0; i<roctable.Rows(); i++)
     {
      if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label))
         return matrix::Zeros(1,1);
      roctable[i][0] = mts.tp_rate;
      roctable[i][1] = mts.fp_rate;
      roctable[i][2] = mts.fn_rate;
      roctable[i][3] = mts.tn_rate;
      roctable[i][4] = mts.precision;
      roctable[i][5] = mts.null_precision;
      roctable[i][6] = mts.mean_error;
      roctable[i][7] = mts.acc;
      roctable[i][8] = mts.b_acc;
      roctable[i][9] = probs[i];
     }
//---
   return roctable;
  }

roc_table() 函数生成一个封装了 ROC 曲线数据的矩阵。其输入参数包括一个真实类别标签的向量、一个预测概率或决策变量的矩阵，以及一个用于在多列矩阵中确定类别成员身份的列索引的无符号长整型整数。最后两个参数定义了目标和非目标的标签。如果发生错误，该函数将返回一个 1x1 的零矩阵。必须注意的是，roc_stats() 和 roc_table() 都是专门为二元分类模型设计的。不遵守此要求将导致一条错误消息。

//+------------------------------------------------------------------+
//| roc curve table display                                          |
//+------------------------------------------------------------------+
string roc_table_display(matrix &out)
  {
   string output,temp;

   if(out.Rows()>=10)
     {
      output = "TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH";
      for(ulong i = 0; i<out.Rows(); i++)
        {
         temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf",
                             out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]);
         StringAdd(output,temp);
        }
     }
   return output;
  }

roc_table_display() 函数接受一个矩阵参数（理想情况下是先前调用 roc_table() 的输出），并将数据格式化为表格形式的字符串表示。

ROC 曲线下面积

ROC 曲线下面积（AUC）为分类器性能提供了一个简洁的单值指标，解决了完整 ROC 曲线细节过多的问题。虽然 ROC 曲线直观地描绘了真正例率和假正例率之间的权衡，但 AUC 量化了模型区分不同类别的整体能力。一个无用的模型，在 ROC 图上表现为一条对角线，其 AUC 为 0.5，表示随机性能。相反，一个完美的模型，其 ROC 曲线紧贴左上角，AUC 达到 1.0。因此，AUC 越高，表示模型性能越好。计算 AUC 涉及确定 ROC 曲线下方的面积，并且由于测试数据集中固有的统计变异，通常简单的求和就足以进行精确估计，无需进行复杂的数值积分。

AUC 具有一个重要的统计学解释：它代表了一个分类器将随机抽取的正例实例排在随机抽取的负例实例之上的概率。这一特性使得 AUC 与 Wilcoxon 秩和检验（也称为 Mann-Whitney U 检验）等价。

Wilcoxon 秩和检验是一种非参数统计方法，用于评估两个独立组之间的差异，而不假设数据服从正态分布。它通过对所有观测值进行排序，并比较组间的秩和，从而评估中位数的差异。

此外，AUC 与基尼系数有着内在的联系。具体来说，基尼系数是由机会对角线与 ROC 曲线之间面积的两倍得出的。基尼系数是衡量分布不平等程度的指标，量化了分布内的离散程度，范围从 0（完全平等）到 1（最大不平等）。在收入分配的背景下，它反映了收入水平的差距。从图形上看，基尼系数定义为洛伦兹曲线与完全平等线之间的面积，与完全平等线下面积的比值。

在 roc_curves.mqh 中定义的函数 roc_auc() 计算二元分类问题的 AUC，并可选择将计算限制在特定的最大 FPR 范围内。它以真实类别标签和预测概率作为输入，以及一个可选的目标标签和最大 FPR。如果最大 FPR 为 1.0，它计算标准的 AUC。否则，它会计算 ROC 曲线，使用 searchsorted 找到曲线上对应于最大 FPR 的点，在该点处对 TPR 进行插值，然后使用梯形法则计算截至该最大 FPR 的部分 AUC。最后，它将这个部分 AUC 标准化为一个介于 0.5 和 1.0 之间的分数，从而有效地提供了在指定 FPR 范围内的分类器性能度量。

//+------------------------------------------------------------------+
//|  area under the curve                                            |
//+------------------------------------------------------------------+
double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0)
  {
   vector all_labels = np::unique(true_classes);

   if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   if(max_fpr == 1.0)
     {
      vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
      return auc[0];
     }

   matrix tpr,fpr,threshs;

   if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs))
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   vector xp(1);
   xp[0] = max_fpr;
   vector stop;

   if(!np::searchsorted(fpr.Row(0),xp,true,stop))
     {
      Print(__FUNCTION__, " ", __LINE__, " searchsorted failed ");
      return EMPTY_VALUE;
     }

   vector xpts(2);
   vector ypts(2);

   xpts[0] = fpr[0][long(stop[0])-1];
   xpts[1] = fpr[0][long(stop[0])];
   ypts[0] = tpr[0][long(stop[0])-1];
   ypts[1] = tpr[0][long(stop[0])];

   vector vtpr = tpr.Row(0);
   vtpr = np::sliceVector(vtpr,0,long(stop[0]));
   vector vfpr = fpr.Row(0);
   vfpr = np::sliceVector(vfpr,0,long(stop[0]));

   if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1))
     {
      Print(__FUNCTION__, " ", __LINE__, " error  ", GetLastError());
      return EMPTY_VALUE;
     }

   vfpr[vfpr.Size()-1] = max_fpr;

   vector yint = np::interp(xp,xpts,ypts);


   vtpr[vtpr.Size()-1] = yint[0];

   double direction = 1.0;

   vector dx = np::diff(vfpr);

   if(dx[dx.ArgMin()]<0.0)
      direction = -1.0;

   double partial_auc = direction*np::trapezoid(vtpr,vfpr);

   if(partial_auc == EMPTY_VALUE)
     {
      Print(__FUNCTION__, " ", __LINE__, " trapz failed ");
      return EMPTY_VALUE;
     }

   double minarea = 0.5*(max_fpr*max_fpr);
   double maxarea = max_fpr;

   return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea));
  }

max_fpr 参数有助于计算 ROC 曲线的部分面积，从而能够评估分类器在定义的 FPR 值范围内的性能。此功能在强调较低 FPR 阈值下的性能的场景中尤为突出。此外，在分析不平衡数据集时也很有优势，因为在这种情况下，ROC 曲线可能会受到大量真负例的过度影响。使用此参数可以对曲线的相关区域进行重点评估。

虽然接收者操作特征（ROC）曲线为分类器评估提供了一个有用的框架，但在确定分类器的绝对优势时，其应用需要仔细考虑，尤其是在纳入错误分类成本时。尽管 AUC 提供了一个评估分类器质量的指标，但性能的比较评估需要一种更细致的方法。为了充分解决成本考虑，有必要回到基础的混淆矩阵。

传统的分类范式通常优先考虑准确率最大化，隐含地假设所有错误分类的成本是统一的。相比之下，成本敏感分类承认与不同错误类型相关的差异成本，旨在最小化错误的总体成本，而不仅仅是优化准确率。例如，在一个用于识别有前途的投资股票的分类器中，错失机会（假负例）的成本可能被认为不如假正例的成本严重。为每种错误分类类型分配成本，就会产生一个成本矩阵。该矩阵阐明了与不同预测结果相关的成本，指明了因错误预测（如假正例和假负例）而产生的惩罚或损失，并可能包含正确预测的成本。下面展示了一个假设的混淆矩阵及其对应的成本矩阵。

成本矩阵

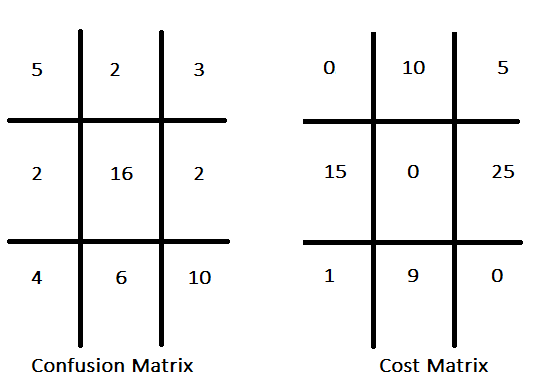
成本矩阵通常在其对角线上具有零值，这表示与正确预测相关的零成本，这是一个普遍但非强制性的约定。给定一个为所有错误分类类型定义的成本结构，混淆矩阵中封装的信息可以聚合为一个单一的性能指标。一个基本方法是将每种错误分类类型的频率乘以其相应的成本，然后将这些乘积相加。然而，该指标的有效性取决于数据集的类别比例是否能准确反映现实世界应用中遇到的情况。

一个更稳健的成本敏感性能度量是每个样本的期望成本。该指标通过将混淆矩阵的样本计数按其各自的行总和进行归一化得出，从而产生给定真实类别下被分类类别的条件概率。然后，将这些概率乘以成本矩阵中相应的成本，并在每行上将乘积相加，得出每个类别成员的期望成本。随后，这些特定于类别的成本按每个类别中样本的期望比例进行加权，然后相加，产生每个样本的总期望成本。估计现实世界场景中的期望类别比例，需要对部署环境中数据的底层分布有全面的了解。用于此估计的方法包括：

历史数据分析，即检查现有记录以提供可靠的类别比例估计。例如，在医疗诊断中，患者记录可以阐明疾病的患病率。

咨询领域专家，其专业知识可以完善或验证通过其他方式获得的估计。

当可以收集新数据时，实施代表性抽样技术，确保样本能准确反映现实世界的分布，特别是在不平衡的数据集中。分层抽样可以进一步确保所有类别得到充分代表，即使在分布不均的情况下也是如此。

一个类别中样本的期望比例在形式上等同于先验概率。在二元分类的特定背景下，令
q 表示一个样本属于目标类别的先验概率。进一步，定义 p1 为 I 类错误（假正例）的概率，c1 代表其相关成本；p2 为 II 类错误（假负例）的概率，c2 代表其相关成本。在许多应用中，q 可以通过理论或经验手段确定，成本 c1 和 c2 是已知的，无论是精确的还是合理的近似值。因此，这三个量可以被视为固定参数。错误概率 p1 和 p2 由分类阈值决定。期望成本由以下公式表示。

重新整理此方程得到：

重排后的成本公式

这证明了对于任何给定期望成本，p1 和 p2 之间存在线性关系。当这种线性关系在 ROC 曲线上进行图形化表示时，其斜率由先验概率 q 和成本比 c2/c1 决定。期望成本的变化会产生一组平行线，位置更低且更靠右的线表示更高的成本。该线与 ROC 曲线在两点相交，表明有两个阈值产生等效但次优的成本。完全位于 ROC 曲线左上方和右侧的线代表了模型无法达到的性能。与 ROC 曲线相切的线表示可实现的最优成本。

这一分析强调，AUC 不一定提供分类模型实际性能的确定性度量。虽然 AUC 是一个有效的整体质量指标，但在考虑运营成本时，其效用会降低，因为它在成本敏感的应用中可能产生误导性的结论。

多于两个类别的决策问题

将 ROC 曲线框架扩展到多类别分类需要采用特定的适应策略。主要采用两种方法：一对一，也称为一对所有，以及一对一方法。OvR 策略通过将每个类别视为正类，而将其余所有类别合并为负类，从而将多类别问题转化为多个二元分类任务，对于 n 个类别，这会产生 n 条 ROC 曲线。相反，OvO 方法为所有可能的类别对构建二元分类问题，产生 n(n-1)/2 条 ROC 曲线。

为了聚合从这些二元分类中得出的性能指标，采用了平均技术。微平均通过考虑所有类别中的所有实例来计算全局 TPR 和 FPR，从而为每个实例分配相等的权重。另一方面，宏平均独立计算每个类别的 TPR 和 FPR，然后对它们求平均，从而为每个类别分配相等的权重，这种方法在特定于类别的性能至关重要时特别有用。因此，多类别 ROC 曲线的解释取决于所选的分解策略（OvR 或 OvO）和平均方法（微平均或宏平均），因为这些选择显著影响最终的性能评估。

MQL5 中用于 ROC 曲线和 AUC 的内置函数

在 MQL5 中，受试者工作特征（ROC）曲线和曲线下面积（AUC）的计算通过专用功能得以实现。The

ReceiverOperatingCharacteristic()向量方法用于生成 ROC 曲线可视化所需的必要值。该方法在代表真实类别标签的向量上操作。第一个参数是一个概率或决策值的矩阵，其结构为列对应于类别数量。第二个参数，一个 ENUM_AVERAGE_MODE 枚举的变量，指定了平均方法。值得注意的是，此函数仅支持 AVERAGE_NONE、AVERAGE_BINARY 和 AVERAGE_MICRO。成功执行后，假正例率（FPR）、真正例率（TPR）和相关的阈值会被写入指定的矩阵，即最后三个参数。该方法返回一个指示执行成功的布尔值。

AUC 计算通过 ClassificationScore() 向量方法执行。与 ROC 方法类似，它在真实类别标签的向量上调用，并需要一个预测概率或决策值的矩阵。第二个参数，一个 ENUM_CLASSIFICATION_METRIC 枚举，必须设置为 CLASSIFICATION_ROC_AUC 以指定 AUC 计算。与 ROC 方法不同，此函数支持 ENUM_AVERAGE_MODE 的所有值。该方法返回一个计算出的面积的向量，其基数取决于平均模式和数据集中存在的类别数量。

为了阐明各种平均模式的影响，开发了 ROC_Demo.mq5 脚本。该脚本利用鸢尾花数据集和一个逻辑回归模型来解决用户可配置的二元或多类别分类问题。完整的脚本代码如下提供。

//+------------------------------------------------------------------+
//|                                                     ROC_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<logistic.mqh>
#include<ErrorDescription.mqh>
#include<Generic/SortedSet.mqh>
//---
enum CLASSIFICATION_TYPE
  {
   BINARY_CLASS = 0,//binary classification problem
   MULITI_CLASS//multiclass classification problem
  };
//--- input parameters
input double   Train_Test_Split = 0.5;
input int      Random_Seed = 125;
input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS;
input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj());
//---
   matrix data = np::readcsv("iris.csv");
   data = np::sliceMatrixCols(data,1);
//---
   if(classification_problem == BINARY_CLASS)
      data = np::sliceMatrixRows(data,0,100);
//---
   ulong rindices[],trainset[],testset[];
   np::arange(rindices,int(data.Rows()));
//---
//---
   if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset))
     {
      Print(__LINE__, "  error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   CSortedSet<ulong> test_set(rindices);
//---
   test_set.ExceptWith(trainset);
//---
   test_set.CopyTo(testset);
//---
   matrix testdata = np::selectMatrixRows(data,testset);
   matrix test_predictors = np::sliceMatrixCols(testdata,0,4);
   vector test_targets = testdata.Col(4);
   matrix traindata = np::selectMatrixRows(data,trainset);
   matrix train_preditors = np::sliceMatrixCols(traindata,0,4);
   vector train_targets = traindata.Col(4);
//---
   logistic::Clogit logit;
//--
   if(!logit.fit(train_preditors,train_targets))
     {
      Print(" error training logistic model ");
      return;
     }
//---
   matrix y_probas = logit.probas(test_predictors);
   vector y_preds = logit.predict(test_predictors);
//---
   vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode);
//---
   if(auc.Size()>0)
      Print(" AUC ", auc);
   else
      Print(" AUC error ", ErrorDescription(GetLastError()));
//---
   matrix fpr,tpr,threshs;
   if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs))
     {
      Print(" ROC error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   string legend;
   for(ulong i = 0; i<auc.Size(); i++)
     {
      string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]);
      StringAdd(legend,temp);
     }

   CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500);
   if(CheckPointer(roc)!=POINTER_INVALID)
     {
      Sleep(7000);
      roc.Destroy();
      delete roc;
      ChartRedraw();
     }
  }
//+------------------------------------------------------------------+

首先，检查一个二元分类问题，平均模式设置为 AVERAGE_BINARY。该模式在目标类别被标记为 1 的假设下计算 ROC 曲线和 AUC，这遵循了 ROC 曲线生成中固有的基本目标/非目标范式。使用这些配置执行脚本所产生的输出表明，AUC 值向量包含一个单一元素。此外，FPR、TPR 和阈值矩阵各自都包含一行。

ROC 演示脚本输出 - 二元分类

MK      0       12:45:28.930    ROC_Demo (Crash 1000 Index,M5)   AUC [1]

要检查标签 1 以外的目标类别的 ROC 曲线和相关 AUC，应将平均模式设置为 AVERAGE_NONE。在此模式下，ReceiverOperatingCharacteristic() 和 ClassificationScore() 函数将每个类别独立地作为目标进行评估，并提供相应的结果。使用 AVERAGE_NONE 和一个二元分类问题执行脚本会产生以下输出。在此实例中，ROC 图显示了两条曲线，代表了 FPR 和 TPR 矩阵中各自行的绘图。还计算了两个 AUC 值。

ROC 演示 - 二元分类 - 无平均

CK      0       16:42:43.249    ROC_Demo (Crash 1000 Index,M5)   AUC [1,1]

结果的呈现与类别标签的顺序相对应。例如，在上述脚本所描绘的二元分类问题中，标签为 0 和 1，TPR、FPR 和阈值矩阵的第一行代表了当标签 0 被视为目标类别时的 ROC 曲线值，而第二行则与标签 1 作为目标相关。此排序约定同样适用于 AUC 值。值得注意的是，这种结果格式在从多类别数据集计算的 ROC 统计中是一致的。在二元分类场景中，使用 AVERAGE_NONE 和 AVERAGE_BINARY 以外的平均选项会调用与多类别数据集处理相对应的计算方法。相反，在多类别分类中，AVERAGE_BINARY 会触发错误。然而，AVERAGE_MICRO、AVERAGE_MACRO 和 AVERAGE_WEIGHTED 都会产生一个单一的、聚合的 AUC 值。

ROC 演示 - 多类别 - 无平均

LL      0       17:27:13.673    ROC_Demo (Crash 1000 Index,M5)   AUC [1,0.9965694682675815,0.9969135802469137]

AVERAGE_MICRO 平均模式通过将独热编码的真实类别矩阵的每个元素视为一个独立的标签，来全局计算 ROC 曲线和 AUC。这种方法通过首先对真实类别标签进行独热编码，生成一个列数对应于类别数量的矩阵，从而将多类别问题转化为二元分类问题。然后，该矩阵与预测的决策值或概率矩阵一起，被扁平化为一个单列结构。随后的 ROC 曲线和 AUC 计算在这些扁平化的容器上执行。此方法产生了涵盖所有类别的综合性能指标，为每个实例分配相等的权重。这在类别显著不平衡的场景中特别有利，可以减轻对多数类的偏见。演示脚本的经验结果说明了这种行为。

ROC 演示 - 多类别 - 微平均

RG      0       17:26:51.955    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9984000000000001]

AVERAGE_MACRO 平均模式采用一种不同的策略来处理类别不平衡。每个类别被独立评估，根据其各自的类别概率计算 AUC。最终的 AUC 则由这些单个 AUC 值的算术平均值导出。值得注意的是，MQL5 文档指出 ReceiverOperatingCharacteristic() 方法不支持 AVERAGE_MACRO。ClassificationScore() 方法在多类别数据集中采用 OvR 技术进行 AUC 计算。使用 AVERAGE_MACRO 执行脚本证实了 AUC 计算成功，而 ROC 曲线生成如预期般失败。

ER      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   AUC [0.997827682838166]
NF      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

AVERAGE_WEIGHTED 平均模式的操作与 AVERAGE_MACRO 类似，除了最终的聚合步骤。它不是简单的算术平均，而是计算加权平均值，其中权重由真实类别标签的类别分布决定。这种方法产生的最终 AUC 值考虑了数据集中的主导类别。与 AVERAGE_MACRO 类似，ReceiverOperatingCharacteristic() 不支持 AVERAGE_WEIGHTED。脚本输出了这种行为的示例。

IN      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9978825995807129]
HO      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

结论

ROC 曲线是用于可视化和评估分类器的有效工具。与准确率、错误率或错误成本等标量指标相比，它们对分类性能提供了更全面的评估。通过将分类器性能与类别偏斜和错误成本解耦，它们相比包括精确率-召回率曲线在内的其他评估方法具有优势。然而，与任何评估指标一样，明智地应用 ROC 图需要对其固有特性和局限性有透彻的理解。预计本文将有助于增进与 ROC 曲线相关的通用知识，并促进社区内采用改进的评估实践。

文件名	文件描述
MQL5/Scripts/ROC_Demo.mq5	用于演示 MQL5 内置 ROC 曲线相关函数的脚本。
MQL5/Scripts/ ROC_curves_table_demo.mq5	演示生成各种基于 ROC 的性能指标的脚本。
MQL5/Include/logisitc.mqh	包含实现逻辑回归的 Clogit 类定义的头文件。
MQL5/Include/roc_curves.mqh	实现用于二元分类性能评估的各种实用程序的自定义函数的头文件。
MQL5/Include/np.mqh	各种向量和矩阵实用程序函数的头文件。
MQL5/Files/iris.csv	鸢尾花数据集的 CSV 文件。