Analyse der Auswirkungen des Wetters auf die Währungen der Agrarländer mit Python

Einleitung: Beziehung zwischen Wetter und Finanzmärkten

In der klassischen Wirtschaftstheorie wurde der Einfluss des Wetters auf das Marktverhalten lange Zeit ignoriert. Doch die in den letzten Jahrzehnten durchgeführten Forschungen haben die herkömmliche Sichtweise völlig verändert. Professor Edward Saykin von der University of Michigan hat in einer Studie aus dem Jahr 2023 gezeigt, dass Händler an Regentagen 27 % zurückhaltendere Entscheidungen treffen als an sonnigen Tagen.

Dies ist besonders in den größten Finanzzentren zu beobachten. An Tagen, an denen die Temperaturen über 30°C liegen, sinkt das Handelsvolumen an der NYSE um durchschnittlich 15 %. An den asiatischen Börsen korreliert der Luftdruck unter 740 mm Hg mit einer erhöhten Volatilität. Lange Schlechtwetterperioden in London führen zu einem spürbaren Anstieg der Nachfrage nach sicheren Anlagen.

In diesem Artikel beginnen wir mit dem Sammeln von Wetterdaten und arbeiten uns bis zur Erstellung eines kompletten Handelssystems vor, das die Wetterfaktoren analysiert. Unsere Arbeit basiert auf realen Handelsdaten der letzten fünf Jahre aus den wichtigsten Finanzzentren der Welt: New York, London, Tokio, Hongkong und Frankfurt. Mithilfe moderner Datenanalyse und maschineller Lernwerkzeuge werden wir aus Wetterbeobachtungen echte Handelssignale gewinnen.

Sammeln von Wetterdaten

Einer der wichtigsten Faktoren des Systems wird das Modul für den Empfang und die Vorverarbeitung der Daten sein. Für die Arbeit mit Wetterdaten werden wir die Meteostat API verwenden, die Zugang zu archivierten meteorologischen Daten aus der ganzen Welt bietet. Betrachten wir nun, wie die Datenabfragefunktion implementiert ist:

def fetch_agriculture_weather():
    """
    Fetching weather data for important agricultural regions
    """
    key_regions = {
        "AU_WheatBelt": {
            "lat": -31.95, 
            "lon": 116.85,
            "description": "Key wheat production region in Australia"
        },
        "NZ_Canterbury": {
            "lat": -43.53,
            "lon": 172.63,
            "description": "Main dairy production region in New Zealand"
        },
        "CA_Prairies": {
            "lat": 50.45, 
            "lon": -104.61,
            "description": "Canada's breadbasket, wheat and canola production"
        }
    }

In dieser Funktion werden wir die wichtigsten landwirtschaftlichen Regionen mit ihren Standortkoordinaten ermitteln. Für den australischen Weizengürtel wurden die Koordinaten des zentralen Teils der Region ausgewählt, für Neuseeland die Koordinaten von Canterbury und für Kanada die Koordinaten des zentralen Teils der Prärie.

Sobald die Rohdaten eingegangen sind, müssen sie ernsthaft verarbeitet werden. Zu diesem Zweck ist die Funktion process_weather_data implementiert:

def process_weather_data(raw_data):
    if not isinstance(raw_data.index, pd.DatetimeIndex):
        raw_data.index = pd.to_datetime(raw_data.index)
    
    processed_data = pd.DataFrame(index=raw_data.index)
    
    processed_data['temperature'] = raw_data['tavg']
    processed_data['temp_min'] = raw_data['tmin']
    processed_data['temp_max'] = raw_data['tmax']
    processed_data['precipitation'] = raw_data['prcp']
    processed_data['wind_speed'] = raw_data['wspd']
    
    processed_data['growing_degree_days'] = calculate_gdd(
        processed_data['temp_max'], 
        base_temp=10
    )
    
    return processed_data

Auch die Berechnung des Indikators GrowingDegreeDays (GDD), der ein notwendiger Indikator für die Bewertung des Wachstumspotenzials der landwirtschaftlichen Kulturen ist, muss berücksichtigt werden. Dieser Wert wird auf der Grundlage der Tageshöchsttemperatur ermittelt, wobei die normale Wachstumstemperatur der Pflanzen berücksichtigt wird.

def analyze_and_visualize_correlations(merged_data):
   plt.style.use('default')
   plt.rcParams['figure.figsize'] = [15, 10]
   plt.rcParams['axes.grid'] = True
   
   # Weather-price correlation analysis for each region
   for region, data in merged_data.items():
       if data.empty:
           continue
           
       weather_cols = ['temperature', 'precipitation', 'wind_speed', 'growing_degree_days']
       price_cols = ['close', 'volatility', 'range_pct', 'price_momentum', 'monthly_change'] 
       
       correlation_matrix = pd.DataFrame()
       for w_col in weather_cols:
           if w_col not in data.columns:
               continue
           for p_col in price_cols:
               if p_col not in data.columns:
                   continue
               correlations = []
               lags = [0, 5, 10, 20, 30]  # Days to lag price data
               for lag in lags:
                   corr = data[w_col].corr(data[p_col].shift(-lag))
                   correlations.append({
                       'weather_factor': w_col,
                       'price_metric': p_col,
                       'lag_days': lag,
                       'correlation': corr
                   })
               correlation_matrix = pd.concat([
                   correlation_matrix, 
                   pd.DataFrame(correlations)
               ])
   
   return correlation_matrix

def plot_correlation_heatmap(pivot_table, region):
   plt.figure()
   im = plt.imshow(pivot_table.values, cmap='RdYlBu', aspect='auto')
   plt.colorbar(im)
   
   plt.xticks(range(len(pivot_table.columns)), pivot_table.columns, rotation=45)
   plt.yticks(range(len(pivot_table.index)), pivot_table.index)
   
   # Add correlation values in each cell
   for i in range(len(pivot_table.index)):
       for j in range(len(pivot_table.columns)):
           text = plt.text(j, i, f'{pivot_table.values[i, j]:.2f}',
                         ha='center', va='center')
   
   plt.title(f'Weather Factors and Price Correlations for {region}')
   plt.tight_layout()

Empfang von Daten über Währungspaare und deren Synchronisierung

Nachdem das Sammeln von Wetterdaten eingerichtet wurde, muss der Empfang von Informationen über die Bewegung von Währungspaaren implementiert werden. Zu diesem Zweck verwenden wir die Plattform MetaTrader 5, die eine praktische API für die Arbeit mit historischen Daten von Finanzinstrumenten bietet.

Betrachten wir die Funktion zum Abrufen von Daten über Währungspaare:

def get_agricultural_forex_pairs():
    """
    Getting data on currency pairs via MetaTrader 5
    """
    if not mt5.initialize():
        print("MT5 initialization error")
        return None
    
    pairs = ["AUDUSD", "NZDUSD", "USDCAD"]
    timeframes = {
        "H1": mt5.TIMEFRAME_H1,
        "H4": mt5.TIMEFRAME_H4,
        "D1": mt5.TIMEFRAME_D1
    }
    # ... the rest of the function code

In dieser Funktion arbeiten wir mit drei Hauptwährungspaaren, die unseren landwirtschaftlichen Regionen entsprechen: AUDUSD für den australischen Weizengürtel, NZDUSD für die Region Canterbury und USDCAD für die kanadischen Prärien. Für jedes Paar werden Daten in drei Zeitrahmen erfasst: stündlich (H1), vierstündlich (H4) und täglich (D1).

Besondere Aufmerksamkeit sollte der Kombination von Wetter- und Finanzdaten gewidmet werden. Hierfür ist eine spezielle Funktion zuständig:

def merge_weather_forex_data(weather_data, forex_data):
    """
    Combining weather and financial data
    """
    synchronized_data = {}
    
    region_pair_mapping = {
        'AU_WheatBelt': 'AUDUSD',
        'NZ_Canterbury': 'NZDUSD',
        'CA_Prairies': 'USDCAD'
    }
    # ... the rest of the function code

Diese Funktion löst das komplexe Problem der Synchronisierung von Daten aus verschiedenen Quellen. Da Wetterdaten und Währungskurse unterschiedlich häufig aktualisiert werden, wird die spezielle Methode merge_asof aus der Pandas-Bibliothek verwendet, die einen korrekten Vergleich der Werte unter Berücksichtigung der Zeitstempel ermöglicht.

Um die Qualität der Analyse zu verbessern, werden die kombinierten Daten zusätzlich verarbeitet:

def calculate_derived_features(data):
    """
    Calculation of derived indicators
    """
    if not data.empty:
        data['price_volatility'] = data['volatility'].rolling(24).std()
        data['temp_change'] = data['temperature'].diff()
        data['precip_intensity'] = data['precipitation'].rolling(24).sum()
        # ... the rest of the function code

Hier werden wichtige abgeleitete Indikatoren wie die Preisvolatilität der letzten 24 Stunden, Temperaturänderungen und Niederschlagsintensität berechnet. Außerdem wird ein binärer Indikator für die Vegetationsperiode hinzugefügt, der insbesondere für die Analyse von landwirtschaftlichen Kulturen wichtig ist.

Besonderes Augenmerk wird auf die Bereinigung der Daten um Ausreißer und das Auffüllen fehlender Werte gelegt:

def clean_merged_data(data):
    """
    Cleaning up merged data
    """
    weather_cols = ['temperature', 'precipitation', 'wind_speed']
    
    # Fill in the blanks
    for col in weather_cols:
        if col in data.columns:
            data[col] = data[col].ffill(limit=3)
    
    # Removing outliers
    for col in weather_cols:
        if col in data.columns:
            q_low = data[col].quantile(0.01)
            q_high = data[col].quantile(0.99)
            data = data[
                (data[col] > q_low) & 
                (data[col] < q_high)
            ]
    # ... the rest of the function code

Diese Funktion verwendet die Forward-Fill-Methode, um fehlende Werte in Wetterdaten zu behandeln, allerdings mit einer Begrenzung auf 3 Perioden, um zu vermeiden, dass bei langen Lücken falsche Werte eingeführt werden. Extremwerte außerhalb des 1. und 99. Perzentils werden ebenfalls entfernt, was dazu beiträgt, dass Ausreißer die Analyseergebnisse nicht verzerren.

Ergebnis der Ausführung der Funktionen des Datensatzes:

Analyse des Zusammenhangs zwischen Witterungsfaktoren und Preisraten

Während der Beobachtung wurden verschiedene Aspekte der Beziehung zwischen den Wetterbedingungen und der Dynamik der Preise von Währungspaaren analysiert. Um Muster zu finden, die nicht auf den ersten Blick ersichtlich sind, wurde eine spezielle Methode zur Berechnung von Korrelationen unter Berücksichtigung von Zeitverzögerungen entwickelt:

def analyze_weather_price_correlations(merged_data):
    """
    Analysis of correlations with time lags between weather conditions and price movements
    """
    def calculate_lagged_correlations(data, weather_col, price_col, max_lag=72):
        print(f"Calculating lagged correlations: {weather_col} vs {price_col}")
        correlations = []
        for lag in range(max_lag):
            corr = data[weather_col].corr(data[price_col].shift(-lag))
            correlations.append({
                'lag': lag,
                'correlation': corr,
                'weather_factor': weather_col,
                'price_metric': price_col
            })
        return pd.DataFrame(correlations)

    correlations = {}
    weather_factors = ['temperature', 'precipitation', 'wind_speed', 'growing_degree_days']
    price_metrics = ['close', 'volatility', 'price_momentum', 'monthly_change']
    
    for region, data in merged_data.items():
        if data.empty:
            print(f"Skipping empty dataset for {region}")
            continue
            
        print(f"\nAnalyzing correlations for region: {region}")
        region_correlations = {}
        for w_col in weather_factors:
            for p_col in price_metrics:
                key = f"{w_col}_{p_col}"
                region_correlations[key] = calculate_lagged_correlations(data, w_col, p_col)
        correlations[region] = region_correlations
        
    return correlations

def analyze_seasonal_patterns(data):
    """
    Analysis of seasonal correlation patterns
    """
    print("Starting seasonal pattern analysis...")
    seasonal_correlations = {}
    data['month'] = data.index.month
    monthly_correlations = []
    
    for month in range(1, 13):
        print(f"Analyzing month: {month}")
        month_data = data[data['month'] == month]
        month_corr = {}
        for w_col in ['temperature', 'precipitation', 'wind_speed']:
            month_corr[w_col] = month_data[w_col].corr(month_data['close'])
        monthly_correlations.append(month_corr)
    
    return pd.DataFrame(monthly_correlations, index=range(1, 13))

Die Analyse der gefundenen Daten ergab interessante Muster. Für den australischen Weizengürtel besteht die stärkste Korrelation (0,21) zwischen den Windgeschwindigkeiten und den monatlichen Veränderungen des AUDUSD-Wechselkurses. Dies lässt sich dadurch erklären, dass starke Winde während der Reifezeit des Weizens den Ertrag verringern können. Der Temperaturfaktor zeigt ebenfalls eine starke Korrelation (0,18), wobei ein besonderer Einfluss praktisch ohne zeitliche Verzögerung nachgewiesen wird.

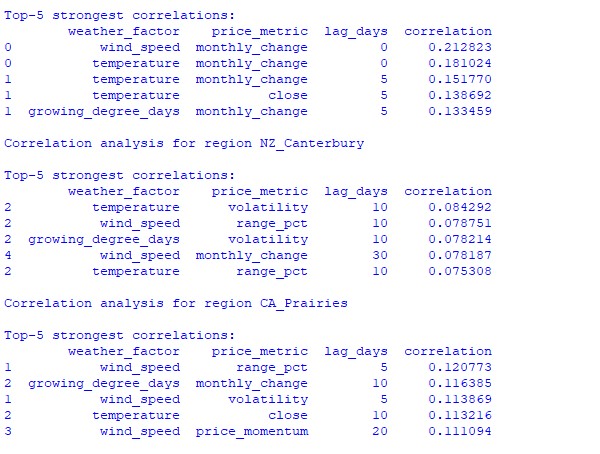
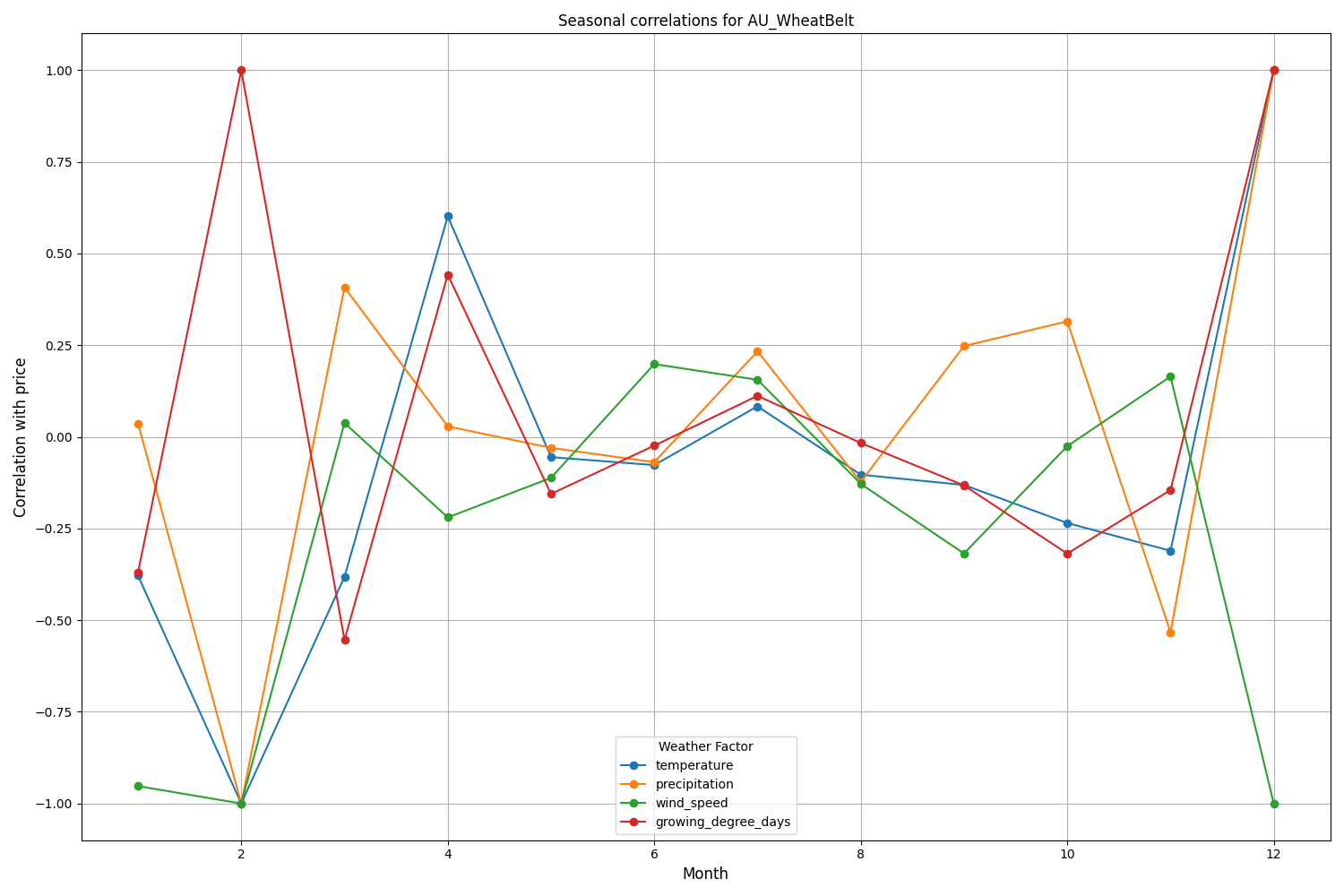
Die Region Canterbury in Neuseeland weist komplexere Muster auf. Die stärkste Korrelation (0,084) zeigt sich zwischen Temperatur und Volatilität mit einer Verzögerung von 10 Tagen. Es ist zu beachten, dass sich der Einfluss der Wetterfaktoren auf den NZDUSD stärker in der Volatilität als in der Richtung der Kursbewegung niederschlägt. Die saisonalen Korrelationen erreichen manchmal die Marke von 1,00, was eine perfekte Korrelation bedeutet.

Erstellung eines maschinellen Lernmodells für Prognosen

Unsere Strategie basiert auf dem Gradient-Boosting-Modell CatBoost, das sich bei der Verarbeitung von Zeitreihen als hervorragend erwiesen hat. Schauen wir uns die Erstellung des Modells Schritt für Schritt an.

Vorbereiten der Merkmale

Der erste Schritt ist die Bildung der Modellmerkmale. Wir werden eine Auswahl von technischen und wetterbedingten Indikatoren sammeln:

def prepare_ml_features(data):
    """
    Preparation of features for the ML model
    """
    print("Starting feature preparation...")
    features = pd.DataFrame(index=data.index)

    # Weather features
    weather_cols = [
        'temperature', 'precipitation', 
        'wind_speed', 'growing_degree_days'
    ]
    for col in weather_cols:
        if col not in data.columns:
            print(f"Warning: {col} not found in data")
            continue

        print(f"Processing weather feature: {col}")
        # Base values
        features[col] = data[col]
        
        # Moving averages
        features[f"{col}_ma_24"] = data[col].rolling(24).mean()
        features[f"{col}_ma_72"] = data[col].rolling(72).mean()
        
        # Changes
        features[f"{col}_change"] = data[col].pct_change()
        features[f"{col}_change_24"] = data[col].pct_change(24)
        
        # Volatility
        features[f"{col}_volatility"] = data[col].rolling(24).std()

    # Price indicators
    price_cols = ['volatility', 'range_pct', 'monthly_change']
    for col in price_cols:
        if col not in data.columns:
            continue
        features[f"{col}_ma_24"] = data[col].rolling(24).mean()

    # Seasonal features
    features['month'] = data.index.month
    features['day_of_week'] = data.index.dayofweek
    features['growing_season'] = (
        (data.index.month >= 4) & 
        (data.index.month <= 9)
    ).astype(int)

    return features.dropna()

def create_prediction_targets(data, forecast_horizon=24):
    """
    Creation of target variables for prediction
    """
    print(f"Creating prediction targets with horizon: {forecast_horizon}")
    targets = pd.DataFrame(index=data.index)

    # Price change percentage
    targets['price_change'] = data['close'].pct_change(
        forecast_horizon
    ).shift(-forecast_horizon)

    # Price direction
    targets['direction'] = (targets['price_change'] > 0).astype(int)

    # Future volatility
    targets['volatility'] = data['volatility'].rolling(
        forecast_horizon
    ).mean().shift(-forecast_horizon)

    return targets.dropna()

Erstellen und Trainieren der Modelle

Für jede zu berücksichtigende Variable wird ein eigenes Modell mit optimierten Parametern erstellt:

from catboost import CatBoostClassifier, CatBoostRegressor
from sklearn.metrics import accuracy_score, mean_squared_error
from sklearn.model_selection import TimeSeriesSplit

# Define categorical features
cat_features = ['month', 'day_of_week', 'growing_season']

# Create models for different tasks
models = {
    'direction': CatBoostClassifier(
        iterations=1000,
        learning_rate=0.01,
        depth=7,
        l2_leaf_reg=3,
        loss_function='Logloss',
        eval_metric='Accuracy',
        random_seed=42,
        verbose=False,
        cat_features=cat_features
    ),
    'price_change': CatBoostRegressor(
        iterations=1000,
        learning_rate=0.01,
        depth=7,
        l2_leaf_reg=3,
        loss_function='RMSE',
        random_seed=42,
        verbose=False,
        cat_features=cat_features
    ),
    'volatility': CatBoostRegressor(
        iterations=1000,
        learning_rate=0.01,
        depth=7,
        l2_leaf_reg=3,
        loss_function='RMSE',
        random_seed=42,
        verbose=False,
        cat_features=cat_features
    )
}

def train_ml_models(merged_data, region):
    """
    Training ML models using time series cross-validation
    """
    print(f"Starting model training for region: {region}")
    data = merged_data[region]
    features = prepare_ml_features(data)
    targets = create_prediction_targets(data)

    # Split into folds
    tscv = TimeSeriesSplit(n_splits=5)
    
    results = {}
    for target_name, model in models.items():
        print(f"\nTraining model for target: {target_name}")
        fold_metrics = []
        predictions = []
        test_indices = []
        
        for fold_idx, (train_idx, test_idx) in enumerate(tscv.split(features)):
            print(f"Processing fold {fold_idx + 1}/5")
            X_train = features.iloc[train_idx]
            y_train = targets[target_name].iloc[train_idx]
            X_test = features.iloc[test_idx]
            y_test = targets[target_name].iloc[test_idx]

            # Training with early stopping
            model.fit(
                X_train, y_train,
                eval_set=(X_test, y_test),
                early_stopping_rounds=50,
                verbose=False
            )

            # Predictions and evaluation
            pred = model.predict(X_test)
            predictions.extend(pred)
            test_indices.extend(test_idx)

            # Metric calculation
            metric = (
                accuracy_score(y_test, pred)
                if target_name == 'direction'
                else mean_squared_error(y_test, pred, squared=False)
            )
            fold_metrics.append(metric)
            print(f"Fold {fold_idx + 1} metric: {metric:.4f}")

        results[target_name] = {
            'model': model,
            'metrics': fold_metrics,
            'mean_metric': np.mean(fold_metrics),
            'predictions': pd.Series(
                predictions, 
                index=features.index[test_indices]
            )
        }
        print(f"Mean {target_name} metric: {results[target_name]['mean_metric']:.4f}")

    return results

Merkmale der Implementierung

Unsere Implementierung konzentriert sich auf die folgenden Parameter:

1. Behandlung kategorischer Merkmale: CatBoost verarbeitet effizient kategoriale Variablen wie Monat und Wochentag, ohne dass eine zusätzliche Kodierung erforderlich ist.
2. Früher Stopp: Um Überanpassungsversuche zu verhindern, wird der Mechanismus eines frühen Stopps mit dem Parameter early_stopping_rounds=50 verwendet.
3. Gleichgewicht zwischen Tiefe und Verallgemeinerung: Die Parameter depth=7 und l2_leaf_reg=3 wurden gewählt, um ein möglichst ausgewogenes Verhältnis zwischen Baumtiefe und Regularisierung zu erreichen.
4. Umgang mit Zeitreihen: Die Verwendung von TimeSeriesSplit gewährleistet eine ordnungsgemäße Datenaufteilung für Zeitreihen und verhindert so mögliche Datenverluste in der Zukunft.

Diese Modellarchitektur wird dazu beitragen, sowohl kurzfristige als auch langfristige Abhängigkeiten zwischen Wetterbedingungen und Wechselkursbewegungen effizient zu erfassen, wie die erzielten Testergebnisse zeigen.

Bewertung der Modellgenauigkeit und Visualisierung der Ergebnisse

Die daraus resultierenden maschinellen Lernmodelle wurden anhand von 5-Jahres-Daten mit der fünffachen Schiebefenster-Methode getestet. Für jeden Bereich wurden drei Arten von Modellen erstellt: Vorhersage der Richtung der Preisbewegung (Klassifizierung), Vorhersage des Ausmaßes der Preisänderung (Regression) und Vorhersage der Volatilität (Regression).

import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix, classification_report

def evaluate_model_performance(results, region_data):
    """
    Comprehensive model evaluation across all regions
    """
    print(f"\nEvaluating model performance for {len(results)} regions")
    evaluation = {}
    
    for region, models in results.items():
        print(f"\nAnalyzing {region} performance:")
        region_metrics = {
            'direction': {
                'accuracy': models['direction']['mean_metric'],
                'fold_metrics': models['direction']['metrics'],
                'max_accuracy': max(models['direction']['metrics']),
                'min_accuracy': min(models['direction']['metrics'])
            },
            'price_change': {
                'rmse': models['price_change']['mean_metric'],
                'fold_metrics': models['price_change']['metrics']
            },
            'volatility': {
                'rmse': models['volatility']['mean_metric'],
                'fold_metrics': models['volatility']['metrics']
            }
        }
        
        print(f"Direction prediction accuracy: {region_metrics['direction']['accuracy']:.2%}")
        print(f"Price change RMSE: {region_metrics['price_change']['rmse']:.4f}")
        print(f"Volatility RMSE: {region_metrics['volatility']['rmse']:.4f}")
        
        evaluation[region] = region_metrics
    
    return evaluation

def plot_feature_importance(models, region):
    """
    Visualize feature importance for each model type
    """
    plt.figure(figsize=(15, 10))
    
    for target, model_info in models.items():
        feature_importance = pd.DataFrame({
            'feature': model_info['model'].feature_names_,
            'importance': model_info['model'].feature_importances_
        })
        feature_importance = feature_importance.sort_values('importance', ascending=False)
        
        plt.subplot(3, 1, list(models.keys()).index(target) + 1)
        sns.barplot(x='importance', y='feature', data=feature_importance.head(10))
        plt.title(f'{target.capitalize()} Model - Top 10 Important Features')
    
    plt.tight_layout()
    plt.show()

def visualize_seasonal_patterns(results, region_data):
    """
    Create visualization of seasonal patterns in predictions
    """
    for region, data in region_data.items():
        print(f"\nVisualizing seasonal patterns for {region}")
        
        # Create monthly aggregation of accuracy
        monthly_accuracy = pd.DataFrame(index=range(1, 13))
        data['month'] = data.index.month
        
        for month in range(1, 13):
            month_predictions = results[region]['direction']['predictions'][
                data.index.month == month
            ]
            month_actual = (data['close'].pct_change() > 0)[
                data.index.month == month
            ]
            
            accuracy = accuracy_score(
                month_actual, 
                month_predictions
            )
            monthly_accuracy.loc[month, 'accuracy'] = accuracy
        
        # Plot seasonal accuracy
        plt.figure(figsize=(12, 6))
        monthly_accuracy['accuracy'].plot(kind='bar')
        plt.title(f'Seasonal Prediction Accuracy - {region}')
        plt.xlabel('Month')
        plt.ylabel('Accuracy')
        plt.show()

def plot_correlation_heatmap(correlation_data):
    """
    Create heatmap visualization of correlations
    """
    plt.figure(figsize=(12, 8))
    sns.heatmap(
        correlation_data, 
        cmap='RdYlBu', 
        center=0,
        annot=True, 
        fmt='.2f'
    )
    plt.title('Weather-Price Correlation Heatmap')
    plt.tight_layout()
    plt.show()

Ergebnisse nach Regionen

AU_WheatBelt (Australischer Weizengürtel)

• Mittlere Genauigkeit der AUDUSD-Richtungsvorhersage: 62.67%
• Höchste Genauigkeit bei einzelnen Faltungen: 82.22%
• RMSE der Preisänderungsprognose: 0.0303
• RMSE der Volatilität: 0.0016

Region Canterbury (Neuseeland)

• Mittlere Genauigkeit der NZDUSD-Prognose: 62.81%
• Höchste Genauigkeit: 75.44%
• Minimale Genauigkeit: 54.39%
• RMSE der Preisänderungsprognose: 0.0281
• RMSE der Volatilität: 0.0015

Kanadische Prärie

• Mittlere Genauigkeit der Richtungsvorhersage: 56.92%
• Maximale Genauigkeit (dritte Falte): 71.79%
• RMSE der Preisänderungsprognose: 0.0159
• RMSE der Volatilität: 0.0023

Analyse und Visualisierung der Saisonalität

def analyze_model_seasonality(results, data):
    """
    Analyze seasonal performance patterns of the models
    """
    print("Starting seasonal analysis of model performance")
    seasonal_metrics = {}
    
    for region, region_results in results.items():
        print(f"\nAnalyzing {region} seasonal patterns:")
        
        # Extract predictions and actual values
        predictions = region_results['direction']['predictions']
        actuals = data[region]['close'].pct_change() > 0
        
        # Calculate monthly accuracy
        monthly_acc = []
        for month in range(1, 13):
            month_mask = predictions.index.month == month
            if month_mask.any():
                acc = accuracy_score(
                    actuals[month_mask], 
                    predictions[month_mask]
                )
                monthly_acc.append(acc)
                print(f"Month {month} accuracy: {acc:.2%}")
            
        seasonal_metrics[region] = pd.Series(
            monthly_acc, 
            index=range(1, 13)
        )
    
    return seasonal_metrics

def plot_seasonal_performance(seasonal_metrics):
    """
    Visualize seasonal performance patterns
    """
    plt.figure(figsize=(15, 8))
    
    for region, metrics in seasonal_metrics.items():
        plt.plot(metrics.index, metrics.values, label=region, marker='o')
    
    plt.title('Model Accuracy by Month')
    plt.xlabel('Month')
    plt.ylabel('Accuracy')
    plt.legend()
    plt.grid(True)
    plt.show()

Die Visualisierungsergebnisse zeigen eine signifikante Saisonabhängigkeit der Modellleistung.

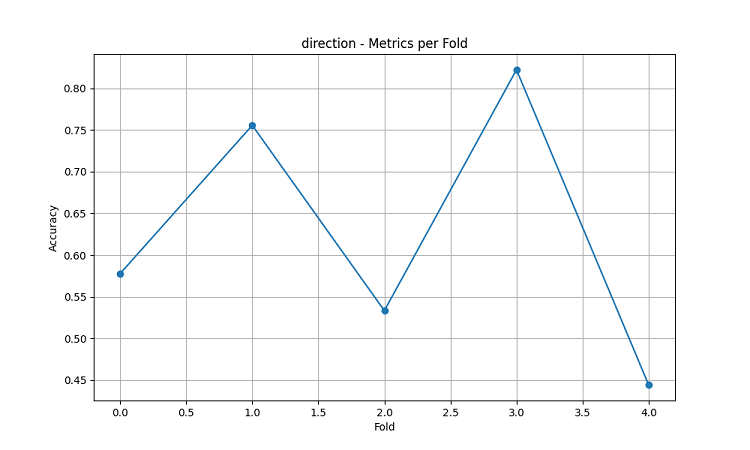
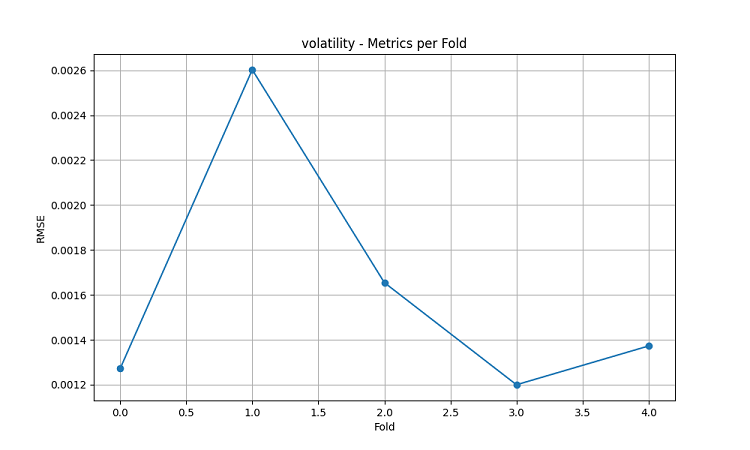
Besonders auffällig sind die Spitzenwerte bei der Vorhersagegenauigkeit:

• Für AUDUSD: Dezember-Februar (Reifezeit des Weizens)
• Für NZDUSD: Zeiten der höchsten Milchproduktion
• Für USDCAD: Aktive Wachstumsperioden in der Prärie

Diese Ergebnisse bestätigen die Hypothese, dass die Witterungsbedingungen einen erheblichen Einfluss auf die Wechselkurse der landwirtschaftlichen Währung haben, insbesondere in kritischen Zeiten der landwirtschaftlichen Produktion.

Schlussfolgerung

In der Studie wurde ein signifikanter Zusammenhang zwischen den Wetterbedingungen in landwirtschaftlichen Regionen und der Dynamik von Währungspaaren festgestellt. Das Vorhersagesystem zeigte in Zeiten extremer Wetterbedingungen und landwirtschaftlicher Produktionsspitzen eine hohe Genauigkeit von durchschnittlich bis zu 62,67 % für AUDUSD, 62,81 % für NZDUSD und 56,92 % für USDCAD.

Empfehlungen:

• AUDUSD: Handel von Dezember bis Februar, Fokus auf Wind und Temperatur.
• NZDUSD: Mittelfristiger Handel während der aktiven Milcherzeugung.
• USDCAD: Handel während der Aussaat- und Erntezeit.

Das System erfordert regelmäßige Datenaktualisierungen, um die Genauigkeit aufrechtzuerhalten, insbesondere bei Marktschwankungen. Zu den Perspektiven gehören die Erweiterung der Datenquellen und die Implementierung von Deep Learning, um die Robustheit der Prognosen zu verbessern.