Algorithmen zur Optimierung mit Populationen: Der Algorithmus intelligenter Wassertropfen (IWD)
281
0
Inhalt
1. Einführung
2. Der Algorithmus
3. Geänderte Version von SDSm
4. Testergebnisse
1. Einführung
Das Flussbett ist eine der anmutigsten Schöpfungen der Natur, in der jeder Wassertropfen (drop) seine Rolle im einzigartigen Tanz des Lebens spielt. Mit jedem Kilometer des Weges bildet der Fluss seine neuen Grenzen und strahlt majestätisch seine Energie und Weisheit aus. Wie dieses Naturphänomen strebt auch der Optimierungsalgorithmus der Intelligenten Wassertropfen nach Harmonie und Perfektion in seiner Funktionsweise, indem er die Prinzipien der Selbstorganisation und der Interaktion zwischen den Teilchen nutzt. Dieser Algorithmus spiegelt die Größe der Natur und ihre Fähigkeit wider, ein Gleichgewicht zu schaffen und aufrechtzuerhalten, was ihn zu einem wichtigen Instrument für die Optimierung und Lösung komplexer Probleme macht.
Jeder Fluss hat sein eigenes Tal, das durch Erosionsprozesse unter dem Einfluss von Oberflächen- und Grundwasser entsteht. Der tiefste Teil dieses Tals, der von einem Flusslauf in den Boden geschnitten wurde, wird als Bett bezeichnet. Der Hauptteil der Flussströmung und die Bodensedimente bewegen sich entlang des Flusses.
Das Relief des Flussbettes ändert sich ständig. Steine und Sand, die vom Wasser mitgerissen werden, bilden Kämme und Gräben, die das Bett in einem spitzen Winkel durchziehen. An Biegungen können Flüsse einen neuen Weg auswaschen und Altarme bilden - Abschnitte des alten Kanals, die sich allmählich in einen See mit eigenem Ökosystem verwandeln und schließlich austrocknen oder zu einem Sumpf werden.
Wenn wir Flüsse in der Natur beobachten, bemerken wir viele Windungen und Kurven entlang ihres Weges. Es stellt sich die Frage, warum diese Wendungen entstanden sind und ob es eine Logik oder einen Grund dafür gibt. Wenn ja, können wir die in Flüssen vorkommenden Mechanismen ausnutzen und infolgedessen intelligente Algorithmen auf ihrer Grundlage entwerfen und entwickeln? Der IWD-Algorithmus ist ein Versuch, einige der Prozesse, die in natürlichen Flüssen ablaufen, zu modellieren und in einen Algorithmus umzusetzen.
IWD ist einer der relativ neuen Algorithmen im Bereich der Schwarmintelligenz. Es simuliert die Dynamik von Flusssystemen. IWD ist ein populationsbasierter Algorithmus, bei dem jeder Wassertropfen eine Lösung darstellt, und das Teilen von Wassertropfen während der Suche zu besseren Lösungen führt.
Im Jahr 2007 entwickelte der iranische Wissenschaftler Hamed Shah-Hosseini einen Algorithmus für das Verhalten von intelligenten Tropfen. Der IWD-Algorithmus besteht aus mehreren künstlichen Wassertropfen, die in der Lage sind, durch Interaktion ihre Umgebung so zu verändern, dass sie den optimalen Weg des geringsten Widerstands finden. Der IWD-Algorithmus ist ein konstruktiver populationsorientierter Optimierungsalgorithmus.
2. Der Algorithmus
IWD ist ein Modell, bei dem Wassertropfen den optimalen Weg zu ihrem Ziel finden, indem sie den Lauf eines Flusses verändern. Dies wird durch drei wichtige Parameter begünstigt. Durch ihre eigene Geschwindigkeit sind die Tropfen in der Lage, Erde vom Grund des Flusses aufzunehmen. Je höher die Geschwindigkeit, desto mehr Erde kann jeder Tropfen mit sich führen, bzw. desto freier wird der Weg für nachfolgende Agenten. Die Durchflussmenge erhöht sich, wenn keine Erde zu reinigen ist. Der optimale Weg ist derjenige, der die geringste Menge an Erde enthält und auf dem die höchste Geschwindigkeit erreicht werden kann. Mit Hilfe von IWD ist es möglich, eine Optimierungsstrategie zu implementieren, bei der zufällige Agenten auf intelligente Weise miteinander interagieren, sodass sie gemeinsam den Flusslauf verändern und einen optimalen Pfad schaffen, auf dem keine Erde angetroffen wird und die Durchflussrate der Agenten so hoch wie möglich wird.
Grundlegende Prinzipien:
- ein Wassertropfen bevorzugt einen Weg mit weniger Erde
- ein Wassertropfen bevorzugt einen kürzeren Weg, wenn er zwischen mehreren Routen auf dem Weg von der Quelle zum Ziel wählen muss.
- Die Schwierigkeit eines Weges hängt von der Menge der Erde ab, der ihn bedeckt. Ein Weg mit mehr Erde gilt als schwieriger, während ein Weg mit weniger Erde als leichter gilt.
In der Natur sind viele Wassertropfen in Flüssen zu beobachten, wo sie riesige Massen (Schwärme von Wassertropfen) bilden. Die Wege, auf denen natürliche Flüsse fließen, wurden durch Schwärme von Wassertropfen geschaffen. Schwärme von Wassertropfen (Flüsse) sind Teil der Umwelt, die durch den Schwarm erheblich verändert wurde und sich auch in Zukunft verändern kann. Außerdem hat die Umgebung selbst einen erheblichen Einfluss auf die Wege der Wassertropfen. Sie stoßen auf den Widerstand der Flussufer. Einem Schwarm von Wassertropfen wird zum Beispiel von den Teilen der Umgebung, die harte Erde bilden, mehr Widerstand entgegengesetzt als von den Teilen, die die weiche Erde bilden. Der natürliche Verlauf eines Flusses ist das Ergebnis des Wettbewerbs zwischen Wassertropfen und der Umwelt, die sich ihrer Bewegung widersetzt.
Eines der Merkmale eines Wassertropfens, der in einen Fluss fließt, ist seine Geschwindigkeit. Ein weiteres Merkmal von Erde ist, dass jeder Fluss nur eine bestimmte Menge aufnehmen kann. Ein Wassertropfen ist also in der Lage, eine gewisse Menge an Erde von einem Ort zum anderen zu transportieren. Diese Erde wird von schnellen auf langsame Partikel übertragen. Das bedeutet, dass sich die vom Fluss mit der schnellen Strömung mitgeführte Erde an einem Ort mit langsamer Strömung absetzen wird.
Während dieser Übergangszeit werden drei offensichtliche Veränderungen eintreten:
- die Geschwindigkeit eines Wassertropfens steigt
- die Erdsättigung der Wassertropfen nimmt zu
- zwischen diesen beiden Punkten nimmt die Menge der Erde im Bett ab (Grafikpunkte)
Oben wurde festgestellt, dass jeder Wassertropfen seine eigene Geschwindigkeit hat. Diese Geschwindigkeit spielt eine direkte Rolle bei der Ansammlung von Erde im Flussbett. Ein Wassertropfen mit hoher Geschwindigkeit nimmt mehr Erde auf als ein Tropfen mit langsamerer Geschwindigkeit. So entfernen Wassertropfen mit einer schnelleren Geschwindigkeit mehr Erde der Flusserde als Wassertropfen mit einer langsameren Geschwindigkeit. Der Erdabtrag hängt also von der Geschwindigkeit des Wassertropfens ab.
Die Geschwindigkeit eines Wassertropfens nimmt auf einem Weg mit niedrigem Erdniveau stärker zu als auf einem Weg mit hohem Erdniveau. So kann der fließende Wassertropfen auf einem Weg mit wenig Erde mehr Erde aufnehmen und eine höhere Geschwindigkeit erreichen, während ein Weg mit viel Erde zu einer Verringerung der Geschwindigkeit führt.
Im IWD-Algorithmus sind Tropfen also durch zwei Haupteigenschaften gekennzeichnet:
- Geschwindigkeit (speed)
- Erde (soil)
Diese beiden Eigenschaften können sich während des Algorithmus ändern. IWD-Tropfen bewegen sich von einer Quelle zu einem Ziel und beginnen ihre Reise mit einer Anfangsgeschwindigkeit und ohne Bodenkontakt. Auf ihrer Reise bewegen sich die Wassertropfen durch eine Umgebung, aus der ein Teil der Erde entfernt wurde, und können eine gewisse Geschwindigkeit erreichen. Es wird davon ausgegangen, dass die IWD iterativ durchgeführt wird. Die Tropfengeschwindigkeit nimmt von der aktuellen Stelle zur nächsten um einen Betrag zu, der nicht linear proportional zum Kehrwert der Erde zwischen den beiden Stellen ist:
vel = vel (t-1) + Av / [Bv + Cv * soil^2(i,j)]
wobei: Av, Bv, Cv sind Geschwindigkeitsverhältnisse (Inputs), während soil (i,j) die Menge der Erde zwischen den Scheitelpunkten des Graphen ist.
Daher kann sich der IWD-Tropfen auf einem Weg mit weniger Erde schneller bewegen als auf einem Weg mit mehr Erde.
Der IWD-Tropfen sammelt auf seinem Weg durch die Umwelt Erde ein. Diese Erde wird von dem Weg entfernt, der die beiden Orte verbindet. Die Menge an Erde, die einem IWD-Tropfen zugefügt wird, ist nicht linear proportional zu der Zeit, die benötigt wird, um den IWD von seinem aktuellen Standort zum nächsten zu bewegen. Diese Zeitspanne wird anhand einfacher physikalischer Gesetze für lineare Bewegungen berechnet:
time(i,j,vel) = R / vel
wobei R ein Abstand zwischen zwei Punkten ist.
Menge der dem Tropfen zugesetzten Erde:
dSoil(i,j) = As / [Bs + Cs * time(i,j,vel)]
wobei: As, Bs und Cs sind die Erdeinwaschungsverhältnisse.
Die neue Menge an Erde auf dem Pfad zwischen den Punkten sieht dann so aus:
soil (i+1,j+1) = Po * soil(i,j) + Pn * dSoil(i,j)
wobei Po und Pn die Verhältnisse der Veränderung der Erdmenge sind.
Die Zeit, die für die Bewegung aufgewendet wird, ist also umgekehrt proportional zur Geschwindigkeit der Bewegung und direkt proportional zur Entfernung zwischen zwei Punkten. Mit anderen Worten: Erde ist ein quantitativer Indikator für Informationen über die Umwelt. Diese Gleichungen bestimmen die Vorliebe der Wassertropfen, Wege mit niedrigem Füllung gegenüber solchen mit hohem Füllung zu wählen. Diese Pfadauswahl wird durch Anwendung einer gleichmäßigen Zufallsverteilung auf die verfügbaren Pfade erreicht. Die Wahrscheinlichkeit, den nächsten Pfad zu wählen, ist umgekehrt proportional zum Erdlevel der verfügbaren Pfade. Daher haben Pfade mit geringerem Füllniveau eine höhere Chance, von IWD-Tropfen ausgewählt zu werden.
Der ursprüngliche IWD-Algorithmus wurde vom Autor entwickelt, um optimale Pfadprobleme zu lösen, wie z.B. Graphen-Suchprobleme und Travelling-Salesman-Probleme. Dieser Algorithmus ist jedoch nicht geeignet, um die Probleme zu lösen, die wir in unseren Tests betrachten. Daher ist es notwendig, den IWD-Algorithmus zur Lösung unserer Optimierungsprobleme anzupassen. Im Gegensatz dazu sind die in den Artikeln über Optimierungsalgorithmen für die Bevölkerung beschriebenen Algorithmen in der Lage, Probleme jeder Art zu lösen, einschließlich Graphen-Suchprobleme. In den vorangegangenen Artikeln wurde bereits ein ähnlicher hochspezialisierter Algorithmus vorgestellt, der einer Überarbeitung bedurfte, nämlich der „Ameisenkolonie (ACO)“.
Um IWD an die Fähigkeit anzupassen, jedes beliebige Optimierungsproblem zu lösen, und damit IWD in Wettbewerben für Populationsalgorithmen konkurrieren kann, muss zunächst festgelegt werden, wie der Prozess der Erdablagerung und -bewegung anzuwenden ist. Wir können nicht dem Ansatz des ACO-Algorithmus folgen, bei dem die Pheromone dem Wert der Fitnessfunktion entsprechen. Im Falle der IWD ist Erde ein dynamischer Parameter und entspricht nicht proportional der Fitness.
Es entstand die Idee, die Koordinaten in Sektoren aufzuteilen, ähnlich wie man ein Flusstal in Abschnitte mit gleicher Fläche unterteilt. Der Gedanke dahinter ist, dass, wenn sich die Position des Tropfens (Agenten) verbessert, die Menge der Erde in den entsprechenden Sektoren entlang aller Koordinaten abnimmt. Die quantitative Veränderung der Erdmenge wird durch die Differenz der Veränderung der Fitnessfunktion in den letzten beiden Iterationen bestimmt, die über alle Wassertropfen hinweg durch die Differenz zwischen der maximalen und minimalen Veränderung der Fitness normalisiert wird.
Das Verhalten der Wassertropfenbewegung basiert auf einer zufälligen Auswahl von Sektoren, die die geringste Menge an Erde aufweisen, d. h., die Wahrscheinlichkeit ist proportional zur Menge der Erde in dem entsprechenden Sektor. Wir werden die besten Koordinaten in allen Bereichen im globalen „Flussbett“-Speicher ablegen. Nachdem ein Wassertropfen einen Sektor ausgewählt hat, wird versucht, die gespeicherte Koordinate so zu verbessern, dass die Wahrscheinlichkeit der neuen Koordinate einem quadratischen Gesetz gehorcht, demzufolge die neue Koordinate mit höherer Wahrscheinlichkeit näher an der vorherigen Koordinate liegt als weiter entfernt. Die Breite des Bereichs, in dem die neue Koordinate liegen wird, wird durch einen externen Parameter bestimmt und in Teilen der Sektorgröße ausgedrückt. Die Aufteilung einer Koordinate in Sektoren und die Wahrscheinlichkeitsverteilung der neuen Koordinate sind in Abbildung 1 dargestellt.
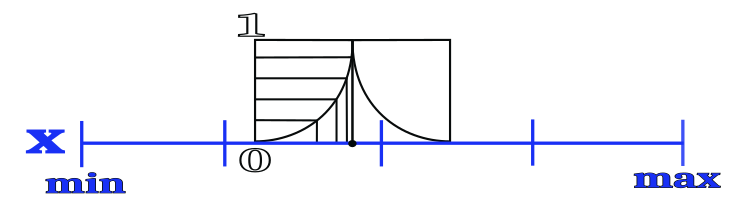
Bild 1. Einteilung der Koordinate in Sektoren und die Wahrscheinlichkeitsverteilung der Wahl einer neuen Koordinate in der Nähe der besten bekannten Koordinate
Auf der Grundlage der obigen Bestimmungen und Konzepte des IWD-Algorithmus können wir einen Pseudocode erstellen, der in die folgenden Schritte unterteilt ist:
- Zufällige Erzeugung von Wassertropfen (erste Iteration)
- FF berechnen
- Aktualisieren des besten Gesamtergebnisses
- Zufällige Erzeugung von Wassertropfen (zweite Iteration)
- FF berechnen
- Aktualisieren des besten Gesamtergebnisses
- Berechnen der Veränderung der Höhe jedes Wassertropfens (aktuelle und vorherige Höhe)
- Aktualisierungshöhen nach Sektoren
- Neue Tropfen (Auswahl eines Sektors nach dem Zufallsprinzip, ein Tropfen in der Nähe eines bekannten Lochs)
- FF berechnen
- Aktualisieren des besten Gesamtergebnisses
- Wiederholung ab S. 7
Kommen wir nun zur Codeanalyse.
Stellen wir den „Wassertropfen“-Suchagenten als S_Drop-Struktur dar, die die folgenden Felder enthält:
- Init (int coords): Die Funktion initialisiert ein Strukturobjekt mit der Anzahl der Koordinaten „coords“ als Argument. Innerhalb der Funktion werden die Größen der Arrays „c“ und „rSection“ bis zur angegebenen Anzahl von Koordinaten geändert. Die Variablen „f“, „fPrev“ und „altChange“ werden ebenfalls initialisiert.
- c: Das Array zum Speichern von Koordinaten.
- rSection: Das Array zum Speichern von Flussabschnitten.
- f: Der Fitnessindikator für einen bestimmten Tropfen.
- fPrev: vorheriger Fitnesswert.
- altChange: Höhenänderung.
struct S_Drop { void Init (int coords) { ArrayResize (c, coords); ArrayResize (rSection, coords); f = -DBL_MAX; fPrev = -DBL_MAX; altChange = 0.0; } double c []; //coordinates int rSection []; //river section (number of cells: number of coordinates, cell value: sector index on the coordinate) double f; //fitness double fPrev; //previous fitness double altChange; //change in altitude };
Wir benötigen einen Speicher, in dem eine Beschreibung des Flusses (die besten Koordinaten der Tiefen und die Tiefen selbst) gespeichert werden, daher nennen wir die Struktur S_Riverbed:
- riverbedDepth: das Array zur Speicherung der Flussbetttiefen; die Anzahl der Zellen im Array entspricht der Anzahl der Sektoren an der Koordinate, und der Wert jeder Zelle ist die Flussbetttiefe im entsprechenden Sektor.
- coordOnSector: das Array zum Speichern einer bestimmten Koordinate der tiefsten Stelle eines Sektors, die Anzahl der Zellen im Array entspricht der Anzahl der Sektoren auf der Koordinate, und der Wert jeder Zelle ist die Koordinate auf dem entsprechenden Sektor.
//—————————————————————————————————————————————————————————————————————————————— struct S_Riverbed //riverbed { double riverbedDepth []; //riverbed depth double coordOnSector []; //coordinate on the sector }; //——————————————————————————————————————————————————————————————————————————————
Wir deklarieren die Klasse C_AO_IWDm (m = modifiziert), die einen künstlichen Optimierungsalgorithmus auf der Grundlage von Wassertropfen implementiert. Nachfolgend finden Sie eine Beschreibung der einzelnen Klassenelemente:
Eigenschaften der Klasse:
- cB: Array zur Speicherung der besten Koordinaten
- fB: speichert den Wert der Zielfunktion für die besten Koordinaten
- p: Array für Partikel (Wassertropfen)
- Die Felder „rangeMax“, „rangeMin“ und „rangeStep“ werden zur Festlegung des Suchbereichs verwendet.
Methoden der Klasse:
- Init: Initialisierung des Objekts der Klasse C_AO_IWDm mit den angegebenen Parametern: „coordsP“ - Anzahl der Koordinaten, „popSizeP“ - Größe der Bevölkerung, „sectorsNumberP“ - Anzahl der Sektoren und „waterViscosityP“ - Wasserviskosität.
- Bewegen: Wassertropfen bewegen
- Revision: eine Revision des Zustands der Wassertropfen durchführen
- coords: Anzahl der Koordinaten
- popSize: Anzahl der Tropfen
- sectorsNumbe: Anzahl der Sektoren
- waterViscosity: Viskositätsverhältnis des Wassers in Teilen der Sektorgröße
- sectorSpace: Größe des Sektors
- rb: Array von Koordinaten zur Beschreibung des Flussbetts
- iterationCounter
- revision: Flag, das die Notwendigkeit einer Revision anzeigt
- SeInDiSp: Berechnet einen neuen Koordinatenwert in einem bestimmten Bereich mit einem bestimmten Schritt
- RNDfromCI: erzeugt eine Zufallszahl in einem bestimmten Intervall
- Skalierung: Skalierung der Zahl auf den angegebenen Bereich
//—————————————————————————————————————————————————————————————————————————————— class C_AO_IWDm { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Drop p []; //particles (drops) public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordsP, //coordinates number const int popSizeP, //population size const int sectorsNumberP, //sectors number const double waterViscosityP); //water viscosity (>= 1) public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coords; //coordinates number private: int popSize; //population size private: int sectorsNumber; //sectors number private: double waterViscosity; //water viscosity private: double sectorSpace []; //sector space private: S_Riverbed rb []; //riverbed private: int iterationCounter; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init initialisiert das Objekt der Klasse C_AO_IWDm mit den angegebenen Parametern: Anzahl der Koordinaten, Anzahl der Tropfen, Anzahl der Sektoren, Wasserviskosität.
Diese Methode bewirkt Folgendes:
1. Setzt den Zufallszahlengenerator zurück.
2. Initialisiert den Wert der Zielfunktion „fB“ mit dem Wert „-DBL_MAX“.
3. Setzt den Iterationszähler auf Null.
4. Setzt die Anzahl der „coords“-Koordinaten und die „popSize“-Populationsgröße auf die angegebenen Werte.
5. Setzt „sectorsNumber“ und „waterViscosity“ auf die angegebenen Werte.
6. Ändert die Größe des Arrays „sectorSpace“ in „coord“.
7. Ändern Sie die Größe des Arrays „p“ in „popSize“ und initialisieren Sie jeden Wassertropfen im Array „p“.
8. Ändert die Arraygrößen von „rangeMax“, „rangeMin“, „rangeStep“ und „cB“ auf „coords“.
9. Ändert die Größe des Arrays „rb“ auf „coords“ und initialisiert jedes Element des Arrays „rb“, einschließlich der Arrays „riverbedDepth“ und „coordOnSector“, und setzt sie auf ihre Standardwerte.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_IWDm::Init (const int coordsP, //coordinates number const int popSizeP, //population size const int sectorsNumberP, //sectors number const double waterViscosityP) //water viscosity (>= 1) { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; iterationCounter = 0; coords = coordsP; popSize = popSizeP; sectorsNumber = sectorsNumberP; waterViscosity = waterViscosityP; ArrayResize (sectorSpace, coords); ArrayResize (p, popSize); for (int i = 0; i < popSize; i++) p [i].Init (coords); ArrayResize (rangeMax, coords); ArrayResize (rangeMin, coords); ArrayResize (rangeStep, coords); ArrayResize (cB, coords); ArrayResize (rb, coords); for (int i = 0; i < coords; i++) { ArrayResize (rb [i].riverbedDepth, sectorsNumber); ArrayResize (rb [i].coordOnSector, sectorsNumber); ArrayInitialize (rb [i].riverbedDepth, 0.0); ArrayInitialize (rb [i].coordOnSector, -DBL_MAX); } } //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns die Methode Moving() abschnittsweise an.
Dieser Codeblock wird nur bei der ersten und zweiten Iteration ausgeführt. Es berechnet und legt die Größe jedes Sektors „sectorSpace“ für jede Koordinate fest. Die Sektorgröße wird bestimmt, indem der Bereich der Werte „rangeMax - rangeMin“ durch die Anzahl der Sektoren „sectorsNumber“ geteilt wird.
Als Nächstes werden die Tropfen mit Anfangswerten initialisiert, die auf zufälligen Werten in bestimmten Bereichen mit einer gleichmäßigen Verteilung basieren.
//---------------------------------------------------------------------------- if (iterationCounter == 0) { for (int i = 0; i < coords; i++) sectorSpace [i] = (rangeMax [i] - rangeMin [i]) / sectorsNumber; } //1,4------------------------------------------------------------------------- if (iterationCounter == 0 || iterationCounter == 1) { double min = 0.0; double max = 0.0; int s = 0; for (int i = 0; i < popSize; i++) { p [i].fPrev = p [i].f; for (int c = 0; c < coords; c++) { s = (int)(RNDfromCI (0, sectorsNumber)); if (s >= sectorsNumber) s = sectorsNumber - 1; p [i].rSection [c] = s; min = rangeMin [c] + sectorSpace [c] * s; max = min + sectorSpace [c]; p [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]); } } for (int i = 0; i < popSize; i++) p [i].fPrev = p [i].f; return; }
Das Codeschnipsel berechnet und normalisiert dann die altChange für jeden Wassertropfen in der Population. Die einzige Raffinesse in diesem Code besteht darin, die Gleichheit der maximalen und minimalen Höhenänderung zu überprüfen, um eine Division durch „0“ zu vermeiden. In diesem Fall gehen wir davon aus, dass sich die Höhe der Wassertropfen nicht verändert hat.
Der Wert „altChange“ für jeden Wassertropfen wird als normalisierter Wert berechnet, der im Bereich von 0 bis 1 liegt. Die Normalisierung erfolgt durch Subtraktion von „minAltChange“ von „altChange“ und Teilung des Ergebnisses durch die Differenz zwischen „maxAltChange“ und „minAltChange“.
//7--------------------------------------------------------------------------- double maxAltChange = -DBL_MAX; double minAltChange = DBL_MAX; double altChange = 0.0; double randSC = 0.0; //random selection component double maxRC = 0.0; double nowRC = 0.0; int indSector = 0; for (int i = 0; i < popSize; i++) { altChange = fabs (p [i].f - p [i].fPrev); p [i].altChange = altChange; if (altChange < minAltChange) minAltChange = altChange; if (altChange > maxAltChange) maxAltChange = altChange; } if (minAltChange == maxAltChange) { for (int i = 0; i < popSize; i++) { p [i].altChange = 0.0; } } else { for (int i = 0; i < popSize; i++) { altChange = p [i].altChange; p [i].altChange = (altChange - minAltChange) / (maxAltChange - minAltChange); } }
Das folgende Codefragment aktualisiert die Tiefe des Flussbetts für jede Koordinate, wenn der aktuelle Wert der Fitnessfunktion größer ist als der vorherige Wert für den entsprechenden Tropfen. Dadurch können wir Höhenänderungen berücksichtigen und die Form des Flussbettes beeinflussen. Jedes Mal, wenn ein Tropfen seine Position verbessert, nehmen wir also an, dass sich das Flussbett verändert hat.
//8--------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (p [i].f > p [i].fPrev) { for (int c = 0; c < coords; c++) { rb [c].riverbedDepth [p [i].rSection [c]] += p [i].altChange; } } }
Der folgende Codeschnipsel führt zwei grundlegende Aktionen aus, um die Koordinaten der Agenten zu ändern, die die Suchstrategie bereitstellen:
- Ein Wassertropfen wählt zufällig einen anderen Wassertropfen aus der Population aus und leiht sich von ihm die Sektornummer, so sind die kombinatorischen Eigenschaften des Algorithmus gewährleistet.
- Ein Wassertropfen wählt nach dem Zufallsprinzip einen Sektor des Flusses im Verhältnis zu der bekannten Tiefe in jedem Sektor aus.
Sobald der Sektor ausgewählt ist, erzeugen wir eine neue Koordinate für den Wassertropfen mit einer gleichmäßigen Verteilung, wenn der Sektor von einem anderen Tropfen genommen wurde, und mit einer quadratischen Funktionsverteilung, wenn der Sektor aus den im Flussbett gespeicherten Informationen ausgewählt wurde. Der resultierende Wert für jede Koordinate wird in den akzeptablen Bereich gebracht.
//9--------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { n = (int)(RNDfromCI (0, popSize)); if (n >= popSize) n = popSize - 1; if (p [n].f > p [i].f) { p [i].rSection [c] = p [n].rSection [c]; min = rangeMin [c] + sectorSpace [c] * p [i].rSection [c]; max = min + sectorSpace [c]; p [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]); } else { randSC = RNDfromCI (0.0, 1.0); nowRC = rb [c].riverbedDepth [0] * randSC; maxRC = nowRC; indSector = 0; for (int r = 1; r < sectorsNumber; r++) { nowRC = rb [c].riverbedDepth [r] * randSC; if (nowRC > maxRC) { maxRC = nowRC; indSector = r; } } if (rb [c].coordOnSector [indSector] == -DBL_MAX) { min = rangeMin [c] + sectorSpace [c] * indSector; max = min + sectorSpace [c]; p [i].c [c] = RNDfromCI (min, max); } else { double x = RNDfromCI (-1.0, 1.0); double y = x * x; double pit = 0.0; double dif = Scale (y, 0.0, 1.0, 0.0, sectorSpace [c] * waterViscosity, false); pit = rb [c].coordOnSector [indSector]; pit += x > 0.0 ? dif : -dif; p [i].c [c] = pit; } min = rangeMin [c] + sectorSpace [c] * indSector; max = min + sectorSpace [c]; p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); p [i].rSection [c] = indSector; } } }
Als Nächstes wird der vorherige Fitnesswert „fPrev“ für jeden Wassertropfen aktualisiert, wenn der aktuelle Wert der Zielfunktion „f“ größer ist als der vorherige Wert. Auf diese Weise können wir Änderungen in der Zielfunktion verfolgen und diese Informationen im Algorithmus verwenden, um Entscheidungen über die Wahl des nächsten Schritts zu treffen.
for (int i = 0; i < popSize; i++) { if (p [i].f > p [i].fPrev) p [i].fPrev = p [i].f; }
Betrachten wir abschließend die Revisionsmethode. Sie dient der Aktualisierung der besten Lösung „cB“ und des entsprechenden Werts der Fitnessfunktion. Wenn bei der aktuellen Iteration eine bessere Lösung gefunden wird, speichern wir die Koordinate des entsprechenden Sektors. So merkt sich das Flussbett die tiefsten Stellen in jedem Sektor bei jeder Koordinate. In dieser Methode erhöhen wir den Iterationszähler „iterationCounter“ um eins, sodass wir in der Methode Moving entsprechend der Iterationen navigieren und Aktionen durchführen können.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_IWDm::Revision () { //3,6,11---------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (p [i].f > fB) { fB = p [i].f; ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY); for (int c = 0; c < coords; c++) { rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c]; } } else { for (int c = 0; c < coords; c++) { if (rb [c].coordOnSector [p [i].rSection [c]] == -DBL_MAX) { rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c]; } } } } iterationCounter++; } //——————————————————————————————————————————————————————————————————————————————
3. Geänderte Version von SDSm
Wir werden die Ergebnisse des IWDm-Algorithmus später betrachten, aber sie brachten uns auf die Idee, zu versuchen, einen anderen Algorithmus zu verbessern, den besten in der Bewertung - SDS, da sowohl IWDm als auch SDS ähnliche Entitäten (Branchen bzw. Restaurants) verwenden. Die im IWD angewandte Methode der Positionsverfeinerung mit Hilfe einer quatratischen Wahrscheinlichkeitsverteilung hat dazu beigetragen, die SDS noch besser zu machen: Die beste Methode der Positionsverfeinerung hatte einen großen Einfluss auf die endgültigen Testergebnisse. Der einzige Unterschied besteht darin, dass in SDSm die Verteilung abgeschnitten wird, wenn sie gegenüber einem benachbarten Restaurant liegt..
Es wurden Änderungen an der Revisionsmethode des SDS-Algorithmus vorgenommen, und aufgrund signifikanter Änderungen in der Verteilung der neuen Koordinaten innerhalb des Restaurants (vorher war sie gleichmäßig) und der Testergebnisse wurde dem Algorithmus der Index „m“ zugewiesen.
Im Code sehen wir, dass die Funktion Research nun für die Verteilung der Zufallsvariablen zuständig ist, die als Argumente das Verhältnis der Verteilungsbreite, die Adresse des Restaurants, die Größe des Restaurants, den kleinstmöglichen Wert entlang der Koordinate, den Schritt entlang der Koordinate, die Fitness beim vorherigen Schritt und die Koordinate, die wir zu verbessern versuchen, erhält.
Mit dem SDSm-Algorithmus versuchen wir, drei Arten von Koordinaten (Gerichte in Restaurants) zu verbessern:
- die Koordinate des Gesprächspartner-Kandidaten
- die beste Koordinate in einem zufällig ausgewählten Restaurant (genau wie in IWDm für ein Flussbett, speichern wir in SDSm die besten Koordinaten für alle Restaurants - das ist so, als ob wir eine Liste der besten Gerichte in allen Restaurants der Stadt speichern)
- unsere eigene Koordinate für das entsprechende Restaurant
Die Verhältnisse der Wahrscheinlichkeitsverteilungsbreite könnten in die externen Parameter aufgenommen werden, aber ich habe dies nicht getan, um die meiner Meinung nach besten Werte einzustellen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SDSm::Revision () { /* here is the old code, no changes */ for (int i = 0; i < populationSize; i++) { for (int c = 0; c < coords; c++) { n = (int)(RNDfromCI (0, populationSize)); if (n >= populationSize) n = populationSize - 1; if (cands [n].fPrev > cands [i].fPrev) { cands [i].raddr [c] = cands [n].raddrPrev [c]; Research (0.25, cands [i].raddr [c], restSpace [c], rangeMin [c], rangeStep [c], cands [n].cPrev [c], cands [i].c [c]); } else { rnd = RNDfromCI (0.0, 1.0); if (rnd < probabRest) { n = (int)(RNDfromCI (0, restNumb)); if (n >= restNumb) n = restNumb - 1; cands [i].raddr [c] = n; Research (1.0, cands [i].raddr [c], restSpace [c], rangeMin [c], rangeStep [c], rb [c].coordOnSector [n], cands [i].c [c]); } else { cands [i].raddr [c] = cands [i].raddrPrev [c]; Research (0.25, cands [i].raddr [c], restSpace [c], rangeMin [c], rangeStep [c], cands [i].cPrev [c], cands [i].c [c]); } } } } } //——————————————————————————————————————————————————————————————————————————————
Hier ist die „magische“ Research-Funktion, die es ermöglichte, den vorherigen Testführer um mehr als 12 % zu verbessern.
Die Funktion bewirkt Folgendes:
- Es wird eine Zufallszahl im Bereich [-1,0;1,0] erzeugt,
- der sich ergebende Wert wird in Schritten entsprechend der Größe des Restaurants mit dem Verteilungsskalierungsfaktor skaliert,
- er wird zu der aktuellen aktualisierten Koordinate hinzugefügt,
- die Restaurantgrenzen werden festgelegt,
- die Zahl wird in akzeptable Werte umgewandelt, entsprechend dem Schritt des optimierten Parameters mit Trimmen entlang der Restaurantgrenzen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SDSm::Research (const double ko, const int raddr, const double restSpaceI, const double rangeMinI, const double rangeStepI, const double pitOld, double &pitNew) { double x = RNDfromCI(-1.0, 1.0); double y = x * x; double pit = pitOld; double min = 0.0; double max = 0.0; double dif = Scale(y, 0.0, 1.0, 0.0, restSpaceI * ko, false); pit += x > 0.0 ? dif : -dif; min = rangeMinI + restSpaceI * raddr; max = min + restSpaceI; pitNew = SeInDiSp (pit, min, max, rangeStepI); } //——————————————————————————————————————————————————————————————————————————————
4. Testergebnisse
IWD Testergebnisse:
C_AO_IWDm:50;10;3.0
=============================
5 Rastrigin's; Func runs 10000 result: 63.304838882364926
Score: 0.78438
25 Rastrigin's; Func runs 10000 result: 49.20424466627239
Score: 0.60967
500 Rastrigin's; Func runs 10000 result: 39.68464591598694
Score: 0.49172
=============================
5 Forest's; Func runs 10000 result: 0.6975685023058024
Score: 0.39458
25 Forest's; Func runs 10000 result: 0.19878497533879688
Score: 0.11244
500 Forest's; Func runs 10000 result: 0.0569274044494088
Score: 0.03220
=============================
5 Megacity's; Func runs 10000 result: 3.44
Score: 0.28667
25 Megacity's; Func runs 10000 result: 1.088
Score: 0.09067
500 Megacity's; Func runs 10000 result: 0.28480000000000005
Score: 0.02373
=============================
All score: 2.82606
Die Ergebnisse in der Vergleichstabelle sind, gelinde ausgedrückt, unterdurchschnittlich.
SDSm Testergebnisse:
C_AO_SDSm:100;100;0.05
=============================
5 Rastrigin's; Func runs 10000 result: 80.65976429448276
Score: 0.99942
25 Rastrigin's; Func runs 10000 result: 79.95659847225565
Score: 0.99071
500 Rastrigin's; Func runs 10000 result: 57.23107170601535
Score: 0.70913
=============================
5 Forest's; Func runs 10000 result: 1.7241883676504082
Score: 0.97529
25 Forest's; Func runs 10000 result: 1.497160007591401
Score: 0.84687
500 Forest's; Func runs 10000 result: 0.29481739063639945
Score: 0.16676
=============================
5 Megacity's; Func runs 10000 result: 10.559999999999999
Score: 0.88000
25 Megacity's; Func runs 10000 result: 6.824000000000001
Score: 0.56867
500 Megacity's; Func runs 10000 result: 1.2384
Score: 0.10320
=============================
All score: 6.24004
Die Ergebnisse von SDSm sind wirklich beeindruckend.
Die animierte Visualisierung des IWDm-Algorithmus zeigt ein gewisses Maß die Fähigkeit, potenziell gute Suchregionen zu clustern, was besonders bei der Rastrigin-Funktion auffällt. Aber die langen flachen Abschnitte des Konvergenzgraphen zeigen, wo der Algorithmus merklich stecken geblieben ist.
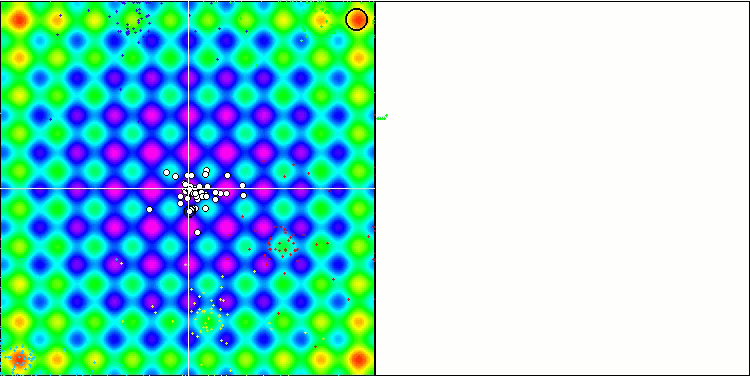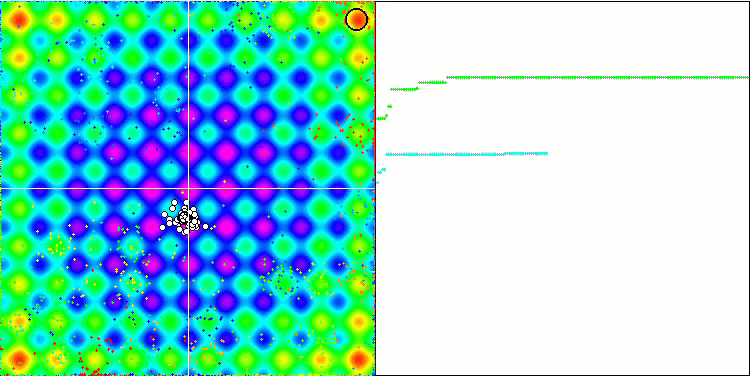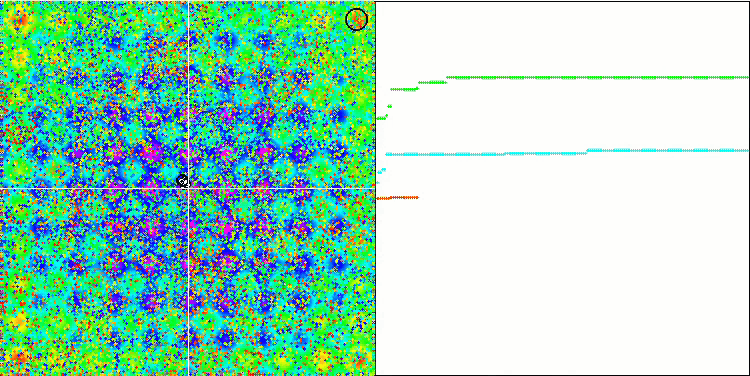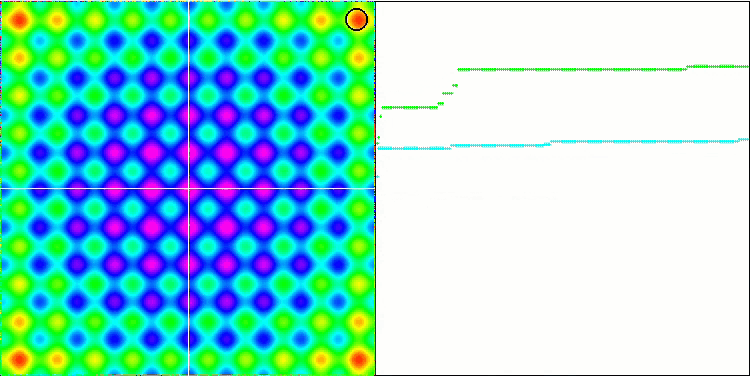
IWDm mit der Testfunktion Rastrigin-.
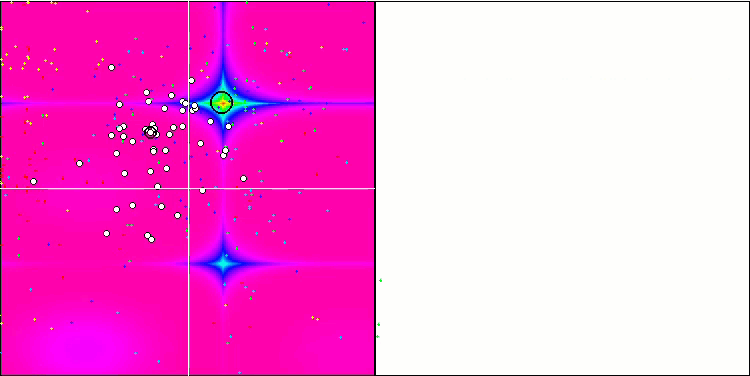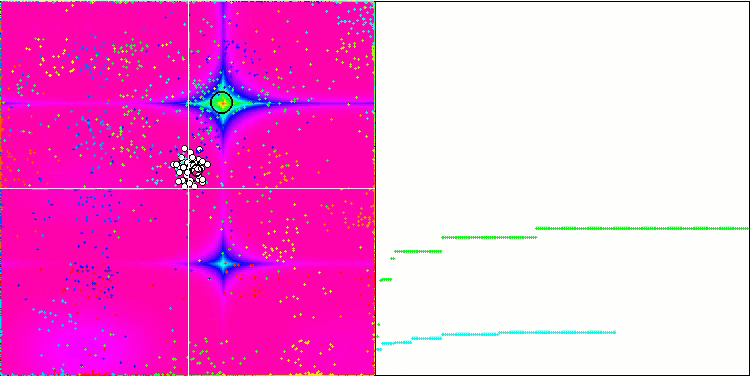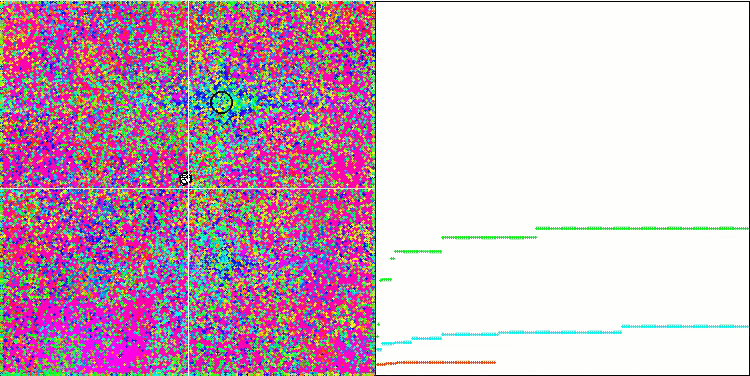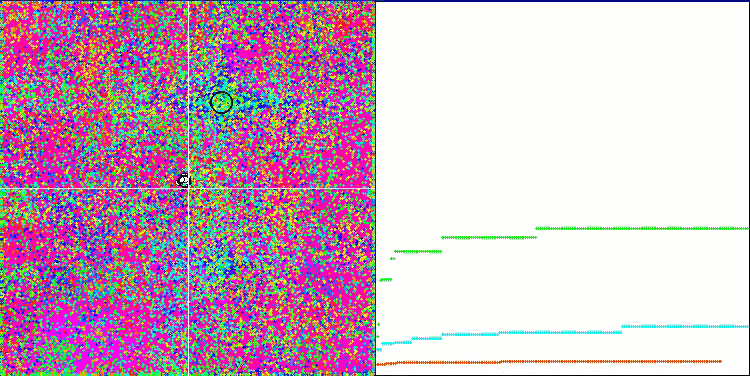
IWDm mit der Testfunktion Forest.
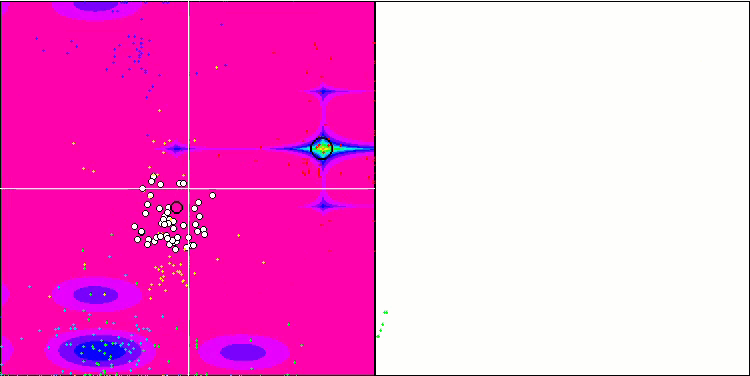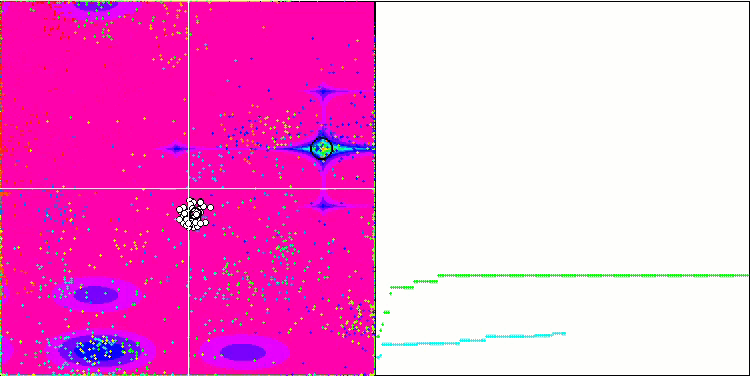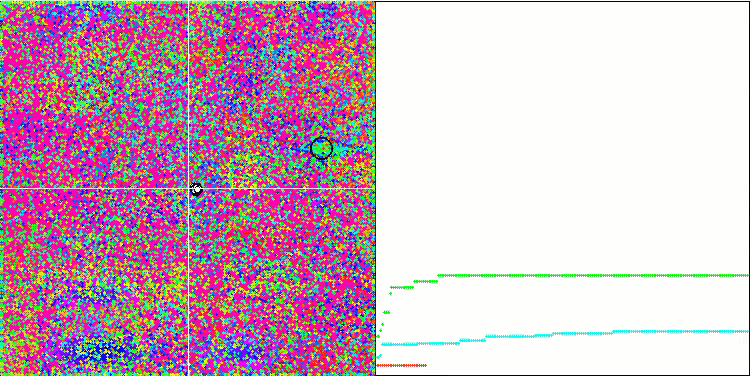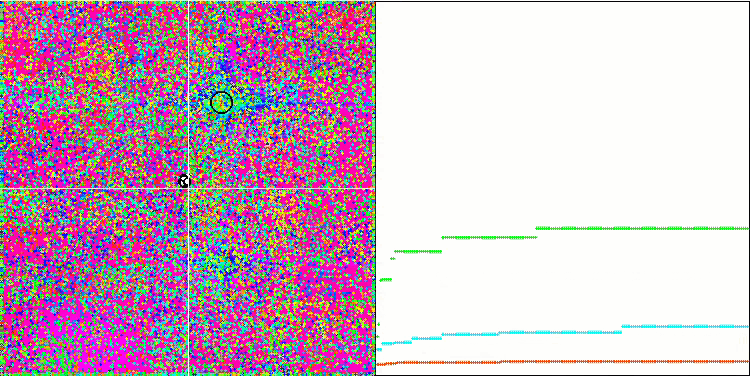
IWDm mit der Testfunktion Megacity.
In diesem Artikel wurde der IWDm-Algorithmus untersucht, der unter 22 Algorithmen den 19. Platz bzw. den 4. Platz von unten belegte und damit den bekannten und beliebten PSO-Algorithmus überholte. IWDm zeigt die besten Ergebnisse bei glatten Funktionen. Die stetige Verbesserung der Konvergenzkurven bei allen drei Testfunktionen lässt hoffen, dass der Algorithmus mit zunehmender Iterationszahl weiter konvergiert, aber dann schwinden die praktische Bedeutung und die Zweckmäßigkeit seiner Anwendung. Die Testbedingungen sind streng: 10.000 Iterationen, nicht mehr und nicht weniger.
Darüber hinaus ist der modifizierte SDSm-Algorithmus zu erwähnen, der 7 von 9 möglichen ersten Plätzen belegte. Dieser Algorithmus ist ein echter „Alleskönner“ unter den Optimierungsalgorithmen. Die Verbesserung der SDSm-Ergebnisse im Vergleich zur herkömmlichen SDS bei den „scharfen“ Forest- und komplexen diskreten Megacity-Funktionen ist besonders auffällig (bei der letztgenannten Funktion beträgt die Verbesserung fast 30 % bei 1000 Parametern). So sehen wir neben dem Hauptthema des Artikels - IWD - einen neuen und großartigen Gast am Tisch - SDSm. Die Animation des SDS-Betriebs können Sie hier sehen. Um zu sehen, wie SDSm funktioniert, führen Sie das Testskript aus dem Archiv aus, das sich in dem Ordner mit SDS befindet.
| # | AO | Beschreibung | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (diskret) | Megacity final | Final result | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | |||||||
| 1 | SDSm | stochastische Diffusionssuche M | 0.99809 | 1.00000 | 0.69149 | 2.68958 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 100.000 |
| 2 | SDS | stochastische Diffusionssuche | 0.99737 | 0.97322 | 0.58904 | 2.55963 | 0.96778 | 0.93572 | 0.79649 | 2.69999 | 0.78696 | 0.93815 | 0.71804 | 2.44315 | 88.208 |
| 3 | SSG | Setzen, Säen und Wachsen | 1.00000 | 0.92761 | 0.51630 | 2.44391 | 0.72654 | 0.65201 | 0.83760 | 2.21615 | 0.54782 | 0.61841 | 0.99522 | 2.16146 | 77.678 |
| 4 | HS | Harmoniesuche | 0.99676 | 0.88385 | 0.44686 | 2.32747 | 0.99882 | 0.68242 | 0.37529 | 2.05653 | 0.71739 | 0.71842 | 0.41338 | 1.84919 | 70.647 |
| 5 | IWO | Optimierung mit invasiven Unkräutern | 0.95828 | 0.62227 | 0.27647 | 1.85703 | 0.70690 | 0.31972 | 0.26613 | 1.29275 | 0.57391 | 0.30527 | 0.33130 | 1.21048 | 48.267 |
| 6 | ACOm | Ameisen-Kolonie-Optimierung M | 0.34611 | 0.16683 | 0.15808 | 0.67103 | 0.86785 | 0.68980 | 0.64798 | 2.20563 | 0.71739 | 0.63947 | 0.05579 | 1.41265 | 47.419 |
| 7 | MEC | Evolutionäre Berechnung des Geistes | 0.99270 | 0.47345 | 0.21148 | 1.67763 | 0.60691 | 0.28046 | 0.21324 | 1.10061 | 0.66957 | 0.30000 | 0.26045 | 1.23002 | 44.061 |
| 8 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.92400 | 0.43407 | 0.24120 | 1.59927 | 0.58309 | 0.23477 | 0.13842 | 0.95629 | 0.52174 | 0.24079 | 0.17001 | 0.93254 | 37.845 |
| 9 | FAm | Firefly-Algorithmus M | 0.59825 | 0.31520 | 0.15893 | 1.07239 | 0.51012 | 0.29178 | 0.41704 | 1.21894 | 0.24783 | 0.20526 | 0.35090 | 0.80398 | 33.152 |
| 10 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.78170 | 0.30347 | 0.19313 | 1.27829 | 0.53774 | 0.14799 | 0.11177 | 0.79750 | 0.40435 | 0.19474 | 0.13859 | 0.73768 | 29.784 |
| 11 | BA | Fledermaus-Algorithmus | 0.40526 | 0.59145 | 0.78330 | 1.78002 | 0.20817 | 0.12056 | 0.21769 | 0.54641 | 0.21305 | 0.07632 | 0.17288 | 0.46225 | 29.488 |
| 12 | CSS | Suche geladener Systeme | 0.56605 | 0.68683 | 1.00000 | 2.25289 | 0.14065 | 0.01853 | 0.13638 | 0.29555 | 0.07392 | 0.00000 | 0.03465 | 0.10856 | 27.914 |
| 13 | GSA | Algorithmus für die Schwerkraftsuche | 0.70167 | 0.41944 | 0.00000 | 1.12111 | 0.31623 | 0.25120 | 0.27812 | 0.84554 | 0.42609 | 0.25525 | 0.00000 | 0.68134 | 27.807 |
| 14 | BFO | Optimierung der bakteriellen Futtersuche | 0.67203 | 0.28721 | 0.10957 | 1.06881 | 0.39655 | 0.18364 | 0.17298 | 0.75317 | 0.37392 | 0.24211 | 0.18841 | 0.80444 | 27.549 |
| 15 | EM | elektromagnetismusähnlicher Algorithmus | 0.12235 | 0.42928 | 0.92752 | 1.47915 | 0.00000 | 0.02413 | 0.29215 | 0.31628 | 0.00000 | 0.00527 | 0.10872 | 0.11399 | 18.981 |
| 16 | SFL | schlurfender Froschsprung | 0.40072 | 0.22021 | 0.24624 | 0.86717 | 0.20129 | 0.02861 | 0.02221 | 0.25211 | 0.19565 | 0.04474 | 0.06607 | 0.30646 | 13.201 |
| 17 | MA | Affen-Algorithmus | 0.33192 | 0.31029 | 0.13582 | 0.77804 | 0.10000 | 0.05443 | 0.07482 | 0.22926 | 0.15652 | 0.03553 | 0.10669 | 0.29874 | 11.771 |
| 18 | FSS | Fischschulsuche | 0.46812 | 0.23502 | 0.10483 | 0.80798 | 0.12825 | 0.03458 | 0.05458 | 0.21741 | 0.12175 | 0.03947 | 0.08244 | 0.24366 | 11.329 |
| 19 | IWDm | intelligente Wassertropfen M | 0.26459 | 0.13013 | 0.07500 | 0.46972 | 0.28568 | 0.05445 | 0.05112 | 0.39126 | 0.22609 | 0.05659 | 0.05054 | 0.33322 | 10.434 |
| 20 | PSO | Partikelschwarmoptimierung | 0.20449 | 0.07607 | 0.06641 | 0.34696 | 0.18873 | 0.07233 | 0.18207 | 0.44313 | 0.16956 | 0.04737 | 0.01947 | 0.23641 | 8.431 |
| 21 | RND | zufällig | 0.16826 | 0.09038 | 0.07438 | 0.33302 | 0.13480 | 0.03318 | 0.03949 | 0.20747 | 0.12175 | 0.03290 | 0.04898 | 0.20363 | 5.056 |
| 22 | GWO | Grauer-Wolf-Optimierung | 0.00000 | 0.00000 | 0.02093 | 0.02093 | 0.06562 | 0.00000 | 0.00000 | 0.06562 | 0.23478 | 0.05789 | 0.02545 | 0.31812 | 1.000 |
Zusammenfassung
Der ursprüngliche IWD-Algorithmus wurde vom Autor entwickelt, um Probleme bei der Suche nach kürzesten Wegen zu lösen, z. B. in der Transportlogistik, beim Netzwerk-Routing und bei der Suche nach optimalen Wegen in geografischen Informationssystemen. In diesem Artikel wurden seine Fähigkeiten und Leistungen bei diesen spezifischen Aufgaben nicht untersucht, und der neue modifizierte IWDm-Algorithmus, der als universeller Algorithmus vorgestellt wurde, konnte keine beeindruckenden Ergebnisse vorweisen. Die Erhöhung der Anzahl der Sektoren führte leider nicht zu einer Steigerung der Effizienz des Algorithmus.
Die Funktionsweise des IWDm-Algorithmus hinterließ bei mir jedoch das Gefühl, dass das volle Potenzial dieses eleganten Algorithmus noch nicht voll ausgeschöpft wurde. Die Idee, den Suchraum in Sektoren aufzuteilen und deren Bewertung zu berücksichtigen, die auf der Modellierung der Erdbewegung im Flussbett beruht, erscheint sehr interessant. Die Ergebnisse zeigten, dass ein solcher Ansatz, wie z. B. die Speicherung der besten Gerichte in jedem Restaurant, und vielleicht mit einer Verzerrung der Wahrscheinlichkeit eines neuen Punktes in der Nähe des vorherigen, die Leistung des SDS-Algorithmus deutlich verbessert.
Wenn wir die Anzahl der Restaurants im neuen SDSm erhöhen (der Standardparameter ist 100) und die Koordinaten in kleinere Gebiete unterteilen (der SDS-Parameter ist 1000), werden die Ergebnisse schlechter. Das bedeutet, dass bei diesem Ansatz die Wahl eines einzelnen Restaurants wichtiger wird und ein bestimmter Punkt in seiner Nähe an Bedeutung verliert (der Algorithmus wird zu einem normalen SDS). Das bedeutet, dass die quadratische Wahrscheinlichkeitsverteilung bei einer bestimmten Größe der Sektoren den größten Einfluss auf die Koordinaten hat. Dies ist eine Art Gleichgewicht zwischen den im Algorithmus vorhandenen Methoden, die sich in ihren Zielen unterscheiden.
Die wichtigste Erkenntnis aus diesem Artikel ist, dass es unmöglich ist, definitiv zu sagen, welche Methode bei den einzelnen Suchstrategien die beste oder die schlechteste ist. Die Verwendung unterschiedlicher Methoden kann einige Algorithmen verschlechtern und andere erheblich verbessern. Wichtig ist die Kombination der in Optimierungsalgorithmen verwendeten Methoden, nicht die Methoden selbst.
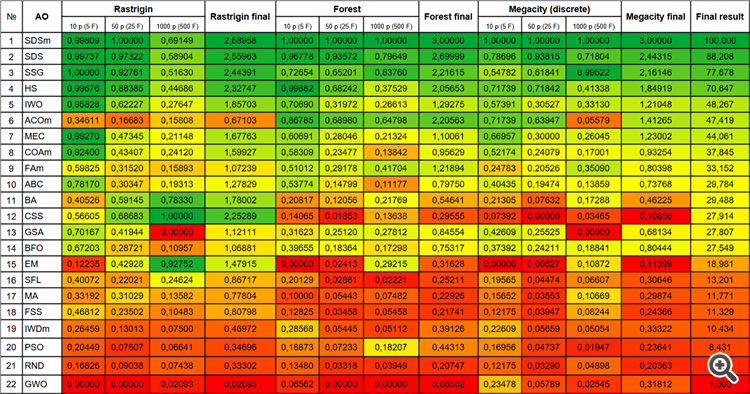
Bild 2. Farbabstufung der Algorithmen gemäß den einschlägigen Tests
Das Histogramm der Algorithmus-Testergebnisse finden Sie unten (auf einer Skala von 0 bis 100, je höher, desto besser, im Archiv finden Sie ein Skript zur Berechnung der Bewertungstabelle nach der in diesem Artikel beschriebenen Methode):
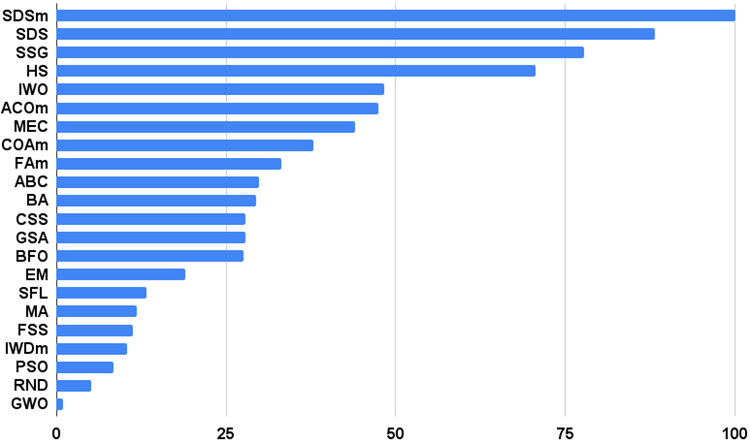
Abb. 3. Histogramm der Endergebnisse der Testalgorithmen
Vor- und Nachteile des modifizierten Algorithmus für intelligente Wassertropfen (IWDm):
Vorteile:
1. Eine kleine Anzahl von externen Parametern.
Nachteile
1. Schlechte Ergebnisse bei glatten und diskreten Funktionen.
2. Geringe Konvergenz.
3. Tendenz, in lokalen Extremen stecken zu bleiben.
Dem Artikel ist ein Archiv mit aktualisierten Versionen der in früheren Artikeln beschriebenen Algorithmuscodes beigefügt. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13730
Python, ONNX und MetaTrader 5: Erstellen eines RandomForest-Modells mit RobustScaler und PolynomialFeatures zur Datenvorverarbeitung
Neuronale Netze leicht gemacht (Teil 65): Abstandsgewichtetes überwachtes Lernen (DWSL)
Bauen Sie Ihr erstes Modell einer Glass-Box mit Python und MQL5
Algorithmen zur Optimierung mit Populationen: Differenzielle Evolution (DE)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.