
Neuronale Netze im Handel: Superpoint Transformer (SPFormer)
Einführung
Die Segmentierung von Objekten ist eine komplexe Aufgabe, bei der es nicht nur um die Erkennung von Objekten in einer spärlichen Punktwolke geht, sondern auch um die Erstellung einer präzisen Maske für jedes Objekt.
Moderne Methoden können in 2 Gruppen eingeteilt werden:
- Ansätze auf Basis von Annahmen
- Ansätze auf Basis des Clusterings
Annahmenbasierte Methoden behandeln die 3D-Objektsegmentierung als eine Top-Down-Pipeline. Sie erzeugen zunächst Regionsvorschläge und bestimmen dann Objektmasken innerhalb dieser Regionen. Diese Methoden scheitern jedoch häufig an der geringen Anzahl von Punktwolken. In 3D-Raum verfügt der Begrenzungsrahmen über einen großen Freiheitsgrad, was die Komplexität der Näherung erhöht. Außerdem sind Punkte in der Regel nur auf Teilen der Oberfläche eines Objekts vorhanden, was die Lokalisierung der geometrischen Zentren erschwert. Qualitativ minderwertige Regionsvorschläge beeinträchtigen den blockbasierten bipartiten Abgleich und verschlechtern die Modellleistung weiter.
Im Gegensatz dazu folgen clusterbasierte Methoden einer Bottom-up-Pipeline. Sie sagen punktweise, semantische Kennzeichnungen und Instanzmittelpunktsverschiebungen voraus. Dann fassen sie die verschobenen Punkte und semantischen Vorhersagen zu Instanzen zusammen. Diese Methoden haben jedoch ihre eigenen Grenzen. Ihre Abhängigkeit von semantischen Segmentierungsergebnissen kann zu ungenauen Vorhersagen führen. Außerdem verlängert der Zwischenschritt der Datenaggregation sowohl die Trainings- als auch die Inferenzzeit.
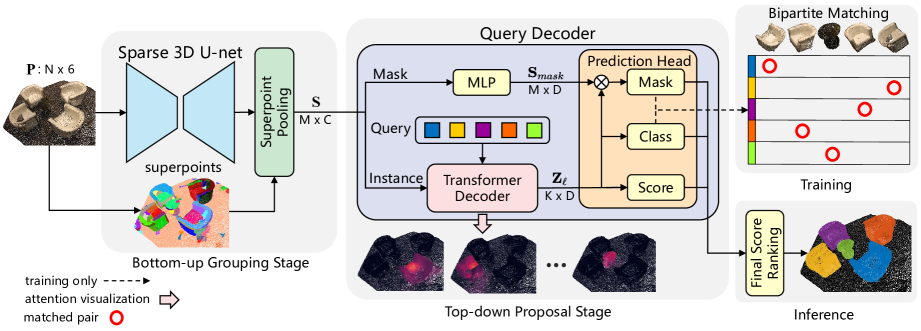
Um diese Einschränkungen zu beseitigen und die Stärken beider Ansätze zu nutzen, haben die Autoren von „Superpoint Transformer for 3D Scene Instance Segmentation“ eine neuartige zweistufige Ende-zu-Ende-Methode für die 3D-Objektsegmentierung namens Superpoint Transformer (SPFormer) vor. Der SPFormer gruppiert bottom-up potenzielle Objekte aus Punktwolken zu Superpunkten und schlägt Instanzen über Abfragevektoren in einer Top-down-Methode vor.
In der Bottom-up-Gruppierungsphase wird ein spärliches 3D-U-Netz verwendet, um Merkmale auf Punktebene zu extrahieren. Es wird eine einfache Punkt-Pooling-Ebene eingeführt, um Objekte auf Punktebene zu Superpunkten zusammenzufassen. Diese Superpunkte verwenden geometrische Muster zur Darstellung homogener Nachbarpunkte. Die daraus resultierenden potenziellen Objekte machen eine Überwachung durch indirekte semantische und Zentrumsabstandsbezeichnungen überflüssig. Die Autoren betrachten die Superpunkte als eine potenzielle Darstellung der 3D-Szene auf mittlerer Ebene und verwenden direkt Instanzkennzeichnungen zum Trainieren des Modells.
In der Top-down-Vorschlagsphase wird ein neuer Decoder des Transformers mit Abfragen eingeführt. Diese Abfragevektoren sagen Instanzen auf der Grundlage der Superpoint-Merkmale in einer Top-down-Pipeline voraus. Die lernfähigen Abfragevektoren erfassen die Instanzinformationen durch Kreuzaufmerksamkeit der Superpunkte. Unter Verwendung von Abfragevektoren, die mit Instanzinformationen und Superpoint-Merkmalen angereichert sind, sagt der Decoder direkt Klassenbezeichnungen, Vertrauenswerte und Instanzmasken voraus. Mit dem bipartiten Abgleich auf der Basis von Superpunktmasken ermöglicht SPFormer ein durchgängiges Training, ohne dass ein arbeitsintensiver Aggregationsschritt erforderlich ist. Außerdem erfordert der SPFormer keine Nachbearbeitung, was die Modelleffizienz weiter verbessert.
1. Der Algorithmus von SPFormer
Die von den Autoren vorgeschlagene Architektur des SPFormer-Modells ist logisch in verschiedene Blöcke unterteilt. Zunächst wird ein spärliches 3D-U-Netz verwendet, um Objektmerkmale auf der unteren Punktebene zu extrahieren. Unter der Annahme, dass die Eingabepunktwolke N Punkte enthält, wird jeder Punkt durch RGB-Farbwerte und XYZ-Koordinaten charakterisiert. Zur Regularisierung der Rohdaten schlagen die Autoren vor, die Punktwolke zu zerstückeln und ein U-Netz-ähnliches Backbone zu verwenden, das aus spärlichen Faltungen besteht, um Punktmerkmale zu extrahieren, die als P′ bezeichnet werden. Im Gegensatz zu clusterbasierten Methoden enthält der vorgeschlagene Ansatz keinen zusätzlichen semantischen Zweig.
Um einen einheitlichen Rahmen zu schaffen, geben die Autoren von SPFormer die extrahierten Punktmerkmale P′ direkt in eine Superpunkt-Pooling-Schicht ein, die auf vorberechneten Punkten basiert. Diese Superpunkt-Pooling-Ebene erhält S-Objekte durch Mittelwertbildung der Punkte innerhalb jedes Superpunkts. Die Superpunkt-Pooling-Ebene skaliert die ursprüngliche Punktwolke zuverlässig herunter, wodurch der Rechenaufwand für die nachfolgende Verarbeitung erheblich gesenkt werden und die Darstellungseffizienz des Modells insgesamt verbessert wird.
Der Decoder der Abfrage (Query) besteht aus zwei Zweigen: Instanz und Maske. Im Maskenzweig wird ein einfaches mehrschichtiges Perzeptron (MLP) verwendet, um Merkmale zu extrahieren, die die Instanzmaske 𝐒mask unterstützen. Der Instanzzweig umfasst eine Reihe von Decoder-Schichten des Transformers. Sie dekodieren lernfähige Abfragevektoren durch Kreuzaufmerksamkeit der Superpunkte.
Nehmen wir an, es gibt K lernbare Abfragevektoren. Wir definieren die Eigenschaften des Abfragevektors für jede Decoder-Ebene des Transformers als Zl vor.
Angesichts der Unregelmäßigkeit und variablen Größe von Superpunkten führen die Autoren eine Transformerstruktur ein, um diese Variabilität in den Eingabedaten zu bewältigen. Die Merkmale des Superpunkts und die lernfähigen Abfragevektoren dienen als Eingabe für den Decoder des Transformers. Die sorgfältig entwickelte Architektur der modifizierten Decoder-Schicht des Transformers ist in der folgenden Abbildung dargestellt.
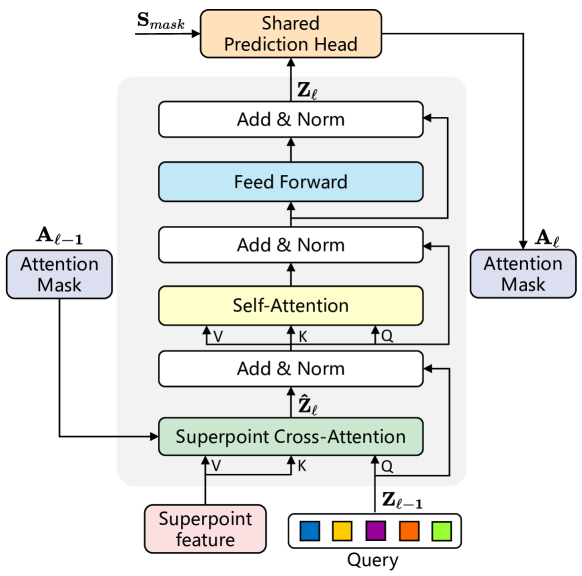
Die Abfragevektoren in SPFormer werden vor dem Training nach dem Zufallsprinzip initialisiert, und die instanzspezifischen Informationen für jede Punktwolke werden ausschließlich durch Kreuzaufmerksamkeit mit Superpunkten gewonnen. Infolgedessen ändert die vorgeschlagene Decoder-Schicht des Transformers die Standardarchitektur, indem die Reihenfolge der Schichten der Selbstaufmerksamkeit (Self-Attention) und der Kreuzaufmerksamkeit (Cross-Attention) im Vergleich zu herkömmlichen Transformer-Decodern umgekehrt wird. Da die Eingaben aus den Eigenschaften des Superpunkt bestehen, entfällt außerdem die Positionskodierung.
Um kontextuelle Informationen über die Kreuzaufmerksamkeit des SuperPoint zu erfassen, werden Aufmerksamkeitsmasken Aij verwendet, die den Einfluss von SuperPoint j auf die Anfrage i darstellen. Auf der Grundlage der vorhergesagten Masken des Superpunkts Ml aus dem Maskenzweig werden die Aufmerksamkeitsmasken des Superpunkts Al unter Verwendung eines Schwellenwertfilters mit τ=0,5 berechnet, einem von den Autoren empirisch ermittelten Wert.
Beim Stapeln der Decoder-Ebenen des Transformers schränken die Aufmerksamkeitsmasken Superpunkts Al die Kreuzaufmerksamkeit dynamisch ein, um sich auf die Instanzregionen im Vordergrund zu konzentrieren.
Unter Verwendung der Anfragevektoren Zl aus dem Instanzzweig setzen die Autoren zwei unabhängige MLPs ein, um die Klassifizierung und die Qualitätsbewertung für jeden Anfragevektor vorherzusagen. Insbesondere wird die Vorhersage „kein Objekt“ hinzugefügt, um während des bipartiten Abgleichs explizit Vertrauenswerte zuzuweisen, wobei alle nicht übereinstimmenden Abfragen als negative Stichproben behandelt werden.
Da die Einstufung der Vorschläge die Leistung der Instanzsegmentierung erheblich beeinflusst und aufgrund des Eins-zu-Eins-Abgleichs die meisten Vorschläge als Hintergrund behandelt werden, kann es außerdem zu Unstimmigkeiten bei der Einstufung kommen. Um dies abzumildern, führen die Autoren einen Bewertungszweig ein, der die Qualität jeder Maskenvorhersage des Superpunkts bewertet und dazu beiträgt, solche Verzerrungen zu korrigieren.
Angesichts der langsamen Konvergenz, die bei Architekturen auf der Basis von Transformern häufig zu beobachten ist, leiten die Autoren die Ausgabe jeder Decoder-Schicht des Transformers in einen gemeinsamen Vorhersagekopf, um Vorschläge zu erzeugen. Während des Trainings werden den Ausgängen der einzelnen Decoder-Schichten Vertrauenswerte zugewiesen, die auf der Basis von Fakten ermittelt wurden. Dieser Ansatz verbessert die Leistung des Modells und ermöglicht es den Abfragevektoren, sich effektiver durch die Schichten zu entwickeln.
Zum Zeitpunkt der Inferenz sagt SPFormer bei einer rohen Eingabepunktwolke direkt K Objektinstanzen zusammen mit ihren Klassenbezeichnungen und der entsprechenden Maske des Superpunks voraus. Die endgültige Maskenbewertung ergibt sich aus dem Mittelwert der Wahrscheinlichkeiten von Superpunkten mit Werten über 0,5 innerhalb jeder vorhergesagten Maske. SPFormer verlässt sich bei der Nachbearbeitung nicht auf die Nicht-Maximum-Unterdrückung, was zu seiner hohen Inferenzgeschwindigkeit beiträgt.
Eine visuelle Darstellung der Architektur SPFormer, wie sie von den Autoren vorgestellt wurde, ist unten abgebildet.
2. Implementation in MQL5
Nachdem wir die theoretischen Aspekte der SPFormer-Methode erläutert haben, gehen wir nun zum praktischen Teil unseres Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen. Ich muss sagen, dass wir heute eine Menge Arbeit vor uns haben. Fangen wir also an.
2.1 Erweitern von OpenCL
Wir beginnen damit, unser bestehendes OpenCL-Programm zu aktualisieren. Die Autoren von SPFormer haben einen neuen Maskierungsalgorithmus vorgeschlagen, der auf vorhergesagten Objektmasken basiert. Der Kerngedanke besteht darin, jede Abfrage nur mit relevanten Superpunkten abzugleichen. Dies unterscheidet sich stark von dem auf der Position der Quelldaten basierenden Ansatz, den wir früher verwendet haben und der im einfachen Transformer vorgeschlagen wurde. Daher müssen wir neue Kernel für die Kreuzaufmerksamkeit und den Rückwärtsdurchlauf entwickeln. Wir beginnen mit der Implementierung des Kernes des Vorwärtsdurchlaufs, MHMaskAttentionOut, der weitgehend vom Kernel des einfachen Transformers übernommen wird. Wir werden jedoch Änderungen vornehmen, um den neuen Maskierungsmechanismus zu berücksichtigen.
Wie bei früheren Implementierungen akzeptiert der Kernel Zeiger auf globale Puffer mit den Entitäten Query, Key und Value, deren Werte vorberechnet werden. Zusätzlich werden Zeiger auf die Puffer für die Aufmerksamkeitskoeffizienten und auf die Puffer für die Ausgabeergebnisse aufgenommen. Außerdem führen wir einen zusätzlichen Zeiger auf einen globalen Maskierungspuffer und einen Maskierungsschwellenparameter ein.
__kernel void MHMaskAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *kv, ///<[in] Matrix of Keys __global float *score, ///<[out] Matrix of Scores __global const float *mask, ///<[in] Mask Matrix __global float *out, ///<[out] Matrix of attention const int dimension, ///< Dimension of Key const int heads_kv, const float mask_level ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
Wie bisher planen wir, den Kernel in einem dreidimensionalen Aufgabenraum (Query, Key, Heads) zu starten. Wir werden lokale Arbeitsgruppen bilden, die den Datenaustausch zwischen Threads innerhalb derselben Query über Aufmerksamkeitsköpfe hinweg ermöglichen. Im Hauptteil der Methode wird sofort der aktuelle Ablauf der Operationen im Aufgabenraum bestimmt und die Parameter des Aufgabenraums festgelegt.
Als Nächstes berechnen wir die Offsets in den Datenpuffern und speichern die erhaltenen Werte in lokalen Variablen.
const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k;
Anschließend wird die entsprechende Aufmerksamkeitsmaske für den aktuellen Thread ausgewertet und andere Hilfskonstanten vorbereitet.
const bool b_mask = (mask[shift_s] < mask_level); const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
Nun erstellen wir ein Array im lokalen Speicher, um Daten zwischen den Threads der Arbeitsgruppe auszutauschen.
__local float temp[LOCAL_ARRAY_SIZE];
Anschließend berechnen wir die Summe der Exponentialwerte der Abhängigkeitskoeffizienten innerhalb einer einzigen Abfrage. Dazu erstellen wir eine Schleife, die iterativ einzelne Summen berechnet und sie in ein lokales Datenfeld schreibt.
//--- sum of exp uint count = 0; if(k < ls) { temp[k] = 0; do { if(b_mask || q_id >= (count * ls + k)) if((count * ls) < (kunits - k)) { float sum = 0; int sh_k = 2 * dimension * heads_kv * count * ls; for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d + sh_k]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; temp[k] = temp[k] + sum; } count++; } while((count * ls + k) < kunits); } barrier(CLK_LOCAL_MEM_FENCE);
Dann summieren wir alle Werte des lokalen Datenfeldes.
do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Beachten Sie, dass bei der lokalen Summierung die Werte unter Berücksichtigung der Maske berechnet wurden. Nun können wir die normalisierten Werte der Aufmerksamkeitskoeffizienten unter Berücksichtigung der Maskierung berechnen.
//--- score float sum = temp[0]; float sc = 0; if(b_mask || q_id >= (count * ls + k)) if(sum != 0) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Bei der Berechnung der Aufmerksamkeitskoeffizienten wurden die Werte für maskierte Elemente auf Null gesetzt. Daher können wir nun die einfache Algorithmen verwenden, um die Ergebnisse des Blocks der Kreuzaufmerksamkeit zu berechnen.
for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE); //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
Das Upgrade für den Backpropagation-Kernel, MHMaskAttentionInsideGradients, ist weniger umfangreich. Er kann punktweise aufgerufen werden. Der Punkt ist, dass die Nullsetzung der Abhängigkeitskoeffizienten während des Vorwärtsdurchlaufs es uns ermöglicht, den einfachen Algorithmus zu verwenden, um den Fehlergradienten auf die Entitäten von Query, Key und Value (Abfrage, Schlüssel, Wert) zu verteilen. Dies ermöglicht es uns jedoch nicht, den Fehlergradienten auf die Maske zu übertragen. Daher fügen wir dem einfachen Algorithmus einen Maskenanpassungsgradienten hinzu.
__kernel void MHMaskAttentionInsideGradients(__global const float *q, __global float *q_g, __global const float *kv, __global float *kv_g, __global const float *mask, __global float *mask_g, __global const float *scores, __global const float *gradient, const int kunits, const int heads_kv, const float mask_level ) { ........ ........ //--- Mask's gradient for(int k = q_id; k < kunits; k += qunits) { float m = mask[shift_s + k]; if(m < mask_level) mask_g[shift_s + k] = 0; else mask_g[shift_s + k] = 1 - m; } }
Beachten Sie, dass die entsprechenden Maskeneinträge auf „1“ normiert sind. Bei irrelevanten Masken wird der Fehlergradient auf Null gesetzt, da sie keinen Einfluss auf die Ausgabe des Modells haben.
Damit ist die Implementierung des OpenCL-Kernels abgeschlossen. Sie können den vollständigen Quellcode der neuen Kernel in den angehängten Dateien einsehen.
2.2 Erstellen der Methodenklasse des SPFormer
Nachdem die Modifikationen des OpenCL-Programms abgeschlossen sind, gehen wir nun zum Hauptprogramm über. Hier erstellen wir eine neue Klasse CNeuronSPFormer, die die Funktionsweise des Kernels von der voll vernetzten Schicht CNeuronBaseOCL erben wird. Aufgrund des Umfangs und der Spezifität der für SPFormer erforderlichen Anpassungen habe ich beschlossen, nicht von bereits implementierten Kreuzaufmerksamkeits-Blöcken zu erben. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronSPFormer : public CNeuronBaseOCL { protected: uint iWindow; uint iUnits; uint iHeads; uint iSPWindow; uint iSPUnits; uint iSPHeads; uint iWindowKey; uint iLayers; uint iLayersSP; //--- CLayer cSuperPoints; CLayer cQuery; CLayer cSPKeyValue; CLayer cMask; CArrayInt cScores; CLayer cMHCrossAttentionOut; CLayer cCrossAttentionOut; CLayer cResidual; CLayer cQKeyValue; CLayer cMHSelfAttentionOut; CLayer cSelfAttentionOut; CLayer cFeedForward; CBufferFloat cTempSP; CBufferFloat cTempQ; CBufferFloat cTempSelfKV; CBufferFloat cTempCrossKV; //--- virtual bool CreateBuffers(void); virtual bool AttentionOut(CNeuronBaseOCL *q, CNeuronBaseOCL *kv, const int scores, CNeuronBaseOCL *out, CNeuronBaseOCL *mask, const int units, const int heads, const int units_kv, const int heads_kv, const int dimension, const float mask_level = 0.5f); virtual bool AttentionInsideGradients(CNeuronBaseOCL *q, CNeuronBaseOCL *kv, const int scores, CNeuronBaseOCL *out, CNeuronBaseOCL *mask, const int units, const int heads, const int units_kv, const int heads_kv, const int dimension, const float mask_level = 0.5f); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSPFormer(void) {}; ~CNeuronSPFormer(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSPFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Die vorgestellte Klassenstruktur umfasst eine große Anzahl von Variablen und verschachtelten Objekten, von denen viele Namen tragen, die mit denen übereinstimmen, die wir zuvor in Implementierungen von aufmerksamkeitsbezogenen Klassen verwendet haben. Dies ist kein Zufall. Wir werden uns mit der Funktionsweise aller Objekte während des Implementierungsprozesses vertraut machen.
Achten Sie darauf, dass alle internen Objekte als statisch deklariert sind, sodass wir sowohl den Konstruktor als auch den Destruktor leer lassen können. Die Initialisierung sowohl von geerbten als auch von neu deklarierten Mitgliedern erfolgt ausschließlich in der Init-Methode. Wie Sie wissen, enthalten die Parameter der Init-Methode Schlüsselkonstanten, die explizit die Architektur des erstellten Objekts definieren.
bool CNeuronSPFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Im Körper der Methode rufen wir sofort die gleichnamige Methode der Elternklasse auf, in der die Initialisierung der geerbten Objekte und Variablen durchgeführt wird.
Danach speichern wir die erhaltenen Konstanten sofort in den internen Variablen der Klasse.
iWindow = window; iUnits = units_count; iHeads = heads; iSPUnits = units_sp; iSPWindow = window_sp; iSPHeads = heads_sp; iWindowKey = window_key; iLayers = MathMax(layers, 1); iLayersSP = MathMax(layers_to_sp, 1);
Im nächsten Schritt initialisieren wir ein kleines MLP, um einen Vektor lernfähiger Abfragen zu erzeugen.
//--- Init Querys CNeuronBaseOCL *base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(iWindow * iUnits, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *buf = base.getOutput(); if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite()) return false; if(!cQuery.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base.Init(0, 1, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cQuery.Add(base)) return false;
Als Nächstes erstellen wir einen Block zur Extraktion der Superpunkte. Hier erzeugen wir einen Block von 4 aufeinanderfolgenden neuronalen Schichten, deren Architektur sich an die Größe der ursprünglichen Sequenz anpasst. Wenn die Länge der Sequenz am Eingang der nächsten Schicht ein Vielfaches von 2 ist, dann verwenden wir einen Faltungsblock mit Verbindung der Residuen, der die Größe der Sequenz um das Zweifache reduziert.
//--- Init SuperPoints for(int r = 0; r < 4; r++) { if(iSPUnits % 2 == 0) { iSPUnits /= 2; CResidualConv *residual = new CResidualConv(); if(!residual) return false; if(!residual.Init(0, r+2, OpenCL, 2*iSPWindow, iSPWindow, iSPUnits, optimization, iBatch)) return false; if(!cSuperPoints.Add(residual)) return false; }
Andernfalls verwenden wir eine einfache Faltungsschicht, die 2 benachbarte Elemente der Sequenz mit einer Schrittweite von 1 Element analysiert. Die Länge der Sequenz wird also um 1 verringert.
else { iSPUnits--; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, r+2, OpenCL, 2*iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, iBatch)) return false; if(!cSuperPoints.Add(conv)) return false; } }
Wir haben die Datenvorverarbeitungsobjekte initialisiert. Als Nächstes werden die internen Schichten des modifizierten Transformer-Decoders initialisiert. Zu diesem Zweck erstellen wir lokale Variablen für die vorübergehende Speicherung von Zeigern auf Objekte und organisieren eine Schleife mit einer Anzahl von Iterationen, die der angegebenen Anzahl interner Schichten des Decoders entspricht.
CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL; for(uint l = 0; l < iLayers; l++) { //--- Cross Attention //--- Query conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 6, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false; //--- Key-Value if(l % iLayersSP == 0) { conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 7, OpenCL, iSPWindow, iSPWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch)) return false; if(!cSPKeyValue.Add(conv)) return false; }
Hier werden zunächst die internen Schichten initialisiert, die die Entität von Query, Key and Value erzeugen. Der Tensor von Key-Value wird nur bei Bedarf erzeugt.
Hier fügen wir auch eine Maskenerstellungsebene hinzu. Zu diesem Zweck wird eine Faltungsschicht verwendet, die für alle Abfragen Maskierungskoeffizienten für jedes einzelne Element der Superpunktfolge erzeugt. Da wir den mehrköpfigen Aufmerksamkeits-Algorithmus verwenden, werden wir auch Koeffizienten für jeden Aufmerksamkeitskopf erzeugen. Um die Werte zu normalisieren, verwenden wir die Aktivierungsfunktion sigmoide.
//--- Mask conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 8, OpenCL, iSPWindow, iSPWindow, iUnits * iHeads, iSPUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(SIGMOID); if(!cMask.Add(conv)) return false;
An dieser Stelle sei darauf hingewiesen, dass wir bei der Durchführung von Kreuzaufmerksamkeit die Aufmerksamkeitskoeffizienten der Superpunktabfragen benötigen. Daher führen wir eine Transposition des erhaltenen Maskierungstensors durch.
transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, l * 14 + 9, OpenCL, iSPUnits, iUnits * iHeads, optimization, iBatch)) return false; if(!cMask.Add(transp)) return false;
Der nächste Schritt ist die Vorbereitung von Objekten für die Aufzeichnung der Ergebnisse der Kreuzaufmerksamkeit. Wir beginnen mit der mehrköpfigen Aufmerksamkeit.
//--- MH Cross Attention out base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, l * 14 + 10, OpenCL, iWindow * iUnits * iHeads, optimization, iBatch)) return false; if(!cMHCrossAttentionOut.Add(base)) return false;
Dann machen wir das Gleiche für die komprimierte Darstellung.
//--- Cross Attention out conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 11, OpenCL, iWindow * iHeads, iWindow * iHeads, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cCrossAttentionOut.Add(conv)) return false;
Als Nächstes fügen wir eine Ebene für die Summierung mit den Originaldaten hinzu.
//--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, l * 14 + 12, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false;
Es folgt ein Block zur Selbstaufmerksamkeit. Auch hier erzeugen wir die Entitäten von Query, Key und Value, aber diesmal verwenden wir die Ergebnisse der Kreuzaufmerksamkeit.
//--- Self-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l*14+13, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false; //--- Key-Value if(l % iLayersSP == 0) { conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l*14+14, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQKeyValue.Add(conv)) return false; }
Dann fügen wir Objekte für die Aufzeichnung der Ergebnisse der mehrköpfigen Aufmerksamkeit und der komprimierten Werte hinzu.
//--- MH Attention out base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, l * 14 + 15, OpenCL, iWindow * iUnits * iHeads, optimization, iBatch)) return false; if(!cMHSelfAttentionOut.Add(base)) return false; //--- Attention out conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 16, OpenCL, iWindow * iHeads, iWindow * iHeads, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cSelfAttentionOut.Add(conv)) return false;
Wir fügen eine Ebene hinzu, um diese mit den Ergebnissen der Kreuzaufmerksamkeit zu summieren,
//--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, l * 14 + 17, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false;
dann einen FeedForward-Block mit einer Residuen-Verbindung.
//--- FeedForward conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 18, OpenCL, iWindow, iWindow, iWindow * 4, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, l * 14 + 19, OpenCL, iWindow * 4, iWindow * 4, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false; //--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, l * 14 + 20, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false; if(!base.SetGradient(conv.getGradient())) return false;
Um unnötige Datenkopien zu vermeiden, kombinieren wir die Fehlergradientenpuffer der letzten Schicht des FeedForward-Blocks und der Verbindungsschicht der Residuen. Wir führen eine ähnliche Operation für den Ergebnispuffer und die Fehlergradienten der oberen Ebene in der letzten inneren Schicht durch.
if(l == (iLayers - 1)) { if(!SetGradient(conv.getGradient())) return false; if(!SetOutput(base.getOutput())) return false; } }
Es sei darauf hingewiesen, dass wir bei der Initialisierung der Objekte keinen Puffer für die Daten der Aufmerksamkeitskoeffizienten angelegt haben. Die Erstellung und Initialisierung interner Objekte wurde in eine eigene Methode ausgelagert.
//--- SetOpenCL(OpenCL); //--- return true; }
Nach der Initialisierung der internen Objekte geht es an die Konstruktion der Weiterleitungsmethoden. Wir werden den Algorithmus der Methoden zum Aufruf der oben erstellten Kernel einer unabhängigen Studie überlassen. Es gibt nichts besonders Neues an ihnen. Wir beschränken uns auf den Algorithmus der Methode FeedForward der obersten Ebene, in der wir eine klare Abfolge von Aktionen des Algorithmus SPFormer aufbauen werden.
bool CNeuronSPFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *superpoints = NeuronOCL; CNeuronBaseOCL *neuron = NULL, *inputs = NULL, *q = NULL, *kv_cross = NULL, *kv_self = NULL;
In den Methodenparametern erhalten wir einen Zeiger auf das Quelldatenobjekt. Im Hauptteil der Methode deklarieren wir eine Reihe von lokalen Variablen für die vorübergehende Speicherung von Zeigern auf Objekte.
Als Nächstes lassen wir die resultierenden Rohdaten durch das Superpoint-Extraktionsmodell laufen.
//--- Superpoints for(int l = 0; l < cSuperPoints.Total(); l++) { neuron = cSuperPoints[l]; if(!neuron || !neuron.FeedForward(superpoints)) return false; superpoints = neuron; }
Und wir erzeugen einen Vektor von Abfragen.
//--- Query neuron = cQuery[1]; if(!neuron || !neuron.FeedForward(cQuery[0])) return false;
Damit sind die vorbereitenden Arbeiten abgeschlossen. Wir erstellen eine Schleife zur Iteration durch die internen neuronalen Schichten unseres Decoders.
inputs = neuron; for(uint l = 0; l < iLayers; l++) { //--- Cross Attentionn q = cQuery[l * 2 + 2]; if(!q || !q.FeedForward(inputs)) return false; if((l % iLayersSP) == 0) { kv_cross = cSPKeyValue[l / iLayersSP]; if(!kv_cross || !kv_cross.FeedForward(superpoints)) return false; }
Hier bereiten wir zunächst die Entitäten Query, Key und Value vor.
Erzeugen wir die Masken.
neuron = cMask[l * 2]; if(!neuron || !neuron.FeedForward(superpoints)) return false; neuron = cMask[l * 2 + 1]; if(!neuron || !neuron.FeedForward(cMask[l * 2])) return false;
Dann führen wir den Algorithmus der Kreuzaufmerksamkeit durch, der die Maskierung berücksichtigt.
if(!AttentionOut(q, kv_cross, cScores[l * 2], cMHCrossAttentionOut[l], neuron, iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey)) return false;
Wir werden die Ergebnisse der mehrköpfigen Aufmerksamkeit auf die Größe eines Abfragetensors reduzieren.
neuron = cCrossAttentionOut[l]; if(!neuron || !neuron.FeedForward(cMHCrossAttentionOut[l])) return false;
Danach werden die Daten der beiden Informationsströme summiert und normalisiert.
q = inputs; inputs = cResidual[l * 3]; if(!inputs || !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Auf den Kreuzaufmerksamkeits-Block folgt der Selbstaufmerksamkeits-Algorithmus. Hier generieren wir die Entitäten Query, Key und Value erneut, aber bereits auf der Grundlage der Ergebnisse der Kreuzaufmerksamkeit.
//--- Self-Attention q = cQuery[l * 2 + 3]; if(!q || !q.FeedForward(inputs)) return false; if((l % iLayersSP) == 0) { kv_self = cQKeyValue[l / iLayersSP]; if(!kv_self || !kv_self.FeedForward(inputs)) return false; }
In diesem Stadium verwenden wir keine Maskierung. Daher geben wir beim Aufruf der Aufmerksamkeits-Methode NULL anstelle des Maskenobjekts an.
if(!AttentionOut(q, kv_self, cScores[l * 2 + 1], cMHSelfAttentionOut[l], NULL, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Wir reduzieren die Ergebnisse der mehrköpfigen Aufmerksamkeit auf die Größe des Abfragetensors.
neuron = cSelfAttentionOut[l]; if(!neuron || !neuron.FeedForward(cMHSelfAttentionOut[l])) return false;
Dann summieren wir ihn mit dem Vektor der Kreuzaufmerksamkeitsergebnisse und normalisieren die Daten.
q = inputs; inputs = cResidual[l * 3 + 1]; if(!inputs || !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Als Nächstes werden, ähnlich wie beim einfachen Transformer, Daten durch FeedForward weitergeleitet. Danach geht es weiter mit der nächsten Iteration der Schleife durch die internen Schichten.
//--- FeedForward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.FeedForward(inputs)) return false; neuron = cFeedForward[l * 2 + 1]; if(!neuron || !neuron.FeedForward(cFeedForward[l * 2])) return false; q = inputs; inputs = cResidual[l * 3 + 2]; if(!inputs || !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; } //--- return true; }
Bevor wir zur nächsten Iteration der Schleife übergehen, speichern wir einen Zeiger auf das letzte Objekt der aktuellen inneren Schicht in der Variablen inputs.
Nach erfolgreichem Abschluss aller Iterationen der internen Schleife über die Schichten des Decoders geben wir das boolesche Ergebnis der Operationen der Methode an das aufrufende Programm zurück.
Der nächste Schritt besteht darin, die Methoden für den Rückwärtsdurchlauf zu entwickeln. Von besonderem Interesse ist die Methode, die für die Verteilung des Fehlergradienten auf alle Elemente unseres Modells auf der Grundlage ihres Beitrags zum Gesamtergebnis verantwortlich ist: calcInputGradients.
bool CNeuronSPFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Diese Methode empfängt einen Zeiger auf das vorangehende Objekt der neuronalen Schicht, das die Eingabedaten während des Vorwärtsdurchlaufs geliefert hat. Das Ziel besteht nun darin, den Fehlergradienten zurück zu dieser Schicht zu übertragen, und zwar im Verhältnis dazu, wie die Eingabe die Ausgabe des Modells beeinflusst hat.
Innerhalb des Methodenkörpers wird zunächst der empfangene Zeiger validiert, da eine Fortsetzung mit einer ungültigen Referenz alle nachfolgenden Operationen sinnlos machen würde.
Dann deklarieren wir eine Reihe lokaler Variablen für die vorübergehende Speicherung von Zeigern auf Objekte, die in der Gradientenberechnung verwendet werden.
CNeuronBaseOCL *superpoints = cSuperPoints[cSuperPoints.Total() - 1]; CNeuronBaseOCL *neuron = NULL, *inputs = NULL, *q = NULL, *kv_cross = cSPKeyValue[cSPKeyValue.Total() - 1], *kv_self = cQKeyValue[cQKeyValue.Total() - 1];
Wir setzen Puffer für die vorübergehende Speicherung von Zwischendaten zurück.
if(!cTempSP.Fill(0) || !cTempSelfKV.Fill(0) || !cTempCrossKV.Fill(0)) return false;
Dann organisieren wir eine Rückwärtsschleife durch die internen Schichten unseres Decoders.
for(int l = int(iLayers - 1); l >= 0; l--) { //--- FeedForward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2 + 1])) return false;
Wie Sie sich vielleicht erinnern, haben wir bei der Initialisierung des Klassenobjekts die Zeiger auf die Fehlergradientenpuffer der oberen Ebene und die Verbindungsschicht der Residuen durch die Zeiger der letzten Schicht von FeedForward ersetzt. Diese Konstruktion ermöglicht es uns, den Rückwärtsdurchgang direkt aus FeedForward zu starten, ohne dass wir Fehlergradienten aus dem Puffer der oberen Ebene und der Verbindungsschicht der Residuen manuell an die letzte Schicht von FeedForward weiterleiten müssen.
Anschließend propagieren wir den Fehlergradienten bis hinunter zur Verbindungsschicht der Residuen des Selbstaufmerksamkeits-Blocks.
neuron = cResidual[l * 3 + 1]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2])) return false;
Danach summieren wir den Fehlergradienten aus den beiden Datenströmen und leiten ihn an die Ergebnisschicht der Selbstaufmerksamkeit weiter.
if(!SumAndNormilize(((CNeuronBaseOCL*)cResidual[l * 3 + 2]).getGradient(), neuron.getGradient(), ((CNeuronBaseOCL*)cSelfAttentionOut[l]).getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Dann verteilen wir den erhaltenen Fehlergradienten auf die Aufmerksamkeitsköpfe.
//--- Self-Attention neuron = cMHSelfAttentionOut[l]; if(!neuron || !neuron.calcHiddenGradients(cSelfAttentionOut[l])) return false;
Wir erhalten Zeiger auf die Entitäts-Puffer von Query, Key und Value der Selbstaufmerksamkeit. Falls erforderlich, setzen wir den Puffer für die Akkumulation von Zwischenwerten zurück.
q = cQuery[l * 2 + 3]; if(((l + 1) % iLayersSP) == 0) { kv_self = cQKeyValue[l / iLayersSP]; if(!kv_self || !cTempSelfKV.Fill(0)) return false; }
Dann übertragen wir den Fehlergradienten entsprechend dem Einfluss der Leistungsergebnisse des Modells auf sie.
if(!AttentionInsideGradients(q, kv_self, cScores[l * 2 + 1], neuron, NULL, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Wir haben die Möglichkeit geschaffen, einen Key-Value-Tensor für mehrere interne Schichten des Decoders zu verwenden. Je nach dem Index der aktuellen internen Schicht summieren wir daher den erhaltenen Wert mit dem zuvor akkumulierten Fehlergradienten in den temporären Datenakkumulationspuffer oder den Gradientenpuffer der entsprechenden Schicht von Key-Value.
if(iLayersSP > 1) { if((l % iLayersSP) == 0) { if(!SumAndNormilize(kv_self.getGradient(), GetPointer(cTempSelfKV), kv_self.getGradient(), iWindowKey, false, 0, 0, 0, 1)) return false; } else { if(!SumAndNormilize(kv_self.getGradient(), GetPointer(cTempSelfKV), GetPointer(cTempSelfKV), iWindowKey, false, 0, 0, 0, 1)) return false; } }
Dann propagieren wir den Fehlergradienten bis hinunter zur Verbindungsschicht der Residuen des Kreuzaufmerksamkeit-Blocks. Hier übergeben wir zunächst den Fehlergradienten aus der Entität Query.
inputs = cResidual[l * 3]; if(!inputs || !inputs.calcHiddenGradients(q, NULL)) return false;
Und dann fügen wir, falls erforderlich, den Fehlergradienten aus dem Informationsfluss von Key-Value hinzu.
if((l % iLayersSP) == 0) { CBufferFloat *temp = inputs.getGradient(); if(!inputs.SetGradient(GetPointer(cTempQ), false)) return false; if(!inputs.calcHiddenGradients(kv_self, NULL)) return false; if(!SumAndNormilize(temp, GetPointer(cTempQ), temp, iWindow, false, 0, 0, 0, 1)) return false; if(!inputs.SetGradient(temp, false)) return false; }
Als Nächstes addieren wir den Fehlergradienten aus dem Fluss der Residuen der Selbstaufmerksamkeit und leiten den erhaltenen Wert an die Kreuzaufmerksamkeit weiter.
if(!SumAndNormilize(((CNeuronBaseOCL*)cSelfAttentionOut[l]).getGradient(), inputs.getGradient(), ((CNeuronBaseOCL*)cCrossAttentionOut[l]).getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Danach müssen wir den Fehlergradienten durch den Kreuzaufmerksamkeit-Block verteilen. Zunächst wird der Fehlergradient auf die Aufmerksamkeitsköpfe verteilt.
//--- Cross Attention neuron = cMHCrossAttentionOut[l]; if(!neuron || !neuron.calcHiddenGradients(cCrossAttentionOut[l])) return false;
Wie bei der Selbstaufmerksamkeit erhalten wir Zeiger auf die Entitätsobjekte Query, Key und Value.
q = cQuery[l * 2 + 2]; if(((l + 1) % iLayersSP) == 0) { kv_cross = cSPKeyValue[l / iLayersSP]; if(!kv_cross || !cTempCrossKV.Fill(0)) return false; }
Dann propagieren wir den Fehlergradienten durch den Aufmerksamkeitsblock. In diesem Fall fügen wir jedoch einen Zeiger auf das Maskierungsobjekt hinzu.
if(!AttentionInsideGradients(q, kv_cross, cScores[l * 2], neuron, cMask[l * 2 + 1], iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey)) return false;
Der Fehlergradient der Query-Entität wird an die vorherige Decoderschicht oder an den Query-Vektor weitergegeben. Die Wahl des Objekts hängt von der aktuellen Decoderebene ab.
inputs = (l == 0 ? cQuery[1] : cResidual[l * 3 - 1]); if(!inputs.calcHiddenGradients(q, NULL)) return false;
Hier fügen wir den Fehlergradienten entlang des Informationsflusses der Verbindung der Residuen hinzu.
if(!SumAndNormilize(inputs.getGradient(), ((CNeuronBaseOCL*)cCrossAttentionOut[l]).getGradient(), inputs.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
In diesem Stadium haben wir die Gradientenausbreitung entlang des Abfragevektors abgeschlossen. Allerdings müssen wir den Fehlergradienten noch durch den Superpoint verteilen. Dazu prüfen wir zunächst, ob es notwendig ist, Gradienten aus dem Key-Value-Tensor zu propagieren. Ist dies der Fall, werden die berechneten Gradienten in dem Puffer akkumuliert, der die zuvor akkumulierten Fehlergradienten enthält.
if((l % iLayersSP) == 0) { if(!superpoints.calcHiddenGradients(kv_cross, NULL)) return false; if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), GetPointer(cTempSP), iSPWindow, false, 0, 0, 0, 1)) return false; }
Dann verteilen wir den Fehlergradienten aus dem Maskengenerierungsmodell.
neuron = cMask[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cMask[l * 2 + 1]) || !DeActivation(neuron.getOutput(), neuron.getGradient(), neuron.getGradient(), neuron.Activation())) return false; if(!superpoints.calcHiddenGradients(neuron, NULL)) return false;
Außerdem addieren wir den erhaltenen Wert zu dem zuvor aufgelaufenen Fehlergradienten. Bitte beachten Sie die aktuelle Decoderschicht.
if(l == 0) { if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), superpoints.getGradient(), iSPWindow, false, 0, 0, 0, 1)) return false; } else if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), GetPointer(cTempSP), iSPWindow, false, 0, 0, 0, 1)) return false; }
Im Falle der Analyse der ersten Decoderschicht (die in unserer Implementierung der letzten Iteration der Schleife entspricht) wird der Gesamtgradient im Puffer der letzten Schicht des Superpoint-Modells gespeichert. Andernfalls akkumulieren wir den Fehlergradienten in einem temporären Puffer zur Zwischenspeicherung.
Wir fahren dann mit der nächsten Iteration der Kehrschleife über die internen Schichten des Decoders fort.
Sobald der Fehlergradient erfolgreich durch alle internen Schichten des Transformer-Decoders propagiert wurde, besteht der letzte Schritt darin, den Gradienten durch die Schichten des Superpoint-Modells zu verteilen. Da das Superpoint-Modell eine lineare Struktur hat, können wir einfach eine umgekehrte Iterationsschleife über seine Schichten organisieren.
for(int l = cSuperPoints.Total() - 2; l >= 0; l--) { superpoints = cSuperPoints[l]; if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[l + 1])) return false; }
Am Ende der Methodenoperationen übergeben wir den Fehlergradienten an die Quelldatenschicht aus dem Superpoint-Modell und geben das logische Ergebnis der Ausführung der Methodenoperationen an das aufrufende Programm zurück.
if(!NeuronOCL.calcHiddenGradients(superpoints, NULL)) return false; //--- return true; }
In diesem Stadium haben wir den Prozess der Ausbreitung des Fehlergradienten durch alle internen Komponenten und Eingabedaten entsprechend ihrem Einfluss auf die Gesamtleistung des Modells implementiert. Der nächste Schritt besteht darin, die trainierbaren Parameter des Modells zu optimieren, um den Gesamtfehler zu minimieren. Diese Vorgänge werden in der Methode updateInputWeights durchgeführt.
Es ist wichtig zu beachten, dass alle trainierbaren Parameter des Modells in den internen Objekten unserer Klasse gespeichert sind. Und der Optimierungsalgorithmus für diese Parameter wurde bereits in diese Objekte implementiert. Daher reicht es aus, im Rahmen der Parameteraktualisierungsmethode nacheinander die entsprechenden Methoden der verschachtelten Objekte aufzurufen. Ich möchte Sie ermutigen, die Anwendung dieser Methode unabhängig zu überprüfen. Zur Erinnerung: Der vollständige Quellcode der neuen Klasse und aller ihrer Komponenten ist in den beigefügten Materialien enthalten.
Die Architektur der trainierbaren Modelle, zusammen mit allen unterstützenden Programmen für das Training und die Interaktion mit der Umgebung, wurde vollständig aus früheren Arbeiten übernommen. An der Architektur des Encoders wurden nur geringfügige Anpassungen vorgenommen. Ich empfehle Ihnen auch, diese selbst zu erkunden. Der vollständige Code für alle Klassen und Dienstprogramme, die bei der Entwicklung dieses Artikels verwendet wurden, ist im Anhang enthalten. Wir gehen nun zur letzten Phase unserer Arbeit über: Training und Test des Modells.
3. Tests
In diesem Artikel haben wir unsere Interpretation der in der Methode SPFormer vorgeschlagenen Ansätze in einem beträchtlichen Umfang umgesetzt. Wir gehen nun zur Trainings- und Testphase des Modells über, in der wir die Akteurs-Politik anhand realer historischer Daten bewerten.
Um die Modelle zu trainieren, verwenden wir reale, historische Daten des Instruments EURUSD mit dem H1-Zeitrahmen für das gesamte Jahr 2023. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Der Trainingsalgorithmus wurde aus früheren Veröffentlichungen übernommen, ebenso wie die unterstützenden Programme für Training und Auswertung.
Die trainierte Akteurs-Politik wurde im Strategietester des MetaTrader 5 unter Verwendung echter historischer Daten für Januar 2024 getestet, wobei alle anderen Parameter unverändert blieben. Die Testergebnisse werden im Folgenden vorgestellt.
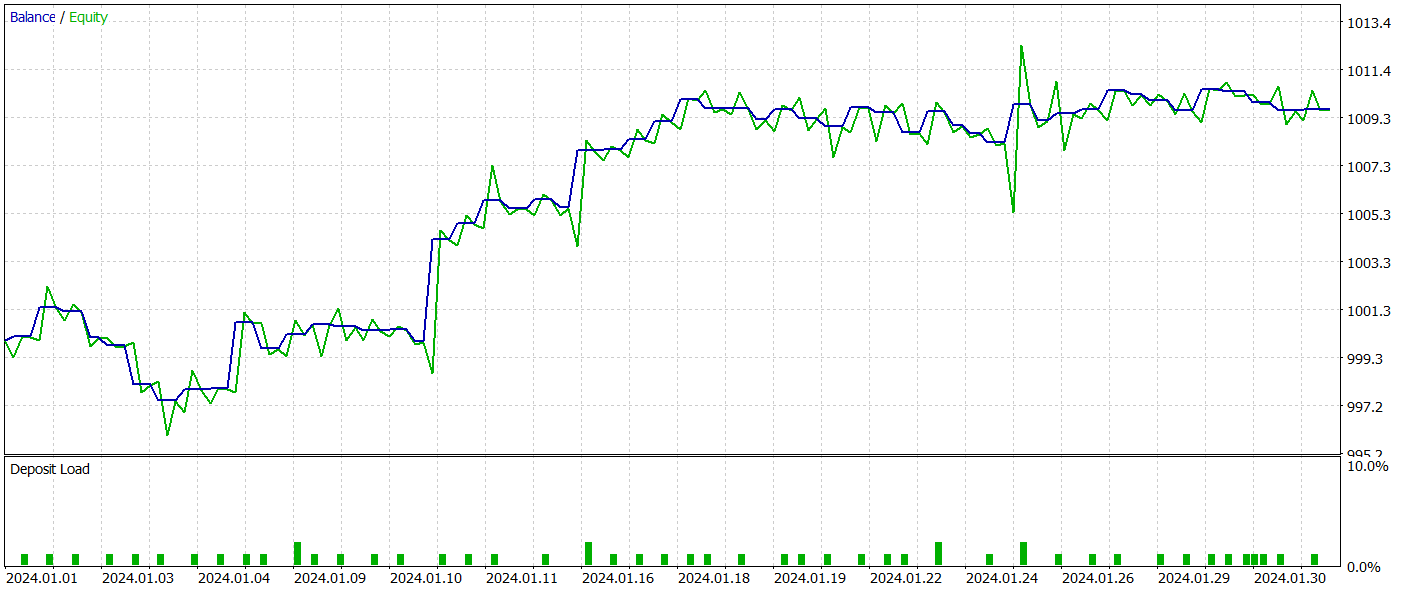
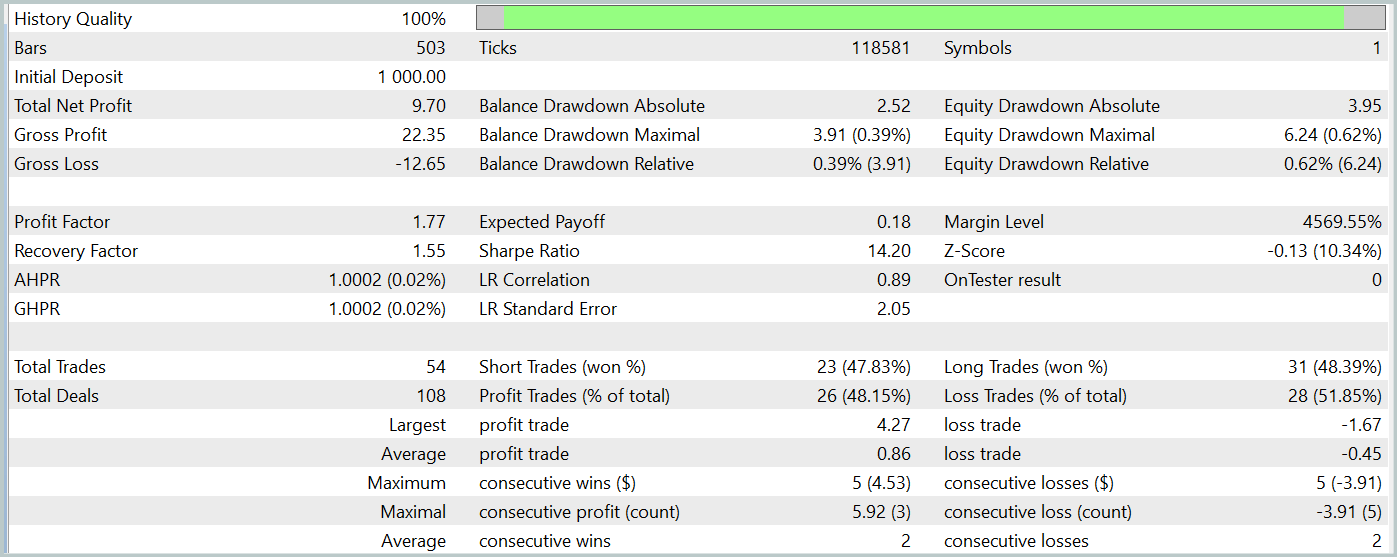
Während des Testzeitraums tätigte das Modell 54 Abschlüsse, von denen 26 mit Gewinn abgeschlossen wurden. Dies machte 48 % aller Handelsoperationen aus. Das durchschnittliche gewinnbringende Handelsgeschäft ist 2-mal höher als der vergleichbare Wert für Operationen mit Verlust. Dies ermöglichte es dem Modell, während des Testzeitraums einen Gewinn zu erzielen.
Es ist jedoch wichtig darauf hinzuweisen, dass die begrenzte Anzahl von Handelsgeschäften während des Testzeitraums keine ausreichende Grundlage für die Bewertung der langfristigen Zuverlässigkeit und Leistung des Modells darstellt.
Schlussfolgerung
Die Methode SPFormer zeigt Potenzial für die Anpassung an Handelsanwendungen, insbesondere für die Segmentierung von Marktdaten und die Vorhersage von Marktsignalen. Im Gegensatz zu traditionellen Modellen, die sich stark auf Zwischenschritte stützen und oft empfindlich auf Rauschen in den Daten reagieren, kann dieser Ansatz direkt mit Superpoint-Darstellungen von Marktinformationen arbeiten. Die Verwendung von Transformer-Architekturen zur Vorhersage von Marktmustern ermöglicht eine vereinfachte Verarbeitung, eine höhere Vorhersagegenauigkeit und eine schnellere Entscheidungsfindung in Handelsszenarien.
Im praktischen Teil dieses Artikels wird unsere Implementierung der vorgeschlagenen Konzepte mit MQL5 vorgestellt. Wir haben auf der Grundlage dieser Konzepte Modelle trainiert und ihre Wirksamkeit anhand echter historischer Daten getestet. Die Testergebnisse zeigten, dass das Modell in der Lage ist, Gewinne zu erwirtschaften, was auf ein vielversprechendes Potenzial für reale Anwendungen schließen lässt. Die hier vorgestellten Implementierungen sind jedoch nur für Demonstrationszwecke gedacht. Vor dem Einsatz des Modells in realen Handelsumgebungen ist es unerlässlich, ein ausgedehntes Training über längere Zeiträume sowie eine gründliche Validierung und Prüfung durchzuführen, um Robustheit und Zuverlässigkeit zu gewährleisten.
Referenzen Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15928
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wirtschaftsprognosen: Erkunden des Potenzials von Python
Wirtschaftsprognosen: Erkunden des Potenzials von Python
 Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (I)
Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (I)
 Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (II)
Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (II)
 African Buffalo Optimierung (ABO)
African Buffalo Optimierung (ABO)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Mate dies ist sehr interessant, aber sehr fortgeschritten für mich!
Vielen Dank für den Austausch, lernen Schritt für Schritt.