
Neuronale Netze im Handel: Erforschen lokaler Datenstrukturen
Einführung
Die Aufgabe der Objekterkennung in Punktwolken gewinnt zunehmend an Bedeutung. Die Effizienz der Lösung dieser Aufgabe hängt stark von den Informationen über die Struktur der lokalen Regionen ab. Die spärliche und unregelmäßige Natur von Punktwolken führt jedoch oft zu unvollständigen und verrauschten lokalen Strukturen.
Die herkömmliche faltungsbasierte Objekterkennung beruht auf festen Kerneln, die alle benachbarten Punkte gleich behandeln. Infolgedessen werden zwangsläufig unverbundene oder verrauschte Punkte von anderen Objekten in die Analyse einbezogen.
Der Transformer hat seine Wirksamkeit bei der Bewältigung verschiedener Aufgaben bewiesen. Im Vergleich zur Faltung kann der Mechanismus der Selbstaufmerksamkeit (Self-Attention) verrauschte oder irrelevante Punkte adaptiv herausfiltern. Dennoch wendet der pure Transformer auf alle Elemente einer Sequenz die gleiche Transformationsfunktion an. Bei diesem isotropen Ansatz werden räumliche Beziehungen und lokale Strukturinformationen wie Richtung und Entfernung von einem zentralen Punkt zu seinen Nachbarn nicht berücksichtigt. Wenn die Positionen der Punkte neu angeordnet werden, bleibt das Ergebnis des Transformers unverändert. Dies erschwert die Erkennung der Richtungsabhängigkeit von Objekten, die für die Erkennung von Preismustern entscheidend ist.
Die Autoren des Artikels „SEFormer: Structure Embedding Transformer for 3D Object Detection“ zielten darauf ab, die Stärken beider Ansätze zu kombinieren, indem eine neue Transformer-Architektur entwickelt wurde - Structure-Embedding transFormer (SEFormer), das in der Lage ist, lokale Strukturen unter Berücksichtigung von Richtung und Entfernung zu kodieren. Der vorgeschlagene SEFormer lernt verschiedene Transformationen für Value (Wert) der Punkte aus unterschiedlichen Richtungen und Entfernungen. Folglich spiegeln sich Änderungen in der lokalen räumlichen Struktur in der Ausgabe des Modells wider, was einen Schlüssel zur genauen Erkennung der Objektrichtung darstellt.
Auf der Grundlage des vorgeschlagenen Modules des SEFormer wird in der Studie ein Multiskalennetzwerk für die 3D-Objekterkennung eingeführt.
1. Der Algorithmus von SEFormer
Die örtliche und räumliche Invarianz der Faltung steht im Einklang mit der induktiven Verzerrung in Bilddaten. Ein weiterer entscheidender Vorteil der Faltung ist ihre Fähigkeit, strukturelle Informationen in den Daten zu kodieren. Die Autoren der Methode von SEFormer zerlegen die Faltung in eine zweistufige Operation: Transformation und Aggregation. Während des Transformationsschritts wird jeder Punkt mit einem entsprechenden Kernel wδ multipliziert. Diese Werte werden dann einfach mit einem festen Aggregationskoeffizienten α=1 summiert. Bei der Faltung werden die Kernel je nach Richtung und Abstand vom Kernelzentrum unterschiedlich gelernt. Folglich ist die Faltung in der Lage, die lokale räumliche Struktur zu kodieren. Bei der Aggregation werden jedoch alle benachbarten Punkte gleich behandelt (α=1). Der Standard-Faltungsoperator verwendet einen statischen und starren Kernel, aber Punktwolken sind oft unregelmäßig und sogar unvollständig. Folglich werden bei der Faltung unweigerlich irrelevante oder verrauschte Punkte in das resultierende Merkmal aufgenommen.
Im Vergleich zur Faltung bietet der Mechanismus der Selbstaufmerksamkeit im Transformer eine effektivere Methode, um unregelmäßige Formen und Objektgrenzen in Punktwolken zu erhalten. Für eine Punktwolke, die aus N Elementen 𝒑=[p1,…, pN], besteht, berechnet der Transformer die Antwort für jeden Punkt wie folgt:
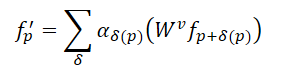
Dabei steht αδ für die Selbstaufmerksamkeitskoeffizienten zwischen Punkten in der lokalen Nachbarschaft, während 𝑾v die Transformation der Value bezeichnet. Im Vergleich zum statischen α=1 bei der Faltung ermöglichen die Selbstaufmerksamkeitskoeffizienten eine adaptive Auswahl von Punkten für die Aggregation, wodurch der Einfluss von nicht verwandten Punkten effektiv ausgeschlossen wird. Allerdings wird auf alle Punkte im Transformer dieselbe Transformation von Value angewandt, was bedeutet, dass die strukturelle Kodierungsfähigkeit, die der Faltung innewohnt, nicht gegeben ist.
In Anbetracht der obigen Ausführungen haben die Autoren des SEFormer festgestellt, dass die Faltung in der Lage ist, die Datenstruktur zu kodieren, während Transformer diese effektiv bewahren können. Daher besteht die einfache Idee darin, einen neuen Operator zu entwickeln, der die Vorteile von Faltung und Transformer vereint. Dies führte zum Vorschlag von SEFormer, der wie folgt formuliert werden kann:
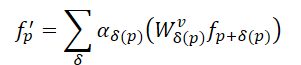
Der Hauptunterschied zwischen SEFormer und dem puren Transformer liegt in der Transformationsfunktion der Value, die auf der Grundlage der relativen Positionen der Punkte gelernt wird.
Angesichts der Unregelmäßigkeit von Punktwolken folgen die Autoren von SEFormer dem Paradigma des Point Transformer, indem sie unabhängig voneinander benachbarte Punkte um jeden Query-Punkt herum abtasten, bevor sie sie an den Transformer weitergeben. Bei ihrer Methode entschieden sich die Autoren für eine Rasterinterpolation zur Erzeugung von Schlüsselpunkten. Um jeden analysierten Punkt herum werden mehrere virtuelle Punkte erzeugt, die auf einem vordefinierten Raster angeordnet sind. Der Abstand zwischen zwei Gitterelementen ist auf d festgelegt.
Diese virtuellen Punkte werden dann anhand ihrer nächsten Nachbarn in der analysierten Punktwolke interpoliert. Im Vergleich zu traditionellen Sampling-Methoden wie K-Nächste Nachbarn (KNN) liegt der Vorteil des Rastersamplings in seiner Fähigkeit, die Punktauswahl aus verschiedenen Richtungen zu erzwingen. Die Rasterinterpolation ermöglicht eine genauere Darstellung der lokalen Struktur. Da jedoch ein fester Abstand d für die Gitterinterpolation verwendet wird, verwenden die Autoren eine Strategie mit mehreren Radien, um die Flexibilität bei der Probenahme zu erhöhen.
SEFormer konstruiert einen Speicherpool mit mehreren Transformationsmatrizen (𝑾v) von Value. Die interpolierten Schlüsselpunkte suchen nach ihren entsprechenden 𝑾v auf der Grundlage ihrer relativen Koordinaten in Bezug auf den ursprünglichen Punkt. Infolgedessen werden ihre Merkmale unterschiedlich umgewandelt. Dies ermöglicht es SEFormer, strukturelle Informationen zu kodieren - eine Fähigkeit, die dem ursprünglichen Transformer fehlt.
Bei dem von den Autoren vorgeschlagenen Objekterkennungsmodell wird zunächst ein auf 3D-Faltung basierendes Grundgerüst erstellt, um mehrskalige Voxelmerkmale zu extrahieren und erste Vorschläge zu generieren. Das Faltungs-Backbone transformiert den rohen Input in eine Reihe von Voxel-Merkmalen mit Downsampling-Faktoren von 1×, 2×, 4× und 8×. Diese Merkmale unterschiedlichen Maßstabs werden auf verschiedenen Tiefenebenen verarbeitet. Nach der Merkmalsextraktion wird das 3D-Volumen entlang der Z-Achse komprimiert und in eine 2D-Merkmalskarte aus der Vogelperspektive (BEV) umgewandelt. Diese BEV-Karten werden dann zur Erstellung erster Objektvorhersagen verwendet.
Als Nächstes aggregiert die vorgeschlagene räumliche Modulationsstruktur die multiskaligen Merkmale [𝑭1, 𝑭2, 𝑭3, 𝑭4] zu mehreren punktuellen Einbettungen 𝑬. Beginnend mit 𝑬init werden die Schlüsselpunkte aus der kleinsten Merkmals-Map 𝑭1 für jedes analysierte Element interpoliert. Die Autoren verwenden m verschiedene Gitterabstände d, um mehrskalige Sätze von Schlüsselmerkmalen zu erzeugen, die als 𝑭1,1, 𝑭2,1,…, 𝑭m,1. bezeichnet werden. Diese Multi-Radius-Strategie verbessert die Fähigkeit des Modells, mit der spärlichen und unregelmäßigen Verteilung von Punktwolken umzugehen. Dann werden m parallele SEFormer-Blöcke angewendet, um m aktualisierte Einbettungen 𝑬1,1, 𝑬2,1,...,𝑬m,1 zu erzeugen. Diese Einbettungen werden verkettet und mit Hilfe eines reinen Transformers in eine einheitliche Einbettung 𝑬1 umgewandelt. 𝑬1 wiederholt dann den zuvor beschriebenen Prozess und aggregiert [𝑭2, 𝑭3, 𝑭4] zu der endgültigen Einbettung 𝑬final. Im Vergleich zu den ursprünglichen Voxelmerkmalen 𝑭 ist die endgültige Einbettung 𝑬final eine detailliertere strukturelle Darstellung des lokalen Gebiets.
Auf der Grundlage der sich ergebenden Einbettungen auf Punktebene 𝑬finalDer von den Autoren vorgeschlagene Modellkopf fasst sie zu mehreren Einbettungen auf Objektebene zusammen, um die endgültigen Objektvorschläge zu erstellen. Genauer gesagt wird jeder Vorschlag der ersten Stufe in mehrere kubische Unterregionen unterteilt, von denen jede mit den umgebenden punktförmigen Objekteinbettungen interpoliert wird. Aufgrund der geringen Größe der Punktwolke sind einige Regionen oft leer. Bei herkömmlichen Ansätzen werden die Merkmale aus nicht leeren Regionen einfach addiert. Im Gegensatz dazu ist SEFormer in der Lage, Informationen sowohl aus bevölkerten als auch aus leeren Regionen zu nutzen. Die verbesserten strukturellen Einbettungsfähigkeiten von SEFormer ermöglichen eine umfassendere strukturelle Darstellung auf Objektebene, wodurch genauere Vorschläge generiert werden.
Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.
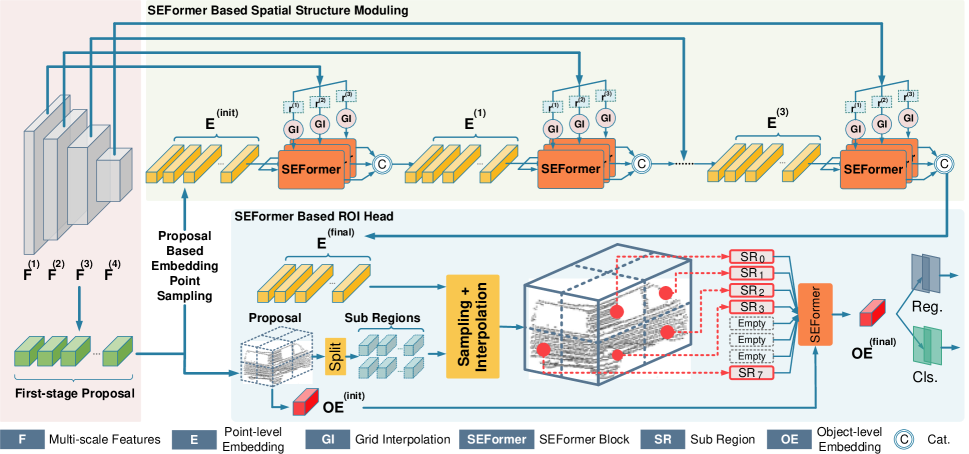
2. Implementation in MQL5
Nachdem wir die theoretischen Aspekte der vorgeschlagenen Methode SEFormer erläutert haben, kommen wir nun zum praktischen Teil unserer Arbeit, in dem wir unsere Interpretation der vorgeschlagenen Ansätze umsetzen. Betrachten wir zunächst die Architektur unseres künftigen Modells.
Für die anfängliche Merkmalsextraktion schlagen die Autoren der SEFormer-Methode die Verwendung einer voxelbasierten 3D-Faltung vor. In unserem Fall kann der Merkmalsvektor eines einzelnen Balkens jedoch wesentlich mehr Attribute enthalten. Daher scheint dieser Ansatz für unsere Zwecke weniger effizient zu sein. Daher schlage ich vor, auf unseren früheren Ansatz zurückzugreifen, bei dem die Merkmale mit Hilfe eines spärlichen Aufmerksamkeitsblocks mit unterschiedlicher Aufmerksamkeitskonzentration aggregiert werden.
Der zweite hervorzuhebende Punkt ist die Konstruktion eines Gitters um den untersuchten Punkt. Bei der von den SEFormer-Autoren gestellten Aufgabe der 3D-Objekterkennung können die Daten entlang der Höhendimension komprimiert werden, was die Analyse von Objekten auf flachen Karten ermöglicht. In unserem Fall ist die Datendarstellung jedoch multidimensional, und jede Dimension kann zu einem bestimmten Zeitpunkt eine entscheidende Rolle spielen. Wir können es uns nicht leisten, die Daten entlang einer einzigen Dimension zu komprimieren. Außerdem stellt die Konstruktion eines „Gitters“ in einem hochdimensionalen Raum eine große Herausforderung dar. Die Anzahl der Elemente steigt geometrisch mit der Anzahl der zu analysierenden Merkmale. Meines Erachtens besteht eine effektivere Lösung in diesem Szenario darin, das Modell die optimalen Schwerpunktpunkte im mehrdimensionalen Raum lernen zu lassen.
In Anbetracht der obigen Ausführungen schlage ich vor, unser neues Objekt zu bauen, indem wir die Kernfunktionalität von der Klasse CNeuronPointNet2OCL erben. Die allgemeine Struktur der neuen Klasse CNeuronSEFormer wird im Folgenden dargestellt.
class CNeuronSEFormer : public CNeuronPointNet2OCL { protected: uint iUnits; uint iPoints; //--- CLayer cQuery; CLayer cKey; CLayer cValue; CLayer cKeyValue; CArrayInt cScores; CLayer cMHAttentionOut; CLayer cAttentionOut; CLayer cResidual; CLayer cFeedForward; CLayer cCenterPoints; CLayer cFinalAttention; CNeuronMLCrossAttentionMLKV SEOut; CBufferFloat cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, int scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronSEFormer(void) {}; ~CNeuronSEFormer(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, uint center_points, uint center_window, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSEFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
In der oben dargestellten Struktur können wir bereits eine vertraute Liste von überschreibbaren Methoden und eine Reihe von verschachtelten Objekten sehen. Die Namen einiger dieser Komponenten erinnern vielleicht an die Architektur desTransformers - und das ist kein Zufall. Die Autoren von SEFormer hatten das Ziel, den Algorithmus des ursprünglichen Transformers zu verbessern. Aber das Wichtigste zuerst.
Alle internen Objekte unserer Klasse werden statisch deklariert, sodass wir den Konstruktor und Destruktor leer lassen können. Die Initialisierung sowohl der deklarierten als auch der geerbten Komponenten erfolgt in der Methode Init, deren Parameter, wie Sie wissen, die Kernkonstanten enthalten, die die Architektur des zu erstellenden Objekts definieren.
bool CNeuronSEFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, uint center_points, uint center_window, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets, optimization_type, batch)) return false;
Zusätzlich zu den Parametern, die wir bereits kennen, führen wir nun die Anzahl der trainierbaren Zentren und die Dimensionalität des Vektors, der ihren Zustand repräsentiert, ein.
Es ist wichtig zu beachten, dass die Architektur unseres Blocks so konzipiert ist, dass die Dimensionalität des Deskriptorvektors des Schwerpunkts von der Anzahl der Merkmale, die zur Beschreibung eines einzelnen analysierten Balkens verwendet werden, abweichen kann.
Innerhalb des Methodenkörpers beginnen wir wie üblich mit dem Aufruf der entsprechenden Methode der übergeordneten Klasse, die bereits die Mechanismen zur Parametervalidierung und Initialisierung der geerbten Komponenten implementiert. Wir überprüfen lediglich das logische Ergebnis der Ausführung der übergeordneten Methode.
Danach speichern wir mehrere Architekturparameter, die bei der Ausführung des zu erstellenden Algorithmus benötigt werden.
iUnits = units_count; iPoints = MathMax(center_points, 9);
Als Array von internen Objekten habe ich CLayer-Objekte verwendet. Um ihre korrekte Funktion zu ermöglichen, übergeben wir einen Zeiger auf das OpenCL-Kontextobjekt.
cQuery.SetOpenCL(OpenCL); cKey.SetOpenCL(OpenCL); cValue.SetOpenCL(OpenCL); cKeyValue.SetOpenCL(OpenCL); cMHAttentionOut.SetOpenCL(OpenCL); cAttentionOut.SetOpenCL(OpenCL); cResidual.SetOpenCL(OpenCL); cFeedForward.SetOpenCL(OpenCL); cCenterPoints.SetOpenCL(OpenCL); cFinalAttention.SetOpenCL(OpenCL);
Um die Schwerpunktrepräsentation zu lernen, erstellen wir einen kleinen MLP, der aus 2 aufeinanderfolgenden, voll verbundenen Schichten besteht.
//--- Init center points CNeuronBaseOCL *base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(iPoints * center_window * 2, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *buf = base.getOutput(); if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite()) return false; if(!cCenterPoints.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base.Init(0, 1, OpenCL, iPoints * center_window * 2, optimization, iBatch)) return false; if(!cCenterPoints.Add(base)) return false;
Beachten Sie, dass wir die doppelte Anzahl von Zentren erstellen. Auf diese Weise schaffen wir 2 Sätze von Schwerpunkten und simulieren die Konstruktion eines Gitters mit unterschiedlichen Skalen.
Und dann werden wir einen Zyklus erstellen, in dem wir interne Objekte entsprechend der Anzahl der Feature-Skalierungsebenen initialisieren.
Ich möchte Sie daran erinnern, dass wir in der übergeordneten Klasse die ursprünglichen Daten mit zwei Koeffizienten für die Aufmerksamkeitskonzentration aggregieren. Dementsprechend wird unsere Schleife 2 Iterationen enthalten.
//--- Inside layers for(int i = 0; i < 2; i++) { //--- Interpolation CNeuronMVCrossAttentionMLKV *cross = new CNeuronMVCrossAttentionMLKV(); if(!cross || !cross.Init(0, i * 12 + 2, OpenCL, center_window, 32, 4, 64, 2, iPoints, iUnits, 2, 2, 2, 1, optimization, iBatch)) return false; if(!cCenterPoints.Add(cross)) return false;
Für die Zentroid-Interpolation verwenden wir einen Kreuzaufmerksamkeitsblock, der die aktuelle Darstellung der Zentroide mit dem Satz der analysierten Eingabedaten abgleicht. Der Kerngedanke dieses Prozesses besteht darin, einen Satz von Zentren zu ermitteln, der die Eingabedaten am genauesten und effektivsten in lokale Regionen unterteilt. Auf diese Weise wollen wir die Struktur der Eingabedaten lernen.
Als Nächstes gehen wir zur Initialisierung der Blockkomponenten von SEFormer über, wie von den ursprünglichen Autoren vorgeschlagen. Dieser Block dient dazu, die Einbettungen der analysierten Punkte mit strukturellen Informationen über die Punktwolke anzureichern. Technisch gesehen wenden wir einen Kreuzaufmerksamkeits-Mechanismus von den analysierten Punkten zu unseren Zentroiden an, die bereits mit Strukturinformationen der Punktwolke angereichert wurden.
Hier verwenden wir eine Faltungsschicht, um die Query-Entität auf der Grundlage der Einbettungen der analysierten Punkte zu erzeugen.
//--- Query CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 3, OpenCL, 64, 64, 64, iUnits, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false;
In ähnlicher Weise erzeugen wir Key-Entitäten, aber hier verwenden wir die Darstellung von Zentroiden.
//--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 4, OpenCL, center_window, center_window, 32, iPoints, 2, optimization, iBatch)) return false; if(!cKey.Add(conv)) return false;
Die Autoren von SEFormer schlagen vor, für jedes Element der Sequenz eine eigene Transformationsmatrix zu verwenden, um die Entität von Value zu erzeugen. Daher wenden wir eine ähnliche Faltungsschicht an, wobei die Anzahl der Elemente in der Sequenz auf 1 gesetzt wird. Gleichzeitig wird die gesamte Anzahl der Zentren als Parameter der Eingabevariablen übergeben. Dieser Ansatz ermöglicht es uns, das gewünschte Ergebnis zu erzielen.
//--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 5, OpenCL, center_window, center_window, 32, 1, iPoints * 2, optimization, iBatch)) return false; if(!cValue.Add(conv)) return false;
Alle unsere Kernel wurden jedoch mit dem Kreuzaufmerksamkeits-Algorithmus erstellt, um mit einem verketteten Tensor von Entitäten von Key-Value (Schlüssel-Wert) zu arbeiten. Um also keine Änderungen an OpenCL vorzunehmen, fügen wir einfach die Verkettung der angegebenen Tensoren hinzu.
//--- Key-Value base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 6, OpenCL, iPoints * 2 * 32 * 2, optimization, iBatch)) return false; if(!cKeyValue.Add(base)) return false;
Die Matrix der Abhängigkeitskoeffizienten wird nur im Kontext von OpenCL verwendet und bei jedem Vorwärtsdurchlauf neu berechnet. Daher ist es nicht sinnvoll, diesen Puffer im Hauptspeicher anzulegen. Wir erstellen ihn also nur im Kontextspeicher von OpenCL.
//--- Score int s = int(iUnits * iPoints * 4); s = OpenCL.AddBuffer(sizeof(float) * s, CL_MEM_READ_WRITE); if(s < 0 || !cScores.Add(s)) return false;
Als Nächstes erstellen wir eine Ebene für die Aufzeichnung von mehrköpfigen Aufmerksamkeitsdaten.
//--- MH Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 7, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!cMHAttentionOut.Add(base)) return false;
Wir fügen auch eine Faltungsschicht hinzu, um die erzielten Ergebnisse zu skalieren.
//--- Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 8, OpenCL, 64, 64, 64, iUnits, 1, optimization, iBatch)) return false; if(!cAttentionOut.Add(conv)) return false;
Nach dem Algorithmus vom Transformer werden die Ergebnisse der Selbstaufmerksamkeit mit den Originaldaten summiert und normalisiert.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 9, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false;
Als Nächstes fügen wir 2 Schichten des FeedForward-Blocks hinzu.
//--- Feed Forward conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 10, OpenCL, 64, 64, 256, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, i * 12 + 11, OpenCL, 256, 64, 64, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false;
Und ein Objekt zur Organisation der restlichen Kommunikation.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, i * 12 + 12, OpenCL, iUnits * 64, optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient(), true)) return false; if(!cResidual.Add(base)) return false;
Beachten Sie, dass wir in diesem Fall den Gradientenfehlerpuffer innerhalb der Restverbindungsschicht außer Kraft setzen. Auf diese Weise lässt sich das Kopieren von Gradientenfehlerdaten aus der Restschicht in die letzte Schicht des FeedForward-Blocks vermeiden.
Um das SEFormer-Modul abzuschließen, schlagen die Autoren vor, einen reinen Transformer zu verwenden. Ich habe mich jedoch für eine anspruchsvollere Architektur entschieden, indem ich ein szenenabhängiges Aufmerksamkeitsmodul eingebaut habe.
//--- Final Attention CNeuronMLMHSceneConditionAttention *att = new CNeuronMLMHSceneConditionAttention(); if(!att || !att.Init(0, i * 12 + 13, OpenCL, 64, 16, 4, 2, iUnits, 2, 1, optimization, iBatch)) return false; if(!cFinalAttention.Add(att)) return false; }
In diesem Stadium haben wir alle Komponenten einer einzelnen internen Schicht initialisiert und gehen nun zur nächsten Iteration der Schleife über.
Nach Abschluss aller Iterationen der Initialisierungsschleife der internen Schicht ist es wichtig zu beachten, dass wir die Ausgaben der einzelnen internen Schichten nicht einzeln verwenden. Logischerweise könnte man sie zu einem einzigen Tensor verketten und diesen vereinheitlichten Tensor an die übergeordnete Klasse übergeben, um die globale Punktwolkeneinbettung zu erzeugen. Natürlich müssten wir den resultierenden Tensor zunächst auf die erforderlichen Dimensionen skalieren. In diesem Fall habe ich mich jedoch für einen anderen Ansatz entschieden. Stattdessen verwenden wir einen Cross-Attention-Block, um die Daten auf der unteren Ebene mit Informationen aus den höheren Ebenen anzureichern.
if(!SEOut.Init(0, 26, OpenCL, 64, 64, 4, 16, 4, iUnits, iUnits, 4, 1, optimization, iBatch)) return false;
Am Ende der Methode wird ein Hilfspuffer für die temporäre Datenspeicherung initialisiert.
if(!cbTemp.BufferInit(buf_size, 0) || !cbTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Danach geben wir das logische Ergebnis der Ausführung der Methodenoperationen an das aufrufende Programm zurück.
In diesem Stadium haben wir die Arbeit an der Initialisierungsmethode des Klassenobjekts abgeschlossen. Nun gehen wir dazu über, den Algorithmus des Vorwärtsdurchlaufa in der Methode feedForward zu konstruieren. Wie Sie wissen, erhalten wir in den Parametern dieser Methode einen Zeiger auf das Quelldatenobjekt.
bool CNeuronSEFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL;
Im Körper der Methode werden einige lokale Variablen deklariert, um Zeiger auf interne Objekte vorübergehend zu speichern. Und dann erzeugen wir eine Darstellung der Zentren.
//--- Init Points if(bTrain) { neuron = cCenterPoints[1]; if(!neuron || !neuron.FeedForward(cCenterPoints[0])) return false; }
Beachten Sie, dass wir die Schwerpunktdarstellung nur während des Modelltrainings erzeugen. Während des Betriebs sind die Schwerpunktpunkte statisch. Wir brauchen sie also nicht bei jedem Durchlauf zu erzeugen.
Als nächstes organisieren wir eine Schleife durch die internen Schichten,
//--- Inside Layers for(int l = 0; l < 2; l++) { //--- Segmentation Inputs if(l > 0 || !cTNetG) { if(!caLocalPointNet[l].FeedForward((l == 0 ? NeuronOCL : GetPointer(caLocalPointNet[l - 1])))) return false; } else { if(!cTurnedG) return false; if(!cTNetG.FeedForward(NeuronOCL)) return false; int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false; if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject())) return false; }
Im Hauptteil werden zunächst die Quelldaten segmentiert (der Algorithmus ist der übergeordneten Klasse entlehnt). Dann reichern wir die Zentren mit den erhaltenen Daten an.
//--- Interpolate center points neuron = cCenterPoints[l + 2]; if(!neuron || !neuron.FeedForward(cCenterPoints[l + 1], caLocalPointNet[l].getOutput())) return false;
Als Nächstes gehen wir zum Aufmerksamkeitsmodul mit Datenstrukturkodierung über. Zunächst extrahieren wir die entsprechenden inneren Schichten aus den Arrays.
//--- Structure-Embedding Attention
q = cQuery[l];
k = cKey[l];
v = cValue[l];
kv = cKeyValue[l];
Dann erzeugen wir nacheinander alle notwendigen Entitäten.
//--- Query if(!q || !q.FeedForward(GetPointer(caLocalPointNet[l]))) return false; //--- Key if(!k || !k.FeedForward(cCenterPoints[l + 2])) return false; //--- Value if(!v || !v.FeedForward(cCenterPoints[l + 2])) return false;
Die Ergebnisse des Erzeugens von Key und Value werden zu einem einzigen Tensor verkettet.
if(!kv || !Concat(k.getOutput(), v.getOutput(), kv.getOutput(), 32 * 2, 32 * 2, iPoints)) return false;
Danach können wir die klassischen Methoden der mehrköpfigen Selbstaufmerksamkeit anwenden.
//--- Multi-Head Attention neuron = cMHAttentionOut[l]; if(!neuron || !AttentionOut(q.getOutput(), kv.getOutput(), cScores[l], neuron.getOutput())) return false;
Wir skalieren die erhaltenen Daten auf die Größe der Originaldaten.
//--- Scale neuron = cAttentionOut[l]; if(!neuron || !neuron.FeedForward(cMHAttentionOut[l])) return false;
Dann summieren wir die beiden Informationsströme und normalisieren die resultierenden Daten.
//--- Residual q = cResidual[l * 2]; if(!q || !SumAndNormilize(caLocalPointNet[l].getOutput(), neuron.getOutput(), q.getOutput(), 64, true, 0, 0, 0, 1)) return false;
Ähnlich wie beim Encoder des reinen Transformers verwenden wir den FeedForward-Block, gefolgt von einer Assoziation der Residuen und Datennormalisierung.
//--- Feed Forward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.FeedForward(q)) return false; neuron = cFeedForward[l * 2 + 1]; if(!neuron || !neuron.FeedForward(cFeedForward[l * 2])) return false; //--- Residual k = cResidual[l * 2 + 1]; if(!k || !SumAndNormilize(q.getOutput(), neuron.getOutput(), k.getOutput(), 64, true, 0, 0, 0, 1)) return false;
Wir leiten die erhaltenen Ergebnisse durch den Aufmerksamkeitsblock und berücksichtigen dabei die Szene. Und dann geht es weiter mit der nächsten Iteration der Schleife.
//--- Final Attention neuron = cFinalAttention[l]; if(!neuron || !neuron.FeedForward(k)) return false; }
Nachdem alle Operationen der inneren Schicht erfolgreich abgeschlossen sind, reichern wir die kleineren Punkteinbettungen mit großräumigen Informationen an.
//--- Cross scale attention if(!SEOut.FeedForward(cFinalAttention[0], neuron.getOutput())) return false;
Und dann übertragen wir das erhaltene Ergebnis, um eine globale Einbettung der analysierten Punktwolke zu bilden.
//--- Global Point Cloud Embedding if(!CNeuronPointNetOCL::feedForward(SEOut.AsObject())) return false; //--- result return true; }
Am Ende der Methode des Vorwärtsdurchlaufs geben wir dem aufrufenden Programm einen booleschen Wert zurück, der den Erfolg der Operationen anzeigt.
Wie man sieht, führt die Implementierung des Algorithmus des Vorwärtsdurchlaufs zu einer ziemlich komplexen Informationsflussstruktur, die alles andere als linear ist. Wir beobachten die Verwendung von Verbindungen der Residuen. Einige Komponenten stützen sich auf zwei Datenquellen. Außerdem kreuzen sich die Datenströme an mehreren Stellen. Diese Komplexität hat natürlich den Entwurf des Algorithmus des Rückwärtsdurchlaufs beeinflusst, den wir in der Methode calcInputGradients implementiert haben.
bool CNeuronSEFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Diese Methode erhält einen Zeiger auf die vorhergehende Ebene als Parameter. Während des Vorwärtsdurchlaufs lieferte diese Schicht die Eingabedaten. Nun müssen wir ihm den Fehlergradienten zurückgeben, der dem Einfluss der Eingabedaten auf die endgültige Ausgabe des Modells entspricht.
Innerhalb des Methodenkörpers wird der erhaltene Zeiger sofort validiert, da eine Fortsetzung mit einer ungültigen Referenz alle nachfolgenden Operationen sinnlos machen würde.
Wir deklarieren auch eine Reihe lokaler Variablen, um vorübergehend Zeiger auf interne Komponenten zu speichern.
CNeuronBaseOCL *neuron = NULL, *q = NULL, *k = NULL, *v = NULL, *kv = NULL; CBufferFloat *buf = NULL;
Danach verteilen wir den Fehlergradienten von der globalen Einbettung der Punktwolke auf unsere internen Schichten.
//--- Global Point Cloud Embedding if(!CNeuronPointNetOCL::calcInputGradients(SEOut.AsObject())) return false;
Beachten Sie, dass wir im Vorwärtsdurchlauf das Endergebnis durch den Aufruf der Methode der übergeordneten Klasse erhalten haben. Um den Fehlergradienten zu erhalten, müssen wir daher die entsprechende Methode der übergeordneten Klasse verwenden.
Als Nächstes wird der Fehlergradient in Ströme unterschiedlicher Größenordnung aufgeteilt.
//--- Cross scale attention neuron = cFinalAttention[0]; q = cFinalAttention[1]; if(!neuron.calcHiddenGradients(SEOut.AsObject(), q.getOutput(), q.getGradient(), ( ENUM_ACTIVATION)q.Activation())) return false;
Dann organisieren wir eine umgekehrte Schleife durch die internen Schichten.
for(int l = 1; l >= 0; l--) { //--- Final Attention neuron = cResidual[l * 2 + 1]; if(!neuron || !neuron.calcHiddenGradients(cFinalAttention[l])) return false;
Hier verteilen wir den Fehlergradienten zunächst auf die Ebene der Residuen-Verbindungsschicht.
Ich möchte Sie daran erinnern, dass wir bei der Initialisierung der internen Objekte den Fehlergradientenpuffer der Restverbindungsschicht durch einen ähnlichen Puffer der Schicht aus dem FeedForward-Block ersetzt haben. Jetzt können wir das unnötige Kopieren von Daten überspringen und den Fehlergradienten sofort an die darunter liegende Ebene weitergeben.
//--- Feed Forward neuron = cFeedForward[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2 + 1])) return false;
Anschließend wird der Fehlergradient auf die Restverbindungsschicht des Aufmerksamkeitsblocks übertragen.
neuron = cResidual[l * 2]; if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2])) return false;
Hier addieren wir den Fehlergradienten aus 2 Informationsströmen und übertragen den Gesamtwert an den Aufmerksamkeitsblock.
//--- Residual q = cResidual[l * 2 + 1]; k = neuron; neuron = cAttentionOut[l]; if(!neuron || !SumAndNormilize(q.getGradient(), k.getGradient(), neuron.getGradient(), 64, false, 0, 0, 0, 1)) return false;
Danach verteilen wir den Fehlergradienten auf die Aufmerksamkeitsköpfe.
//--- Scale neuron = cMHAttentionOut[l]; if(!neuron || !neuron.calcHiddenGradients(cAttentionOut[l])) return false;
Mit Hilfe der Algorithmen des ursprünglichen Transformers wird der Fehlergradient auf die Entitätsebene Query, Key und Value übertragen.
//--- MH Attention q = cQuery[l]; kv = cKeyValue[l]; k = cKey[l]; v = cValue[l]; if(!AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), cScores[l], neuron.getGradient())) return false;
Als Ergebnis dieser Operation erhalten wir 2 Tensoren mit den Fehlergradienten: auf der Ebene von Query und des verketteten Key-Value-Tensors. Verteilen wir die Fehlergradienten Key und Value auf die Puffer der entsprechenden internen Ebenen.
if(!DeConcat(k.getGradient(), v.getGradient(), kv.getGradient(), 32 * 2, 32 * 2, iPoints)) return false;
Dann können wir den Fehlergradienten vom Query-Tensor auf die Ebene der ursprünglichen Datensegmentierung übertragen. Es gibt jedoch einen Vorbehalt. Für die letzte Schicht ist dieser Vorgang nicht besonders schwierig. Für die erste Schicht speichert der Gradientenpuffer jedoch bereits Informationen über den Fehler aus der nachfolgenden Segmentierungsebene. Und wir müssen sie bewahren. Deshalb überprüfen wir den Index der aktuellen Ebene und ersetzen gegebenenfalls die Zeiger auf die Datenpuffer.
if(l == 0) { buf = caLocalPointNet[l].getGradient(); if(!caLocalPointNet[l].SetGradient(GetPointer(cbTemp), false)) return false; }
Als Nächstes verteilen wir den Fehlergradienten.
if(!caLocalPointNet[l].calcHiddenGradients(q, NULL)) return false;
Falls erforderlich, summieren wir die Daten der 2 Informationsströme mit anschließender Rückgabe des entfernten Zeigers auf den Datenpuffer.
if(l == 0) { if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 64, false, 0, 0, 0, 1)) return false; if(!caLocalPointNet[l].SetGradient(buf, false)) return false; }
Als Nächstes wird der Fehlergradient der restlichen Verbindungen des Aufmerksamkeitsblocks hinzugefügt.
neuron = cAttentionOut[l]; //--- Residual if(!SumAndNormilize(caLocalPointNet[l].getGradient(), neuron.getGradient(), caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1)) return false;
Der nächste Schritt besteht darin, den Fehlergradienten auf die Ebene unserer Zentren zu verteilen. Hier müssen wir den Fehlergradienten sowohl von der Key- als auch von der Value-Entität verteilen. Auch hier werden wir die Substitution von Zeigern auf Datenpuffer verwenden.
//--- Interpolate Center points neuron = cCenterPoints[l + 2]; if(!neuron) return false; buf = neuron.getGradient(); if(!neuron.SetGradient(GetPointer(cbTemp), false)) return false;
Danach wird der erste Fehlergradient von der Entität Key übertragen.
if(!neuron.calcHiddenGradients(k, NULL)) return false;
Allerdings ist es die erste nur für die letzte Schicht, aber für die erste enthält sie bereits Informationen über den Fehlergradienten aus dem Einfluss auf das Ergebnis der nachfolgenden Schicht. Deshalb überprüfen wir den Index der analysierten inneren Schicht und fassen gegebenenfalls die Daten aus den beiden Informationsströmen zusammen.
if(l == 0) { if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1)) return false; } else { if(!SumAndNormilize(GetPointer(cbTemp), GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 0.5f)) return false; }
In ähnlicher Weise propagieren wir den Gradienten des Fehlers von der Entität Value und fassen die Daten aus zwei Informationsströmen zusammen.
if(!neuron.calcHiddenGradients(v, NULL)) return false; if(!SumAndNormilize(buf, GetPointer(cbTemp), buf, 1, false, 0, 0, 0, 1)) return false;
Danach geben wir den zuvor entfernten Zeiger auf den Fehlergradientenpuffer zurück.
if(!neuron.SetGradient(buf, false)) return false;
Anschließend wird der Fehlergradient zwischen den Zentren der vorherigen Schicht und den segmentierten Daten der aktuellen Schicht verteilt.
neuron = cCenterPoints[l + 1]; if(!neuron.calcHiddenGradients(cCenterPoints[l + 2], caLocalPointNet[l].getOutput(), GetPointer(cbTemp), (ENUM_ACTIVATION)caLocalPointNet[l].Activation())) return false;
Gerade um diesen spezifischen Fehlergradienten zu erhalten, haben wir zuvor die Puffer in der Schwerpunktschicht übersteuert. Außerdem ist zu beachten, dass der Gradientenpuffer in der Datensegmentierungsschicht bereits einen großen Teil der relevanten Informationen enthält. Deshalb speichern wir in dieser Phase den Fehlergradienten in einem temporären Datenpuffer und summieren dann die Daten der beiden Informationsflüsse.
if(!SumAndNormilize(caLocalPointNet[l].getGradient(), GetPointer(cbTemp), caLocalPointNet[l].getGradient(), 64, false, 0, 0, 0, 1)) return false;
In diesem Stadium haben wir den Fehlergradienten auf alle neu deklarierten internen Objekte verteilt. Dennoch müssen wir den Fehlergradienten auf die Datensegmentierungsschichten verteilen. Wir leihen uns diesen Algorithmus vollständig von der Methode der übergeordneten Klasse.
//--- Local Net neuron = (l > 0 ? GetPointer(caLocalPointNet[l - 1]) : NeuronOCL); if(l > 0 || !cTNetG) { if(!neuron.calcHiddenGradients(caLocalPointNet[l].AsObject())) return false; } else { if(!cTurnedG) return false; if(!cTurnedG.calcHiddenGradients(caLocalPointNet[l].AsObject())) return false; int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMulGrad(neuron.getOutput(), neuron.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), cTurnedG.getGradient(), neuron.Neurons() / window, window, window)) return false; if(!OrthoganalLoss(cTNetG, true)) return false; //--- CBufferFloat *temp = neuron.getGradient(); neuron.SetGradient(cTurnedG.getGradient(), false); cTurnedG.SetGradient(temp, false); //--- if(!neuron.calcHiddenGradients(cTNetG.AsObject())) return false; if(!SumAndNormilize(neuron.getGradient(), cTurnedG.getGradient(), neuron.getGradient(), 1, false, 0, 0, 0, 1)) return false; } } //--- return true; }
Nachdem alle Iterationen unserer internen Schleife abgeschlossen sind, geben wir einen booleschen Wert zurück, der den Erfolg der Methodenausführung an das aufrufende Programm anzeigt.
Damit haben wir sowohl den Vorwärtsdurchlauf als auch den Algorithmus der Gradientenverteilung durch die internen Komponenten unserer neuen Klasse implementiert. Was bleibt, ist die Implementierung der Methode updateInputWeights, die für die Aktualisierung der trainierbaren Parameter zuständig ist. In diesem Fall sind alle trainierbaren Parameter in den verschachtelten Komponenten gekapselt. Dementsprechend besteht die Aktualisierung der Parameter unserer Klasse lediglich darin, die entsprechenden Methoden in jedem der internen Objekte nacheinander aufzurufen. Dieser Algorithmus ist recht einfach, und ich schlage vor, diese Methode der unabhängigen Erforschung zu überlassen.
Zur Erinnerung: Die vollständige Implementierung der Klasse CNeuronSEFormer und alle ihre Methoden finden Sie in den beigefügten Dateien. Dort finden Sie auch die zuvor deklarierten Unterstützungsmethoden, die innerhalb dieser Klasse überschrieben werden können.
Abschließend ist anzumerken, dass die Gesamtarchitektur des Modells weitgehend aus dem vorherigen Artikel übernommen wurde. Die einzige Änderung, die wir vorgenommen haben, war das Ersetzen einer einzelnen Ebene im Encoder des Umgebungszustands.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSEFormer; { int temp[] = {BarDescr, 8}; // Variables, Center embedding if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } { int temp[] = {HistoryBars, 27}; // Units, Centers if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = LatentCount; // Output Dimension descr.step = int(true); // Use input and feature transformation descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Das Gleiche gilt für alle Programme, die für die Interaktion mit der Umwelt und das Training der Modelle verwendet werden und die vollständig aus dem vorherigen Artikel übernommen wurden. Deshalb werden wir sie jetzt nicht diskutieren. Der vollständige Code für alle in diesem Artikel verwendeten Programme ist im Anhang enthalten.
3. Tests
Und nun, nachdem wir eine beträchtliche Menge an Arbeit hinter uns gebracht haben, kommen wir zum letzten - und vielleicht den am meisten erwarteten - Teil des Prozesses: das Trainieren der Modelle und das Testen der daraus resultierenden Akteurspolitik an realen historischen Daten.
Wie immer verwenden wir zum Trainieren der Modelle reale historische Daten des Instruments EURUSD mit dem Zeitrahmen H1 für das gesamte Jahr 2023. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Der Algorithmus für das Training des Modells wurde aus früheren Artikeln übernommen, ebenso wie die Programme, die sowohl für die Ausbildung als auch für die Tests verwendet wurden.
Zum Testen der trainierten Akteurspolitik verwenden wir reale historische Daten vom Januar 2024, wobei alle anderen Parameter unverändert bleiben. Die Testergebnisse werden im Folgenden vorgestellt.
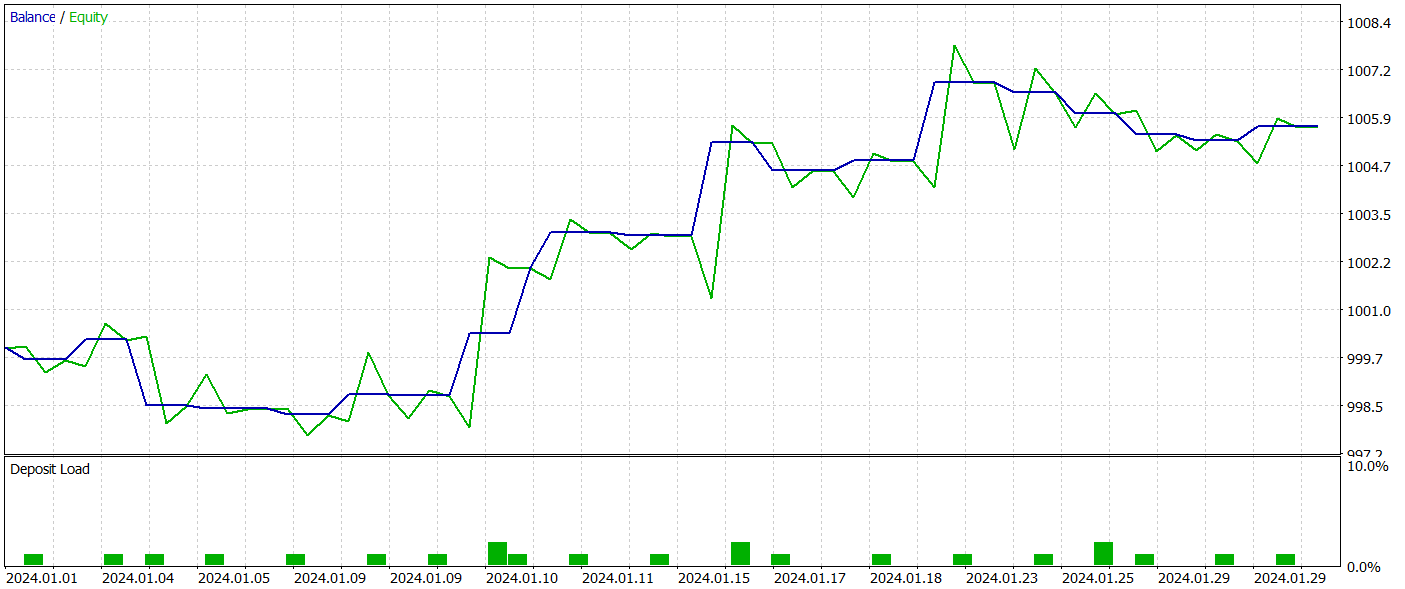
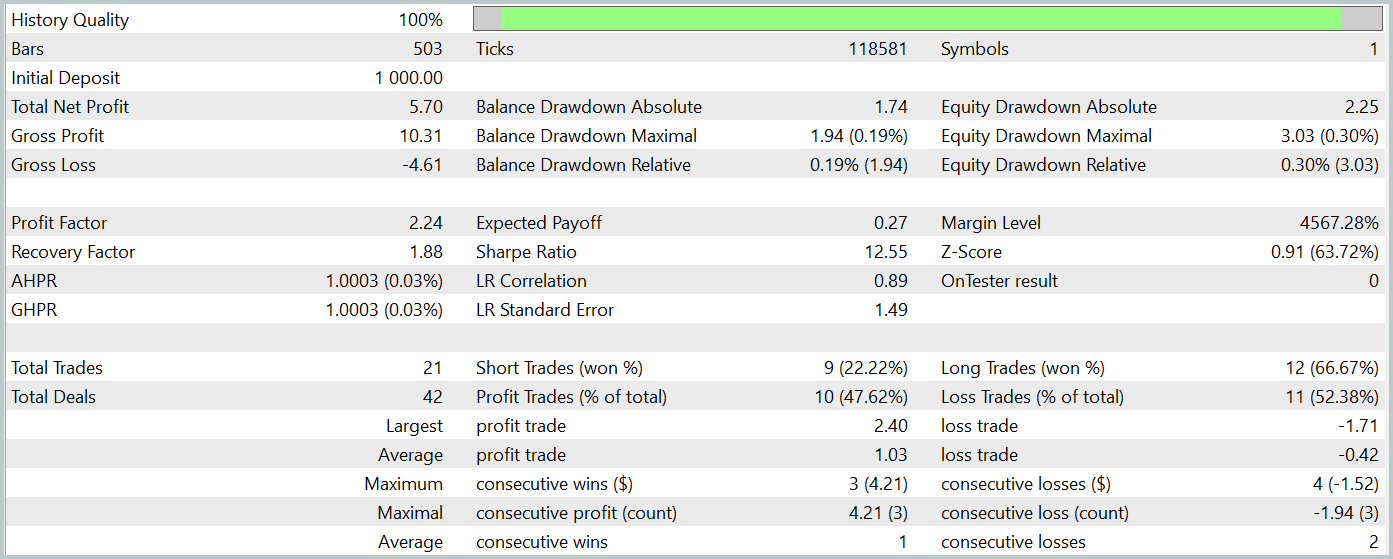
Während des Testzeitraums führte das trainierte Modell 21 Handelsgeschäfte aus, von denen etwas mehr als 47 % mit Gewinn abgeschlossen wurden. Erwähnenswert ist, dass die Kaufpositionen eine deutlich höhere Rentabilität aufwiesen (66 % gegenüber 22 %). Es ist klar, dass ein zusätzliches Modelltraining erforderlich ist. Dennoch war das durchschnittliche gewinnbringende Handelsgeschäft 2,5 Mal größer als der Durchschnitt der mit einem Verlust, sodass das Modell während des Testzeitraums insgesamt einen Gewinn erzielen konnte.
Meiner subjektiven Meinung nach erwies sich das Modell als ziemlich schwer. Dies ist wahrscheinlich zu einem großen Teil auf die Verwendung von szenekonditionierten Aufmerksamkeitsmechanismen zurückzuführen. Die Anwendung eines ähnlichen Ansatzes mit der Methode HyperDet3D brachte bessere Ergebnisse bei geringerem Rechenaufwand hervor.
Allerdings lassen die geringe Anzahl von Handelsgeschäften und der kurze Testzeitraum in beiden Fällen keine endgültigen Rückschlüsse auf die langfristige Wirksamkeit der Methode zu.
Schlussfolgerung
Die Methode SEFormer ist gut für die Analyse von Punktwolken geeignet und erfasst lokale Abhängigkeiten auch unter verrauschten Bedingungen - ein Schlüsselfaktor für genaue Vorhersagen. Dies eröffnet vielversprechende Möglichkeiten für präzisere Vorhersagen von Marktbewegungen und verbesserte Entscheidungsstrategien.
Im praktischen Teil dieses Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit Hilfe von MQL5 umgesetzt und das Modell auf realen historischen Daten trainiert und getestet. Die Ergebnisse zeigen das Potenzial der vorgeschlagenen Methode. Vor dem Einsatz des Modells in realen Handelsszenarien ist es jedoch unerlässlich, es über einen längeren historischen Zeitraum zu trainieren und die trainierte Strategie umfassend zu testen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15882
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay-Systems (Teil 66): Abspielen des Dienstes (VII)
Entwicklung eines Replay-Systems (Teil 66): Abspielen des Dienstes (VII)
 Finden von nutzerdefinierten Währungspaar-Mustern in Python mit MetaTrader 5
Finden von nutzerdefinierten Währungspaar-Mustern in Python mit MetaTrader 5
 African Buffalo Optimierung (ABO)
African Buffalo Optimierung (ABO)
 Artificial Showering Algorithm (ASHA)
Artificial Showering Algorithm (ASHA)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Schöner Artikel
Danke!