Algorithmen zur Populationsoptimierung Partikelschwarm (PSO)
365
0
Sie bilden erkennbare Schwärme, die im Sonnenlicht schweben
oder den Gewitterwolken folgen. Es ist möglich, dass sie ihre Energie aus atmosphärischen Entladungen beziehen.
Doch im Moment der Gefahr oder, allgemeiner gesagt, einer plötzlichen Veränderung, die ihre Existenz bedroht, schließen sie sich zusammen...
Stanisław Lem „Der Unbesiegbare“
Inhalt
1. Einführung
Es gibt wahrscheinlich nicht wenige Menschen, die Stanisław Lems wunderbaren Science-Fiction-Bestseller „Der Unbesiegbare“ gelesen haben. Überraschenderweise wurde eine der ersten Beschreibungen der Schwarmintelligenz genau mit der Veröffentlichung dieses Science-Fiction-Romans geboren. Die Geschichte handelt von Robotern, die ohne zentrale Steuerung überleben. Bemerkenswert ist, dass die einfachsten und zahlreichsten Exemplare überlebten und nicht die komplexesten, intelligentesten und mächtigsten.
Im Laufe der Jahrtausende währenden Nekroevolution haben diese Maschinen gelernt, effektiv mit Konkurrenten umzugehen, die sie sowohl an Intelligenz als auch an Energieverfügbarkeit übertrafen. Sie hatten nicht nur mit anderen Robotern zu kämpfen, sondern auch mit der lebendigen Welt des Planeten. Die Elemente der Fantasie in diesem Werk können zuverlässig mit der Evolution und der Natur selbst verglichen werden.
Seit der Antike interessieren sich die Menschen für das Verhalten von Tieren innerhalb einer Gruppe (das so genannte Schwarmverhalten) - wie Vögel funktionieren, wenn ein Schwarm in warme Länder fliegt, wie ein Bienenschwarm Nahrung produziert, wie ein Ameisenvolk überlebt und dabei komplexe Strukturen schafft, wie sich Fische in einem Schwarm verhalten und warum ihr Verhalten so synchronisiert ist. Die Organisation der Individuen in der Gesellschaft, die einige Muster eines gut koordinierten integralen Organismus aufweist, regt zu neuen Ideen im Bereich der algorithmischen Optimierung an.
Schwarmintelligenz beschreibt die Simulation des kollektiven Verhaltens eines selbstorganisierenden Systems. Es gibt eine ziemlich große Anzahl solcher Algorithmen. In der kanonischen Version, die 1995 von J. Kennedy und R. Eberhart verfasst wurde, wurde das dieser Methode zugrunde liegende Modell durch Vereinfachung des Reynolds-Modells gewonnen. Infolge dieser Vereinfachung begannen die einzelnen Individuen der Population als separate Objekte zu erscheinen, die keine Größe, aber eine gewisse Geschwindigkeit haben.
Aufgrund der extremen Ähnlichkeit mit materiellen Teilchen wurden die daraus resultierenden einfachen Objekte als Teilchen bezeichnet, und ihre Population wurde als Schwarm bezeichnet. Zu jedem Zeitpunkt (bei jeder Iteration) haben die Teilchen einen Positions- und Geschwindigkeitsvektor im Raum. Für jede Position des Teilchens wird der entsprechende Wert der Zielfunktion berechnet, und auf dieser Grundlage ändert das Teilchen nach bestimmten Regeln seine Position und Geschwindigkeit im Suchraum. Bei der Bestimmung der nächsten Position des Partikels wird die Information über die beste Position unter allen anderen benachbarten Partikeln, die den Aufgaben der Fitnessfunktion entspricht, berücksichtigt.
Beispiele für Schwarmalgorithmen:
- Partikelschwarm-Verfahren
- Ameisen-Algorithmus
- Bienen-Algorithmus:
- Künstliches Immunsystem
- Grauer-Wolf-Algorithmus
- Fledermaus-Algorithmus
- Schwerkraft-Suchalgorithmus
- Altruismus-Algorithmus
- und viele andere
Der Übergang von der Modellierung kollektiven Verhaltens zur kollektiven Optimierung basiert auf der folgenden biologischen Idee: Organismen schließen sich in Kolonien zusammen, um ihre Lebensbedingungen zu verbessern. Jeder Organismus in der Kolonie hat im Durchschnitt eine bessere Überlebenschance im Kampf gegen Fressfeinde, die Kolonie kann im Vergleich zu einzelnen Organismen effizienter Nahrung suchen, verarbeiten und speichern usw. Mit anderen Worten: Jede Kolonie von Organismen löst während der gesamten Zeit ihres Bestehens verschiedene Optimierungsprobleme mit unterschiedlichem Effizienzgrad, z. B. die Maximierung der Nahrungsmenge bei gleichzeitiger Minimierung der Verluste durch Raubtiere. Diese Überlegungen bildeten die Grundlage für die Konstruktion verschiedener mathematischer Optimierungsmethoden.
Der Partikelschwarm ist einer der bekanntesten und beliebtesten Optimierungsalgorithmen seit seiner Einführung. Viele Autoren der verschiedenen Implementierungen behaupten, dass der Algorithmus sehr effektiv bei der Optimierung komplexer Funktionen mit vielen Argumenten ist und sich sogar für das Training neuronaler Netze eignet.
In diesem Artikel werde ich versuchen herauszufinden, ob der Algorithmus tatsächlich für die Lösung komplexer Probleme geeignet ist. In der klassischen Version des Algorithmus und in vielen seiner Modifikationen gibt es erhebliche Einschränkungen, die damit zusammenhängen, dass die optimierte Funktion glatt und kontinuierlich sein muss, was bedeutet, dass er für diskrete Funktionen völlig ungeeignet ist. Im Rahmen der Artikelserie werden jedoch alle betrachteten Algorithmen so verändert (wenn es Einschränkungen gibt), dass die Mängel beseitigt werden, damit die Algorithmen zumindest rein technisch funktionieren. Mit anderen Worten, alle Algorithmen müssen unabhängig von der Glattheit der Funktionen sein (wie z. B. bei den Problemen der Händler) und dürfen keine Einschränkungen hinsichtlich des Argumentationsschritts haben.
2. Grundsätze des Algorithmus
Während der vorherige Artikel eine Einführung in die Welt der Optimierung war, wurde das Prinzip der Interaktion des Hauptprogramms (EA, Skript, Indikator) mit dem Kern des Optimierungsalgorithmus nicht behandelt. Es ist wichtig, darauf zu achten, denn ein aufmerksamer Leser wird sich in jedem Fall die Frage stellen, warum Algorithmen und Beispielprogramme so geschrieben sind. Die bestehenden Versionen von Optimierungsalgorithmen sind so aufgebaut, dass sich der Algorithmus auf die Fitnessfunktion wie auf ein externes Objekt bezieht, während der Algorithmus das ausführbare Hauptprogramm ist.
Die folgende Abbildung 1 zeigt ein Diagramm, in dem der Algorithmus die optimierten Parameter an die Fitnessfunktion übergibt und den Fitnesswert zurückerhält (Bewertungskriterium). Dieses System ist für die Erstellung eines Programms zur Lösung von Problemen durch die Nutzer, einschließlich der Händler, ungeeignet. Warum ist es unangenehm? Wir können zum Beispiel nicht sagen, dass ein Prüfer im Laufe der Geschichte gelaufen ist.
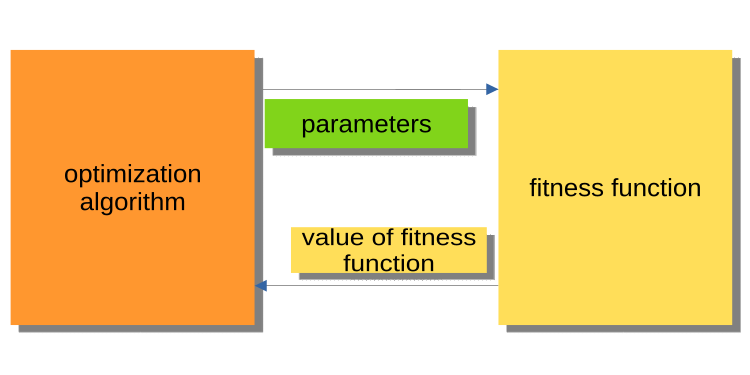
Abb. 1. Interaktion zwischen PSO und Fitnessfunktion
Die in Abb. 2 dargestellte Struktur ist wesentlich praktischer. Der Optimierungsalgorithmus ist hier kein eigenständiges Programm, sondern ein separates Modul oder eine „Black Box“. Dieses Modul hat die Parameter „min“, „max“ und „step“ für jedes optimierte Argument. Das MQL-Programm empfängt auf Anfrage optimierte Argumente und gibt die Fitnesswerte oder, mit anderen Worten, die Werte der Fitnessfunktionen zurück. Diese Struktur ermöglicht den Aufbau einer Reihe sehr flexibler Lösungen, von der Verwendung der automatischen Optimierung in Expert Advisors bis hin zum Schreiben eines eigenen Optimierungsmanagers.
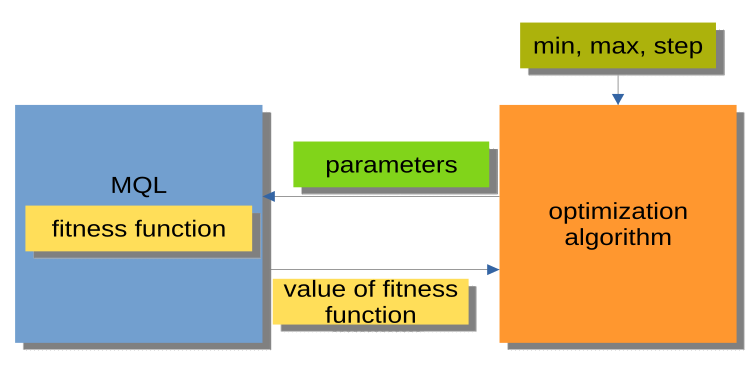
Abb. 2. Interaktion zwischen MQL-Programm und PSO
Es ist auch erwähnenswert, dass die Organisation von Aufrufen zu Methoden von Optimierungsalgorithmen (MQL-Block in Abb. 2) durch ein allgemeines Schema dargestellt werden kann, das für alle Optimierungsalgorithmen (AO) gleich ist:
Initialisierung
Zyklus der Iterationen (Epochen)
{
1) Method_АО_1
2) Ermittlung von Fitnesswerten für jede Variante der optimierten Parameter
3) Method_АО_2
}
Es werden also nur drei öffentliche Methoden verwendet: Initialization_АО_0, Method_АО_1 und Method_АО_2. Dies ist ausreichend, um den Optimierungsprozess in Anwenderprojekten jeder Komplexität zu organisieren.
Der PSO-Arbeitsablauf selbst ist in Abbildung 3 dargestellt und umfasst die folgenden logischen Schritte:
- Zufällige Partikelgenerierung (erste Iteration)
- Ermittlung des Fitnesswerts für jedes Partikel
- Ermittlung des Fitnesswerts für alle Partikel im Allgemeinen
- Einstellung der Partikelgeschwindigkeit
- Haltepunkt oder Übergang zu Schritt 2
- Abschluss des Programms.
Abb. 3. PSO-Arbeitsablauf
Betrachten wir den Partikelschwarm-Algorithmus etwas genauer.
Das Schwarmintelligenzsystem besteht aus vielen Partikeln, die sowohl miteinander als auch mit der Umwelt interagieren. Jedes Teilchen folgt einfachen Regeln, obwohl es kein zentrales Verhaltenskontrollsystem gibt, das jedem Teilchen sagt, was es zu tun hat. Lokale und zufällige Interaktionen zwischen ihnen führen zum Entstehen eines intelligenten Gruppenverhaltens, das nicht von Einzelpersonen gesteuert wird.
Wenn wir eine Analogie zu einer Herde ziehen, dann können wir sagen, dass alle Teilchen einfache Aufgaben erfüllen müssen:
- Überschneidungen mit anderen Partikeln vermeiden;
- Anpassen ihre Geschwindigkeit an die Geschwindigkeit der sie umgebenden Teilchen;
- Versuch einen relativ geringen Abstand zwischen sich und der Umwelt zu halten.
Der PSO-Algorithmus beginnt mit einer Initialisierung der Population. In einem zweiten Schritt werden die Fitnesswerte jedes Partikels berechnet, woraufhin die individuellen und globalen Bestwerte aktualisiert werden und anschließend die Geschwindigkeit und Position der Partikel. Bei der Verwendung von PSO wird eine mögliche Lösung eines numerischen Optimierungsproblems durch die Position der Partikel dargestellt. Darüber hinaus hat jedes Teilchen eine aktuelle Geschwindigkeit, die seine absolute Größe und Richtung zu einer neuen, vermeintlich besseren Lösung/Position widerspiegelt.
Das Partikel speichert auch seinen Fitnesswert, die aktuelle Position, die beste bekannte Position (eine frühere Position mit der besten bekannten Fitness) und die Fitness der besten bekannten Position. Die Schritte zwei bis vier werden wiederholt, bis die Abschlussbedingung erfüllt ist. In der ersten Iteration werden alle Partikel zerstreut, um die beste Lösung zu finden (Exploration). Jedes Teilchen wird bewertet. Die besten Lösungen für die Nachbarschaftstopologie werden gefunden, und die persönlichen und globalen besten Partikel für jedes Mitglied des Schwarms werden aktualisiert. Konvergenz wird erreicht, indem alle Partikel zu dem Partikel mit der besten Lösung hingezogen werden.
Obwohl der PSO-Algorithmus in seinem Kern recht einfach ist, müssen wir ihn verstehen, um den Code in diesem Artikel an unsere Bedürfnisse anpassen zu können. PSO ist ein iterativer Prozess. Bei jeder Iteration in der Hauptverarbeitungsschleife wird zunächst die aktuelle Geschwindigkeit der einzelnen Partikel aktualisiert. Dabei werden die aktuelle Geschwindigkeit des Partikels, seine lokalen Informationen und die globalen Informationen des Schwarms berücksichtigt. Die Position jedes Partikels wird dann mit dem Wert der neuen Geschwindigkeit des Partikels aktualisiert.
Mathematisch sehen diese beiden Gleichungen zur Aktualisierung der Partikelkoordinaten wie folgt aus:
v(t+1) = w * v(t) + c1 * rp * (p(t) – x(t)) + (c2 * rg * (g(t) – x(t))
x(t+1) = x(t) + v(t+1)
Der Prozess der Positionsaktualisierung ist eigentlich viel einfacher als die vorgeschlagenen Gleichungen. Die erste Gleichung dient der Aktualisierung der Geschwindigkeit des Teilchens.
Der Ausdruck v(t+1) bezeichnet die Geschwindigkeit zum Zeitpunkt t+1. Die neue Geschwindigkeit hängt von drei Bedingungen ab.
- Die erste: w * v(t). Der Faktor w wird als Gewichtsanteil der Trägheit bezeichnet und ist einfach eine Konstante; v(t) ist die aktuelle Geschwindigkeit zum Zeitpunkt t.
- Der zweite Term: c1 * rp * (p(t) - x(t)). Der Faktor c1 ist eine Konstante, die als kognitiver (oder persönlicher bzw. lokaler) Gewichtsanteil bezeichnet wird. Der rp-Multiplikator ist eine Zufallsvariable aus dem Bereich [0, 1]. Die Vektorgröße p(t) ist die beste bisher gefundene Position des Teilchens, und die Vektorgröße x(t) ist die aktuelle Position des Teilchens.
- Der dritte Term: Aktualisierung der Geschwindigkeit c2 * rg * (g(t) - x(t). Der Faktor c2 ist eine Konstante, die als sozialer (oder globaler) Gewichtsanteil bezeichnet wird. Der Multiplikator rg ist eine Zufallsvariable im Bereich [0, 1]. Der Wert des g(t)-Vektors ist die beste bekannte Position, die bisher von einem der Teilchen im Schwarm gefunden wurde. Sobald die neue Geschwindigkeit v(t+1) bestimmt ist, wird sie zur Berechnung der neuen Position x(t+1) des Teilchens verwendet.
3. Klassische Umsetzung
Eine logische Einheit, die einen Satz von Koordinaten im Raum (optimierte Parameter) beschreibt, ist ein Partikel, der als Struktur dargestellt werden kann, wobei c[] die Koordinaten des Partikels sind, cB[] die besten Koordinaten des Partikels für alle Iterationen sind, v[] die Geschwindigkeit für jede der Koordinaten des Partikels ist, ff - der aktuelle Fitnesswert des Partikels, ffB - der beste Fitnesswert des Partikels für alle Iterationen. Im Konstruktor der Partikelstruktur initialisieren wir die Werte von ff und ffB mit dem kleinstmöglichen Wert, der durch den Typ „double“ dargestellt werden kann, da der Algorithmus darauf ausgelegt ist, das Maximum der Funktion zu finden (um das Minimum zu finden, genügt es, ein „-“-Zeichen vor den resultierenden Fitnesswert zu setzen).
//—————————————————————————————————————————————————————————————————————————————— struct S_Particles { public: double c []; //coordinates double cB []; //best coordinates double v []; //velocity double ff; //the value of the fitness function double ffB; //best value fitness function S_Particles () { ff = -DBL_MAX; ffB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Implementieren wir den PSO-Algorithmus als eine Klasse mit nur drei öffventlichen Methoden: InitPS(), Preparation () und Dwelling() (Initialization_АО_0, Method_АО_1 und Method_АО_2). Von den privaten Methoden sind GenerateRNDparticles() und ParticleMovement() einzigartig für PSO, während der Rest bereits im vorherigen Artikel besprochen wurde. Das Array der Struktur p[] ist ein Schwarm von Partikeln. Zusätzlich zu der Tatsache, dass jedes Partikel Fitnesswerte, seine eigenen Koordinaten und die besten Koordinaten hat, hat der Schwarm als Ganzes die besten Koordinaten cB und den besten Fitnesswert ffB.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_PSO { public: //---------------------------------------------------------------------------- S_Particles p []; //particles double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double ffB; //FF of the best coordinates void InitPS (const int params, //number of opt. parameters const int size, //swarm size const double inertiaP, //inertia const double selfBoostP, //boost const double groupBoostP); //group boost void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- int swarmSize; //swarm size int parameters;//number of optimized parameters double inertia; double selfBoost; double groupBoost; bool dwelling; void GenerateRNDparticles (); void ParticleMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode InitPS() ist für die Initialisierung des Algorithmus vor Beginn der Optimierung gedacht(Initialization_АО_0). Die Werte der Methodenargumente werden den privaten Mitgliedern der Methode zugewiesen, und die Größe wird dem Schwarm und den internen Parametern der einzelnen Partikel im Schwarm zugewiesen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::InitPS (const int paramsP, const int sizeP, const double inertiaP, const double selfBoostP, const double groupBoostP) { ffB = -DBL_MAX; parameters = paramsP; swarmSize = sizeP; ArrayResize (rangeMax, parameters); ArrayResize (rangeMin, parameters); ArrayResize (rangeStep, parameters); dwelling = false; inertia = inertiaP; selfBoost = selfBoostP; groupBoost = groupBoostP; ArrayResize (p, swarmSize); for (int i = 0; i < swarmSize; i++) { ArrayResize (p [i].c, parameters); ArrayResize (p [i].cB, parameters); ArrayResize (p [i].v, parameters); } ArrayResize (cB, parameters); } //——————————————————————————————————————————————————————————————————————————————
Die Methode Preparation() wird bei jeder Iteration (Epoche) zuerst aufgerufen (Method_АО_1). Die Methode ist einfach, aber sehr wichtig. Je nachdem, ob die Methode bei der ersten Epoche oder bei nachfolgenden Epochen (bestimmt durch das Verweil-Flag ) aufgerufen wird, wird der Schwarm-Fitnesswert zurückgesetzt und eine zufällige Schwarm-Population erzeugt, oder die Partikel bewegen sich zu neuen Koordinaten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::Preparation () { if (!dwelling) { ffB = -DBL_MAX; GenerateRNDparticles (); dwelling = true; } else ParticleMovement (); } //——————————————————————————————————————————————————————————————————————————————
Eine zufällige Schwarm-Population wird mit der Methode GenerateRNDparticles() erzeugt. Die Partikel haben zufällige Koordinaten in dem für sie angegebenen Bereich und eine zufällige Geschwindigkeit für jede der Koordinaten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::GenerateRNDparticles () { for (int s = 0; s < swarmSize; s++) { for (int k = 0; k < parameters; k++) { p [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); p [s].c [k] = SeInDiSp (p [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); p [s].cB [k] = p [s].c [k]; p [s].v [k] = RNDfromCI (0.0, (rangeMax [k] - rangeMin [k]) * 0.5); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode ParticleMovement() löst den Algorithmus zum Verschieben von Partikeln an neue Positionen aus. Um dies zu erreichen, muss die Geschwindigkeit für jede Koordinate nach der oben genannten Gleichung berechnet werden. Ich weiß nicht, warum der Begriff „Geschwindigkeit“ verwendet wird, da es sich im Grunde um einen Verschiebungswert handelt, d. h. um die Differenz zwischen dem Ort, an dem sich das Teilchen gerade befindet, und dem Ort, an dem es sich bewegen sollte. Nachdem wir diese Differenz für jede der Koordinaten berechnet haben, addieren wir sie einfach zu den aktuellen Werten. Anschließend prüfen wir, ob es inakzeptabel ist, die Min/Max-Grenzen der optimierten Parameter (bei einem Partikel sind dies die Koordinaten) mit einem bestimmten Schritt zu überschreiten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::ParticleMovement () { double rp; //random component of particle movement double rg; double velocity; double posit; double positBest; double groupBest; for (int i = 0; i < swarmSize; i++) { for (int k = 0; k < parameters; k++) { rp = RNDfromCI (0.0, 1.0); rg = RNDfromCI (0.0, 1.0); velocity = p [i].v [k]; posit = p [i].c [k]; positBest = p [i].cB [k]; groupBest = cB [k]; p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit); p [i].c [k] = posit + p [i].v [k]; p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Dwelling() ist die dritte öffentliche Methode des für die Optimierung verwendeten Algorithmus(Methode-АО_2). Ziel der Methode ist es, die besten Koordinaten und Fitnesswerte jedes einzelnen Partikels im Vergleich zu seiner vorherigen Leistung zu aktualisieren, sowie die Fitness des Schwarms und die besten Koordinaten des Schwarms zu aktualisieren, falls erforderlich. Die Methode wird nach der Ermittlung der Fitnesswerte in der Iterationsschleife aufgerufen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSO::Dwelling () { for (int i = 0; i < swarmSize; i++) { //remember the best position for the particle if (p [i].ff > p [i].ffB) { p [i].ffB = p [i].ff; for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k]; } if (p [i].ff > ffB) { ffB = p [i].ff; for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Die Funktion zur Diskretisierung der „double“-Zahl mit einem bestimmten Schritt im angegebenen Bereich.
//—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_PSO::SeInDiSp (double in, double inMin, double inMax, double step) { if (in <= inMin) return (inMin); if (in >= inMax) return (inMax); if (step == 0.0) return (in); else return (inMin + step * (double)MathRound ((in - inMin) / step)); } //——————————————————————————————————————————————————————————————————————————————
Die Funktion zur Ermittlung einer zufälligen „double“-Zahl in einem bestimmten Bereich.
//—————————————————————————————————————————————————————————————————————————————— // Random number generator in the custom interval double C_AO_PSO::RNDfromCI (double min, double max) { if (min == max) return (min); double Min, Max; if (min > max) { Min = max; Max = min; } else { Min = min; Max = max; } return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0))); } //——————————————————————————————————————————————————————————————————————————————
Der theoretische Teil ist erledigt. Kommen wir zur Praxis.
Da ich bei der Konstruktion von Algorithmen dieselbe Struktur wie im ersten Artikel der Serie verwende (und dies auch in Zukunft tun werde), die in Abb. 2 beschrieben ist, wird es für uns nicht schwierig sein, den Algorithmus mit dem Prüfstand zu verbinden.
Beim Ausführen des Stands werden ähnliche Animationen wie die unten gezeigten zu sehen sein. In diesem Fall können wir deutlich sehen, wie sich ein Schwarm von Teilchen verhält. Der Schwarm verhält sich wirklich wie ein Schwarm in der Natur. Auf der Wärmekarte der Funktion bewegt sie sich in Form einer dichten Wolke.
Wie Sie sich vielleicht erinnern, bezeichnet der schwarze Kreis das globale Optimum (max) der Funktion, während der schwarze Punkt die besten durchschnittlichen Koordinaten des Suchalgorithmus zum Zeitpunkt der aktuellen Iteration angibt. Lassen Sie mich erklären, woher die Durchschnittswerte kommen. Die Wärmekarte hat zweidimensionale Koordinaten, und die zu optimierende Funktion kann Hunderte von Variablen (Messungen) umfassen. Daher wird das Ergebnis nach Koordinaten gemittelt.
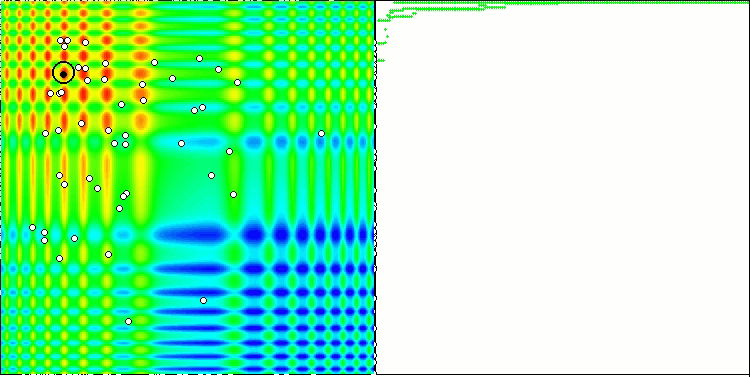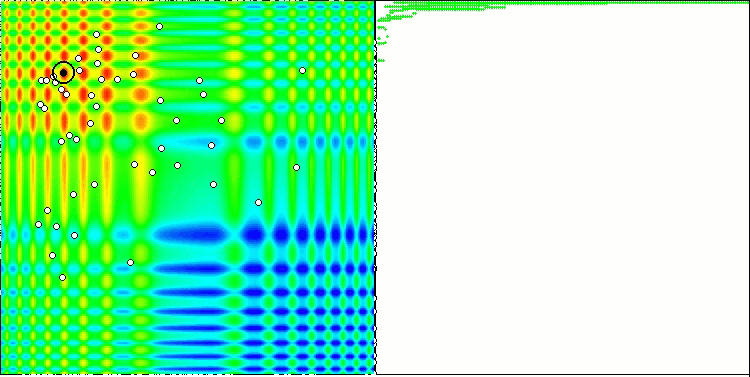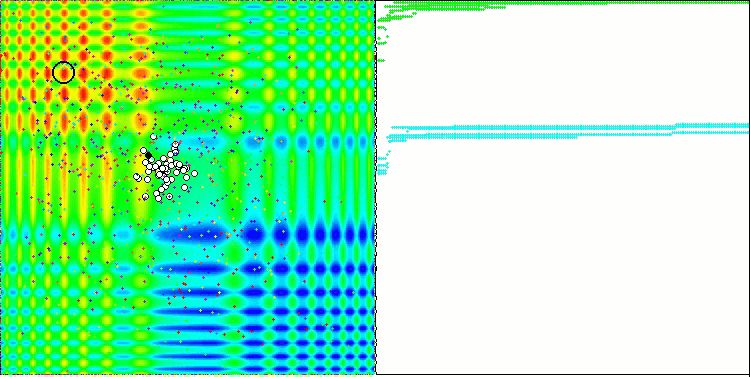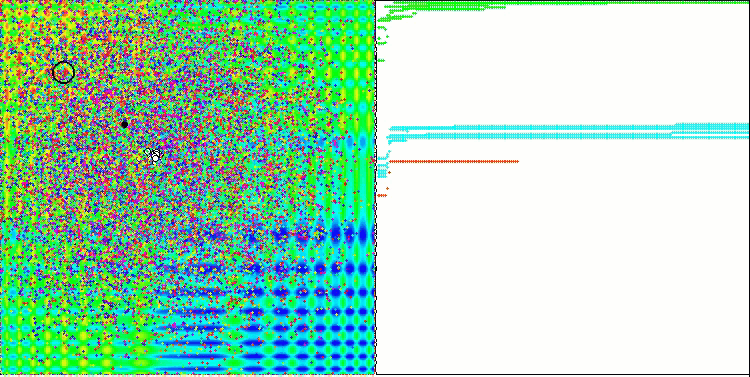
PSO auf die Skin Funktion.
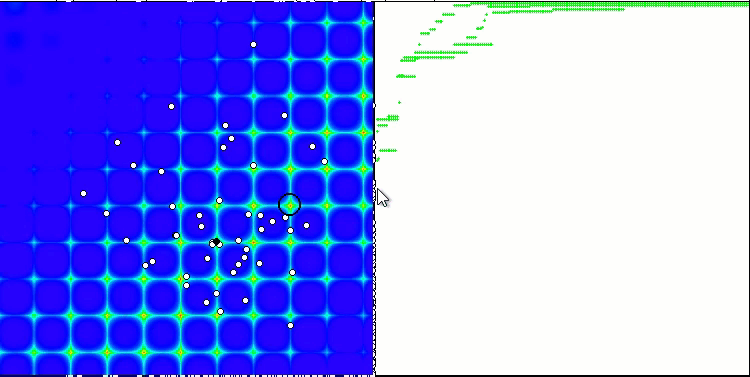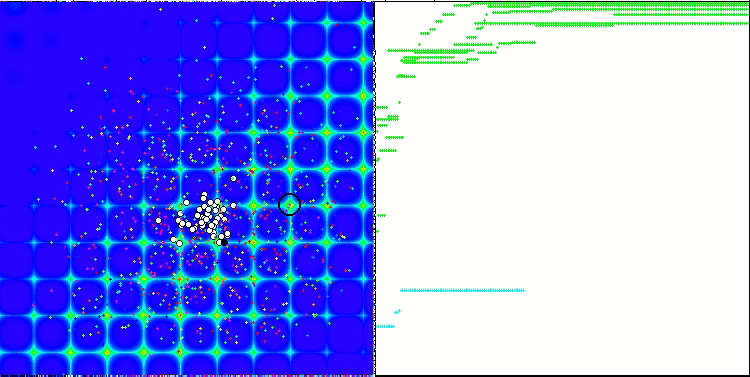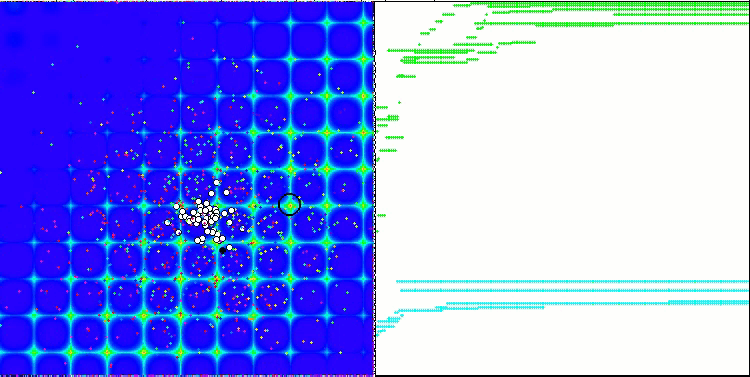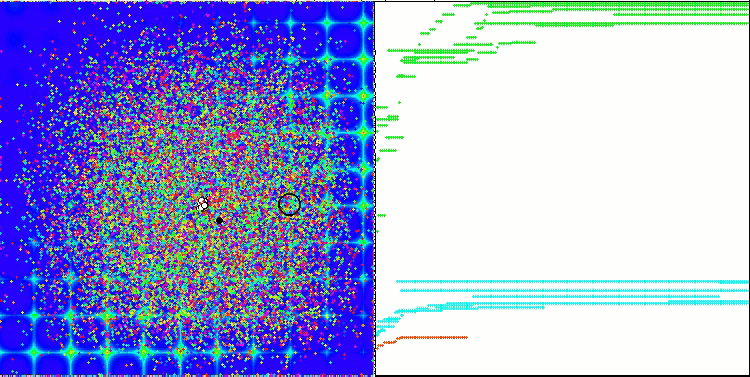
PSO auf dem Forest Testfunktion.
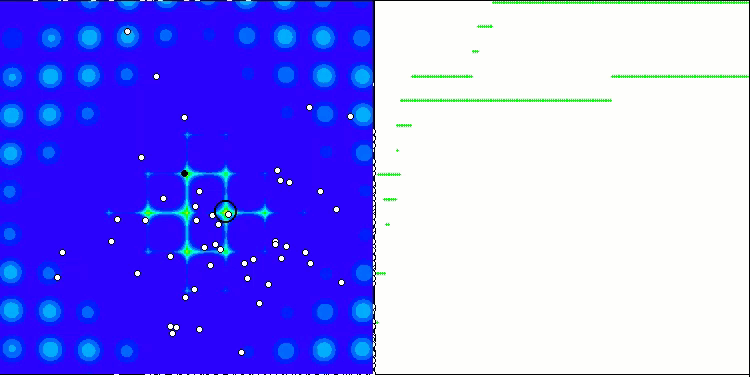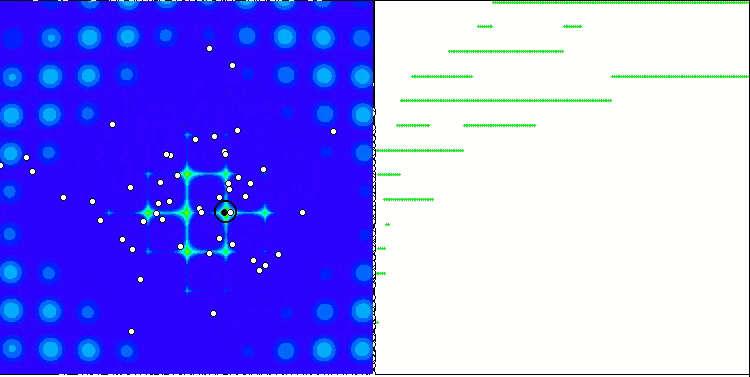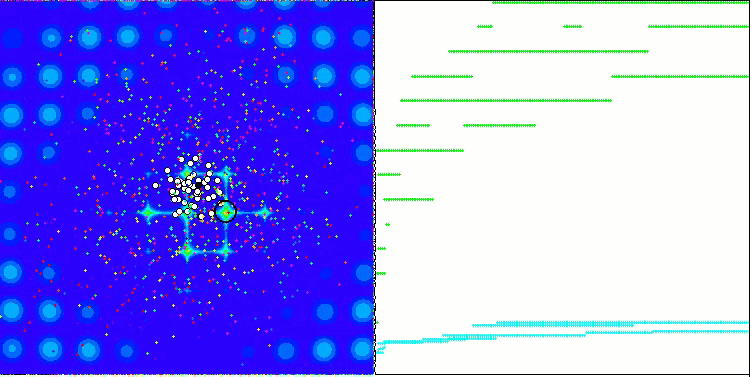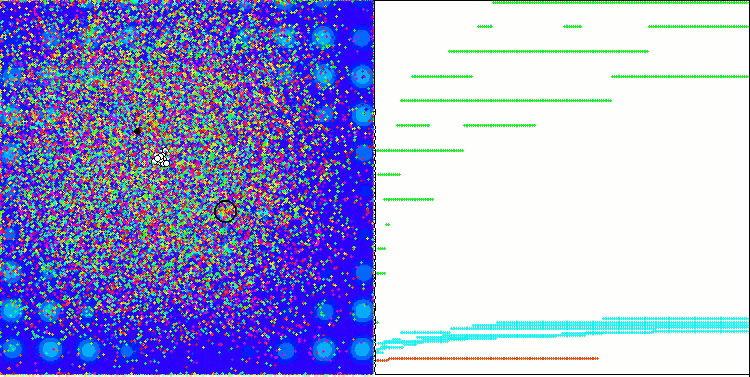
PSO auf der Megacity Testfunktion.
Wie Sie in der Animation sehen können, haben die Tests gezeigt, dass PSO recht gut mit der glatten ersten Funktion zurechtkommt, allerdings nur bei der Optimierung von zwei Variablen. Mit zunehmender Dimension des Suchraums nimmt die Effizienz des Algorithmus stark ab. Dies ist vor allem bei der zweiten und dritten Funktion zu beobachten. Die Ergebnisse sind deutlich schlechter als bei dem im vorigen Artikel beschriebenen Zufallsalgorithmus. Wir werden auf die Ergebnisse zurückkommen und sie bei der Erstellung einer vergleichenden Ergebnistabelle im Detail diskutieren.
Wenn man sieht, wie der berühmte PSO-Algorithmus schmählich gegen den Zufallsalgorithmus verliert, möchte man ihm vielleicht eine zweite Chance geben. Im nächsten Abschnitt werde ich versuchen, den PSO-Algorithmus zu ändern.
4. Geänderte Version
Meiner Meinung nach hat PSO folgende Schwächen:
1) Jede der Koordinaten wird zwangsläufig mit einer Wahrscheinlichkeit von nahezu 1 verändert. Das bedeutet, dass jedes Teilchen des Schwarms bei jeder Iteration im besten Fall irgendwo im lokalen Extrembereich der globalen Region oszilliert, während es im schlimmsten Fall nie genau den Punkt des globalen Extrembereichs trifft. Dies impliziert ein charakteristisches Merkmal des Algorithmus - das Steckenbleiben in lokalen Extrema, d.h. schlechte Konvergenz.
2) Der Algorithmus funktioniert nicht gut mit diskreten Funktionen, teilweise wegen des ersten Fehlers. Die Partikelkoordinaten springen zu den nächstgelegenen „Bereichen“ der Oberfläche der zu optimierenden Funktion, ohne dass die Umgebung eines lokalen Extremums im Detail untersucht werden kann.
3) Schwache Fähigkeit des Algorithmus, neue Bereiche zu erkunden. Der Schwarm konzentriert sich irgendwo an einem Ort, ohne zu versuchen, dem lokalen „Loch“ zu entkommen. Einige Autoren erwähnen Versuche, eine Implementierung einer Multi-Schwarm-Modifikation zu schaffen, aber die Fragen der Optimierung komplexer multivariabler Funktionen bleiben offen, da das Prinzip der gegenseitigen Distanz unklar ist, da nicht nur das Prinzip der gemeinsamen Bewegung erfüllt sein muss, sondern auch die Möglichkeit der gegenseitigen Abstoßung. Andernfalls hat eine solche Implementierung keinen Sinn, da die einzelnen Schwärme einfach in einem Gebiet oder an einem Punkt zusammenlaufen. Gleichzeitig wird die Optimierung einfacher ein- oder zweistufiger Funktionen mit einfachsten Methoden und hervorragender Konvergenz durchgeführt.
Was können wir also tun, um den Algorithmus zu verbessern?
Es ist offensichtlich (wenn auch nicht unbedingt richtig), dass wir die besten individuellen Koordinaten von anderen Partikeln an die Partikel weitergeben müssen. Je besser die Gesamtkoordinaten des „Spender“-Partikels sind, desto größer ist die Wahrscheinlichkeit, die Koordinaten zu passieren. Die Verschiebung der Wahrscheinlichkeit, ein Teilchen zu wählen, ist in Abb. 4 schematisch dargestellt. Wir erzeugen eine Zufallszahl von 0 bis 1, transformieren die resultierende Zahl mit einer Parabelfunktion und skalieren sie dann auf den Bereich der Seriennummern der Partikel im Schwarm von 0 bis SwarmSize-1. Dazu müssen wir einen zusätzlichen Parameter für PSOm (den modifizierten Algorithmus) einführen - die Wahrscheinlichkeit des Kopierens der Koordinate - und wir müssen den Schwarm so sortieren, dass die Partikel umso besser sind, je näher sie sich am Index 0 befinden.
Fig. 4. Verschobene Teilchenauswahlwahrscheinlichkeit
Ändern wir die Methode ParticleMovement() leicht ab. Wir erzeugen eine Zufallszahl [0;1]. Wenn die Zahl größer ist als der Parameter „copy“, dann führen wir die üblichen, oben beschriebenen Operationen mit dem Teilchen durch, andernfalls kopieren wir die Koordinate eines anderen Teilchens mit dem Index, der gemäß der in Abb. 4 grafisch dargestellten Regel gewählt wurde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSOm::ParticleMovement () { double rp; //random component of particle movement double rg; double velocity; double posit; double positBest; double groupBest; for (int i = 0; i < swarmSize; i++) { for (int k = 0; k < parameters; k++) { rp = RNDfromCI (0.0, 1.0); rg = RNDfromCI (0.0, 1.0); double rC = RNDfromCI (0.0, 1.0); if (rC > copy) { velocity = p [i].v [k]; posit = p [i].c [k]; positBest = p [i].cB [k]; groupBest = cB [k]; p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit); p [i].c [k] = posit + p [i].v [k]; p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); } else p [i].c [k] = p [GetPartcileAdress ()].cB [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Dwelling() sollte ebenfalls geändert werden. Hinzufügen des Aufrufs der Sortierfunktion SortParticles().
//—————————————————————————————————————————————————————————————————————————————— void C_AO_PSOm::Dwelling () { for (int i = 0; i < swarmSize; i++) { //remember the best position for the particle if (p [i].ff > p [i].ffB) { p [i].ffB = p [i].ff; for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k]; } if (p [i].ff > ffB) { ffB = p [i].ff; for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k]; } } SortParticles (); } //——————————————————————————————————————————————————————————————————————————————
Die Funktion GetParticleAdress() bietet eine Auswahl der Adresse eines Partikels mit einer zum besten Partikel verschobenen Wahrscheinlichkeit.
//—————————————————————————————————————————————————————————————————————————————— //shift of probability in the smaller party (to an index 0) int C_AO_PSOm::GetParticleAdress () { double x = RNDfromCI (-1.0, 0.0); x = x * x; x = Scale (x, 0.0, 1.0, 0, swarmSize - 1); x = SeInDiSp (x, 0, swarmSize - 1, 1); return ((int)x); } //——————————————————————————————————————————————————————————————————————————————
Die Funktion SortParticles() ist der bekannte Sortieralgorithmus Bubblesort.
//—————————————————————————————————————————————————————————————————————————————— //Sorting of particles void C_AO_PSOm::SortParticles () { //---------------------------------------------------------------------------- int cnt = 1; int t0 = 0; double t1 = 0.0; //---------------------------------------------------------------------------- // We will put indexes in the temporary array for (int i = 0; i < swarmSize; i++) { ind [i] = i; val [i] = p [i].ffB; //ffPop [i]; } while (cnt > 0) { cnt = 0; for (int i = 0; i < swarmSize - 1; i++) { if (val [i] < val [i + 1]) { t0 = ind [i + 1]; t1 = val [i + 1]; ind [i + 1] = ind [i]; val [i + 1] = val [i]; ind [i] = t0; val [i] = t1; cnt++; } } } // On the received indexes create the sorted temporary population for (int u = 0; u < swarmSize; u++) pT [u] = p [ind [u]]; // Copy the sorted array back for (int u = 0; u < swarmSize; u++) p [u] = pT [u]; } //——————————————————————————————————————————————————————————————————————————————
Die Funktion zur Skalierung einer Zahl von einem Zahlenbereich in einen anderen.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_PSOm::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } //——————————————————————————————————————————————————————————————————————————————
5. Testergebnisse
Lassen Sie uns abschließend die Ergebnisse der aktuellen Forschung zusammenfassen. Leider hat sich der PSO-Algorithmus nicht bewährt, so sehr ich auch auf gute Ergebnisse gehofft hatte. Die Studien zeigten die schwache Konvergenz für diskrete Funktionen mit Brüchen und mit einer großen Anzahl von Argumenten. Ein Versuch, den Algorithmus zu modifizieren, war erfolglos, die Ergebnisse waren noch schlechter als die der klassischen Implementierung.
Die Erhöhung des Kopierparameters auf Werte nahe 0,8 führt immer noch zu sofortiger Konvergenz, allerdings nur für die erste glatte Funktion in den Tests und mit nur zwei Argumenten. Bei anderen Tests verschlechtert dieser Parameter die Ergebnisse nur. Die klassische Implementierung von PSO konnte nur bei der Skin-Funktion mit 1000 Argumenten etwas Interessantes zeigen. Andere Tests erwiesen sich als mittelprächtig.
Das endgültige Testergebnis beträgt 0,47695 für den klassischen Algorithmus und 0,45144 für den modifizierten Algorithmus . Die Testergebnisse sind in der Tabelle aufgeführt. Der Prüfstand erlaubt es uns, die Anzahl der Testläufe in den Einstellungen auszuwählen (Standard ist 5), sodass die Leser statistisch genauere Ergebnisse erhalten können, wenn sie diesen Parameter höher einstellen, wenn es die Rechenleistung erlaubt.
| AO | Durchläufe | Skin | Forest | Megacity (diskret) | Endgültiges Ergebnis | ||||||
| 2 Parameter (1 F) | 40 Parameter (20 F) | 1000 Parameter (500 F) | 2 Parameter (1 F) | 40 Parameter (20 F) | 1000 Parameter (500 F) | 2 Parameter (1 F) | 40 Parameter (20 F) | 1000 Parameter (500 F) | |||
| RND | 1000 | 0.98744 | 0.61852 | 0.49408 | 0.89582 | 0.19645 | 0.14042 | 0.77333 | 0.19000 | 0.14283 | 0.51254 |
| 10 000 | 0.99977 | 0.69448 | 0.50188 | 0.98181 | 0.24433 | 0.14042 | 0.88000 | 0.20133 | 0.14283 | ||
| PSO | 1000 | 0.98436 | 0.72243 | 0.65483 | 0.71122 | 0.15603 | 0.08727 | 0.53333 | 0.08000 | 0.04085 | 0.47695 |
| 10 000 | 0.99836 | 0.72329 | 0.65483 | 0.97615 | 0.19640 | 0.09219 | 0.82667 | 0.10600 | 0.04085 | ||
| PSOm | 1000 | 0.96678 | 0.64727 | 0.57654 | 0.80616 | 0.13388 | 0.06800 | 0.53333 | 0.08067 | 0.04211 | 0.45144 |
| 10 000 | 0.99505 | 0.64986 | 0.57654 | 0.90401 | 0.18194 | 0.07104 | 0.74667 | 0.10400 | 0.04211 | ||
Zusammenfassend lässt sich sagen, dass PSO zu einer schnellen und vorzeitigen Konvergenz an den durchschnittlichen optimalen Punkten und zu einer langsamen Konvergenz im Bereich der verfeinerten Suche führt (da die Fähigkeit zur lokalen Suche gering ist). Einfach ausgedrückt: Der Algorithmus ist sehr schwach und eignet sich nicht für die Optimierung komplexer und vor allem diskreter Funktionen, insbesondere von Funktionen mit mehreren Argumenten.
Es gibt mehrere Ansätze, die zur Verbesserung von PSO im Allgemeinen verwendet werden können. Die Schwarmgröße ist einer der wichtigsten Faktoren. Eine höhere Schwarmgröße kann die Wahrscheinlichkeit einer schnelleren und genaueren Konvergenz erhöhen. Bei praktischen Problemen gibt es jedoch oft einen Schwellenwert für die Anzahl der Durchläufe der Fitnessfunktion, und eine Erhöhung der Schwarmgröße verringert nur proportional die Anzahl der Epochen und damit die Möglichkeit der Schwarmentwicklung.
Der zweite Ansatz besteht darin, ein Gleichgewicht zwischen Erkundung und Nutzung herzustellen. Zu Beginn der Iterationen besteht aufgrund des hohen Explorationsgrades eine hohe Chance, eine Lösung nahe dem globalen Optimum zu finden. Am Ende der Iteration würde ein hoher Ausnutzungsgrad dem Partikel die Chance geben, die genaueste Lösung in dem vielversprechenden Gebiet zu finden. Die Voroptimierung vor dem Schwarmstadium durch andere Methoden ist eine weitere Technik, die zur Verbesserung der grundlegenden Leistung von PSO eingesetzt werden kann und die heutzutage recht häufig verwendet wird. Die Zuweisung unterschiedlicher Aufgaben oder Ziele an jede Untergruppe kann die Effektivität des PSO bei Multitasking-Problemen ebenfalls erhöhen.
Ein weiterer Ansatz zur Verbesserung der Leistung des PSO besteht darin, die Komponenten der Geschwindigkeitsgleichung zu bestimmen (dynamische Geschwindigkeitsregelung). Ein solcher Ansatz kann Partikel in verschiedene Richtungen schicken und zu einer schnelleren Konvergenz zum globalen Optimum führen, aber das ist nur eine Annahme.Vorteile:
- Der Algorithmus ist sehr einfach und anspruchslos gegenüber Rechenressourcen, der Code arbeitet sehr schnell, da die klassische Implementierung nicht einmal Arrays sortiert.
- Der Algorithmus leistet gute Arbeit bei glatten Funktionen. Bisher ist PSO der klare Tabellenführer bei der Optimierung von glatten Funktionen mit mehreren Argumenten.
Nachteile
- Die geringe Qualität der Studie zur optimierten Funktion. Der Algorithmus kann nicht zur Lösung von Problemen eingesetzt werden, bei denen eine Reihe von eindeutigen Lösungen erforderlich ist.
- Geringe Geschwindigkeit und Konvergenzgenauigkeit.
- Untauglichkeit für die Optimierung diskreter Funktionen.
- Fast vollständige Nicht-Skalierbarkeit.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11386
Datenwissenschaft und maschinelles Lernen (Teil 09): Der Algorithmus K-Nächste-Nachbarn (K-Nearest Neighbors, KNN)
Lernen Sie, wie man ein Handelssystem mit den Fraktalen entwickelt
Neuronale Netze leicht gemacht (Teil 28): Gradientbasierte Optimierung
DoEasy. Steuerung (Teil 20): Das WinForms-Objekt SplitContainer
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.