雲モデル最適化(ACMO)：理論

内容

1. はじめに
2. アルゴリズムの実装

はじめに

最適化アルゴリズムにおいて最適解を見つけ出すことの重要性は、近年ますます増しています。その中でも特に興味深いアプローチの一つが、メタヒューリスティック手法である雲モデル最適化(ACMO: Atmosphere Clouds Model Optimization)です。この手法は数学的には高度であるものの、自然の現象に基づいており、シンプルかつ明快に説明できます。 

現実の大気と同様に、雲が形成され移動する広大な仮想空間を想像してみてください。そこでは天候が単なる条件の集合ではなく、湿度や気圧といった要素がすべての判断に影響を及ぼす生きたシステムとして機能しています。ACMOはこのような自然の力学に着想を得て、雲の形成と変化の原理を使いながら、空における雲の振る舞いになぞらえて解空間を探索し、最適な経路を模索するのです。このアルゴリズムはYanらによって提案され、2013年に発表されました。

本稿では、潜在的な解となる雲が生成する「空」の準備から始まり、仮想の空間を雲が移動し、気象条件に応じて適応・変化する様子まで、ACMOアルゴリズムの各ステップを順に追っていきます。この魅力的なプロセスを追体験しながら、雲がまるで研究チームのように、無数の可能性の中から最適解を見出そうとする姿を垣間見ることができるでしょう。このアルゴリズムの仕組みを一緒に解き明かしながら、その動作を段階的に理解していきましょう。

ACMOの核心は、自然界における雲の振る舞いをモデル化し、それをもとに最適化問題を解決することにあります。アルゴリズムは、以下の3つの主要な雲の特性を活用します。

• 生成：雲は湿度の高い領域に発生するため、アルゴリズムは既知の最適解の周辺を集中的に探索できます。
• 移動：雲は仮想の解空間内を移動し、解の多様性を保ちながら探索範囲を拡大します。これにより、局所最適に陥るリスクを軽減できます。
• 拡散：雲は検索空間全体に広がり、幅広い候補解をカバーします。これにより、大域最適解に到達する可能性が高まります。

アルゴリズムの実装

ACMOアルゴリズムの概念はかなり複雑なため、簡単なところから徐々に段階を踏んで理解していきましょう。ここでは、アルゴリズムの基本的なアイデアをできる限り平易に説明します。

1. 「空」の準備：まず仮想の空を創り出すことを想像してください。この空は複数の領域に分割されており、それぞれの領域には個別の湿度（＝解の質）と気圧（＝探索の蓄積経験）が設定されています。

2. 雲の生成：雲は最も「湿った」領域にのみ出現します。各雲は多数の水滴で構成されており、それぞれの水滴が問題に対する潜在的な解を表します。

3. 雲の移動：雲はほとんど静止せず、高気圧の領域から低気圧の領域へと移動していきます。これは、現実の大気で風が高気圧から低気圧へ吹く原理と同じです。

4. 雲の形状の変化：雲は移動することで大きくなります。この拡大の程度は、移動先と移動元の気圧差に依存します。

5. 蒸発：各ステップで雲は少しずつ水滴を失い、それによって湿度が低下します。雲が一定以上に「乾燥」してしまうと、完全に消滅します。

6. 「気象」の更新：雲が移動するたびに、各領域の湿度と気圧の値が再計算されます。もし雲が良好な解を見つけた場合、その領域の湿度は増加します。

7. 繰り返し：手順2〜6を繰り返すことで、雲は仮想空間のより広範な領域を探索し、最適な解を求めて進化していきます。

8. 完了：あらかじめ指定された繰り返し回数に到達するか、あるいは十分に良好な解が得られた時点で、アルゴリズムは停止します。

このアルゴリズムは、巨大な迷路（探索空間）の中で宝物（最適解）を探すために、複数の探索チーム（雲）を派遣するようなものです。各チームはそれぞれ独自の方法で探索をおこない、領域ごとに変化する「気象」を通じて互いに情報を共有しながら、やがて最良の経路を協力して見つけ出すのです。

図1：領域ごとに密度、湿度、大きさが異なる雲。雨滴の降水量は正規分布に従う

まず、下の表を使用して、ACMOの外部パラメータとその目的を理解しましょう。

パラメータ	目的
popSize（個体数）	水滴の個体数、固定サイズの個体数、雲全体に分布する水滴
cloudsNumber（雲の量）	雲の数
regionsNumber（領域の数）	最適化される各パラメータは同じ数の領域に分割される
dMin（最小ドロップ数）	雲の中の雨滴の平均数に対する最小雨滴数。雲が乾燥しているとみなされる閾値
λ（閾値係数）	雨（水滴）発生を伴う雲が形成される領域の閾値湿度係数
γ（乾燥率）	各反復で雲の水分量を減らす乾燥率
EnM0（初期エントロピー）	出現時の雲の幅
HeM0（初期ハイパーエントロピー）	ハイパーエントロピー：出現時の雲の密度。このパラメータは正規分布の形状を規定する。

次に、ACMOアルゴリズムの手順を見てみましょう。

1. 初期化

• 検索空間UをMD個の領域Uiに分割する
• 各領域の湿度値HUiと気圧PUiを初期化する
• アルゴリズムパラメータ（閾値係数λ、乾燥率γ、初期エントロピーEnM0、初期ハイパーエントロピーHeM0など）を設定する

2. 雲の生成

• 湿度HUiが動的に計算された閾値Htを超える複数の領域Sを定義する
• Sの各領域Uiについて：
• CenterCk = Center (Ui)という式を使用して雲の中心CenterCkを計算する
• 初期エントロピーEnM0、HeM0およびζ収縮比に基づいて、エントロピーEnCkとハイパーネトロピーHeCkを計算する
• 中心CenterCk、エントロピーEnCk、ハイパーエントロピーHeCkを持つ雲Ckを生成する

3. 湿度と気圧の最新情報

• 各Ui領域の湿度値HUiと気圧PUiを更新する

4. 雲の移動フェーズ

• 各雲Ckについて：
• 現在の領域と選択した隣接領域の間との気圧差に基づいて、移動方向を決定する
• 雲Ckを低気圧の方向に移動させる

5. 雲の拡散フェーズ

• 各雲Ckについて：
• 気圧差に基づき、水滴（解候補）が他の領域へ拡散するかを判断する
• 雲Ckの水滴を、隣接するより低い気圧の領域へ拡散させる

6. 湿度と気圧の最新情報

• 雲の移動と拡散後の各領域Uiの湿度値HUiと気圧PUiを更新する

7. 終了条件の確認

• 反復カウンタtをインクレメントする
• t < tmaxの場合、2（雲の生成）に進む
• t >= tmaxの場合、アルゴリズムは終了する

要点

• Ui個の領域が検索空間を形成し、各領域は湿度HUiと気圧PUiによって特徴付けられる
• 雲Ckは、湿度が十分な領域(HUi > Ht)でのみ生成される
• 雲の移動や拡散は、領域間の気圧差の影響を受けて起こる
• 湿度と気圧の値は、雲の移動と拡散のサイクルごとに更新される

それでは、主な雲の操作について詳しく見ていきましょう。

1. Cloudmove (C)操作は、雲の移動を担当します。

1.1 各雲Ckについて

• 検索空間Uからランダムなターゲット領域Fを選択する
• 雲が現在位置する領域Eとターゲット領域Fの間の気圧差ΔPを計算する
• F領域の気圧がE領域よりも低い場合(ΔP > 0)、雲Ckはより低気圧の領域に向かって移動する
• 気圧差と雲のエントロピーに基づいて、雲の移動速度Vkを計算する
• 雲Ckの中心はVkだけ移動する
• 雲Ck内の水分量は蒸発によりγ * 100%減少する
• 水滴の数nkがdN閾値未満になった場合、雲Ckを雲集合Cから削除する（雲は実際には削除されず、エントロピーとハイパーエントロピーの初期値が設定され、現在の反復に合わせて調整された状態で、湿度が閾値を超える領域に移動される）

このように、雲は低気圧の領域へと移動しながら、そのエネルギー（＝水分量）を徐々に失っていきます。この移動メカニズムは、自然界の雲の物理的挙動を反映しています。

2. Cloudspread (C)操作は、雲の拡散を司ります。

2.1 各雲Ckについて：

• 雲の中心が位置する現在の領域Eを取得する
• 移動フェーズ後に雲の中心が移動する領域Gを取得する
• 現在の領域と新しい領域間の気圧差ΔP = PE - PGを計算する
• 領域EとGが異なる場合は、拡散係数α = ΔP / ΔPmaxを計算する
• 領域EとGが同じ場合は、α = 0.3（基本伝播速度）を設定する
• 新しい雲エントロピーEnCk = EnCk × (1 + α)を計算する（ここでαは分布係数）
• 雲の新しいハイパーエントロピーHeCk = HeCk × (1 + α)を計算する（つまり、伝播係数に比例して増加する）
• 雲Ckのエントロピーが5 × EnM0を超えるか、その中の水分量がdNの閾値未満の場合、雲Ckを雲集合Cから「削除」する

操作1と2の主な考え方

• 領域間の気圧差が大きいほど、雲の移動速度は速くなる
• エントロピーの増加により探索空間の拡張が可能になる
  
• ハイパーエントロピーの増加により、空間の詳細な探索が促進される
• 雲の消滅条件：エントロピーが5 × EnM0を超える、または水分量がdN未満になる

アルゴリズムの記述において、1つの雲がカバーできる領域数に制限は明示されていません。アルゴリズムでは、雲Ckの中心が位置する現在の領域Eと、移動後の中心が位置する新しい領域Gの2 つの領域のみが考慮されます。しかし、各反復で雲はサイズを増して隣接領域へと拡大し、水滴が落ちる領域の湿度と気圧は上昇します。このように、1つの雲は順次複数の領域を移動することができますが、任意の時点でアルゴリズムが扱うのは常に「現在の領域」と「新しい領域」の2つだけです。つまり、雲の移動と水滴の降下（＝解の適用）は別々に扱われます。雲と水滴は同一の存在ではなく、アルゴリズム内では異なる概念として扱われています。

アルゴリズムは、雲の位置を更新し、新しいエントロピーとハイパーエントロピーを計算し、消滅条件を満たしているかをチェックしますが、雲がカバーできる領域数に明示的な制限は設けていません。

図2：低気圧に向かう領域を横切る雲の移動

アルゴリズムの説明から明らかなように、この手法において「適合度関数」を持つのは雲ではなく領域であり、その適合度関数とは、領域における湿度を指します。このアルゴリズムにおける雲の役割は、ある領域に何滴の雨が降るかを示す指標として機能する点にあります。以下に要点を示します。

1. 各領域は独自の気圧Pを持ち、この気圧が雲の伝播速度を決定します。
2. 雲Ck水滴を「所有」しているわけではなく、現在の領域E および新たに移動する領域Gにどれだけの水滴が落ちるかを示す指標として機能します。
3. 雲が領域Eから領域Gへ移動するかどうかは、気圧勾配ΔP = PE - PGによって決定されます。
4. 水滴は特定の雲に属しているわけではなく、雲が存在する領域に降ります。

したがって、このシステムにおける「気象」の動態を決定づける主要な主体は雲ではなく領域であることが分かります。この点こそが、本アルゴリズムと従来のマルチポピュレーション型アルゴリズムとの本質的な違いであると強調できます。

気圧は探索空間内の各領域にとって重要な特徴であり、雲の移動方向（高気圧領域から低気圧領域へ）を決定する要因となります。概念的には、ある領域が評価されるたび（その領域にある点の目的関数が計算されるたび）に、その領域の気圧が増加します。これは、ある領域を探索すればするほど、その領域の「気圧」が高まり、アルゴリズムが他の未探索領域への探索を促されるという考え方を反映しています。

著者のアルゴリズムによれば、雲の形状の変化は、雲が現在存在している領域と、これから移動する新しい領域との間に生じる気圧差に応じて発生します。具体的には、以下のようにして変化が生じます。

• 気圧差ΔP = PE - PGが大きい場合、それは雲が大きく異なる気圧の領域へ移動していることを意味し、その移動速度は速くなる
• 気圧差ΔPが小さい場合は、雲が似た気圧値の領域に移動していることを意味し、その移動速度は遅くなる

さらに、アルゴリズムの説明によれば、最初の反復におけるエントロピーとハイパーエントロピーの値は次のように決定されます。

1. 初期エントロピーEnM0 = Ij / A、ここで

• Aはレベル6に設定されている
• Ijはj次元の領域の長さ

2. 初期エントロピーHeM0はレベル0.5に設定されます。

アルゴリズムのエントロピーによって、雲が広がる範囲（サイズ）が決まります。最初の反復では、雲は少なくとも1つの検索領域全体をカバーする必要があります。

ハイパーエントロピーは雲の「厚さ」に影響し、正規分布の形状、言い換えれば雲内の水滴の密度を制御します。初期値0.5は、薄すぎる雲と濃すぎる雲の間のバランスをとるために実験的に選択されます。

1. エントロピーは反復ごとに増加します。これは、雲が徐々に「伸びて」、より広い探索領域をカバーし、局所最適解に陥るのを避けるのに役立つことを意味します。
2. ハイパーエントロピーは逆に、雲の中心部における密度を高めます。その結果、雲は有望な領域に対する解の精緻化をおこないます。

このアプローチにより、アルゴリズムは探索範囲の拡大と解の洗練化の両立を可能にし、同時に局所最適からの脱出能力も維持することができます。

多次元空間では、雲の領域インデックスの定義は少し複雑になりますが、原則は同じです。以下がその仕組みです。

• 検索空間はすべての次元にわたって領域に分割される。次元数をD、各次元をM区間に分割すると、領域の総数はM × Dになる。
• この場合の領域インデックスは単なる番号ではなく、各次元における位置を示す座標の集合である。アルゴリズムは、雲の中心が各次元でどの区間に属しているかを調べることで、その雲が属する領域インデックスを決定する。

たとえば、3次元(D = 3(の空間があり、各次元が10(M = 10)区間に分割されているとします。このとき、領域インデックスが(3, 7, 2)の場合、それは「第1次元で3番目の区間、第2次元で7番目、第3次元で2番目の区間」を表しています。

ここで注意すべきなのは、雲の中心は、必ずしもその雲の中で最良の水滴（解）を示すものではないという点です。以下のような重要なポイントがあります。

• 雲の中心は、雲が生成された領域内における「ある種の中間点（代表点）」として定義される
• 雲内の最良の水滴ドとは、目的関数の評価（＝適合度）が最も高かったものを指す
• アルゴリズムには、各領域における「領域湿度値(UiH: region humidity value）」という概念があり、これはその領域で得られた最良の適合度値を表す。これは雲の中心ではなく、最良のドロップに対応している
• 雲の中心は、探索空間における雲の位置決定や雲の移動計算に用いられるが、それが最良解であるとは限らない

したがって、このアルゴリズムにおいて、雲の中心と最良の水滴は異なる概念です。雲の中心は検索空間における雲の移動と配置の基準として使用され、一方で最良の水滴は、その領域において現時点で見つかった最良解（最適値）を表します。

このアプローチにより、アルゴリズムは、雲の中心を用いて検索空間全体を効率的に探索しつつ、領域ごとに落下した最良の水滴（解）を追跡・保存することで、解の質を高める戦略的な探索が可能になります。

ACMO アルゴリズムには、特定の条件下で雲が破壊または消滅するメカニズムが組み込まれています。主なケースは以下の通りです。

1. 水分不足

• 各雲には一定量の水分が割り当てられている
• 水分量が閾値dNを下回った場合、乾燥しすぎているとみなされ、雲は消滅する
• これは、自然界で小さな雲が消えていく現象に類似している

2. エントロピー過多

• 雲のエントロピーは、雲がどれだけ広がっているかを示す
• エントロピーが初期エントロピーの5倍(5 × EnM0)を超えると、雲は拡散しすぎと判断され、消滅する

これは、拡がりすぎて薄まり、空気中に消えてしまう雲のイメージです。

3. 自然蒸発

• 雲が移動するたびに、その水分量は一定の割合(γ * 100%)で減少する
• この減少の後に水分量がdN未満になると、雲は自然に蒸発するように消える

これは実世界での雲の蒸発現象に相当します。

4. 雲の合体

• アルゴリズムの標準仕様としては明示されていないが、一部の ACMO バリアントでは雲が合体することがある
• 合体が起こると、一方の雲（通常は小さい方）が消滅し、他方に吸収されるように見える

これらの雲破壊メカニズムは、探索空間内の非有望な解を排除し、リソースを有望な領域に集中させるための重要な戦略です。 

雲がすべて低気圧領域に集まったらどうなるのだろうかと疑問に思うかもしれません。しかしながら、低気圧領域とは「探索されていない領域」であり、「質の悪い解」ではないことに注意が必要です。仮にすべての雲が最低圧領域に集まったとしても、それらの領域は雲の活動によって次第に気圧が上昇します。そして、ある時点で新たに低圧となる領域が出現し、雲はそちらへと自然に移動するようになります。

つまり、雲は常に動き続けており、高品質な解の領域にも、あまり探索されていない領域にも適応的に移動します。さらに、雲の蒸発・拡散・破壊のメカニズムにより、破壊された雲の代わりに新しい雲が生成され、探索が継続されます。これにより、探索空間における有望な領域の改良サイクルが再び開始されるのです。

新しい雲Ckの中心を決定します。ある領域において湿度値が一定の閾値Hₜを超えた場合、その領域から新しい雲が生成される可能性があります。湿度閾値Ht は次の式を使用して動的に計算されます。

Ht = Hmin + λ * (Hmax - Hmin)、ここで

• HminとHmax：検索エリア全体の最小湿度と最大湿度
• λ：実験的テストに基づく閾値係数は0.7

エントロピーとハイパーエントロピーの計算。新しい雲のエントロピーの重要度EnMは検索中に減少し、次の式で設定されます。

EnMt = ζ * EnM0、ここでζは次の式で計算される圧縮比です。

ζ = 1 / (1 + e^(- (8 - 16 * (t / tmax))))

新しく生成される雲のハイパーエントロピーは、反復ごとに増加します。

HeMt = ζ * HeM0、ここでζは次の式を使用して計算される膨張率として機能します。

ζ = 1 / (1 + e^(8 - 16 * (t / tmax)))、ここで

• EnM0j：初期エントロピーは0.2
  
• HeM0：初期ハイパーエントロピーは0.5
• t：現在の反復
• tmax：最大反復回数

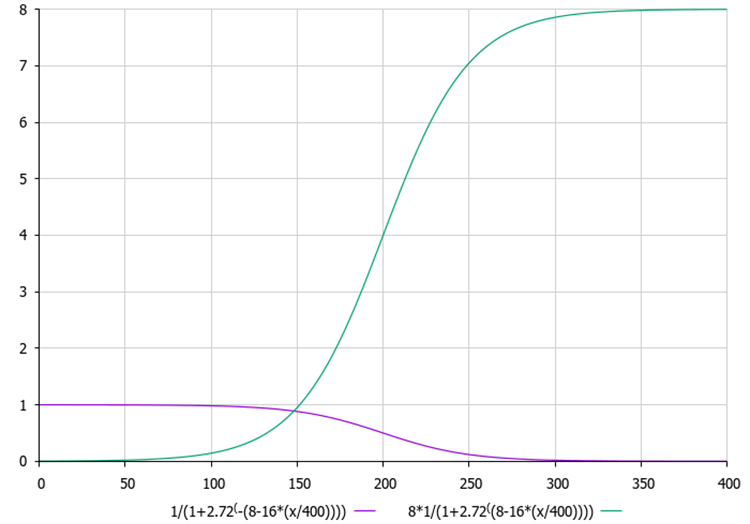
図3：現在のエポックに応じた新しい雲のエントロピーとハイパーエントロピーのグラフ

雲の移動速度は次の法則に従います。

Vk = β * EnCk、ここでβは次の式で表されます。

β = (PCk - PF) / (PMax - PMin)、ここで

• βは大気圧係数
• PMaxおよびPMin：検索空間内の最大および最小大気圧
  
• PCkおよびPF：現在の領域と目標領域の気圧
• EnCk：現在の雲エントロピー
  

ACMO雲運動モデルの理論全体がわかったので、アルゴリズムコードの実装を始めましょう。

気象特性を持つ領域を表すために使用されるS_ACMO_Region構造体について説明します。S_ACMO_Region構造体には複数のフィールドが含まれており、各フィールドは領域に関する情報を格納します。

構造体フィールド

• humidity：領域の湿度レベル
• pressure：領域の大気圧
• centre：中心点を示す座標のベクトルの形式での領域の中心
• x：領域内で気圧が最も高い点

Init()：構造体フィールドの初期値を設定する初期化メソッド

• humidity「-DBL_MAX 」という値で初期化され、非常に低い湿度レベルを示す
• pressure：気圧はまだ測定されていないため、ゼロに初期化される

S_ACMO_Region構造体は、さまざまな領域の気候条件に関する情報を保存および処理する必要がある気象モデルで使用されます。Init ()メソッドは、構造体が使用前に適切に初期化されることを保証します。 

//——————————————————————————————————————————————————————————————————————————————
// Region structure
struct S_ACMO_Region
{
    double humidity; //humidity in the region
    double pressure; //pressure in the region
    double centre;   //the center of the region
    double x;        //point of highest pressure in the region

    void Init ()
    {
      humidity = -DBL_MAX;
      pressure = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

次に、S_ACMO_AreaとS_ACMO_Cloudの2つの構造体について詳しく検討します。

 1. S_ACMO_Area構造体は、構造S_ACMO_Regionによって記述された領域の配列で構成される領域を表し、特定のエリア内の複数の領域に関する情報を含みます。

 2. S_ACMO_Cloud構造体は、雲とその特性を表します。以下は構造体フィールドです。

• center []：雲の中心の座標を格納する配列
• entropy []：各座標の雲エントロピー値の配列
  
• entropyStart []：初期エントロピー値の配列
• hyperEntropy：ハイパーエントロピー値
  
• regionIndex []：雲が属する領域のインデックスの配列
• droplets：雲の中の水滴の数（雲の湿度を表す従来の概念）

Init (int coords)メソッドは、構造体内の配列を初期化し、渡されたcoordsパラメータに応じて配列のサイズを変更します。

両方の構造は気象モデルで領域や雲を表現し、分析するために使用されます。S_ACMO_Areaは領域をグループ化するために使用され、 S_ACMO_Cloudは雲の特性を記述するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
struct S_ACMO_Area
{
    S_ACMO_Region regions [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Cloud structure
struct S_ACMO_Cloud
{
    double center       [];    // cloud center
    double entropy      [];    // entropy
    double entropyStart [];    // initial entropy
    double hyperEntropy;       // hyperEntropy
    int    regionIndex  [];    // index of regions
    double droplets;           // droplets

    void Init (int coords)
    {
      ArrayResize (center,       coords);
      ArrayResize (entropy,      coords);
      ArrayResize (entropyStart, coords);
      ArrayResize (regionIndex,  coords);
      droplets = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

別のC_AOクラスから継承されたC_AO_ACMOクラスを見てみましょう。以下は、クラスの一般的な構造体です。

1. アルゴリズムの外部パラメータの役割を果たすクラスパラメータ

• popSize：集団のサイズ
• cloudsNumber：雲の数
• regionsNumber：次元あたりの領域の数
• dMin：雲の中の平均滴数に対する最小滴数
• EnM0およびHeM0：エントロピーとハイパーエントロピーの初期値
• λ：雨量領域を決定するための閾値係数
• γ：弱化の速度

2. パラメータ配列

• params：各要素にパラメータの名前と値が含まれる構造体の配列

3.   メソッド

• SetParams ()：「params」配列からのモデルパラメータ
• Init ()：指定された検索境界、ステップ、エポック数でモデルを初期化する
• Moving ()：雲の移動を担当する
• Revision ()：モデルの状態のリビジョンを実行する
• MoveClouds ()：雲の移動を担当する
• GetRegionIndex ()：指定されたポイントの領域インデックスを取得する
• RainProcess()：雨を処理する
• DropletsDistribution ()：雲の上に水滴を分散させる
• UpdateRegionProperties ()：領域のプロパティを更新する
• GenerateClouds ()：雲を生成する
• CalculateHumidityThreshold ()：湿度閾値を計算する
• CalculateNewEntropy ()：雲の新しいエントロピーを計算する

4. クラスメンバー

   S_ACMO_Area areas []：さまざまな領域に関する情報を含む

   S_ACMO_Cloud clouds []：雲の特性に関する情報を含む

   epochs、epochNow、dTotal、entropy []、minGpなどのprivate変数は、モデルと計算の状態を追跡するために使用されます。

C_AO_ACMOクラスは、大気中の雲をシミュレートして移動することを目的としています。雲の状態、雲の動き、領域との相互作用を管理できるさまざまなパラメータとメソッドが含まれています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACMO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACMO () { }
  C_AO_ACMO ()
  {
    ao_name = "ACMO";
    ao_desc = "Atmospheric Cloud Model Optimization";
    ao_link = "https://www.mql5.com/ja/articles/15849";

    popSize       = 50;    //population size

    cloudsNumber  = 5;     // Number of clouds
    regionsNumber = 10;    // Number of regions per dimension  (M)
    dMin          = 0.2;   // Minimum number of drops relative to the average number of drops in the clouds (dN)
    EnM0          = 1.0;   // Initial value of entropy
    HeM0          = 0.5;   // Initial value of hyperentropy
    λ             = 0.7;   // Threshold factor (threshold of the rainiest regions)
    γ             = 0.2;   // Weaken rate

    ArrayResize (params, 8);

    params [0].name = "popSize";       params [0].val = popSize;

    params [1].name = "cloudsNumber";  params [1].val = cloudsNumber;
    params [2].name = "regionsNumber"; params [2].val = regionsNumber;
    params [3].name = "dMin";          params [3].val = dMin;
    params [4].name = "EnM0";          params [4].val = EnM0;
    params [5].name = "HeM0";          params [5].val = HeM0;
    params [6].name = "λ";             params [6].val = λ;
    params [7].name = "γ";             params [7].val = γ;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    cloudsNumber  = (int)params [1].val;
    regionsNumber = (int)params [2].val;
    dMin          = params      [3].val;
    EnM0          = params      [4].val;
    HeM0          = params      [5].val;
    λ             = params      [6].val;
    γ             = params      [7].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    cloudsNumber;  // Number of clouds
  int    regionsNumber; // Number of regions per dimension (M)
  double dMin;          // Minimum number of drops relative to the average number of drops in the clouds (dN)
  double EnM0;          // Initial value of entropy
  double HeM0;          // Initial value of hyperentropy
  double λ;             // Threshold factor
  double γ;             // Weaken rate


  S_ACMO_Area   areas  [];
  S_ACMO_Cloud  clouds [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  int    dTotal;         // Maximum total number of droplets (N)
  double entropy [];     // Entropy
  double minGp;          // Minimum global pressure


  void   MoveClouds                 (bool &rev);
  int    GetRegionIndex             (double point, int ind);
  void   RainProcess                (bool &rev);
  void   DropletsDistribution       (double &clouds [], int &droplets []);

  void   UpdateRegionProperties     ();

  void   GenerateClouds             ();
  double CalculateHumidityThreshold ();
  void   CalculateNewEntropy        (S_ACMO_Cloud &cl, int t);
};
//——————————————————————————————————————————————————————————————————————————————

次に、雲モデルのパラメータを初期化するC_AO_ACMOクラスのInitメソッドを見てみましょう。

1. このメソッドは、モデルパラメータの境界とステップを記述する 3 つの配列（rangeMinP、rangeMaxP、rangeStepP）を受け入れます。4番目のパラメータはepochsPです。デフォルトでは0に設定されており、エポックの数を指定します。

2. StandardInitメソッドを呼び出して基本的な初期化を実行します。成功しなかった場合、メソッドはfalseを返します。

3. 変数の初期化：このメソッドは、エポックの合計数を設定し、現在のエポックを0にリセットします。

4. パラメータの初期化

• dTotal：集団サイズと同じに設定される
• dMin：集団と雲の数の関係を考慮して再計算される

5. 配列メモリの割り当て：このメソッドは、座標の数に応じてentropy配列とareas配列のサイズを変更します。

6. エントロピーと領域の初期化

• エントロピー値は各c座標ごとに計算される
• 各r領域に対して、Init ()メソッドが呼び出され、領域が初期化される
• 領域の中心は、最小値と最大値の平均値に領域数を掛けて計算される
• 次に、中心はSeInDiSpメソッドを実行し、値を特定の範囲に正規化する
• x座標は領域に対して設定される（最高湿度値は、デフォルトでは領域の中央に配置される）
  

7. 雲の初期化

• 雲の量に応じてclouds配列のサイズを変更する
• 各雲に対してInitメソッドが呼び出され、パラメータが初期化される

Initメソッドは、雲モデルの基本的なセットアップと初期化を実行し、さらなるシミュレーションに必要なパラメータ、配列サイズ、および値を設定します。最初に親クラスの標準的な初期化を実行し、次に座標、領域、雲に関連する特定のパラメータを構成するように構成されています。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACMO::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  //----------------------------------------------------------------------------
  dTotal       = popSize;
  dMin         = dMin * (popSize / (double)cloudsNumber);

  ArrayResize (entropy, coords);
  ArrayResize (areas,   coords);

  for (int c = 0; c < coords; c++)
  {
    entropy [c] = (rangeMax [c] - rangeMin [c]) / regionsNumber;

    ArrayResize (areas [c].regions, regionsNumber);

    for (int r = 0; r < regionsNumber; r++)
    {
      areas [c].regions [r].Init ();
      areas [c].regions [r].centre = rangeMin [c] + entropy [c] * (r + 0.5);
      areas [c].regions [r].centre = u.SeInDiSp (areas [c].regions [r].centre, rangeMin [c], rangeMax [c], rangeStep [c]);
      areas [c].regions [r].x      = areas [c].regions [r].centre;
    }
  }

  ArrayResize (clouds, cloudsNumber);
  for (int i = 0; i < cloudsNumber; i++) clouds [i].Init (coords);

  minGp = DBL_MAX;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

まとめ

本記事では、多次元最適化問題の解決を目的として設計された、気象現象を模倣したユニークかつ魅力的なアルゴリズム「ACMO」の世界を探りました。一見すると複数の集団を扱うアルゴリズムのように見えるACMOですが、詳しく分析することでその独自性と革新性が明らかになります。

このモデルは、「雲」「領域」「水滴」という3つの主要構成要素に基づいています。これらはそれぞれ独立して機能しますが、相互に連携することで、各要素が重要な役割を果たす調和のとれた効率的な最適化システムを形成しています。雲は解の多様性を担い、領域は探索空間を分割し、水滴は異なる解の間を移動・評価する役割を持ちます。この絶妙な連携により、ACMOアルゴリズムは独創性に富みつつ、実用的な最適化ツールとしての可能性を秘めています。

記事の後半では、理論的な枠組みから一歩進んで、ACMOアルゴリズムをさまざまなテスト関数上で実験的に評価し、その性能や強みを明らかにしていきます。さらに、得られた結果を通じて、この革新的なモデルを実社会の複雑な課題へ応用する新たな可能性を探っていく予定です。