MetaTrader 5 / Testador
English Русский 中文 Español Deutsch 日本語
preview
Optimização por nuvens atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Prática

Optimização por nuvens atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Prática

MetaTrader 5 — Testador | 26 fevereiro 2025, 08:40
67 0
Andrey Dik
Andrey Dik

Conteúdo

  1. Introdução
  2. Implementação do algoritmo
  3. Resultados dos testes


Introdução

No mundo da ciência, onde tecnologia e natureza se cruzam, surgiu a ideia única do algoritmo metaheurístico ACMO (Atmospheric Cloud Model Optimization), que otimiza problemas complexos. No artigo anterior, analisamos tecnicamente sua implementação, que modela o processo de formação e movimento das nuvens na atmosfera com base em vários parâmetros meteorológicos. Na primeira parte, criamos uma classe para gerenciar a modelagem das nuvens, contendo métodos para inicialização, movimento, atualização das propriedades das regiões e outros processos.

Dividimos o espaço de busca em regiões. Definimos os valores iniciais de umidade e pressão em cada uma. Estabelecemos os parâmetros do modelo, como entropia inicial, hiperentropia, valor limite de umidade para a formação de nuvens, entre outros. A próxima etapa foi a geração de nuvens ao selecionar uma área com alta umidade. Calculamos o centro da nuvem, sua entropia e hiperentropia. Atualizamos os parâmetros meteorológicos de umidade e pressão nas regiões após a geração das nuvens. Implementamos o movimento das nuvens para áreas de baixa pressão e a subsequente atualização de suas características, dependendo de seu deslocamento entre regiões, bem como sua dissipação. 

O que ainda precisa ser feito? É preciso implementar funções para a distribuição e a redistribuição aleatórias de gotas entre as nuvens. Também é necessário concluir o processo de chuva e atualizar a solução global. Testar o modelo em nossas funções de teste com diferentes parâmetros para avaliar seu desempenho e precisão. Faremos alterações no processo de chuva e na formação de gotas para implementar um intercâmbio mais completo de informações sobre regiões promissoras na população.


Implementação do algoritmo

Descreveremos todo o processo meteorológico na forma de pseudocódigo, o que nos permitirá, com base nele, compilar a versão final do algoritmo:

1. Na primeira época, distribuição aleatória das nuvens:
   EnCk = EnM0;
   HeCk = HeM0;
//------------------------------------------------------------------------------
1.1 Movimento das nuvens em direção às regiões de menor pressão:
   β = deltaP / normP
   d = Tck.x - Cck.c
   VC = β * d;
   Ck = Ck + VC

   alteração da quantidade de gotas após o movimento:
   nk = nk × (1 - γ)

   alteração da entropia e hiperentropia:
   α = ΔP / ΔPmax;
   EnCk = EnCk * (1 + α)
   HeCk = HeCk * (1 - α)
//------------------------------------------------------------------------------
2. Processo de chuva, precipitação de gotas:
   distribuição das gotas entre as nuvens proporcionalmente à umidade da região
   aumento do número de gotas existentes nas nuvens
//------------------------------------------------------------------------------
3. Cálculo da função de aptidão para as gotas
//------------------------------------------------------------------------------
4. Atualização da solução global e da pressão mínima nas regiões onde as gotas precipitaram
//------------------------------------------------------------------------------
5. Verificação da dissipação das nuvens e criação de novas em regiões para substituir as dissipadas acima do limite:
   regra de dissipação devido à expansão além do valor permitido (ruptura da nuvem):
   En > 5 * EnM0_t
   regra de dissipação quando o teor de umidade está abaixo do valor crítico (secagem da nuvem):
   dCk < dMin

   valor limite acima do qual as regiões podem formar nuvens:
   HT = H_min + λ * (H_max - H_min);
//------------------------------------------------------------------------------
6. Calcular a entropia e a hiperentropia para novas nuvens:
   En = EnM0 / (1 + 2.72 ^ (-(8 - 16 * (t / maxT))))
   He = HeM0 / (1 + 2.72 ^ ((8 - 16 * (t / maxT))))

Então, vamos continuar. Analisaremos o método "Moving" da classe "C_AO_ACMO". O método executa duas operações: "MoveClouds (revision)" — responsável pelo movimento das nuvens — e "RainProcess (revision)" — que processa o processo de chuva, dependendo do estado das nuvens, bem como do parâmetro "revision". O método "Moving" executa duas ações principais relacionadas à dinâmica das nuvens e ao processo de chuva. Ele encapsula a lógica de movimento das nuvens e sua interação com a precipitação. Assim, o método "Moving" é responsável por atualizar o estado das nuvens e da chuva no contexto da simulação do clima.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Moving ()
{
  MoveClouds       (revision);
  RainProcess      (revision);
}
//——————————————————————————————————————————————————————————————————————————————

Vamos analisar detalhadamente o método "MoveClouds" da classe "C_AO_ACMO":

1. O primeiro bloco (se "rev" for "false"), o método cria nuvens com centros aleatórios. Para cada nuvem e cada coordenada: Para cada agente e cada coordenada:

  • Gera-se um valor aleatório para o centro da nuvem dentro dos intervalos definidos (função "RNDfromCI").
  • O centro é ajustado usando "SeInDiSp" para normalizar os valores.
  • Determina-se o índice da região onde a nuvem está localizada com a função "GetRegionIndex".
  • Definem-se os valores de entropia e entropia inicial para a nuvem.
  • Define-se o valor inicial da hiperentropia "hyperEntropy".
O método conclui a execução.

2. Segundo bloco (se "rev" for igual a "true"):

  • Se "rev" for igual a "true", o método começa a procurar regiões com a menor pressão.
  • Criam-se arrays para armazenar os índices das regiões com menor umidade "lHind" e para a normalização da pressão "normP".

3. Laço para encontrar a região com a menor pressão:

  • Para cada coordenada "c", determina-se a pressão mínima e máxima entre todas as regiões.
  • O índice da região com a menor pressão é armazenado no array "lHind".
  • A pressão normalizada para cada coordenada é armazenada em "normP".

5. Movimento das nuvens para cada uma delas e cada coordenada:

  • Se a nuvem já estiver na região com a menor pressão, a iteração é ignorada.
  • Seleciona-se aleatoriamente uma região-alvo com menor pressão.
  • Calcula-se a diferença de pressão entre a região atual e a região-alvo.
  • Normaliza-se o valor da pressão e calcula-se a velocidade de deslocamento da nuvem "VC".
  • O centro da nuvem é atualizado considerando a velocidade de deslocamento.
  • O índice da região é atualizado.
  • A entropia da nuvem é atualizada conforme a variação da pressão.
  • Reduz-se a quantidade de umidade na nuvem e atualiza-se a hiperentropia, limitando seu valor ao máximo de 8.

O método "MoveClouds" é responsável por movimentar as nuvens para regiões com menor pressão, atualizando seus parâmetros, como entropia e hiperentropia. O método implementa um modelo dinâmico que reflete as mudanças na atmosfera.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::MoveClouds (bool &rev)
{
  //----------------------------------------------------------------------------
  if (!rev)
  {
    //creating clouds with random centers---------------------------------------
    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        clouds [i].center [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        clouds [i].center [c] = u.SeInDiSp  (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

        clouds [i].entropy      [c] = entropy [c] * EnM0;
        clouds [i].entropyStart [c] = clouds [i].entropy [c];
      }

      clouds [i].hyperEntropy = HeM0;
    }

    return;
  }

  //search for the region with the lowest pressure------------------------------
  int targetRegion = 0;

  int lHind []; //lowest humidity index
  ArrayResize     (lHind, coords);
  ArrayInitialize (lHind, 0);

  double normP [];
  ArrayResize (normP, coords);
  double minP;
  double maxP;

  for (int c = 0; c < coords; c++)
  {
    minP =  DBL_MAX;
    maxP = -DBL_MAX;

    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].pressure < areas [c].regions [lHind [c]].pressure)
      {
        lHind [c] = r;
      }

      if (areas [c].regions [r].pressure < minP) minP = areas [c].regions [r].pressure;
      if (areas [c].regions [r].pressure > maxP) maxP = areas [c].regions [r].pressure;
    }

    normP [c] = maxP - minP;
  }

  //moving the cloud to a region with less pressure-----------------------------
  int    clRegIND = 0;
  double deltaP   = 0.0;
  double α        = 0.0; // Entropy factor
  double β        = 0.0; // Atmospheric pressure factor
  double VC       = 0.0; // Cloud velocity
  double d        = 0.0; // Cloud direction

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      //find a region with lower pressure---------------------------------------
      if (clouds [i].regionIndex [c] == lHind [c]) continue;

      clRegIND = clouds [i].regionIndex [c];

      do targetRegion = u.RNDminusOne (regionsNumber);
      while (areas [c].regions [clRegIND].pressure < areas [c].regions [targetRegion].pressure);

      //------------------------------------------------------------------------
      deltaP = areas [c].regions [clRegIND].pressure - areas [c].regions [targetRegion].pressure;

      β = deltaP / normP [c];
      d = areas [c].regions [targetRegion].x - areas [c].regions [clRegIND].centre;

      VC = β * d;

      clouds [i].center      [c] += VC;
      clouds [i].center      [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

      α = β;
      clouds [i].entropy [c] *=(1 + α);
    }

    clouds [i].droplets     *=(1 - γ);
    clouds [i].hyperEntropy *=(1 + α);
    if (clouds [i].hyperEntropy > 8) clouds [i].hyperEntropy = 8;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Em seguida, analisaremos o método "GetRegionIndex" da classe "C_AO_ACMO". Descrição do método:

1. Cálculo da posição da região. O índice da região "regPos", onde um determinado ponto "point" está localizado, é calculado e arredondado para baixo até o número inteiro mais próximo usando a função "floor".
2. Verificação de limites. Este bloco verifica se o índice calculado "regPos" ultrapassa os valores permitidos (ou seja, não pode exceder o número máximo de regiões permitidas).
3. O método retorna o índice da região onde o ponto está localizado.

O método "GetRegionIndex" é projetado para determinar o índice da região onde um determinado ponto está localizado dentro de um intervalo definido. Ele leva em consideração o número de regiões e processa corretamente os casos em que o ponto está no limite do intervalo. 

//——————————————————————————————————————————————————————————————————————————————
int C_AO_ACMO::GetRegionIndex (double point, int ind)
{
  int regPos = (int)floor ((point - rangeMin [ind]) / ((rangeMax [ind] - rangeMin [ind]) / regionsNumber));

  if (regPos >= regionsNumber) regPos = regionsNumber - 1;

  return regPos;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos descrever o próximo método "RainProcess" da classe "C_AO_ACMO":

2. Inicialização de arrays:

  • São criados dois arrays: "cloud" para armazenar os valores das nuvens e "drops" para armazenar a quantidade de gotas de chuva para cada nuvem.
  • Ambos os arrays são ajustados em tamanho de acordo com a quantidade de nuvens "cloudsNumber".

3. Inicialização do array "cloud":

  • Se "rev" for igual a "false", todos os elementos do array "cloud" são inicializados com o valor "1.0".
  • Caso contrário, o array "cloud" é inicializado com o valor "0.0" e, em seguida, ocorre o cálculo da umidade para cada nuvem.

4. Cálculo da umidade:

  • Para cada nuvem e cada coordenada, calcula-se a umidade com base nas regiões.
  • Se a umidade não for igual a "-DBL_MAX", ela é adicionada ao elemento correspondente do array "cloud". Caso contrário, é adicionado o valor mínimo de gota "minGp".

5. Distribuição das gotas:

  • Chama-se o método "DropletsDistribution" para distribuir as gotas com base nos valores do array "cloud".

6. Laço principal do processamento das gotas, para cada nuvem e cada gota:

  • Calculam-se os valores "dist", "centre", "xMin", "xMax".
  • Gera-se o valor "x" usando a distribuição normal (gaussiana).
  • Se "x" ultrapassar os limites do intervalo, ele é ajustado com o método "RNDfromCI".
  • O valor de "x" é normalizado com o método "SeInDiSp" e armazenado no array "a".

Após o processamento de todas as gotas de cada nuvem, o número total de gotas na nuvem é atualizado. Assim, o método "RainProcess" modela o processo de precipitação das nuvens, considerando a umidade e a distribuição das gotas. Ele inicializa os arrays, calcula a umidade para cada nuvem, distribui as gotas de chuva e gera valores para cada uma com base na distribuição normal. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int r = 0; r < regionsNumber; r++)
        {
          humidity = areas [c].regions [clouds [i].regionIndex [r]].humidity;
          if (humidity != -DBL_MAX) cloud [i] += humidity;
          else                      cloud [i] += minGp;
        }
      }
    }
  }

  DropletsDistribution (cloud, drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;
  int    dCNT   = 0;

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [dCNT].c [c] = x;
      }

      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

O próximo método, "DropletsDistribution", da classe "C_AO_ACMO", é projetado para distribuir as gotas de chuva entre as nuvens com base em sua umidade. Vamos analisá-lo passo a passo.

2. Inicialização das variáveis:

  • minHumidity - inicializada com o valor máximo, para permitir encontrar a menor umidade.
  • indMinHumidity - armazena o índice da nuvem com a menor umidade.
  • totalHumidity - usado para armazenar a soma da umidade de todas as nuvens.

3. Soma da umidade: neste laço, soma-se a umidade de todas as nuvens e identifica-se a nuvem com a menor umidade.

4. Distribuição proporcional das gotas: para cada nuvem, calcula-se a quantidade de gotas proporcional à sua umidade em relação à umidade total. Esse valor é armazenado no array "droplets".

5. Distribuição das gotas restantes:

  • Primeiro, calcula-se o número total de gotas distribuídas "totalDrops".
  • Em seguida, calcula-se a quantidade de gotas restantes "remainingDrops".
  • Se houver gotas restantes, elas são adicionadas à nuvem com a menor umidade.

O método "DropletsDistribution" distribui as gotas de chuva entre as nuvens de maneira eficiente, considerando a umidade. Primeiro, as gotas são distribuídas proporcionalmente e, depois, o método ajusta a distribuição, adicionando as gotas restantes à nuvem com a menor umidade. Isso garante uma modelagem mais realista do processo de precipitação, mantendo o número constante de gotas, conforme o tamanho da população definido nos parâmetros externos do algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::DropletsDistribution (double &cloud [], int &droplets [])
{
  double minHumidity    = DBL_MAX;
  int    indMinHumidity = -1;
  double totalHumidity  = 0; //total amount of humidity in all clouds

  for (int i = 0; i < ArraySize (cloud); i++)
  {
    totalHumidity += cloud [i];

    if (cloud [i] < minHumidity)
    {
      minHumidity = cloud [i];
      indMinHumidity = i;
    }
  }

  // Filling the droplets array in proportion to the value in clouds
  for (int i = 0; i < ArraySize (clouds); i++)
  {
    droplets [i] = int((cloud [i] / totalHumidity)*popSize); //proportional distribution of droplets
  }

  // Distribute the remaining drops, if any
  int totalDrops = 0;

  for (int i = 0; i < ArraySize (droplets); i++)
  {
    totalDrops += droplets [i];
  }

  // If not all drops are distributed, add the remaining drops to the element with the lowest humidity
  int remainingDrops = popSize - totalDrops;

  if (remainingDrops > 0)
  {
    droplets [indMinHumidity] += remainingDrops; //add the remaining drops to the lightest cloud
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" da classe "C_AO_ACMO" executa a atualização do estado do sistema. Vamos analisar o método em detalhes:

1. Laço pelos elementos do array "a" (população de agentes de otimização). Nesse laço, ocorre a iteração por todos os elementos do array "a" com tamanho "popSize":

  • Se o valor de aptidão "f" do elemento atual for maior que o valor máximo de aptidão atual "fB", "fB" é atualizado, e o índice "ind" é definido como o índice atual.
  • Além disso, ocorre a busca pelo valor mínimo de aptidão "f" entre todos os elementos do array. Se o valor atual for menor que "minGp", "minGp" é atualizado.

2. Cópia de dados: se for encontrado um elemento com o valor máximo de aptidão "f" (ou seja, se "ind" não for igual a -1), os dados do array "c" do elemento "a[ind]" são copiados para o array "cB".

3. Atualização das propriedades da região: chama-se o método "UpdateRegionProperties", que atualiza os parâmetros de umidade e pressão nas diferentes regiões.

4. Geração de nuvens: chama-se o método "GenerateClouds", responsável pelo desaparecimento das nuvens antigas e pela criação de novas.

5. Atualização do estado:

  • Define-se a variável "revision" como "true", indicando que o estado inicial do sistema foi processado.
  • Incrementa-se o contador "epochNow" para acompanhar o número de épocas.

O método "Revision" é responsável por atualizar o estado do sistema relacionado às nuvens. Ele encontra o valor máximo de aptidão "f", atualiza os parâmetros correspondentes, inicializa novas nuvens e atualiza as propriedades das regiões. Esse método é essencial para garantir que os dados do modelo estejam sempre atualizados e que o sistema se adapte às mudanças.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f < minGp) minGp = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  UpdateRegionProperties (); //updating humidity and pressure in the regions
  GenerateClouds         (); //disappearance of clouds and the creation of new ones

  revision = true;
  epochNow++;
}
//——————————————————————————————————————————————————————————————————————————————

O método "GenerateClouds" da classe "C_AO_ACMO" é responsável pela criação de nuvens e pelo gerenciamento do seu estado, levando em conta vários fatores, como umidade e entropia. Descrição do método:

1. Cálculo do limite de umidade: chama-se a função "CalculateHumidityThreshold", que retorna o valor limite de umidade necessário para a formação das nuvens.

2. Estrutura para armazenar os índices das regiões:

  • Define-se a estrutura "S_Areas", que contém um array de índices das regiões aptas à formação de nuvens. 
  • O array "ar" é inicializado com um tamanho igual ao número de coordenadas "coords".

3. Coleta de informações sobre as regiões: nesse laço duplo, cada região é verificada em relação ao limite de umidade. Se a umidade da região for superior ao limite, o índice dessa região é adicionado ao array "regsIND" da estrutura "S_Areas".

4. Verificação das condições de dissipação das nuvens:

  • Para cada nuvem, verifica-se se sua entropia excede um limite predefinido (5 vezes a entropia inicial). Se isso ocorrer, a nuvem é considerada dissipada.
  • Em seguida, verifica-se se a quantidade de umidade na nuvem está abaixo do valor mínimo "dMin", o que também pode levar à dissipação da nuvem.

5. Criação de uma nova nuvem nas regiões mais úmidas:

  • Se uma nuvem se dissipar, cria-se uma nova nuvem em uma das regiões mais úmidas. Para cada coordenada, um índice de região é escolhido aleatoriamente, e a nuvem recebe novas coordenadas centrais e um novo índice de região.
  • Em seguida, chama-se a função "CalculateNewEntropy", que recalcula a entropia com base na época atual para a nova nuvem.

O método "GenerateClouds" gerencia o processo de criação e dissipação das nuvens com base na umidade e na entropia. Ele coleta informações sobre as regiões propícias à formação de nuvens, verifica a possibilidade de dissipação das nuvens existentes e gera novas nuvens nas regiões apropriadas. Esse método é essencial para o gerenciamento dinâmico do estado das nuvens no modelo.                                                                                                                                                    

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::GenerateClouds ()
{
  //Collecting statistics of regions capable of creating clouds-----------------
  double Ht = CalculateHumidityThreshold ();

  struct S_Areas
  {
      int regsIND []; //index of the potential region
  };

  S_Areas ar [];
  ArrayResize (ar, coords);

  int sizePr = 0;

  for (int i = 0; i < coords; i++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [i].regions [r].humidity > Ht)
      {
        sizePr = ArraySize (ar [i].regsIND);
        sizePr++;
        ArrayResize (ar [i].regsIND, sizePr, coords);
        ar [i].regsIND [sizePr - 1] = r;
      }
    }
  }

  //Check the conditions for cloud decay----------------------------------------
  bool   cloudDecay = false;

  for (int i = 0; i < cloudsNumber; i++)
  {
    cloudDecay = false;

    //checking the cloud for too much entropy-----------------------------------
    for (int c = 0; c < coords; c++)
    {
      if (clouds [i].entropy [c] > 5.0 * clouds [i].entropyStart [c])
      {
        //Print ("Disintegration of cloud #", i, " - tore at epoch ", epochNow);
        cloudDecay = true;
        break;
      }
    }

    //checking the cloud for decay----------------------------------------------
    if (!cloudDecay)
    {
      if (clouds [i].droplets < dMin)
      {
        //Print ("Disintegration of cloud #", i, " - dried up at epoch ", epochNow);
        cloudDecay = true;
      }
    }

    //if the cloud has decayed--------------------------------------------------
    int regIND = 0;

    if (cloudDecay)
    {
      //creating a cloud in a very humid region---------------------------------
      for (int c = 0; c < coords; c++)
      {
        regIND = u.RNDminusOne (ArraySize (ar [c].regsIND));
        regIND = ar [c].regsIND [regIND];

        clouds [i].center      [c] = areas [c].regions [regIND].x;
        clouds [i].regionIndex [c] = regIND;
      }

      CalculateNewEntropy (clouds [i], epochNow);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateHumidityThreshold" da classe "C_AO_ACMO" é responsável por calcular o limite de umidade necessário para a formação das nuvens. Vamos detalhar o processo passo a passo:

1. Laço duplo para encontrar a umidade mínima. O laço externo percorre todas as coordenadas "coords", enquanto o laço interno percorre todos os "regionsNumber" em cada coordenada. Se a umidade da região não for igual a "-DBL_MAX", ocorre a verificação: se a umidade atual for menor que o valor atual de "H_min", "H_min" é atualizado.

2. O método retorna um valor que representa "H_min" aumentado pelo produto de "λ" pela diferença entre "H_max" e "H_min", o que define o limite de umidade necessário para a formação das nuvens.

O método "CalculateHumidityThreshold" calcula o limite de umidade com base na umidade mínima entre todas as regiões e ajusta esse valor considerando a umidade máxima e o coeficiente "λ". Isso permite determinar as condições sob as quais as nuvens podem se formar, levando em conta o estado do ambiente.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACMO::CalculateHumidityThreshold ()
{
  double H_max = fB;
  double H_min = DBL_MAX;

  for (int c = 0; c < coords; c++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].humidity != -DBL_MAX)
      {
        if (areas [c].regions [r].humidity < H_min)
        {
          H_min = areas [c].regions [r].humidity;
        }
      }
    }
  }

  return H_min + λ * (H_max - H_min);
}
//——————————————————————————————————————————————————————————————————————————————

O método "CalculateNewEntropy" da classe "C_AO_ACMO" é responsável por calcular a nova entropia e a hiperentropia das nuvens representadas pela estrutura "S_ACMO_Cloud". Vamos analisá-lo:

1. Cálculo da entropia:

  • O laço percorre todas as coordenadas "coords".
  • Para cada coordenada, calcula-se o novo valor de entropia "cl.entropy[c]", usando a fórmula: En = (entropy [c] * EnM0) / (1 + e ^ (-(8 - 16 * (t / epochs)))).
  • Os valores cl.entropyStart[c] e cl.entropy[c] são inicializados com "entropy[c]", servindo para preservar o valor inicial da entropia.

2. Cálculo da hiperentropia: He = 1 / (1 + e ^ (8 - 16 * (t / epochs))).

3. A hiperentropia é escalada pelo método "Scale" do objeto "u", permitindo ajustar o valor da hiperentropia dentro do intervalo definido (de 0 a 8), usando os parâmetros "HeM0" e 8.0.

O método "CalculateNewEntropy" atualiza os valores de entropia e hiperentropia das nuvens com base no tempo atual "t" e nos parâmetros definidos. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::CalculateNewEntropy (S_ACMO_Cloud &cl, int t)
{
  //----------------------------------------------------------------------------
  //En: 1/(1+2.72^(-(8-16*(t/maxT))))
  for (int c = 0; c < coords; c++)
  {
    cl.entropy      [c] = entropy [c] * EnM0 / (1.0 + pow (M_E, (-(8.0 - 16.0 * (t / epochs)))));
    cl.entropyStart [c] = cl.entropy [c] = entropy [c];
  }

  //----------------------------------------------------------------------------
  //He: 1/(1+2.72^((8-16*(t/maxT))))
  cl.hyperEntropy = 1.0 / (1.0 + pow (M_E, ((8.0 - 16.0 * (t / epochs)))));

  cl.hyperEntropy = u.Scale (cl.hyperEntropy, 0.0, 8.0, HeM0, 8.0);
}
//——————————————————————————————————————————————————————————————————————————————

En and He 2

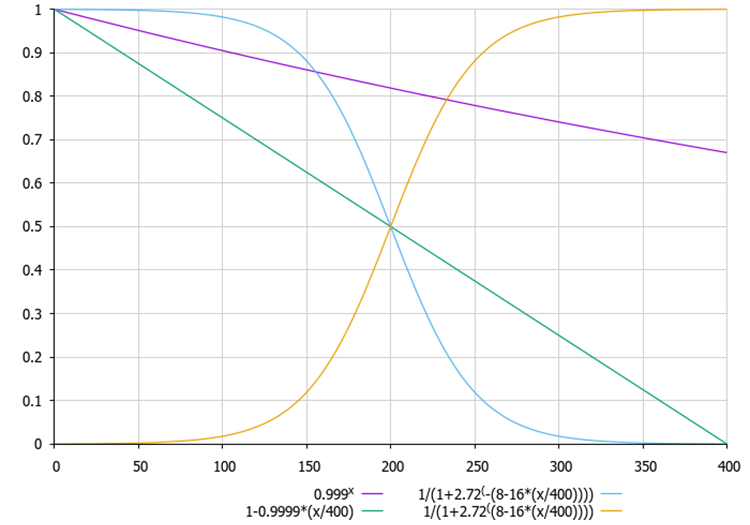
Figura 1. Variantes de fórmulas para calcular o coeficiente ζ dependendo da época atual. Você pode selecionar uma fórmula e experimentar o algoritmo com cada uma delas (as linhas estão comentadas no código).


Resultados dos testes

Vamos para os testes do algoritmo. O modelo meteorológico de formação de nuvens, conforme planejado pelos autores, funciona da seguinte forma:

//original version
ACMO|Atmospheric Cloud Model Optimization|50.0|5.0|10.0|0.2|5.0|5.0|0.9|0.2|
=============================
5 Hilly's; Func runs: 10000; result: 0.6017884495404766
25 Hilly's; Func runs: 10000; result: 0.3426222382089618
500 Hilly's; Func runs: 10000; result: 0.2526410178225118
=============================
5 Forest's; Func runs: 10000; result: 0.4780554376190664
25 Forest's; Func runs: 10000; result: 0.261057831391174
500 Forest's; Func runs: 10000; result: 0.17318135866144563
=============================
5 Megacity's; Func runs: 10000; result: 0.3507692307692307
25 Megacity's; Func runs: 10000; result: 0.16153846153846158
500 Megacity's; Func runs: 10000; result: 0.09632307692307775
=============================
All score: 2.71798 (30.20%)

Infelizmente, os resultados ficaram muito aquém do esperado. Embora o modelo apresente uma abordagem elegante para a formação de nuvens, com várias fórmulas e lógicas projetadas para evitar o aprisionamento em extremos, a convergência do algoritmo foi baixa. Falta uma interação direta e uma troca de informações entre os agentes das melhores soluções — um recurso que normalmente melhora o desempenho de qualquer algoritmo. Como resultado, decidi adicionar o intercâmbio de informações por meio de uma transmissão probabilística de dados das gotas melhores para as piores. Vamos ver os resultados:

ACMOm|Atmospheric Cloud Model Optimization|50.0|4.0|10.0|0.2|0.2|2.0|0.9|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.9032099148349984
25 Hilly's; Func runs: 10000; result: 0.48545807643133143
500 Hilly's; Func runs: 10000; result: 0.30403284557071203
=============================
5 Forest's; Func runs: 10000; result: 0.8026793420899985
25 Forest's; Func runs: 10000; result: 0.3785708322859447
500 Forest's; Func runs: 10000; result: 0.1917777390119122
=============================
5 Megacity's; Func runs: 10000; result: 0.6230769230769231
25 Megacity's; Func runs: 10000; result: 0.244
500 Megacity's; Func runs: 10000; result: 0.10795384615384714
=============================
All score: 4.04076 (44.90%)

Os resultados melhoraram significativamente. Portanto, a ideia foi bem-sucedida. A proposta consiste em transferir, com certa probabilidade, informações sobre a melhor solução das gotas superiores para outras gotas das nuvens, desde que apresentem maior umidade (o que, no contexto do algoritmo, representa a aptidão). 

Por fim, para cada nuvem, atualiza-se o número total de gotas (indicador de umidade da nuvem), adicionando o valor correspondente do array "drops". O método "RainProcess" implementa o mecanismo que modela o processo de precipitação, levando em conta a umidade, a distribuição das gotas e a interação com a população. As alterações no código foram destacadas em verde.

Para cada valor gerado de "x", seleciona-se um índice aleatório "p" da população. Dependendo da probabilidade (95%), os valores no array "a", que representa a população ou o conjunto de soluções, são atualizados. Ao final, o número total de gotas liberadas para cada nuvem é atualizado, somando-se o valor correspondente do array "drops".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        humidity = areas [c].regions [clouds [i].regionIndex [c]].humidity;
       
        if (humidity != -DBL_MAX) cloud [i] += humidity;

        else                      cloud [i] += minGp;
      }
    }
  }

  DropletsDistribution (cloud, drops);
  //ArrayPrint (drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;

  int    dCNT   = 0;


  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        int p = u.RNDminusOne (popSize);

        if (a [p].f > a [dCNT].f)
        {
          if (u.RNDprobab () < 0.95) a [dCNT].c [c] = a [p].c [c];
        }

        else
        {
          a [dCNT].c [c] = x;
        }
      }
      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ao visualizar o funcionamento do algoritmo, observa-se o seguinte: há boa convergência, com longos trechos suaves no gráfico de convergência, quando há poucos parâmetros a serem otimizados, o que indica uma certa tendência ao aprisionamento em extremos locais. No entanto, esse problema diminui à medida que o número de parâmetros aumenta.

As nuvens na visualização aparecem como aglomerados densos, mas, ao ajustar diferentes configurações de parâmetros externos (como a quantidade de regiões, nuvens, entropia inicial e valor limite de secagem), é possível simular a aparência de nuvens flutuando no céu, como na natureza real.

Hilly

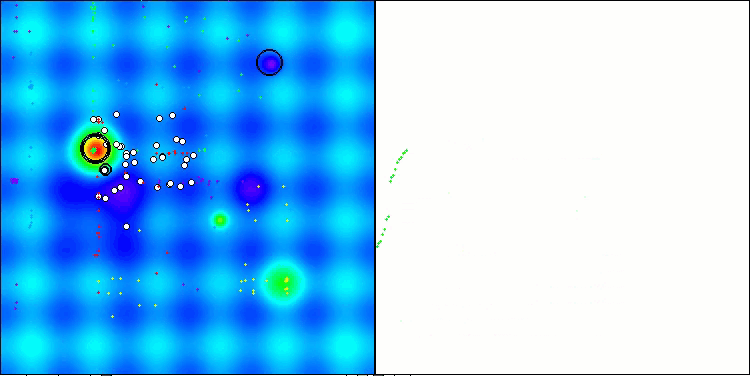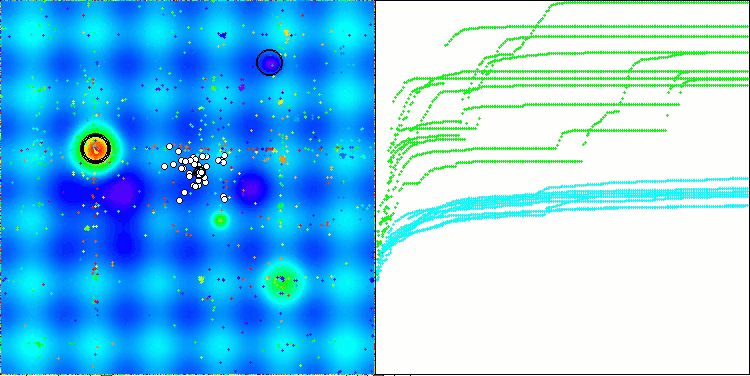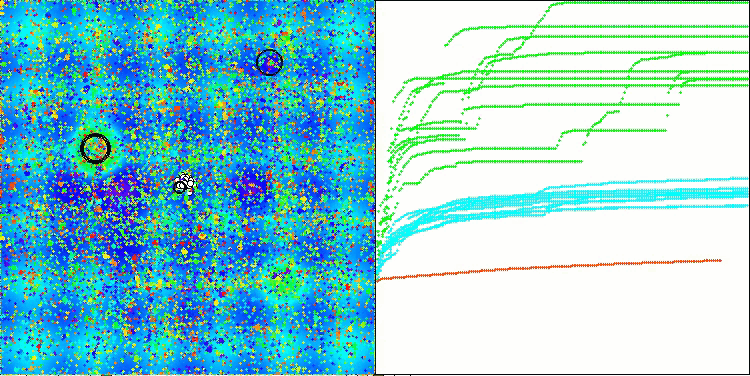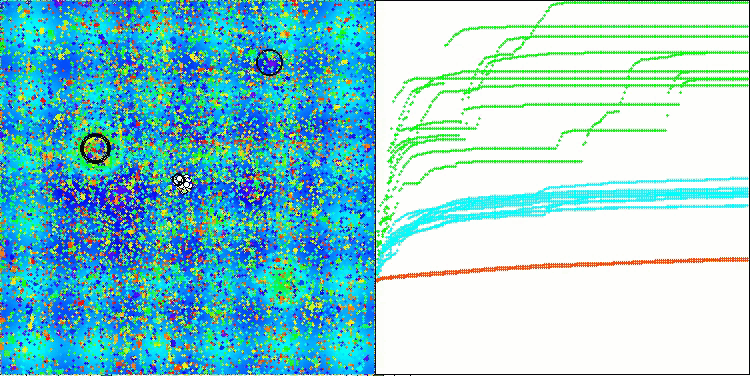
ASO na função de teste Hilly

Forest

ASO na função de teste Forest

Megacity

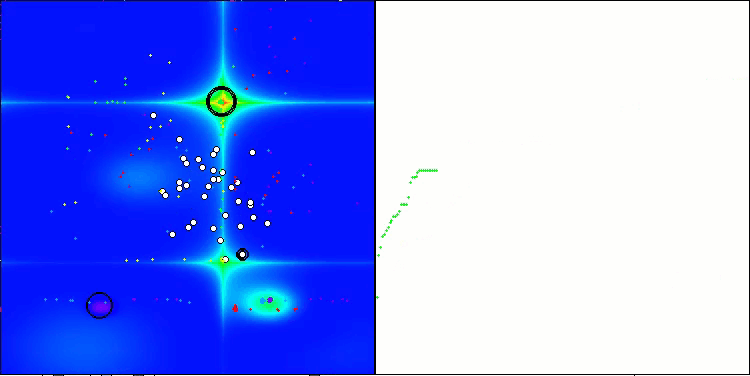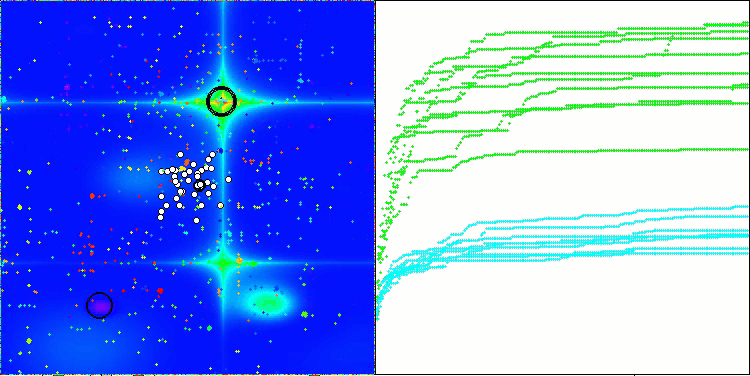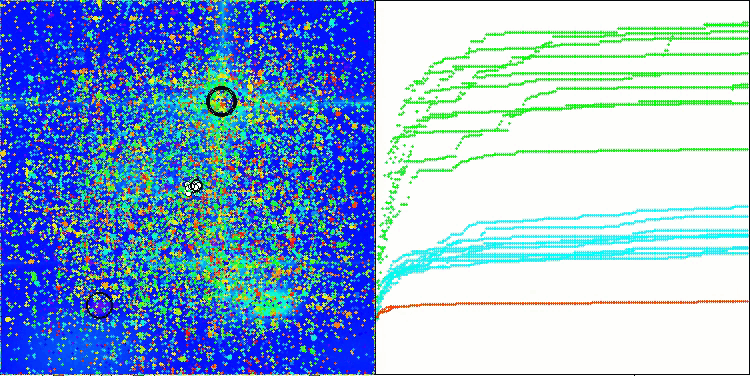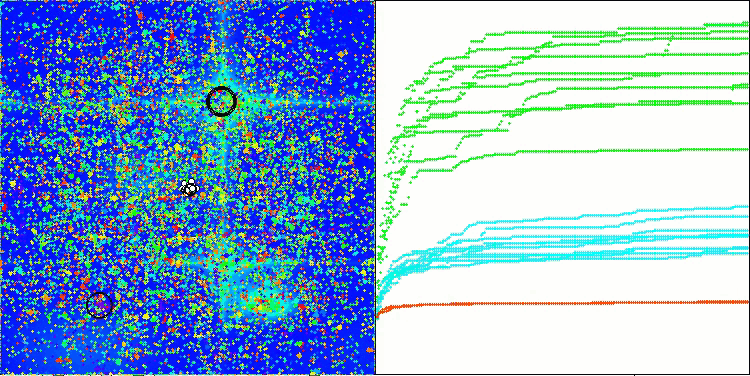
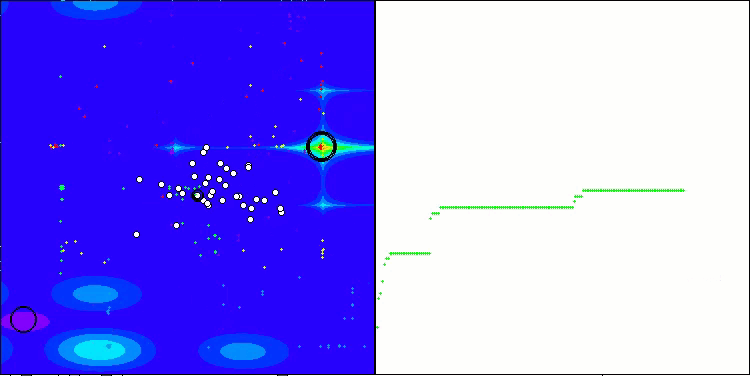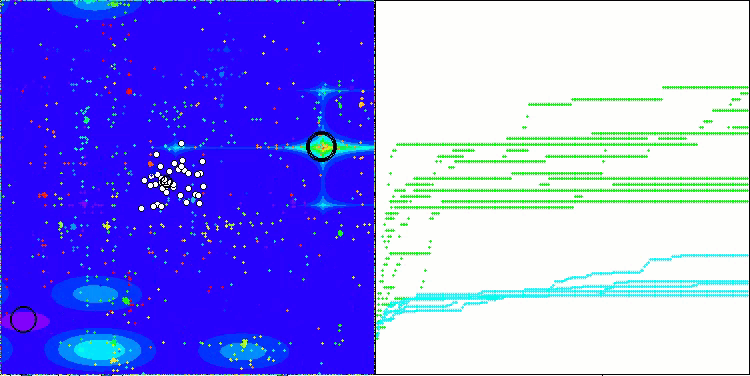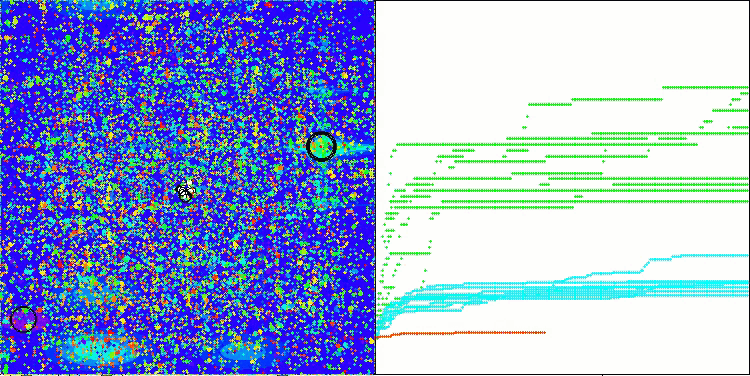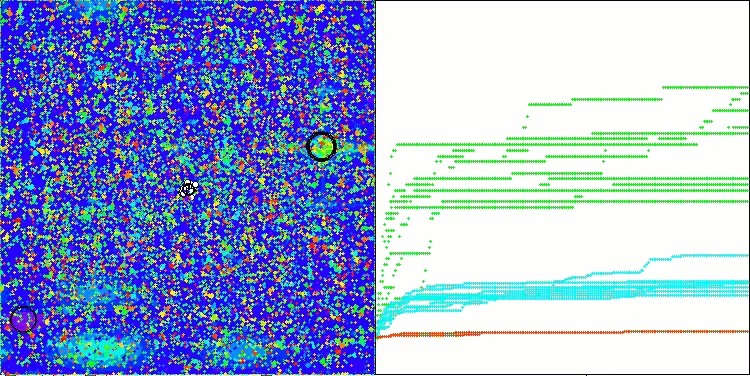
ASO na função de teste Megacity

Os testes da versão modificada do algoritmo posicionaram-no em 27º lugar, um desempenho relativamente estável. Vale destacar que a tabela agora sempre inclui 45 algoritmos e, com cada novo algoritmo, a diferença entre os anteriores e os subsequentes tende a diminuir. Portanto, pode-se afirmar que a tabela representa um ranking dos melhores algoritmos conhecidos. 

№ AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS across neighbourhood search 0,94948 0,84776 0,43857 2,23581 1,00000 0,92334 0,39988 2,32323 0,70923 0,63477 0,23091 1,57491 6,134 68,15
2 CLA code lock algorithm 0,95345 0,87107 0,37590 2,20042 0,98942 0,91709 0,31642 2,22294 0,79692 0,69385 0,19303 1,68380 6,107 67,86
3 AMOm animal migration ptimization M 0,90358 0,84317 0,46284 2,20959 0,99001 0,92436 0,46598 2,38034 0,56769 0,59132 0,23773 1,39675 5,987 66,52
4 (P+O)ES (P+O) evolution strategies 0,92256 0,88101 0,40021 2,20379 0,97750 0,87490 0,31945 2,17185 0,67385 0,62985 0,18634 1,49003 5,866 65,17
5 CTA comet tail algorithm 0,95346 0,86319 0,27770 2,09435 0,99794 0,85740 0,33949 2,19484 0,88769 0,56431 0,10512 1,55712 5,846 64,96
6 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44
7 AAm archery algorithm M 0,91744 0,70876 0,42160 2,04780 0,92527 0,75802 0,35328 2,03657 0,67385 0,55200 0,23738 1,46323 5,548 61,64
8 ESG evolution of social groups 0,99906 0,79654 0,35056 2,14616 1,00000 0,82863 0,13102 1,95965 0,82333 0,55300 0,04725 1,42358 5,529 61,44
9 SIA simulated isotropic annealing 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76
10 ACS artificial cooperative search 0,75547 0,74744 0,30407 1,80698 1,00000 0,88861 0,22413 2,11274 0,69077 0,48185 0,13322 1,30583 5,226 58,06
11 ASO anarchy society optimization 0,84872 0,74646 0,31465 1,90983 0,96148 0,79150 0,23803 1,99101 0,57077 0,54062 0,16614 1,27752 5,178 57,54
12 TSEA turtle shell evolution algorithm 0,96798 0,64480 0,29672 1,90949 0,99449 0,61981 0,22708 1,84139 0,69077 0,42646 0,13598 1,25322 5,004 55,60
13 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06
14 CRO chemical reaction optimisation 0,94629 0,66112 0,29853 1,90593 0,87906 0,58422 0,21146 1,67473 0,75846 0,42646 0,12686 1,31178 4,892 54,36
15 BSA bird swarm algorithm 0,89306 0,64900 0,26250 1,80455 0,92420 0,71121 0,24939 1,88479 0,69385 0,32615 0,10012 1,12012 4,809 53,44
16 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79
17 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95
18 BCOm bacterial chemotaxis optimization M 0,75953 0,62268 0,31483 1,69704 0,89378 0,61339 0,22542 1,73259 0,65385 0,42092 0,14435 1,21912 4,649 51,65
19 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22
20 TSm tabu search M 0,87795 0,61431 0,29104 1,78330 0,92885 0,51844 0,19054 1,63783 0,61077 0,38215 0,12157 1,11449 4,536 50,40
21 BSO brain storm optimization 0,93736 0,57616 0,29688 1,81041 0,93131 0,55866 0,23537 1,72534 0,55231 0,29077 0,11914 0,96222 4,498 49,98
22 WOAm wale optimization algorithm M 0,84521 0,56298 0,26263 1,67081 0,93100 0,52278 0,16365 1,61743 0,66308 0,41138 0,11357 1,18803 4,476 49,74
23 AEFA artificial electric field algorithm 0,87700 0,61753 0,25235 1,74688 0,92729 0,72698 0,18064 1,83490 0,66615 0,11631 0,09508 0,87754 4,459 49,55
24 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31
25 BFO-GA bacterial foraging optimization - ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93
26 ABHA artificial bee hive algorithm 0,84131 0,54227 0,26304 1,64663 0,87858 0,47779 0,17181 1,52818 0,50923 0,33877 0,10397 0,95197 4,127 45,85
27 ACMO atmospheric cloud model optimization 0,90321 0,48546 0,30403 1,69270 0,80268 0,37857 0,19178 1,37303 0,62308 0,24400 0,10795 0,97503 4,041 44,90
28 ASBO adaptive social behavior optimization 0,76331 0,49253 0,32619 1,58202 0,79546 0,40035 0,26097 1,45677 0,26462 0,17169 0,18200 0,61831 3,657 40,63
29 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55
30 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81
31 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54
32 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21
33 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44
34 NMm Nelder-Mead method M 0,73807 0,50598 0,31342 1,55747 0,63674 0,28302 0,08221 1,00197 0,44667 0,18667 0,04028 0,67362 3,233 35,92
35 FAm firefly algorithm M 0,58634 0,47228 0,32276 1,38138 0,68467 0,37439 0,10908 1,16814 0,28667 0,16467 0,04722 0,49855 3,048 33,87
36 GSA gravitational search algorithm 0,64757 0,49197 0,30062 1,44016 0,53962 0,36353 0,09945 1,00260 0,32667 0,12200 0,01917 0,46783 2,911 32,34
37 BFO bacterial foraging optimization 0,61171 0,43270 0,31318 1,35759 0,54410 0,21511 0,05676 0,81597 0,42167 0,13800 0,03195 0,59162 2,765 30,72
38 ABC artificial bee colony 0,63377 0,42402 0,30892 1,36671 0,55103 0,21874 0,05623 0,82600 0,34000 0,14200 0,03102 0,51302 2,706 30,06
39 BA bat algorithm 0,59761 0,45911 0,35242 1,40915 0,40321 0,19313 0,07175 0,66810 0,21000 0,10100 0,03517 0,34617 2,423 26,93
40 AAA algae adaptive algorithm 0,50007 0,32040 0,25525 1,07572 0,37021 0,22284 0,16785 0,76089 0,27846 0,14800 0,09755 0,52402 2,361 26,23
41 SA simulated annealing 0,55787 0,42177 0,31549 1,29513 0,34998 0,15259 0,05023 0,55280 0,31167 0,10033 0,02883 0,44083 2,289 25,43
42 IWDm intelligent water drops M 0,54501 0,37897 0,30124 1,22522 0,46104 0,14704 0,04369 0,65177 0,25833 0,09700 0,02308 0,37842 2,255 25,06
43 PSO particle swarm optimisation 0,59726 0,36923 0,29928 1,26577 0,37237 0,16324 0,07010 0,60572 0,25667 0,08000 0,02157 0,35823 2,230 24,77
44 Boids boids algorithm 0,43340 0,30581 0,25425 0,99346 0,35718 0,20160 0,15708 0,71586 0,27846 0,14277 0,09834 0,51957 2,229 24,77
45 MA monkey algorithm 0,59107 0,42681 0,31816 1,33604 0,31138 0,14069 0,06612 0,51819 0,22833 0,08567 0,02790 0,34190 2,196 24,40


Considerações finais

Foram apresentadas duas versões do algoritmo: a original e a modificada. A versão modificada inclui pequenas alterações, mas melhora significativamente o desempenho graças ao intercâmbio de informações na população. Isso demonstra que até mesmo ajustes sutis na lógica do algoritmo podem resultar em ganhos consideráveis de eficiência em diversas tarefas.

Gostei muito da ideia por trás do algoritmo, pois ela visa evitar o aprisionamento em extremos. Ele adota uma lógica complexa e em várias etapas para mover nuvens das zonas de alta pressão para as de baixa pressão, resultando em precipitação. No entanto, isso não foi suficiente para alcançar uma convergência satisfatória. Por isso, busquei uma modificação, introduzindo o intercâmbio de informações na população, o que ajudou a melhorar a convergência — um dos aspectos fundamentais de qualquer algoritmo de otimização.

Uma característica particular do algoritmo é que nenhuma nuvem permanece no mesmo lugar por muito tempo. À medida que a pressão aumenta na região, a nuvem é empurrada para uma nova área inexplorada. Esse mecanismo foi projetado pelos autores como uma forma de evitar o aprisionamento em extremos locais. No entanto, ao tentar melhorar a convergência do algoritmo, aumentou-se a probabilidade de aprisionamento, o que, infelizmente, comprometeu parcialmente a característica principal que me levou a considerar a aplicação dessa abordagem em outros algoritmos de otimização. O desenvolvimento de qualquer algoritmo de otimização sempre envolve um equilíbrio entre a resistência ao aprisionamento e a obtenção de uma solução precisa. Se desejado, a probabilidade de troca de informações pode ser ajustada no código; atualmente, ela está em 95%, o que aumenta a resiliência.

O algoritmo representa uma base sólida e um conjunto interessante de técnicas, como regras para a formação de umidade nas regiões, distribuição de pressão entre elas e a possibilidade de aplicar leis físicas de aceleração e inércia, dependentes da massa das nuvens, entre outras ideias. Por isso, ele se torna uma ferramenta valiosa para pesquisadores.

Tab

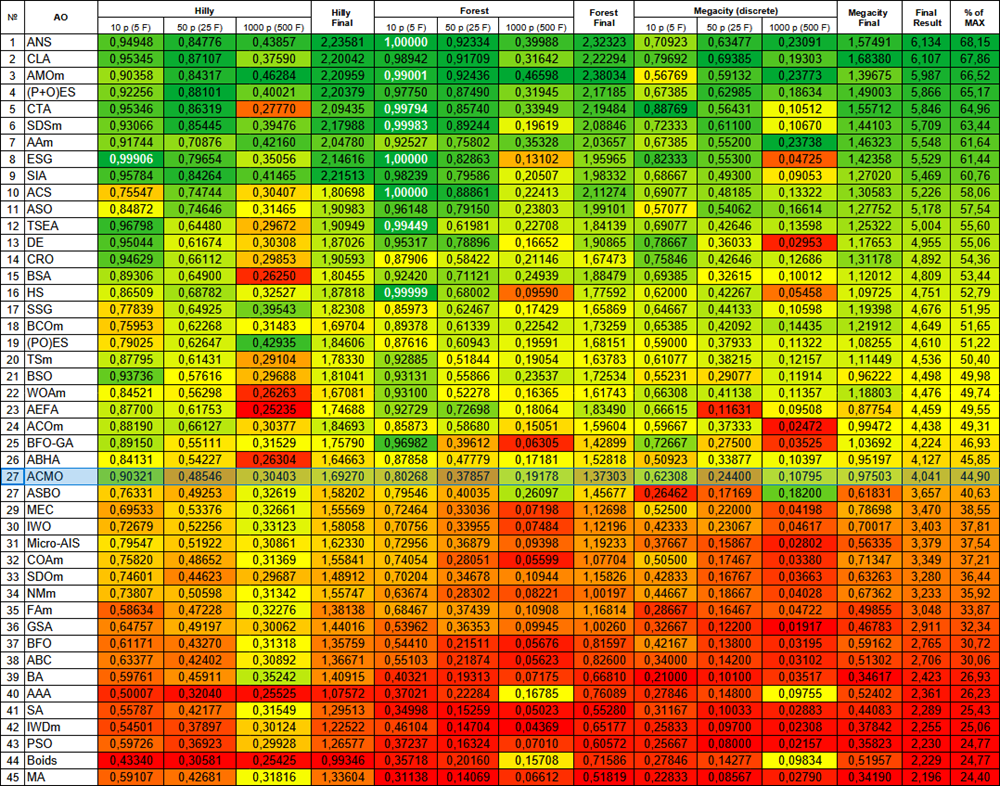
Figura 2. Histograma dos resultados do teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo há um script para calcular a tabela de classificação)

chart

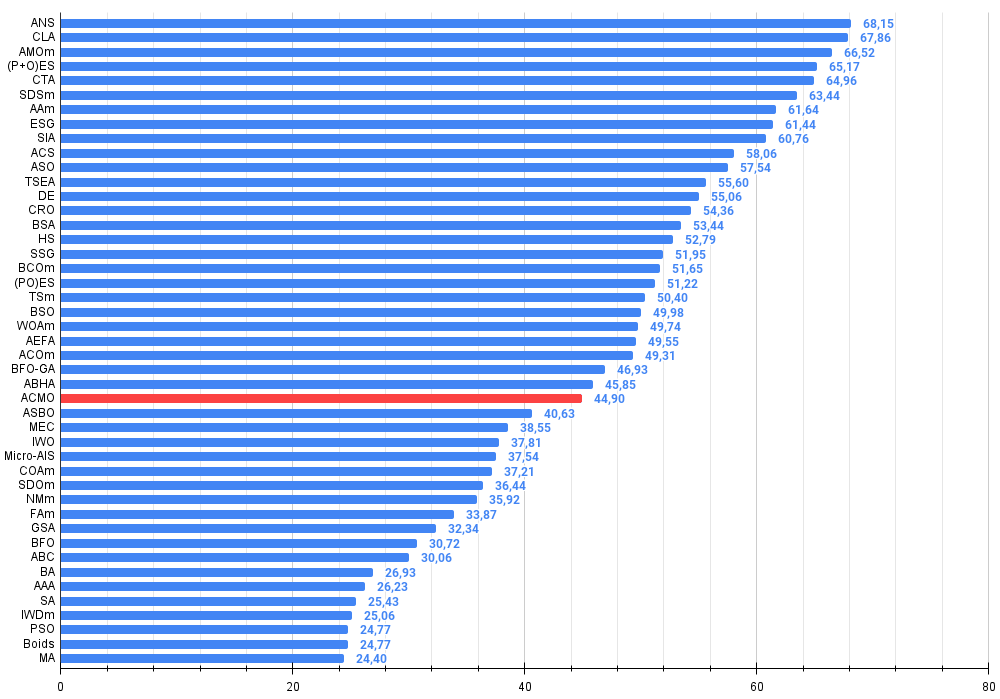
Figura 3. Graduação de cores dos algoritmos para os respectivos testes. Os resultados destacados em branco são maiores ou iguais a  0.99

Prós e contras do algoritmo ACMO:

Prós:

  1. Mecanismos embutidos para evitar o aprisionamento.
  2. Boa convergência.
  3. Escalabilidade razoável.

Contras:

  1. Grande número de parâmetros externos.
  2. Implementação complexa.
  3. Dificuldade em ajustar os parâmetros para equilibrar aprisionamento e convergência.

Um arquivo contendo as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos foram modificados para melhorar as capacidades de busca. As conclusões e análises apresentadas no artigo baseiam-se nos resultados dos experimentos realizados.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15921

Arquivos anexados |
Baixar como ZIP
ACMO.zip (39.7 KB)
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão
Redes neurais em trading: Explorando a estrutura local dos dados Redes neurais em trading: Explorando a estrutura local dos dados
A identificação eficaz e a preservação da estrutura local dos dados de mercado em meio ao ruído são tarefas cruciais no trading. Embora o uso do mecanismo Self-Attention tenha mostrado bons resultados no processamento desses dados, o método clássico não leva em conta as características locais da estrutura original. Neste artigo, proponho conhecer um algoritmo capaz de considerar essas dependências estruturais.
Simulação de mercado (Parte 09): Sockets (III) Simulação de mercado (Parte 09): Sockets (III)
Este artigo é continuação do artigo anterior. Aqui vamos ver como o Expert Advisor será implementado. Mas principalmente como deverá ser feito o código do servidor. Isto por que, o código que foi visto no artigo anterior não é o suficiente para que possamos de fato fazer com que as coisas funcionem como deverão. Então é necessário que você veja ambos artigos para compreender mais profundamente o que estará acontecendo.
Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 7): Refinando nosso modelo para o desenvolvimento de EA Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 7): Refinando nosso modelo para o desenvolvimento de EA
Neste artigo, vamos nos aprofundar na preparação detalhada do nosso indicador para o desenvolvimento de Expert Advisor (EA). Nossa discussão abrangerá refinamentos adicionais na versão atual do indicador para melhorar sua precisão e funcionalidade. Além disso, vamos introduzir novos recursos que marcam pontos de saída, abordando uma limitação da versão anterior, que identificava apenas os pontos de entrada.
Do básico ao intermediário: Eventos (I) Do básico ao intermediário: Eventos (I)
Com base em tudo que já foi mostrado e visto até este ponto. Acredito que já podemos começar a implementar algum tipo de aplicação para ser executada diretamente no gráfico de algum ativo. Mas antes mesmo de podermos fazer isto, precisamos falar de uma coisa que para iniciantes é bastante confusa. Que é justamente o fato de que o aplicações desenvolvidas em MQL5, e voltadas para serem vistas em um gráfico, não são criadas da mesma forma que vimos até este momento. Neste artigo começaremos a entender um pouco melhor sobre isto.