Algoritmo de arquearia — Archery Algorithm (AA)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

Em um cenário no qual as tarefas se tornam cada vez mais complexas e os recursos, mais escassos, a otimização não é apenas uma necessidade, mas um verdadeiro exercício de arte algorítmica no mundo moderno. Como encontrar a melhor solução entre inúmeras possibilidades? Como minimizar custos, aumentar a eficiência e obter o máximo de lucro? Essas questões preocupam especialistas das mais diversas áreas, desde a economia até a engenharia, passando pelas ciências sociais e pela ecologia. Antes de abordar um problema de otimização, é fundamental modelar corretamente o desafio, definindo as variáveis-chave e as relações matemáticas que reproduzam adequadamente a realidade. A otimização tem amplo uso em finanças e trading, ajudando não apenas a desenvolver novas estratégias de investimento, mas também a aprimorar as já existentes. Contudo, apesar da versatilidade das abordagens, os métodos de otimização podem ser divididos, de forma geral, em duas categorias: determinísticos e estocásticos.

Os métodos determinísticos, como a descida de gradiente, oferecem soluções rigorosas e previsíveis, usando derivadas matemáticas para encontrar o ótimo, o que permite modelar diversos cenários de maneira eficiente. No entanto, quando as tarefas se tornam não lineares ou multidimensionais, sua eficácia pode diminuir drasticamente. Nesses casos, entram em cena os métodos estocásticos, que, baseados em processos aleatórios, conseguem encontrar soluções aceitáveis em condições complexas, tornando-se especialmente úteis em ambientes de mercado voláteis.

A combinação de métodos determinísticos e estocásticos é essencial nas abordagens modernas de otimização. Ao integrá-los, os analistas conseguem criar modelos mais flexíveis e adaptáveis, capazes de lidar tanto com condições estáveis quanto com cenários em constante mudança. Isso melhora a qualidade das previsões e minimiza os riscos, o que é vital para o sucesso na gestão de investimentos.

Neste artigo, apresentamos uma nova abordagem para a resolução de problemas de otimização: o Algoritmo de Arquearia (Archery Algorithm, AA). Desenvolvido por Fatemeh Ahmadi Zeidabadi e colegas, o algoritmo foi publicado em fevereiro de 2022. Inspirado na arte do arco e flecha, esse método propõe soluções quase-ótimas, atualizando as posições dos membros da população no espaço de busca com base em um elemento selecionado aleatoriamente. Testaremos a eficácia do AA em funções-alvo padrão e compararemos os resultados obtidos com os de outros algoritmos já conhecidos. Ao nos aprofundarmos nos detalhes, revelaremos como essa abordagem inovadora pode transformar nossa compreensão sobre a otimização e abrir novos horizontes para a resolução de problemas complexos.

Implementação do algoritmo

O Algoritmo de Arquearia (AA) é um método estocástico de otimização totalmente novo, projetado para encontrar soluções ótimas e inspirado no comportamento do arqueiro ao mirar no alvo.  O AA simula o processo de disparo de flechas em direção ao alvo. Cada membro da população representa uma solução potencial para o problema de otimização, e suas posições no espaço de busca são atualizadas com base no desempenho de um membro "alvo" escolhido aleatoriamente, de modo semelhante ao ajuste da mira de um arqueiro conforme o ponto que deseja atingir.

A população é representada como uma matriz, em que cada linha corresponde a um membro (solução) e cada coluna representa uma dimensão do problema. Essa estrutura permite avaliar e atualizar sistematicamente as soluções com base em seus valores da função objetivo. O desempenho de cada membro é medido por meio dessa função, que quantifica a qualidade da solução encontrada. Os resultados são armazenados em um vetor, permitindo ao algoritmo comparar a eficácia das diferentes soluções.

O alvo é dividido em seções, cuja largura corresponde ao desempenho dos membros da população. Calcula-se uma função de probabilidade para determinar a chance de cada membro ser selecionado com base em seu valor da função objetivo, garantindo que os arqueiros mais eficientes tenham maior probabilidade de serem escolhidos. Então, um membro da população é selecionado aleatoriamente com base na probabilidade acumulada, imitando a escolha de um alvo pelo arqueiro. Essa seleção influencia a forma como as posições dos outros membros são atualizadas. O algoritmo atualiza a posição de cada arqueiro no espaço de busca por meio de equações específicas. A atualização depende do valor da função objetivo do arqueiro escolhido em comparação ao valor atual. Esse processo inclui um elemento de aleatoriedade para explorar o espaço de busca. O AA opera de forma iterativa, atualizando a população até que a condição de parada seja alcançada (número máximo de iterações). Durante esse processo, o algoritmo monitora a melhor solução encontrada.

Na versão original do algoritmo AA apresentada acima, a matriz é descrita como a população e os vetores como os membros dessa população. No entanto, o texto não especifica operações particulares associadas ao trabalho com matrizes. Na realidade, o algoritmo envolve ações padrão com agentes de busca, semelhantes às observadas na maioria dos algoritmos previamente analisados.

Vale também destacar que a expressão "o alvo é dividido em seções, cuja largura corresponde ao desempenho dos membros da população" sugere o uso do método de roleta para a seleção. Nesse caso, a probabilidade de escolha de um setor é proporcional à sua largura.

Assim, formulações complexas que descrevem muitos conceitos podem ser explicadas de maneira muito mais simples, o que pode facilitar significativamente a implementação prática da ideia.

O Algoritmo de Arquearia, portanto, é um método de otimização baseado em população, que utiliza os princípios de tiro ao alvo para conduzir a busca por soluções ótimas. Ele combina elementos de aleatoriedade com distribuição normal para explorar e explorar o espaço de busca. Os principais componentes do algoritmo são:

1. População de agentes (arqueiros)
2. Vetor de probabilidades e probabilidades acumuladas
3. Mecanismo de herança (ausente na versão original)
4. Mecanismo de atualização de posições
5. Parâmetro de intensidade de aprendizado (I)

Para começar, apresentamos o pseudocódigo do algoritmo:

Inicialização:
    Criar uma população de tamanho popSize de agentes
    Para cada agente:
        Inicializar uma posição aleatória dentro do intervalo de busca
        Inicializar a posição anterior e a adaptabilidade

Ciclo principal:
    Enquanto a condição de parada não for atingida:
        Para cada agente i na população:
            Calcular o vetor de probabilidades P e as probabilidades acumuladas C
            
            Para cada coordenada c:
                Selecionar o arqueiro k usando a probabilidade acumulada
                
                Se (número_aleatório < probabilidade_de_herança):
                    nova_posição[c] = posição_arqueiro_k[c]
                Caso contrário:
                    I = arredondar(1 + número_aleatório_de_0_a_1) // Parâmetro de intensidade de aprendizado
                    gaussiano_aleatório = gerar_número_gaussiano (média = 0, mín = -1, máx = 1)
                    
                    Se (adaptabilidade_do_arqueiro_k > adaptabilidade_do_agente_i):
                        nova_posição[c] = posição_anterior[c] + gaussiano_aleatório * (posição_arqueiro_k[c] - I * posição_anterior[c])
                    Caso contrário:
                        nova_posição[c] = posição_anterior[c] + gaussiano_aleatório * (posição_anterior[c] - I * posição_arqueiro_k[c])
                
                Restringir nova_posição[c] dentro do intervalo de busca
            
            Atualizar a posição do agente i
        
        Avaliar a adaptabilidade de todos os agentes
        Atualizar a melhor solução global
        Para cada agente:
            Se a nova adaptabilidade for melhor que a anterior:
                Atualizar a posição anterior e a adaptabilidade

Retornar a melhor solução encontrada

Características da implementação no código:

1. O algoritmo utiliza uma abordagem probabilística para selecionar os arqueiros dos quais os agentes devem aprender.
2. O mecanismo de herança permite que os agentes copiem diretamente as posições de arqueiros bem-sucedidos com certa probabilidade.
3. Na atualização das posições, é usada a distribuição gaussiana para introduzir aleatoriedade no processo de aprendizado dos arqueiros.
4. O algoritmo mantém as melhores posições anteriores dos agentes, proporcionando uma "memória" das boas soluções.
5. A implementação incluirá um mecanismo para restringir as novas posições dentro do intervalo permitido de busca.
6. O parâmetro de intensidade de aprendizado (I), descrito pelos autores, será utilizado para ajustar o grau de influência da posição atual na nova posição.

O parâmetro I (intensidade de aprendizado) é uma variável aleatória que pode assumir o valor 1 ou 2. Ele é definido da seguinte forma: I = arredondar para o inteiro mais próximo (1 + número_aleatório entre 0 e 1). Isso significa que I será igual a 1 com uma probabilidade de 0,5 e igual a 2 com a mesma probabilidade. O papel do parâmetro I no algoritmo é:

1. Quando I = 1, o algoritmo realiza ajustes menores na posição.
2. Quando I = 2, o algoritmo pode fazer mudanças mais drásticas na posição.

Agora vamos diretamente ao desenvolvimento do código do algoritmo. Descreveremos a estrutura do "arqueiro" — "S_AA_Agent", que representa um agente no algoritmo de otimização com múltiplas coordenadas no espaço de soluções e contém informações sobre seu desempenho na função de aptidão. 

• cPrev[] — um array que armazena as coordenadas anteriores do agente.
  
• fPrev — uma variável que guarda o valor anterior de aptidão (fitness) do agente.   

O método "Init" prepara o agente para a execução, definindo valores iniciais para suas coordenadas e aptidão. Em seguida, o valor de "fPrev" é definido como o menor valor possível para o tipo "double", pois a adaptabilidade ainda não foi calculada.

//——————————————————————————————————————————————————————————————————————————————
struct S_AA_Agent
{
    double cPrev []; // previous coordinates
    double fPrev;    // previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Vamos analisar a classe "C_AO_AAm", que implementa o próprio algoritmo e herda da classe "C_AO". 

• popSize indica o tamanho da população.
• inhProbab representa a probabilidade de herança de uma característica de outro arqueiro.

Em seguida, ocorre a inicialização do array params com tamanho 2, onde são armazenados os parâmetros do algoritmo: tamanho da população e probabilidade de herança.

• O método SetParams define os parâmetros do algoritmo com base nos valores armazenados no array params. Ele extrai os valores para popSize e inhProbab, convertendo-os para os tipos correspondentes.
• Init é o método responsável por inicializar o algoritmo, aceitando como parâmetros os limites mínimos e máximos de busca, o passo de busca e o número de épocas.
• Os métodos Moving e Revision são responsáveis pela lógica de movimentação dos agentes no espaço de soluções e pela sua revisão (atualização). 

S_AA_Agent agent[] é o array de agentes que será utilizado para a execução da otimização.

A classe C_AO_AAm implementa o algoritmo de otimização, enquanto os métodos SetParams, Init, Moving e Revision controlam a configuração e o comportamento do algoritmo durante sua execução. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AAm () { }
  C_AO_AAm ()
  {
    ao_name = "AAm";
    ao_desc = "Archery Algorithm M";
    ao_link = "https://www.mql5.com/en/articles/15782";

    popSize   = 50;    // population size
    inhProbab = 0.3;

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "inhProbab"; params [1].val = inhProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    inhProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // step search
             const int     epochsP = 0);  // number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double  inhProbab; //probability of inheritance

  S_AA_Agent agent [];

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

O método Init na classe C_AO_AAm é responsável por inicializar o algoritmo de otimização. Ele aceita quatro parâmetros: arrays para os limites mínimos e máximos de busca, o passo de busca e o número de épocas, que por padrão são definidos como zero.

• Se a inicialização padrão for bem-sucedida, o método então ajusta o tamanho do array agent para corresponder ao valor definido por popSize. Isso permite a criação da quantidade necessária de agentes que serão utilizados no algoritmo.
• No laço for, cada agente do array é inicializado por meio do método Init, que define as coordenadas iniciais para cada agente.
  

Ao final, o método retorna true, indicando que a inicialização do algoritmo foi concluída com sucesso. Assim, o método Init garante a preparação do algoritmo para execução, configurando os parâmetros necessários e criando os agentes que participarão do processo de otimização.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAm::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método Moving na classe C_AO_AAm é responsável pelo deslocamento dos agentes no espaço de soluções, com base em suas posições atuais e nos valores da função que estão otimizando. Vamos analisar sua execução em partes:

• Se o método for chamado pela primeira vez (revision igual a false), cada agente e cada coordenada recebem um valor aleatório dentro dos limites definidos por rangeMin e rangeMax.
• Em seguida, esse valor é ajustado por meio do método SeInDiSp, que garante que o valor esteja de acordo com o passo definido.

Após essa etapa, o sinalizador revision é definido como true, e o método conclui sua execução.

• Em seguida, são criados dois arrays: P, para as probabilidades, e C, para as probabilidades acumuladas.
• O pior valor da função, F_worst, é identificado para normalizar os valores da função de aptidão dos agentes.
• Em seguida, as probabilidades de cada agente são calculadas e normalizadas de modo que sua soma seja igual a 1.
• As probabilidades acumuladas C são calculadas com base nas probabilidades P.
• Para cada agente e cada coordenada, ocorre a seleção de um arqueiro-parceiro, com base na probabilidade acumulada.
• Se o valor aleatório for menor que a probabilidade de herança definida, inhProbab, o agente assume a coordenada do arqueiro escolhido (garantindo a herança das características conforme a probabilidade definida).
  
• Caso contrário, o agente atualiza sua posição com base em uma fórmula que leva em conta a posição atual, um valor aleatório e a posição do arqueiro-parceiro.
• Por fim, o novo valor da coordenada também é ajustado com o método SeInDiSp.

O método Moving implementa o deslocamento dos agentes no espaço de soluções, considerando suas posições atuais e os valores da função. Ele utiliza métodos probabilísticos para selecionar as direções de movimento e atualizar as posições.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        // Update position using Eq. (5) and (6)
        double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);

        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método Revision na classe C_AO_AAm é responsável por atualizar as informações sobre os melhores agentes da população. Este método executa as seguintes ações:

• A variável "ind" é inicializada com o valor "-1". Ela será usada para armazenar o índice do agente com o melhor valor da função de aptidão.
• O laço for percorre todos os agentes da população (popSize). Se o valor da função do agente atual a[i].f for maior que o melhor valor atual fB:
• fB é atualizado com o novo melhor valor a[i].f
• O índice desse agente é armazenado na variável ind.

Após a conclusão do laço, se ind for diferente de -1, a função ArrayCopy é chamada para copiar as coordenadas do melhor agente do array a para o array cB. Um segundo laço for percorre todos os agentes da população:

• Se o valor da função do agente atual a[i].f for maior que seu valor anterior de aptidão agent[i].fPrev:
• O valor anterior fPrev é atualizado para o novo valor.
• As coordenadas atuais do agente são copiadas para o array cPrev por meio de ArrayCopy.

O método Revision serve para atualizar as informações sobre a melhor solução global, além de atualizar as melhores posições dos agentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Resultados dos testes

Modifiquei ligeiramente o algoritmo. O algoritmo original dos autores não prevê a troca direta de informações entre arqueiros. A troca ocorre indiretamente por meio da interação das coordenadas com a distribuição normal, então considerei necessário adicionar esse intercâmbio de informações. Para isso, foi incluído um parâmetro adicional, inhProbab, responsável por implementar essa troca com uma probabilidade definida.

if (u.RNDbool () < inhProbab)
{
  x = a [k].c [c];
}

Os resultados apresentados a seguir correspondem à versão original do algoritmo, conforme concebido pelos autores.

AA|Archery Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6699547926310098
25 Hilly's; Func runs: 10000; result: 0.37356238340164605
500 Hilly's; Func runs: 10000; result: 0.257542163368952
=============================
5 Forest's; Func runs: 10000; result: 0.38166669771790607
25 Forest's; Func runs: 10000; result: 0.199300365268835
500 Forest's; Func runs: 10000; result: 0.15337954055780398
=============================
5 Megacity's; Func runs: 10000; result: 0.4076923076923077
25 Megacity's; Func runs: 10000; result: 0.17907692307692308
500 Megacity's; Func runs: 10000; result: 0.10004615384615476
=============================
All score: 2.72222 (30.25%)

O algoritmo obteve 30,25% nos testes. No entanto, com minha modificação, o desempenho foi aprimorado em mais de 13%. Abaixo estão os resultados obtidos pela versão modificada:

Assim, decidi adotar a versão modificada do algoritmo e incluí-la na tabela de classificação.
=============================
5 Hilly's; Func runs: 10000; result: 0.9353194829441194
25 Hilly's; Func runs: 10000; result: 0.6798262991897616
500 Hilly's; Func runs: 10000; result: 0.2596620178276653
=============================
5 Forest's; Func runs: 10000; result: 0.5735062785421186
25 Forest's; Func runs: 10000; result: 0.22007188891556378
500 Forest's; Func runs: 10000; result: 0.1486980566819649
=============================
5 Megacity's; Func runs: 10000; result: 0.6307692307692309
25 Megacity's; Func runs: 10000; result: 0.344
500 Megacity's; Func runs: 10000; result: 0.10193846153846249
=============================
All score: 3.89379 (43.26%)

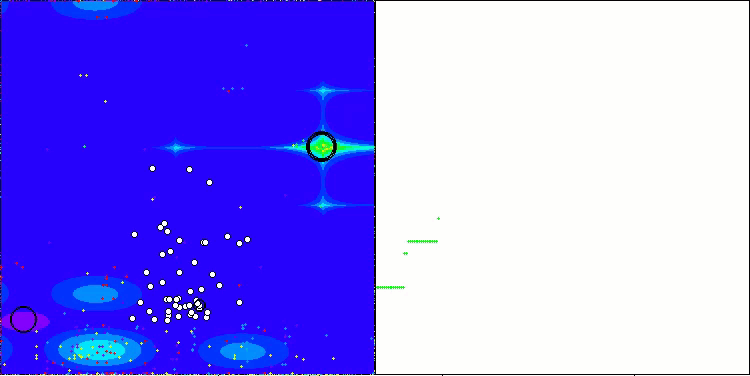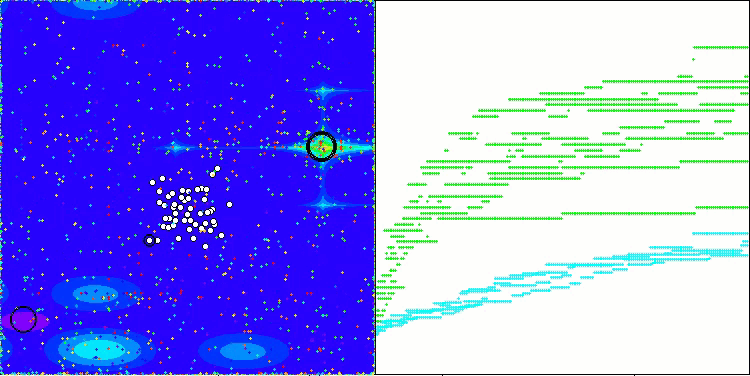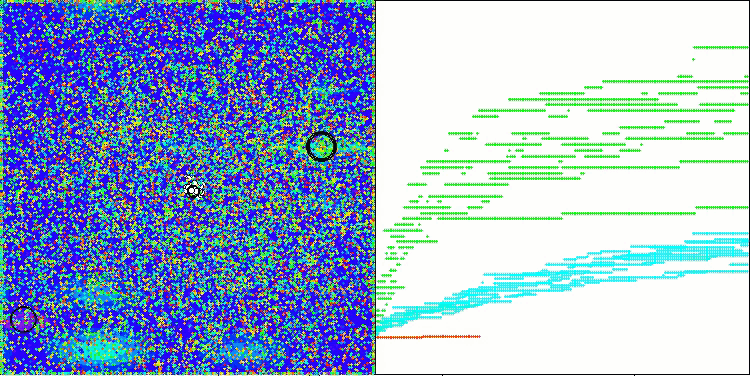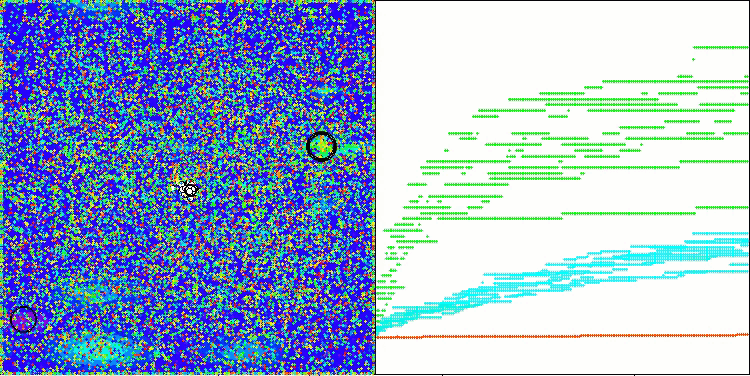
A visualização a seguir mostra como o algoritmo se comporta. Acredito que o desempenho é satisfatório. Embora haja alguma variação nos resultados, ela não é crítica e ocorre apenas em funções com um número reduzido de coordenadas.

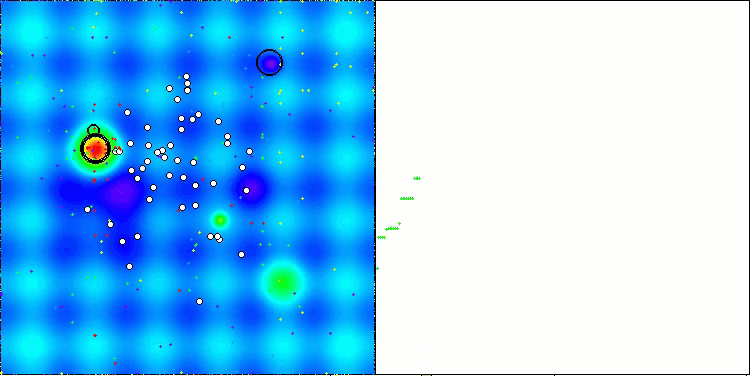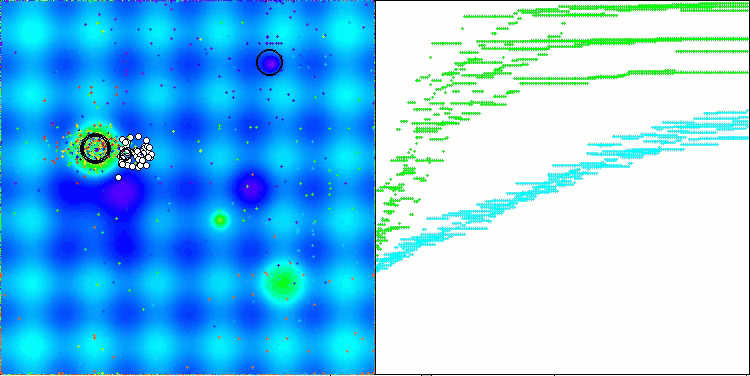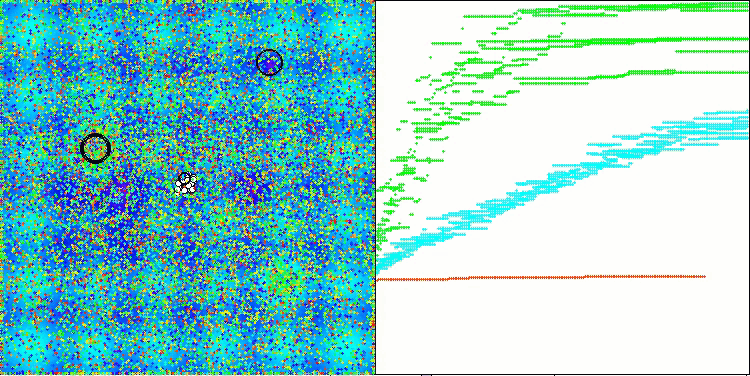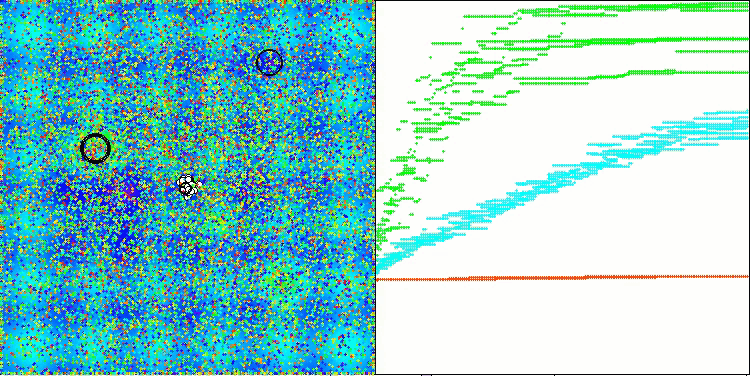
AAm na função de teste Hilly

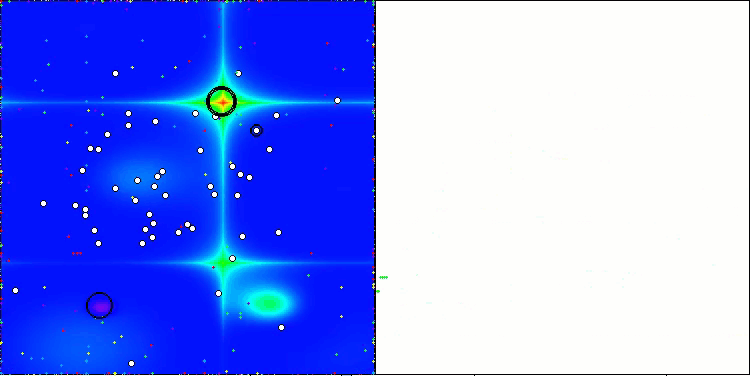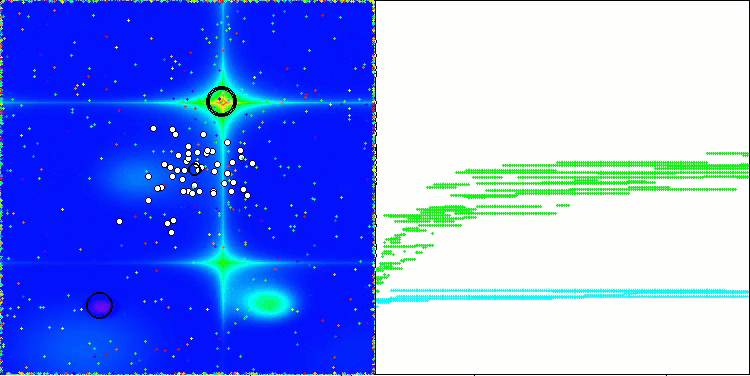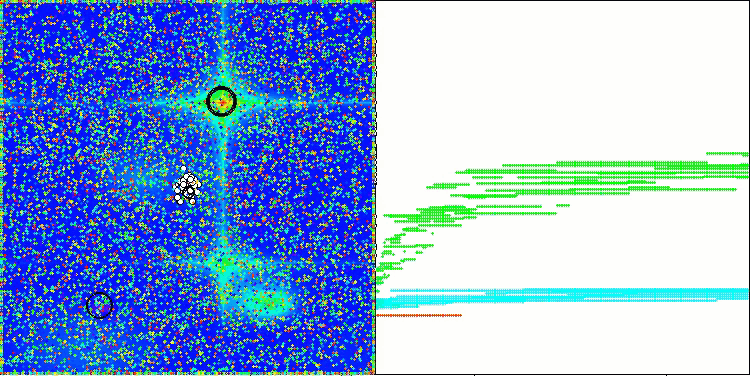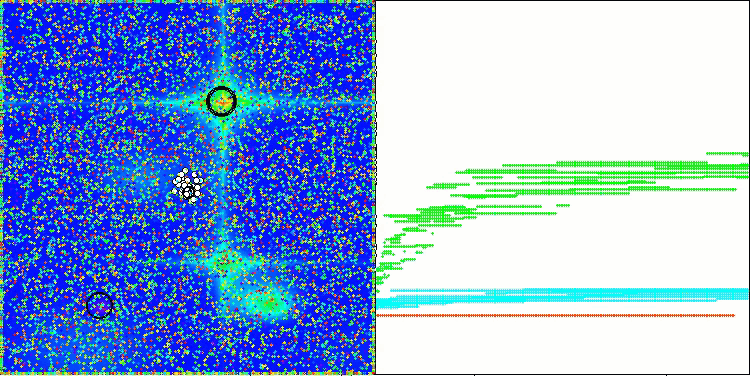
AAm na função de teste Forest

AAm na função de teste Megacity

Com base nos testes realizados, a versão modificada do algoritmo ocupa a 26ª posição.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
18	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
19	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
20	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
21	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
22	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
23	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
24	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
25	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
26	AAm	archery algorithm M	0,93532	0,67983	0,25966	1,87481	0,57351	0,22007	0,14870	0,94228	0,63077	0,34400	0,10194	1,07671	3,894	43,26
27	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
28	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
29	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
30	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
31	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
32	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
33	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
34	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
35	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
36	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
37	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
38	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
39	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
40	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
41	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
42	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
43	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
44	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
45	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38

Considerações finais

Foram apresentadas duas versões do algoritmo: a original, proposta pelos autores, e minha versão modificada, que inclui pequenas alterações, mas proporciona um ganho significativo em termos de desempenho. Este artigo demonstra claramente que até mesmo ajustes mínimos na lógica do algoritmo podem resultar em melhorias notáveis na eficiência em diferentes tarefas. Fica evidente também que descrições excessivamente complexas podem dificultar a compreensão do funcionamento do algoritmo, tornando seu aprimoramento mais desafiador. Por outro lado, quando conceitos complexos são explicados de forma simples, abre-se caminho para soluções mais eficazes.

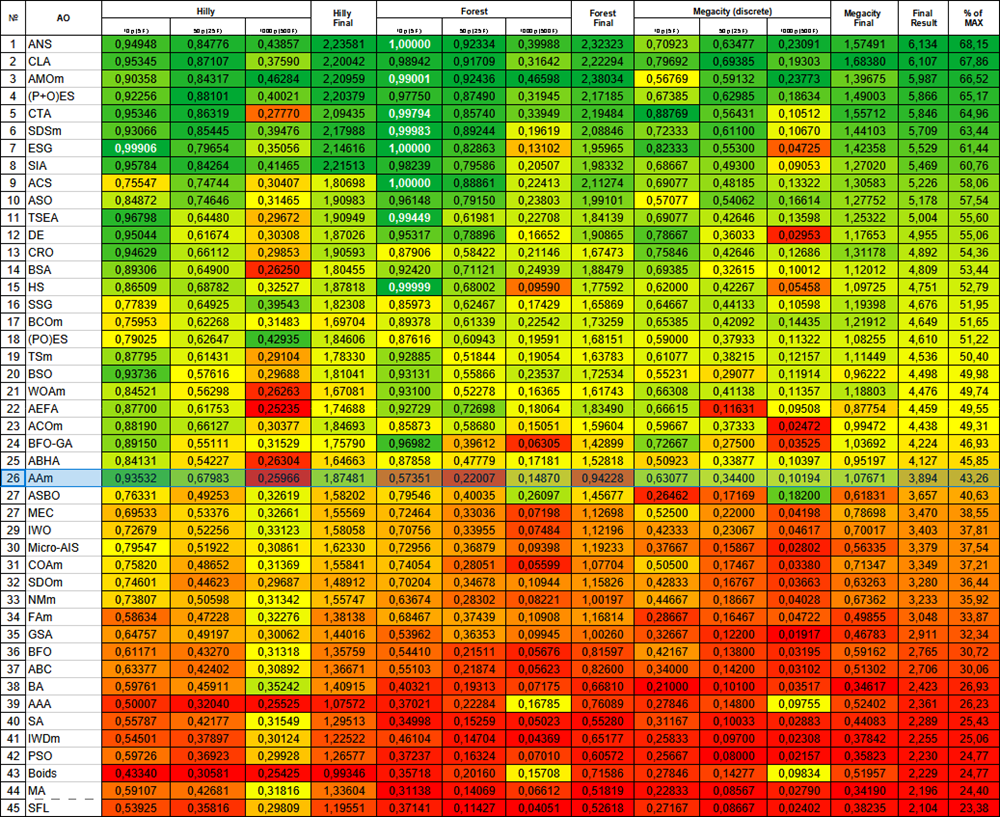
Figura 1. Graduação de cores dos algoritmos para os respectivos testes. Os resultados destacados em branco são maiores ou iguais a  0.99

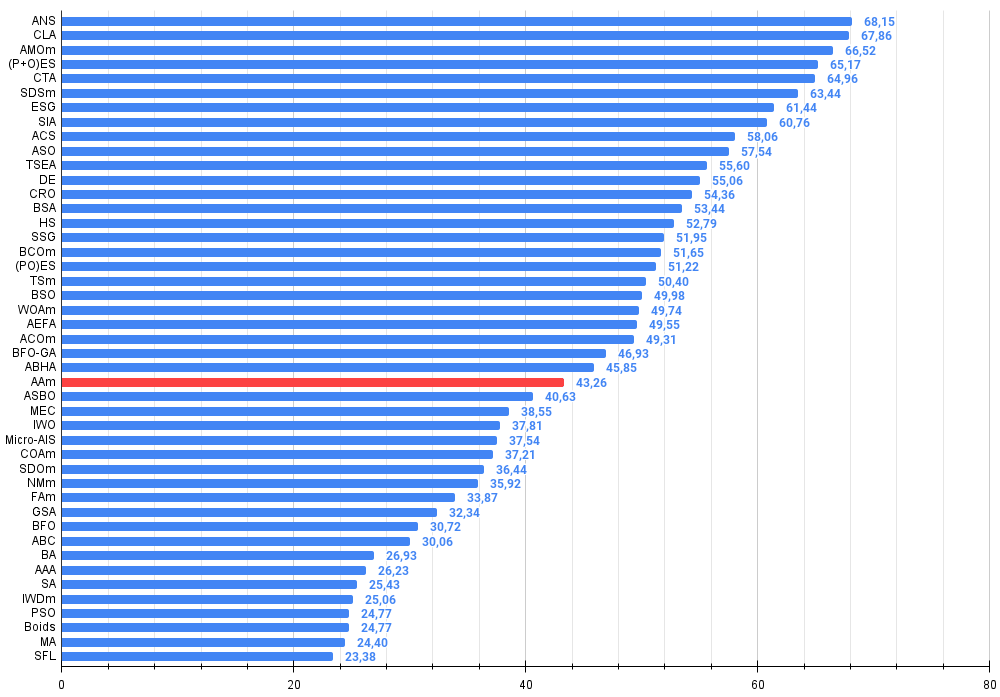
Figura 2. Histograma dos resultados do teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo há um script para calcular a tabela de classificação)

Quando o artigo estava quase pronto para publicação, tive uma ideia que decidi pôr à prova. E se, seguindo a lógica dos autores sobre alvos e arqueiros que usam o método de "roleta" para seleção, alterássemos o tamanho dos próprios alvos de forma inversamente proporcional à qualidade das soluções encontradas? Se a solução for boa, ela deve ser aprimorada e explorada em sua proximidade. Caso contrário, se o resultado for pouco significativo, a zona de busca deve ser ampliada para identificar novas direções potencialmente promissoras.

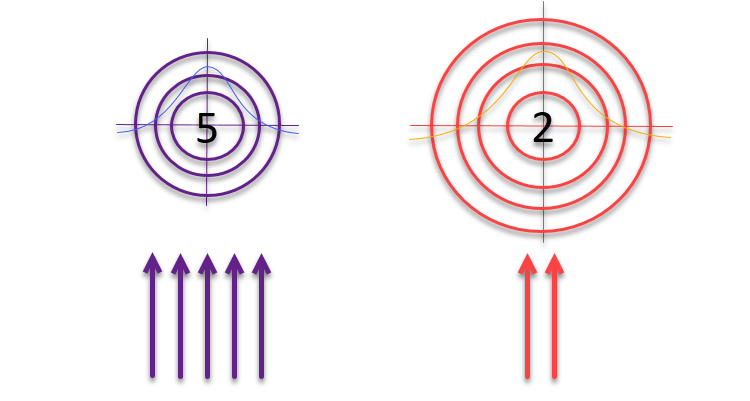
Figura 3. O número de flechas que atingem os alvos é diretamente proporcional à qualidade dos próprios alvos, enquanto o tamanho dos alvos é inversamente proporcional à sua qualidade. 

Vamos analisar o código que implementa essa ideia de ajuste dinâmico dos alvos em função da qualidade das soluções.

void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX; // a[ArrayMaximum(a, WHOLE_ARRAY, 0, popSize)].f;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst; ////F_worst - a[i].f;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;
  
  double maxFF = fB;
  double minFF = DBL_MAX;
  double prob1;
  double prob2;
  
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < minFF) minFF = a [i].f;
  } 

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        
        // Update position using Eq. (5) and (6)
        //double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);
        /*
        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
        */
        
        prob1 = u.Scale (a [i].f, minFF, maxFF, 0, 1);
        prob2 = u.Scale (a [k].f, minFF, maxFF, 0, 1);
        
        x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2);  
        
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//—

1. Na seção comentada da versão original, era usada uma estrutura condicional "if-else" para determinar como a posição do agente seria atualizada. Essa lógica foi removida e substituída por um novo cálculo.

2. Três novas linhas de código foram introduzidas:

prob1 = u.Scale(a[i].f, minFF, maxFF, 0, 1);
prob2 = u.Scale(a[k].f, minFF, maxFF, 0, 1);

x = agent[i].cPrev[c] + rnd * (a[k].c[c] - agent[i].cPrev[c]) * (1 - prob1 - prob2);

Essas linhas implementam uma nova abordagem para calcular a posição atualizada:

a) São calculadas duas variáveis probabilísticas, prob1 e prob2, utilizando a função Scale, que normaliza os valores de adaptabilidade dos agentes i e k em um intervalo de 0 a 1, com base nos valores mínimo e máximo de aptidão, minFF e maxFF.

b) Em seguida, a nova posição x é calculada com base nessas probabilidades. Ela utiliza a posição anterior i do agente agent[i].cPrev[c], a posição k do arqueiro selecionado a[k].c[c] e um fator aleatório rnd.

c) Agora, o movimento é influenciado pela soma das aptidões de ambos os agentes, subtraída de 1. Esse fator atua como um coeficiente de escala, permitindo expandir ou contrair o alvo de forma inversamente proporcional à aptidão dos arqueiros selecionados. Quanto menos experientes forem os arqueiros, maior será a dispersão das flechas, embora a distribuição das probabilidades de acerto ainda siga uma distribuição normal.

Agora, vejamos o resultado:

Assim, decidi adotar a versão modificada do algoritmo e incluí-la na tabela de classificação.
=============================
5 Hilly's; Func runs: 10000; result: 0.9174358826544864
25 Hilly's; Func runs: 10000; result: 0.7087620527831496
500 Hilly's; Func runs: 10000; result: 0.42160091427958263
=============================
5 Forest's; Func runs: 10000; result: 0.9252690259821034
25 Forest's; Func runs: 10000; result: 0.7580206359203926
500 Forest's; Func runs: 10000; result: 0.353277934084795
=============================
5 Megacity's; Func runs: 10000; result: 0.6738461538461538
25 Megacity's; Func runs: 10000; result: 0.552
500 Megacity's; Func runs: 10000; result: 0.23738461538461658
=============================
All score: 5.54760 (61.64%)

Os resultados são animadores, com uma melhora significativa no desempenho do algoritmo. A visualização a seguir destaca a convergência consistente do algoritmo e a identificação de regiões relevantes na superfície da função.

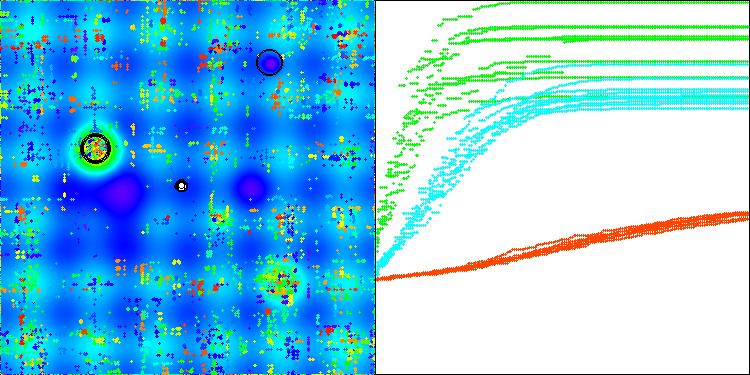
AAm na função de teste Hilly

Realizaremos mais um pequeno experimento. Os resultados anteriores foram obtidos subtraindo a soma das probabilidades dos arqueiros de um.

//x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2); 
 x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (2 - prob1 - prob2);  

A principal mudança agora é subtrair a soma das probabilidades não de 1, mas de 2. Vamos entender como essa simples modificação pode impactar o comportamento do algoritmo:

• Na versão anterior, o resultado dessa operação poderia ser negativo caso a aptidão de ambos os arqueiros fosse alta, levando ao efeito de "mutação" nas coordenadas resultantes do novo arqueiro.
  
• Na nova versão, o multiplicador resulta em um valor entre 0 e 2.

Essa mudança leva a movimentos mais amplos dos agentes, resultando em uma exploração mais agressiva do espaço de soluções, já que os agentes passam a dar passos maiores em cada atualização de posição.

Como mostram os resultados do algoritmo, essa modificação melhorou a convergência em funções de complexidade média, mas também levou a uma queda no desempenho em funções de alta dimensionalidade (destacadas em amarelo). Assim, decidi adotar a versão modificada do algoritmo e incluí-la na tabela de classificação. No entanto, o algoritmo ainda obteve uma pontuação final superior.

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9053229410164233
25 Hilly's; Func runs: 10000; result: 0.8259118221071665
500 Hilly's; Func runs: 10000; result: 0.2631661675236262
=============================
5 Forest's; Func runs: 10000; result: 0.9714247249319152
25 Forest's; Func runs: 10000; result: 0.9091052022399436
500 Forest's; Func runs: 10000; result: 0.2847632249786224
=============================
5 Megacity's; Func runs: 10000; result: 0.7169230769230768
25 Megacity's; Func runs: 10000; result: 0.6378461538461538
500 Megacity's; Func runs: 10000; result: 0.10473846153846252
=============================
All score: 5.61920 (62.44%)

O resultado anterior parece mais prático e será mantido como a versão principal do algoritmo AAm modificado. A tabela de classificação com gradiente térmico atualizada mostra que o AAm agora ocupa uma honrosa 7ª posição. O algoritmo pode ser descrito como bem equilibrado, com boa convergência em funções de diferentes dimensões, sendo recomendado para a resolução de diversas tarefas.

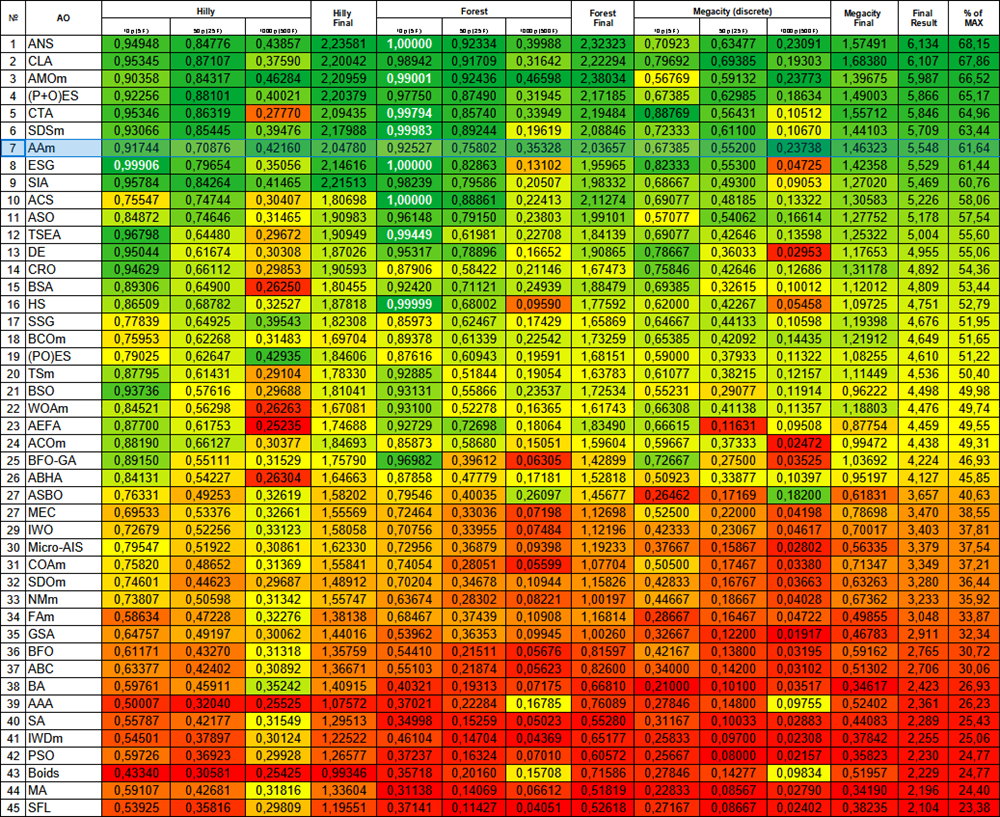
Figura 4. Graduação de cores dos algoritmos para os respectivos testes. Os resultados destacados em branco são maiores ou iguais a  0.99

Prós e contras do algoritmo AAA:

Prós:

1. Razoavelmente rápido.
2. Auto-adaptável.
   
3. Apenas um parâmetro externo.
4. Boa convergência.
5. Boa escalabilidade.
6. Implementação simples (apesar das descrições complexas dos autores).
   

Contras:

1. Tendência leve a ficar preso em funções de baixa dimensionalidade.
   

A adição de novos algoritmos à tabela de classificação começou a gerar dificuldades, tornando-a menos legível. Por isso, decidi limitar o número de algoritmos a serem comparados a 45, adotando agora um formato de eliminação direta. Para facilitar o acesso dos leitores a todas as análises, preparei um arquivo HTML com a lista de todos os algoritmos analisados e organizados conforme seu ranking na tabela. Esse arquivo já acompanha os artigos há algum tempo e reserva uma pequena surpresa para quem o abre pela primeira vez.

O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5