PythonとMQL5における局所的特徴量選択の適用

はじめに

金融市場の分析においては、市場の基礎的な状況が変化することで、指標の有効性も変わることがよくあります。たとえば、ボラティリティの変動により、市場のレジームが変わると、それまで信頼できていた指標が機能しなくなることがあります。このような変動性のために、トレーダーが使用する指標は多様化しています。なぜなら、どのような市場状況においても一貫して良好なパフォーマンスを示す単一の指標は存在しないからです。機械学習の観点からは、このような動的な市場環境に対応できる柔軟な特徴量選択手法が求められます。

一般的な特徴量選択アルゴリズムの多くは、特徴空間全体で予測性能が高い特徴量を優先します。これらの特徴量は、目的変数との関係が非線形であったり、他の特徴の影響を受けていたりする場合でも選ばれる傾向にあります。しかし、最新の非線形モデルでは、局所的に強い予測力を持つ特徴量や、特定の特徴量空間内で目的変数との関係が変化する特徴量から、有用な情報を引き出すことが可能です。そのため、このような大域的なバイアスは課題となる可能性があります。

本記事では、Narges Armanfard、James P. Reilly、Majid Komeiliによる論文「Local Feature Selection for Data Classification」で提案された局所特徴量選択アルゴリズムを取り上げます。この手法は、従来の選択手法では見落とされがちな、大域的には有用性が限定的であっても、局所的には高い予測力を持つ特徴を特定することを目的としています。まずアルゴリズムの概要を説明し、その後、Pythonによる実装を通じて、MetaTrader 5向けの分類モデルを構築する手順を解説します。

局所特徴量選択

機械学習の成功には、問題解決に寄与する有益な特徴量を選択することが不可欠です。教師あり分類においては、特徴量がデータのカテゴリを効果的に識別できることが求められます。しかし、有益でない特徴量はノイズを引き起こし、モデルの性能を低下させる可能性があるため、それらを見分けることはしばしば困難です。このため、特徴量選択は予測モデルの構築において重要な初期ステップとされています。

従来の手法は、すべてのデータに対して共通の最適な特徴量サブセットを求めるのに対し、局所特徴量選択(LFS: Local Feature Selection)は、特定の局所領域ごとに最適なサブセットを選択します。この柔軟性は、非定常データの扱いにおいて特に有効です。さらにLFSは、異なるサンプル間で使用される特徴量サブセットの違いを考慮する分類器を組み込んでいます。これは、クラス単位のクラスタリングを通じて実現され、クラス内距離を最小化しつつ、クラス間距離を最大化するような特徴量が選択されます。

このアプローチでは、重複する領域内で局所的に最適な特徴量サブスペースを識別し、各サンプルが複数の特徴量空間で表現されるようにします。この概念をより明確に理解するために、通信会社が顧客の解約（チャーン）を予測し、アカウントを閉鎖する可能性のある顧客を特定しようとするシナリオを考えてみましょう。同社は以下のようなさまざまな顧客属性（特徴量）を収集しています。

• 顧客在籍期間：顧客がどのくらいの期間、当社と契約しているか
• 月額料金：顧客が毎月支払っている金額
• 顧客の体重と身長
• カスタマーサービスへの問い合わせ回数：顧客がサポートに問い合わせた頻度

たとえば、長期間にわたって契約を続けている忠実な顧客を2人選んだ場合、上記の各特徴量において両者の差はごくわずかであることが予想されます。これは彼らが同じクラス（解約しない顧客）に属しているためです。一方で、長年の契約者と、契約後すぐに解約した顧客を比較すると、体重や身長にはそれほど差がないかもしれませんが、その他の関連性の高い予測変数（例：在籍期間やサポートへの連絡頻度）では明確な違いが見られる可能性があります。

忠実な顧客は在籍期間が長く、より高額なプランを選択しやすく、問題が発生した場合には解約せずにカスタマーサポートに連絡する傾向が強いでしょう。一方、体重や身長のような特徴量は平均的で、これらの顧客タイプを区別するうえで有効な手がかりにはなりません。

個々の特徴量に対して、顧客間の距離（たとえばユークリッド距離）をペアで分析することで、有効な予測変数はクラス間距離が大きく、無関係な特徴量はクラス間距離が小さいことが確認できます。したがって、クラス内距離が小さく、クラス間距離が大きいような特徴量が選択されることになります。

このようなアプローチは一見すると有効に見えますが、データ内の局所的な変動性を十分に捉えきれないという問題があります。これに対処するには、予測力が特徴量空間の異なる領域（局所領域）でどのように変化するかを考慮する必要があります。たとえば、2つのクラスを持つデータセットを考えてみましょう。このうち1つのクラスが、さらに2つの異なるサブセットに分かれているとします。このデータセットの特徴量x₁およびx₂を用いた散布図を想像すると、最初のサブセットはx₁によってクラス1と明確に分離できる一方で、x₂では難しいというケースがあります。逆に、2番目のサブセットではx₂による分離が有効であり、x₁では不十分です。

クラス間の分離のみを考慮すると、各サブセットで実際に有効なのはどちらか一方の特徴量だけであるにもかかわらず、アルゴリズムが誤ってx₁とx₂の両方を選択してしまう可能性があります。これは、アルゴリズムが各サブセット内の小さく重要な距離よりも、2つのサブセット間に存在する大域的に大きな距離を優先してしまうために起こります。この問題に対処するため、引用論文の著者は距離に対する重み付けスキームを導入しました。具体的には、距離が近いサンプル対には高い重みを、遠いサンプル対には低い重みを与えることで、クラス内の外れ値の影響を抑制することができます。このアプローチでは、クラスの所属情報（クラスメンバーシップ）と距離の大域的分布の両方が考慮されます。

要約すると、論文で提案されているLFSアルゴリズムは2つの要素があります。1番目の要素は、各サンプルごとに最適な特徴量のサブセットを選択する特徴量選択プロセスを含みます。2番目の要素は、推論時に、テストサンプルと各クラスとの局所的な類似度を評価するメカニズムを通じて分類をおこないます。

特徴量選択

このセクションでは、LFS法における学習手順を、少し数学的な記述を交えながら段階的に説明します。まず、訓練データの想定構造から始めます。局所特徴量選択はN個の訓練サンプル、Z種類のクラスラベル、およびM個の特徴量候補（予測子）からなるデータセットに対して実装されます。

訓練データは、行列Xとして表され、各行がサンプル、各列が異なる特徴量候補に対応します。つまり、行列XはN行M列の構造を持ちます。各サンプルは、Xの第i行としてX(i)と記述されます。クラスラベルは、別の列ベクトルYに格納されており、各ラベルはX内の対応するサンプル（行）にマッピングされます。

LFS法の目的は、各訓練サンプルX(i)に対して、どの特徴量がそのクラスラベルの決定に最も関連するかを示すM次元のバイナリベクトルF(i)を求めることです。すべてのサンプルについてF(i)を並べた行列Fは、Xと同じ次元になります。

アルゴリズムではユークリッド距離を用いて、現在のサンプルと同じクラスラベルを持つ他のサンプルとの平均距離を最小化し、異なるクラスラベルを持つサンプルとの平均距離を最大化することを目指します。加えて、距離には重みを導入することで、現在のサンプルと近傍にあるサンプルを優先的に扱うようにします。このために重み列ベクトルWを使用します。ただし、WやF(i)は初期状態では未知であるため、これらを同時に推定するために反復的な最適化手順が用いられます。

クラス内距離とクラス間距離の計算

以下のセクションで説明する各ステップは、最適なF(i)ベクトルを決定するために、単一のサンプルX(i)に対して実行される計算に関係します。プロセスは、まずFのすべての要素を0に初期化し、重みをすべて1に設定するところから始まります。次に、X(i)に関してクラス内距離およびクラス間距離を計算します。距離計算にF(i)ベクトルを組み込むことで、値が1に設定された、すなわち「関連があると判断された特徴量」のみが考慮されるようになります。数学的な取り扱いを簡便にするために、ユークリッド距離は2乗され、以下のような距離の計算式が導出されます。

囲まれた「×」の記号は、要素ごとの乗算（アダマール積）を表す演算子です。クラス内距離およびクラス間距離は、先ほどの式を用いて計算されますが、Xの異なるj番目の行要素を用いる点が異なります。クラス内距離は、サンプルX(i)と同じクラスラベルを持つX(j)に対して計算されます。

クラス間距離は、Y(i)とは異なるクラスラベルを持つj要素を使用して計算されます。

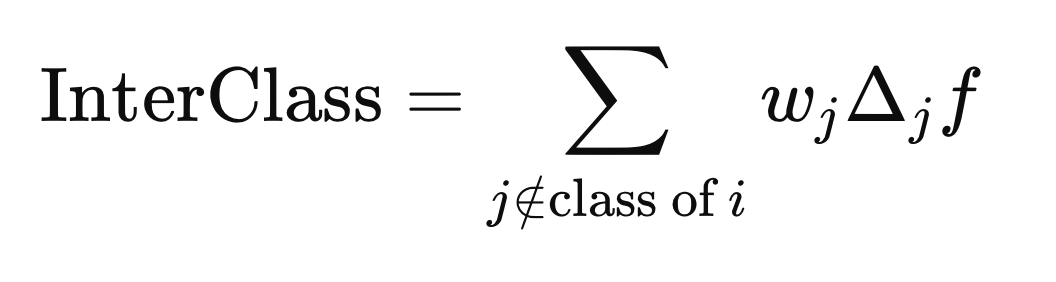
重みの計算

2つのサンプル間の距離を定義する際にFベクトルが用いられるとき、その距離はF(i)によって定義された行列空間内で測定されていると解釈されます。重み付けでは、クラスラベルが異なるためにサンプルにペナルティを課すべきではありません。F(i)はまだ最適ではないため、近傍の基準を定義するために選択された変数はまだ不明です。この問題に対処するために、引用された論文では、重みの改良の以前の反復から計算された重みを平均化する手法を採用しています。

2つのサンプル間の距離の定義にFベクトルが含まれる場合、それはF(i)によって定義された距離空間内で計算されます。最適な重みの計算は、以下の式のように、F(z)と呼ばれる別の距離空間で距離を定義することによって行われます。最適な重みの計算は、以下の式で示されるように、F(z)と呼ばれる別の距離空間で距離を定義することによって実行されます。

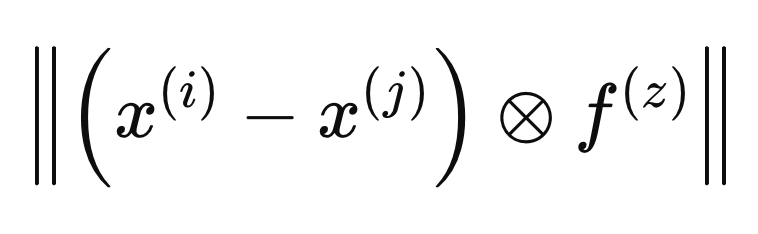
異なるクラスにあるという理由だけで重みがサンプルにペナルティを与えないようにするために、F(z)によって定義された距離空間内のX(i)と同じクラスの他のすべてのサンプル間の最小距離を計算します。

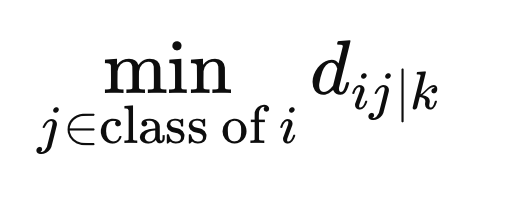
さらに、異なるクラスラベルを持つサンプルからX(i)までの最小距離を計算します。

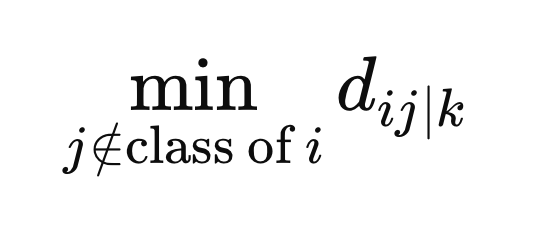
これらは重みを定義するために必要な最終値です。重みは、特定の距離空間zに対する距離と最小距離の差の負の指数関数として、すべての距離空間を通じて平均化することによって計算されます。

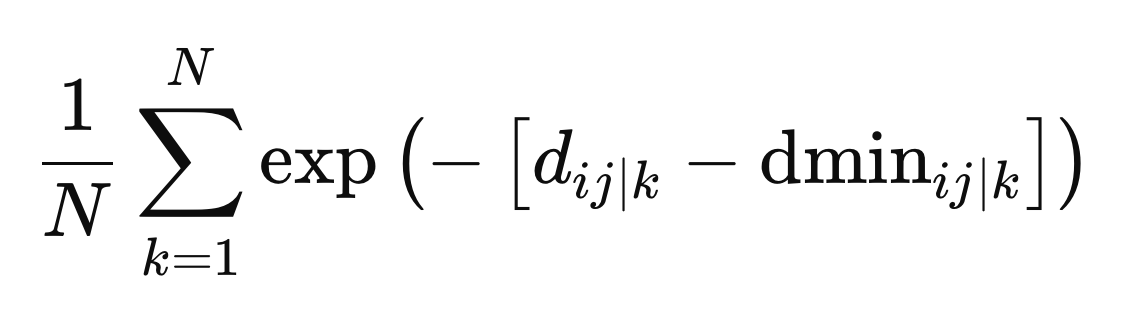
相反する目的

この段階では、最適な重みが求められ、クラス間分離とクラス内分離のバランスを取るという課題に取り組むことができます。具体的には、2つの相反する目的、つまり「クラス内分離を最小化する（同一クラス内のデータをできるだけ似たものにする）」と「クラス間分離を最大化する（異なるクラスをできるだけ異なるものにする）」という目的をどのように調整するかが問題となります。同じ予測子セットで両方を完璧に達成することは通常不可能です。

これらの相反する目標を調整するために有効なアプローチは、イプシロン制約法です。この方法では、まず1つの最適化問題（通常は最大化問題）を解決し、その後、最大化した関数が所定のしきい値を超えるように制約を加えて、最小化問題に取り組みます。

まず、クラス間の分離を最大化し、この関数の最大値を記録します。この最大値はイプシロン(ϵ)で表され、可能な限り最大のクラス間分離を示します。次に、パラメータβ（0から1の範囲）を使って、クラス内分離を最小化しますが、このときの制約として、「最小化後のクラス間分離がβϵ以上でなければならない」という条件がつきます。

パラメータβは、2つの目標間のバランスを取るための妥協要因として機能します。βが1の場合、クラス間分離が最優先され、βが0の場合はクラス内分離の最小化に焦点が移ります。両方の最適化タスクには共通して4つの制約が課せられます。

• Fのすべての要素は0以上1以下であること
• Fベクトルの要素の合計は、活性化できる予測子の最大数を制限するユーザー指定のハイパーパラメータ以下であること
• 各サンプルにおいて少なくとも1つの予測子が選ばれるよう、Fベクトルの要素の合計が1以上であること
  

クラス内最小化の際には、最初の最大化操作からの追加の制約があります。最大化された関数の値は、少なくともβとϵの積と同じかそれ以上である必要があります。

このように、目的関数と制約はすべて線形で構成されており、これはこの最適化問題が線形計画問題であることを意味します。標準的な線形計画問題は、超えてはならないしきい値を指定する制約に従って、目的関数を最大化することを目的としています。

線形計画法では、線形制約の下で線形目的関数を最適化します。通常「z」と表記される目的関数は、決定変数の線形結合として定義されます。制約は線形不等式または等式として表現され、決定変数の値を制限します。ユーザーが指定する制約に加えて、決定変数には暗黙的な非負制約があり、不等式の右辺にも非負制約が課されます。

標準形式では、決定変数が非負であり、制約は「以下」の不等式として表現されることが想定されていますが、これらの制限は変換によって緩和可能です。不等式の両辺に-1を掛けることで、「以上」の不等式や負の右辺を扱うことができます。また、決定変数に負の係数が含まれる場合には、新しい変数を導入することで正の係数に変換できます。

内点法は、特に大規模な最適化タスクを扱う際に、線形計画問題を効率的に解くアルゴリズムとして有効です。私たちのPython実装では、この手法を用いて最適なソリューションを効率よく見つけ出します。収束に達すると、最適なF(i)ベクトルが得られます。ただし、これらの値は必要な形式（1または0）にはなっていない点に注意が必要です。これは、LFS法の最終ステップで修正されます。

ベータ版試験

計算されたF(i)ベクトルの問題は、それがバイナリ値ではなく実数値で構成されていることです。LFS手順の目的は、各サンプルに対して最も関連性の高い変数を特定することであり、これは各要素が0または1のいずれかであるバイナリF行列によって表されます。値0は、対応する変数が無関係と見なされるか、スキップされることを意味します。

F(i)ベクトルの実数値をバイナリ値に変換するために、モンテカルロ法を用いて最適なバイナリ表現を探索します。これは、ユーザーが指定した回数だけプロセスを繰り返すことによって行われ、この回数はLFS法における重要なハイパーパラメータとなります。各反復では、各予測子候補を最初に1に設定したバイナリベクトルから開始し、連続値のF(i)をその予測子が選ばれる確率として用います。次に、このバイナリベクトルが最小化手続きの制約を満たしているかどうかを確認し、目的関数値を計算します。目的関数の値が最も小さかったバイナリベクトルが、最終的なF(i)ベクトルとして選択されます。

特徴量選択のための後処理

LFSは各サンプルごとに最適な予測子候補を個別に選択するため、単一の決定的な予測子セットを提示するのは現実的ではありません。この問題に対処するために、各予測子が最適なサブセットに含まれた回数を集計します。これにより、ユーザーは出現頻度に基づいてしきい値を設定し、最も頻繁に選ばれた予測子を最も関連性が高いものとして識別できます。重要なのは、このセット内で予測子が関連性を持つからといって、その予測子単独で有用であるとは限らず、他の予測子との相互作用の中で価値が生まれている可能性があるという点です。

これはLFSの大きな利点のひとつです。すなわち、単体では目立たないものの、他の予測子との組み合わせにおいて重要性を発揮するような変数を特定できる点です。このような前処理は、変数間の複雑な関係性を捉えるのに優れた、現代的な予測モデルにとって非常に有用です。LFSは、無関係な予測子を除去することでモデリングプロセスを簡素化し、最終的にモデルの性能を向上させることができます。

Python実装：LFSpy

このセクションでは、LFSアルゴリズムの実際の応用について説明します。まずは特徴量選択手法としての利用に焦点を当て、続いてデータ分類機能についても簡単に触れます。すべてのデモンストレーションは、特徴量選択とデータ分類の両方の機能を備えたLFSアルゴリズムの実装であるLFSpyパッケージを用いてPythonで実施します。このパッケージはPyPIで公開されており、詳細な情報もそちらで確認できます。

まず、LFSpyパッケージをインストールします。

pip install LFSpy

次に、LFSpyからLocalFeatureSelectionクラスをインポートします。

from LFSpy import LocalFeatureSelection

パラメトリックコンストラクタを呼び出すことによって、LocalFeatureSelectionのインスタンスを作成できます。

lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)

コンストラクタは次のオプションパラメータをサポートします。

パラメータ名	データ型	詳細
alpha	integer	すべての予測子候補のうち選択された予測子の最大数。デフォルト値は19です。
gamma	double	局所領域内で異なるクラスラベルを持つサンプルと同じクラスラベルを持つサンプルの比率を制御する許容レベル。デフォルト値は0.2です。
tau	integer	データセット全体の反復回数（従来の機械学習のエポック数に相当）。デフォルトは2ですが、この値を1桁の数字（通常は5以下）に設定することをお勧めします。
sigma	double	距離に基づいて観測の重み付けを制御します。値が1より大きい場合、重み付けが減少します。デフォルトは1です。
n_beta	integer	連続したFベクトルをその2進数に変換するときにテストされるベータ値の数。
nrrp	integer	ベータ試験の反復回数。この値は少なくとも500である必要があり、訓練データセットのサイズに応じて増加します。デフォルトは2000です。
knn	integer	特に分類タスクに適用されます。分類のために比較する最も近い近傍の数を指定します。デフォルト値は1です。

LFSpyクラスのインスタンスを初期化した後、少なくとも2つの入力パラメータ（候補予測子で構成される訓練サンプルの2次元行列と、対応するクラスラベルの1次元配列）を持つfit()メソッドを使用します。

lfs.fit(xtrain,ytrain)

モデルが適合されると、fstarを呼び出すことでF包含行列が返されます。この行列は、選択された特徴量を示す1と0で構成されています。なお、この行列は学習サンプルの配置に対して転置された形になっている点に注意してください。

fstar = lfs.fstar

predict()メソッドは、学習したモデルに基づいてテストサンプルを分類し、テストデータに対応するクラスラベルを返すために使用されます。

predicted_classes = lfs.predict(test_samples)

score()メソッドは、予測されたクラスラベルを既知のラベルと比較することによってモデルの精度を計算します。正しく分類されたテストサンプルの割合を返します。

accuracy = lfs.score(test_data,test_labels)

LFSpyの例

最初の実用的なデモンストレーションとして、[−1,1][−1,1]の範囲内で数千個の均一分布のランダム変数を生成します。これらの変数は、指定された列数の行列に配置されます。次に、任意の2つの列の値が両方とも負か両方とも正かに応じて、各行に対応する{0,1}ラベルのベクトルを作成します。このデモンストレーションの目的は、LFSメソッドがこのデータセット内で最も関連性の高い予測子を識別できるかどうかを判断することです。Fバイナリ包含行列で各予測変数が選択された回数（1で示される）を合計して結果を評価します。このテストを実装するコードを以下に示します。

import numpy as np
import pandas as pd
from LFSpy import LocalFeatureSelection
from timeit import default_timer as timer

#number of random numbers to generate
datalen = 500 

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our training data
xtrain = data
ytrain = class_labels

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#start timer
start = timer()

#train the model
lfs.fit(xtrain,ytrain)

#output training duration
print("Training done in ", timer()-start , " seconds. ")

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
ibins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0])

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(original_crits.shape[0]):
   print( f" Variable at column {i}, selected {original_crits[i]} %")

以下はLFSdemo.pyを実行したときの出力です。

Training done in  45.84896759999992  seconds. 
Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable at column 0, selected 19.0 %
Python   Variable at column 1, selected 81.0 %
Python   Variable at column 2, selected 87.0 %
Python   Variable at column 3, selected 20.0 %
Python   Variable at column 4, selected 18.0 %

クラスを予測する上での役割が同じであるにもかかわらず、関連する変数の1つが他の変数よりわずかに頻繁に選択されたのは興味深いことです。これは、データ内の微妙なニュアンスが選択プロセスに影響を与えている可能性があることを示唆しています。明らかに、両方の変数が無関係な予測変数よりも一貫して頻繁に選ばれており、クラスを決定する上での重要性を示しています。このアルゴリズムの実行速度が比較的遅いのは、シングルスレッドで動作しているためであり、大規模なデータセットに対してはパフォーマンスが低下する可能性があります。

データ分類のためのLFS

LFSの局所的な性質を考慮すると、従来の大域的に偏った特徴量選択方法と比べて、分類器の構築にはより多くの労力が必要です。参照されている論文では提案された分類器アーキテクチャについて説明されていますが、ここでは詳述しません。詳細について興味のある読者は引用された論文を参照することをお勧めします。このセクションでは、実装に焦点を当てます。

LocalFeatureSelectionクラスのpredict()メソッドは、クラス間の類似性を評価します。このメソッドは、訓練データの構造に一致するテストデータを受け取り、訓練されたLFSモデルによって学習されたパターンに基づいて予測されたクラスラベルを返します。次のコードデモンストレーションでは、前回のスクリプトを拡張してLFS分類器モデルを構築し、それをJSON形式でエクスポートし、MQL5スクリプトを使用してロードした後、サンプル外データセットを分類します。LFSモデルをエクスポートするためのコードはJsonModel.pyに含まれており、このファイルはLocalFeatureSelectionモデルの状態とパラメータをJSONファイルにシリアル化するlfspy2json()関数を定義します。これにより、モデルをMQL5コードで簡単に読み取り、使用できる形式で保存でき、MetaTrader 5との統合が容易になります。以下に完全なコードを示します。

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com

from LFSpy import LocalFeatureSelection
import json 

MQL5_FILES_FOLDER = "MQL5\\FILES"
MQL5_COMMON_FOLDER = "FILES"

def lfspy2json(lfs_model:LocalFeatureSelection, filename:str):
    """
    function export a LFSpy model to json format 
    readable from MQL5 code.
    
    param: lfs_model should be an instance of LocalFeatureSelection
    param: filename or path to file where lfs_model
    parameters will be written to
    
    """
    if not isinstance(lfs_model,LocalFeatureSelection):
        raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "alpha":lfs_model.alpha,
            "gamma":lfs_model.gamma,
            "tau":lfs_model.tau,
            "sigma":lfs_model.sigma, 
            "n_beta":lfs_model.n_beta,
            "nrrp":lfs_model.nrrp,
            "knn":lfs_model.knn,
            "rr_seed":lfs_model.rr_seed,
            "num_observations":lfs_model.training_data.shape[1],
            "num_features":lfs_model.training_data.shape[0],
            "training_data":lfs_model.training_data.tolist(),
            "training_labels":lfs_model.training_labels.tolist(),
            "fstar":lfs_model.fstar.tolist()
          }
          
    
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

この関数は、LocalFeatureSelectionオブジェクトとファイル名を入力として受け取ります。モデルのパラメータをJSONオブジェクトとしてシリアル化し、指定されたファイル名で保存します。また、このモジュールは、標準的なMetaTrader 5インストールにおいてアクセス可能なフォルダーのディレクトリパスを表す2つの定数、MQL5_FILES_FOLDERとMQL5_COMMON_FOLDERも定義します。これは、MetaTrader 5との統合のための解決策の一部に過ぎません。残りの部分はMQL5コードで実装されており、その内容はlfspy.mqhに記載されています。このインクルードファイルには、推論の目的でJSON形式で保存されたLFSモデルを読み込むためのClfspyクラスの定義が含まれています。以下に完全なコードを示します。

//+------------------------------------------------------------------+
//|                                                        lfspy.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>
//+------------------------------------------------------------------+
//|structure of model parameters                                     |
//+------------------------------------------------------------------+
struct LFS_PARAMS
  {
   int               alpha;
   int               tau;
   int               n_beta;
   int               nrrp;
   int               knn;
   int               rr_seed;
   int               sigma;
   ulong             num_features;
   double            gamma;
  };
//+------------------------------------------------------------------+
//|  class encapsulates LFSpy model                                  |
//+------------------------------------------------------------------+
class Clfspy
  {
private:
   bool              loaded;
   LFS_PARAMS        model_params;
   matrix train_data,
          fstar;
   vector            train_labels;
   //+------------------------------------------------------------------+
   //|  helper function for parsing model from file                     |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      model_params.alpha = (int)jsonmodel["alpha"].ToInt();
      model_params.tau = (int)jsonmodel["tau"].ToInt();
      model_params.sigma = (int)jsonmodel["sigma"].ToInt();
      model_params.n_beta = (int)jsonmodel["n_beta"].ToInt();
      model_params.nrrp = (int)jsonmodel["nrrp"].ToInt();
      model_params.knn = (int)jsonmodel["knn"].ToInt();
      model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt();
      model_params.gamma = jsonmodel["gamma"].ToDbl();

      ulong observations = (ulong)jsonmodel["num_observations"].ToInt();
      model_params.num_features = (ulong)jsonmodel["num_features"].ToInt();

      if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) ||
         !fstar.Resize(model_params.num_features,observations))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }


      for(int i=0; i<int(model_params.num_features); i++)
        {
         for(int j = 0; j<int(observations); j++)
           {
            if(i==0)
               train_labels[j] = jsonmodel["training_labels"][j].ToDbl();
            train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl();
            fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl();
           }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| helper classification function                                   |
   //+------------------------------------------------------------------+
   matrix            classification(matrix &testing_data)
     {
      int N = int(train_labels.Size());
      int H = int(testing_data.Cols());

      matrix out(H,2);

      for(int i = 0; i<H; i++)
        {
         vector column = testing_data.Col(i);
         vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn);
         if(!out.Row(result,i))
           {
            Print(__FUNCTION__, " row insertion failure ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| internal feature classification function                         |
   //+------------------------------------------------------------------+
   vector            class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn)
     {
      int N = int(targets.Size());
      int n_nt_cls_1 = (int)targets.Sum();
      int n_nt_cls_2 = N - n_nt_cls_1;
      int M = int(patterns.Rows());
      int NC1 = 0;
      int NC2 = 0;
      vector S = vector::Zeros(N);

      S.Fill(double("inf"));

      vector NoNNC1knn = vector::Zeros(N);
      vector NoNNC2knn = vector::Zeros(N);
      vector NoNNC1 = vector::Zeros(N);
      vector NoNNC2 = vector::Zeros(N);
      vector radious = vector::Zeros(N);
      double r = 0;
      int k = 0;
      for(int i = 0; i<N; i++)
        {
         vector fs = f_star.Col(i);
         matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
         vector testpr = test * fs;
         vector mtestpr = (-1.0 * testpr);
         matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false);
         vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0)));
         vector min1 = dist;
         np::sort(min1);
         vector min_uniq = np::unique(min1);
         int m = -1;
         int no_nereser = 0;
         vector NN(dist.Size());
         while(no_nereser<int(knn))
           {
            m+=1;
            double a1  = min_uniq[m];
            for(ulong j = 0; j<dist.Size(); j++)
               NN[j]=(dist[j]<=a1)?1.0:0.0;
            no_nereser = (int)NN.Sum();
           }
         vector bitNN = np::bitwiseAnd(NN,targets);
         vector Not = np::bitwiseNot(targets);
         NoNNC1knn[i] = bitNN.Sum();
         bitNN = np::bitwiseAnd(NN,Not);
         NoNNC2knn[i] = bitNN.Sum();
         vector A(fs.Size());
         for(ulong v =0; v<A.Size(); v++)
            A[v] = (fs[v]==0.0)?1.0:0.0;
         vector f1(patterns.Cols());
         vector f2(patterns.Cols());
         if(A.Sum()<double(M))
           {
            for(ulong v =0; v<A.Size(); v++)
               A[v] = (A[v]==1.0)?0.0:1.0;
            matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols());
            amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false);
            matrix patternsp = patterns*amask;
            vector testp = test*(amask.Col(0));
            vector testa = patternsp.Col(i) - testp;
            vector col = patternsp.Col(i);
            matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false);
            double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum()));
            vector Dist_pat  = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0)));
            vector eerep = Dist_pat;
            np::sort(eerep);
            int remove = 0;
            if(targets[i] == 1.0)
              {
               vector unq = np::unique(eerep);
               k = -1;
               NC1+=1;
               if(remove!=1)
                 {
                  int Next = 1;
                  while(Next == 1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() - 1.0;
                     double nocls2clst = f2tn.Sum();
                     if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum() - 1.0;
                        nocls2clst = f2tn.Sum();
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC1[i]>NoNNC2[i])
                        S[i] = 1.0;
                    }
                 }
              }
            if(targets[i] == 0.0)
              {
               vector unq = np::unique(eerep);
               k=-1;
               NC2+=1;
               int Next;
               if(remove!=1)
                 {
                  Next =1;
                  while(Next==1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() ;
                     double nocls2clst = f2tn.Sum() -1.0;
                     if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum();
                        nocls2clst = f2tn.Sum() -1.0;
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC2[i]>NoNNC1[i])
                        S[i] = 1.0;
                    }
                 }
              }
           }
         radious[i] = r;
        }
      vector q1 = vector::Zeros(N);
      vector q2 = vector::Zeros(N);
      for(int i = 0; i<N; i++)
        {
         if(NoNNC1[i] > NoNNC2knn[i])
            q1[i] = 1.0;
         if(NoNNC2[i] > NoNNC1knn[i])
            q2[i] = 1.0;
        }

      vector ntargs = np::bitwiseNot(targets);
      vector c1 = np::bitwiseAnd(q1,targets);
      vector c2 = np::bitwiseAnd(q2,ntargs);

      double sc1 = c1.Sum()/NC1;
      double sc2 = c2.Sum()/NC2;

      if(sc1==0.0 && sc2==0.0)
        {
         q1.Fill(0.0);
         q2.Fill(0.0);

         for(int i = 0; i<N; i++)
           {
            if(NoNNC1knn[i] > NoNNC2knn[i])
               q1[i] = 1.0;
            if(NoNNC2knn[i] > NoNNC1knn[i])
               q2[i] = 1.0;

            if(!targets[i])
               ntargs[i] = 1.0;
            else
               ntargs[i] = 0.0;
           }

         c1 = np::bitwiseAnd(q1,targets);
         c2 = np::bitwiseAnd(q2,ntargs);

         sc1 = c1.Sum()/NC1;
         sc2 = c2.Sum()/NC2;
        }

      vector out(2);

      out[0] = sc1;
      out[1] = sc2;

      return out;
     }
public:
   //+------------------------------------------------------------------+
   //|    constructor                                                   |
   //+------------------------------------------------------------------+
                     Clfspy(void)
     {
      loaded = false;
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+
                    ~Clfspy(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  load a LFSpy trained model from file                            |
   //+------------------------------------------------------------------+
   bool              load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false)
     {
      loaded = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();
      if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         loaded = fromJSON(js);
        }
      return loaded;
     }
   //+------------------------------------------------------------------+
   //|   make a prediction based specific inputs                        |
   //+------------------------------------------------------------------+
   vector            predict(matrix &inputs)
     {
      if(!loaded)
        {
         Print(__FUNCTION__, " No model available, Load a model first before calling this method ");
         return vector::Zeros(1);
        }

      if(inputs.Cols()!=train_data.Rows())
        {
         Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)");
         return vector::Zeros(1);
        }

      matrix testdata = inputs.Transpose();

      matrix probs = classification(testdata);
      vector classes = vector::Zeros(probs.Rows());

      for(ulong i = 0; i<classes.Size(); i++)
         if(probs[i][0] > probs[i][1])
            classes[i] = 1.0;

      return classes;

     }
   //+------------------------------------------------------------------+
   //| get the parameters of the loaded model                           |
   //+------------------------------------------------------------------+
   LFS_PARAMS        getmodelparams(void)
     {
      return model_params;
     }


  };
//+------------------------------------------------------------------+

このクラスでは、ユーザーが理解する必要がある主なメソッドが2つあります。

• load()メソッド：エクスポートされたLFSモデルを指すファイル名を入力として受け取る
• predict()メソッド：必要な数の列を持つ行列を受け取り、入力行列の行数に対応するクラスラベルのベクトルを返す
  

実際にどのように機能するかを見てみましょう。まずはPythonコードから始めます。ファイルLFSmodelExportDemo.pyは、ランダムに生成された数値を使用してサンプル内およびサンプル外のデータセットを準備します。サンプル外データはCSVファイルとして保存されます。LFSモデルはサンプル内データを使用して訓練され、その後シリアル化されJSON形式で保存されます。次に、サンプル外データを使用してモデルをテストし、その結果を記録して、後でMetaTrader 5で実行した同じテストと比較できるようにします。Pythonコードを以下に示します。

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports
import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER
from os import path
from sklearn.metrics import accuracy_score, classification_report

#initialize MT5 terminal
if not mt5.initialize():
    print("MT5 initialization failed ")
    mt5.shutdown()
    exit() # stop the script if mt5 not initialized
  
#we want to get the path to the MT5 file sandbox
#initialize TerminalInfo instance    
terminal_info = mt5.terminal_info()

#model file name
filename = "lfsmodel.json"

#build the full path
modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename)

#number of random numbers to generate
datalen = 1000

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our data
train_size = 100
xtrain = data[:train_size,:]
ytrain = class_labels[:train_size]

#load testing data (out of sample)
test_data = data[train_size:,:]
test_labels = class_labels[train_size:]

#here we prepare the out of sample data for export using pandas
#the data will be exported in a single csv file
colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])]
testdata = pd.DataFrame(test_data,columns=colnames)

#the last column will be the target labels
testdata["c_labels"]=test_labels

#display first 5 samples
print("Out of sample dataframe head \n", testdata.head())
#display last 5 samples
print("Out of sample dataframe tail \n", testdata.tail())

#build the full path of the csv file
testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv")

#try save the file
try:
    testdata.to_csv(testdatafilepath)
except Exception as e:
    print(" Error saving iris test data ")
    print(e) 
else:
    print(" test data successfully saved to csv file ")  

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#train the model
lfs.fit(xtrain,ytrain)

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
bins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0])
index = np.argsort(percents)[::-1]

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(percents.shape[0]):
   print(f" Variable  {colnames[index[i]]}, selected {percents[index[i]]} %")


#conduct out of sample test of trained model
accuracy = lfs.score(test_data,test_labels)
print(f" Out of sample accuracy is {accuracy*100.0} %")


#export the model
try:
    lfspy2json(lfs,modelfilepath)
except Exception as e:
    print(" Error saving lfs model ")
    print(e)
else:
   print("lfs model saved to \n ", modelfilepath)

次に、MetaTrader 5スクリプト「LFSmodelImportDemo.mq5」に焦点を移します。ここでは、Pythonスクリプトによって生成されたサンプル外データを読み取り、訓練済みのモデルを読み込みます。次に、サンプル外データセットをテストし、その結果をPythonテストから取得された結果と比較します。MQL5コードを以下に示します。

//+------------------------------------------------------------------+
//|                                           LFSmodelImportDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<lfspy.mqh>
//script inputs
input string OutOfSampleDataFile = "testdata.csv";
input bool   OutOfSampleDataInCommonFolder = false;
input string LFSModelFileName = "lfsmodel.json";
input bool   LFSModelInCommonFolder = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder);
   
   if(testdata.Rows()<1)
    {
     Print(" failed to read csv file ");
     return;
    }
    
   
   vector testlabels = testdata.Col(testdata.Cols()-1);
   testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1);
   
  
   Clfspy lfsmodel;
   
   if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder))
    {
     Print(" failed to load the iris lfs model ");
     return;
    }
    
   vector y_pred = lfsmodel.predict(testdata);
   
   vector check = MathAbs(testlabels-y_pred);
   
   Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %");
  }
//+------------------------------------------------------------------+

以下は、Pythonスクリプト「LFSmodelExportDemo.py」を実行したときの出力です。

Python  Out of sample dataframe head 
Python         var_1     var_2     var_3     var_4     var_5  c_labels
Python  0  0.337773 -0.210114 -0.706754  0.940513  0.434695         1
Python  1 -0.009701 -0.119561 -0.904122 -0.409922  0.619245         1
Python  2  0.442703  0.295811  0.692888  0.618308  0.682659         1
Python  3  0.694853  0.244405 -0.414633 -0.965176  0.929655         0
Python  4  0.120284  0.247607 -0.477527 -0.993267  0.317743         0
Python  Out of sample dataframe tail 
Python          var_1     var_2     var_3     var_4     var_5  c_labels
Python  95  0.988951  0.559262 -0.959583  0.353533 -0.570316         0
Python  96  0.088504  0.250962 -0.876172  0.309089 -0.158381         0
Python  97 -0.215093 -0.267556  0.634200  0.644492  0.938260         0
Python  98  0.639926  0.526517  0.561968  0.129514  0.089443         1
Python  99 -0.772519 -0.462499  0.085293  0.423162  0.391327         0
Python  test data successfully saved to csv file 

Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable  var_3, selected 87.0 %
Python   Variable  var_2, selected 81.0 %
Python   Variable  var_4, selected 20.0 %
Python   Variable  var_1, selected 19.0 %
Python   Variable  var_5, selected 18.0 %
Python   Out of sample accuracy is 92.0 %
Python  lfs model saved to 
Python    C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json

以下は、MQL5スクリプト「LFSmodelImportDemo.mq5」を実行したときの出力です。

LFSmodelImportDemo (BTCUSD,D1)  Accuracy is 92.0 %

結果を比較すると、両方のプログラムからの出力が一致しており、モデルのエクスポート方法が期待どおりに機能していることがわかります。

結論

局所特徴量選択（LFS）は、特に金融市場のような動的な環境に適した革新的な特徴量選択のアプローチを提供します。LFSは、局所的に関連する特徴を識別することで、単一の大域特徴量セットに依存する従来の方法の制限を克服します。このアルゴリズムは、さまざまなデータパターンへの適応性、非線形関係の管理能力、相反する目的のバランスを取る能力を備えており、機械学習モデルを構築するための貴重なツールとなります。LFSpyパッケージはLFSの実用的な実装を提供しますが、特に大規模なデータセットにおいて、計算効率をさらに最適化できる余地があります。結論として、LFSは複雑で進化するデータを特徴とする分野における分類タスクに対して、有望なアプローチを提供します。

ファイル名	詳細
Mql5/include/np.mqh	さまざまな行列およびベクトルユーティリティ関数の一般的な定義を含むインクルードファイル
Mql5/include/lfspy.mqh	MetaTrader 5プログラムでLFSモデル推論機能を提供するClfspyクラスの定義を含むインクルードファイル
Mql5/scripts/JsonModel.py	LFSモデルをJSON形式でエクスポートできるようにする関数の定義を含むローカルPythonモジュール
Mql5/scripts/LFSdemo.py	ランダム変数を使用した特徴量選択にLocalFeatureSelectionクラスを使用する方法を示すPythonスクリプト
Mql5/scripts/LFSmodelExportDemo.py	MetaTrader 5で使用するためにLFSモデルをエクスポートする方法を示すPythonスクリプト
Mql5/scripts/LFSmodelImportDemo.mq5	エクスポートされたLFSモデルをMetaTrader 5プログラムにロードして使用する方法を示すMQL5スクリプト