Algoritmo de otimização de migração animal (AMO)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

Migração animal: harmonia e estratégia da natureza. Os animais geralmente migram entre locais de invernada e reprodução, seguindo rotas que se desenvolveram ao longo de séculos de evolução. Essas viagens sazonais não são deslocamentos aleatórios, mas sim trajetórias cuidadosamente planejadas que levam a regiões mais favoráveis para sua sobrevivência e reprodução. Dependendo da estação do ano, os animais se deslocam em busca de alimento, abrigo e condições adequadas para a reprodução, guiados pelas necessidades naturais de seu grupo e pelos instintos que os movem. Cada jornada representa não apenas uma luta pela sobrevivência, mas também uma manifestação de harmonia com a natureza, na qual cada indivíduo desempenha um papel único no ecossistema.

Por exemplo, as renas do norte migram por grandes distâncias em busca de melhores pastagens, enquanto aves como grous e gansos realizam longos voos entre locais de invernada e ninhos, utilizando rotas específicas transmitidas de geração em geração. Essas migrações não apenas garantem a sobrevivência das espécies, mas também sustentam o ecossistema como um todo, contribuindo para a polinização de plantas e a dispersão de sementes.

A inspiração vem da natureza. O algoritmo AMO (Animal Migration Optimization) foi proposto em 2013 pelo pesquisador Xiantao Li. A ideia principal desse algoritmo é modelar o processo de migração sazonal dos animais em busca de condições ideais para sobrevivência e reprodução na natureza. Ele se baseia na observação do comportamento de animais migratórios, como aves, peixes e mamíferos. Esses animais se deslocam sazonalmente entre locais de invernada e reprodução, seguindo regras naturais de interação desenvolvidas durante a migração.

O algoritmo AMO imita três componentes principais do deslocamento dos animais por longas distâncias: evitar colisões com vizinhos, mover-se na mesma direção que o grupo (bando) e manter uma distância adequada entre os indivíduos. Esses princípios não apenas ajudam a evitar conflitos, mas também sustentam o comportamento coletivo, essencial para a sobrevivência na natureza selvagem.

Etapas de otimização no algoritmo AMO. O algoritmo incorpora dois estágios principais de otimização em uma única iteração:

• Processo de migração: durante essa fase, a posição do indivíduo é atualizada levando em conta seus vizinhos.
  
• Atualização da população: nesta fase, ocorre a substituição parcial de indivíduos por novos, com uma probabilidade que depende da posição do indivíduo no grupo.

A modelagem do comportamento coletivo dos animais migratórios pode ser uma abordagem eficiente para resolver problemas complexos de otimização. O algoritmo tenta equilibrar a exploração do espaço de busca e a exploração das melhores soluções encontradas, imitando os processos naturais que ocorrem na natureza.

2. Implementação do algoritmo

No modelo algorítmico da migração animal, a principal ideia é a criação de "zonas" concêntricas ao redor de cada animal. Na zona de repulsão, o animal central busca se afastar de seus vizinhos para evitar colisões. O algoritmo de migração animal, segundo os autores, é dividido em dois principais processos:

1. Processo de migração animal Para descrever a vizinhança restrita dos indivíduos, é utilizada uma topologia em anel. Por conveniência, o tamanho da vizinhança é definido como cinco para cada dimensão. A topologia da vizinhança permanece fixa e é determinada com base nos índices dos indivíduos na população. Se o índice de um animal for "j", seus vizinhos terão os índices [j - 2, j - 1, j, j + 1 e j + 2]. Caso o índice do animal seja "1", seus vizinhos serão [N - 1, N, 1, 2, 3], e assim sucessivamente. Após a formação da topologia de vizinhança, um vizinho é selecionado aleatoriamente, e a posição do indivíduo é atualizada levando em conta o posicionamento desse vizinho. Essa é a descrição dada pelos autores do algoritmo original. No entanto, a restrição no número de vizinhos pode ser parametrizada no algoritmo, permitindo a realização de experimentos para encontrar o número ideal de vizinhos a fim de garantir a máxima eficiência do algoritmo.

2. Processo de atualização da população No processo de atualização da população, o algoritmo simula como alguns animais deixam o grupo enquanto outros se juntam à população. Os indivíduos podem ser substituídos por novos animais com uma probabilidade "p", que é definida com base na qualidade da função de aptidão. A população é ordenada de forma decrescente conforme os valores da função de aptidão, o que significa que a probabilidade de um indivíduo com a melhor aptidão ser substituído é 1/N, enquanto a de um indivíduo com a pior aptidão é 1.

Os processos de migração animal e atualização da população, conforme a versão do autor, podem ser descritos de forma algorítmica conforme apresentado abaixo.

Processo de migração animal:

1. Para cada animal:    a. Determinar a vizinhança topológica do animal (5 vizinhos mais próximos).
   b. Escolher um vizinho aleatório da lista de vizinhos.    
   c. Atualizar a posição do animal na direção do vizinho selecionado pela fórmula:
      x_j_new = x_j_old + r * (x_neighbor - x_j_old), onde:

• x_j_new — nova posição do j-ésimo animal,
  
• x_j_old — posição atual,
• x_neighbor — posição do vizinho selecionado,
• r — número aleatório de uma distribuição normal.
  

   d. Avaliação da nova posição do animal utilizando a função objetivo.

Processo de atualização da população:

1. Ordenar os animais de acordo com os valores da função objetivo em ordem decrescente. 2. Para cada animal:    a. Calcular a probabilidade de substituição do animal por um novo animal aleatório:

      p = 1.0 - (1.0 / (x + 1)), onde x é o ranking (índice) do i-ésimo animal na lista ordenada.

   b. Se um número aleatório for menor que p, substituir o animal (modificar a coordenada para a média das coordenadas de dois animais aleatoriamente selecionados da população).    c. Caso contrário, o animal permanece inalterado.

3. Avaliação da nova população utilizando a função objetivo.

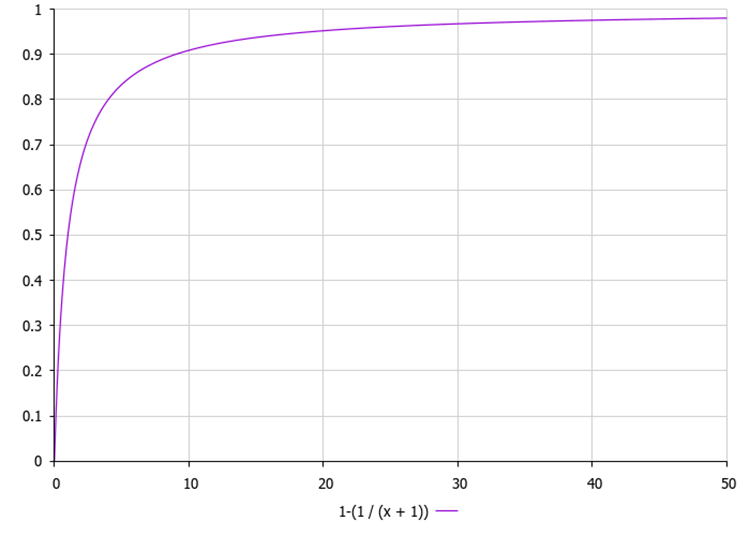
Figura 1. Gráfico da probabilidade de alteração de um indivíduo, dependendo de sua posição na população, onde "x" representa o índice do indivíduo na população.

Agora, passamos à escrita do pseudocódigo do algoritmo de migração animal AMO.

1. Inicialização da população de animais com posições aleatórias.

2. Laço principal:

   a. Para cada animal:

      Determinar a vizinhança topológica.
      Selecionar um vizinho aleatório.
      Atualizar a posição do animal na direção do vizinho.
      Avaliar a nova posição.

   b. Ordenar a população com base nos valores da função objetivo.

   c. Substituir probabilisticamente os piores indivíduos por novos.

   d. Avaliar a população atualizada.

   e. Atualizar a melhor solução encontrada.

3. Repetir a partir do passo 2 até que se atinja o critério de parada estabelecido.

Agora que compreendemos o algoritmo, podemos seguir para a implementação do código. Vamos analisar detalhadamente a classe "C_AO_AMO":

1. A classe "C_AO_AMO" herda da classe base "C_AO", permitindo o uso de suas funcionalidades e sua ampliação.

2. No construtor, são definidas as principais características do algoritmo, como nome, descrição e referência ao artigo. Além disso, são inicializados os parâmetros do algoritmo, incluindo o tamanho da população, o desvio padrão e o número de vizinhos.

3. popSize, deviation, neighborsNumberOnSide — variáveis que determinam o tamanho da população, o desvio padrão e a quantidade de vizinhos de cada lado que serão considerados na migração.

4. SetParams — método responsável por atualizar os parâmetros do algoritmo com base nos valores armazenados no array "params".

5. Init — método de inicialização, que recebe arrays para valores mínimos e máximos do intervalo, passos e número de épocas. 

6. Moving() — método que gerencia o deslocamento dos agentes no espaço de busca. "Revision()" — método que verifica e atualiza o estado dos agentes na população.

7. S_AO_Agent population [] — array que armazena a população atual de agentes (animais). "S_AO_Agent pTemp []" — array temporário utilizado para ordenação da população.

8. GetNeighborsIndex — método privado utilizado para obter os índices dos vizinhos de um agente específico.

A classe "C_AO_AMO" implementa o algoritmo de otimização baseado na migração animal, fornecendo os métodos e parâmetros necessários para sua configuração e execução. Ela herda funcionalidades da classe base, permitindo sua ampliação e modificação conforme os requisitos da tarefa.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AMOm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AMOm () { }
  C_AO_AMOm ()
  {
    ao_name = "AMOm";
    ao_desc = "Animal Migration Optimization M";
    ao_link = "https://www.mql5.com/en/articles/15543";

    popSize               = 50;   // Population size
    deviation             = 8;
    neighborsNumberOnSide = 10;

    ArrayResize (params, 3);

    params [0].name = "popSize";               params [0].val = popSize;

    params [1].name = "deviation";             params [1].val = deviation;
    params [2].name = "neighborsNumberOnSide"; params [2].val = neighborsNumberOnSide;
  }

  void SetParams ()
  {
    popSize               = (int)params [0].val;

    deviation             = params      [1].val;
    neighborsNumberOnSide = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double deviation;
  int    neighborsNumberOnSide;

  S_AO_Agent population []; // Animal population
  S_AO_Agent pTemp      []; // Temporary animal population

  private: //-------------------------------------------------------------------
  int   GetNeighborsIndex (int i);
};
//——————————————————————————————————————————————————————————————————————————————

A seguir, analisaremos o código do método "Init" da classe "C_AO_AMO". Descrição de cada parte do método:

1. rangeMinP [], rangeMaxP [], rangeStepP [] — arrays para definir os valores mínimos e máximos dos intervalos dos parâmetros a serem otimizados e seus passos.

2. O método "StandardInit" realiza a inicialização padrão com base nos intervalos fornecidos.

3. Ajuste do tamanho dos arrays "population" e "pTemp" para "popSize".

4. A inicialização dos agentes percorre todos os elementos do array "population", inicializando cada agente utilizando o método "Init", passando o número de coordenadas "coords". 

5. Se todas as operações forem concluídas com sucesso, o método retorna "true".

O método "Init" da classe "C_AO_AMO" é responsável pela inicialização da população de agentes, levando em conta os intervalos e parâmetros definidos.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize);
  ArrayResize (pTemp,      popSize);

  for (int i = 0; i < popSize; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Em seguida, analisaremos o método "Moving" da classe "C_AO_AMO", que gerencia o deslocamento dos agentes na população. Principais partes do código:

1. Verificação do estado "revision":

• Se "revision" for "false", significa que o método está sendo chamado pela primeira vez ou após um reset. Nesse caso, a população é inicializada.
• Para cada indivíduo da população (de "0" até "popSize") e para cada coordenada (de "0" até "coords"), são gerados valores aleatórios dentro do intervalo permitido ("rangeMin" e "rangeMax").
• Esses valores são ajustados utilizando a função "SeInDiSp", que os corrige conforme o passo definido ("rangeStep").

2. Definição do flag "revision":

• Após a inicialização, "revision" é definido como "true", e o método é finalizado.

3. Laço principal de migração:

• Se "revision" for "true", o método segue para a lógica principal da migração.
• Para cada indivíduo, ocorre uma nova iteração pelas coordenadas.
• O método "GetNeighborsIndex(i)" é usado para obter o índice do vizinho que será comparado com o indivíduo atual.
• O "dist" (distância) entre os valores das coordenadas do vizinho e do indivíduo é calculado.
• Com base nessa distância, são determinadas as fronteiras mínima e máxima ("min" e "max") dentro das quais a nova coordenada será definida.

4. Correção dos valores:

• Se as fronteiras calculadas estiverem fora dos limites aceitáveis, elas são ajustadas considerando "rangeMin" e "rangeMax".
• O novo valor da coordenada é gerado com base em uma distribuição normal, utilizando a função "GaussDistribution", levando em conta o desvio padrão "deviation".
• Como no primeiro caso, o novo valor também é ajustado através da função "SeInDiSp".

O método "Moving" é responsável por atualizar as posições dos agentes com base nos seus vizinhos e fatores aleatórios. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    ind1    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;

  for (int i = 0; i < popSize; i++)
  { 
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = a [i].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

A seguir, o código apresenta o método "Revision" da classe "C_AO_AMO". Analisemos cada parte:

1. Busca do melhor indivíduo:

• A variável "ind" é usada para armazenar o índice do indivíduo com a melhor função de aptidão ("f").
• O código percorre toda a população (de "0" até "popSize") e atualiza o valor "fB", caso o indivíduo atual tenha um valor de função superior.
• Se for encontrado um melhor indivíduo, suas características (coordenadas) são copiadas para o array "cB".

2. Laço principal de modificação da população:

• Para cada indivíduo da população (de "0" até "popSize"), a probabilidade "prob" é calculada com base no índice "i".
• Para cada coordenada (de "0" até "coords"), ocorre um teste aleatório comparando com a probabilidade "prob".
• Se um número aleatório for menor que "prob", dois indivíduos aleatórios "ind1" e "ind2" são escolhidos.
• Caso os dois indivíduos sejam iguais, "ind2" é incrementado para evitar a seleção do mesmo indivíduo.
• O novo valor da coordenada do indivíduo atual é calculado como a média das coordenadas de dois indivíduos selecionados aleatoriamente e, em seguida, corrigido com a função "SeInDiSp", que restringe o valor dentro do intervalo permitido.

3. Atualização da população:

•    Após a conclusão das modificações, toda a população é atualizada copiando os valores do array "a".
•    Em seguida, a função "Sorting" é chamada para ordenar a população com base no valor da função "f".

O uso de condições probabilísticas e da seleção aleatória de indivíduos para atualizar as coordenadas sugere que o método busca a melhor solução possível, considerando as interações entre os vizinhos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  int    ind1 = 0;
  int    ind2 = 0;
  double dist = 0.0;
  double x    = 0.0;
  double min  = 0.0;
  double max  = 0.0;
  double prob = 0.0;
  
  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {  
      if (u.RNDprobab() < prob)
      {
        ind1 = u.RNDminusOne (popSize);
        ind2 = u.RNDminusOne (popSize);

        if (ind1 == ind2)
        {
          ind2++;
          if (ind2 > popSize - 1) ind2 = 0;
        }

        a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [i] = a [i];

  u.Sorting (population, pTemp, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Agora, analisaremos o código do método "GetNeighborsIndex" da classe "C_AO_AMO", que é responsável por obter o índice de um vizinho aleatório para um determinado índice "i", respeitando os limites do array.

1. Inicialização de variáveis:

• "Ncount" — número de vizinhos, determinado pela variável "neighborsNumberOnSide".
• "N" — número total de vizinhos, incluindo o próprio elemento, calculado como "Ncount * 2 + 1".

2. O método utiliza estruturas condicionais para verificar a posição do índice "i" em relação aos limites do array.

3. Tratamento dos primeiros "Ncount" elementos (borda esquerda). Se o índice "i" for menor que "Ncount", significa que ele está no início do array. Nesse caso, o método gera um índice de vizinho aleatório entre "0" e "N-1".

4. Tratamento dos últimos "Ncount" elementos (borda direita). Se o índice "i" for maior ou igual a "popSize - Ncount", significa que ele está no final do array. O método gera um índice de vizinho começando de "popSize - N", garantindo que os limites sejam respeitados.

5. Tratamento de todos os outros elementos. Se o índice "i" estiver no meio do array, o método gera um índice de vizinho deslocado "Ncount" para a esquerda e adiciona um valor aleatório entre "0" e "N-1".

6. Por fim, o método retorna o índice do vizinho gerado.

O método "GetNeighborsIndex" permite obter o índice de um vizinho aleatório para um determinado "i", respeitando os limites do array.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AMO::GetNeighborsIndex (int i)
{
  int Ncount = neighborsNumberOnSide;
  int N = Ncount * 2 + 1;
  int neighborIndex;

  // Select a random neighbor given the array boundaries
  if (i < Ncount)
  {
    // For the first Ncount elements
    neighborIndex = MathRand () % N;
  }
  else
  {
    if (i >= popSize - Ncount)
    {
      // For the last Ncount elements
      neighborIndex = (popSize - N) + MathRand () % N;
    }
    else
    {
      // For all other elements
      neighborIndex = i - Ncount + MathRand () % N;
    }
  }

  return neighborIndex;
}
//——————————————————————————————————————————————————————————————————————————————

Agora que concluímos a implementação do algoritmo, vamos verificar seu funcionamento. Resultados da versão original do algoritmo:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.43676335174918435
25 Hilly's; Func runs: 10000; result: 0.28370099295372453
500 Hilly's; Func runs: 10000; result: 0.25169663266864406
=============================
5 Forest's; Func runs: 10000; result: 0.312993148861033
25 Forest's; Func runs: 10000; result: 0.23960515885149344
500 Forest's; Func runs: 10000; result: 0.18938496103401775
=============================
5 Megacity's; Func runs: 10000; result: 0.18461538461538463
25 Megacity's; Func runs: 10000; result: 0.12246153846153851
500 Megacity's; Func runs: 10000; result: 0.10223076923076994
=============================
All score: 2.12345 (23.59%)

Infelizmente, a versão original apresenta um desempenho fraco na busca, e esses resultados não serão incluídos na tabela de classificação. A análise dos resultados revelou um atraso significativo em relação a outros métodos, o que me levou a repensar profundamente o algoritmo.

Ao examinar a estratégia em detalhes, identifiquei uma falha crítica: a ordenação da população não contribuía para a preservação do material genético dos melhores indivíduos. Ela apenas alterava sua posição topológica, sem modificar sua essência. O impacto da ordenação se limitava à correção da probabilidade de mudança das coordenadas dos indivíduos no espaço de busca, sendo essa probabilidade inversamente proporcional à sua aptidão.

Curiosamente, as novas coordenadas eram geradas exclusivamente com base nos valores já existentes na população, por meio da média entre dois indivíduos selecionados aleatoriamente. A compreensão desses aspectos levou à ideia de expandir a população, integrando os descendentes ao grupo parental antes da ordenação. Essa abordagem não apenas preservaria as melhores combinações genéticas, mas também eliminaria naturalmente os indivíduos menos adaptados. Sem dúvida, a questão da renovação do pool genético da população continua sendo um desafio, mas essa modificação deve aumentar significativamente a dinâmica do processo evolutivo. Para implementar essa ideia, começaremos alterando o método de inicialização, dobrando o tamanho da população parental.

A seguir, apresentamos o código completo da inicialização, onde fica evidente o aumento da população parental.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMOm::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize * 2);
  ArrayResize (pTemp,      popSize * 2);

  for (int i = 0; i < popSize * 2; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Consequentemente, também será necessário ajustar o método "Revision".

//----------------------------------------------------------------------------
for (int i = 0; i < popSize; i++) population [i + popSize] = a [i];

u.Sorting (population, pTemp, popSize * 2);

Após essas modificações, testaremos novamente o algoritmo e compararemos os resultados.

AMOm|Animal Migration Optimization M|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.4759595972704031
25 Hilly's; Func runs: 10000; result: 0.31711543296080447
500 Hilly's; Func runs: 10000; result: 0.2540492181444619
=============================
5 Forest's; Func runs: 10000; result: 0.40387880560608347
25 Forest's; Func runs: 10000; result: 0.27049305409901064
500 Forest's; Func runs: 10000; result: 0.19135802944407254
=============================
5 Megacity's; Func runs: 10000; result: 0.23692307692307696
25 Megacity's; Func runs: 10000; result: 0.14461538461538465
500 Megacity's; Func runs: 10000; result: 0.10109230769230851
=============================
All score: 2.39548 (26.62%)

Neste caso, observamos uma melhora geral de 3%, o que indica um progresso promissor nessa abordagem.

A seguir, tentaremos transferir a modificação probabilística dos indivíduos com base no ranking para o método "Moving". Isso permitirá que as coordenadas dos indivíduos sejam ajustadas imediatamente após a obtenção de novas coordenadas dos vizinhos mais próximos.

//----------------------------------------------------------------------------
int    ind1 = 0;
int    ind2 = 0;
double dist = 0.0;
double x    = 0.0;
double min  = 0.0;
double max  = 0.0;
double prob = 0.0;

for (int i = 0; i < popSize; i++)
{
  prob = 1.0 - (1.0 / (i + 1));
    
  for (int c = 0; c < coords; c++)
  {
    //------------------------------------------------------------------------
    ind1 = GetNeighborsIndex (i);

    dist = fabs (population [ind1].c [c] - a [i].c [c]);

    x    = a [i].c [c];
    min  = x - dist;
    max  = x + dist;

    if (min < rangeMin [c]) min = rangeMin [c];
    if (max > rangeMax [c]) max = rangeMax [c];

    a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      
    //----------------------------------------------------------------------------
    if (u.RNDprobab() < prob)
    {
      ind1 = u.RNDminusOne (popSize);
      ind2 = u.RNDminusOne (popSize);

      if (ind1 == ind2)
      {
        ind2++;
        if (ind2 > popSize - 1) ind2 = 0;
      }

      a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
    }
      
    a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Vamos testar os resultados novamente:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7204154413083147
25 Hilly's; Func runs: 10000; result: 0.4480389094268583
500 Hilly's; Func runs: 10000; result: 0.25286213277651365
=============================
5 Forest's; Func runs: 10000; result: 0.7097109421461968
25 Forest's; Func runs: 10000; result: 0.3299544372347476
500 Forest's; Func runs: 10000; result: 0.18667655927410348
=============================
5 Megacity's; Func runs: 10000; result: 0.41076923076923083
25 Megacity's; Func runs: 10000; result: 0.20400000000000001
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.35829 (37.31%)

Muito melhor, vale a pena continuar. Após alguns experimentos com o código, chegamos à versão final do método "Moving".

//----------------------------------------------------------------------------
  int    ind1    = 0;
  int    ind2    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;
  double prob    = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = population [ind1].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);


      //------------------------------------------------------------------------
      if (u.RNDprobab() < prob)
      {
        if (u.RNDprobab() <= 0.01)
        {
          ind1 = u.RNDminusOne (popSize);
          ind2 = u.RNDminusOne (popSize);

          //if (ind1 == ind2)
          {
            //ind2++;
            //if (ind2 > popSize - 1) ind2 = 0;

            a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
            a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //ind1 = u.RNDminusOne (popSize);
        //a [i].c [c] = population [ind1].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora, passamos do método "Moving" para a versão final do método "Revision" da classe "C_AO_AMO", responsável pela atualização e ordenação da população de agentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [popSize + i] = a [i];

  u.Sorting (population, pTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Com o código finalizado, realizamos novos testes.

3. Resultados dos testes

Saída do algoritmo AMO em um ambiente de testes com funções de avaliação:

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9627642143272663
25 Hilly's; Func runs: 10000; result: 0.8703754433240446
500 Hilly's; Func runs: 10000; result: 0.467183248460726
=============================
5 Forest's; Func runs: 10000; result: 0.9681183408862706
25 Forest's; Func runs: 10000; result: 0.9109372988714968
500 Forest's; Func runs: 10000; result: 0.4719026790932256
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.5886153846153845
500 Megacity's; Func runs: 10000; result: 0.23546153846153978
=============================
All score: 6.14305 (68.26%)

Altos resultados para liderança na tabela de classificação, mas ao custo de uma grande variação nos valores finais em funções de baixa dimensionalidade. Vamos realizar 50 testes, em vez dos habituais 10.

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.903577388020872
25 Hilly's; Func runs: 10000; result: 0.8431723262743616
500 Hilly's; Func runs: 10000; result: 0.46284266807030283
=============================
5 Forest's; Func runs: 10000; result: 0.9900061169785055
25 Forest's; Func runs: 10000; result: 0.9243600311397848
500 Forest's; Func runs: 10000; result: 0.4659761237381695
=============================
5 Megacity's; Func runs: 10000; result: 0.5676923076923077
25 Megacity's; Func runs: 10000; result: 0.5913230769230771
500 Megacity's; Func runs: 10000; result: 0.23773230769230896
=============================
All score: 5.98668 (66.52%)

Agora, os resultados estão mais realistas, embora a eficiência tenha diminuído ligeiramente.

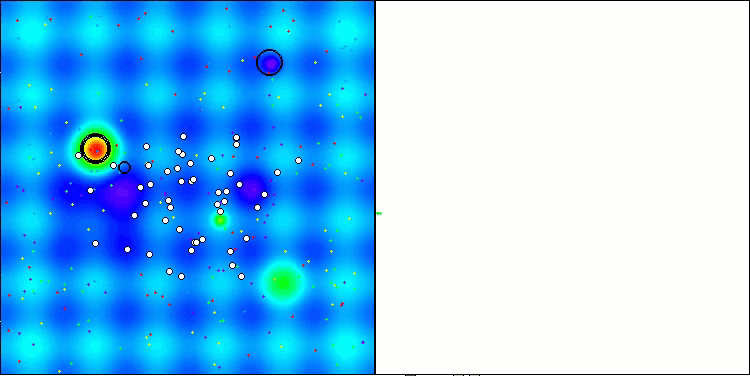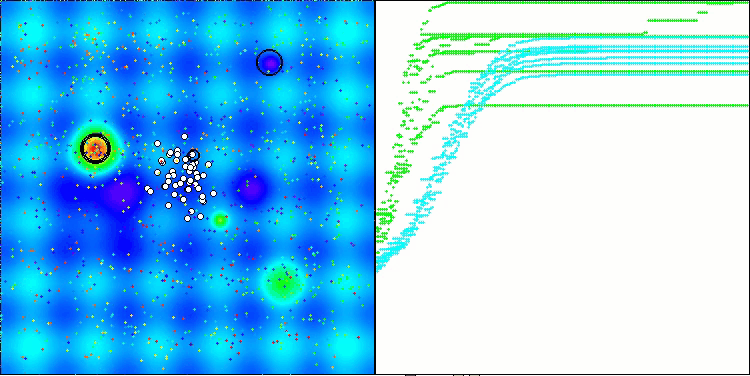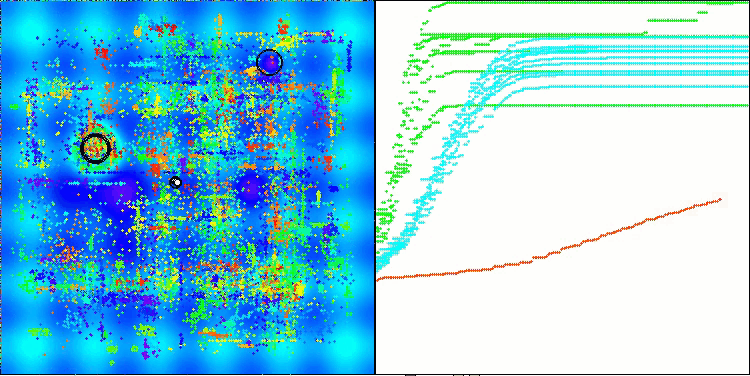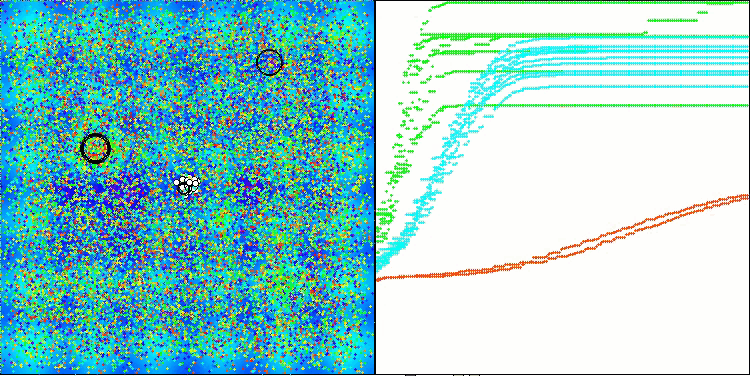
AMOm na função de teste Hilly

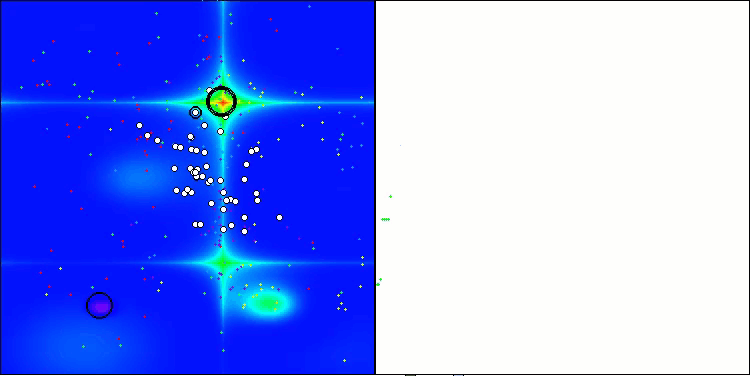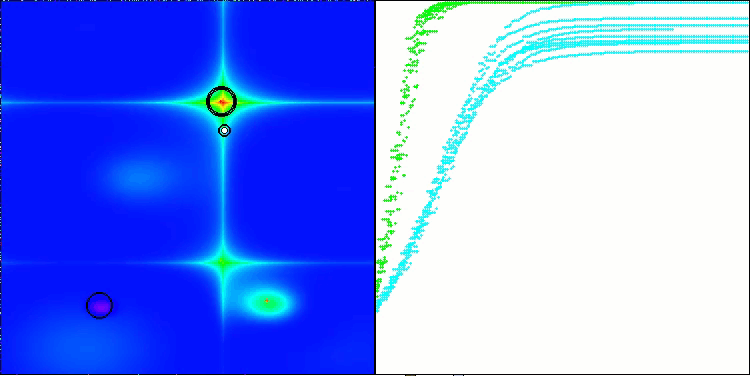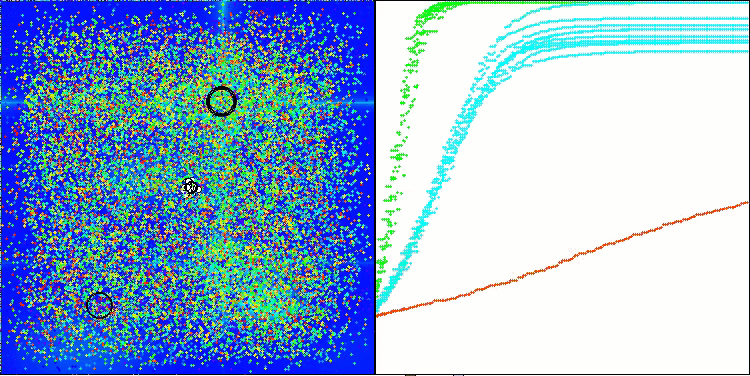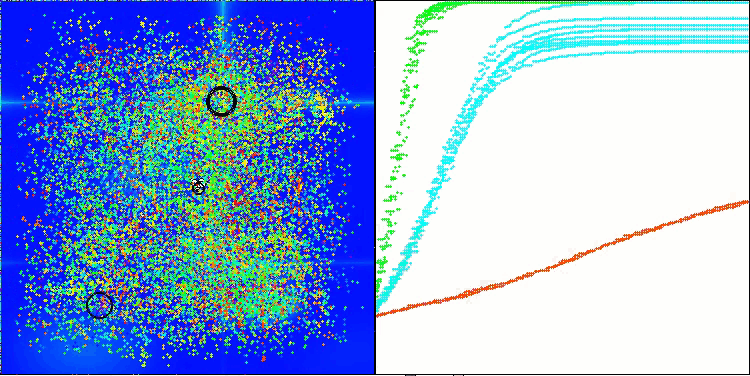
AMOm na função de teste Forest

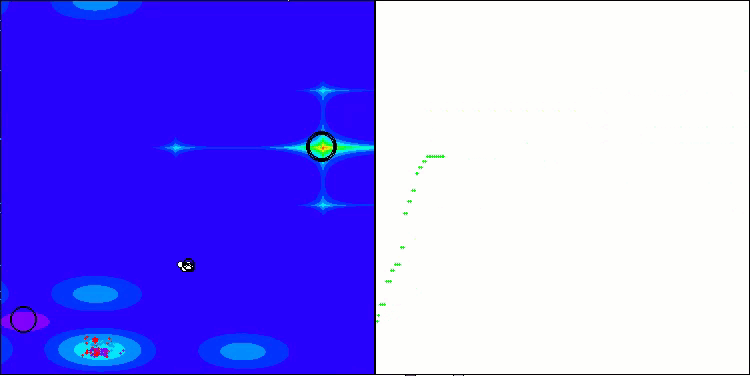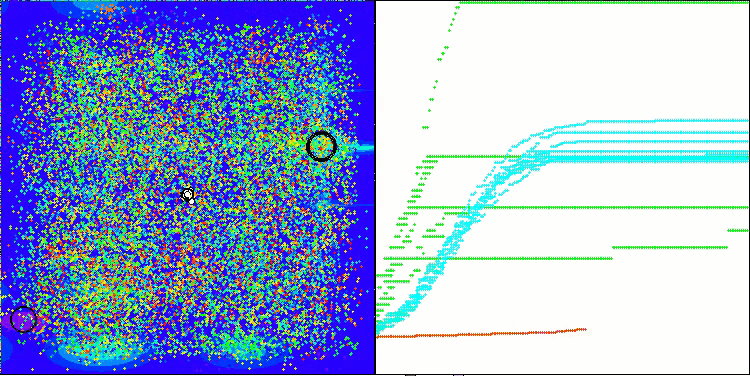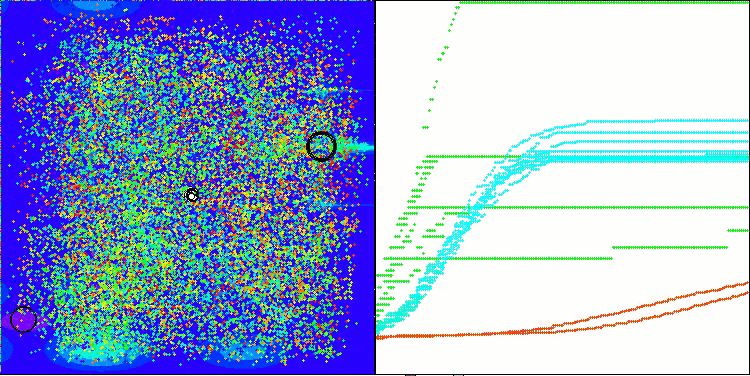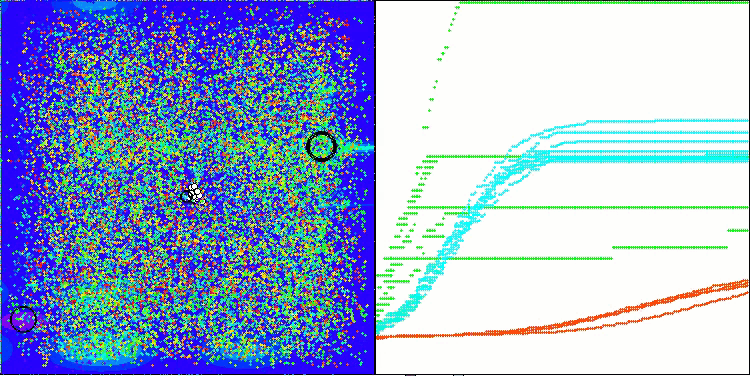
AMOm na função de teste Megacity

Após transformações surpreendentes (lembram daquele clássico filme onde "as calças se transformam... em elegantes bermudas"?), o algoritmo conquista um sólido 3º lugar na tabela de classificação.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
18	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
19	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
20	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
21	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
22	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
23	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
24	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
25	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
26	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
27	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
28	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
29	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
30	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
31	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
32	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
33	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
34	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
35	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
36	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
37	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
38	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
39	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
40	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
41	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
42	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
43	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
44	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
45	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46

Considerações finais

Com base nos resultados do algoritmo AMOm nas funções de teste, podemos tirar as seguintes conclusões: apesar da variação dos valores em funções de baixa dimensionalidade, o algoritmo demonstra excelente escalabilidade em funções de alta dimensionalidade. As principais modificações feitas na versão original melhoraram significativamente o seu desempenho. Neste caso, o aumento do tamanho da população parental em duas vezes (para ordenação junto com os descendentes) e a mudança na sequência das etapas do algoritmo permitiram a obtenção de uma gama mais ampla de soluções diversas. Esse algoritmo é um exemplo claro de como a aplicação de técnicas adicionais para sua modificação pode levar a melhorias substanciais, algo que nem sempre ocorre com outros algoritmos de otimização. 

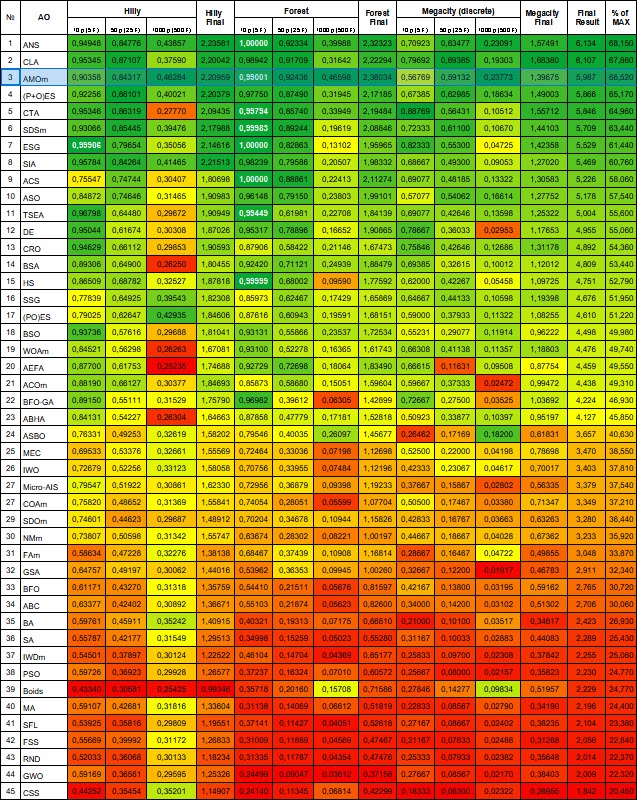
Figura 2. Graduação de cores dos algoritmos para os respectivos testes. Os resultados iguais ou superiores a 0.99 estão destacados em branco.

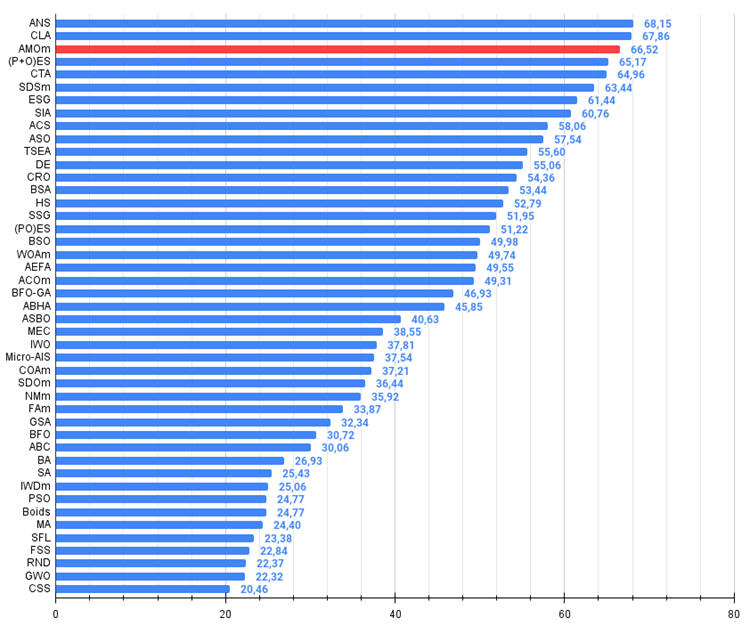
Figura 3. Histograma dos resultados dos testes dos algoritmos (escala de 0 a 100, quanto maior, melhor),

onde 100 é o resultado teórico máximo possível; no arquivo anexo há um script para o cálculo da tabela de classificação)

Prós e contras do algoritmo AMOm:

Prós:

1. Excelente taxa de convergência.
2. Alta escalabilidade.
3. Poucos parâmetros.
4. Implementação simples.

Contras:

1. Variação dos resultados em funções de baixa dimensionalidade.

O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos conduzidos.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355