Animal Migration Optimization (AMO) algorithm

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

Animal migration: harmony and nature strategy of nature. Animals typically migrate between wintering and breeding grounds, following well-established paths developed over centuries of evolution. These seasonal journeys are not random wanderings, but carefully planned routes leading to areas most favorable for their survival and reproduction. Depending on the season, animals move in search of food, shelter and suitable conditions for reproduction, guided by the natural needs of their pack and instincts. Each such journey is not only a struggle for existence, but also a manifestation of harmony with nature, where each individual plays a unique role in the overall ecosystem.

For example, reindeer migrate vast distances in search of better grazing land, and birds, such as cranes and geese, make long flights between wintering and nesting grounds, using specific routes that are passed down from generation to generation. These migrations not only ensure the survival of individual species, but also support the ecosystem as a whole, facilitating the pollination of plants and the dispersal of seeds.

Inspiration from nature. AMO (Animal Migration Optimization) algorithm was proposed in 2013 by researcher Xiantao Li. The main idea of this algorithm is to model the process of seasonal migration of animals in search of optimal conditions for life and reproduction in nature. The algorithm was inspired by observing the behavior of migratory animals such as birds, fish and mammals. These animals make seasonal movements between wintering and breeding grounds, following certain rules of interaction developed by nature during migration.

The AMO algorithm simulates three main components of animal movement over long distances: avoiding collisions with neighboring individuals, moving in the same direction as the flock (group), and maintaining sufficient distance between each other. These principles not only help avoid conflicts, but also maintain collective behavior, which is critical for survival in the wild.

Optimization stages in the AMO algorithm. The algorithm includes two key stages of optimization in one iteration:

• Migration: During this stage, the position of the individual is updated taking into account its neighbors.
  
• Population renewal: at this stage, individuals are partially replaced by new ones, with a probability depending on the position of the individual in the flock.

Modeling the collective behavior of migratory animals can be an effective approach to solving complex optimization problems. The algorithm tries to balance exploration of the search space and exploitation of the best solutions found, mimicking natural processes.

2. Algorithm implementations

In this algorithmic model of animal migration, the basic concept is to create concentric "zones" around each animal. In the repulsion zone, the animal tends to move away from its neighbors to avoid collisions. The algorithm of animal migration, according to the author, is divided into two main processes:

1. Animal migration. A topological ring is used to describe a limited neighborhood of individuals. For convenience, the neighborhood length is set to five for each dimension. The neighborhood topology remains stationary and is determined based on the indices of an individual in the population. If the animal's index is "j", then its neighbors have indexes [j - 2, j - 1, j, j + 1 and j + 2]. If the index of an animal is "1", its neighbors will have indices [N - 1, N, 1, 2, 3] and so on. Once the neighborhood topology is formed, one neighbor is randomly selected and the individual's position is updated to reflect the position of this neighbor. This description is given by the authors of the original algorithm. In this case, the limitation on the number of neighbors can be passed into the parameters of the algorithm in order to find, through experiments, the best number of neighbors to ensure the highest possible efficiency of the algorithm.

2. Population renewal. During the population renewal, the algorithm models how some animals leave the group and others join the population. Individuals can be replaced by new animals with a probability of "p" determined based on the quality of the fitness function. We sort the population in descending order of the fitness function values, which means that the probability of changing an individual with the best fitness is 1/N, while the probability of changing an individual with the worst fitness is 1.

The animal migration and the population renewal, according to the author's version, can be described algorithmically, as shown below.

Animal migration:

1. For each animal: a. Determining the topological neighborhood of an animal (5 nearest neighbors).
   b. Selecting a random neighbor from the neighbors list.    
   c. Updating the animal's position in the direction of the selected neighbor using the following equation:
      x_j_new = x_j_old + r * (x_neighbor - x_j_old), where:

• x_j_new — new position of the j th animal,
  
• x_j_old — current position,
• x_neighbor — selected neighbor position,
• r — random number from a normal distribution.
  

   d. Evaluating the new position of the animal using the objective function.

Population renewal:

1. Sorting animals by the value of the objective function in descending order. 2. For each animal: a. Calculating the probability of replacing an animal with a new random animal:

      p = 1.0 - (1.0 / (x + 1)), where x is a rank (index) of the i th animal in the sorted list.

   b. If a random number is less than p, replace the animal (change the coordinate to the average value of the coordinates of two randomly selected animals from the population).    c. Otherwise, leave the animal unchanged.

3. Estimating a new population using an objective function.

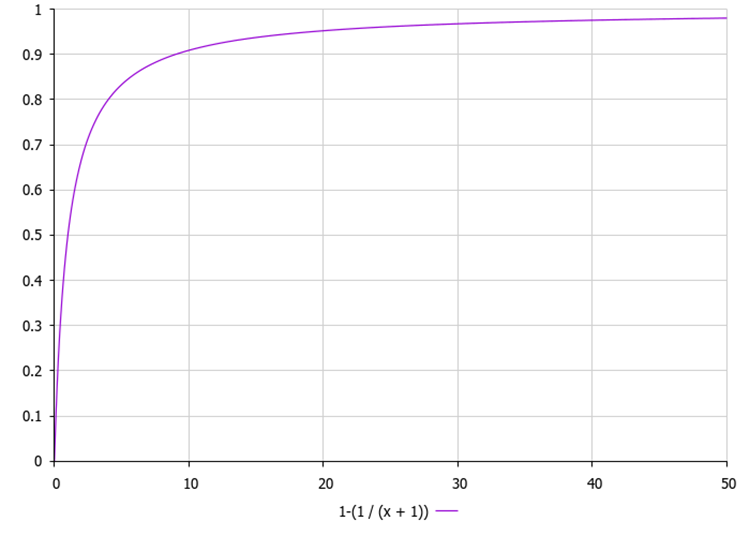
Figure 1. Change probability for an individual depending on its position in the population, where "x" is the index of the individual in the population

Let's write a pseudocode for the AMO animal migration algorithm.

1. Initializing animal population with random positions.

2. Main loop:

   a. For each animal:

      Defining a topological neighborhood.
      Selecting a random neighbor.
      Updating the animal's position in the direction of its neighbor.
      Evaluating a new position.

   b. Sorting the population by the values of the objective function.

   c. Probabilistic replacement of inferior animals with new ones.

   d. Estimating the updated population.

   e. Updating the best solution.

3. Repeat from step 2 until the stop criterion is met.

Now that we are familiar with the algorithm, we can move on to writing the code. Let's take a closer look at the code of the C_AO_AMO class:

1. The C_AO_AMO class is inherited from the C_AO base class, which allows using its functionality and expand it.

2. The constructor specifies the basic characteristics of the algorithm, such as the name, description, and link to the article. The algorithm parameters are also initialized, including the population size, bias, and number of neighbors.

3. popSize, deviation, neighborsNumberOnSide — variables determine the population size, standard deviation, and the number of neighbors on one side that will be taken into account during migration.

4. SetParams — the method is responsible for updating the algorithm parameters based on the values stored in the params array.

5. Init — initialization method that accepts arrays for the minimum and maximum range values, steps, and number of epochs. 

6. Moving () — the method is responsible for moving agents in the search space, Revision () — the method checks and updates the state of agents in the population.

7. S_AO_Agent population [] — the array stores the current population of agents (animals), S_AO_Agent pTemp [] — temporary array to use when sorting the population.

8. GetNeighborsIndex — private method used to obtain neighbor indices for a specific agent.

The C_AO_AMO class implements an optimization algorithm based on animal migration, providing the necessary methods and parameters for setting up and executing the algorithm. It inherits functionality from the base class, which allows us to extend and modify its behavior depending on the task requirements.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AMOm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AMOm () { }
  C_AO_AMOm ()
  {
    ao_name = "AMOm";
    ao_desc = "Animal Migration Optimization M";
    ao_link = "https://www.mql5.com/en/articles/15543";

    popSize               = 50;   // Population size
    deviation             = 8;
    neighborsNumberOnSide = 10;

    ArrayResize (params, 3);

    params [0].name = "popSize";               params [0].val = popSize;

    params [1].name = "deviation";             params [1].val = deviation;
    params [2].name = "neighborsNumberOnSide"; params [2].val = neighborsNumberOnSide;
  }

  void SetParams ()
  {
    popSize               = (int)params [0].val;

    deviation             = params      [1].val;
    neighborsNumberOnSide = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double deviation;
  int    neighborsNumberOnSide;

  S_AO_Agent population []; // Animal population
  S_AO_Agent pTemp      []; // Temporary animal population

  private: //-------------------------------------------------------------------
  int   GetNeighborsIndex (int i);
};
//——————————————————————————————————————————————————————————————————————————————

Next, let's consider the Init method code of the C_AO_AMO class. Description of each part of the method:

1. rangeMinP [], rangeMaxP [], rangeStepP [] — arrays for determining the minimum and maximum ranges of optimized parameters and their steps.

2. The StandardInit method performs standard initialization based on the passed ranges.

3. Resizing the population and pTemp arrays on popSize.

4. Initialization of agents is carried out on all elements of the population array and initializes each agent using the Init method passing the number of coords coordinates to it. 

5. If all operations are successful, the method returns true.

The Init method of the C_AO_AMO class is responsible for initializing the agent population considering the given ranges and parameters.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize);
  ArrayResize (pTemp,      popSize);

  for (int i = 0; i < popSize; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Next we will look at the Moving method of the C_AO_AMO class responsible for the movement of agents in the population. Main parts of the code:

1. Check the revision status:

• If revision is equal to false, the method is called for the first time or after a reset. In this case, population is initialized.
• For each individual in the population (from 0 to popSize) and for each coordinate (from 0 to coords), random values are generated in the specified range (rangeMin and rangeMax).
• These values are then handled by the SeInDiSp function, which adjusts them taking into account the specified step (rangeStep).

2. Setting the revision flag:

• After the initialization, revision is set to true, and the method terminates.

3. Basic migration cycle:

• If revision is equal to true, the method switches to the main migration logic.
• For each individual, iteration over the coordinates occurs again.
• GetNeighborsIndex(i) is used to obtain the index of the neighbor the current individual will be compared to.
• The dist distance between the coordinates of the neighbor and the current individual is calculated.
• Based on this distance, the minimum and maximum boundaries (min and max), in which the new coordinate is located, are determined.

4. Adjusting the values:

• If the calculated boundaries are outside the acceptable range, they are adjusted to take into account rangeMin and rangeMax.
• Then the new coordinate value is calculated using the normal distribution (GaussDistribution function), which allows taking into account the standard deviation (deviation).
• As in the first case, the new value is also handled using SeInDiSp.

The Moving method is responsible for updating the positions of agents depending on their neighbors and random factors. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    ind1    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;

  for (int i = 0; i < popSize; i++)
  { 
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = a [i].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The following code is the Revision method of the C_AO_AMO. Let's look at it piece by piece:

1. Finding the best individual:

• The ind variable is used to store the index of the individual with the best function (f).
• Passing through the entire population (from 0 to popSize), the code updates the fB value if the current individual has the best function value.
• If the best individual is found, its characteristics (coordinates) are copied into the cB array.

2. The basic cycle of population change:

• For each individual in the population (from 0 to popSize), the prob probability is calculated, which depends on the i index.
• For each coordinate (from 0 to coords), a random comparison is made with the prob probability.
• If the random number is less than prob, two random individuals ind1 and ind2 are selected.
• If both individuals match, ind2 is increased to avoid selecting the same individual.
• The new coordinate value of the current individual is calculated as the average of the coordinates of two random individuals, and then adjusted using the SeInDiSp function, which limits the value to a given range.

3. Population update:

•    Once the changes are complete, the entire population is updated by copying the values from the a array.
•    The Sorting function is called next. It sorts the population by the f function.

The use of probabilistic conditions and random selection of individuals to update coordinate values suggests that the method aims to find an optimal solution based on the interaction between neighbors.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  int    ind1 = 0;
  int    ind2 = 0;
  double dist = 0.0;
  double x    = 0.0;
  double min  = 0.0;
  double max  = 0.0;
  double prob = 0.0;
  
  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {  
      if (u.RNDprobab() < prob)
      {
        ind1 = u.RNDminusOne (popSize);
        ind2 = u.RNDminusOne (popSize);

        if (ind1 == ind2)
        {
          ind2++;
          if (ind2 > popSize - 1) ind2 = 0;
        }

        a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [i] = a [i];

  u.Sorting (population, pTemp, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Finally, let's consider the code of the GetNeighborsIndex method of the C_AO_AMO class responsible for obtaining the index of a random neighbor for the specified i index taking into account the array boundaries.

1. Initialization of variables:

• Ncount — number of neighbors determined by the neighborsNumberOnSide variable.
• N — total number of neighbors, including the element itself, is defined as Ncount * 2 + 1.

2. The method uses conditional statements to check the position of the i index relative to the array boundaries.

3. Handling the first Ncount elements (borders on the left). If the i index is less than Ncount, this means that it is at the beginning of the array. In this case, the method generates a random neighbor index from 0 to N-1.

4. Handling the last Ncount elements (borders on the right). If the i index is greater than or equal to popSize - Ncount, this means that it is at the end of the array. The method generates a neighbor index starting from popSize - N to take into account the boundaries.

5. Handling all other elements. If the index of i is somewhere in the middle of the array, the method generates a neighbor index that is offset by Ncount to the left and adds a random value from 0 to N-1.

6. At the end, the method returns the generated neighbor index.

The GetNeighborsIndex method allows getting the index of a random neighbor for a given index of i considering the array boundaries.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AMO::GetNeighborsIndex (int i)
{
  int Ncount = neighborsNumberOnSide;
  int N = Ncount * 2 + 1;
  int neighborIndex;

  // Select a random neighbor given the array boundaries
  if (i < Ncount)
  {
    // For the first Ncount elements
    neighborIndex = MathRand () % N;
  }
  else
  {
    if (i >= popSize - Ncount)
    {
      // For the last Ncount elements
      neighborIndex = (popSize - N) + MathRand () % N;
    }
    else
    {
      // For all other elements
      neighborIndex = i - Ncount + MathRand () % N;
    }
  }

  return neighborIndex;
}
//——————————————————————————————————————————————————————————————————————————————

Now, once we have finished writing the algorithm, let's check how it works. Results of the original version of the algorithm:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.43676335174918435
25 Hilly's; Func runs: 10000; result: 0.28370099295372453
500 Hilly's; Func runs: 10000; result: 0.25169663266864406
=============================
5 Forest's; Func runs: 10000; result: 0.312993148861033
25 Forest's; Func runs: 10000; result: 0.23960515885149344
500 Forest's; Func runs: 10000; result: 0.18938496103401775
=============================
5 Megacity's; Func runs: 10000; result: 0.18461538461538463
25 Megacity's; Func runs: 10000; result: 0.12246153846153851
500 Megacity's; Func runs: 10000; result: 0.10223076923076994
=============================
All score: 2.12345 (23.59%)

Unfortunately, the original version shows weak search qualities. Such indicators will not be included in the rating table. Analysis of the results revealed a significant gap between the algorithm and other participants, which prompted me to deeply rethink it.

Upon closer examination of the strategy, a key flaw was discovered: population sorting did not contribute to the accumulation of genetic material from the best individuals. It only changed their topological arrangement without affecting their essence. The influence of sorting was limited to only adjusting the probability of changing the coordinates of individuals in the search space, and this probability is inversely proportional to their fitness.

It is noteworthy that the new coordinates were formed exclusively on the basis of those already existing in the population, by averaging the values of two randomly selected individuals. Recognition of these nuances led to the idea of expanding the population in order to integrate the offspring into the parent group before sorting. This approach will not only preserve the best genetic combinations, but also naturally displace less adapted individuals. Undoubtedly, the problem of updating the gene pool of the population remains relevant, but the proposed modification should significantly increase the dynamics of the evolutionary process. To implement this idea, we start by changing the initialization method by doubling the size of the parent population.

Let us present the initialization code in full, where we can see the doubling of the parent population.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMOm::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize * 2);
  ArrayResize (pTemp,      popSize * 2);

  for (int i = 0; i < popSize * 2; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Accordingly, it is necessary to correct the Revision method:

//----------------------------------------------------------------------------
for (int i = 0; i < popSize; i++) population [i + popSize] = a [i];

u.Sorting (population, pTemp, popSize * 2);

After the appropriate adjustments, we will test the algorithm again and compare the results:

AMOm|Animal Migration Optimization M|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.4759595972704031
25 Hilly's; Func runs: 10000; result: 0.31711543296080447
500 Hilly's; Func runs: 10000; result: 0.2540492181444619
=============================
5 Forest's; Func runs: 10000; result: 0.40387880560608347
25 Forest's; Func runs: 10000; result: 0.27049305409901064
500 Forest's; Func runs: 10000; result: 0.19135802944407254
=============================
5 Megacity's; Func runs: 10000; result: 0.23692307692307696
25 Megacity's; Func runs: 10000; result: 0.14461538461538465
500 Megacity's; Func runs: 10000; result: 0.10109230769230851
=============================
All score: 2.39548 (26.62%)

In this case, we see an improvement in the overall result by 3%, which indicates the chances of success on the chosen path.

Next, we will try to pass the probabilistic change of individuals depending on rank to the Moving method. This will allow changes to be made to the coordinates of individuals immediately after receiving new coordinates from their nearest neighbors.

//----------------------------------------------------------------------------
int    ind1 = 0;
int    ind2 = 0;
double dist = 0.0;
double x    = 0.0;
double min  = 0.0;
double max  = 0.0;
double prob = 0.0;

for (int i = 0; i < popSize; i++)
{
  prob = 1.0 - (1.0 / (i + 1));
    
  for (int c = 0; c < coords; c++)
  {
    //------------------------------------------------------------------------
    ind1 = GetNeighborsIndex (i);

    dist = fabs (population [ind1].c [c] - a [i].c [c]);

    x    = a [i].c [c];
    min  = x - dist;
    max  = x + dist;

    if (min < rangeMin [c]) min = rangeMin [c];
    if (max > rangeMax [c]) max = rangeMax [c];

    a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      
    //----------------------------------------------------------------------------
    if (u.RNDprobab() < prob)
    {
      ind1 = u.RNDminusOne (popSize);
      ind2 = u.RNDminusOne (popSize);

      if (ind1 == ind2)
      {
        ind2++;
        if (ind2 > popSize - 1) ind2 = 0;
      }

      a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
    }
      
    a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Let's check the results again:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7204154413083147
25 Hilly's; Func runs: 10000; result: 0.4480389094268583
500 Hilly's; Func runs: 10000; result: 0.25286213277651365
=============================
5 Forest's; Func runs: 10000; result: 0.7097109421461968
25 Forest's; Func runs: 10000; result: 0.3299544372347476
500 Forest's; Func runs: 10000; result: 0.18667655927410348
=============================
5 Megacity's; Func runs: 10000; result: 0.41076923076923083
25 Megacity's; Func runs: 10000; result: 0.20400000000000001
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.35829 (37.31%)

That is much better and worth continuing. After some experiments with the code, we got the final version of the Moving method:

//----------------------------------------------------------------------------
  int    ind1    = 0;
  int    ind2    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;
  double prob    = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = population [ind1].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);


      //------------------------------------------------------------------------
      if (u.RNDprobab() < prob)
      {
        if (u.RNDprobab() <= 0.01)
        {
          ind1 = u.RNDminusOne (popSize);
          ind2 = u.RNDminusOne (popSize);

          //if (ind1 == ind2)
          {
            //ind2++;
            //if (ind2 > popSize - 1) ind2 = 0;

            a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
            a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //ind1 = u.RNDminusOne (popSize);
        //a [i].c [c] = population [ind1].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Let's move on from the Moving method to the final version of the Revision method of the C_AO_AMO responsible for updating and sorting the agent population.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [popSize + i] = a [i];

  u.Sorting (population, pTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Once the code is finally formed, we move on to testing again.

3. Test results

AMO test stand results:

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9627642143272663
25 Hilly's; Func runs: 10000; result: 0.8703754433240446
500 Hilly's; Func runs: 10000; result: 0.467183248460726
=============================
5 Forest's; Func runs: 10000; result: 0.9681183408862706
25 Forest's; Func runs: 10000; result: 0.9109372988714968
500 Forest's; Func runs: 10000; result: 0.4719026790932256
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.5886153846153845
500 Megacity's; Func runs: 10000; result: 0.23546153846153978
=============================
All score: 6.14305 (68.26%)

We can see high results in the rating table. However, the price is a high spread of final values on small dimension functions. Let's perform 50 tests instead of the usual 10.

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.903577388020872
25 Hilly's; Func runs: 10000; result: 0.8431723262743616
500 Hilly's; Func runs: 10000; result: 0.46284266807030283
=============================
5 Forest's; Func runs: 10000; result: 0.9900061169785055
25 Forest's; Func runs: 10000; result: 0.9243600311397848
500 Forest's; Func runs: 10000; result: 0.4659761237381695
=============================
5 Megacity's; Func runs: 10000; result: 0.5676923076923077
25 Megacity's; Func runs: 10000; result: 0.5913230769230771
500 Megacity's; Func runs: 10000; result: 0.23773230769230896
=============================
All score: 5.98668 (66.52%)

Now the results are more realistic, but the efficiency has also decreased slightly.

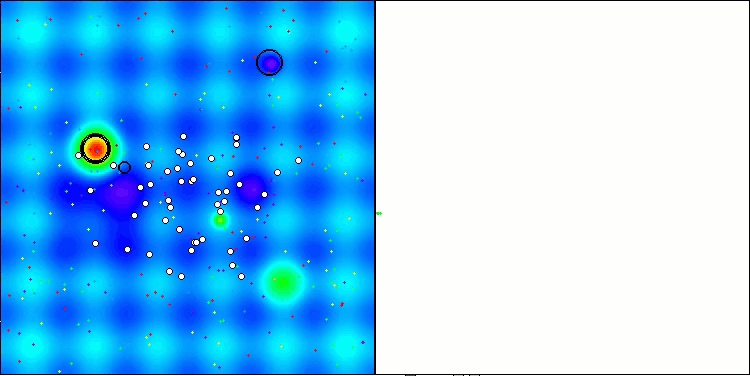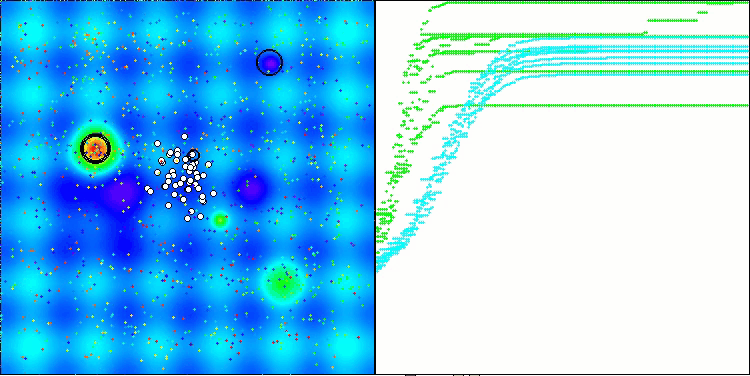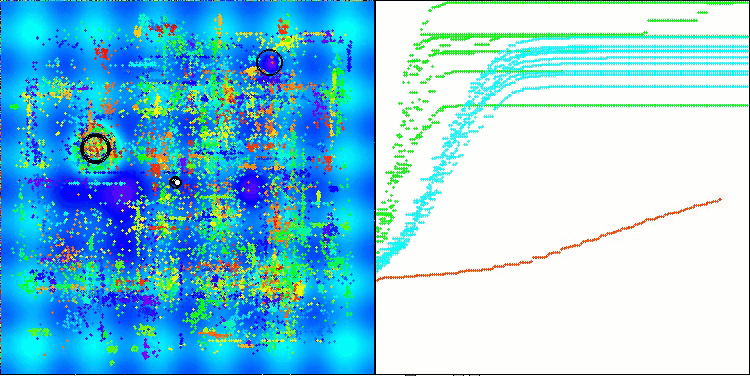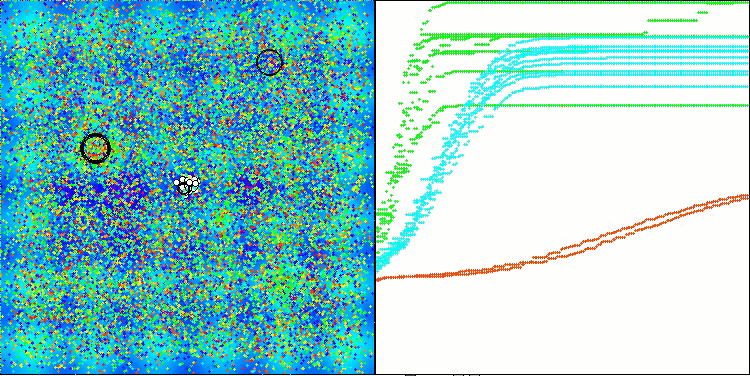
 AMOm on the Hilly function

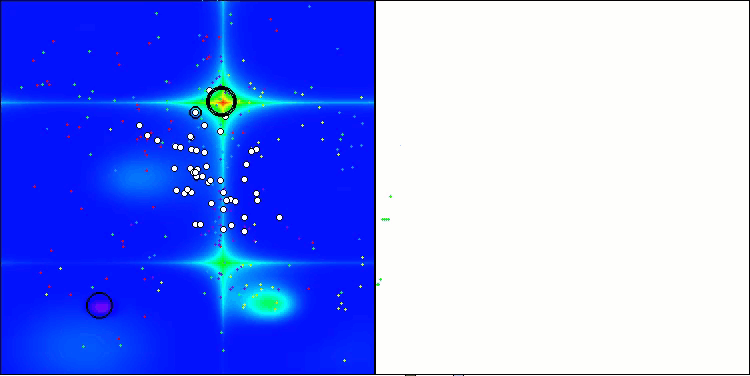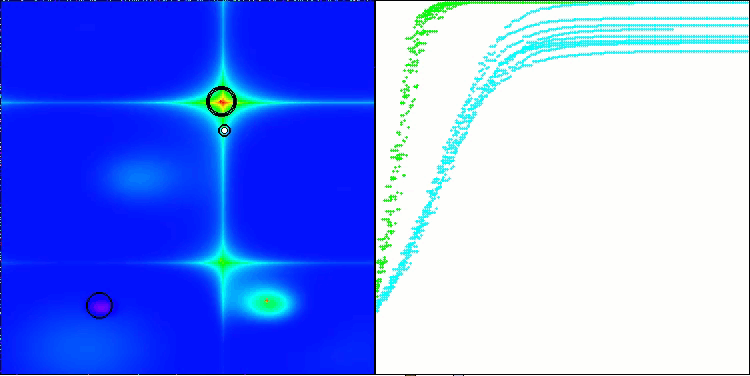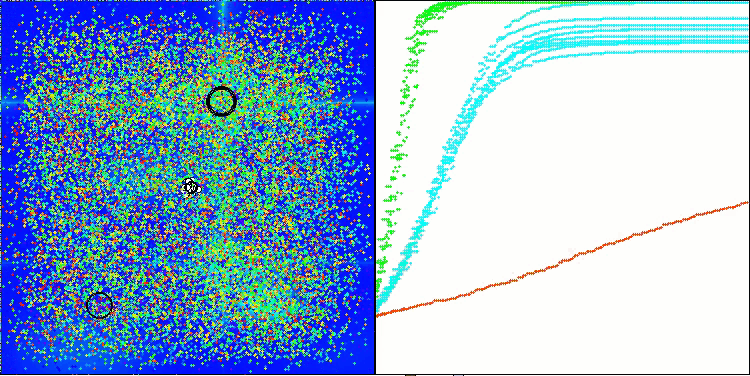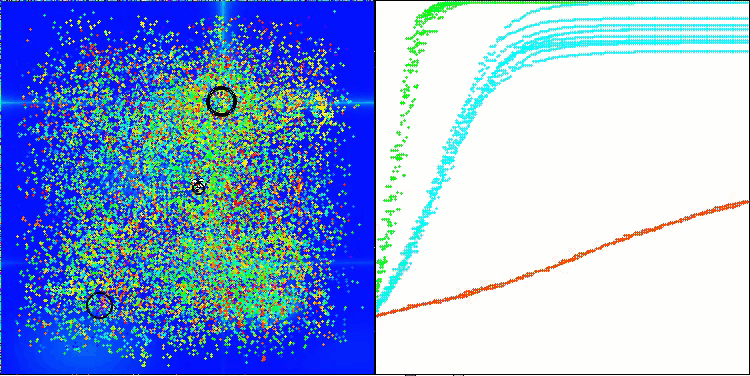
AMOm on the Forest function

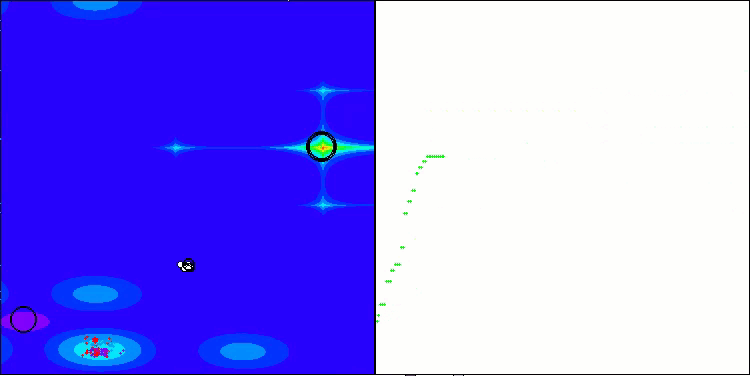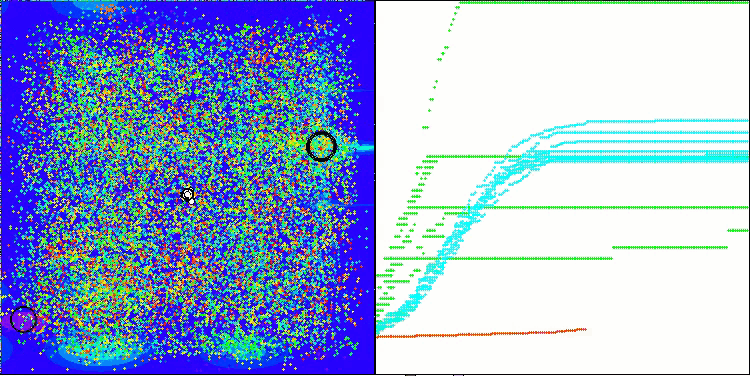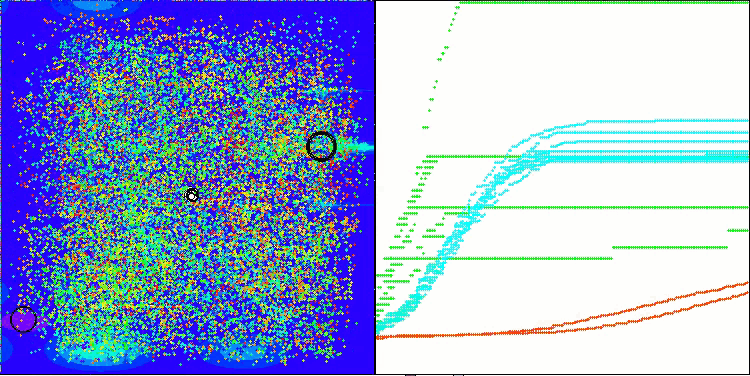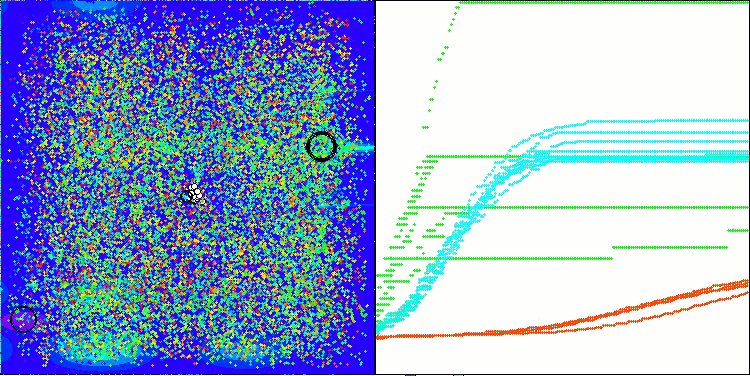
AMOm on the Megacity function

After some amazing transformations, the algorithm confidently takes the third place in the rating table.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	turtle shell evolution algorithm	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
19	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
20	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
21	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
22	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
23	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
24	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
25	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
26	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
27	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
28	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
29	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
30	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
31	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
32	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
33	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
34	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
35	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
36	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
37	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
38	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
39	Boids	boids algorithm	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
40	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
41	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
42	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
43	RND	random	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
44	GWO	grey wolf optimizer	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
45	CSS	charged system search	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46

Summary

Based on the results of the AMOm algorithm on test functions, the following conclusions can be drawn: despite the spread of values on small dimension functions, the algorithm shows excellent scalability on large dimension ones. The major changes made to the original version of the algorithm significantly improved its performance. In this case, doubling the parent population (for sorting together with the daughter individuals) and changing the sequence of execution of the algorithm stages made it possible to obtain a wider range of diverse solutions. This algorithm became a clear example of the possibilities of using additional techniques for its modification, which led to significant improvements. This became possible due to the improvement of the algorithm logic itself, which does not always work in relation to other optimization algorithms. 

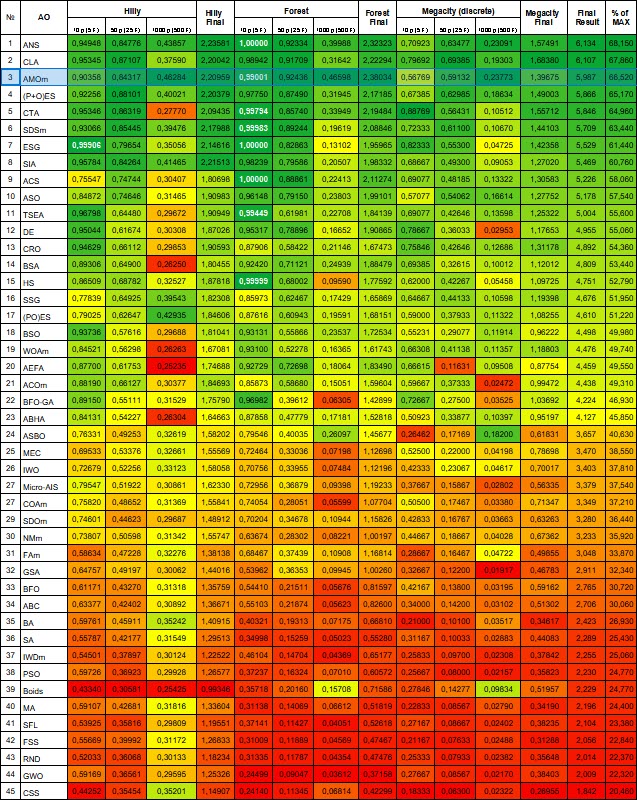
Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

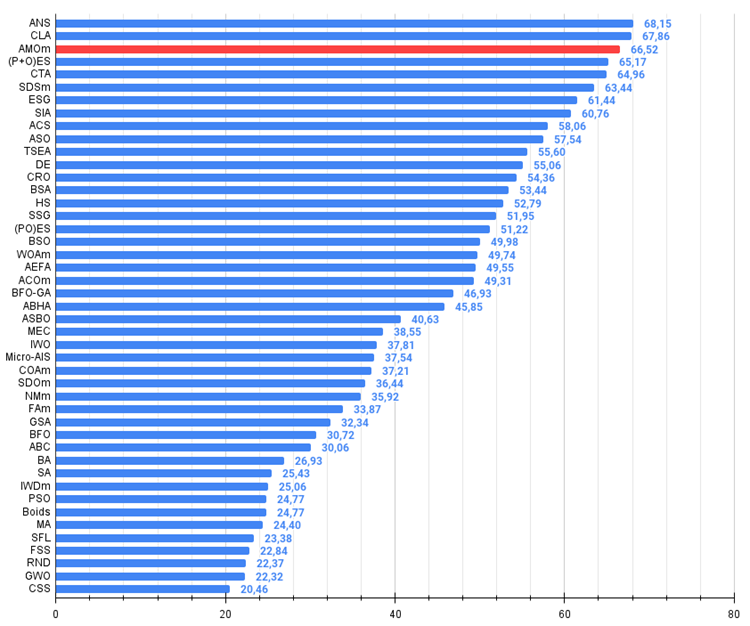
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

AMOm pros and cons:

Advantages:

1. Excellent convergence.
2. High scalability.
3. Few parameters.
4. Simple implementation.

Disadvantages:

1. Scatter of results on low-dimensional functions.

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355