初級から中級へ：演算子

はじめに

ここに掲載されている資料は、教育目的のみのものです。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。

前回の「初級から中級へ：変数(III)」では、定義済みの変数や関数を解釈するための面白い方法について探りました。しかし、ここまでに触れた内容は、すべて新米プログラマー、特に小規模な個人プロジェクトに取り組むプログラマーがよく直面する大きな課題に繋がっています。それは、異なるデータ型の取り扱いに関する問題です。

「初級から中級へ：変数(II)」でも簡単に触れましたが、MQL5ではデータがさまざまな型に分類されています。しかし、データ型を正確に説明するためには、まず適切な文脈を確立することが不可欠です。そしてその文脈こそが、この記事のテーマである基本的な演算子にあたります。データ型について効果的に議論する前に、これらの演算子を理解することが重要です。

このトピックは一見単純に感じるかもしれませんが、だからこそ非常に大切です。多くのコーディングミスは、この基本的な概念の理解不足から生じることが多いのです。

それでは、この記事の最初のトピックに入りましょう。

データ型と演算子

型のない言語では、演算子やデータ型について特に議論する必要はない場合が多いです。例えば、「10を3で割る」という演算をおこなうと、問題なく期待通りの結果が得られることが一般的です。しかし、MQL5やC、C++のような強い型付けがされている言語では、この単純な除算が1つの結果ではなく、2つの異なる結果を生むことになります。場合によっては、さらに多くのケースが存在することもありますが、これらの追加のケースについては後の説明で詳しく見ていきます。今は、2つの異なる結果が得られる可能性に注目していきます。

「ちょっと待ってください。2つの結果ですか。そんなの意味がないでしょう。冗談でしょう。10を3で割ったら、結果はいつでも3.3333...です。それ以外に答えはないはずです。」もしあなたがそう考えているのであれば、この記事はまさにあなたのためのものです。ここでの目的は、プログラミングにおいて物事が常に一見した通りに進むわけではないことを理解していただくことです。

まずは、繰り返し小数を扱うよりも簡単ですが、それでも1つの操作で全く異なる2つの結果が得られるケースを見てみましょう。以下に、簡単なコード例を示します。こちらです。

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print(5 / 2);
7. }
8. //+------------------------------------------------------------------+

コード01

こちらのシンプルなコード01は、しばしば大きな混乱を引き起こす興味深い概念を説明するために役立ちます。MetaTrader 5ターミナルで実行しなくても、6行目で実行される操作の結果がすでに分かると思っていらっしゃるかもしれません。しかし、ちょっとお待ちください。本当に、その値が何になるかを正確にお判りでしょうか。意外に思われるかもしれませんが、その答えは、計算に使われるデータ型によって異なります。もちろん、予想される結果は2.5ですが、コード01を実行すると、ターミナルには2と表示されるはずです。でも、なぜでしょうか。コンピューターはこんな簡単な計算もわからないのでしょうか。実際、コンピューターは算術演算を本質的に理解しているわけではありません。現実には、コンピューターは足し算は得意ですが、その他の数学的演算はあまり得意ではありません。

だまそうとしていると思われるかもしれませんが、まったくそんなことはありません。からくりのように見えるかもしれませんが、これは基本的な事実です。コンピューターは足し算だけは得意でも、分数計算には苦労します。たとえば、コンピューターに2つの分数を足すように頼んだ場合、必ずしも正しい結果が得られるわけではありません。これは、コンピューターのメモリ内で数値がどのように表現されているかに起因します。

コンピューターは、0と1の状態、つまりオンとオフしか理解できません。2や3といった数値を直接認識するわけではなく、ブール論理を使ってデータを処理し、計算をおこなっています。この方法で計算が実行されるため、私たちが求める結果を得ることができるのです。しかし、電卓に5÷2と入力すれば、当然2.5が表示されます。では、なぜMQL5は2.5ではなく2を返すのか。

ここで登場するのがデータ型です。6行目では、どちらの値も整数型（int）です。そのため、コンパイラは出力も整数型でなければならないと判断します。一方、電卓では結果を整数や浮動小数点数（小数とも呼ばれる）にすることができます。この点が、特に初心者プログラマーが混乱しがちな部分です。動的型付け言語では結果が常に同じになることが多いですが、MQL5のような強く型付けされた言語では、データ型の定義方法によって結果が異なります。

このコード01を修正して、正しい結果である2.5を表示させるには、次のように修正する必要があります。

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print((double)(5 / 2));
7. }
8. //+------------------------------------------------------------------+

コード02

コード02で見たような変更を加えれば、結果は明白になります。このプロセスは、型キャスティング（型変換）として知られています。MQL5のドキュメントには、他の多くのプログラミング言語のリファレンスと同様に、この概念についての詳細な説明があります。

MQL5の場合、型変換のセクションを参照することができます。そこでは暗黙的な変換がどのように機能し、より複雑な型（典型的にはdouble）を常に優先するかが図解で説明されています。その一例を以下に示します。

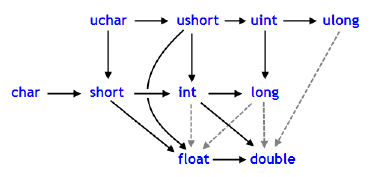
図01

データ型の相対的なスケールについては、すでにドキュメントで説明されているので、ここではその詳細には触れません。しかし、好奇心旺盛な読者は、なぜこのようなエラーが発生するのかと不思議に思うかもしません。

これを理解することで、他の多くの概念を把握することができます。例えば、ある数学的な演算をおこなうと、時として正しくない、あるいは無意味な結果が得られるのはなぜでしょう。ある値が最初は正しいように見えても、後で使うと間違っているように見えるのはなぜでしょうか。

これらの矛盾は、コンピュータのメモリにおけるデータの表現方法に起因します。これをきちんと説明するために、新しいトピックを紹介しましょう。

ビット幅

「初級から中級へ：変数(II)」の最後で、メモリに保存されるさまざまなデータ型の制限を示す表を見ました。しかし、重要な点があります。浮動小数点型（doubleやfloat）は、整数型（intやushortなど）とは同じように表現されません。今回は、整数値にのみ焦点を当てます。浮動小数点数については、後ほど詳しく説明します。浮動小数点演算を盲目的に信頼すると、深刻な誤差を招く可能性があるからです。

まず、整数値を最も基本的な単位であるビットに分解してみましょう。型が表現できる最大値は、使用されるビット数に2を累乗した値に相当します。例えば、4ビットの場合、16個の異なる値を表現できます。10ビットの場合は、1024個の値を表現できます。

ただし、これは正の値にのみ適用されます。負の値の場合は、少し調整が必要です。符号付き整数では、その範囲は、2の（ビット数 - 1）乗から、その負の対応値から1を引いた範囲になります。最初は少し分かりづらいかもしれませんが、実際にはとても簡単です。例えば、同じ4ビットで、正負両方の値を表現すると、-8から7の範囲になります。10ビットだと、-512から511まで表現できます。しかし、ちょっと待ってください。-8から8、あるいは-512から512にすべきではないでしょうか。結局のところ、8と7を足すと16ではなく15になり、512と511を足すと1024ではなく1023になります。なぜこうなるのでしょうか。欠けている値はゼロです。ゼロは範囲内で1つの位置を占めているため、カウントがわずかにずれているのです。

さらに詳しく理解するためには、負の数がどのようにメモリに保存されるかを知る必要があります。次の図を見てみましょう。

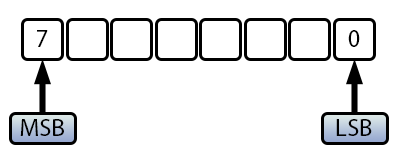
図02

ここでは、符号なし文字(uchar)または符号付き文字(char)を表すことができる8ビット値を見ています。その違いは最上位ビット(MSB)にあります。uchar（符号なし）の場合、すべての値が正であり（u接頭辞で示される）、MSBは問題ではなく、0から255までの値（合計256の値）を許容します。しかし、char（符号付き）の場合は、MSBが値の正負を決定します。MSBが1の場合、値は負となり、MSBが0の場合、値は正となります。このため、正の値を0から127まで数えることができます。しかし、ゼロは符号なしであり、MSBがオンで他のビットがオンでない唯一のケースであるため、-128と解釈され、「負のゼロ」というものは存在しません。これはまた、負の値の場合、可能な値の半分と比較して、カウントが常に余分な値を持つ理由も説明します。

面白いと思いませんか。しかし、これからさらに面白くなります。上記の説明を理解した方なら、たぶん、多くのプログラミング言語に存在するABSやMathAbs関数がどのように負の値を正の値に変換し、またその逆も可能であるかをすでに理解していることでしょう。この変換をおこなうには、MSBの状態を変更すればよいのです。

しかし、自分の行動に注意を払わなければ、予期しないことが起こる可能性があります。例えば、2つの正の値、例えば100と40を足すと、負の値になることがあります。「待って、何？両方の数字が正なら、和も正でなければならないでしょう。」日常的な数学ではそうです。しかし、コンピュータでは、物事が必ずしも期待通りに動くとは限りません。この現象を次のコード例で見てみましょう。下記のコードをご覧ください。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     char    value1 = 100,
07.             value2 = 40,
08.             Result;
09. 
10.     Result = value1 + value2;
11.     Print(value1, " + ", value2, " = ", Result);
12. }
13. //+------------------------------------------------------------------+

コード03

このコードを実行すると、次のような結果が画面に表示されます。

図03

「これは何ですか。ありえません。」いや、読者の皆さん、ありえなくありません。実際、この記事を執筆する必要があった理由がまさにここにあります。強い型付けが行われている言語では、適切なデータ型を選択することが計算結果に直接影響を与えるということを理解しなければなりません。この基本的な概念を理解していないために、多くのプログラマーは苦労しています。さらに、こうした一見単純な問題に対する認識が不足しているために、多くの人々が誤った認識を持っています。しかし、適切な理解がなければ、正確さや安全性について誤った保証を信じることになりかねません。

さて、あなたはおそらくこう思うかもしれません。「正の数なら127まで、負の数なら-128までの範囲を持つデータ型を使うより、8ビットではなく32ビットのint型を使った方が良いのでは？」その通り、読者の皆さん、それは理にかなった解決策に思えるでしょう。しかし、ここでの本当の問題は、それだけではありません。問題は、どんなに大きなデータ型を使っても、最終的に表現できる最大値に達してしまうということです。そうなれば、計算が何らかの形で破綻することになります。現在、私たちはまだ整数型の話をしていますが、浮動小数点数を扱うとさらに複雑さが増します。

そのため、浮動小数点演算に進む前に、まず整数演算を理解することが非常に重要です。しかし、ここで覚えておくべき重要なポイントがあります。それは、常に大きなデータ型を使えるわけではないということです。この制約は特に文字列を扱う際に顕著です。これがさらに複雑になります。文字列、または文字のシーケンスは、8ビットまたは16ビットでエンコードできます。ほとんどの場合、コンピュータはASCIIテーブルに依存しています。これは、コンピュータの黎明期に作られた8ビットのエンコーディング規格です。しかし、ASCIIはすべての文字を表現するには不十分だったため、追加の符号化方式が開発されました。そのため、一部のプログラムでは16ビットエンコーディングを使っています。しかし、16ビットエンコーディングを使ったからといって、無限の可能性が得られるわけではありません。それは、最上位ビット(MSB)を15の位置にシフトすることで、単に表現できる値の範囲を256から65,536に拡張するだけです。

それでも、文字列は単なる値の配列に過ぎませんが、その配列が広範囲の表現を可能にします。例えば、MQL5では、最大の定義済み型(ulong)が64ビットに制限されているにもかかわらず、128ビットの値を作成することができます。では、なぜこれが可能なのでしょうか。実は簡単です。シーケンスの各ビットがオンまたはオフになることで、どのように値に寄与するかを理解すれば、アクティブなビットの値を合計することができます。そうすることで、まるで魔法のように、任意の値を表現する能力を得ることができるのです。

これが、コード03で100と40を足すと-116になる理由です。この文脈での-116は、実際には+140を意味します。一見不思議に思えるかもしれませんが、2進数で値を調べると、以下のようになります。

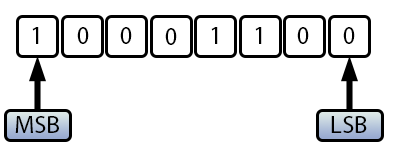
図04

言い換えれば、同じ2進数値でも、ある場合には正として解釈され、別の場面では負として解釈されることがあります。これは、最上位ビット(MSB)の扱い方によるものです。このため、特にループを作成する際には非常に注意が必要です。適切に管理されていないと、型に関する問題が発生し、計算やループが予測できない挙動を示すことになります。見た目には全てが正しく動作しているように見えても、型の選択ミスや与えられた型の最大値を超えることによって、プログラム全体が制御不可能に陥る恐れがあります。

先ほど、より大きなデータ型を使用することでこの問題を解決できると述べましたが、なぜこのアプローチがすべてのケースでうまくいくわけではないのでしょうか。その答えは、MSBのシフト方法にあります。この効果は、下の画像で確認できます。

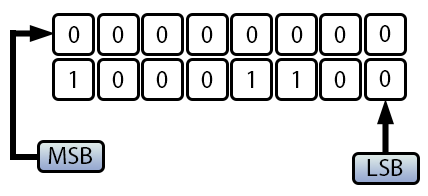
図05

シンプルな概念でしょう。これでとりあえず算術演算の基本はカバーしました。しかし、これまで述べてきたことはすべて算術演算子に関するものです。次に検討する必要があるもう 1 つの重要な演算子のカテゴリは、論理演算子です。これらの概念をきちんと分けて説明するために、新しいトピックに移ります。

論理演算子

論理演算子はビットレベルで動作します。バイトやビットのセット全体に適用できる場合もありますが、主にビットレベルで機能するように設計されています。最初は少し混乱するかもしれませんが、時間が経つにつれて、それが理にかなっていることがわかるでしょう。算術演算子が計算の実行に使われるのに対し、論理演算子は条件の評価に使われます。通常、論理演算は値が特定の条件を満たすかどうかを確認します。これらの演算子は制御構造と組み合わせて使うと最も効果的なので、ここでは簡単な概要だけを説明し、今後のトピックに備えることにします。

論理演算子は条件文とともに使うとその意味がより明確になりますが、単純な演算にも利用できます。実際、CPUの演算は基本的に算術演算よりも論理演算の方が多いと言えます。算術論理演算ユニット(ALU)が「算術」と「論理」の両方の名前を持っていることを考えると、論理演算がCPUの機能にとって基本的であることがわかります。

論理演算子には、主にAND、OR、NOT、そして一部のプログラミング言語で使われるXORがあります。これに加えて、右シフト演算と左シフト演算も存在します。これらの単純な演算はすべて、計算論理の基盤を形成します。実際には、これらの基本的な操作を組み合わせることで、あらゆる計算が実行可能です。これはCPUの「頭脳」であるALUが動作する原理そのものです。

ここで、MQL5のドキュメント（または他のプログラミング言語のリファレンス）を見て、「でも、論理演算子には>や<、その他の比較演算子もあるのでは？」という疑問が湧くかもしれません。いい質問です。確かに、いくつかのプログラミング言語では便宜上、追加の論理演算子や比較関数を提供しています。しかし、ハードウェアレベルでは、これらの操作はプログラミング言語で表現される方法よりもはるかに単純です。ここでのポイントは、これらの実装を批判することではありません。実際、これらはプログラミングを格段に簡単にしてくれます。例えば、2つの値を比較する最も簡単な方法は、引き算を使うことです。しかし、代わりにビットごとのXOR演算を使う方法もあります。もしすべてのビットが一致すれば、結果はゼロとなり、いずれかのビットが異なれば、値は等しくないことになります。減算をおこなう場合、MSB（最上位ビット）を分析することで、その結果がゼロ（等しい）、負（小さい）、または正（大きい）であるかを判断することができます。これにより、明示的な比較演算子を使用せずに数値間の関係を明確にすることができるのです。

この概念を明確にするために、ある値が他の値より大きいか、小さいか、あるいは等しいかを判断する簡単な例を見てみましょう。そのために、以下のコードスニペットを使用します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     short   value1 = 230,
07.             value2 = 250;
08. 
09.     Print("Result #1: ", value1 - value2);
10.     Print("Result #2: ", value2 - value1);
11.     Print("Result #3: ", value2 ^ value1);
12. }
13. //+------------------------------------------------------------------+

コード04

ここでは、シンプルで典型的な値分析システムを紹介します。このコードを実行すると、ターミナルに次のような結果が表示されます。

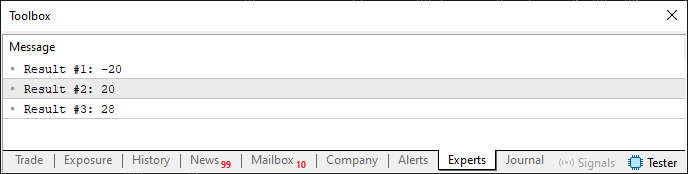
図06

ここで、ある値が他の値より大きいか、小さいか、あるいは等しいかを判断することに関して、先に述べたことに注意してください。さらに面白くするために、16ビットの符号付き値を使い、65,536通りの値を表現できるようにしています。しかし、これは符号付き値であり、負と正の両方の数値を保持できるため、その範囲は-32,768から32,767までとなります。8ビットの範囲内の値を分析するだけであれば、ある値が他の値より大きいか、小さいか、または等しいかを判断するのに問題はありません。しかし、16ビットの値であれば、-255から255までの広い範囲を表現することができ、素晴らしいです。ただし、これをさらに良くする方法もありますが、その前にいくつかの概念を説明しなければならないため、今回は触れません。それでも、コード04は非常に魅力的で楽しいものです。

では、ここで何が起こっているのかを整理してみましょう。値1は値2より明らかに小さいため、一方の値を他方から引くと負の値になり、最初の値が本当に小さいことが確認できます。これはコード04の9行目でおこなわれています。一方、10行目では、値2から値1を引くと結果が正となり、値2が値1より大きいことが示されます。最後に11行目では、値が等しいかどうかを比較して確認します。結果がゼロでないことから、この2つの値は同じではないと結論できます。

この概念は非常に興味深いものです。さらに面白いのは、ALU（算術論理演算ユニット）には減算演算がないことに気づく点です。実際、ALUで実行される演算は基本的に加算といくつかの論理演算の組み合わせであり、加算演算でさえ、論理演算に還元することができます。

しかし、これを正確に示すためには、制御演算をいくつか使用する必要があります。この記事ではまだ制御演算について説明していないので、ALUレベルでどのように実装されるかについては触れません。しかし、今後の記事で詳しく解説する予定ですのでご安心ください。これらのテクニックを理解し実装できるようになれば、インジケーターやスクリプト、エキスパートアドバイザー(EA)の作成を超えて、MQL5を使ってより高度でエキサイティングなタスクにも取り組めるようになります。

この実装をデモンストレーションするかどうかはまだ決めていません。なぜなら、本記事の主な目的はあくまで教育的なものだからです。しかし、少し考えてみるつもりです。

シフト演算子に関しては、MQL5のドキュメントでほとんど触れられていないため、まだ適切に表現されていない部分もあります。しかし、これらの演算子は非常に特定の目的を持ち、特定のタスクを実行するために設計されています。そのため、一般的なMQL5コードでは、特にインジケーターやEAでの使用は少ないです。しかし、MQL5で作成されたアプリケーションで画像を扱う場合には、これらの演算子がより頻繁に使用されます。

それでも、非常に特殊な目的で使われるものであれば、他の用途にも適用できる場合があります。そのようなタスクについては、制御演算を扱う際に取り上げる予定です。

最終的な考察

この記事では、強く型付けされた言語で作業する際に大きな影響を与える、プログラミングの重要なポイントをいくつか取り上げました。ここで紹介した概念の中には、多くの方にとって新しいものもあるかもしれませんが、実際にはこのトピックの表面をなぞったに過ぎません。読者の皆さんには、MQL5の基本的なドキュメントをじっくりと学び、理解を深めることをお勧めします。さらに、ブールロジックについても積極的に研究するとよいでしょう。ブールロジックは非常にシンプルな概念ですが、コーディングにおける多くの計算を簡潔にするのに役立ちます。また、正負の値の扱い方やその微妙な違いを理解することは、長期的に見ても大きな強みとなるでしょう。

添付ファイルには、本記事で取り上げた4つのコードのうち3つを収録しているので、ご自身のペースで学習を進めてください。次回は、制御演算（演算子）について解説します。ここからが本当にエキサイティングな展開となり、いよいよプログラミングの醍醐味が味わえることでしょう。では、また次回お会いしましょう。