Ciclos y trading
71
11
Introducción
La principal tarea a la que se enfrenta un trader es predecir los movimientos de precios. Los comerciantes construyen sus pronósticos basándose en un modelo u otro. Uno de los modelos más simples y visuales es el modelo de movimiento cíclico de precios.
La idea básica detrás de cualquier patrón cíclico es que varios factores interactúan para crear ciclos en el movimiento de precios. Estos ciclos pueden diferir entre sí en su duración y fuerza. Si conoces los parámetros de estos ciclos, entonces las operaciones de trading serán muy sencillas: abrir una posición de compra cuando el ciclo haya alcanzado su mínimo, vender cuando el ciclo haya alcanzado su máximo.
Veamos cómo se puede utilizar este modelo en la práctica.
Ciclo simple
Cuando describimos ciclos, solemos aplicar las funciones trigonométricas seno y coseno. Pero el ciclo se puede definir de otra manera, con la ayuda de diferencias finitas.
Por ejemplo, consideremos una ecuación en la que la segunda diferencia es proporcional al valor de la serie temporal:
Esta es una ecuación de oscilador armónico. A primera vista, no tiene nada de especial. Pero esta ecuación tiene una propiedad interesante. Si el valor de la relación R está en el rango de 0 a 4, entonces esta ecuación solo puede pertenecer a una sinusoide. Esta relación depende del período del ciclo N. En otras palabras, su valor puede elegirse de tal manera que la ecuación reaccione sólo a ciclos con una determinada frecuencia:
Ahora veamos cómo se puede aplicar esta ecuación en la práctica. Si lo aplicamos a precios p[], necesitaremos el valor del nivel m alrededor del cual fluctúa el precio.
Para evitar calcular el valor de este nivel medio, recurriré a un pequeño truco. Recordemos qué sucede matemáticamente cuando un ciclo alcanza un punto máximo o mínimo. En estos momentos la primera derivada cambia de signo.
En lugar de la derivada, utilizaremos la primera diferencia de la ecuación original. Éste es el difícil destino del comerciante: buscar las diferencias en las diferencias. Pero este enfoque simplifica enormemente los cálculos. Solo necesitamos establecer el valor del ratio R. La forma final de la ecuación es la siguiente:
Además, llamaré a dichas ecuaciones ecuaciones de algoritmos comerciales. Basándonos en esta ecuación podemos crear una estrategia de trading. En primer lugar, haré una pequeña adición: podemos utilizar cualquier versión de la media móvil convencional en lugar del precio actual. La esencia de la estrategia en sí es muy simple. La apertura y cierre de posiciones se produce cuando cambia el signo de la ecuación:
- De negativo a positivo: abrir compra, cerrar venta.
- De positivo a negativo: abrir vender, cerrar comprar.
El cambio de equilibrio de EA puede ser así.
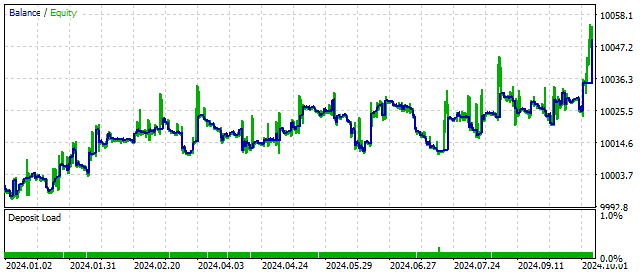
Esta estrategia comercial tiene perspectivas. Pero necesita algunas mejoras.
Ciclo con amortiguación
La estrategia que analizamos anteriormente tiene un grave inconveniente. Se basa en el supuesto de que el ciclo continuará durante mucho tiempo. En la vida real, el ciclo depende de muchos factores externos y puede colapsar casi inmediatamente después de comenzar.
Para eliminar este inconveniente, podemos utilizar el modelo de oscilador armónico con amortiguación de oscilaciones. La ecuación de dicho ciclo también se establece mediante diferencias finitas:
El parámetro S determina la rapidez con la que desaparecen las oscilaciones. Cuanto mayor sea su valor, más rápida será la amortiguación. El valor crítico de este parámetro se puede encontrar utilizando la siguiente ecuación:
A partir de este valor, el movimiento del oscilador se vuelve no oscilatorio.
Ya sabemos qué hacer con tal ecuación. Necesitamos encontrar su primera diferencia, que generará señales comerciales.
Al agregar un nuevo parámetro, la estrategia comercial puede volverse más flexible y rentable. Por ejemplo, así es como se ve el cambio de equilibrio en un valor crítico de S.
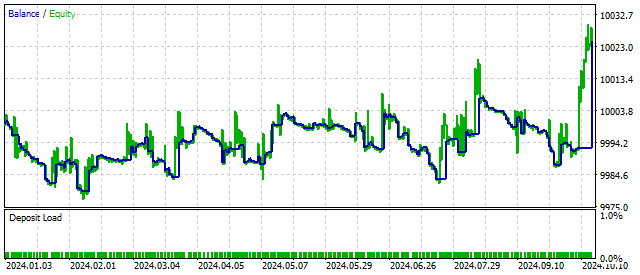
Por definición, el parámetro S debe ser positivo. Pero este requisito no es obligatorio. Si establecemos un valor negativo para este parámetro, la ecuación original describirá oscilaciones con una amplitud cada vez mayor. De esta manera, EA puede reaccionar al inicio del ciclo y posiblemente aumentar la rentabilidad. Los resultados comerciales en este caso podrían verse así:
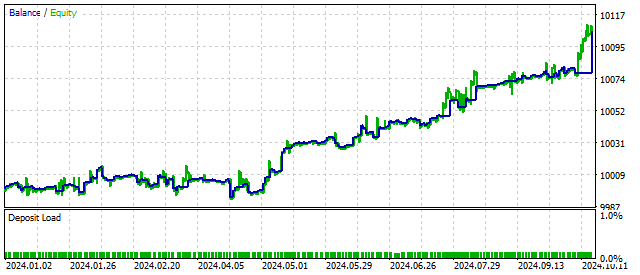
Como puede ver, hacer que el modelo de ciclo sea más complejo puede mejorar los resultados comerciales. Intentemos complicar aún más el modelo.
Ondas de Elliott
La Teoría de las Ondas de Elliott se conoce desde hace mucho tiempo y se utiliza ampliamente en el comercio. Intentemos aplicar el modelo cíclico a las Ondas de Elliott.
Las primeras cinco Ondas de Elliott se pueden simular como la suma de dos sinusoides con diferentes amplitudes y períodos:
En este caso se deberán cumplir las siguientes condiciones:
Como resultado podemos obtener algo como esto:
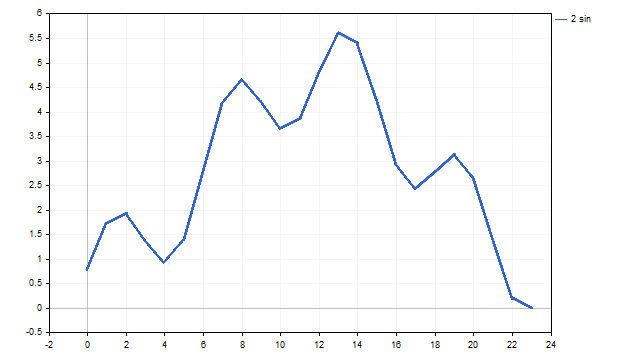
No se ve exactamente como en los libros: es un poco angular, pero bastante similar.
Podemos simular la suma de dos senoides utilizando diferencias finitas:
Donde 
— el valor de la diferencia finita de orden n, en la lectura del precio con índice i. Ya sabemos qué hacer con esta ecuación: hallar la diferencia a partir de la suma de las diferencias y obtener señales de trading:
El uso de la suma de dos senos paranasales permite ajustar el EA a situaciones de mercado más complejas. El uso de este algoritmo comercial puede conducir tanto a un aumento de las entradas al mercado como a una mejora de su rentabilidad.
Este es el resultado que puede mostrar un EA basado en el principio de Ondas de Elliott:
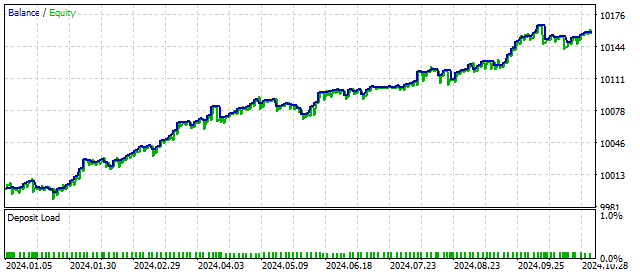
Como puede ver, incluso una pequeña complicación del modelo cíclico puede traer resultados positivos.
Oscilador armónico generalizado
Ya hemos analizado tres modelos basados en el oscilador armónico. Cada uno de estos modelos se construyó sobre sus propios supuestos iniciales. Pero como resultado, todavía obtuvimos cierta suma de diferencias finitas.
Podemos construir un modelo más general. La esencia de este modelo es muy simple: primero tomamos la diferencia de un orden predeterminado y las sumamos a las diferencias de órdenes inferiores, hasta el primero. En este caso, cada diferencia de orden bajo se toma con su propia relación de ponderación.
Por ejemplo, tomé la diferencia del séptimo orden. Entonces la ecuación para el algoritmo de trading será la siguiente:
Un modelo de este tipo puede incluir una amplia variedad de combinaciones de ciclos y su comportamiento. Hemos visto anteriormente que hacer el modelo más complejo mejora los resultados comerciales. En este caso la variación del saldo podrá ser la siguiente:
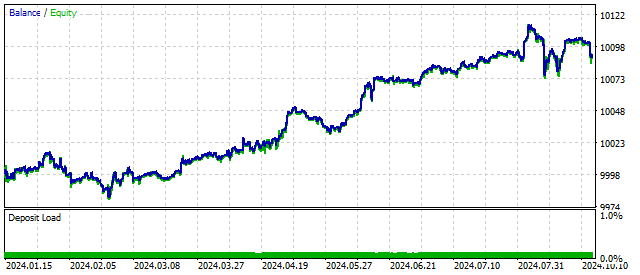
Aumentar el orden de la diferencia principal hace que el modelo sea más flexible. El oscilador generalizado solo reaccionará a ciertas combinaciones de precios. En otras palabras, busca ciertos patrones. Al mismo tiempo, hay que recordar que cuanto mayor sea el orden del oscilador, con menos frecuencia se producirán sus patrones.
Otra característica de este algoritmo es que las proporciones pueden variar dentro de límites muy amplios. Incluso evaluar estos límites puede resultar difícil. Por otra parte, la selección de ratios permite configurar el algoritmo de tal forma que responda a patrones no cíclicos en el comportamiento de los precios.
Osciladores no lineales
Los modelos lineales son simples e intuitivos. Pero el comportamiento de los precios en el mercado también puede ser no lineal. Por ejemplo, un cambio brusco en el precio es más fácil de describir utilizando modelos no lineales. La principal ventaja de los modelos no lineales es que pueden describir el comportamiento de series temporales muy complejas. Cuando escuchas las palabras «caos» y «estocasticidad», lo más probable es que estés tratando con modelos no lineales.
Uno de los modelos más simples es el oscilador de firma. Su ecuación es en muchos aspectos similar a la del oscilador armónico. La Función signo se utiliza como función no lineal. La ecuación del algoritmo comercial se ve así:
Donde 'sign' es la función de signo.
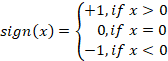
Gracias a esta característica, el oscilador puede funcionar en 5 modos diferentes. Los modos de cambio dependen del movimiento del precio. La no linealidad del oscilador nos da la esperanza de que el comercio con su ayuda será más flexible y estable. El cambio de equilibrio utilizando este algoritmo podría verse así:
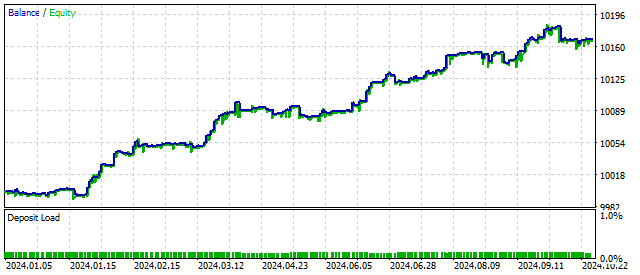
Ahora, consideremos un oscilador con no linealidad cuadrática. Su ecuación es muy sencilla:
Para poder aplicar esta ecuación en la práctica, necesitamos refinarla un poco.
En primer lugar, necesitamos un nivel promedio alrededor del cual fluctúe el precio. Permítanme recordarles que en lugar de precios reales podemos utilizar su valor suavizado (SMA). Entonces el nivel promedio será igual al valor promedio de las medias móviles.
Calcular el promedio de los promedios puede parecer un poco intimidante al principio. En 1910, Andréi Márkov publicó su obra «Cálculo de diferencias finitas» (Calculating Finite Differences). En este trabajo, demostró que tomar un promedio de un gran número de SMA es equivalente a aplicar un LWMA a todos los valores de la serie de tiempo. Una vez más, las diferencias finitas han simplificado los cálculos.
La ecuación para el algoritmo de trading del oscilador cuadrático será la siguiente:
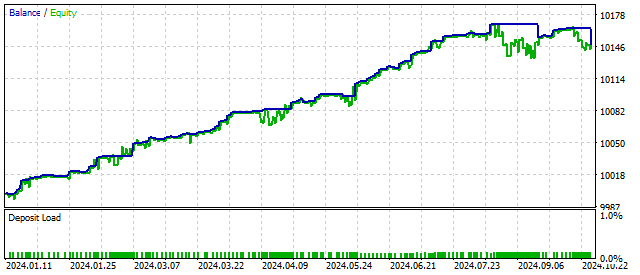
La no linealidad cuadrática permite cambiar los modos de funcionamiento del oscilador con mayor suavidad, pero con una amplitud mayor. Esto puede mejorar los resultados comerciales.
Otro ejemplo de no linealidad cuadrática es el Oscilador de van der Pol. Este oscilador fue uno de los primeros ejemplos de simulación del caos determinista. Debido a sus propiedades, la ecuación de Van der Pol ha encontrado aplicación no solo en la teoría de la oscilación, sino también en otras áreas, como la física, la biología, etc.
El oscilador de Van der Pol en sí es una modificación del oscilador con no linealidad cuadrática, y la ecuación para su algoritmo comercial se ve así:
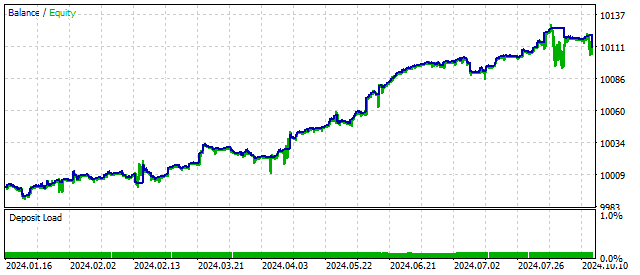
A primera vista, este oscilador debería ser inestable. De hecho, sus parámetros pueden cambiar en un rango bastante amplio sin afectar los resultados comerciales.
En 1918, Georg Duffing investigó la ecuación de un oscilador con no linealidad cúbica. Este oscilador también puede simular un comportamiento caótico de los precios. Pero tiene una característica más: dependiendo de las condiciones externas y de sus parámetros, este oscilador puede estar en dos estados estables.
La ecuación del algoritmo de trading del oscilador de Duffing es la suma de un oscilador armónico de tercer grado y un binomio cúbico:
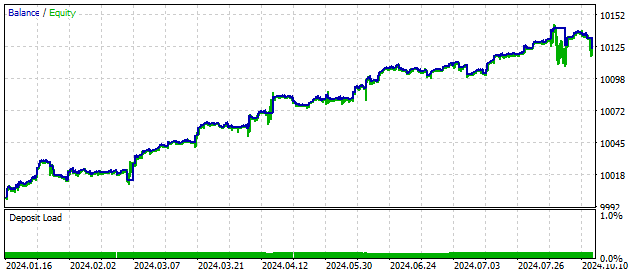
El rendimiento de este oscilador es comparable a otros modelos no lineales.
En general, se pueden crear muchos modelos no lineales. Cualquier función no lineal puede convertirse en un generador de caos. La no linealidad de los tres osciladores anteriores se basaba en algunos principios e ideas físicos. La econofísica es una dirección útil, pero no es en absoluto necesario seguirla en todo momento.
Por ejemplo, agregaré no linealidad al algoritmo comercial basado en la función logarítmica:
Te preguntarás: ¿de dónde salieron estos logaritmos y con qué fundamento los agregué? Mi respuesta será muy sencilla: así lo quise.
Pero si tengo tiempo para pensar en la respuesta, será un poco diferente. ¿Cuál es la diferencia entre precios consecutivos? Digamos 100 puntos. ¿Y qué pasa con la diferencia entre los logaritmos de estos precios? ¿Habrá algo más allí además de ceros? Aquí está mi nueva respuesta: a la izquierda tenemos un oscilador regular y a la derecha tenemos un filtro que puede influir en la apertura de posiciones. El filtro sólo se mostrará cuando el precio se mueva fuertemente. Comprobamos su funcionamiento.
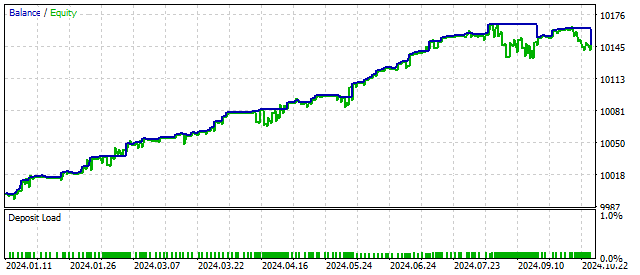
El resultado es similar al funcionamiento de un oscilador con no linealidad cuadrática. El filtro está funcionando. Pero es importante recordar que todas las ideas deben probarse primero en el probador antes de aplicarlas en la práctica.
Fuerzas externas
Hasta ahora hemos estado analizando osciladores autónomos. Imagínese un péndulo. Se balancea uniformemente de un lado a otro. Sus ciclos se repiten una y otra vez. Por qué este péndulo oscila, por qué oscila de esta manera particular, son preguntas que no podemos responder. Este es un ejemplo de un oscilador de funcionamiento libre.
Ahora, empuja ese péndulo. Primero de una manera, luego de la otra. Los ciclos del péndulo comenzaron a cambiar: su frecuencia instantánea y su amplitud cambiaron. Bajo la influencia de fuerzas externas, el péndulo dejó de ser autónomo.
Intentemos aplicar el mismo enfoque al oscilador armónico. Su ecuación cambiará y se verá así:
Donde F[n] es una fuerza externa. ¿Qué clase de fuerza es ésta, cómo actúa, hacia dónde se dirige? No sé nada al respecto. Simplemente supongo que existe. Y ahora surge la pregunta: ¿está justificada tal complicación del modelo? Vamos a responderlo.
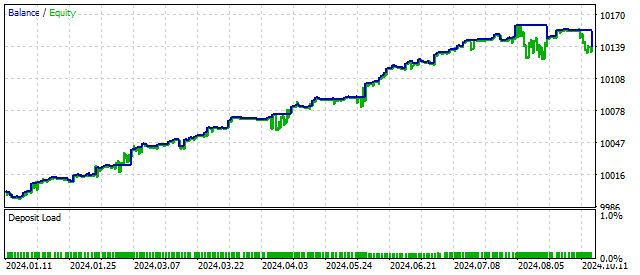
Obtuve este resultado asumiendo que esta fuerza externa está relacionada con los valores de los precios de la siguiente manera:
Hice esta suposición por una sola razón: hablé de diferencias finitas a lo largo del artículo y en este caso también utilicé las proporciones de la segunda diferencia. Eres libre de hacer tus propias suposiciones. Por ejemplo, la fuerza externa puede estar relacionada con la diferencia entre los precios de cierre y apertura, los volúmenes de ticks, etc. También puedes agregar un elemento de no linealidad:
Después de todo, esta fuerza desconocida puede depender de varios componentes. Resume lo más que puedas durante el mayor tiempo posible. Cualquier suposición que usted haga puede tener un impacto positivo en los resultados de sus operaciones.
Conclusión
Como puedes ver, el uso de patrones cíclicos en el trading está bastante justificado. La principal ventaja de estos modelos es que tienen cientos de combinaciones de parámetros que dan un resultado estable durante un largo período de tiempo. El comerciante debe seleccionar varias docenas de opciones que no se correlacionen entre sí.
En este artículo solo he mencionado algunos de los osciladores más populares. Todavía existen bastantes soluciones que se pueden utilizar para construir modelos cíclicos (entre otras cosas).
Probé el EA en las siguientes condiciones: EURUSD, H1, 2024.01.01 - 2024.10.30
Para escribir este artículo se utilizaron los siguientes programas:
| Nombre | Tipo | Descripción |
|---|---|---|
| Harmonic Oscillator | EA |
|
| Damped Harmonic Oscillator | EA |
|
| scr Elliott wave | Script |
|
| Elliott wave | EA |
|
| Generalized Harmonic Oscillator | EA | Valor admisible de ratios: -1000 ... +1000 |
| Sign Oscillator | EA | |
| Quadratic Oscillator | EA | |
| Van der Pol Oscillator | EA | |
| Duffing Oscillator | EA | |
| Log Oscillator | EA | |
| Non-Autonomous Oscillator | EA |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16494
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
Redes neuronales en el trading: Agente multimodal con herramientas complementarias (Final)
Dominando los registros (Parte 1): Conceptos fundamentales y primeros pasos en MQL5
Particularidades del trabajo con números del tipo double en MQL4
Modelos de regresión no lineal en la bolsa de valores
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Este es un gran artículo, pero también es un tarro de galletas, tantas alternativas para probar. ¿Has pensado en construir un mecanismo adaptativo que evalúe las condiciones del mercado e intente elegir la mejor optimización para las condiciones actuales?
Una forma de adaptarse es evaluar varios ciclos a la vez. Además, esto es más fácil de lo que parece. Por ejemplo, se puede hacer así. El primer ciclo - toma los recuentos seguidos. El segundo ciclo - tome las muestras de precios una tras otra. Y así sucesivamente. La combinación de estos ciclos dará una imagen única del estado del mercado en este momento.
🚫 Banderas rojas:
Parámetros por defecto inutilizables:
iPeriod = 870 , R = -940 , S = 450 → valores absurdos para operaciones a corto plazo.
No se activan operaciones:
El EA evalúa la señal sólo una vez por cada nueva barra, y los umbrales lógicos de la señal casi nunca se alcanzan con los parámetros por defecto.
CalcLWMA() utiliza acumuladores estáticos en el original - causando resultados totalmente inválidos en el tiempo.
No hay backtest o validación en el código - y el indicador no se proporciona en el artículo para la inspección visual en tiempo real.
Presume de crecimiento de la renta variable sin pruebas compartibles o enlaces MQ5 Signals.
Se jacta de crecimiento de las acciones sin proporcionar ninguna prueba o referencias a MQ5 Signals.
1. Sobre lo absurdo de los valores - usted lo sabe mejor
2. El EA abre posiciones cuando se abre una nueva barra. Si necesita alguna otra lógica, puede implementar todo usted mismo
3. debería estar claro en el artículo que CalcWMA se utiliza para calcular la media de todos los SMAs.