Redes neuronales en el trading: Optimización del Transformer para la previsión de series temporales (LSEAttention)
217
0
Introducción
La previsión de series temporales multidimensionales resulta fundamental en diversos campos (finanzas, sanidad, etc.) en los que se aborda la tarea de predecir valores futuros a partir de datos históricos. Esta tarea se hace especialmente difícil en las previsiones a largo plazo, ya que en este caso se necesitan modelos capaces de captar eficazmente las correlaciones y dependencias a largo plazo de las series temporales multidimensionales. Las investigaciones recientes se centran en el uso de la arquitectura delTransformer para la previsión de series temporales gracias a su capacidad para captar interacciones temporales complejas mediante el mecanismo de Self-Attention. Sin embargo, a pesar del potencial existente, los métodos actuales de previsión de series temporales multidimensionales siguen basándose más en modelos lineales, lo cual plantea dudas sobre la eficacia de la arquitectura del Transformer en este contexto.
El mecanismo de Self-Attention que subyace en esta arquitectura del Transformer se formula del siguiente modo:
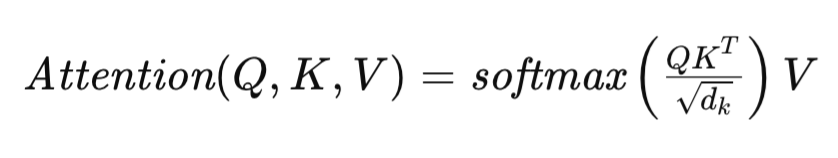
donde Q, K y V representan las matrices Query, Key y Value respectivamente, y dk denota la dimensionalidad de los vectores de descripción de un elemento de secuencia en dichas matrices. Esta formulación permite al Transformer evaluar dinámicamente la importancia de los distintos elementos de la secuencia original, lo que facilita la búsqueda de interdependencias complejas en los datos.
Varias técnicas de adaptación de la arquitectura del Transformer se aplican a la previsión de series temporales a largo plazo. Por ejemplo, el FEDformer aplica un módulo de Fourier avanzado que logra una complejidad lineal en tiempo y espacio, lo que mejora significativamente la escalabilidad y la eficiencia para procesar secuencias largas.
PatchTST abandona la atención puntual y se centra en el nivel de parches en lugar de en pasos temporales individuales, lo cual permite al modelo captar una información semántica más amplia de las series temporales multidimensionales, que es fundamental para una previsión eficaz a largo plazo.
En visión por computadora y procesamiento del lenguaje natural, las matrices de atención pueden experimentar un colapso de entropía o de rango. Este problema se agrava en la previsión de series temporales debido a las frecuentes fluctuaciones inherentes a los datos temporales, lo cual provoca una importante degradación del rendimiento del modelo. Las causas fundamentales del colapso de entropía siguen siendo poco conocidas, por lo que resulta necesario seguir investigando sus mecanismos subyacentes y su impacto en el rendimiento de los modelos. Los autores del artículo "LSEAttention is All You Need for Time Series Forecasting" precisamente intentan solucionar estos problemas.
1. El algoritmo LSEAttention
El objetivo de la previsión multidimensional de series temporales es determinar los valores P futuros más probables para cada uno de los canales C, representados como un tensor Y ∈ RC×P. Esta predicción se basa en datos históricos de series temporales de longitud L con C canales encapsulados en un array de datos inicial X ∈ RC×L. Para resolver el problema que nos ocupa, necesitaremos entrenar un modelo predictivo fωRC×L →RC×P con los parámetros ω, para minimizar el error cuadrático medio (MSE) entre los valores predichos y los reales.
El Transformer se basa en gran medida en su mecanismo de Self-Attention puntual para captar las asociaciones temporales. Sin embargo, dicha dependencia puede conducir a un fenómeno conocido como colapso de la atención, en el que las matrices de atención convergen a valores idénticos en todos los conjuntos de datos de origen y tienden hacia matrices idénticas. Esto provoca una mala generalización de los datos por parte del modelo.
Los autores del método LSEAttention establecen una analogía entre la determinación de los coeficientes de dependencia mediante la función SoftMax y LSE (Log-Sum-Exp) y sugieren que esta es la fuente del problema de inestabilidad numérica, que puede ser la causa principal del colapso de la atención.
El número de condicionamientos de una función determina su sensibilidad a pequeños cambios en los datos de origen. Un número de condicionamientos alto indica que pequeñas perturbaciones de los datos de entrada pueden provocar cambios significativos en la salida.
Esta inestabilidad puede manifestarse en forma de problemas como la sobreatención o el colapso de la entropía, caracterizados por matrices de atención con valores diagonales excesivamente altos (que indican desbordamiento) y valores no diagonales extremadamente bajos (que indican subdesbordamiento).
Para resolver los problemas anteriores, se propone el módulo LSEAttention, que integra el truco Log-Sum-Exp(LSE) junto con la función de activación de la unidad lineal de error gaussiano (GELU). El truco LSE mitiga la inestabilidad numérica derivada del desbordamiento y el subdesbordamiento gracias a la normalización. La función SoftMax puede reformularse usando LSE de la siguiente manera:
donde el exponente de LSE(x) denota la magnitud exponencial de la función log-sum-exp, aumentando la estabilidad numérica.
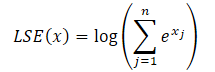
Aprovechando la propiedad de los grados siempre podemos representar el valor del exponente de cualquier número como el producto de dos valores exponenciales.
donde a es la constante usada para la normalización. En la práctica, el valor máximo suele usarse como constante. Sustituiremos el producto de los exponentes en la fórmula LSE y tomaremos el valor total más allá del signo de suma:
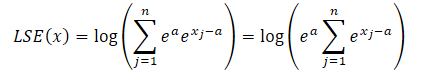
El logaritmo del producto será igual a la suma de los logaritmos, mientras que el logaritmo natural del valor exponencial será igual al exponente de la potencia. Esto nos permitirá simplificar la expresión presentada:
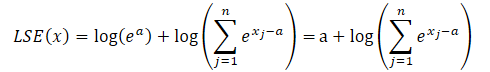
Ahora sustituiremos la expresión obtenida en la función SoftMax y utilizaremos la propiedad de las potencias:
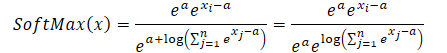
Resulta sencillo ver que el valor exponencial de la constante común al numerador y al denominador es decreciente. Mientras que el exponente del logaritmo natural es igual a la expresión sublogarítmica. Así, obtendremos una expresión SoftMax numéricamente estable.
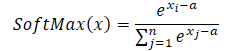
Cuando usamos el valor máximo como constante (a = max(x)), siempre obtenemos x-a menor o igual que 0. En tal caso, el valor exponencial de x-a oscilará entre 0 y 1, sin incluir 0. En consecuencia, el denominador de la función estará en el intervalo (1, n].
Además, los autores del framework LSEAttention sugieren usar la función de activación GELU, que posibilita una activación probabilística más suave. Esto ayuda a estabilizar los valores extremos de la probabilidad logarítmica antes de aplicar la función exponencial, mitigando de esta forma las transiciones bruscas en las estimaciones de atención. Al aproximar la función ReLU mediante una curva suave que incorpora la función de distribución acumulativa (CDF) de una distribución normal estándar, GELU reduce los cambios bruscos en las activaciones que pueden producirse con la ReLU tradicional. Esta propiedad resulta especialmente ventajosa para estabilizar los mecanismos de atención basados en el Transformer, en los que los cambios bruscos de activación pueden provocar inestabilidad numérica y explosión de gradientes.
La función GELU se define formalmente del siguiente modo:
donde Φ(x) representa la CDF de la distribución normal estándar. Esta formulación garantiza que GELU aplique distintos niveles de escalado a las entradas según su magnitud, lo cual reduce la amplificación de los valores extremos. La naturaleza suave y probabilística de GELU permite una transición gradual de los valores de entrada, lo que a su vez mitiga el impacto de las grandes fluctuaciones de gradiente durante el entrenamiento.
Esta propiedad adquiere importancia cuando se combina con el truco Log-Sum-Exp(LSE), que normaliza la función SoftMax de forma numéricamente estable. Juntos, LSE y GELU evitan el desbordamiento y el subdesbordamiento en las operaciones exponenciales en SoftMax, lo que redunda en un rango estabilizado de estimaciones de atención. Esta sinergia aumenta la robustez de los modelos del Transformer al garantizar una buena distribución de los ratios de atención entre los tokens. En última instancia, esto logra gradientes más estables y una mejor convergencia durante el entrenamiento.
En las arquitecturas de Transformer tradicionales, la función de activación ReLU (Rectified Linear Unit) utilizada en el bloque Feed Forward (FFN) es propensa al problema de la "ReLU moribunda", en el que las neuronas pueden quedar inactivas y generar cero para todos los valores de entrada negativos. Esto conduce a estas neuronas a un escenario de gradiente cero, lo que detiene su proceso de aprendizaje y contribuye a la inestabilidad durante el entrenamiento.
Para resolver los problemas anteriores, se utiliza una ReLU paramétrica (PReLU) como función de activación alternativa. La PReLU introduce una inclinación entrenable para entradas negativas, lo que permite una salida distinta de cero incluso cuando la entrada es negativa. Esta adaptación no solo alivia el problema de la ReLU moribunda, sino que también facilita una transición más suave entre activaciones negativas y positivas, mejorando así la capacidad del modelo para aprender en todas las regiones del espacio de valores inicial. La presencia de un gradiente distinto de cero para valores negativos mejora el flujo de gradiente, lo que resulta crucial para entrenar arquitecturas más profundas. En consecuencia, el uso de PReLU contribuye a la estabilidad general del entrenamiento y ayuda a mantener las representaciones activas, lo que en última instancia logra un mejor rendimiento del modelo.
En el Transformer de series temporales LSEAttention(LATST), los autores del framework también añaden la normalización reversible de los datos, que resulta especialmente eficaz para tratar las discrepancias entre la distribución de los datos de entrenamiento y de prueba en los problemas de predicción de series temporales.
La arquitectura conserva el mecanismo temporal tradicional de Self-Attention integrado en el módulo LSEAttention.
En general, la arquitectura LATST consta de una estructura de Transformer de un solo nivel aumentada por módulos de sustitución, lo cual permite un aprendizaje adaptativo preservando la robustez de los mecanismos de atención. Este diseño facilita la modelización eficaz de las dependencias temporales y mejora el rendimiento en las tareas de pronóstico de series temporales. A continuación le mostramos la visualización del framework realizada por el autor.
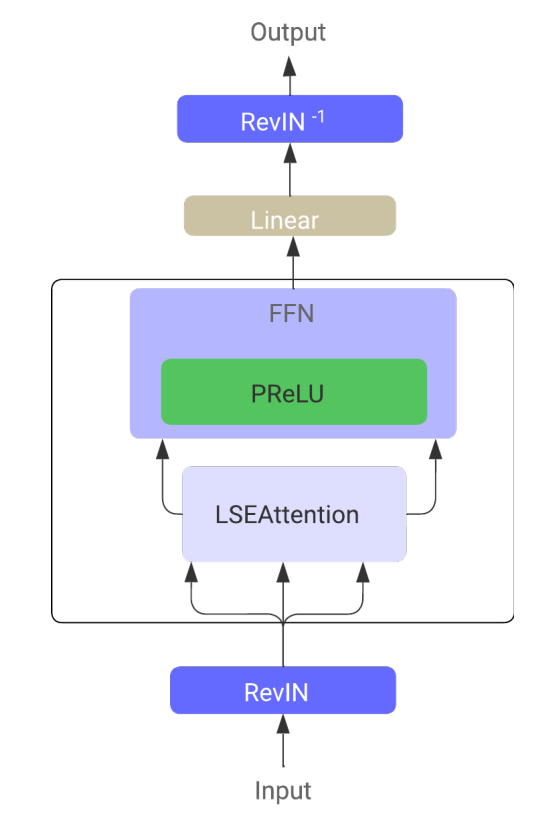
2. Implementación con MQL5
Tras considerar los aspectos teóricos del framework LSEAttention, pasaremos a la parte práctica de nuestro trabajo, en la que consideraremos una de las variantes de implementación de los enfoques propuestos mediante MQL5. Y aquí debemos decir que este artículo será diferente de todos los que hemos hecho antes. La cuestión es que en esta implementación, no crearemos un nuevo objeto para aplicar los enfoques propuestos. En su lugar, añadiremos los enfoques propuestos a las clases que ya se han implementado.
2.1 Ajuste de la capa SoftMax
Tomemos, por ejemplo, la clase CNeuronSoftMaxOCLdentro de la cual se organiza la capa de funciones SoftMax. Utilizaremos mucho esta clase como capa independiente de nuestro modelo y como parte de varios frameworks de trabajo. En concreto, usaremos el objeto CNeuronSoftMaxOCL al crear el módulo de agrupación basado en dependencias CNeuronMHAttentionPooling que hemos utilizado en varios trabajos recientes. Y resulta bastante lógico añadir a nuestro algoritmo el enfoque del cálculo numéricamente estable de los valores de la función SoftMax.
Para ello, modificaremos el funcionamiento del kernel SoftMax_FeedForward. En los parámetros del kernel, obtendremos los punteros a dos búferes de datos: el búfer de valores iniciales y el búfer de resultados.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs) { const uint total = (uint)get_local_size(0); const uint l = (uint)get_local_id(0); const uint h = (uint)get_global_id(1);
Luego planificaremos la ejecución del kernel en un espacio de tareas bidimensional. El tamaño de la primera dimensión será igual al número de valores normalizados dentro de una secuencia unitaria. En la segunda dimensión, indicaremos el número de secuencias unitarias (o cabezas de normalización). En esta caso, además, añadiremos los flujos a los grupos de trabajo dentro de secuencias unitarias individuales.
En el cuerpo del kernel, identificaremos inmediatamente el flujo actual a través de todas las dimensiones del espacio de tareas.
Aquí es donde declararemos un array de datos en la memoria local que se utilizará para el intercambio de datos dentro de los grupos de trabajo.
__local float temp[LOCAL_ARRAY_SIZE];
Y definiremos las constantes de desplazamiento en los búferes de datos globales hasta los elementos correspondientes.
const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE); uint shift_head = h * total;
Para reducir las operaciones de acceso a la memoria global, copiaremos los datos iniciales en las variables locales y controlaremos los valores obtenidos.
float inp = inputs[shift_head + l]; if(isnan(inp) || isinf(inp) || inp<-120.0f) inp = -120.0f;
Observe que estamos limitando el valor inicial a -120, que es casi lo mismo que el valor mínimo de grado para calcular un exponente de tipo float y es una forma adicional de evitar la subestimación. No limitaremos el umbral superior de valores, ya que combatiremos el desbordamiento restando el valor máximo.
A continuación tendremos que determinar el valor máximo de la secuencia unitaria analizada. Para ello, organizaremos un ciclo de recogida de valores máximos en subsecuencias separadas del grupo de trabajo y los escribiremos en los elementos del array local.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp); barrier(CLK_LOCAL_MEM_FENCE); }
Luego determinaremos el valor máximo de nuestro array local creando un ciclo adicional de enumeración de los valores.
uint count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float max_value = temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Después guardaremos el valor máximo obtenido de los elementos del grupo de trabajo actual en una variable local y nos aseguraremos de sincronizar los flujos en esta fase. Es muy importante para nosotros que todos los flujos del grupo de trabajo conserven el valor máximo correcto antes de cambiar posteriormente los elementos del array de memoria local.
Ahora podemos restar el valor del elemento máximo del valor original. También en este caso comprobaremos el umbral inferior de valores. Al fin y al cabo, cuando restamos un valor máximo positivo, corremos el riesgo de salirnos del rango de valores aceptables. A continuación, calcularemos el exponente del valor ajustado.
inp = fmax(inp - max_value, -120); float inp_exp = exp(inp); if(isinf(inp_exp) || isnan(inp_exp)) inp_exp = 0;
Y con la ayuda de dos ciclos consecutivos efectuaremos la suma de los valores exponenciales obtenidos dentro del grupo de trabajo. El algoritmo de ciclo es similar al anterior, utilizado para encontrar el valor máximo. Solo modificaremos la operación en el cuerpo de los ciclos.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? temp[l] : 0) + inp_exp; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); if(l + count < ls) temp[l + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Y ahora que tenemos todos los valores necesarios, podremos calcular los valores finales de la función SoftMax dividiendo cada valor exponencial individual por su suma dentro del grupo de trabajo.
//--- float sum = temp[0]; outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f); }
Luego guardaremos el resultado de las operaciones realizadas en el elemento correspondiente del búfer global de resultados.
Aquí cabe señalar que los cambios introducidos en el algoritmo para calcular la función SoftMax en la pasada directa no requieren una revisión de los algoritmos del pasada inversa. Como se desprende de los cálculos matemáticos presentados en la parte teórica de este artículo, el uso del truco LSE no modifica los valores finales de la función. Por consiguiente, el impacto de los datos originales en el resultado final seguirá siendo el mismo. Y somos libres de usar el algoritmo de distribución del gradiente de error ya disponible.
2.2 Modificación del módulo de atención relativa
Sin embargo, debemos señalar que no siempre utilizamos el algoritmo SoftMax como una capa independiente. En casi todas nuestras implementaciones de los distintos usos de los bloques de Self-Attention, hemos implementado su ejecución dentro de un único kernel de construcción de funcionalidad de atención. Echemos un vistazo ahora al módulo de atención relativa CNeuronRelativeSelfAttention. En él, todo el algoritmo Self-Attention modificado se implementa dentro del kernel MHRelativeAttentionOut. Y, por supuesto, es importante que consigamos un proceso de entrenamiento estable para todos nuestros modelos, independientemente de su arquitectura. Por todo ello, tenemos trabajo por hacer para implementar un SoftMax numéricamente estable en todos los algoritmos similares. Al mismo tiempo, dejaremos los parámetros del kernel y del espacio de tareas sin cambios en la medida de lo posible. Esto es exactamente lo que hicimos al actualizar el kernel MHRelativeAttentionOut.
Sin embargo, debemos considerar que los cambios en los parámetros del kernel y el espacio de tareas de su colocación en la cola de ejecución deben ir acompañados de los cambios correspondientes en todos los métodos envolventes de dicho kernel del programa principal. De lo contrario, existe el riesgo de obtener un error crítico del programa al poner el kernel en la cola de ejecución. Esto se aplica no solo a los cambios en el espacio global de tareas, sino también a los cambios en el tamaño de los grupos de trabajo.
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_local_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_local_size(1); const int heads = get_global_size(2);
En el cuerpo del kernel, identificaremos el flujo actual en el espacio de tareas, como antes. También definiremos todas las dimensionalidades del espacio de tareas.
Aquí también definiremos una serie de constantes necesarias, entre las que se encuentran tanto los punteros de desplazamiento en los búferes de datos globales como algunos valores auxiliares.
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension);
Después declararemos un array en la memoria local, que utilizaremos para intercambiar datos entre los flujos del grupo de trabajo.
__local float temp[LOCAL_ARRAY_SIZE];
Para determinar el coeficiente de atención, según el algoritmo de Self-Attention vainilla, primero tendremos que realizar una operación de multiplicación en los dos vectores correspondientes de los tensores Query y Key. Sin embargo, los autores del framework R-MAT han añadido más elementos de desplazamiento global y dependiente del contexto. La igualdad en el tamaño de todos los vectores utilizados nos permitirá realizar operaciones dentro de un único ciclo con un número de iteraciones igual al tamaño de los vectores. El cuerpo del ciclo realizará la multiplicación por elementos de los elementos de los vectores correspondientes con la posterior suma de los valores obtenidos.
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef;
Luego corregiremos el resultado obtenido por la raíz cuadrada de la dimensionalidad de los vectores. Los autores del Transformador vainilla afirman que esta operación mejora la estabilidad del modelo. Y nosotros no vamos a discutirlo.
Además, los valores obtenidos se traducen al área de valores de probabilidad con la ayuda de la función SoftMax. Aquí añadiremos las operaciones del algoritmo para mejorar la estabilidad numérica. Primero tendremos que determinar el valor máximo entre los coeficientes obtenidos dentro de un grupo de trabajo. Para ello, dividiremos todos los flujos del grupo de trabajo en varios subgrupos, cada uno de los cuales escribirá su valor máximo en uno de los elementos de nuestro array en la memoria local.
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); }
Después organizaremos un ciclo para determinar el valor máximo entre los elementos del array.
uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Y calcularemos el valor exponencial a partir de la capacidad de atención actual menos el valor máximo. Y no olvidaremos de sincronizar los flujos, ya que en el siguiente paso cambiaremos los valores de los elementos del array local y corremos el riesgo de sobrescribir el valor del elemento máximo antes de que sea utilizado por todos los flujos del grupo de trabajo.
sc = exp(fmax(sc - temp[0], -120)); if(isnan(sc) || isinf(sc)) sc = 0; barrier(CLK_LOCAL_MEM_FENCE);
El siguiente paso consistirá en calcular la suma de los valores exponenciales obtenidos dentro del grupo de trabajo. Para ello, al igual que antes, usaremos un algoritmo de dos ciclos consecutivos.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Y ahora podremos llevar los coeficientes de atención al terreno de los valores probabilísticos dividiendo los valores actuales por la suma total.
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Después almacenaremos los valores obtenidos en los elementos correspondientes del búfer de datos global y sincronizaremos los flujos de operaciones dentro del grupo de trabajo.
Por último, tendremos que calcular la suma ponderada de los elementos del tensor Value para cada elemento de la secuencia original. Como ya sabrá, deberemos ponderar los valores según los factores de atención mencionados. Dentro de un mismo elemento de secuencia, esta operación se representará multiplicando el vector de los coeficientes de atención por el tensor Value, al que los autores del framework R-MAT han añadido un tensor de desplazamiento global.
Para realizar las operaciones anteriores, crearemos un sistema de ciclos cuyo ciclo exterior iterará los elementos del último cambio del tensor Value.
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0;
En el cuerpo del ciclo, cada flujo calculará su valor para el elemento correspondiente, que luego se sumará en el grupo de trabajo mediante dos ciclos consecutivos anidados.
//--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
La suma de los valores obtenidos por parte de uno de los flujos del grupo de trabajo se almacenará en el elemento correspondiente del búfer global de resultados.
//--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); barrier(CLK_LOCAL_MEM_FENCE); } }
Después, los flujos de operaciones del grupo de trabajo se sincronizarán y pasaremos a la siguiente iteración del ciclo.
Como hemos comentado anteriormente, la realización de cambios en el algoritmo de la función SoftMax no afectará a la dependencia de los resultados respecto a los datos originales. Por lo tanto, para la funcionalidad de pasada inversa, utilizaremos los algoritmos implementados anteriormente sin modificaciones.
2.3 Función de activación GELU
Además de la estabilización numérica de la función SofMax, los autores del framework LSEAttention proponen utilizar la función de activación GELU. Los autores de esta función de activación proponen dos variantes de su aplicación. Una de ellas se presenta a continuación.
La aplicación de una función de este tipo no es difícil. Nos limitaremos a aumentar la función de cálculo de activación con una nueva variante.
float Activation(const float value, const int function) { if(isnan(value) || isinf(value)) return 0; //--- float result = value; switch(function) { case 0: result = tanh(clamp(value, -20.0f, 20.0f)); break; case 1: //Sigmoid result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f))); break; case 2: //LReLU if(value < 0) result *= 0.01f; break; case 3: //SoftPlus result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value)))); break; case 4: //GELU result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f))); break; default: break; } //--- return result; }
No obstante, tras la simplicidad oculta de la pasada directa nos esperaba la tarea ciertamente difícil de implementar la pasada inversa de esta función. La cuestión es que la derivada de GELU depende del valor inicial y de la sigmoide. Y en nuestra implementación estándar, no tenemos tales valores.
Y no hay forma de expresar exactamente la derivada de la función GELU mediante el resultado de la pasada directa que tenemos. Así que hemos tenido que recurrir a algunas heurísticas y aproximaciones.
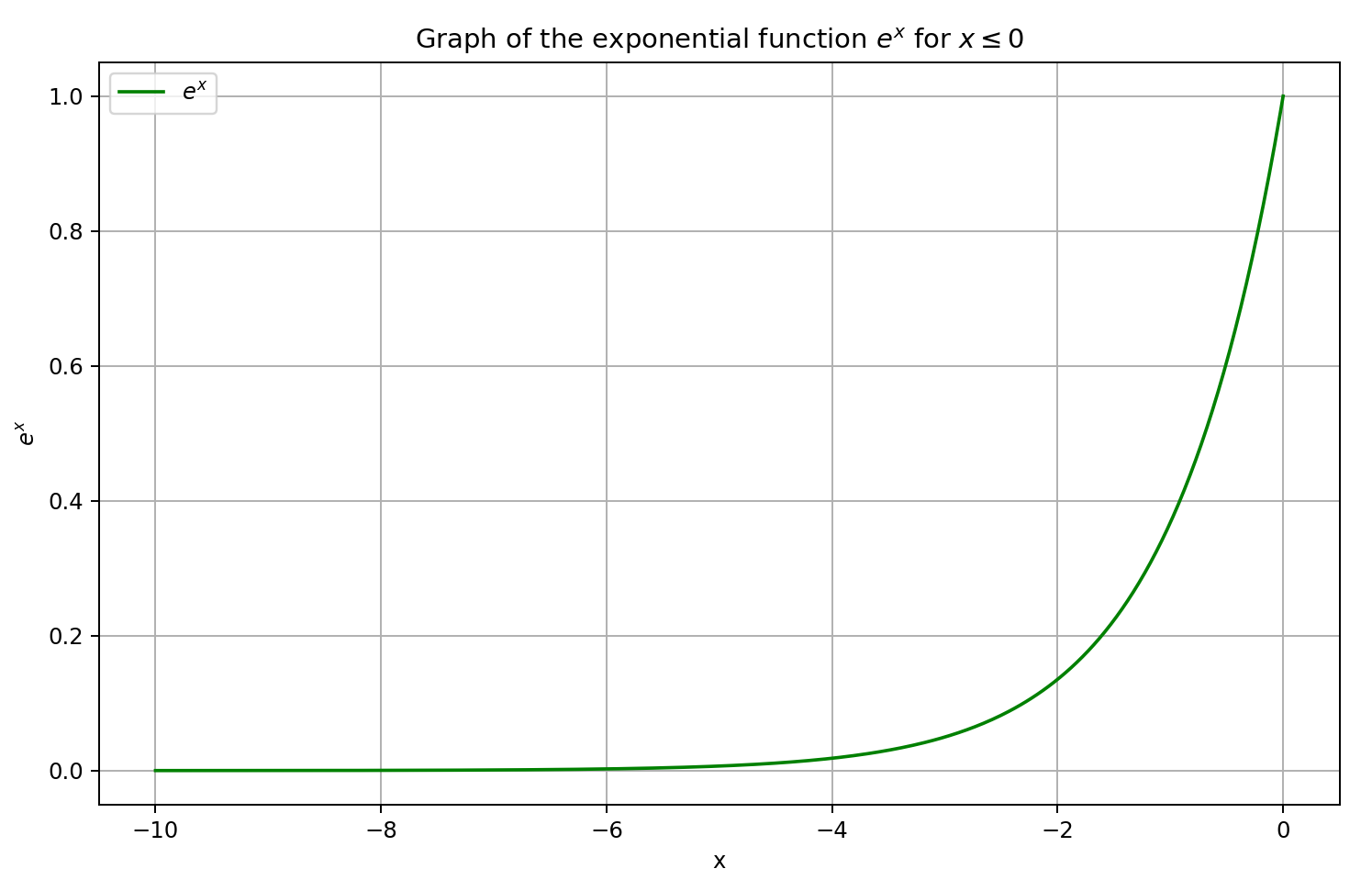
En primer lugar, vamos a recordar el gráfico sigmoide.
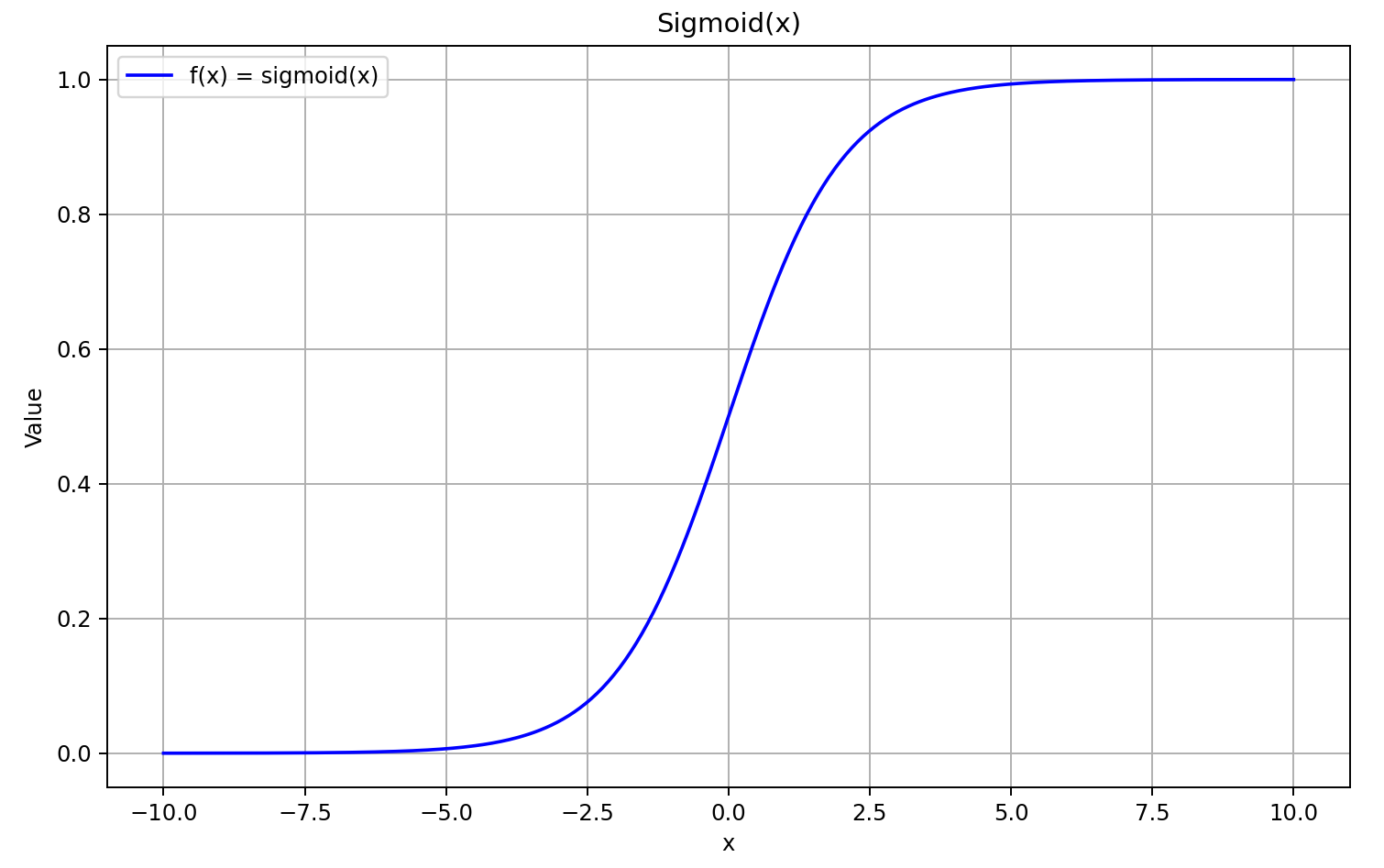
Para valores del argumento superiores a "5" tiende a "1", mientras que para valores inferiores a "-5" tiende a "0". Por lo tanto, para valores suficientemente negativos de X, la derivada de GELU tenderá a "0" como el multiplicador izquierdo de la ecuación tiende a "0". Y para valores positivos suficientemente grandes de X, la derivada tenderá a "1" ya que ambos multiplicadores tienden a "1". Todo esto se ve confirmado por el gráfico siguiente:
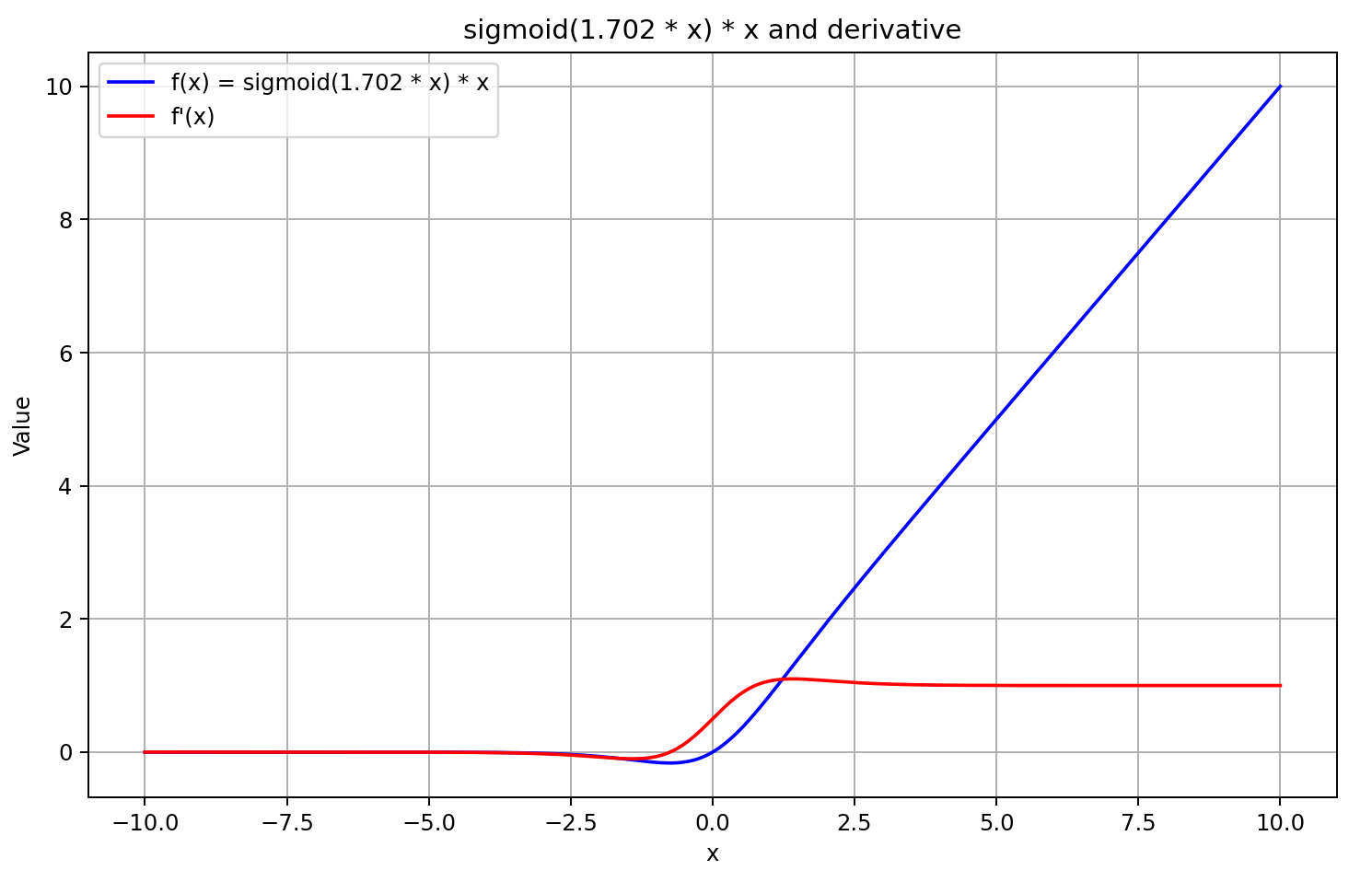
Guiándonos por los supuestos anteriores, aproximaremos la derivada como la sigmoide del resultado de la pasada directa multiplicada por 5. Este enfoque nos ofrecerá un cálculo relativamente rápido del valor de la derivada con una buena aproximación para resultados de GELU mayores o iguales a "0". Y en valores negativos de la función tras una pasada directa, la derivada se fijará en 0,5, lo cual no permitirá seguir entrenando el modelo, al tiempo que la derivada real de la función tenderá a "0" y bloqueará la transmisión del gradiente de error.
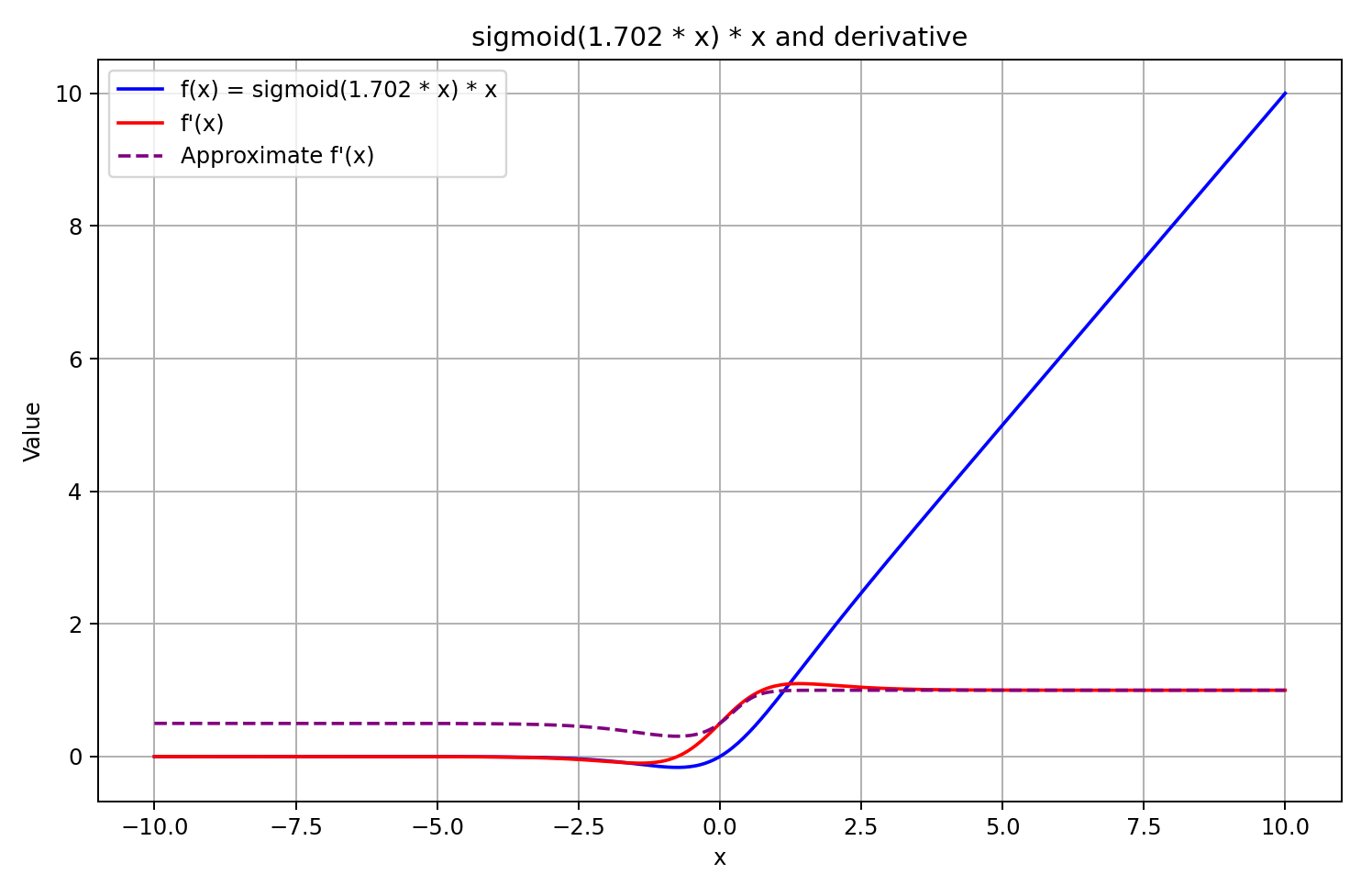
La decisión está tomada. Pongámonos manos a la obra. Para ello, añadiremos un elemento más a la función para calcular la derivada.
float Deactivation(const float grad, const float inp_value, const int function) { float result = grad; //--- if(isnan(inp_value) || isinf(inp_value) || isnan(grad) || isinf(grad)) result = 0; else switch(function) { case 0: //TANH result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value; result *= 1.0f - pow(inp_value, 2.0f); break; case 1: //Sigmoid result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value; result *= inp_value * (1.0f - inp_value); break; case 2: //LReLU if(inp_value < 0) result *= 0.01f; break; case 3: //SoftPlus result *= Activation(inp_value, 1); break; case 4: //GELU if(inp_value < 0.9f) result *= Activation(5 * inp_value, 1); break; default: break; } //--- return clamp(result, -MAX_GRAD, MAX_GRAD); }
Tenga en cuenta que solo calcularemos la función de activación cuando el valor del resultado de la pasada directa sea inferior a "0,9". En otros casos, tomaremos la derivada como "1", lo que resulta coherente con la realidad. De este modo, reduciremos el número de operaciones realizadas en la distribución del gradiente de error.
Los autores del framework sugieren utilizar la función GELU para crear no linealidad entre las capas del bloque FeedForward. En la clase CNeuronRMAT , utilizaremos como bloque especificado un módulo convolucional con retroalimentación CResidualConv. Vamos a cambiar en él la función de activación entre capas. Esta operación se realizará en el método de inicialización de la clase. Las modificaciones puntuales se resaltarán en el código con un guión bajo.
bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false; //--- if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch)) return false; if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[0].SetActivationFunction(GELU); if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch)) return false; if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[1].SetActivationFunction(None); //--- ........ ........ ........ //--- return true; }
Con esto concluirá nuestro trabajo sobre la aplicación de los enfoques propuestos por los autores del framework LSEAttention. El código completo de todas las modificaciones se encuentra en el anexo. Allí encontrará también el código completo de todos los programas utilizados en la elaboración de este artículo.
Debemos decir que todos los programas de interacción con el entorno y de entrenamiento de modelos se han trasladado al completo del artículo anterior. Asimismo, la arquitectura de los modelos se ha mantenido sin cambios. Así que resultará aún más interesante evaluar el resultado del entrenamiento del modelo. Al fin y al cabo, solo los enfoques aplicados pueden afectar al resultado del entrenamiento.
3. Simulación
En este artículo, hemos implementado los enfoques necesarios para optimizar el algoritmo del Transformer vainilla propuesto por los autores del framework LSEAttention para la previsión de series temporales. Como ya hemos dicho, este artículo se diferencia de los presentados anteriormente. No hemos creado nuevas capas neuronales como habíamos hecho antes. Por el contrario, hemos aplicado los planteamientos propuestos en sitios ya realizados. De hecho, hemos tomado el framework HypDiff implementado en el artículo anterior y añadido algunas optimizaciones de algoritmos que no afectaban a la arquitectura del modelo. A menos, por supuesto, que consideremos el cambio de la función de activación en el bloque FeedForward. Sin embargo, los enfoques introducidos han ajustado ligeramente las operaciones computacionales, añadiéndoles estabilidad numérica. Y, obviamente, nos interesa ver cómo afecta esto a los resultados del entrenamiento del modelo.
Para que el experimento resulte más puro, hemos repetido por entero el algoritmo de entrenamiento del modelo HypDiff. Para el entrenamiento, hemos usado la misma muestra de entrenamiento. Sin embargo, esta vez no lo hemos actualizado iterativamente. Sí, esto puede afectar negativamente a los resultados del entrenamiento, pero nos permitirá comparar correctamente el rendimiento del modelo antes y después de optimizar el algoritmo.
Para validar los resultados del entrenamiento del modelo, hemos utilizado los datos históricos reales del primer trimestre de 2024. Ahora le presentamos los resultados de las mismas.
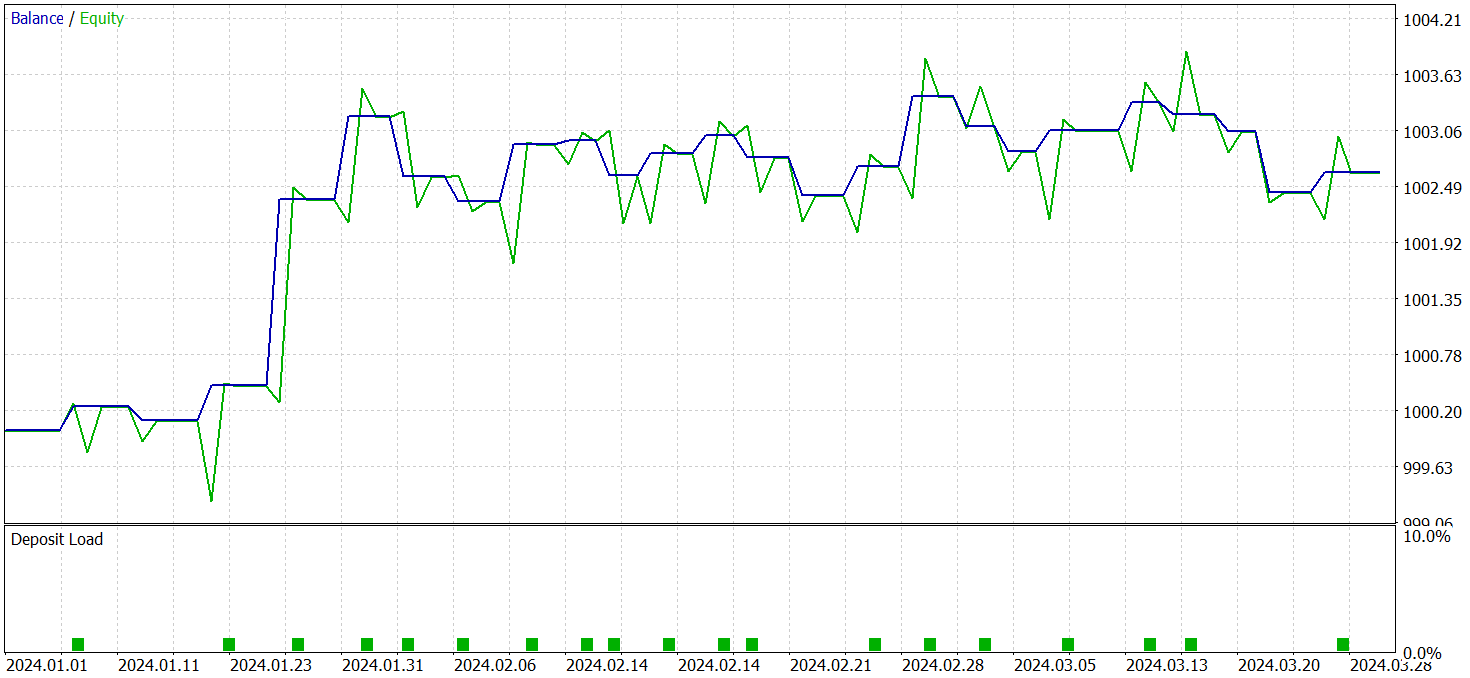
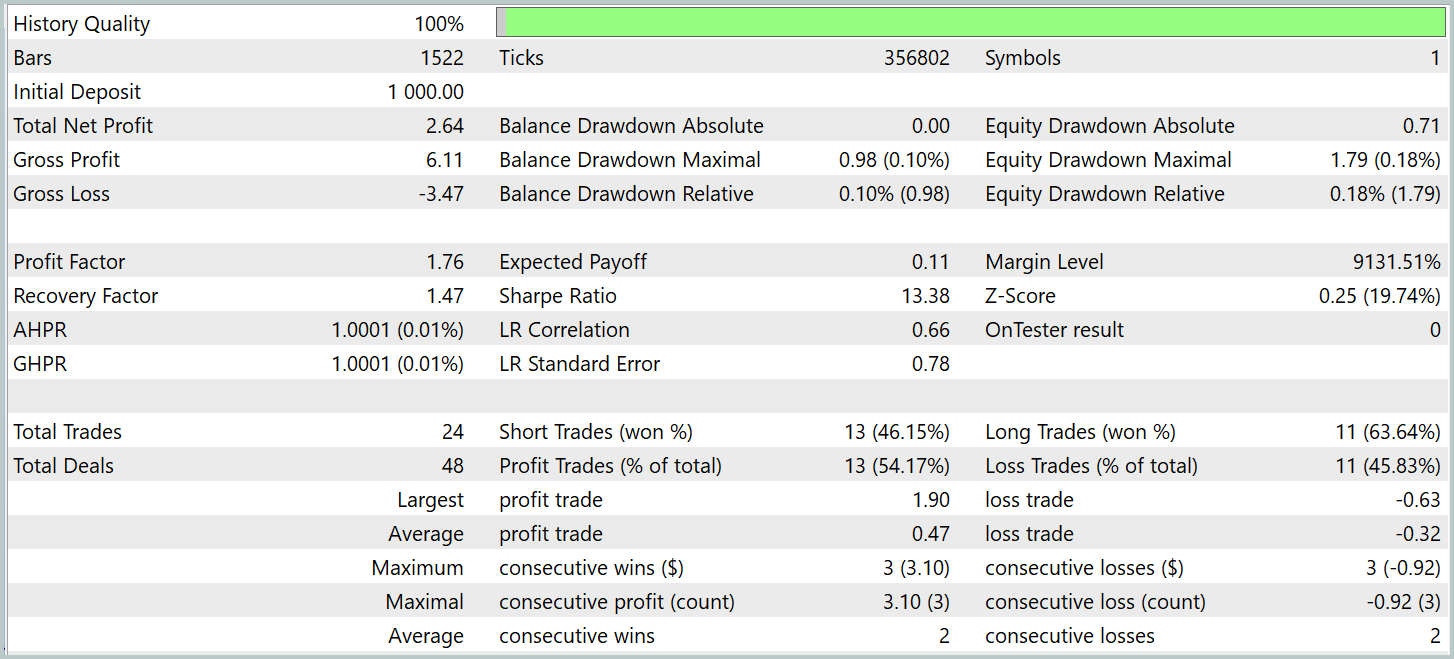
Debemos decir que los resultados del modelo en la muestra de prueba antes y después de la modificación son bastante parecidos. Durante el periodo de prueba, el modelo actualizado ha realizado 24 transacciones. La desviación respecto al modelo básico ha sido de 1 transacción en el nivel de margen de error. Ambos modelos han realizado 13 transacciones rentables. La única mejora visible es la ausencia de reducciones en el mes de febrero.
Conclusión
El método LSEAttention supone un desarrollo de los mecanismos de atención especialmente eficaz en tareas que requieren una gran robustez frente al ruido y la variabilidad de los datos. La principal ventaja de LSEAttention es el uso del suavizado logarítmico implementado mediante la función Log-Sum-Exp. Así se evitan los efectos de desbordamiento numérico y el desvanecimiento, cuya importancia para las redes neuronales profundas es crítica.
En la parte práctica, hemos implementado los enfoques propuestos usando MQL5 en objetos previamente implementados. Asimismo, hemos entrenado y probado los modelos utilizando los enfoques propuestos con datos históricos reales. Según los resultados de las pruebas, podemos concluir que los enfoques propuestos mejoran la estabilidad del proceso de aprendizaje de los modelos.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16360
Operar con noticias de manera sencilla (Parte 4): Mejora del rendimiento
El análisis volumétrico de redes neuronales como clave de las tendencias futuras
Algoritmo de búsqueda orbital atómica - Atomic Orbital Search (AOS) Modificación
Integración de Smart Money Concepts (SMC), Order Blocks (OB) y Fibonacci para entradas óptimas
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso