Algoritmo de Algas Artificiales (Artificial Algae Algorithm, AAA)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de la prueba

Introducción

Las algas, algunos de los organismos más antiguos de la Tierra, desempeñan un papel clave en los ecosistemas acuáticos. Hay más de 45.000 especies de algas, que pueden variar mucho en color, forma, tamaño y hábitat. Proporcionan vida a los medios acuáticos, ya que son la base de la dieta de muchas especies animales, y también producen oxígeno mediante la fotosíntesis, lo que las hace importantes para mantener la vida en el planeta. Estos organismos vivos pueden ser unicelulares o pluricelulares, y a menudo forman colonias que funcionan como una sola unidad.

Las algas unicelulares pueden dividirse por mitosis, creando nuevas células que permanecen unidas entre sí para formar una colonia. Las algas multicelulares pueden reproducirse mediante esporas que se propagan en el agua y germinan en nuevos organismos, formando también colonias. Estos asombrosos organismos demuestran cómo pueden utilizarse los procesos biológicos para crear soluciones innovadoras en modelización y optimización matemáticas.

El Algoritmo Artificial de Algas (AAA), propuesto por Uymaz, Tezel y Yel en 2015, es una combinación de fenómeno natural biológico y elegancia matemática. Este algoritmo metaheurístico de optimización se inspira en el fascinante mundo de las microalgas, cuyos hábitos coloniales y capacidades adaptativas sirvieron de base para la creación de un modelo algorítmico de optimización. Inspirado en la capacidad de las microalgas para desplazarse hacia una fuente de luz, adaptarse a condiciones ambientales cambiantes y reproducirse por mitosis para mejorar la fotosíntesis, AAA se desarrolló para modelar matemáticamente estas propiedades únicas.

El algoritmo incluye tres procesos clave: movimiento en espiral, proceso evolutivo y adaptación. Movimiento en espiral: Simula el movimiento tridimensional de las algas en una solución nutritiva, lo que les permite encontrar las condiciones óptimas para su crecimiento. Proceso evolutivo: Asegura la reproducción de las colonias de algas en las condiciones más adecuadas favoreciendo su desarrollo y mejorando las soluciones. Adaptación: Ayuda a las colonias menos exitosas a parecerse más a la colonia más grande, lo que garantiza su supervivencia y su desarrollo posterior.

Implementación del algoritmo

El Algoritmo Artificial de Algas (AAA) se desarrolló para modelar matemáticamente las propiedades de las algas, como su movimiento en espiral, adaptación y proceso evolutivo. Cada colonia de algas representa una posible solución candidata al problema de optimización (y cada célula de la colonia es una coordenada independiente), y estas colonias se combinan para formar una población de algas. Cada colonia se caracteriza por su tamaño, que refleja la calidad de la solución presentada.

En el proceso evolutivo, las colonias de algas que alcanzan condiciones ambientales más adecuadas son capaces de desarrollarse y crecer. Las colonias que no pueden obtener las condiciones adecuadas no se desarrollan y mueren. Una vez completado el movimiento en espiral, las colonias de algas se clasifican según su tamaño. Una célula elegida al azar de la colonia más grande se copia en la misma célula de la colonia más pequeña, completando así el proceso evolutivo.

Las colonias de algas realizan movimientos en espiral en el agua para conseguir mejores condiciones ambientales. Su energía es proporcional al tamaño de la colonia. Durante el desplazamiento pierden energía, pero si llegan a un entorno mejor, recuperan la mitad de la energía perdida. La energía de una colonia es directamente proporcional a la concentración de nutrientes, por lo que cuanta más energía tenga una colonia, mayor será su frecuencia de movimiento.

La fuerza de fricción es otro factor importante que influye en el movimiento en el agua. Las colonias con una superficie menor tienen una mayor amplitud de movimiento porque su superficie de fricción es menor. Las colonias que logran mejores condiciones tienen una mayor superficie de fricción debido a su tamaño, por lo que las colonias ralentizan sus movimientos, lo que les ayuda a explorar las proximidades de la solución encontrada y aumentar su capacidad de búsqueda local.

La adaptación se produce cuando las colonias de algas que no han alcanzado un desarrollo suficiente durante el movimiento en espiral intentan imitar a la colonia más grande. La colonia con el valor de hambre (hunger) más alto se somete a este proceso. Al comienzo de la optimización, el valor de hambre (hunger) de todas las colonias es cero. Durante el movimiento en espiral, el valor de hambre (hunger) de las colonias que no han encontrado una mejor solución aumenta en uno. Después del movimiento en espiral y del proceso evolutivo, la colonia con mayor valor de hambre (hunger) entra en el período de adaptación. Sin embargo, el proceso de adaptación no ocurre en cada iteración. Primero, se selecciona un valor aleatorio entre 0 y 1. Si este valor es menor que el parámetro de adaptación, se realiza la adaptación.

Pasemos a escribir el pseudocódigo AAA:

Inicialización:
    Crear una población de agentes
    Para cada agente:
        Inicializar una posición aleatoria en el espacio de búsqueda
        Inicializar parámetros (tamaño, energía, hambre, etc.)

Bucle principal:
    Hasta que se alcanza el criterio de parada:
        Para cada agente:
            Realizar el movimiento
            Valore la función de aptitud
        
        Actualizar la mejor solución encontrada
        
        Para cada agente:
            Actualizar la energía
            Actualizar tamaño
            Actualizar el hambre
        
        Realizar la evolución
        Realizar la adaptación

Función de movimiento:
    Para cada agente:
        Seleccionar otro agente mediante la selección de torneo
        Para cada coordenada:
            Actualización de la posición del agente mediante la ecuación de movimiento trigonométrico en espiral
            y el coeficiente de fricción

Función EvolutionProcess:
    Encuentre el agente con el tamaño más pequeño
    Sustituye sus coordenadas por las de un agente seleccionado al azar

Función AdaptationProcess:
    Encuentra al agente con más hambre
    Con cierta probabilidad:
        Encuentre el agente de mayor tamaño
        Actualiza las coordenadas del agente hambriento para acercarlo a las coordenadas
        del gran agente
        Restablecer parámetros de agente hambriento

Función EnergyCalculation:
    Calcular la energía en función del tamaño de la colonia, la concentración de nutrientes
    y tasa de crecimiento actual

Función TournamentSelection:
    Selecciona dos agentes al azar
    Devuelve el agente con el mejor valor de la función de ajuste

Enumeremos las ecuaciones utilizadas en el algoritmo. Las ecuaciones 1-5 se refieren directamente a la aplicación de la lógica básica del algoritmo.

1. Inicialización de la población: población = [[x1_1, x1_2, ..., x1_D], [x2_1, x2_2, ..., x2_D], [xN_1, xN_2, ... , xN_D]], donde xj_i - i célula de la j colonia de algas, D - dimensión de la colonia y N - tamaño de la población.

2. Movimiento en espiral: x'i_j = xi_j + α * cos (θ) * τ (Xi) * p; y'i_j = yi_j + α * sen (θ) * τ (Xi) * p; z'i_j = zi_j + r * v, donde (x'i_j, y'i_j, z'i_j) - nuevas coordenadas de la colonia i, α, θ ∈ [0, 2π], p ∈ [-1, 1], r ∈ [-1, 1], v ∈ [-1, 1], τ (Xi) - área de fricción de la colonia i.

3. Proceso evolutivo: biggest = max (Gi), m = celda seleccionada al azar, smallest.xm = mayor.xm.

4. Adaptación: starving = max (Ai); starving.x = starving.x + (biggest.x - starving.x) * rand.

5. Modelo Monod de crecimiento de las algas: μt = μtmax * St / (St + Kt), donde μt es la tasa de crecimiento de las algas en un tiempo dado t, μtmax es una tasa de crecimiento máxima, St - tamaño de la colonia en un tiempo dado t y Kt es una constante de semisaturación.

6. Área de fricción: τ (Xi) = 2π * (3√ (3*Gi) / (4π))^2, donde τ (Xi) es un área de fricción de la colonia i y Gi es un tamaño de la colonia i.

7. Selección de colonia para el movimiento en espiral: la selección de torneo se utiliza para seleccionar la colonia que se desplazará. A continuación lo analizaremos con más detalle.

8. Selección de dimensiones aleatorias para el movimiento en espiral: p, r, v son índices de medida seleccionados al azar y diferentes entre sí.

9. Selección de una colonia vecina para el movimiento en espiral: Xj es una colonia seleccionada por torneo de selección a la que se moverá la colonia Xi.

10. Hambre inicial de todas las colonias: Ai = 0 para todas las i.

11. Aumento del hambre (hunger) en las colonias que no han mejorado la solución: Ai = Ai + 1, si la colonia no ha encontrado una solución mejor.

12. Selección de una colonia con hambre (hunger) máxima: starving = max (Ai).

13. Probabilidad de adaptación: rand < Ap, donde Ap es un parámetro de adaptación.

Las ecuaciones 6-13 describen detalles adicionales de la implementación del algoritmo, como el cálculo del área de fricción, la selección de colonias para el movimiento, la gestión de la inanición de las colonias y la probabilidad de adaptación.

El modelo de Monod se utiliza con bastante frecuencia para describir el crecimiento y el comportamiento de poblaciones en sistemas biológicos. Se basa en los trabajos de Jacques Monod, un bioquímico francés que estudió la cinética del crecimiento de los microorganismos. La tasa de crecimiento poblacional depende de la concentración del sustrato (nutriente). En bajas concentraciones de sustrato, la tasa de crecimiento es proporcional a la concentración y en altas concentraciones alcanza su máximo. En los algoritmos de optimización, el modelo Monod se utiliza para modelar el crecimiento y la adaptación de las poblaciones en algoritmos evolutivos. Durante la optimización, los parámetros de la población cambian dependiendo de los recursos disponibles, lo que permite un modelado más preciso de los procesos biológicos reales.

Me gustaría llamar su atención sobre la selección del torneo para elegir una colonia. No hemos utilizado este método antes en los algoritmos. Escribamos un guión e imprimamos los resultados para ver claramente la distribución de probabilidades de selección de individuos en la población utilizando este método de selección. La sección de código resaltada en azul participa directamente en la formación de la distribución durante la selección.

input int      PopSize = 50;
input int      Count   = 1000000;
input int      BarWidth = 50; // Histogram width in characters

void OnStart()
{
  int pop[];
  ArrayResize(pop, PopSize);

  for(int i = 0; i < PopSize; i++) pop[i] = PopSize - i;

  Print("Original population:");
  ArrayPrint(pop);

  int tur[];
  ArrayResize(tur, PopSize);
  ArrayInitialize(tur, 0);

  int ind1 = 0, ind2 = 0;

  for(int i = 0; i < Count; i++)
  {
    ind1 = MathRand() % PopSize;
    ind2 = MathRand() % PopSize;

    if(pop[ind1] > pop[ind2]) tur[ind1]++;
    else                      tur[ind2]++;
  }

  Print("Probability distribution (in %):");

  double maxPercentage = 0;
  double percentages[];
  ArrayResize(percentages, PopSize);

  for(int i = 0; i < PopSize; i++)
  {
    percentages[i] = (double)tur[i] / Count * 100;
    if(percentages[i] > maxPercentage) maxPercentage = percentages[i];
  }

  for(int i = 0; i < PopSize; i++)
  {
    int barLength = (int)((percentages[i] / maxPercentage) * BarWidth);
    string bar = "";
    for(int j = 0; j < barLength; j++) bar += "|";

    PrintFormat("%2d: %5.2f%% %s", i, percentages[i], bar);
  }
}

A continuación se muestra el resultado de ejecutar un script para visualizar la distribución de probabilidad de elegir cada individuo de la población:

Población original:
20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1
Distribución de probabilidad (en %):
 0:  9.76% ||||||||||||||||||||||||||||||||||||||||||||||||||
 1:  9.24% |||||||||||||||||||||||||||||||||||||||||||||||
 2:  8.74% ||||||||||||||||||||||||||||||||||||||||||||
 3:  8.22% ||||||||||||||||||||||||||||||||||||||||||
 4:  7.77% |||||||||||||||||||||||||||||||||||||||
 5:  7.27% |||||||||||||||||||||||||||||||||||||
 6:  6.74% ||||||||||||||||||||||||||||||||||
 7:  6.26% ||||||||||||||||||||||||||||||||
 8:  5.78% |||||||||||||||||||||||||||||
 9:  5.25% ||||||||||||||||||||||||||
10:  4.75% ||||||||||||||||||||||||
11:  4.22% |||||||||||||||||||||
12:  3.73% |||||||||||||||||||
13:  3.25% ||||||||||||||||
14:  2.75% ||||||||||||||
15:  2.25% |||||||||||
16:  1.75% ||||||||
17:  1.25% ||||||
18:  0.77% |||
19:  0.25% |

La distribución de probabilidades disminuye linealmente, lo que permite seleccionar las colonias con más posibilidades de buenas soluciones, pero las opciones menos eficientes también tienen posibilidades de ser seleccionadas. Este enfoque de la selección no depende de los valores absolutos de la aptitud de los individuos, lo que proporciona una amplia gama de diversidad de soluciones.

En artículos anteriores, ya hemos considerado ecuaciones para cambiar la distribución de probabilidades durante la selección, pero con la capacidad de proporcionar una disminución tanto lineal como no lineal de las probabilidades, y con menos costes computacionales (para la selección de torneos, se requiere una doble llamada a la función MathRand()).

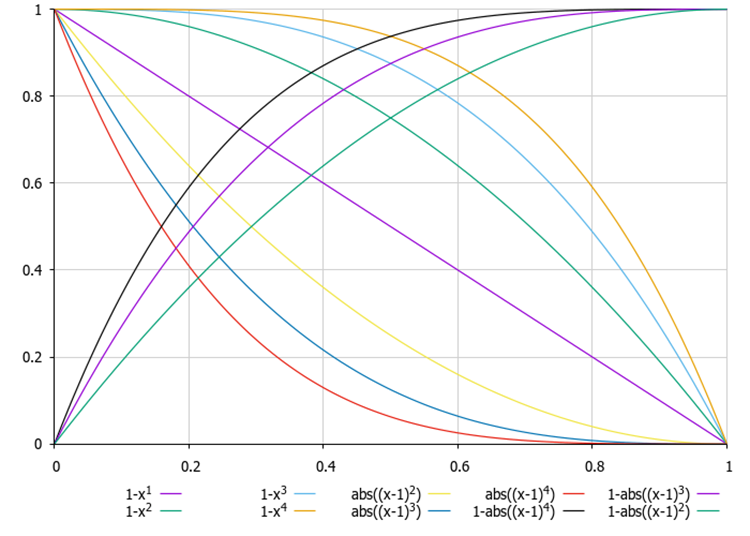
Figura 1. Ejemplos de ecuaciones para cambiar la forma de una distribución de probabilidad, donde x es un número aleatorio distribuido uniformemente en el rango [0.0, 1.0]

Ahora que hemos cubierto todas las complejidades del algoritmo en detalle, podemos comenzar a escribir el código en sí.

Vamos a describir la estructura S_AAA_Agent, que se utilizará para simular la colonia de algas (agente) en el algoritmo. La estructura contiene cuatro campos:

• energy - nivel de energía del agente.
• hunger - nivel de hambre del agente.
• size - Tamaño del agente (altura y longitud de las algas).
  
• friction - relación de fricción que afecta al movimiento del agente.

Init - el método inicializa los miembros de la estructura con valores por defecto. 

Así, la estructura S_AAA_Agent es un modelo de agente simple con características básicas.

//——————————————————————————————————————————————————————————————————————————————
struct S_AAA_Agent
{
  double energy;
  int    hunger;
  double size;
  double friction;

  void Init ()
  {
    energy   = 1.0;
    hunger   = 0;
    size     = 1.0;
    friction = 0.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Escribamos la definición de la clase C_AO_AAA heredada de la clase base C_AO. Esto significa que heredará todos los miembros y métodos de la clase base y podrá extenderlos o sobrescribirlos.

1. En el constructor de la clase, se establecen los valores de varios parámetros relacionados con el algoritmo y también se inicializan:

• popSize  - tamaño de la población.
• adaptationProbability  - probabilidad de adaptación.
• energyLoss - pérdida de energía.
• maxGrowthRate - máxima tasa de crecimiento.
• halfSaturationConstant - constante de media absorción.

Todos estos parámetros se almacenan en la matriz params.

2. El método SetParams actualiza los valores de los parámetros del algoritmo de la matriz params.

3. Las opciones disponibles son:

• Init () - acepta matrices para los valores mínimo y máximo de los parámetros, así como los pasos y el número de épocas.
• Moving () - se encarga de mover o actualizar el estado de los agentes.
• Revision ()  - método para revisar o evaluar un estado.
• EvolutionProcess (), AdaptationProcess (), CalculateEnergy (), TournamentSelection () - los métodos privados son responsables del proceso evolutivo, la adaptación, el cálculo de la energía de las algas y la selección del torneo, respectivamente.
  

Campos de clase:

• adaptationProbability, energyLoss, maxGrowthRate, halfSaturationConstant - variables para almacenar los valores de los parámetros.
• S_AAA_Agent agent []  - conjunto de agentes.
  
• fMin, fMax - valores de aptitud (tamaño de las algas) para una población.

La clase C_AO_AAA es una estructura que permite una cómoda gestión de los parámetros y estados de los agentes, así como la integración en un sistema más amplio basado en la herencia de la clase C_AO.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAA : public C_AO
{
  public: //--------------------------------------------------------------------

  ~C_AO_AAA () { }

  C_AO_AAA ()
  {
    ao_name = "AAA";
    ao_desc = "Algae Adaptive Algorithm";
    ao_link = "https://www.mql5.com/en/articles/15565";

    popSize                = 200;
    adaptationProbability  = 0.2;
    energyLoss             = 0.05;
    maxGrowthRate          = 0.1;
    halfSaturationConstant = 1.0;

    ArrayResize (params, 5);

    params [0].name = "popSize";                params [0].val = popSize;
    params [1].name = "adaptationProbability";  params [1].val = adaptationProbability;
    params [2].name = "energyLoss";             params [2].val = energyLoss;
    params [3].name = "maxGrowthRate";          params [3].val = maxGrowthRate;
    params [4].name = "halfSaturationConstant"; params [4].val = halfSaturationConstant;
  }

  void SetParams ()
  {
    popSize                = (int)params [0].val;
    adaptationProbability  = params      [1].val;
    energyLoss             = params      [2].val;
    maxGrowthRate          = params      [3].val;
    halfSaturationConstant = params      [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double adaptationProbability;
  double energyLoss;
  double maxGrowthRate;
  double halfSaturationConstant;

  S_AAA_Agent agent [];

  private: //-------------------------------------------------------------------
  void   EvolutionProcess    ();
  void   AdaptationProcess   ();
  double CalculateEnergy     (int index);
  int    TournamentSelection ();
  double fMin, fMax;
};
//——————————————————————————————————————————————————————————————————————————————

Veamos en detalle el siguiente método Init de la clase C_AO_AAA:

• rangeMinP - matriz de valores mínimos para cada parámetro.
• rangeMaxP - matriz de valores máximos para cada parámetro.
• rangeStepP - matriz de pasos de cambio para cada parámetro.
• epochsP - número de épocas (por defecto - 0).

Campos de método:

1. El método StandardInit realiza la inicialización estándar con los parámetros pasados. 

2. Cambia el tamaño de la matriz agent a popSize. Esto nos permite preparar un array para almacenar agentes.

3. Establece los valores mínimo y máximo de las funciones utilizadas durante el funcionamiento.

4. El bucle recorre cada agente, inicializándolo mediante el método Init.

5. El bucle interior inicializa las coordenadas de cada agente:

• En primer lugar, la coordenada c se establece aleatoriamente en el rango comprendido entre rangeMin[c] y rangeMax[c] utilizando el método RNDfromCI.
• A continuación, se cambia la coordenada utilizando SeInDiSp, que normaliza los valores.

Si todas las operaciones se realizan correctamente, el método devuelve true. Así, el método Init inicializa el array de agentes con unos rangos y pasos dados para sus coordenadas. Incluye la inicialización estándar, el establecimiento de los límites de la función y la asignación aleatoria de los valores de las coordenadas.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  ArrayResize (agent, popSize);

  fMin = -DBL_MAX;
  fMax =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init ();

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Consideremos el código del método Moving de la clase C_AO_AAA. Estructura general y funcionalidad:

1. Si la variable revision es false, se establece en true, y la función termina. Esto significa que la lógica básica del método Moving no se ejecuta en la primera iteración.

2. El bucle recorre todos los elementos de la población popSize.

3. La selección del torneo se realiza en la función TournamentSelection, que devuelve el índice de uno de los agentes (alga) para su uso posterior.

4. El bucle interior itera sobre cada coordenada (la dimensión del espacio especificada por la variable coords).

5. Se generan tres valores aleatorios: α y β (ángulos) y ρ (el valor en el rango de -1 a 1) utilizando el método u.RNDfromCI.

6. En función del valor de variant (que varía de 0 a 2), se actualizan las coordenadas a[i].c[c]:

• Si variant es 0, se utiliza el coseno del ángulo α.
• Si variant es 1, se utiliza el seno del ángulo β.
• Si variant es 2, se utiliza el valor ρ.

El uso de la variable variant permite simular el movimiento espiral tridimensional de las algas en el espacio multidimensional. La actualización de coordenadas tiene en cuenta la fricción especificada como agent[i].friction.

7. Las coordenadas a[i].c[c] se limitan mediante la función u.SeInDiSp, que establece un valor dentro de un rango y con un paso determinados.

La función Moving implementa el proceso usando cambios aleatorios en las coordenadas de los agentes basados en su estado actual y el estado de otros agentes. El uso de fricción y valores aleatorios nos permite crear dinámicas que simulan el comportamiento de los agentes en el espacio de búsqueda. El código incluye mecanismos que evitan ir más allá de los rangos especificados, lo que es importante para mantener valores de coordenadas válidos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int variant = 0;

    int j = TournamentSelection ();

    for (int c = 0; c < coords; c++)
    {
      double α = u.RNDfromCI (0.0, 2 * M_PI);
      double β = u.RNDfromCI (0.0, 2 * M_PI);
      double ρ = u.RNDfromCI (-1.0, 1.0);

      if (variant == 0) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathCos (α);
      if (variant == 1) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathSin (β);
      if (variant == 2) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * ρ;

      variant++;

      if (variant > 2) variant = 0;

      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Después del método Moving, pasa al método Revision de la clase C_AO_AAA. Este método se encarga de actualizar el estado de los agentes de una población en función de sus características e interacciones. Estructura general:

1. La variable ind se inicializa con el valor de -1. Se utilizará para almacenar el índice del agente con el mejor valor de función.

2. El bucle recorre todos los agentes de la población popSize. Dentro del bucle: si el valor de la función a[i].f supera el máximo actual de fB, 

• Se actualiza el valor máximo de fB.
• El índice del agente con el mejor valor se almacena en la variable ind.
• El agent[i].size tamaño del agente se actualiza según su a[i].f valor de la función de ajuste.
• Se actualizan los valores mínimo fMin y máximo fMax de la función de ajuste para el agente actual.

3. Si se ha encontrado un agente con el máximo valor de ajuste f, sus coordenadas se copian en la matriz cB mediante la función ArrayCopy.

4. Actualización de energía y otros parámetros del agente:

• Su energía se calcula utilizando la función CalculateEnergy.
• Se calcula la fricción, normalizada por fMin y fMax.
• La energía del agente disminuye en energyLoss.
• Si la nueva energía es mayor que la actual, entonces la energía aumenta en la mitad de la pérdida, y el hambre (hunger) del agente se restablece. De lo contrario, aumenta el nivel de hambre.
• Se calcula un factor de crecimiento basado en el tamaño actual del agente y la saciedad, y se actualiza el tamaño del agente.

5. Llamada a procesos: al final de la función, se llama a los métodos EvolutionProcess y AdaptationProcess. Los métodos se encargan de la posterior evolución y adaptación de los agentes en función de su estado actual.

En general, la función Revision se encarga de actualizar el estado de los agentes de una población en función de sus características e interacciones. Incluye análisis, así como la actualización y la llamada a procesos adicionales, lo que permite modelar la dinámica de la población.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;

      ind = i;
    }

    agent [i].size = a [i].f;

    if (a [i].f < fMin) fMin = a [i].f;
    if (a [i].f > fMax) fMax = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].energy   = CalculateEnergy (i);

    agent [i].friction = u.Scale (a [i].f, fMin, fMax, 0.1, 1.0, false);

    agent [i].energy -= energyLoss;

    double newEnergy = CalculateEnergy (i);

    if (newEnergy > agent [i].energy)
    {
      agent [i].energy += energyLoss / 2;
      agent [i].hunger = 0;
    }
    else
    {
      agent [i].hunger++;
    }

    double growthRate = maxGrowthRate * agent [i].size / (agent [i].size + halfSaturationConstant);

    agent [i].size *= (1 + growthRate);
  }

  //----------------------------------------------------------------------------
  EvolutionProcess  ();
  AdaptationProcess ();
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a describir la función EvolutionProcess (). Es responsable de la evolución de los agentes en la población. El propósito principal de esta función es para encontrar el agente menos apto (las algas más bajas) y reemplazar sus coordenadas con las coordenadas de agentes aleatorios más aptos (algas más altas).

1. Encontrar al agente más inadecuado:

• Se inicializa la variable smallestIndex. Almacenará el índice del agente más inadaptado. Inicialmente se establece en 0.
• El bucle recorre todos los agentes (empezando por el primero) y compara su ajuste. Si la ajuste del agente actual es menor que la ajuste del agente con el índice smallestIndex, se actualiza smallestIndex.

2. Copiando coordenadas:

• Se inicializa la variable m para almacenar un índice de agente aleatorio.
• El bucle itera por todas las coordenadas desde 0 hasta coords.
• Dentro del bucle, se llama al método u.RNDminusOne (popSize). Genera el índice aleatorio m en el rango comprendido entre 0 y popSize 1.
• Entonces las coordenadas del agente más inadecuado por índice smallestIndex se sustituyen por las coordenadas de un agente aleatorio por índice m.

La función EvolutionProcess implementa un mecanismo de evolución simple, en el que el agente menos apto de la población recibe las coordenadas de un agente aleatorio. Esta operación forma parte del mecanismo de adaptación, que permite a los agentes mejorar sus características seleccionando coordenadas más acertadas de otros agentes. En general, realiza las funciones combinatorias del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::EvolutionProcess ()
{
  int smallestIndex = 0;

  for (int i = 1; i < popSize; i++)
  {
    if (agent [i].size < agent [smallestIndex].size) smallestIndex = i;
  }

  int m = 0;

  for (int c = 0; c < coords; c++)
  {
    m = u.RNDminusOne (popSize);

    a [smallestIndex].c [c] = a [m].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

Echemos un vistazo más de cerca al código de la función AdaptationProcess (). Es responsable de la adaptación de los agentes en la población, en función de su hambre (hunger) y tamaño. El objetivo principal de la función es cambiar las coordenadas del agente más hambriento si se cumple una determinada condición de probabilidad de adaptación.

1. En busca del agente más hambriento (algas):

• Se inicializa la variable starvingIndex, que almacena el índice del agente más hambriento. Inicialmente se establece en 0.
• El bucle itera por todos los agentes (empezando por el primero) y compara el nivel de hambre. Si el nivel de hambre del agente actual es mayor que el del agente con el índice de starvingIndex, se actualiza starvingIndex.

2. Comprobación de la probabilidad de adaptación:

• Se utiliza el método u.RNDprobab (), que genera un número aleatorio (probabilidad). Si este número es menor que la probabilidad de adaptación dada (adaptationProbability), se ejecuta el siguiente bloque de código.

3. Encontrar la mayor alga - agente:

• De forma similar al primer paso, aquí se busca el índice del agente más alto de la población. Inicialmente, biggestIndex se establece en 0.
• El bucle recorre todos los agentes y actualiza BiggestIndex si el agente actual es superior.

4. Adaptación de coordenadas:

• El bucle itera a través de todas las coordenadas.
• Las coordenadas del agente con el índice de starvingIndex se actualizan añadiendo el valor calculado como la diferencia entre las coordenadas del agente más alto y el agente más hambriento, multiplicado por una probabilidad aleatoria.
• Entonces las coordenadas se normalizan utilizando el método u.SeInDiSp (), que comprueba y ajusta las coordenadas dentro de los límites especificados rangeMin, rangeMax y rangeStep.

5. Actualización del estado del agente:

• El tamaño del agente se actualiza con el valor de ajuste f de la matriz a.
• El nivel hunger se establece en 0, lo que significa que el agente está lleno.
• La energy del agente se establece en 1.0. Este es el valor máximo.

La función AdaptationProcess implementa el mecanismo de adaptación que permite al agente más hambriento mejorar sus coordenadas tomándolas prestadas del agente más alto si se cumple la condición de probabilidad. Esto forma parte de un sistema que imita la selección natural, donde los agentes se adaptan al entorno para mejorar sus posibilidades de supervivencia.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::AdaptationProcess ()
{
  int starvingIndex = 0;

  for (int i = 1; i < popSize; i++) if (agent [i].hunger > agent [starvingIndex].hunger) starvingIndex = i;
  
  if (u.RNDprobab () < adaptationProbability)
  {
    int biggestIndex = 0;

    for (int i = 1; i < popSize; i++) if (agent [i].size > agent [biggestIndex].size) biggestIndex = i;

    for (int j = 0; j < coords; j++)
    {
      a [starvingIndex].c [j] += (a [biggestIndex].c [j] - a [starvingIndex].c [j]) * u.RNDprobab ();

      a [starvingIndex].c [j] = u.SeInDiSp (a [starvingIndex].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }

    agent [starvingIndex].size   = a [starvingIndex].f;
    agent [starvingIndex].hunger = 0;
    agent [starvingIndex].energy = 1.0;
  }
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, tenemos el código de la función CalculateEnergy. Está diseñado para calcular la energía de un determinado agente en función de sus características, como el tamaño de la colonia, el nivel de energía y la concentración de nutrientes. La función devuelve el valor de energía utilizado en otras partes del algoritmo.

1. Inicialización de variables:

• colony_size - obtener la altura de las algas utilizando index.
• max_growth_rate - máxima tasa de crecimiento.
• half_saturation_constant - la mitad de la constante de saturación.

2. Normalización de la función de ajuste: Se calcula el valor normalizado de la concentración de nutrientes. Se calcula como el cociente entre la diferencia entre f (de la matriz a) y el valor mínimo de fMin y el rango comprendido entre fMax y fMin. Añadiendo 1e-10 se evita la división por cero.

3. Obtener la tasa de crecimiento actual: current_growth_rate - obtener el valor actual de la energía del agente, que también se interpreta como la tasa de crecimiento actual.

4. Cálculo de la tasa de crecimiento: growth_rate - se calcula a partir de la tasa de crecimiento máxima, la concentración de nutrientes normalizada y la tasa de crecimiento actual. La ecuación tiene en cuenta el efecto de saturación, por el que la tasa de crecimiento disminuye a medida que aumenta la tasa de crecimiento actual.

5. Cálculo de la energía: energy se calcula como la diferencia entre growth_rate y algunas pérdidas de energía (energyLoss). Este valor muestra cuánta energía recibe el agente después de tener en cuenta las pérdidas.

6. Si la energía calculada es negativa, se establece en0. Esto evita valores energéticos negativos.

7. La función devuelve el valor de energía calculado.

La función CalculateEnergy modela un proceso, en el que un agente gana energía en función de su tasa de crecimiento, el tamaño de la colonia y la concentración de nutrientes. También tiene en cuenta las pérdidas de energía para garantizar un comportamiento realista de los agentes en la simulación. 

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AAA::CalculateEnergy (int index)
{
  double colony_size              = agent [index].size;
  double max_growth_rate          = maxGrowthRate;
  double half_saturation_constant = halfSaturationConstant;

  // Use the normalized value of the fitness function
  double nutrient_concentration = (a [index].f - fMin) / (fMax - fMin + 1e-10);

  double current_growth_rate = agent [index].energy;

  double growth_rate = max_growth_rate * nutrient_concentration / (half_saturation_constant + current_growth_rate) * colony_size;

  double energy = growth_rate - energyLoss;

  if (energy < 0) energy = 0;

  return energy;
}
//——————————————————————————————————————————————————————————————————————————————

El último método consiste en aplicar el mecanismo de selección de torneos. El método TournamentSelection selecciona uno de los dos candidatos de la población en función de sus valores de función de aptitud. Devuelve el índice del candidato que tiene el mejor valor de aptitud. La selección de torneos proporciona selección. Ya hemos considerado anteriormente sus distribuciones de probabilidad entre los agentes de la población.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AAA::TournamentSelection ()
{
  int candidate1 = u.RNDminusOne (popSize);
  int candidate2 = u.RNDminusOne (popSize);

  return (a [candidate1].f > a [candidate2].f) ? candidate1 : candidate2;
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de la prueba

Resultados del banco de pruebas de AAA:

AAA|Algae Adaptive Algorithm|200.0|0.2|0.05|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.5000717048088521
25 Hilly's; Func runs: 10000; result: 0.3203956013467087
500 Hilly's; Func runs: 10000; result: 0.25525273777603685
=============================
5 Forest's; Func runs: 10000; result: 0.37021025883379577
25 Forest's; Func runs: 10000; result: 0.2228350161785575
500 Forest's; Func runs: 10000; result: 0.16784823154308887
=============================
5 Megacity's; Func runs: 10000; result: 0.2784615384615384
25 Megacity's; Func runs: 10000; result: 0.14800000000000005
500 Megacity's; Func runs: 10000; result: 0.097553846153847
=============================
All score: 2.36063 (26.23%)

Tanto la impresión como la visualización del funcionamiento del algoritmo muestran una convergencia débil, lo que confirman los resultados de las pruebas. Por desgracia, no se cumplieron mis expectativas de obtener resultados elevados. Considerando una estrategia de búsqueda compleja para un algoritmo, es difícil determinar las razones de su ineficacia, ya que localiza débilmente el óptimo global. Sin embargo, a pesar de estas deficiencias, el algoritmo sigue teniendo sus ventajas.

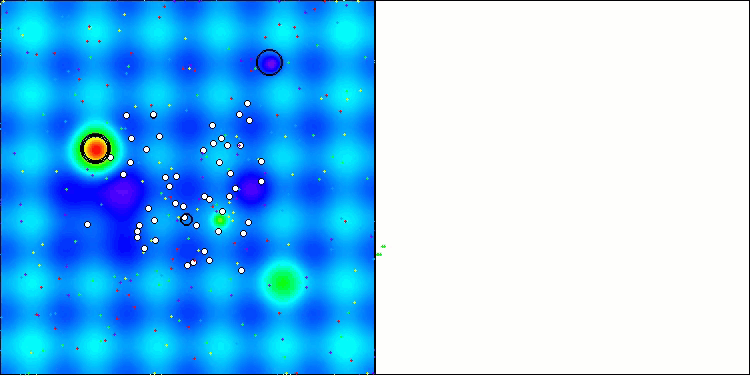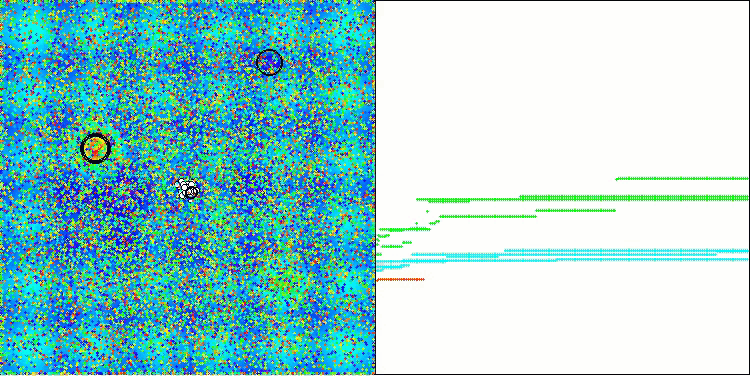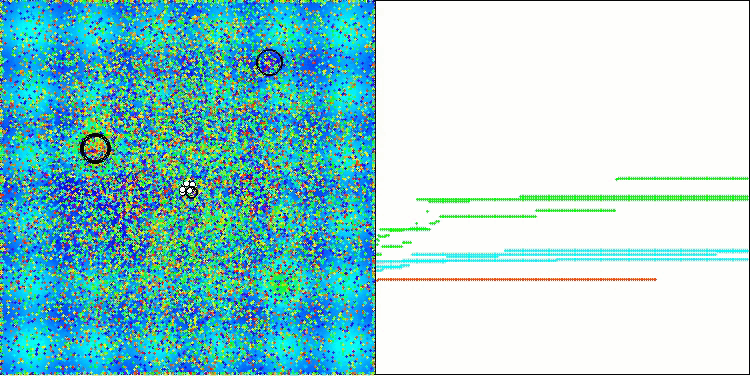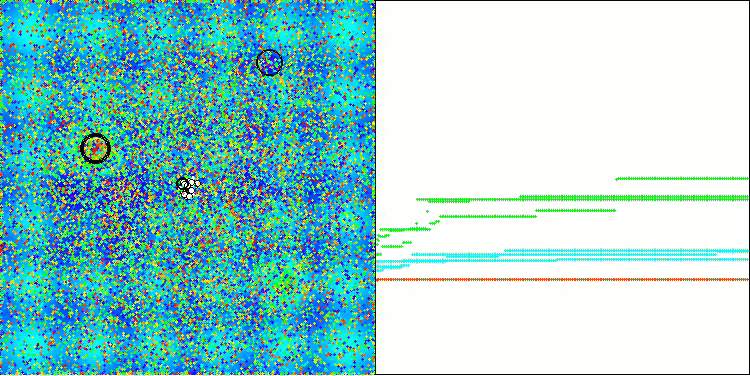
AAA en la función de prueba Hilly.

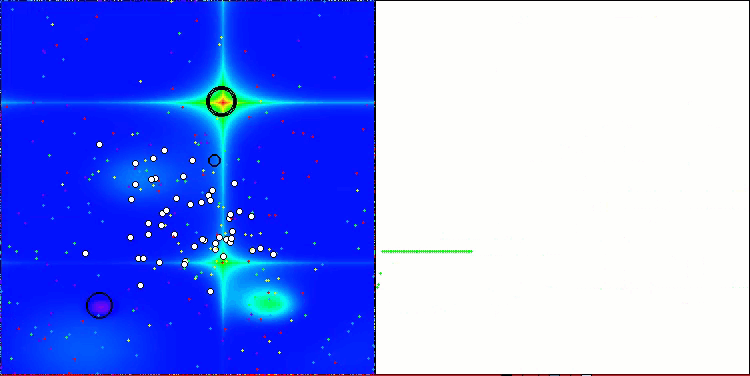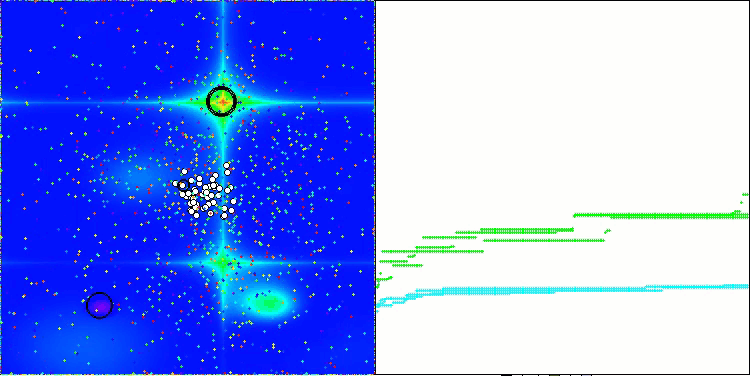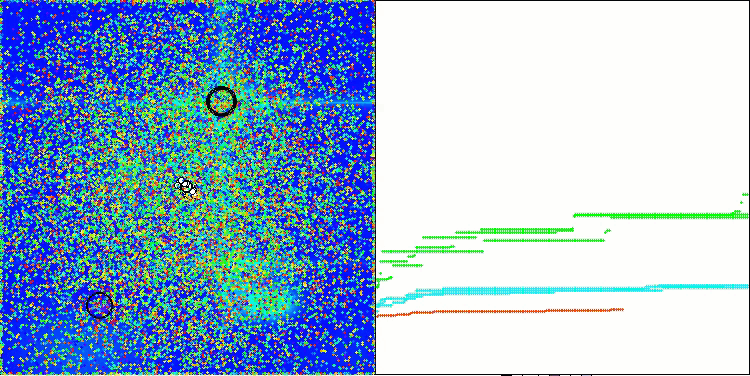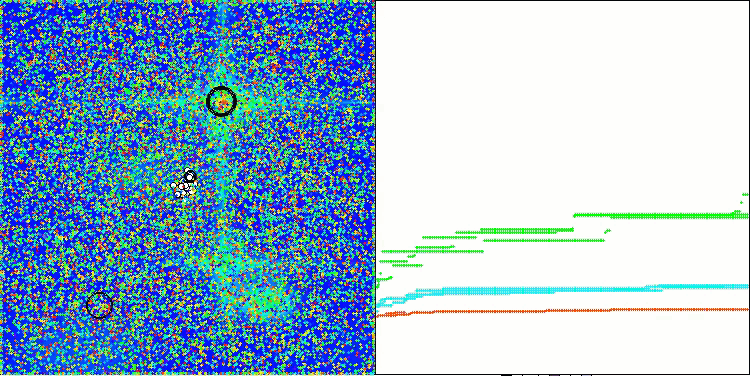
AAA en la función de prueba Forest.

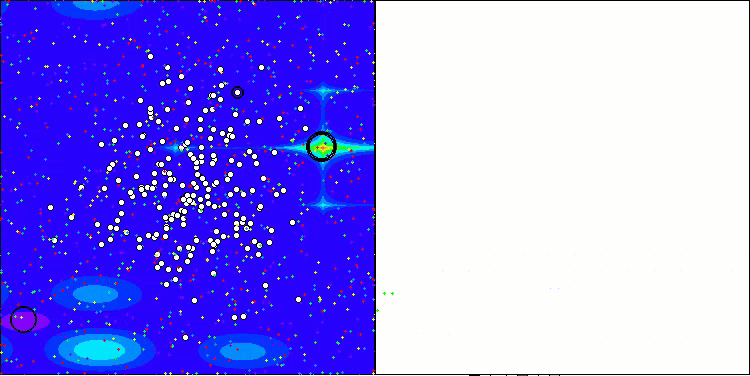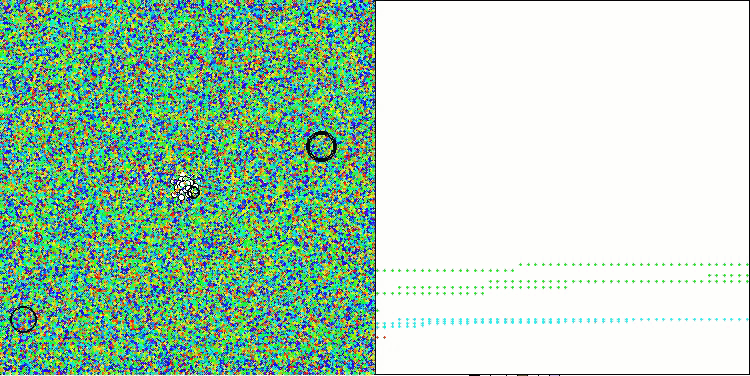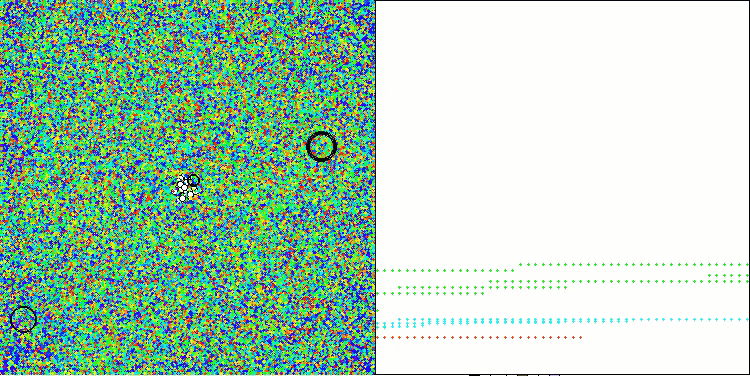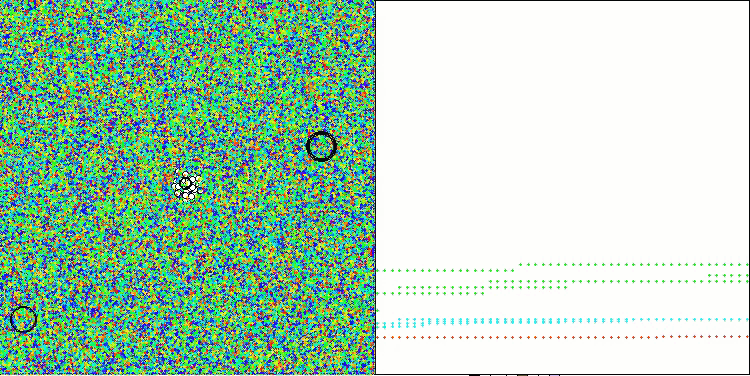
AAA en la función de prueba Megacity.

Según los resultados de la prueba, el algoritmo ocupa el puesto 36 en la tabla de clasificación.

#	AO	Descripción	Hilly			Hilly final	Forest			Forest final	Megacity (discreto)			Megacity final	Resultado final	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	Búsqueda en todo el vecindario (vecinos)	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	Algoritmo de bloqueo de código	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	Optimización de la migración animal M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	Estrategias de evolución (P+O)	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	Algoritmo de cola de cometa	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	Búsqueda de difusión estocástica M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	Evolución de los grupos sociales	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	Recocido isotrópico simulado	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	Búsqueda cooperativa artificial	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	Optimización de la sociedad anárquica	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	Algoritmo de evolución del caparazón de tortuga	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	Evolución diferencial	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	Optimización de reacciones químicas	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	Algoritmo de enjambre de aves	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	Búsqueda de armonía	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	Siembra y crecimiento de plantones	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) Estrategias de evolución	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	BSO	Optimización de la lluvia de ideas	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
19	WOAm	Algoritmo de optimización de ballenas M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
20	AEFA	Algoritmo de campo eléctrico artificial	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
21	ACOm	Optimización de colonias de hormigas M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
22	BFO-GA	Optimización de la alimentación bacteriana - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
23	ABHA	Algoritmo de colmena artificial	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
24	ASBO	Optimización del comportamiento social adaptativo	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
25	MEC	Computación evolutiva de la mente	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
26	IWO	Optimización de malezas invasoras	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
27	Micro-AIS	Microsistema inmunológico artificial	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
28	COAm	Algoritmo de optimización de cuco M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
29	SDOm	Optimización de la dinámica espiral M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
30	NMm	Método de Nelder-Mead M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
31	FAm	Algoritmo de luciérnaga M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
32	GSA	Algoritmo de búsqueda gravitacional	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
33	BFO	Optimización de la búsqueda de alimento bacteriano	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
34	ABC	Colonia de abejas artificial	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
35	BA	Algoritmo de murciélago	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
36	AAA	Algoritmo adaptativo de algas	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
37	SA	Recocido simulado	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
38	IWDm	Gotas de agua inteligentes M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
39	PSO	Optimización del enjambre de partículas	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
40	Boids	Algoritmo de boids	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
41	MA	Algoritmo del mono	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
42	SFL	Salto de rana arrastrado	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
43	FSS	Búsqueda de bancos de peces	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
44	RND	Aleatorio	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
45	GWO	Optimizador de lobo gris	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32

Resumen

La impresión muestra una convergencia baja. Estoy un poco decepcionado con las capacidades del algoritmo: a pesar de utilizar múltiples métodos y una lógica de pasos compleja, ha terminado al final de la tabla. Quizás valga la pena prestar más atención y comprensión a los métodos utilizados, ya que su cantidad no siempre garantiza la calidad. Los lectores son libres de experimentar con él y, si el algoritmo muestra mejores resultados, compártalos. Espero comentarios sobre el artículo.

Los aspectos positivos del algoritmo incluyen buenos resultados en las funciones Forest y Megacity con 1000 variables en comparación con sus competidores más cercanos. Esto demuestra el potencial del algoritmo en términos de escalabilidad para problemas con extremos «agudos» y problemas discretos.

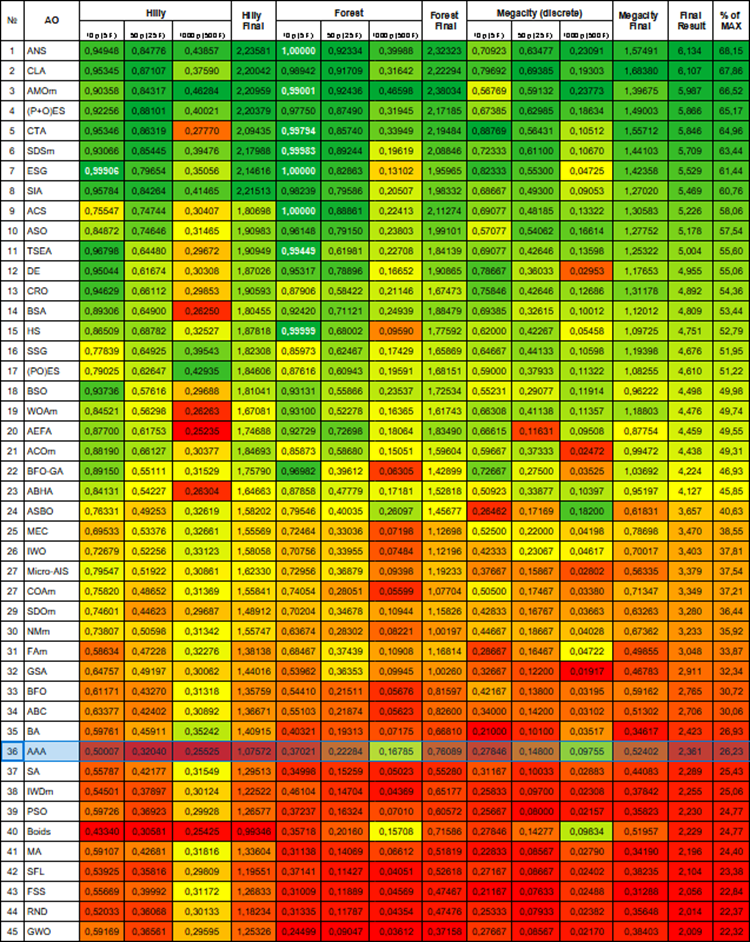
Figura 1. Gradación por colores de los algoritmos según las pruebas pertinentes. Los resultados superiores o iguales a 0,99 se resaltan en blanco.

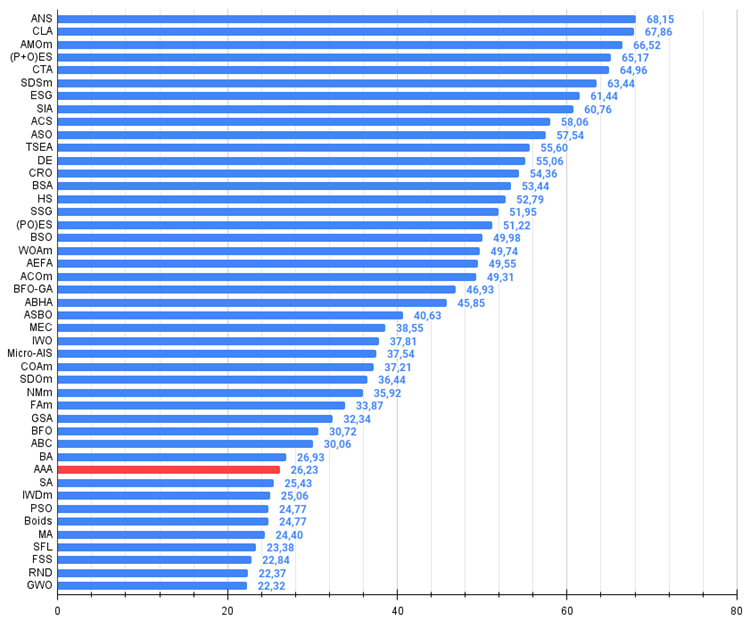
Figura 2. El histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más, mejor,

donde 100 es el máximo resultado teórico posible, el archivo contiene un script para calcular la tabla de clasificación)

Pros y contras de AAA:

Ventajas:

1. Idea prometedora y enfoques innovadores.

Desventajas:

1. Gran cantidad de parámetros (muy difícil de configurar).
   
2. Convergencia débil.
3. Difícil de depurar.

El artículo se acompaña de un archivo con las versiones actuales de los códigos del algoritmo. El autor del artículo no es responsable de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han realizado cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.

• GitHub: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/es/code/49355