Algoritmos de optimización de la población: Algoritmo de búsqueda gravitacional (GSA)

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

El Algoritmo de Búsqueda Gravitacional (GSA) fue propuesto originalmente por E. Rashedi para resolver un problema de optimización, sobre todo para problemas no lineales, siguiendo los principios de la ley de gravitación de Newton. En el algoritmo propuesto, las partículas se tratan como objetos, y su rendimiento se valora en función de sus masas. La gravedad es la tendencia de las masas a acelerarse las unas hacia las otras. Supone una de las cuatro interacciones fundamentales de la naturaleza (las otras son la interacción electromagnética, la interacción nuclear débil y la interacción nuclear fuerte).

Todas las partículas del universo atraen al resto: la gravedad existe en todas partes.  Es la fuerza más débil, pero también la más visible. Gracias al funcionamiento de la fuerza gravitacional, las personas pueden caminar sobre la Tierra y los planetas pueden orbitar alrededor del Sol. La fuerza gravitacional de cualquier objeto es proporcional a la masa del mismo. Así, los objetos con mayor masa tienen más gravedad. La inevitabilidad de la gravedad distingue a esta de todas las demás fuerzas de la naturaleza. El comportamiento de la fuerza gravitacional de Newton se conoce como acción a distancia. Es una ley física general deducida a partir de observaciones empíricas mediante lo que Isaac Newton llamó razonamiento inductivo. Forma parte de la mecánica clásica formulada en el trabajo de Newton «Philosophiae Naturalis Principia Mathematica» («Principios»), publicados por primera vez el 5 de julio de 1687.

Cuando, en abril de 1686, Newton presentó el primer libro de texto inédito a la Royal Society, Robert Hooke afirmó que Newton había obtenido de él la ley de los cuadrados inversos. En el lenguaje actual, la ley establece que cada masa puntual atrae a cualquier otra masa puntual mediante una fuerza que actúa a lo largo de una línea que interseca dos puntos.

2. Descripción del algoritmo

El presente artículo muestra un algoritmo de optimización basado en la ley de la gravedad de Newton: "Cada partícula del universo atrae a todas las demás con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa". En el algoritmo propuesto, los agentes de búsqueda suponen un conjunto de masas que interactúan entre sí basándose en la gravedad newtoniana y las leyes del movimiento. Todos los agentes pueden intercambiar información entre sí, estén donde estén en el espacio de búsqueda, mediante una fuerza de atracción que dependerá de la masa (calculada partiendo de los valores de la función objetivo) y de la distancia entre ellos.

Los agentes se tratan como objetos y su aptitud se mide según su masa. En términos generales (con el algoritmo configurado de forma cercana a las leyes físicas reales), todos estos objetos se atraen entre sí por la fuerza de la gravedad, y dicha fuerza provoca un movimiento global de todos los objetos hacia los objetos de mayor masa. Por consiguiente, las masas interactúan usando una forma directa de acoplamiento, a través de la fuerza gravitacional.

En el GSA clásico, cada partícula posee tres tipos de masas:

(a) Masa activa
(b) Masa pasiva
(c) Masa inerte

En la mayoría de los casos, resulta cómodo y oportuno utilizar la igualdad de estos conceptos para simplificar los códigos y los cálculos y aumentar la eficacia de las capacidades de búsqueda del algoritmo. Por lo tanto, habrá una masa en el algoritmo, en lugar de tres. Las fórmulas de las leyes físicas usadas en el GSA se muestran en la Figura 1.

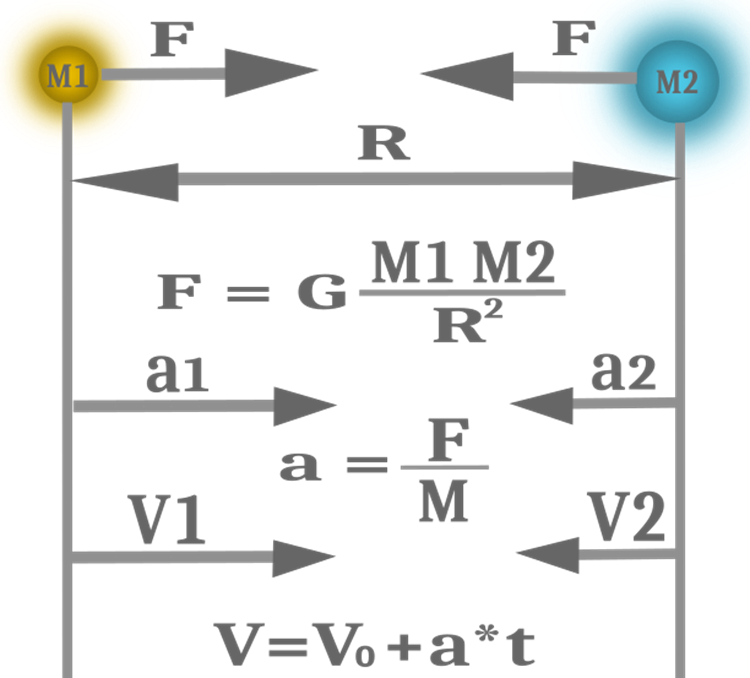
Figura 1. Fuerza gravitacional, aceleración y velocidad.

La posición de las partículas proporciona la solución al problema, mientras que la función de adecuación se usa para calcular las masas. El algoritmo tiene dos etapas: exploración y explotación. Este algoritmo usa las capacidades de reconocimiento al principio para evitar el problema que supone atascarse en un óptimo local, y después explota las áreas de extremos.

El algoritmo de búsqueda gravitacional debe convertir una partícula que se mueve en el espacio en un objeto de una masa determinada. Estos objetos son atraídos por la interacción gravitacional entre sí, y cada partícula en el espacio será atraída por la atracción mutua de otras, creando aceleraciones. Cada partícula es atraída por las demás y se mueve en la dirección de la fuerza. Podemos decir que las partículas con una masa pequeña se desplazan hacia las partículas con una masa mayor, pero los objetos masivos también se desplazan, aunque a una velocidad menor inversamente proporcional a la masa; son los objetos "grandes" los que encuentran la mejor solución, para ello, matizan esta moviéndose a una velocidad lenta en comparación con los objetos "pequeños", que se mueven más rápidamente. El GSA realiza la transferencia de información mediante la interacción entre objetos.

Pasos para el GSA:

1. Inicialización de los agentes
2. Evolución de la aptitud
3. Cálculo de la constante gravitacional
4. Cálculo de las masas de los agentes

1. Inicialización de los agentes.
Todos los agentes se inicializan de manera aleatoria. Cada agente se contempla como una solución candidata. Para que el análisis de estabilidad tenga sentido y sea fiable, resulta crucial especificar las condiciones de equilibrio iniciales. Al fin y al cabo, si el "disco" de objetos inicial no se encuentra en equilibrio, su relajación en los primeros pasos temporales de la simulación puede provocar inestabilidades de poca importancia para nuestra comprensión de la estabilidad de las "galaxias de disco". Desafortunadamente, no conocemos ninguna solución analítica para la densidad, el campo de velocidad y la temperatura de un disco de gas tridimensional en equilibrio hidrostático en el potencial exterior de un halo de materia oscura y/o un disco estelar.

2. Evolución de la aptitud.
La fiabilidad y eficacia del GSA depende del equilibrio entre las capacidades de investigación y explotación. En las iteraciones iniciales del proceso de búsqueda de soluciones, se favorece la exploración del espacio de búsqueda: esto puede conseguirse permitiendo a los agentes usar un tamaño de paso grande en las primeras iteraciones. En iteraciones posteriores, será necesario mejorar el espacio de búsqueda para evitar que se pierdan los óptimos globales. Por consiguiente, las soluciones candidatas deberán tener tamaños de paso pequeños para su uso en iteraciones posteriores.

3. Cálculo de la constante gravitacional.
La constante gravitacional (también conocida como "constante gravitacional universal", "constante gravitacional newtoniana" o "constante gravitacional de Cavendish"), denotada por la letra G, es una constante física empírica que interviene en el cálculo de los efectos gravitacionales en la ley de gravitación universal de Isaac Newton, así como en la teoría general de la relatividad de Albert Einstein. En la ley de Newton, supone una constante de proporcionalidad que relaciona la fuerza gravitacional entre dos cuerpos con el producto de sus masas por el cuadrado inverso de su distancia. En las ecuaciones de campo de Einstein se cuantifica la relación entre la geometría del espacio-tiempo y el tensor energía-momento.

4. Cálculo de las masas de los agentes.
La masa supone la cantidad de materia presente en el espacio.

Pseudocódigo del algoritmo:

1. Generar un sistema de objetos de forma aleatoria.
2. Determinar la aptitud de cada objeto.
3. Actualizar los valores de la constante de gravedad, el cálculo de masas, el mejor y el peor objeto.
4. Calcular las fuerzas que actúan sobre cada coordenada.
5. Calcular las aceleraciones y velocidades de los objetos.
6. Actualizar las posiciones de los objetos.
7. Determinar la aptitud de cada objeto.
8. Repetir desde el paso 3 hasta que se cumpla el criterio de parada.

Vamos a analizar el código del GSA. Para describir un objeto en el sistema de interacción gravitacional necesitaremos la estructura S_Object, que describirá todas las propiedades físicas necesarias del objeto suficientes para realizar la búsqueda gravitacional: with [] - coordenadas en el espacio de búsqueda, v [] - vector de velocidad en cada coordenada (dimensionalidad del array - número de coordenadas), M - masa del objeto (en el GSA la masa es un valor relativo que representa el valor calculado dependiendo de la aptitud máxima y mínima del sistema de objetos), f - valor de aptitud, R [] - distancia euclidiana hasta otros objetos (dimensionalidad del array - número de objetos), F [] - vector de fuerzas en cada una de las coordenadas (dimensionalidad del array - número de coordenadas).

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Vamos a declarar la clase de algoritmo de búsqueda gravitacional C_AO_GSA. De las propiedades físicas de los objetos que intervienen en el algoritmo como agentes, solo necesitamos una cosa: las coordenadas que representan la mejor solución, el valor fB. La clase declara los intervalos de coordenadas permitidos del espacio de búsqueda y el paso. Representemos el sistema de objetos gravitacionales como el array de estructuras S_Object. En el algoritmo clásico solo hay tres parámetros externos: G_constant, a_constant, e_constant, que definen las propiedades de la interacción gravitacional de los objetos, mientras que las otras constantes están incorporadas en las fórmulas de cálculo; sin embargo me ha parecido adecuado poner estas constantes en los parámetros externos del algoritmo, lo cual ofrece una mayor flexibilidad para ajustar las propiedades del algoritmo en su conjunto. Un poco más tarde, veremos con mayor detalle todos los parámetros, ya que influyen mucho en el comportamiento del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

El método público del algoritmo Init () está diseñado para transmitir los parámetros externos del algoritmo a las constantes internas, inicializar las variables de servicio y asignar las dimensiones a los arrays.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

El primer método público llamado en cada iteración es Moving (). Este método contiene toda la física y la lógica del algoritmo de GSA, y es bastante grande, así que lo veremos por partes. Nótese que el método toma como parámetro la iteración actual: el parámetro interviene en el cálculo de la constante de gravedad, ajustando el equilibrio entre exploración y explotación.

La primera iteración supone la fase de inicialización del objeto, y asigna valores aleatorios a todas las coordenadas del objeto dentro de un rango aceptable con una distribución uniforme, comprobando si están fuera de rango. Al inicio del proceso de optimización, todos los objetos tienen una velocidad igual a cero, es decir, se encuentran inmóviles en el espacio de búsqueda en relación con las coordenadas. Nótese que los objetos no tienen masa, por lo que deberían moverse a la velocidad de la luz, pero entonces estaríamos rompiendo las leyes de la física para la primera iteración, porque este momento es algo equivalente al Big Bang. La adaptabilidad de los objetos en este punto es el valor más bajo posible de número double. Al depurar el algoritmo, han surgido dificultades para encontrar errores relacionados con la masa cero, podrá ver la solución a continuación.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

El resto del código Moving () se relaciona con la segunda iteración y siguientes, en las que los objetos ganarán masa, velocidad y aceleración.

En primer lugar, debemos calcular la masa, y como se ha mencionado anteriormente, la masa (por definición, un valor escalar positivo) de los objetos se calcula a partir de los valores de la función de aptitud, por lo que será necesario determinar el valor de aptitud mínimo y máximo, y solo entonces calcular la masa basada en estos valores. En este punto de la iteración anterior, ya hemos obtenido el valor de la función de aptitud.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

En este lugar del código, la masa se calcula usando la fórmula Mo=(Fo-Fmin)/(Fmax-Fmin), donde

• Mo - masa del objeto
• Fo - función de aptitud del objeto
• Fmax - valor de aptitud máximo entre todos los objetos (mejor valor)
• Fmin - valor de aptitud mínimo entre todos los objetos (peor valor)
  

Como podemos ver en la fórmula, la masa solo puede tomar valores positivos comprendidos entre 0 y 1, ambos inclusive. Dado que ya hemos dicho antes que la masa no debe ser cero (de lo contrario la velocidad sería igual a la velocidad de la luz), limitaremos el límite inferior de la masa a 0,1. El valor superior bien puede ser igual a 1. Aquí cabe señalar que si los valores mínimo y máximo de la función de aptitud son iguales, la masa de todos los objetos será la misma para todos e igual a 1. Esto corresponde al caso en que el espacio de búsqueda es homogéneo en la zona donde se encuentran los objetos y todos los objetos son iguales en cuanto a la función de aptitud; asimismo, el movimiento en cualquier dirección tiene la misma prioridad. Parecería que en este caso todos los objetos deberían desplazarse y concentrarse gradualmente hacia un centro de masa común, pero esto no sucede debido a la acción no lineal de la fuerza gravitacional.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Bien, ya hemos calculado la masa de los objetos, ahora necesitamos calcular otro componente de la fórmula R: la distancia euclidiana de cada objeto hasta cada uno de los otros. El cálculo consta de dos ciclos de iteración de objetos y un ciclo de cálculo para cada una de las coordenadas. Como recordaremos, la distancia euclidiana es la raíz de la suma de los cuadrados de las diferencias de coordenadas.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Ahora ya podemos calcular los vectores de fuerza de los objetos. También deberemos iterar por todos los objetos en dos ciclos, además de efectuar otro ciclo para las coordenadas, ya que la velocidad se calcula por separado para cada coordenada. Además, tendremos que añadir una condición para excluir los índices de los objetos que coincidan, de forma que el objeto excluya el cálculo de sí mismo del cálculo de fuerzas. Aquí utilizaremos la conocida fórmula de Newton para calcular la fuerza gravitacional de dos objetos (Figura 1), corrigiendo la distancia por el factor e_constant. Primero calcularemos la constante gravitacional G, que deberá cambiar en cada iteración descendente, suponiendo la intensificación del algoritmo al final de la optimización.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Para que los objetos empiecen a moverse, solo queda calcular la velocidad. La fórmula de la Figura 1 muestra que la aceleración interviene en el cálculo de la velocidad, y que la aceleración es igual a la fuerza que actúa sobre el cuerpo dividida por la masa. Asimismo, la fórmula incluye el tiempo V=V0+a*t, en nuestro algoritmo, el papel del tiempo lo juega la iteración, por lo que el cambio en la velocidad no será otra cosa que el aumento de la velocidad en una iteración. El vector de velocidades ya se ha calculado anteriormente, solo queda dividirlo por la masa; además los autores introducen la perturbación de la fuerza y la perturbación de la velocidad. La perturbación es un número aleatorio que se distribuye uniformemente entre 0 y 1. Esto añade un componente aleatorio al movimiento de los objetos; sin este, el movimiento sería estrictamente determinista y dependería solo de la posición inicial de los cuerpos. Me ha parecido prudente sacar los indicadores de perturbación a los parámetros externos del algoritmo, lo cual permitirá regular el movimiento de los objetos de totalmente determinista a totalmente aleatorio.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

El segundo método obligatorio en cada iteración será Revision (). El método está diseñado para determinar el mejor valor de aptitud en la iteración actual. En un ciclo, iteramos por todos los objetos y sustituimos la mejor solución global.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Vamos a pasar a los resultados de las pruebas. Impresión de los resultados del banco de pruebas con los mejores parámetros del GSA que se han podido encontrar:

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Score: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Score: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Score: 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Score: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Score: 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Score: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Score: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Score: 0.01950

Parámetros del algoritmo:

input double PowerOfdistance_P  = 2.0;   //Power of distance
input double GraviPert_Min_P    = 0.2;   //Gravitational perturbation Min
input double GraviPert_Max_P    = 0.6;   //Gravitational perturbation Max
input double VelocityPert_Min_P = 0.0;   //Velocity perturbation Min
input double VelocityPert_Max_P = 1.0;   //Velocity perturbation Max
input double G_constant_P       = 2.0;   //G constant
input double a_constant_P       = 20.0;  //a constant
input double e_constant_P       = 0.01;  //e constant

PowerOfdistance_P - indicador del grado en que la distancia entre objetos afecta a la formación de los objetos vinculados de forma gravitacional, cuanto mayor sea el grado en la fórmula, menor será la influencia de los objetos sobre otros.

• GraviPert_Min_P - límite inferior del rango de perturbación gravitacional.
• GraviPert_Max_P - límite superior del rango de perturbación gravitacional.
• Cuando GraviPert_Min_P = 1,0 y GraviPert_Max_P = 1,0 no habrá perturbación gravitacional.
• VelocityPert_Min_P - límite inferior del rango de perturbación de la velocidad.
• VelocityPert_Max_P - límite superior del rango de perturbación de la velocidad.

Cuando VelocityPert_Min_P = 1,0 y VelocityPert_Max_P = 1,0 no habrá perturbación de la velocidad.

• G_constante_P es la constante gravitacional y actúa como factor de escala; cuanto mayor sea su valor, más intensas serán las fuerzas gravitacionales y más rápido cambiará la velocidad de los objetos.
• a_constant_P - factor de corrección de la constante gravitacional; tiene por objeto reducir el campo de búsqueda en toda la optimización para afinar los extremos encontrados.
• e_constant_P - factor de corrección para la distancia entre objetos.

Veamos los resultados de la prueba en la visualización. El comportamiento del algoritmo en las funciones de prueba resulta muy peculiar e interesante. En esencia, el experimento muestra visualmente el funcionamiento de las fuerzas gravitacionales. El movimiento de los objetos se ve muy influido por los parámetros externos del algoritmo, al igual que los resultados de optimización resultantes. De inicio, los objetos con velocidad cero se distribuyen aleatoriamente por el espacio de búsqueda y entran en movimiento en la siguiente iteración. Estos ajustes usados en la prueba (los mejores que hemos encontrado) hacen que los objetos se muevan hacia un centro de masa común.

No olvidemos que cada objeto actúa según su gravedad sobre los demás, cuyas leyes de movimiento se describen con bastante precisión en el algoritmo. Cuando los objetos se acercan al centro de masa común, continúan moviéndose, adquiriendo gran velocidad: esto se asemeja a un movimiento pulsante de masa de partículas hacia el centro de masa común y de regreso desde el centro. Tras varias iteraciones, el movimiento de los objetos modifica su trayectoria bajo la influencia del relieve del espacio de la función de aptitud, que actúa como una inhomogeneidad gravitacional, influyendo en la masa de los objetos. Como ya hemos dicho antes, la masa de los objetos se calcula partiendo del valor de la función de aptitud. Aunque es simétrica a lo largo de los ejes, la función Rastrigin tiene un efecto bastante uniforme en el movimiento de los objetos y la descomposición en grupos no resulta especialmente perceptible.

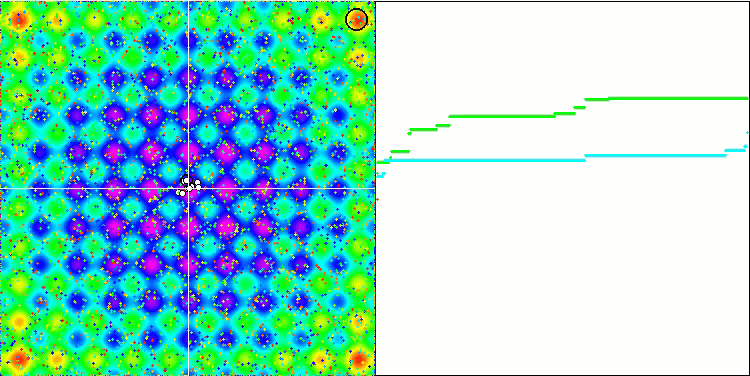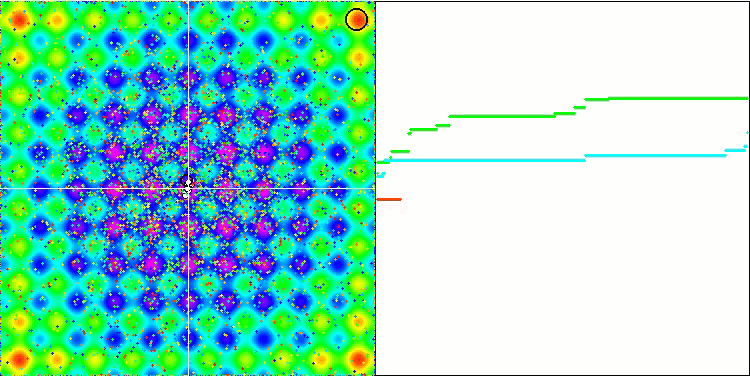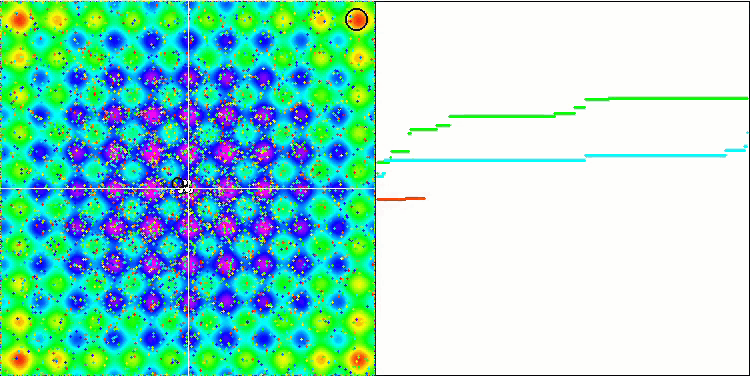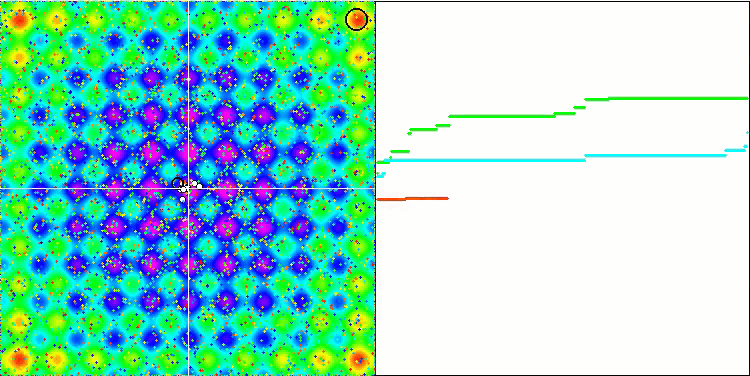
  GSA en la función de prueba Rastrigin.

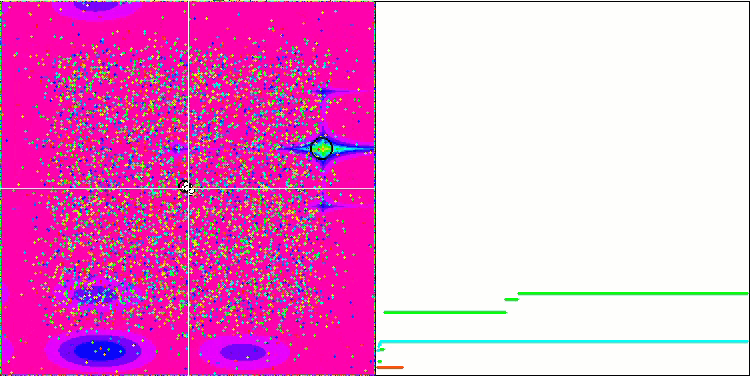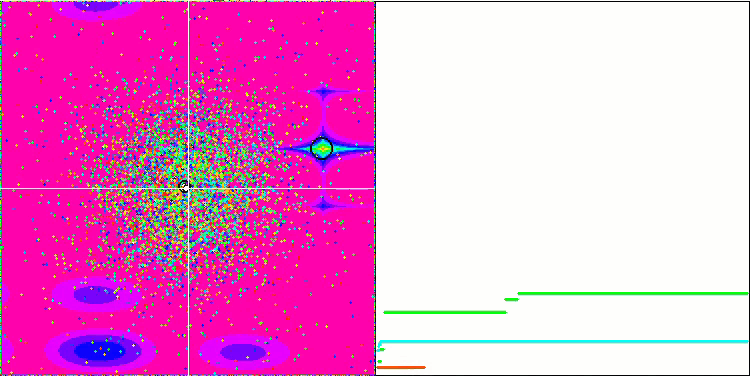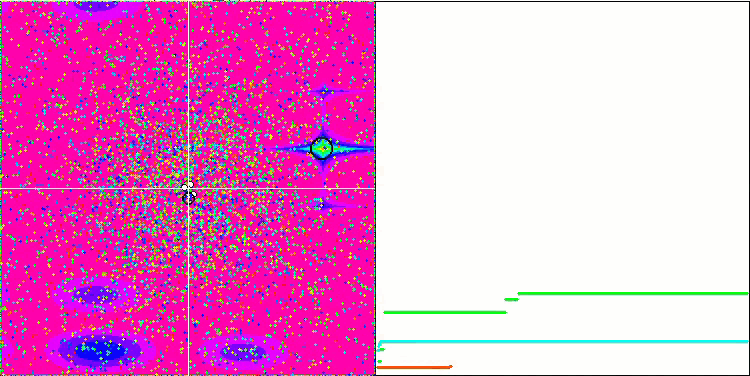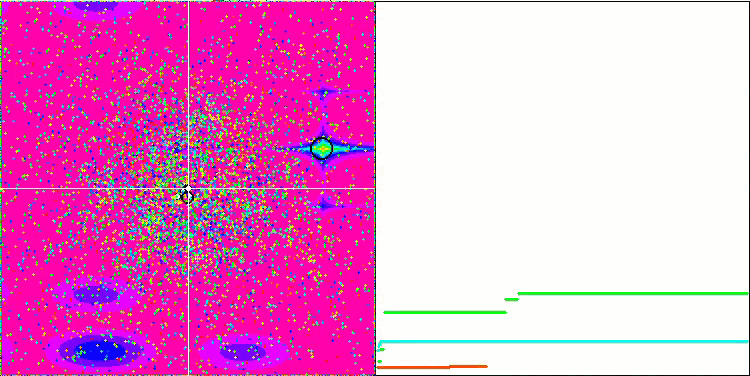
Los objetos muestran un comportamiento aún más interesante en Forest y Megacity. Estas funciones son asimétricas y, por ello, tienen un impacto inhomogéneo en todo el grupo de objetos.

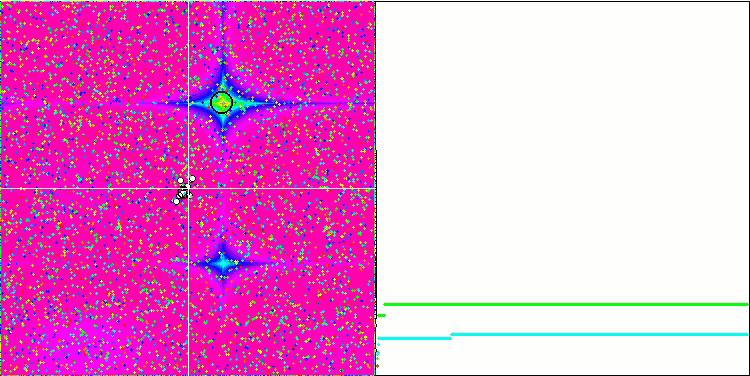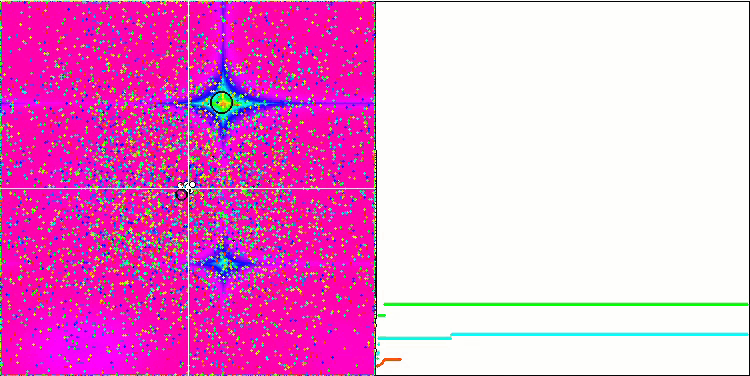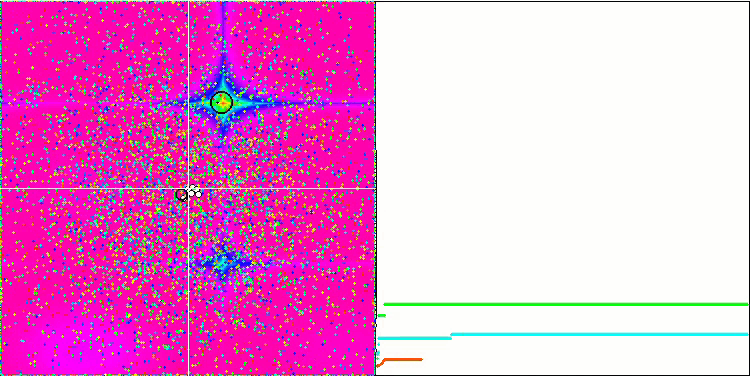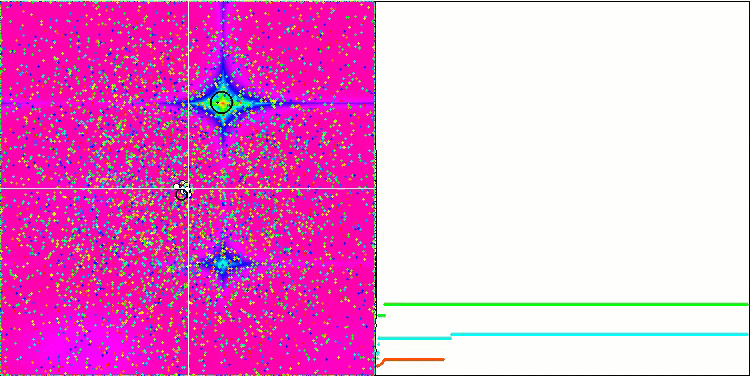
  GSA en la función de prueba Forest.

GSA en la función de prueba Megacity.

Tras mucho experimentar con el GSA, se me ocurrió crear un simulador de movimiento para objetos espaciales. No posee valor práctico, pero nos ofrece una idea de las leyes físicas que se aplican a los sistemas planetarios y estelares. El simulador supone una versión del GSA con los factores de aleatoriedad desactivados. Además, hemos introducido tres objetos que imitan a tres estrellas, una gigante azul, una estrella amarilla y una enana blanca, con parámetros de masa independientes en los ajustes.

Asimismo, hemos creado especialmente para el simulador una nueva función de aptitud, Universe, con un espacio homogéneo. El simulador ilustra cómo el grado (parámetro) de distancia entre los objetos influye en su movimiento mutuo. Así, en la siguiente representación, se aplica el grado 3, en lugar del valor estándar de la ley de Newton, que es 2. Ahora queda claro cómo influye el grado en la formación de sistemas vinculados de forma gravitacional, tales como los sistemas estelares binarios y triples.

Si el grado de distancia fuera mayor en nuestro universo, las galaxias se habrían formado mucho antes de lo que lo hicieron. En la presente animación, podemos ver que ya en las primeras iteraciones han surgido objetos emparejados que orbitan alrededor de un centro de masa común. Como era de esperar, la gigante azul ha reunido el mayor número de objetos a su alrededor en la visualización.

Visualización del simulador de movimiento de objetos espaciales usando como base el algoritmo GSA.

Vamos a analizar los resultados de la prueba de GSA. Las técnicas originales usadas en el algoritmo no le han permitido obtener resultados serios en nuestras pruebas. Las numerosas variaciones de los parámetros probados no han mejorado la convergencia del algoritmo. El algoritmo ha mostrado algunos resultados positivos en relación con otros participantes en la prueba sobre la función Rastrigin suave con 10 variables y Megacity. En las demás pruebas, el GSA obtiene resultados inferiores a la media de la tabla, ocupando el 8º lugar de 12.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
IWO	invasive weed optimization	1,00000	1,00000	0,35295	2,35295	0,79937	0,46349	0,41071	1,67357	0,75912	0,44903	0,94416	2,15231	100,000
ACOm	ant colony optimization M	0,36118	0,26810	0,20182	0,83110	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	0,15901	2,15901	96,805
COAm	cuckoo optimization algorithm M	0,96423	0,69756	0,30792	1,96971	0,64504	0,34034	0,21362	1,19900	0,67153	0,34273	0,48451	1,49877	74,417
FAm	firefly algorithm M	0,62430	0,50653	0,20290	1,33373	0,55408	0,42299	0,64360	1,62067	0,21167	0,28416	1,00000	1,49583	70,740
BA	bat algorithm	0,42290	0,95047	1,00000	2,37337	0,17768	0,17477	0,33595	0,68840	0,15329	0,07158	0,49268	0,71755	59,383
ABC	artificial bee colony	0,81573	0,48767	0,24656	1,54996	0,58850	0,21455	0,17249	0,97554	0,47444	0,26681	0,39496	1,13621	57,393
BFO	bacterial foraging optimization	0,70129	0,46155	0,13988	1,30272	0,41251	0,26623	0,26695	0,94569	0,42336	0,34491	0,53694	1,30521	55,563
GSA	gravitational search algorithm	0,73222	0,67404	0,00000	1,40626	0,31238	0,36416	0,42921	1,10575	0,51095	0,36658	0,00000	0,87753	52,786
FSS	fish school search	0,48850	0,37769	0,13383	1,00002	0,78060	0,05013	0,08423	0,91496	0,00000	0,01084	0,23493	0,24577	20,094
PSO	particle swarm optimisation	0,21339	0,12224	0,08478	0,42041	0,15345	0,10486	0,28099	0,53930	0,08028	0,02385	0,05550	0,15963	14,358
RND	random	0,17559	0,14524	0,09495	0,41578	0,08623	0,04810	0,06094	0,19527	0,00000	0,00000	0,13960	0,13960	8,117
GWO	grey wolf optimizer	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,04119	0,07252	0,30348	1,000

En general, el algoritmo GSA es notablemente sensible a la presencia de un gradiente en la función optimizada, mientras que su baja escalabilidad no permite utilizarlo para tareas serias que contengan muchas variables, por lo que no recomendaría el algoritmo para aplicaciones con redes neuronales y para optimizar sistemas comerciales. Cabe señalar que las capacidades del algoritmo de búsqueda gravitacional, en mi opinión, no se han explorado por completo, y la investigación adicional de los usuarios puede revelar nuevos aspectos positivos desconocidos de este algoritmo tan interesante e inusual desde todos los puntos de vista. Las principales ventajas del algoritmo son su independencia respecto a la mejor solución global encontrada y la posibilidad de que todos los agentes interactúen entre sí. 

Encontrará el histograma con los resultados de la prueba del algoritmo en la Figura 2.

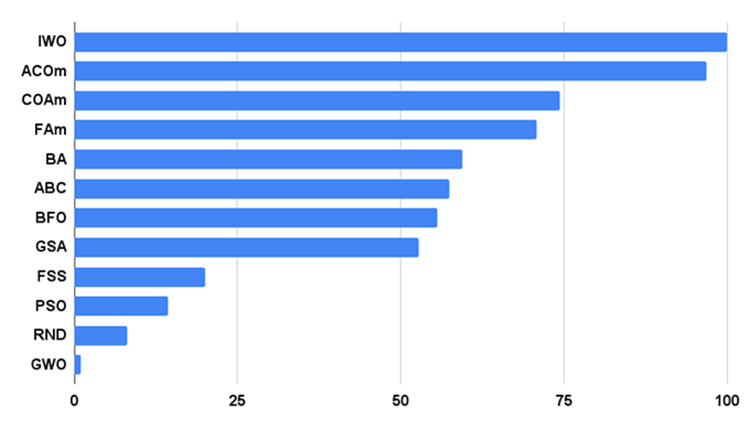
Figura 2. Histograma con los resultados finales de los algoritmos de prueba.

Conclusiones sobre las propiedades del algoritmo de optimización de búsqueda gravitacional (GSA):

Ventajas:
1. Facilidad de implementación.
2. Buen rendimiento en funciones suaves con pocas variables.

Desventajas:
1. Alta complejidad computacional.
2. Malos resultados en las funciones discretas.
3. Mala escalabilidad.