Características del Wizard MQL5 que debe conocer (Parte 43): Aprendizaje por refuerzo con SARSA

Introducción

El aprendizaje por refuerzo (Reinforcement Learning, RL) permite a los sistemas de negociación aprender de su entorno o de los datos del mercado y, de este modo, mejorar su capacidad de negociación con el tiempo. RL permite adaptarse a las condiciones cambiantes del mercado, lo que lo hace adecuado para determinados mercados financieros y valores dinámicos. Los mercados financieros son impredecibles, ya que a menudo se caracterizan por un alto grado de incertidumbre. RL destaca en la toma de decisiones en condiciones de incertidumbre, ya que ajusta continuamente sus acciones en función de la información recibida (recompensas), lo que resulta muy útil para los operadores a la hora de gestionar condiciones de mercado volátiles.

Una comparación paralela a esto podría ser un Asesor Experto que se adjunta a un gráfico y también se optimiza periódicamente a partir del historial de precios reciente para ajustar sus parámetros. RL pretende hacer lo mismo, pero con menos bombo y platillo. En la parte de esta serie dedicada hasta ahora al RL, lo hemos utilizado en su sentido estricto, como un tercer enfoque del aprendizaje automático (además del aprendizaje supervisado y el no supervisado). Aún no lo hemos considerado como un modelo independiente que pueda utilizarse en la elaboración de previsiones.

Eso cambia en este artículo. No solo introducimos un algoritmo RL diferente, SARSA, sino que buscamos implementarlo dentro de otra clase de señal personalizada de asesores expertos ensamblados por el asistente como un modelo de señal independiente. Cuando se utiliza como modelo de señal, el RL automatiza el proceso de toma de decisiones, reduciendo la necesidad de una intervención humana constante, lo que a su vez (al menos en teoría) podría permitir el comercio de alta frecuencia y una respuesta en tiempo real a los movimientos del mercado. Además, al recibir retroalimentación continua de su mecanismo de recompensa, los modelos de RL tienden a aprender a gestionar mejor el riesgo. Esto se consigue penalizando las acciones de alto riesgo con bajas recompensas, lo que tiene como efecto neto que RL minimiza la exposición a operaciones volátiles o deficitarias.

Sin embargo, en principio, el RL también consiste en equilibrar la exploración y la explotación, es decir, equilibrar el intento de nuevas estrategias con el uso de las que ya son rentables. Esto es posible gracias a un enfoque «epsilon-greedy» para actualizar el Q-Map, que es una matriz de acciones en los posibles estados ambientales entre los que un agente puede seleccionar una acción.

También hay otras ventajas de RL que pueden parecer anecdóticas, pero que vale la pena mencionar dado el creciente papel de RL en la IA.

Puede ayudar a optimizar la ejecución de las operaciones bursátiles al aprender el mejor momento y los mejores precios para comprar o vender, basándose en datos históricos y comentarios en tiempo real, mejorando así la rentabilidad. Esto se puede lograr cuando, como modelo de señal base, tal y como ocurre en este artículo, se combina con otra señal, de modo que su función se reduce a determinar el cómo, en situaciones en las que se utilizan órdenes pendientes. Si Q-Map ofrece, por ejemplo, tres acciones de órdenes limitadas, órdenes stop y órdenes de mercado, se pueden ajustar los puntos de entrada de una estrategia ya establecida y familiar.

RL es un poco poco convencional, a diferencia de los modelos lineales tradicionales, y quizá sea más adecuado para aprender y ejecutar estrategias comerciales complejas y no lineales, que posiblemente reflejen mejor el comportamiento real del mercado. RL también es escalable para gestionar múltiples clases de activos o estrategias simultáneamente, dependiendo de cómo se defina su Q-Map y las acciones asociadas, lo que lo convierte en una solución versátil para la gestión de carteras o el trading algorítmico en diversos instrumentos financieros. Por último, es especialmente adecuado para sistemas de toma de decisiones en tiempo real, que no solo incluyen asesores expertos totalmente automatizados, sino que pueden ampliarse para incluir incluso sistemas de negociación semimanuales y asesores expertos, dependiendo de la estrategia y la configuración actual de cada uno.

Introducción a SARSA

SARSA, acrónimo de State-Action-Reward-State-Action (Estado-Acción-Recompensa-Estado-Acción), debe su nombre a la forma en que se actualizan los valores del Q-Map. Este método de actualización de los valores Q difiere claramente del enfoque de aprendizaje Q que analizamos en un artículo anterior en el sentido de que se trata de un enfoque dentro de la política, a diferencia del enfoque fuera de la política que examinamos entonces. De hecho, nuestra implementación de SARSA para este artículo es idéntica a la que utilizamos en aquel artículo cuando presentamos el aprendizaje Q, salvo por la forma en que se actualizan los valores del mapa Q.

El algoritmo de política de SARSA significa que aprende los valores Q en función de las acciones que ya ha tomado, siguiendo su política actual y no las acciones que está a punto de tomar en función del estado actual del entorno. Actualiza los valores Q utilizando la acción que fue elegida por la misma política que sigue. Por otro lado, el aprendizaje Q es un algoritmo fuera de política, lo que significa que actualiza los valores Q utilizando la mejor acción posible del siguiente estado del entorno, independientemente de la acción que haya tomado la política actual. Aprende la política óptima independientemente de las acciones actuales del agente. Implementamos esta actualización de los valores Q para SARSA según la política de la siguiente manera:

//+------------------------------------------------------------------+
// Update Q-value using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q-action from Q-Map
   double _action = Q[act[1]][e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _action *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  if(i == act[0])
      {  continue;
      }
      Q[i][e_row[1]][e_col[1]] += THIS.alpha * (Reward + (THIS.gamma * _action) - Q[act[0]][e_row[1]][e_col[1]]);
   }
}

La regla de actualización SARSA utiliza la acción real realizada en el siguiente estado (Estado → Acción → Recompensa → Estado → Acción). Sigue la política epsilon-greedy para la exploración y el aprendizaje. Esto es muy similar a lo que se analizó con Q-Learning, sin embargo, lo que entonces no estaba claro, pero ahora se ha puesto de relieve, es cómo la selección epsilon-greedy puede dar lugar a resultados muy inconsistentes, ya que el proceso de actualización del Q-Map es aleatorio. Por regla general, cuanto menor es el valor de épsilon, menores son los efectos aleatorios.

Cuando se trata de equilibrar la exploración y la explotación, SARSA tiene un enfoque más equilibrado porque sigue la misma política tanto durante el aprendizaje como durante la toma de decisiones, lo que en teoría significa que es más seguro en entornos inciertos como algunos mercados financieros. Por otro lado, el aprendizaje por refuerzo (Q-Learning) tiende a ser más agresivo, ya que siempre busca la máxima recompensa del siguiente estado, lo que lo hace más propenso a tomar decisiones de alto riesgo en entornos volátiles.

Por lo tanto, SARSA es más adecuado para situaciones en las que es fundamental mantener un equilibrio entre la exploración y la explotación, y el entorno es arriesgado o no estacionario. El mejor ejemplo que se me ocurre para esto sería, por ejemplo, operar con cualquiera de los pares de yenes japoneses. Por el contrario, el aprendizaje por refuerzo (Q-Learning) es más adecuado cuando el entorno es relativamente estable y es más importante encontrar la estrategia óptima que gestionar el riesgo continuo. Una vez más, probablemente el mejor ejemplo de esto podría ser el par EURCHF.

También consideramos otro algoritmo RL, Deep-Q-Networks, en este artículo, y también difiere de SARSA en varios aspectos. A primera vista, la principal diferencia radica en cómo SARSA, al igual que Q-Learning, utiliza una tabla Q para almacenar los valores de estado-acción. Esto limita SARSA a entornos con espacios de estado pequeños, ya que los entornos más grandes hacen que mantener una tabla Q sea poco práctico. Sin embargo, como vimos en ese artículo, las DQN utilizan redes neuronales para aproximar los valores Q de cada par estado-acción, lo que las hace más escalables y eficaces en entornos con espacios de estado grandes o continuos.

En lo que respecta a la repetición de experiencias, SARSA no utiliza esta función, ya que aprende de cada experiencia de forma secuencial. Esto puede conducir a un aprendizaje ineficaz, ya que el agente solo aprende de la experiencia más reciente. Por otro lado, sin embargo, DQN puede implementar la reproducción de experiencias, en la que las experiencias pasadas se almacenan en un búfer y se muestrean aleatoriamente durante el entrenamiento. Esto puede contribuir en gran medida a reducir la correlación entre experiencias consecutivas, lo que a su vez puede conducir a un aprendizaje más estable.

Otra diferencia entre SARSA y DQN radica en el uso de redes objetivo. SARSA no tiene ese concepto, ya que actualiza los valores Q directamente en cada paso basándose en la política actual. Por otro lado, como vimos en el artículo sobre DQN, el uso de una red objetivo junto con la red Q principal para estabilizar el aprendizaje es obligatorio. Con las DQN, la red objetivo se actualiza periódicamente, lo que proporciona actualizaciones estables del valor Q y evita grandes oscilaciones en el aprendizaje.

La escalabilidad y la complejidad son otra forma abstrusa en la que DQN y SARSA difieren, ya que SARSA es más adecuado para problemas más pequeños y sencillos debido a las limitaciones del tamaño de la tabla Q y del aprendizaje basado en políticas. Mientras que DQN está diseñado para problemas más complejos y de alta dimensión, como los que se encuentran en tareas basadas en imágenes o entornos con un gran número de estados. En este artículo sobre SARSA, al igual que en el artículo sobre Q-Learning, estamos limitando nuestros estados de entorno a 9 para mayor brevedad.

En resumen, estos se basan en tres estados simplificados del mercado: alcista, bajista y volátil. Cada uno de estos estados se aplica entonces en un marco temporal corto y en un marco temporal largo para crear una matriz de 3 x 3 que implica 9 estados posibles. En los casos en los que sea necesario tener en cuenta parámetros adicionales, como datos de noticias económicas o la evolución de los precios de los valores relacionados, la continuidad de los valores que pueden adoptar estos datos limita la aplicabilidad de SARSA.

Por último, el aprendizaje de velocidad presenta otra diferencia importante entre SARSA y DQN, dado que SARSA puede ser más lento en entornos complejos debido al proceso de actualización secuencial y a la falta de generalización de la red neuronal. Sin embargo, DQN tiende a ser más rápido en entornos grandes debido a su capacidad para generalizar entre estados similares utilizando una red neuronal, especialmente cuando se combina con el aprendizaje por lotes mediante la repetición de experiencias.

Configuración del entorno MQL5 para SARSA

Para implementar nuestra clase de señal personalizada que utiliza RL y no un MLP u otro algoritmo de aprendizaje automático como modelo base, en esencia, necesitamos simplificar la clase de señal que vimos en el artículo introductorio a RL que se centró en el aprendizaje Q. Ese artículo se basó en un MLP para sus previsiones, con RL restringido al procesamiento de la función de pérdida durante el entrenamiento. El RL entonces, al igual que ahora con SARSA, utiliza el enfoque epsilon-greedy, que guía cuándo elegir aleatoriamente la mejor acción para el agente.

Cuando solo utilizábamos el RL para guiar el proceso de entrenamiento de una MLP, estas elecciones a menudo aleatorias eran «tolerables», ya que el valor de pérdida proporcionado por el entrenamiento no era tan sensible al rendimiento general de la MLP. Sin embargo, ahora que el RL es el modelo y no otro MLP, la selección de acciones aleatorias tiene un impacto desproporcionado en el rendimiento general.

A menudo, en el aprendizaje automático, hay una muestra de entrenamiento y una muestra de prueba. Sin embargo, por costumbre, no proporciono estos datos, pero los menciono e invito al lector a obtener estos dos conjuntos de datos independientes. Por lo general, el conjunto de datos de entrenamiento será ligeramente mayor que el conjunto de datos de prueba y, cuando seguimos este protocolo de separar el entrenamiento de la prueba, el uso de épsilon puede resultar realmente constructivo para el modelo en su conjunto. El Q-Map, que es simplemente una matriz, no se exporta mediante ninguna función del código adjunto, pero esto es relativamente sencillo y cualquier persona interesada en llevarlo más allá para realizar entrenamientos y pruebas independientes tendría que exportar esta matriz como un archivo bin o CSV en su sistema después del entrenamiento, antes de leerlo durante la prueba.

Codificación de la clase de señal personalizada

Nuestra clase de señal personalizada, como se mencionó anteriormente, es una simplificación de lo que teníamos en el artículo sobre el algoritmo Q-Learning, y uno de los principales ajustes es la función get output, que hemos revisado como se indica a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSARSA::GetOutput(int &Output, Cql *QL)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.SetOnPolicy(_reward, _in_e);
      Output = QL.transition_act;
   }
}

La compilación de este código en un Asesor Experto se puede realizar siguiendo las instrucciones que se encuentran aquí y aquí para los nuevos lectores. El Asesor Experto ensamblado se probará con un valor epsilon optimizado, simplemente porque solo estamos demostrando la usabilidad del Asesor Experto. En la práctica, este valor debería guiarse idealmente por el conocimiento propio de la importancia relativa y el significado de los distintos estados del medio ambiente y sus respectivas acciones.

Prueba y depuración de su señal basada en SARSA

Para probar y aprovechar mejor la señal personalizada SARSA, habría que realizar algunos cambios en esta clase de señal, y quizás el más importante sea la incorporación de una función para exportar la matriz Q-Map. Esto permitirá realizar pruebas y formación independientes en el sentido tradicional. Sin embargo, estas capacidades de validación cruzada están integradas en el probador de estrategias, ya que se dispone de pruebas de avance.

También se pueden realizar ajustes adicionales en la forma en que hemos definido los estados del entorno, teniendo en cuenta estados de mercado alternativos, como los niveles de precios absolutos, los valores indicativos del RSI o las bandas de Bollinger, y cruzando esto con marcos temporales alternativos para cada uno de estos puntos de datos. La depuración comenzará con la comprobación de cómo se capturan y actualizan estas variables de estado.

La función de recompensa también debe reflejar con precisión los resultados de las operaciones. Para este artículo, nuestro código utiliza la excursión favorable como porcentaje del rango de precios, en cada nueva barra. Esto se debe a que estamos entrenando simultáneamente un Q-Map y tomando decisiones comerciales basadas en sus ponderaciones de Q-Value en ese momento. Sin duda, esto no es lo ideal, ya que se deberían buscar conjuntos de datos de entrenamiento y pruebas independientes adecuados. Sin embargo, los parámetros de recompensa pueden ser más a largo plazo que los que estamos utilizando aquí si, por ejemplo, tienen en cuenta la rentabilidad y el rendimiento de un asesor experto durante períodos de tiempo más largos.

Para no perseguir ciegamente la rentabilidad del Asesor Experto, también sería una buena idea probar pares individuales de estado-acción y asegurarse de que el EA reacciona correctamente a las condiciones del mercado, tal y como se espera. Por ejemplo, al comprobar las ponderaciones del valor Q en el mapa Q de nuestra versión simplificada para este artículo en la primera coordenada de la cuadrícula 0 y 0, que marca condiciones bajistas a corto y largo plazo, debería tener la ponderación más alta para la acción 0, que representa la venta, y no un «valor ajustado a la curva» que es inconsistente con lo que se debería hacer en mercados bajistas.

La verificación de un equilibrio adecuado entre exploración y explotación, tal y como se aplica mediante la política epsilon-greedy, también es fundamental, aunque esto se puede obtener mediante la optimización del valor epsilon ideal. Sin embargo, esta optimización debería realizarse en un conjunto de datos de entrenamiento independiente en el que los Q-Maps se respalden en pasadas con un mejor rendimiento. Después del entrenamiento, en un conjunto de datos independiente, las pruebas (marcha hacia delante) pueden confirmar o refutar el valor epsilon utilizado.

El entrenamiento retrospectivo debe realizarse con conjuntos de datos de calidad razonable. Los informes del probador de estrategias indican la calidad de los datos utilizados tras una prueba de estrategia, por lo que siempre son un buen indicador de la fiabilidad del entrenamiento. Sin embargo, esta formación implicará la exportación de Q-Maps al final de cada pasada si los resultados de la prueba son mejores que los puntos de referencia anteriores, y los Q-Maps exportados se reutilizarían en rondas de formación posteriores, de modo que estas pasadas de formación adicionales actuarían como épocas al entrenar redes neuronales.

Al final del proceso de entrenamiento, el Q-Map final que proporcione el rendimiento más satisfactorio del Asesor Experto se utilizaría en una única prueba prospectiva para comprobar si el rendimiento del entrenamiento pasado con este Q-Map concreto puede replicarse en un conjunto de datos de prueba aún «no visto». Las jugadas hacia adelante son propias del probador de estrategias, y este artículo aquí puede servir de guía para los lectores que sean nuevos en esto.

Además de la validación cruzada en conjuntos de datos históricos, se podría considerar lo mismo para cuentas reales antes de la implementación completa. Registro de rendimiento, donde se tabulan diferentes Q-Maps junto con el rendimiento de sus respectivos probadores. Esto puede llevarse un paso más allá mediante la implementación de registros detallados en pruebas prospectivas en tiempo real para capturar los estados del mercado, las acciones, las recompensas y las actualizaciones del valor Q, lo que, al menos en teoría, debería ayudar a detectar fallos en la toma de decisiones y ajustar parámetros como la tasa de aprendizaje o la decadencia ε si fuera necesario.

Informes del Probador de estrategias

Las pruebas realizadas en el marco temporal diario para el EURJPY para el año 2022, cuyo único objetivo es demostrar la usabilidad del Asesor Experto, nos dan los siguientes resultados:

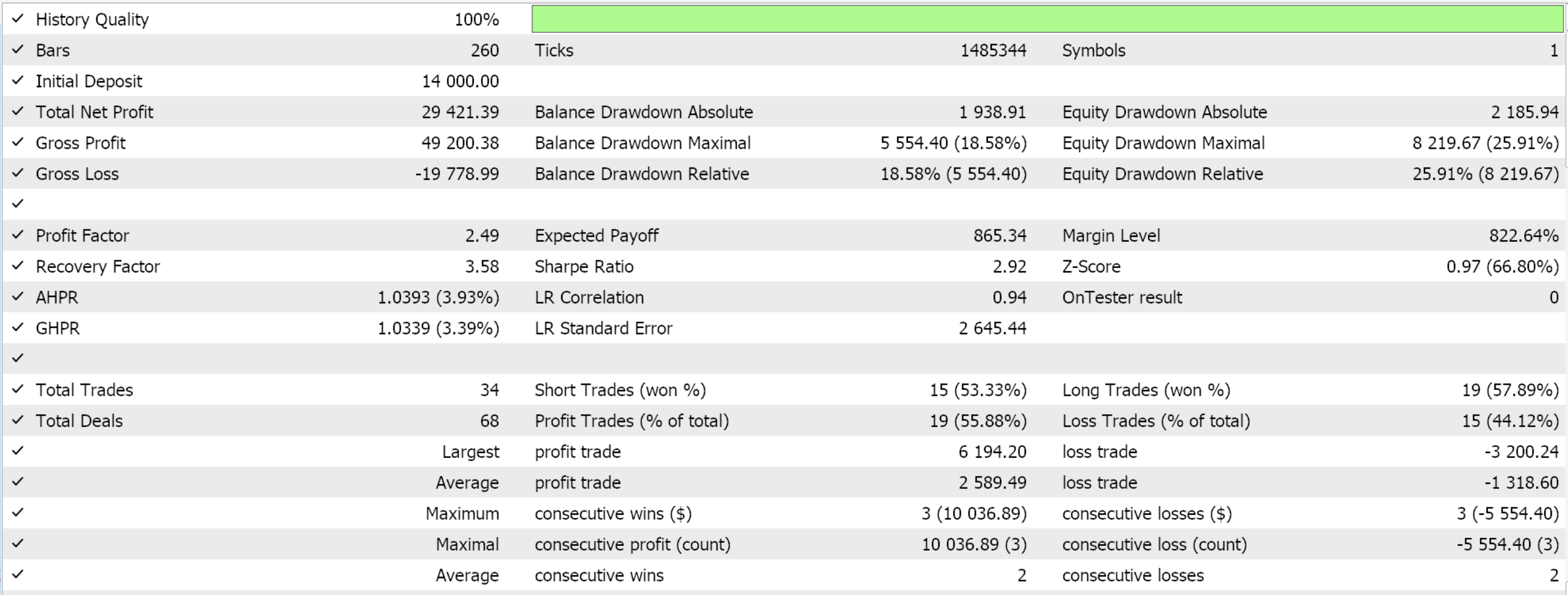
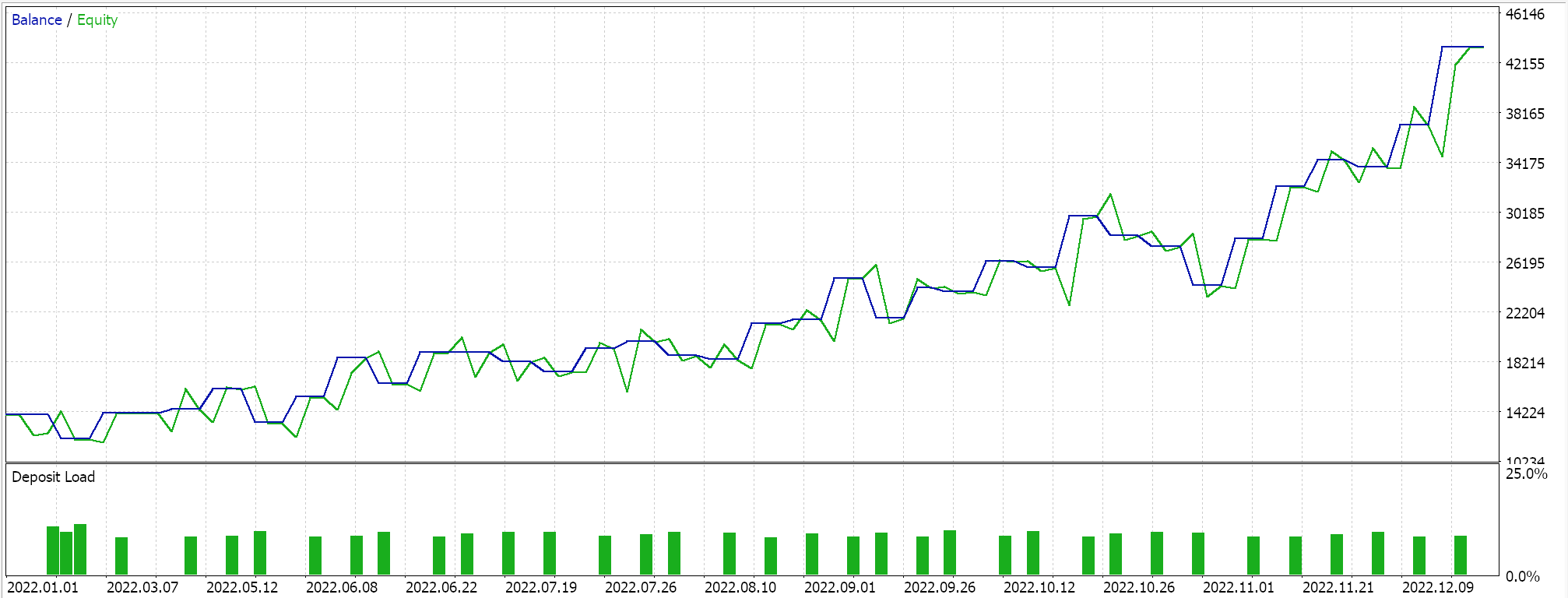
Consideraciones prácticas para SARSA en operaciones en vivo

Dado que SARSA es un algoritmo basado en políticas, incorpora directamente las acciones de la política durante el aprendizaje, lo que lo hace más adaptable a datos ruidosos. El método de valor Q-Map que utilizamos actualiza todos los valores Q en el mapa en proporción a su brecha con respecto a la acción actual, como se muestra en el código de política anterior. Esta actualización sigue a la actualización epsilon-greedy realizada en la función Acción, para equilibrar la exploración (descubrimiento de nuevas estrategias) y la explotación (uso de estrategias conocidas), para ayudar al modelo a evitar el sobreajuste al ruido de corto plazo en los datos del mercado. La selección de la próxima acción que utilizará el agente se realiza a través de un proceso de decisión de Markov, independientemente de si se aplicará la ponderación de Markov al proceso de actualización del valor Q, como vimos en el artículo de Q-Learning anterior. Esto se maneja en la función Action como se muestra a continuación:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//
   int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   transition_act = 0;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q[i][_next_row][_next_col] > Q[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
}

El suavizado temporal mediante un mecanismo de recompensa ayuda a suavizar el ruido a corto plazo al centrarse en la recompensa acumulada a lo largo de múltiples iteraciones temporales. Esto le da al algoritmo la capacidad de aprender patrones más allá del ruido inmediato en los datos. Además, un ajuste continuo de la política garantiza que esta se base tanto en la situación actual como en la futura. Esto puede ayudar a mitigar los efectos de los datos ruidosos al permitir que el algoritmo se adapte a medida que se dispone de más datos, especialmente cuando las condiciones del mercado cambian rápidamente.

SARSA es bastante robusto a la hora de gestionar mercados volátiles, dada su estructura inherente a la hora de seleccionar la acción de transición, tal y como se indica en la función Action, cuyo código se ha compartido anteriormente. Dado un par de coordenadas para el estado actual del entorno, estos dos valores tendrían que convertirse en un único índice, reconocible por la matriz de Markov de la clase QL. Esto lo hacemos utilizando la función «GetMarkov», cuyo código se muestra a continuación:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

Una vez que contamos con este índice, podemos proceder a leer nuestra matriz de Markov fila (representada por este índice) para determinar qué columna tiene el valor de probabilidad más alto. Esta matriz de Markov es particularmente adecuada para esto porque no está protegida ni almacenada de ningún modo como la mayoría de los indicadores comunes. No tiene memoria y esto lo hace muy adaptable a entornos inciertos como cuando la volatilidad es alta. Entonces, de la fila de la matriz de Markov correspondiente al estado actual del entorno, leemos la columna con la mayor probabilidad y su índice nos daría el número entero para el próximo estado del entorno. Este entero nuevamente necesitaría descomponerse en dos valores similares a los que comenzamos, a los que llamamos índice de fila e índice de columna.

Una vez que tenemos estos valores de fila y columna, que representan las coordenadas para el próximo estado, podemos proceder a leer la acción con el valor Q más alto de nuestro mapa Q. El índice de esta acción representaría lo que hemos llamado la “acción de transición”. En resumen, nos enfrentamos a tres posibles acciones: 0-vender, 1-no hacer nada y 2-comprar. Además, el entorno está restringido a tres estados en los tres «marcos temporales» que considera el Q-Map.

Me refiero a «marcos temporales» porque en realidad solo estamos utilizando un único marco temporal. El lector, por supuesto, puede modificar el código y realizar los cambios que considere oportunos. El parámetro de entrada «m_scale» define en qué medida se registran los cambios más importantes en el «marco temporal» al obtener estos cambios de dos niveles que utilizamos para mapear y definir los estados del entorno.

SARSA tiene en cuenta tanto las acciones como las recompensas dentro de la política actual, lo que contribuye a estabilizar el proceso de aprendizaje durante los periodos de alta volatilidad del mercado. Esto evita cambios extremos en la toma de decisiones que podrían surgir a raíz de cambios repentinos en el mercado, lo que lo hace más adecuado para mercados volátiles en comparación con algoritmos fuera de política como el aprendizaje Q. Como se puede ver en nuestro código de función de política compartida anteriormente, actualizamos los valores para la acción indexada 1 y no el índice 0 como había sido el caso para el algoritmo Q-Learning.

Debido a que SARSA evalúa directamente las acciones adoptadas por la política actual, sin mayores problemas se vuelve más cauteloso en entornos altamente volátiles, evitando así estimaciones excesivamente optimistas del valor de las acciones que podrían llevar a malas decisiones durante cambios inesperados del mercado. Además, en mercados volátiles, la exploración ε-greedy de SARSA permite que el modelo explore estrategias más seguras en lugar de tomar acciones de alto riesgo. Esto reduce la probabilidad de grandes pérdidas durante períodos de oscilaciones extremas de precios, al tiempo que brinda al modelo oportunidades para descubrir nuevas estrategias rentables. La exploración de estrategias más seguras proviene de épsilon, que permite una elección aleatoria de acciones y no necesariamente las mejores acciones gratificantes actuales, que, dado un entorno volátil, podrían desmaterializarse rápidamente en recompensas desalentadoras. 

La convergencia a largo plazo de SARSA hacia la política óptima depende de la interacción continua con el entorno. En los mercados financieros, donde las tendencias a largo plazo y los cambios estructurales son la norma, la evaluación iterativa de políticas de SARSA garantiza que los valores Q tenderán a converger con el tiempo, reflejando así estos patrones a largo plazo. 

Personalización de SARSA para estrategias más complejas

La agregación del espacio de estados en SARSA puede ser una forma de desglosar espacios de estados complejos, especialmente en los mercados financieros, donde el espacio de estados (movimientos de precios, indicadores, condiciones del mercado, noticias del calendario económico) puede ser muy amplio y continuo. La agregación del espacio de estados reduciría esta complejidad agrupando estados similares en estados «agregados» o «abstractos». El ejemplo más claro de esto serían los estados ambientales que mencionamos en este artículo, que son simplemente tres cambios inmediatos y otros cambios a más largo plazo. Sin embargo, también se podría hacer un uso más ingenioso de esto al considerar un entorno más multifacético, como un Q-Map que tiene en cada eje, por ejemplo, información sobre el rendimiento a 10 años, tipos de interés de referencia, el índice de precios al productor (IPP), el índice de precios al consumidor (IPC) y la tasa de desempleo.

Dado que los Q-Maps son de doble eje, esta información sería aplicable a cada divisa de un par de divisas negociado. Así que, en lugar de lidiar con las lecturas de valor individuales de cada una de estas métricas, se podrían agrupar de la misma manera que lo hicimos para este artículo, simplemente considerando si cada una de estas métricas aumentó, se mantuvo estable o disminuyó. Estos resultados se utilizarían para determinar qué tipo de índice debe asignarse a cada punto de la matriz Q-Map, del mismo modo que hemos asignado valores de índice en la Q-Map para este artículo.

Conclusión

En este artículo hemos considerado otro algoritmo para el aprendizaje de refuerzo, SARSA, y vale la pena mencionar que la implementación que tuvimos para el primer algoritmo RL que consideró Q-Learning así como el posterior que analizó Deep-Q-Networks, no utilizaron adecuadamente el proceso de decisión de Markov al seleccionar la siguiente acción. En cambio, las cadenas de Markov se proporcionaron simplemente como un mecanismo para ponderar el proceso de actualización. Esto se ha corregido para este artículo, con disculpas, y se adjunta el código fuente completo.