Funciones de activación neuronal durante el aprendizaje: ¿la clave de una convergencia rápida?

Introducción

En el artículo anterior analizamos las propiedades de una red neuronal MLP sencilla como aproximador (aprendizaje por refuerzo) en un asesor comercial. Entonces no prestamos especial atención a las propiedades de las funciones de activación, sino que utilizamos la popular sigmoidea tangente hiperbólica. También en uno de los artículos discutimos las capacidades del conocido y ampliamente utilizado algoritmo ADAM, pero modificado por mí en un método independiente de optimización global basado en la población ADAMm.

En este artículo, profundizaremos en las capacidades de la red neuronal como interpolador de datos (aprendizaje supervisado), centrándonos en las propiedades de las funciones de activación de las neuronas. Así, usaremos el algoritmo de optimización ADAM incorporado en la red neuronal (como es habitual en las aplicaciones de redes neuronales) y estudiaremos el efecto de la función de activación y su derivada en la tasa de convergencia del algoritmo de optimización.

Imagine un río con muchos afluentes. En su estado normal, el agua fluye con libertad, creando un complejo patrón de corrientes y remolinos. Pero, ¿qué pasará si empezamos a construir un sistema de esclusas y presas? Podremos controlar el flujo de agua, dirigirla en la dirección que nos convenga y regular la fuerza de la corriente. La función de activación en las redes neuronales cumple un papel parecido: decide qué señal transmitir y cuál retrasar o atenuar. Sin ella, una red neuronal no sería más que un conjunto de transformaciones lineales.

La función de activación añade dinamismo a la red neuronal, lo cual le permite captar matices sutiles en los datos. Por ejemplo, en un problema de reconocimiento facial, la función de activación ayuda a la red a fijarse en detalles minúsculos como la curva de las cejas o la forma de la barbilla. La elección correcta de la función de activación afectará al modo en que la red neuronal gestiona las distintas tareas. Algunas funciones resultan más adecuadas para las fases iniciales del aprendizaje, ya que proporcionan señales claras y comprensibles. Algunas funciones permiten a la red captar patrones más sutiles en fases avanzadas, mientras que otras eliminan todo lo innecesario, dejando solo lo más importante.

Si no conocemos las propiedades de las funciones de activación, podríamos tener problemas. La red neuronal puede empezar a "tropezar" en tareas sencillas o a "pasar por alto" detalles sustanciales. La principal tarea de las funciones de activación consiste en introducir la no linealidad en la red neuronal y normalizar los valores de salida.

El objetivo de este trabajo es identificar los problemas asociados al uso de distintas funciones de activación y su impacto en la precisión de una red neuronal que pasa por puntos de ejemplos (interpolación) minimizando el error. También veremos si las funciones de activación afectan realmente a la tasa de convergencia, o si se trata de una propiedad del algoritmo de optimización utilizado. Como algoritmo de referencia, aplicaremos un ADAMm poblacional modificado que usará elementos de estocasticidad, y realizaremos pruebas con el ADAMm incorporado en MLP (uso clásico). Este último debería poseer intuitivamente la ventaja de tener acceso directo al gradiente de superficie de la función de aptitud debido a la derivada de la función de activación. Mientras que la población estocástica ADAMm no tendrá acceso a la derivada y desconocerá por completo la superficie del problema de optimización. Veamos qué sale de todo esto y entonces sacaremos conclusiones.

El artículo tiene carácter investigativo, así que la narración seguirá el orden del experimento.

Implementamos una red neuronal MLP con ADAM integrado

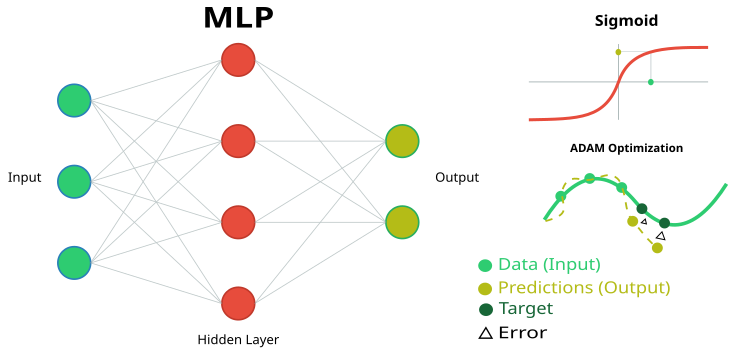
Figura 1. Representación esquemática de la red neuronal MLP y entrenamiento de la misma

Para el presente estudio, necesitaremos un código sencillo y transparente de la red neuronal MLP, sin usar cálculos matriciales especializados e incorporados en el lenguaje MQL5. Esto nos permitirá comprender con claridad qué sucede exactamente en la lógica de la red neuronal, así como entender de qué dependen determinados resultados.

Así, implementaremos un perceptrón multicapa (MLP) con un algoritmo de optimización ADAM (Adaptive Moment Estimation) integrado. La clase y la estructura representarán la parte de la implementación de la red neuronal en la que se definen los componentes principales: neuronas, capas de neuronas y pesos.

1. La clase "C_Neuro" representará una neurona, que será la unidad básica de una red neuronal.

• C_Neuron() — constructor, inicializa los valores de las propiedades "m" y "v" con ceros. Estos valores se utilizarán para el algoritmo de optimización.
• out — valor de salida de la neurona tras la aplicación de la función de activación.
• delta — delta del error utilizado para calcular el gradiente durante el entrenamiento.
• bias — valor de desplazamiento añadido a las entradas de la neurona.
• m y v — se utilizan para almacenar el primer y segundo momento del desplazamiento, utilizados por el método de optimización ADAM.

2. La estructura "S_NeuronLayer" representará una capa de neuronas. "C_Neuron n []" será un array de neuronas en la capa de la red neuronal.

Para almacenar los pesos entre las neuronas, utilizaremos un enfoque orientado a objetos en lugar de simples arrays bidimensionales. La base será la clase "C_Weight", que almacenará no solo el peso de conexión en sí, sino también los parámetros para la optimización: el primer y segundo momentos utilizados en el algoritmo ADAM. La estructura de datos estará organizada jerárquicamente: "S_WeightsLayer" contendrá un array de estructuras "S_WeightsLayerR", que a su vez contendrán arrays de objetos "C_Weight". Esto facilitará la dirección de cualquier peso en la red a través de una cadena de índices comprensible.

Por ejemplo, para referirnos al peso de la conexión entre la primera neurona de la capa cero y la segunda neurona de la capa siguiente, utilizaremos la entrada: wL [0].nOnL [1].nOnR [2].w. Aquí, el primer índice indicará un par de capas vecinas, el segundo índice indicará la neurona en la capa izquierda, y el tercer índice indicará la neurona en la capa derecha.

//——————————————————————————————————————————————————————————————————————————————
// Класс нейрона
class C_Neuron
{
  public:
  C_Neuron ()
  {
    m = 0.0;
    v = 0.0;
  }
  double out;   // Выход нейрона после функции активации
  double delta; // Дельта ошибки
  double bias;  // Смещение
  double m;     // Первый момент смещения
  double v;     // Второй момент смещения
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Структура слоя нейронов
struct S_NeuronLayer
{
    C_Neuron n []; // нейроны в слое
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Класс веса
class C_Weight
{
  public:
  C_Weight ()
  {
    w = 0.0;
    m = 0.0;
    v = 0.0;
  }

  double w; // Вес
  double m; // Первый момент
  double v; // Второй момент
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов справа
struct S_WeightsLayerR
{
    C_Weight nOnR [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов слева
struct S_WeightsLayer
{
    S_WeightsLayerR nOnL [];
};
//——————————————————————————————————————————————————————————————————————————————

La clase "C_MLPa" de perceptrón multicapa (MLP) implementará las funciones básicas de la red neuronal, incluido el aprendizaje con uso de la pasada directa y la propagación inversa del error mediante el algoritmo de optimización ADAM. Veamos lo que este puede hacer:

Estructura de la red:

• La red constará de capas sucesivas: capa de entrada -> capas ocultas -> capa de salida.
• Cada neurona de una capa estará conectada a todas las neuronas de la capa siguiente (red completamente conectada).

Características principales:

• Init — método de creación de una red con la configuración especificada.
• ImportWeights y ExportWeights — carga y guardado de los pesos de la red.
• ForwProp — pasada directa: recepción de la respuesta de la red a los datos de entrada.
• BackProp — aprendizaje de una red basado en la propagación inversa del error.

Parámetros de aprendizaje (algoritmo ADAM):

• alfa (0,001) — rapidez de aprendizaje de la red.
• beta1 (0,9) y beta2 (0,999) — parámetros que ayudan a la red a aprender de forma estable.
• épsilon (1e-8) — número pequeño para proteger contra la división por cero.

Componentes internos:

• BackProp — almacena la información sobre el tamaño de cada capa (layersSize).
• Contiene todas las neuronas (nL) y los pesos entre ellas (wL).
• Lleva la cuenta del número de pesos (wC) y capas (nLC).
• actFunc — utiliza la función de activación seleccionada.
  

En esencia, esta clase es el "cerebro" de una red neuronal que sabe cómo admitir datos de entrada, procesarlos a través de un sistema de neuronas y pesos, producir un resultado y aprender de sus errores, mejorando gradualmente la precisión de sus predicciones.

//+----------------------------------------------------------------------------+
//| Класс многослойного персептрона (MLP)                                      |
//| Реализует прямой проход по полносвязной нейронной сети и обучение методом  |
//| обратного распространения ошибки алгоритмом оптимизации ADAM               |
//| Архитектура: Lin -> L1 -> L2 -> ... Ln -> Lout                             |
//+----------------------------------------------------------------------------+
class C_MLPa
{
  public: //--------------------------------------------------------------------
  ~C_MLPa ()
  {
    delete actFunc;
  }
  C_MLPa ()
  {
    alpha   = 0.001;   // Скорость обучения
    beta1   = 0.9;     // Коэффициент затухания для первого момента
    beta2   = 0.999;   // Коэффициент затухания для второго момента
    epsilon = 1e-8;    // Малая константа для численной стабильности
  }

  // Инициализация сети с заданной конфигурацией, Возвращает общее количество весов в сети или 0 в случае ошибки
  int    Init          (int &layerConfig [], int actFuncType, int seed);
  bool   ImportWeights (double &weights []);  // Импорт весов
  bool   ExportWeights (double &weights []);  // Экспорт весов

  // Прямой проход по сети
  void   ForwProp (double &inLayer  [],  // входные значения
                   double &outLayer []); // значения выходного слоя

  // Обратное распространение ошибки с оптимизацией алгоритмом ADAM
  void   BackProp (double &errors []);

  // Получить общее количество весов в сети
  int    GetWcount () { return wC; }

  // Параметры оптимизации ADAM
  double alpha;          // Скорость обучения
  double beta1;          // Коэффициент затухания для первого момента
  double beta2;          // Коэффициент затухания для второго момента
  double epsilon;        // Малая константа для численной стабильности

  int layersSize    [];  // Размер каждого слоя (количество нейронов)
  S_NeuronLayer  nL [];  // Слои нейронов,                    пример обращения: nLayers [].n [].a
  S_WeightsLayer wL [];  // Слои весов между слоями нейронов, пример обращения: wLayers [].nOnLeft [].nOnRight [].w

  private: //-------------------------------------------------------------------
  int            wC;       // Общее количество весов в сети (включая смещения)
  int            nLC;      // Общее количество слоев нейронов (включая входной и выходной)
  int            wLC;      // Общее количество слоев весов (между слоями нейронов)
  int            t;        // Счетчик итераций
  C_Base_ActFunc *actFunc; // Функции активации и их производные
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" inicializará la estructura del perceptrón multicapa estableciendo el número de neuronas de cada capa, seleccionando la función de activación y generando pesos iniciales para las neuronas. Asimismo, comprobará que la configuración de la red sea correcta y devuelva el número total de pesos necesarios, o 0 en caso de error.

Parámetros:

• layerConfig [] — array que contiene el número de neuronas en cada capa de la red.
• actFuncType — tipo de función de activación que se utilizará en la red neuronal (por ejemplo, sigmoidea, etc.).
• seed — semilla que inicializará un número para el generador de números aleatorios, permitiendo obtener resultados reproducibles al inicializar los pesos.

Lógica de funcionamiento:

1. El método determinará el número de capas basándose en el array "layerConfig" transmitido.
2. Comprobará que el número de capas sea al menos de 2 y que cada capa contenga un número positivo de neuronas. En caso de error, mostrará un mensaje y finalizará la ejecución.
3. Copiará el tamaño de las capas en el array "layersSize" e inicializará los arrays para almacenar las neuronas y los pesos.
4. Calculará el número total de pesos necesarios para conectar neuronas entre capas.
5. Inicializará los pesos utilizando el método Xavier, que, en teoría, ayuda a evitar problemas con gradientes desvanecidos o explosivos.
6. Dependiendo del tipo de función de activación transmitida, creará el objeto de función de activación correspondiente.
7. Inicializará a cero el contador de iteraciones, utilizado en el algoritmo ADAM.
   

//+----------------------------------------------------------------------------+
//| Инициализация сети                                                         |
//| layerConfig - массив с количеством нейронов в каждом слое                  |
//| Возвращает общее количество необходимых весов или 0 при ошибке             |
//+----------------------------------------------------------------------------+
int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed)
{
  nLC = ArraySize (layerConfig);

  if (nLC < 2)
  {
    Print ("Ошибка конфигурации сети! Меньше 2 слоев!");
    return 0;
  }

  // Проверка конфигурации
  for (int i = 0; i < nLC; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Ошибка конфигурации сети! Слой №" + string (i + 1) + " содержит 0 нейронов!");
      return 0;
    }
  }

  wLC = nLC - 1;
  ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY);

  // Инициализация слоев нейронов
  ArrayResize (nL, nLC);
  for (int i = 0; i < nLC; i++)
  {
    ArrayResize (nL [i].n, layersSize [i]);
  }

  // Инициализация слоев весов
  ArrayResize (wL, wLC);
  for (int w = 0; w < wLC; w++)
  {
    ArrayResize (wL [w].nOnL, layersSize [w]);
    for (int n = 0; n < layersSize [w]; n++)
    {
      ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]);
    }
  }

  // Подсчет общего количества весов
  wC = 0;
  for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1];

  // Инициализация весов
  double weights [];  ArrayResize (weights, wC);

  srand (seed);
  
  //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂)))
  double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1]));
  for (int i = 0; i < wC; i++)
  {
    weights [i] = (2.0 * n) * (rand () / 32767.0) - n;
  }

  ImportWeights (weights);

  switch (actFuncType)
  {
    case eActACON:      actFunc = new C_ActACON      (); break;
    case eActAlgSigm:   actFunc = new C_ActAlgSigm   (); break;
    case eActBentIdent: actFunc = new C_ActBentIdent (); break;
    case eActRatSigm:   actFunc = new C_ActRatSigm   (); break;
    case eActSiLU:      actFunc = new C_ActSiLU      (); break;
    case eActSoftPlus:  actFunc = new C_ActSoftPlus  (); break;
    default:            actFunc = new C_ActTanh      (); break;
  }

  t = 0;
  return wC;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar más en profundidad dos métodos: "ImportWeights" y "ExportWeights". Estos métodos están diseñados para importar y exportar los pesos y desplazamientos del perceptrón multicapa. "ImportWeights" — se encargará de importar los pesos y desplazamientos del array "weights" a la estructura de la red neuronal.

El método primero comprobará si el tamaño del array "pesos" coincidirá con el número de pesos almacenados en la variable "wC". Si las dimensiones no coinciden, el método retornará "false" indicando un error.

La variable "wCNT" se utilizará para llevar la cuenta del índice actual en el array "pesos".
Ciclos por las capas y neuronas:

• El ciclo externo iterará cada capa empezando por la segunda capa (índice 1), ya que la primera capa es la capa de entrada y no habrá pesos ni desplazamientos para ella.
• El ciclo interno iterará cada neurona de la capa actual.
• Para cada neurona, se establecerá el valor de desplazamiento "bias" del array "weights" y se incrementará el contador "wCNT".
• El ciclo anidado iterará todas las neuronas de la capa anterior, estableciendo los pesos que conectan las neuronas de la capa actual con las neuronas de la capa anterior.

"ExportWeights" — el método se encargará de exportar los pesos y desplazamientos de la estructura de la red neuronal al array "weights". La lógica del método será similar a la del método "ImportWeights". Ambos métodos permitirán almacenar en un programa externo los pesos y los desplazamientos con respecto a la clase de la red, utilizar la red entrenada en el futuro y usar los algoritmos de optimización externos, como los algoritmos de población.

//+----------------------------------------------------------------------------+
//| Импорт весов и смещений сети                                               |
//+----------------------------------------------------------------------------+
bool C_MLPa::ImportWeights (double &weights [])
{
  if (ArraySize (weights) != wC) return false;

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      nL [ln].n [n].bias = weights [wCNT++];

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++];
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

//+----------------------------------------------------------------------------+
//| Экспорт весов и смещений сети                                              |
//+----------------------------------------------------------------------------+
bool C_MLPa::ExportWeights (double &weights [])
{
  ArrayResize (weights, wC);

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      weights [wCNT++] = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w;
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método "ForwProp" realizará el cálculo secuencial de los valores de todas las capas de un perceptrón multicapa desde la capa de entrada hasta la capa de salida. Tomará valores de entrada, los procesará a través de capas ocultas y generará los valores de salida. Parámetros:

• inLayer [] — array de valores de entrada para la red neuronal (en verde en la figura 1).
• outLayer [] —  array donde se escribirán los valores de la capa de salida después del procesamiento (color amarillo en la figura 1).
  

El método inicializará los valores de activación de las neuronas de la capa de entrada copiando los valores de entrada del array "inLayer" a las neuronas correspondientes.

Procesamiento de las capas ocultas y de salida:

• El ciclo externo recorrerá todas las capas empezando por la segunda (índice 1), ya que la primera será la capa de entrada.
• El ciclo interno recorrerá cada neurona de la capa actual.
• Para cada neurona, se calculará la suma de las entradas ponderadas:
• Se comenzará añadiendo un desplazamiento (bias) a la neurona.
• El ciclo anidado iterará todas las neuronas de la capa anterior, sumando a "val" el producto del valor de salida de la neurona de la capa anterior y el peso correspondiente.
• Una vez calculada la suma, la función de activación se aplicará al valor "val" y el resultado se almacenará en el valor de salida de la neurona de la capa actual.

Una vez procesadas todas las capas, el método copiará los valores de salida de la última capa (capa de salida) en el array "outLayer".

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

El método "BackProp" implementará la propagación inversa del error en un perceptrón multicapa. Luego actualizará los pesos y desplazamientos de todas las capas de salida hacia la entrada usando el algoritmo de optimización ADAM. Lógica de funcionamiento:

La variable "t" se incrementará en uno para llevar la cuenta del número de iteraciones y se utilizará en la fórmula de la lógica de ADAM.

Cálculo de las deltas para todas las capas:

• El ciclo externo iterará las capas en orden inverso, empezando por la capa de salida y terminando por la capa de entrada.
• El ciclo interno iterará las neuronas de la capa actual.
• Si la capa actual es una capa de salida, la delta se calculará como el producto de los errores [nCurr] y la derivada de la función de activación para la neurona de salida.
• Para las capas ocultas, la delta se calculará como la suma de los productos de los deltas de la capa siguiente por los pesos correspondientes.
• La delta se corregirá entonces por la derivada de la función de activación, y el resultado se almacenará en nL [ln].n [nCurr].delta.

Actualización de los desplazamientos usando ADAM:

• El ciclo externo recorrerá todas las capas, empezando por la segunda.
• Para cada neurona de la capa actual, los momentos de desplazamiento "m" y "v" se actualizarán utilizando los parámetros "beta1" y "beta2".
• A continuación, se corregirán los momentos de desplazamiento "m_hat" y "v_hat".
• Por último, el desplazamiento se actualizará utilizando los momentos corregidos.

Actualización de las escalas usando ADAM:

• El ciclo externo atravesará todas las capas de pesos.
• Los ciclos internos recorrerán las neuronas de la capa actual y de la capa siguiente.
• Para cada peso, se calculará un gradiente, que luego se utilizará para actualizar los momentos "m" y "v".
• Tras corregir los momentos de los pesos "m_hat" y "v_hat", las pesos se actualizarán utilizando los momentos corregidos.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Código del banco de pruebas para dibujar las funciones de activación

El banco está diseñado para probar la corrección de varias funciones de activación usadas en redes neuronales, así como para su visualización en forma de gráfico. Las imágenes resultantes se utilizarán más adelante para evaluar visualmente su aspecto. El código es bastante sencillo y no tiene mucho sentido describirlo.

#include <Graphics\Graphic.mqh>
#include <Math\AOs\NeuroNets\MLPa.mqh>

#define SIZE_X 750
#define SIZE_Y 200

//--- input parameters
input E_Act ACT = eActTanh;
input int   CNT = 10000;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  ObjectDelete (ChartID (), "Test");
  double activ [];
  double deriv [];

  //----------------------------------------------------------------------------
  C_Base_ActFunc *act;
  switch (ACT)
  {
    default:            act = new C_ActTanh      (); break;
    case eActAlgSigm:   act = new C_ActAlgSigm   (); break;
    case eActRatSigm:   act = new C_ActRatSigm   (); break;
    
    case eActSoftPlus:  act = new C_ActSoftPlus  (); break;
    case eActBentIdent: act = new C_ActBentIdent (); break;
    case eActSiLU:      act = new C_ActSiLU      (); break;
    
    case eActACON:      act = new C_ActACON      (); break;
    case eActSnake:     act = new C_ActSnake     (); break;
    case eActSERF:      act = new C_ActSERF      (); break;
  }
  
  //----------------------------------------------------------------------------
  ActFuncTest (act, activ, deriv, CNT, -10, 10);
  
  //----------------------------------------------------------------------------
  CGraphic gr_test;
  gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20);
  gr_test.YAxis ().Name (act.GetFuncName () + ": Value");
  gr_test.YAxis ().NameSize (13);
  gr_test.HistorySymbolSize (10);
  gr_test.CurveAdd (activ, ColorToARGB (clrRed,  255), CURVE_LINES, "activ");
  gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv");
  gr_test.CurvePlotAll ();
  gr_test.Redraw (true);
  gr_test.Update ();
  
  //----------------------------------------------------------------------------
  delete act;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max)
{
  Print (act.GetFuncName (), " [", min, "; ", max, "]");
  Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max));
  Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max));

  ArrayResize (arrayAct, testCount);
  ArrayResize (arrayDer, testCount);
  double x    = 0.0;
  double step = (max - min) / testCount;
  
  for (int i = 0; i < testCount; i++)
  {
    x = min + step * i;

    arrayAct [i] = act.Activ (x);
    arrayDer [i] = act.Deriv (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Código de las clases de la función de activación

Existen muchas funciones de activación neuronal diferentes que se utilizan en diversas tareas de redes neuronales. Hemos intentado seleccionar funciones que incluyan tanto la célebre tangente hiperbólica como otras menos conocidas, como la función de activación Snake, excluyendo al mismo tiempo funciones muy similares en apariencia y propiedades. Convencionalmente, podemos dividirlas en tres grupos:

1. Funciones sigmoideas,
2. Interruptores no lineales,
3. Funciones de tipo periódico.

Vamos a implementar la clase básica "C_Base_ActFunc" para las funciones de activación de neuronas. Contendrá dos funciones virtuales: "Activ" para calcular la activación y "Deriv" para calcular la derivada. El método "GetFuncName()" retornará el nombre de la función de activación almacenada en la celda protegida "funcName". La clase está diseñada para que la herencia cree implementaciones concretas de funciones de activación. Mediante la creación de un objeto de función de activación podremos acelerar los cálculos eliminando la necesidad de múltiples usos de "if" y "switch".

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  virtual double Activ (double inp) = 0; // Виртуальная функция активации
  virtual double Deriv (double inp) = 0; // Виртуальная функция производной
  string         GetFuncName () {return funcName;}
  protected:
  string funcName;
};
//——————————————————————————————————————————————————————————————————————————————

La clase "C_ActTanh" implementará la función de activación de tangente hiperbólica y su derivada, y se heredará de la clase básica "C_Base_ActFunc". El constructor de la clase establecerá el nombre de la función de activación en la variable "funcName" como "ActTanh". Método de activación:

• Activ (double x) calculará el valor de la función de activación tangente hiperbólica mediante la fórmula f(x) = 2 / (1 + exp ( − 2  ⋅  (x)) − 1. Esta fórmula convertirá el valor de entrada "x" en un rango de -1 a 1.

Aquí vemos el método de la derivada:

• Deriv(double x) calculará la derivada de la función de activación. La derivada de la tangente hiperbólica se expresará como: f′(x) = 1 − (f (x)) ^ 2, donde f(x) será el valor de la función de activación calculado para la "x" actual. La derivada mostrará a qué velocidad cambiará la función según el valor de entrada.

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh () {funcName = "ActTanh";}

  double Activ (double x)
  {
    return 2.0 / (1.0 + exp (-2 * (x))) - 1.0;
  }

  double Deriv (double x)
  {
    //1 - (f(x))^2
    double fx = Activ (x);
    return 1.0 - fx * fx;
  }
};
//——————————————————————————————————————————————————————————————————————————————

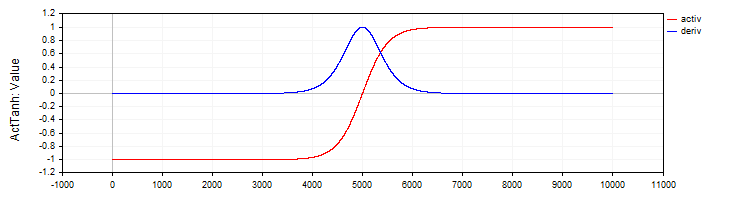
Figura 2. La tangente hiperbólica y su derivada

La clase "C_ActAlgSigm" de forma similar a la clase "C_ActTanh" implementará la sigmoide algebraica como función de activación con los métodos para calcular la activación y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// Алгебраическая сигмоида
class C_ActAlgSigm : public C_Base_ActFunc
{
  public:
  C_ActAlgSigm () {funcName = "ActAlgSigm";}

  double Activ (double x)
  {
    return x / sqrt (1.0 + x * x);
  }

  double Deriv (double x)
  {
    // (1 / sqrt (1 + x * x))^3
    double d = 1.0 / sqrt (1.0 + x * x);
    return d * d * d;
  }
};
//——————————————————————————————————————————————————————————————————————————————

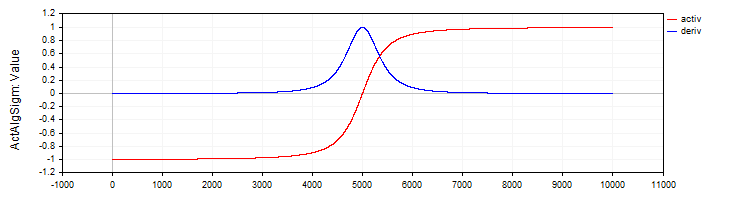
Figura 3. La sigmoide algebraica y su derivada

La clase "C_ActRatSigm" implementará una sigmoide racional con los métodos de activación y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// Рациональная сигмоида
class C_ActRatSigm : public C_Base_ActFunc
{
  public:
  C_ActRatSigm () {funcName = "ActRatSigm";}

  double Activ (double x)
  {
    return x / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    //1 / (1 + abs (x))^2
    double d = 1.0 + fabs (x);
    return 1.0 / (d * d);
  }
};
//——————————————————————————————————————————————————————————————————————————————

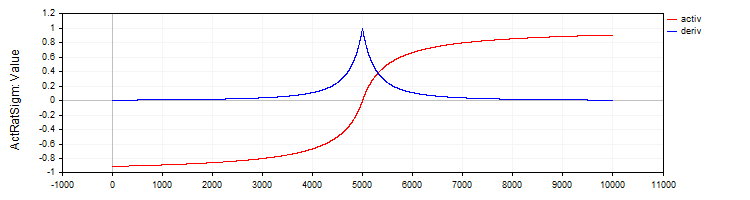
Figura 4. La sigmoide racional y su derivada

La clase "C_ActSoftPlus" implementará la función de activación "Softplus" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// Softplus
class C_ActSoftPlus : public C_Base_ActFunc
{
  public:
  C_ActSoftPlus () {funcName = "ActSoftPlus";}

  double Activ (double x)
  {
    return log (1.0 + exp (x));
  }

  double Deriv (double x)
  {
    return 1.0 / (1.0 + exp (-x));
  }
};
//——————————————————————————————————————————————————————————————————————————————

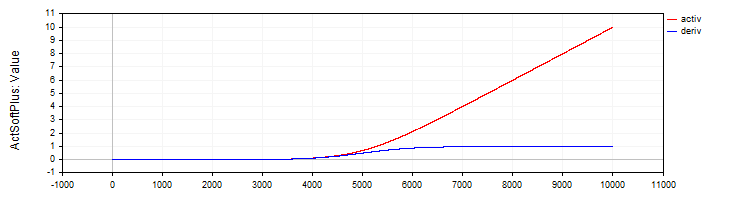
Figura 5. La función SoftPlus y su derivada

La clase "C_ActBentIdent" implementará la función de activación "Bent Identity" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// Bent Identity
class C_ActBentIdent : public C_Base_ActFunc
{
  public:
  C_ActBentIdent () {funcName = "ActBentIdent";}

  double Activ (double x)
  {
    return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x;
  }

  double Deriv (double x)
  {
    return x / (2.0 * sqrt (x * x + 1.0)) + 1.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

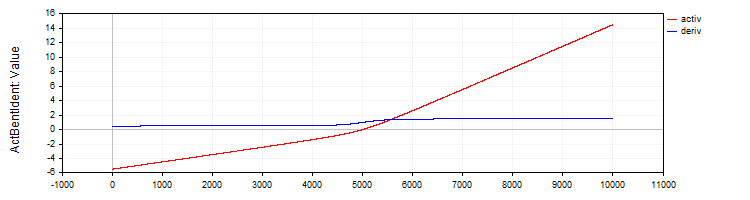
Figura 6. La función "Bent Identity" y su derivada

La clase "C_ActSiLU" presentará la implementación de la función de activación "SiLU" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// SiLU (Swish)
class C_ActSiLU : public C_Base_ActFunc
{
  public:
  C_ActSiLU () {funcName = "ActSiLU";}

  double Activ (double x)
  {
    return x / (1.0 + exp (-x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 0.5;

    // f(x) + (f(x)*(1 - f(x)))/ x
    double fx = Activ (x);
    return fx + (fx * (1.0 - fx)) / x;
  }
};
//——————————————————————————————————————————————————————————————————————————————

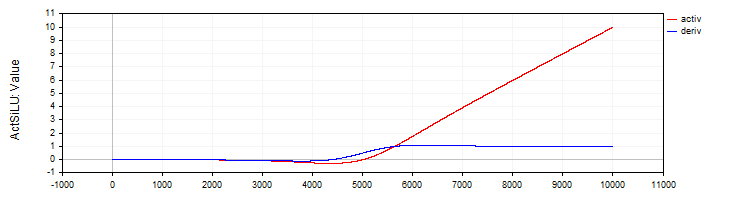
Figura 7. La función "SiLU" y su derivada

La clase "C_ActACON" implementará la función de activación "ACON" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// ACON
class C_ActACON : public C_Base_ActFunc
{
  public:
  C_ActACON () {funcName = "ActACON";}

  double Activ (double x)
  {
    return (x * cos (x) + sin (x)) / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 2.0;

    //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)]
    double sinX   = sin  (x);
    double cosX   = cos  (x);
    double fabsX  = fabs (x);
    double fabsXp = fabsX + 1.0;

    // Разделяем формулу на две части
    double part1 = (2.0 * cosX - x * sinX) / fabsXp;
    double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp);
    return part1 + part2;
  }
};
//——————————————————————————————————————————————————————————————————————————————

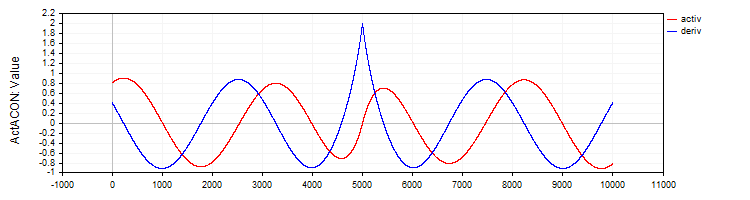
Figura 8. La función ACON y su derivada

La clase "C_ActSERF" implementará la función de activación "SERF" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// SERF (Функция сигмоидально-взвешенного экспоненциального выпрямления)
class C_ActSERF : public C_Base_ActFunc
{
  public:
  C_ActSERF ()
  {
    alpha    = 0.5;
    funcName = "ActSERF";
  }

  double Activ (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));

    if (x >= 0) return sigmoid * x;
    else return sigmoid * (exp (x) - 1.0);
  }

  double Deriv (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));
    double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid);
    double e = exp (x);
    if (x >= 0) return sigmoid + x * sigmoidDeriv;
    else return sigmoid * e + (e - 1.0) * sigmoidDeriv;
  }

  private:
  double alpha;
};
//——————————————————————————————————————————————————————————————————————————————

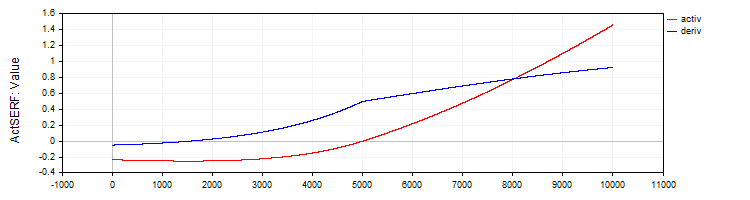
Figura 9. La función SERF y su derivada

La clase "C_ActSNAKE" implementará la función de activación "SNAKE" y su derivada.

//——————————————————————————————————————————————————————————————————————————————
// Snake (Периодическая активационная функция)
class C_ActSnake : public C_Base_ActFunc
{
  public:
  C_ActSnake ()
  {
    frequency = 1;
    funcName  = "ActSnake";
  }

  double Activ (double x)
  {
    double sinx = sin (frequency * x);
    return x + sinx * sinx;
  }

  double Deriv (double x)
  {
    double fx = frequency * x;
    return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency;
  }

  private:
  double frequency;
};
//——————————————————————————————————————————————————————————————————————————————

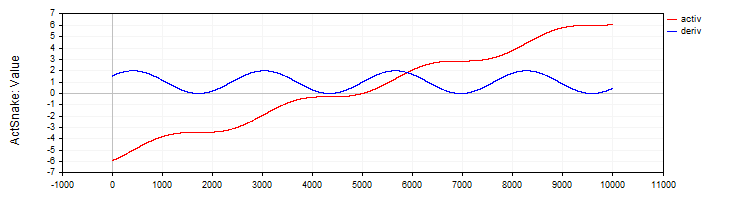
Figura 10. La función SNAKE y su derivada

Ponemos a prueba las funciones de activación

Ahora es el momento de ver cómo se entrena una red MLP con diferentes características de activación. La complejidad de la función de activación para el algoritmo de optimización puede demostrarse claramente en la configuración del MLP 1-1-1 utilizando un solo ejemplo en el entrenamiento (un valor por entrada y un valor objetivo).

A primera vista, esto puede no parecer obvio: ¿por qué iba a generar interés una tarea tan simple? Aquí radica un punto metodológico importante: el uso de un único punto de datos nos permitirá aislar e investigar con precisión la complejidad de la propia función de activación y su impacto en el proceso de optimización. Cuando trabajamos con un gran conjunto de datos, son muchos los factores que influyen en el proceso de aprendizaje: la distribución de los datos, las interdependencias entre ejemplos y la manifestación de su influencia al pasar por la función de activación. Utilizando solo un punto, eliminaremos todos estos factores externos y podremos centrarnos en lo difícil que es para el algoritmo de optimización lidiar con esa función de activación en particular.

La cuestión es que una red neuronal que pase por un único punto de la función interpolada podría tener innumerables variantes de pesos. Esto puede parecer increíble, pero se deduce de la ecuación "in * w + b = out", donde in será la entrada de la red, w será el peso, b será el desplazamiento, y out será la salida de la red para la configuración 1-1.

No hay problemas con esta configuración, sin embargo, aparecerán cuando se añade otra capa, es decir, una configuración 1-1-1. En este caso, incluso el problema más sencillo se convertirá en no trivial para el algoritmo de optimización, ya que el espacio de búsqueda de soluciones se volverá significativamente más complejo: ahora tendremos que encontrar la combinación correcta de pesos a través de la capa intermedia con su función de activación. Precisamente esta complejidad nos permitirá evaluar la eficacia de los distintos algoritmos de optimización a la hora de ajustar los pesos con distintas funciones de activación.

Las siguientes tablas muestran los resultados de los algoritmos ADAM en la implementación clásica y el ADAMm poblacional. Para ambos algoritmos, hemos realizado 10.000 iteraciones, considerando la presencia de una población para el algoritmo de población y manteniendo igual el número total de cálculos de la red neuronal. Las impresiones indican el grano del generador de números pseudoaleatorios (para reproducir las variantes problemáticas de las ejecuciones de entrenamiento), la iteración en la que se ha obtenido el mejor resultado y el resultado en la época actual múltiplo de 1000.

Los pesos se han inicializado con números aleatorios utilizando el método de Xavier para ADAM y números aleatorios en el rango [-10; 10] para ADAMm. Hemos realizado varias pruebas con diferentes granos y seleccionado los peores resultados. El proceso de selección de pesos ha finalizado al alcanzar el número máximo de iteraciones o cuando el error se ha reducido por debajo de 0,000001.

Tabla de resultados de las funciones de activación sigmoidales:

Tanh	AlgSigm	RatSigm
MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Iteración del mejor resultado: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 4 -----Integrated ADAM----- 0: 0.1878131682539310, 0: 0.18781316825393096 0: 0.1878131682539310, 1000: 0.22880505258129305 0: 0.1878131682539310, 2000: 0.2395439537933131 0: 0.1878131682539310, 3000: 0.24376284285887292 0: 0.1878131682539310, 4000: 0.24584964230029535 0: 0.1878131682539310, 5000: 0.2470364071634453 0: 0.1878131682539310, 6000: 0.24777681648987268 0: 0.1878131682539310, 7000: 0.2482702131676117 0: 0.1878131682539310, 8000: 0.24861563983949608 0: 0.1878131682539310, 9000: 0.2488669473265396 Best result iteration: 0, Err: 0.187813 -----Population-based ADAMm----- 0: 0.2481251241755712 1000: 0.0000009070157679 Best result iteration: 1000, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 4 -----Integrated ADAM----- 0: 0.0354471509280691, 0: 0.03544715092806905 0: 0.0354471509280691, 1000: 0.10064226929576263 0: 0.0354471509280691, 2000: 0.13866170841306655 0: 0.0354471509280691, 3000: 0.16067944018111643 0: 0.0354471509280691, 4000: 0.17502946224977484 0: 0.0354471509280691, 5000: 0.18520767592761297 0: 0.0354471509280691, 6000: 0.19285431843628092 0: 0.0354471509280691, 7000: 0.1988366186290051 0: 0.0354471509280691, 8000: 0.20365853142896836 0: 0.0354471509280691, 9000: 0.20763502064394074 Best result iteration: 0, Err: 0.035447 -----Population-based ADAMm----- 0: 0.1928944265733889 Best result iteration: 688, Err: 0.000000

Tabla de resultados de las funciones de activación de tipo SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 131.77685264891647 0: 0.5380138004155748, 2000: 1996.1250363225556 0: 0.5380138004155748, 3000: 8050.259717531171 0: 0.5380138004155748, 4000: 20321.169969814575 0: 0.5380138004155748, 5000: 40601.21872791767 0: 0.5380138004155748, 6000: 70655.44591598355 0: 0.5380138004155748, 7000: 112311.81150857621 0: 0.5380138004155748, 8000: 167489.98562842538 0: 0.5380138004155748, 9000: 238207.27978678182 Best result iteration: 0, Err: 0.538014 -----Population-based ADAMm----- 0: 18.4801637203493884 778: 0.0000022070092175 Best result iteration: 1176, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 185.646717568436 0: 15.1221330593320857, 2000: 1003.1026112225994 0: 15.1221330593320857, 3000: 2955.8393027057205 0: 15.1221330593320857, 4000: 6429.902382962495 0: 15.1221330593320857, 5000: 11774.781156010686 0: 15.1221330593320857, 6000: 19342.379583340015 0: 15.1221330593320857, 7000: 29501.355075464813 0: 15.1221330593320857, 8000: 42640.534930000824 0: 15.1221330593320857, 9000: 59168.850722337185 Best result iteration: 0, Err: 15.122133 -----Population-based ADAMm----- 0: 7818.0964949082390376 Best result iteration: 15, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 2 -----Integrated ADAM----- 0: 0.0021199944516222, 0: 0.0021199944516222444 0: 0.0021199944516222, 1000: 4.924850697388685 0: 0.0021199944516222, 2000: 14.827133542234415 0: 0.0021199944516222, 3000: 28.814259008218087 0: 0.0021199944516222, 4000: 45.93517121925276 0: 0.0021199944516222, 5000: 65.82077308420028 0: 0.0021199944516222, 6000: 88.26782602934948 0: 0.0021199944516222, 7000: 113.15535264604428 0: 0.0021199944516222, 8000: 140.41067538093935 0: 0.0021199944516222, 9000: 169.9878269747845 Best result iteration: 0, Err: 0.002120 -----Population-based ADAMm----- 0: 17.2288020548757288 1000: 0.0000030959186317 Best result iteration: 1150, Err: 0.000001

Tabla de resultados para las funciones de activación periódicas:

ACON	SERF	Snake
MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0,0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0,0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 481, Err: 0.000000	MLP config: 1|1|1, Weights: 4, Función de activación: eActSERF, Semilla: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001

Ahora podemos sacar conclusiones preliminares sobre la complejidad de las funciones de activación para el gradiente clásico ADAM y el ADAMm poblacional. Aunque el ADAM regular tiene información directa sobre el gradiente de la función de activación, es decir, conoce literalmente la dirección del descenso más pronunciado, no ha logrado hacer frente a una tarea aparentemente tan simple. Como resultado, la función más simple para ADAM ha sido ACON, en la que ha logrado minimizar consistentemente el error. Pero funciones como SiLU han resultado un problema para él: en ellas, el error no solo no ha disminuido, sino que ha crecido rápidamente. Resulta obvio que, como ADAM no tenía las condiciones de límite de pesos y desplazamientos, ha elegido la dirección equivocada y aumentado los valores de peso. Los pesos han volado libremente hacia los lados, sin restricciones y literalmente arrastrados por el viento dirigido de la derivada de la función de activación.

El problema solo empeorará si utilizamos más neuronas en las capas, porque cada neurona tomará como entrada la suma de los productos de las salidas de las neuronas de la capa anterior con el peso correspondiente. Por tanto, la suma podría ser tan grande que resulte imposible calcular correctamente la función exponencial.

Como podemos ver, ninguna de las funciones de activación supone un problema para el ADAMm poblacional. Este convergirá de forma estable en todas ellas, y solo en algunas el número de iteraciones superará ligeramente las 1000.

Mejoramos las clases de la función de activación, MLP y ADAM

Para solucionar la situación con los pesos dispersos en la red neuronal, realizaremos cambios en las clases de las funciones de activación. Esto permitirá rastrear los límites de las funciones correspondientes y evitar la acumulación de una gran suma cuando esta se suministre a una neurona, y también limitará los valores de los pesos y los desplazamientos en sí.

Luego añadiremos a la clase básica los métodos "GetBoundUp" y "GetBoundLo", que ofrecerán acceso a los límites de las funciones de activación correspondientes, permitiendo que otras clases o funciones obtengan información sobre los valores permitidos.

A continuación le mostramos el código para la clase básica y la clase de tangente hiperbólica con los cambios realizados (el resto del código no se modificará). Las clases restantes de las otras funciones de activación se implementarán de manera similar, con sus propios límites correspondientes.

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  double         GetBoundUp  () { return boundUp;}
  double         GetBoundLo  () { return boundLo;}
  protected:
  double boundUp;  // верхняя граница входного диапазона
  double boundLo;  // нижняя граница входного диапазона
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh ()
  {
    boundUp  =  6.0;
    boundLo  = -6.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Ahora añadiremos al código del método de pasada directa del MLP una verificación de los valores de suma antes de suministrarlos a la función de activación de neuronas para asegurarnos de que no superen los límites especificados. No tiene sentido aumentar la suma más allá de los límites dados, además, esto permitirá realizar una parada temprana al calcular la suma para una configuración de red con una gran cantidad de neuronas en las capas, lo cual puede acelerar significativamente los cálculos.

Comprobación del límite superior: este fragmento de código verificará si el valor actual de la suma es mayor que el límite superior establecido. Si el valor es mayor que este límite, se establecerá igual a este límite y se finalizará la ejecución del ciclo. El límite inferior se comprobará de manera similar.

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;

        if (val >  actFunc.GetBoundUp ())
        {
          val =  actFunc.GetBoundUp ();
          break;
        }
        if (val < actFunc.GetBoundLo ())
        {
          val = actFunc.GetBoundLo ();
          break;
        }
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

Ahora añadiremos al método de propagación inversa del error el código de verificación de límites. Estos complementos implementarán la lógica para reflejar los valores de desplazamiento y peso de los límites dados hacia el límite inverso. Esto será necesario para garantizar que los valores no caigan fuera de los rangos aceptables, evitando aumentos o disminuciones incontroladas en los pesos y desplazamientos.

La simple poda de los valores en el límite conduciría a un estancamiento en el entrenamiento, ya que el peso simplemente alcanzaría el límite y cambiar los pesos se volvería imposible. Precisamente para prevenir este tipo de situaciones se pone en práctica la reflexión, en lugar de la poda de valores. Esto posibilita una "revitalización" o una especie de "sacudida" al ajustar los pesos y los desplazamientos.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя
  double bias;      // смещение

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
      bias = nL [ln].n [nCurr].bias;

      if (bias < actFunc.GetBoundLo ())
      {
        nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias);  // отражаем от нижней границы
      }
      else
        if (bias > actFunc.GetBoundUp ())
        {
          nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ());  // отражаем от верхней границы
        }
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
        w = wL [lw].nOnL [nCurr].nOnR [nNext].w;

        if (w < actFunc.GetBoundLo ())
        {
          wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w);  // отражаем от нижней границы
        }
        else
          if (w > actFunc.GetBoundUp ())
          {
            wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ());  // отражаем от верхней границы
          }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ahora repetiremos las mismas pruebas de antes y veremos los resultados obtenidos. En estos momentos no hay una explosión de escalas ni un crecimiento en avalancha de errores durante el entrenamiento.

Tabla de resultados de las funciones de activación sigmoidales:

Tanh	AlgSigm	RatSigm
MLP config: 1|1|1, Weights: 4, Activation func: eActTanh, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActAlgSigm, Seed: 2 -----Integrated ADAM----- 0: 0.0095411465043040, 0: 0.009541146504303972 0: 0.0095411465043040, 1000: 0,20977102640908893 0: 0,0095411465043040, 2000: 0.23464558094398064 0: 0,0095411465043040, 3000: 0.23657904914082925 0: 0,0095411465043040, 4000: 0.17812555648593617 0: 0.0095411465043040, 5000: 2.1749975763135927 0: 0,0095411465043040, 6000: 2.2093668968051166 0: 0,0095411465043040, 7000: 2.1657244506071813 0: 0.0095411465043040, 8000: 1.9330415523200173 0: 0.0095411465043040, 9000: 0.10441382194622865 Best result iteration: 0, Err: 0.009541 -----Population-based ADAMm----- 0: 0.2201830630768654 Best result iteration: 750, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActRatSigm, Seed: 1 -----Integrated ADAM----- 0: 1.2866075458561122, 0: 1.2866075458561121 1000: 0,2796061866784148, 1000: 0.2796061866784148 2000: 0.0450819127087337, 2000: 0.04508191270873367 3000: 0.0200306843648248, 3000: 0.020030684364824806 4000: 0.0098744349153286, 4000: 0.009874434915328582 5000: 0.0049448920462547, 5000: 0.00494489204625467 6000: 0.0024344513388710, 6000: 0.00243445133887102 7000: 0.0011602603038120, 7000: 0.0011602603038120354 8000: 0.0005316894732581, 8000: 0.0005316894732581081 9000: 0.0002339388712666, 9000: 0.00023393887126662818 Best result iteration: 9999, Err: 0.000099 -----Population-based ADAMm----- 0: 1.8418367346938778 Best result iteration: 645, Err: 0.000000

Tabla de resultados de las funciones de activación de tipo SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1|1|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 12.377378915308087 0: 0.5380138004155748, 2000: 12.377378915308087 3000: 0,1996421769021168, 3000: 0,19964217690211675 4000: 0,1985425345613517, 4000: 0,19854253456135168 5000: 0,1966512639256550, 5000: 0,19665126392565502 6000: 0,1933509943676914, 6000: 0,1933509943676914 7000: 0,1874142582090466, 7000: 0,18741425820904659 8000: 0,1762132792048514, 8000: 0,17621327920485136 9000: 0,1538331138702293, 9000: 0.15383311387022927 Best result iteration: 9999, Err: 0.109364 -----Population-based ADAMm----- 0: 12.3773789153080873 Best result iteration: 677, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 25.619316876852988 1922: 8.6344718719116980, 2000: 8.634471871911698 1922: 8.6344718719116980, 3000: 8.634471871911698 1922: 8.6344718719116980, 4000: 8.634471871911698 1922: 8.6344718719116980, 5000: 8.634471871911698 1922: 8.6344718719116980, 6000: 8.634471871911698 6652: 4.3033564303197833, 7000: 8.634471871911698 6652: 4.3033564303197833, 8000: 8.634471871911698 6652: 4.3033564303197833, 9000: 7.11489380279475 Best result iteration: 9999, Err: 3.589207 -----Population-based ADAMm----- 0: 25.6193168768529880 Best result iteration: 15, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSiLU, Seed: 4 -----Integrated ADAM----- 0: 0.6585816582701970, 0: 0.658581658270197 0: 0.6585816582701970, 1000: 5.142928362480306 1393: 0,3271208998291733, 2000: 0.32712089982917325 1393: 0.3271208998291733, 3000: 0.32712089982917325 1393: 0.3271208998291733, 4000: 0.4029355474095988 5000: 0.0114993205601383, 5000: 0.011499320560138332 6000: 0.0003946998191595, 6000: 0.00039469981915948605 7000: 0.0000686308316624, 7000: 0.00006863083166239227 8000: 0.0000176901182322, 8000: 0.000017690118232197302 9000: 0.0000053723044223, 9000: 0.000005372304422295116 Best result iteration: 9999, Err: 0.000002 -----Population-based ADAMm----- 0: 19.9499415647445524 1000: 0.0000057228950379 Best result iteration: 1051, Err: 0.000000

Tabla de resultados para las funciones de activación periódicas:

ACON	SERF	Snake
MLP config: 1|1|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0,0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0,0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 300, Eh: 0.000000	MLP config: 1|1|1, Weights: 4, Función de activación: eActSERF, Semilla: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1|1|1, Weights: 4, Activation func: eActSnake, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001

Conclusiones

Bien, vamos a resumir nuestra investigación. Permítame recordarle la esencia del experimento: hemos tomado dos algoritmos de optimización construidos sobre la misma lógica, pero que funcionan de maneras fundamentalmente diferentes. El primero (ADAM clásico) es un optimizador integrado que funciona desde dentro de la red neuronal, con acceso directo a las funciones de activación y a toda la estructura interna, como un navegador con un mapa detallado del área. El segundo (población ADAMm) es un optimizador externo que trabaja con la red neuronal como una "caja negra", sin tener ninguna información sobre su estructura interna y los detalles de la tarea: como un viajero que encuentra su camino guiado solo por las estrellas y la dirección general.

Como objeto de estudio para ambos algoritmos, hemos usado la misma red neuronal. Esto es de vital importancia porque nos permite localizar la fuente de problemas potenciales: si tenemos dificultades al trabajar con ciertas funciones de activación, podemos estar seguros de que no se trata de un problema con la red neuronal en sí, sino con la forma en que el algoritmo de optimización interactúa con dichas funciones.

Esta configuración experimental nos permite ver claramente cómo funcionan diferentes funciones de activación en el contexto de distintos enfoques de optimización. Debemos señalar que deliberadamente no hemos considerado la capacidad de generalización de la red ni su rendimiento con datos nuevos. Nuestro objetivo es estudiar la influencia mutua de las funciones de activación y los algoritmos de optimización, su compatibilidad y la efectividad de su interacción.

Este enfoque nos permite obtener una imagen clara de cómo funcionan las diferentes estrategias de optimización en distintas funciones de activación, sin la influencia de factores extraños. Y los resultados del experimento muestran claramente que a veces un optimizador externo "ciego" puede resultar más efectivo que un algoritmo que tiene información completa sobre la estructura de la red.

En todas las funciones de activación, el ADAMm externo ha mostrado una convergencia rápida y estable, de lo cual podemos concluir que las propiedades de la función de activación no juegan un papel especial para él; por otro lado, el ADAM incorporado clásico ha topado con serios problemas.

Ahora veremos el comportamiento del ADAM integrado en cada una de las funciones de activación y lo resumiremos en las siguientes conclusiones:

1. Funciones problemáticas (convergencia atascada o lenta):

• TanH (tangente hiperbólica)
• AlgSigm (sigmoide algebraica)
• SERF (enderezamiento exponencial ponderado sigmoide)
• Snake (función periódica)

2. Casos exitosos (convergencia):

• RatSigm (sigmoide racional), la mejor de las sigmoides
  
• SoftPlus
• BentIdent (identidad curva)
  
• SiLU (Swish), lal mejor del segundo grupo
  
• ACON (función adaptativa), la mejor de las periódicas
  

3. Patrones:

Las funciones sigmoides clásicas (TanH, AlgSigm) presentan problemas de atascamiento. Las funciones adaptativas más modernas (ACON, SiLU) demuestran mejor convergencia. De las funciones periódicas, ACON muestra convergencia, mientras que Snake se atasca.

Así, en el estudio presentado, se ha desarrollado un enfoque integral para la optimización de redes neuronales que combina el control de los pesos, los límites de la función de activación y el proceso de aprendizaje en un único sistema interconectado. La innovación clave ha sido la introducción de los métodos GetBoundUp y GetBoundLo, que permiten que cada función de activación defina sus propios límites, que luego se utilizarán para controlar los pesos de la red. Este mecanismo se complementa con un sistema de interrupción temprana de la suma cuando se alcanzan los límites, lo que no solo evita cálculos redundantes, especialmente en redes grandes, sino que también garantiza que los valores se controlen antes de aplicar la función de activación.

Un elemento especialmente importante ha sido el mecanismo de reflexión del pesos, que, a diferencia de la poda o normalización tradicionales, evita el estancamiento en el aprendizaje mediante una especie de “sacudida” de los pesos al alcanzar los límites. Esta solución permite mantener la posibilidad de cambiar pesos incluso en situaciones críticas, asegurando la continuidad del proceso de aprendizaje. La integración sistémica de todos estos componentes crea un mecanismo eficaz para evitar la dispersión de los pesos sin perder flexibilidad de entrenamiento, lo que resulta especialmente importante al trabajar con diferentes funciones de activación. Este enfoque integrado no solo resuelve el problema del control de los pesos, sino que también abre nuevas perspectivas para comprender la interacción de varios componentes de una red neuronal durante el proceso de aprendizaje.

El estudio no indica que ADAM sea inútil en el entrenamiento de redes neuronales, sino que solo centra la atención en su respuesta a determinadas funciones de activación. Tal vez para las redes neuronales grandes no exista ninguna alternativa (o sus análogos modernos de los métodos de descenso de gradiente). Este puede ser el próximo tema para considerar la efectividad de ADAM (como representante de los algoritmos de optimización modernos mediante el método de propagación inversa) en el contexto de las redes neuronales a gran escala, así como para estudiar la influencia de la elección de las funciones de activación en la capacidad de generalización de la red y la estabilidad de su funcionamiento con nuevos datos.

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de optimización basados en la población
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	MLPa.mqh	Script	Red neuronal MLP con ADAM
4	Tests and Drawing act func.mq5	Script	Script para la construcción visual de las funciones de activación
5	Test act func in training.mq5	Script	Script de entrenamiento de MLP con ADAM y ADAMm