Redes neuronales en el trading: Mejora de la eficiencia del Transformer mediante la reducción de la nitidez (SAMformer)

Introducción

La previsión de series temporales multidimensionales es un problema de aprendizaje clásico que consiste en analizar series temporales para predecir tendencias futuras a partir de información histórica. Y es una tarea difícil debido a la correlación de las características y las dependencias temporales a largo plazo en las series temporales. Este problema de aprendizaje resulta habitual en aquellas aplicaciones del mundo real en las que las observaciones se recogen de forma secuencial (datos médicos, consumo eléctrico, cotizaciones bursátiles).

Recientemente, las arquitecturas basadas en el Transformer han logrado un rendimiento extraordinario en tareas de procesamiento del lenguaje natural y visión por computadora. El Transformer es particularmente eficaz al trabajar con datos secuenciales, lo que conlleva naturalmente la aplicación de este tipo de soluciones en series temporales. Sin embargo, el estado actual de la previsión de series temporales multidimensionales se consigue con un modelo más sencillo basado en el MLP.

Los trabajos recientes sobre la aplicación del Transformer a los datos de series temporales se han centrado principalmente en implementaciones eficientes que reducen el coste cuadrático de la atención, o en la descomposición de las series temporales para reflejar mejor los patrones subyacentes. No obstante, los autores del artículo "SAMformer: Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention" llaman la atención sobre el problema de la inestabilidad del aprendizaje de los Transformers que se manifiesta en ausencia de datos a gran escala.

En visión por computadora y PNL, se ha descubierto que las matrices de atención pueden sufrir un colapso de entropía o de rango. Luego se propusieron varios enfoques para superar estos problemas. Sin embargo, en el caso de la predicción de series temporales, aún quedan cuestiones abiertas sobre cómo pueden entrenarse eficientemente las arquitecturas de transformadores sin tendencia al sobreentrenamiento. Los autores del citado artículo pretenden demostrar que la eliminación de la inestabilidad del aprendizaje mejora el rendimiento del Transformer en la previsión multidimensional de largo alcance, en contra de las creencias previas sobre sus limitaciones.

1. El algoritmo SAMformer

Hoy vamos a analizar un sistema multidimensional de previsión a largo plazo, dada una serie temporal D-dimensional de longitud L (ventana de visualización retrospectiva). Los datos iniciales se disponen como una matriz 𝐗 ∈ RD×L. El objetivo consistirá en pronosticar los próximos H valores (horizonte de pronóstico), denotados como 𝐘 ∈ RD×H Supongamos que tenemos acceso a un conjunto de entrenamiento que consta de N observaciones. Nuestro objetivo será entrenar un modelo de predicción f𝝎: RD×L→RD×L con parámetros 𝝎 que minimice el error cuadrático medio (MSE) en el conjunto de datos de entrenamiento.

Recientemente se ha demostrado que los transformadores funcionan a la par que las redes neuronales lineales simples entrenadas para proyectar directamente los datos de origen en los valores predichos. Para encontrar las causas de este fenómeno, los autores del framework SAMformer consideran un modelo generativo para un problema de regresión artificial que imita una configuración de previsión de series temporales. Así, usan un modelo lineal para generar un cierto tipo de continuación de las series temporales hacia los datos de origen aleatorios, añadiendo un poco de ruido a los resultados. De este modo, se generan 15000 conjuntos de datos de origen y resultados que se dividen en 10000 muestras de entrenamiento y 5000 para la validación del modelo.

Usando un modelo generativo de este tipo, los autores del SAMformer desarrollan una arquitectura de Transformer que podría resolver eficazmente el problema de la predicción sin una complejidad excesiva. Para ello, proponen simplificar el codificador del Transformer convencional, dejando atrás el bloque de Self-Attention y el enlace residual. En lugar del bloque FeedForward, se usa directamente una capa lineal para predecir los datos posteriores.

Aquí cabe señalar que los autores del framework utilizan la atención canalizada, que simplifica la tarea y reduce el riesgo de hiperparametrización, ya que la matriz de atención se hace mucho más pequeña gracias a L>D. Además, la atención canalizada resulta más apropiada porque la generación de datos sigue al proceso de identificación.

Para determinar el papel de la atención en la resolución de problemas, los autores del framework consideran un modelo denominado Random Transformer. En él, solo se optimiza la capa de predicción, mientras que todos los parámetros del bloque de Self-Attention se fijan en valores aleatorios durante el entrenamiento a nivel de inicialización. Esto obliga al Transformer en cuestión a actuar como un modelo lineal. En la figura siguiente se muestra una comparación de los mínimos locales obtenidos por estos dos modelos tras su optimización mediante el método Adam con el modelo Oracle que corresponde a la solución de mínimos cuadrados (visualización a partir del artículo del autor).

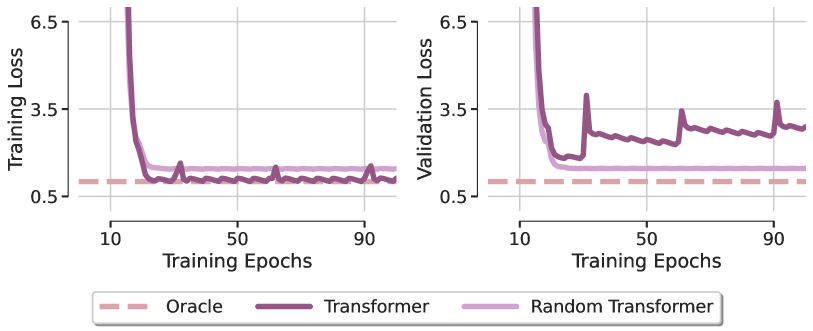
El primer hallazgo sorprendente es que ninguno de los transformadores consigue recuperar la dependencia lineal de la regresión artificial, lo cual pone de manifiesto que la optimización incluso de una arquitectura tan sencilla con un diseño favorable muestra una clara falta de generalización. Esta observación permanece invariable para distintos optimizadores y valores de la tasa de aprendizaje. A partir de esto, los autores del framework concluyen que la escasa capacidad de generalización del Transformer se debe principalmente a problemas en la capacidad de aprendizaje del módulo de atención.

Para comprender mejor el fenómeno descubierto, los autores del SAMformer visualizan las matrices de atención en distintas épocas de aprendizaje, descubriendo que la matriz de atención se aproxima a la matriz de identidad justo después de la primera época y casi no cambia a partir de entonces, especialmente cuando SoftMax amplifica las diferencias en los valores de la matriz. Esto demuestra la aparición de un colapso entrópico de la atención con una matriz de atención de rango completo, lo cual se identifica como una de las razones de la rigidez del entrenamiento de los transformadores.

Los autores del SAMformer también encuentran una relación entre el colapso de la entropía y la nitidez del panorama de pérdidas del Transformer. El Transformer converge a un mínimo más nítido que el Random Transformer, a la vez que posee una entropía mucho menor (la atención respecto a este último se fija en la inicialización, su entropía permanece constante a lo largo del entrenamiento). Estos patrones patológicos sugieren que el Transformer falla debido al colapso de entropía y a la brusquedad de su pérdida en el aprendizaje.

Estudios recientes han demostrado que el panorama de pérdidas del Transformer es más agudo que el de otras arquitecturas. Esto puede explicar la inestabilidad del entrenamiento y el bajo rendimiento del Transformer, especialmente al entrenarse con conjuntos de datos pequeños.

Con el fin de encontrar una solución adecuada para mejorar el rendimiento de la generalización y la estabilidad del aprendizaje, los autores del framework SAMformer investigan dos enfoques. El primero consiste en utilizar un sistema de minimización consciente de la nitidez que sustituya al objetivo de aprendizaje:

donde ρ>0 es el hiperparámetro, y 𝝎 es el parámetro del modelo.

El segundo enfoque consiste en volver a parametrizar todas las matrices de pesos usando la normalización espectral y un escalar entrenado adicional llamado σReparam.

Los resultados ponen de relieve el éxito de la convergencia de la solución propuesta hacia el resultado deseado. Sorprendentemente, esto solo se logra con SAM, ya que σReparam no consigue acercarse al rendimiento óptimo a pesar de maximizar la entropía de la matriz de atención. Además, la nitidez utilizando SAM es varios órdenes de magnitud inferior a la del Transformer, mientras que la entropía de la atención obtenida con SAM se mantiene cercana a la de la línea básica del Transformer, con un ligero aumento en las últimas etapas del entrenamiento. Esto sugiere que el colapso de entropía resulta positivo en este escenario.

Los autores del SAMformer complementan la solución descrita con una normalización reversible de instancias (RevIN). Este método ha demostrado su eficacia a la hora de gestionar el cambio entre los datos de entrenamiento y los de prueba en las series temporales. Como se desprende del estudio presentado anteriormente, el modelo se optimiza usando SAM, lo que obliga al modelo a converger a mínimos locales más planos. En general, se ofrece un modelo del Transformer reducido con un único codificador que se muestra en la figura siguiente (visualización del autor).

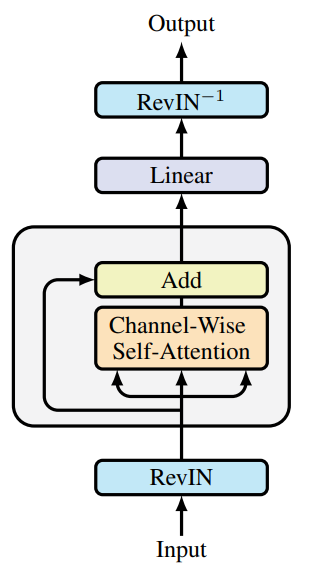
Debemos destacar que el SAMformer preserva la atención de canal representada por la matriz D×D, en contraste con la atención espacial (o temporal) dada por la matriz L×L utilizada en otros modelos. Esto ofrece dos ventajas importantes:

• proporciona invarianza a la permutación de características, eliminando la necesidad de codificación posicional que suele preceder a la capa de atención;
• permite reducir el tiempo y la complejidad de memoria, ya que D≤L en la mayoría de los conjuntos de datos del mundo real.

La atención por canales examina el efecto medio de cada característica sobre las demás en todos los pasos temporales.

2. Implementación con MQL5

Tras considerar los aspectos teóricos del framework SAMformer, pasaremos a la implementación de los enfoques propuestos mediante MQL5. Y aquí es importante definir desde el principio qué implementaremos en nuestros modelos y cómo lo haremos. Veamos con detalle lo que nos ofrecen los autores del framework SAMformer:

• un truncamiento del Codificador del Transformer hasta el nivel de un bloque de Self-Attention con enlace residual;
• atención canalizada;
• normalización reversible;
• optimización de SAM.

El truncamiento del codificador es una cuestión interesante, pero en mi opinión su principal valor práctico reside en la reducción de los parámetros del modelo entrenado. Después de todo, si dejamos a un lado las convenciones, la funcionalidad del modelo no depende de nuestra atribución de capas neuronales individuales al bloque FeedForward del Codificador o al bloque de predicción que los autores del framework colocan detrás del bloque de atención.

Para organizar la atención a través de los canales, solo tendremos que transponer los datos de origen antes de pasarlos a la unidad de atención. Y no necesitamos hacer ningún ajuste para eso.

Con la normalización reversible RevIN ya estamos familiarizados. Solo queda la optimización del modelo mediante el método SAM. El SAM funciona mediante la búsqueda de parámetros situados en vecindarios con un valor de pérdida uniformemente bajo.

El algoritmo de optimización SAM funciona en varias etapas. En primer lugar, a partir de los resultados de la pasada directa, obtenemos el gradiente de error a nivel de los parámetros del modelo. Luego normalizamos los gradientes de error obtenidos y añadimos el gradiente de error normalizado a los parámetros actuales, considerando el factor de nitidez. Repetimos la pasada directa y la distribución del gradiente de error. Luego devolvemos la matriz de pesos a su estado anterior, restando el gradiente normalizado previamente añadido. Y actualizamos los parámetros con uno de los métodos clásicos SGD o Adam. Los autores del framework SAMformer sugieren usar este último.

Y aquí cabe señalar que los autores del método utilizan la normalización de los gradientes de error en todo el modelo. Esto requiere mucho trabajo. Y en este contexto, la cuestión de la reducción del número de parámetros del modelo adquiere mayor relevancia. La solución obvia sería reducir las capas internas y las cabezas de atención. Es exactamente es lo que hacen los autores del framework SAMformer.

Nosotros hemos decidido apartarnos un poco de la implementación del autor en este caso, y normalizar los gradientes de error solo dentro de una única capa neuronal. Además, realizaremos una normalización separada de los gradientes para cada grupo de parámetros que forman el valor de una sola neurona. Y comenzaremos nuestra implementación construyendo nuevos kernels en el lado del programa OpenCL.

2.1 Complementamos el programa OpenCL

Creo que ya se habrá dado cuenta de que en nuestros trabajos utilizamos con mayor frecuencia dos tipos de capas neuronales: las completamente conectadas y las convolucionales. Todos nuestros módulos de atención se basan, de un modo u otro, en el uso de capas de convolución que utilizamos sin solapamiento para analizar y transformar elementos individuales de la secuencia analizada. Por ello, hemos decidido aumentar la funcionalidad de estas dos capas neuronales con la optimización SAM. En el lado del programa OpenCL, crearemos kernels para normalizar el gradiente de error y crear factores de peso ω+ε.

Primero crearemos un kernel para la capa totalmente conectada CalcEpsilonWeights. En los parámetros de este kernel, obtendremos los punteros a los 4 búferes de datos y al factor de dispersión de la nitidez. Tres búferes de datos contendrán la información original, mientras que otro registrará los resultados. 

__kernel void CalcEpsilonWeights(__global const float *matrix_w,
                                 __global const float *matrix_g,
                                 __global const float *matrix_i,
                                 __global float *matrix_epsw,
                                 const float rho
                                )
  {
   const size_t inp = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
   const size_t out = get_global_id(1);

Tenemos previsto invocar este kernel en un espacio de tareas bidimensional con combinación en grupos de trabajo a lo largo de la primera dimensión. En el cuerpo del kernel, identificaremos directamente el flujo actual de operaciones en todas las dimensiones del espacio de tareas.

Después declararemos un array de datos en la memoria local del dispositivo para organizar el proceso de intercambio de datos entre los flujos del grupo de trabajo.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)inputs, (int)LOCAL_ARRAY_SIZE);

En el siguiente paso, definiremos el gradiente de error del elemento analizado como el producto de los elementos correspondientes en los búferes de datos de origen y los gradientes a la salida de la capa. El valor obtenido se ponderará según el valor absoluto del parámetro analizado. Esto atribuirá más peso a los parámetros que más contribuyen al resultado de la capa.

   const int shift_w = out * (inputs + 1) + inp;
   const float w =IsNaNOrInf(matrix_w[shift_w],0);
   float grad = fabs(w) * IsNaNOrInf(matrix_g[out],0) * (inputs == inp ? 1.0f : IsNaNOrInf(matrix_i[inp],0));

Y luego deberemos encontrar la norma L2 de los gradientes de error obtenidos. Para ello, sumaremos los cuadrados de los valores obtenidos dentro de un grupo de trabajo utilizando un array en la memoria local y dos ciclos consecutivos, como hemos hecho en trabajos anteriores.

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

La raíz cuadrada de la suma obtenida será la norma buscada de los gradientes. Con su ayuda encontraremos el valor corregido del parámetro.

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7), w);
//---
   matrix_epsw[shift_w] = epsw;
  }

Y guardaremos el valor obtenido en el elemento correspondiente del búfer global de resultados.

El kernel CalcEpsilonWeightsConv, que realiza el ajuste inicial de los parámetros de la capa de convolución, se construirá de forma similar. Sin embargo, como ya sabrá, la capa de convolución tiene sus propias peculiaridades. Posee menos parámetros, pero cada parámetro interactúa con múltiples elementos de la capa de datos de origen y participa en la generación de los valores de múltiples elementos en el búfer de resultados. En consecuencia, el gradiente de error de un parámetro se generará recogiendo su fracción de varios elementos del búfer de resultados.

La especificidad de la capa de convolución también quedará patente en los parámetros del kernel. Aquí vemos la aparición de dos constantes adicionales que definen el tamaño de la secuencia de origen y el paso de la ventana de datos de origen.

__kernel void CalcEpsilonWeightsConv(__global const float *matrix_w,
                                     __global const float *matrix_g,
                                     __global const float *matrix_i,
                                     __global float *matrix_epsw,
                                     const int inputs,
                                     const float rho,
                                     const int step
                                    )
  {
//---
   const size_t inp = get_local_id(0);
   const size_t window_in = get_local_size(0) - 1;
   const size_t out = get_global_id(1);
   const size_t window_out = get_global_size(1);
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

También aumentaremos la dimensionalidad del espacio de tareas a 3. La primera dimensión se corresponderá con la ventana de datos de origen analizados ampliada por el elemento de desplazamiento. En la segunda dimensión, especificaremos el número de filtros de convolución. La tercera será responsable del número de secuencias independientes en los datos de origen. Como antes, agregaremos los flujos de transacciones en grupos de trabajo por la primera dimensión.

En el cuerpo del kernel, identificaremos el flujo actual de operaciones en todas las dimensiones del espacio de tareas. A continuación, inicializaremos el array de datos en la memoria local del contexto OpenCL para intercambiar información dentro del grupo de trabajo.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)(window_in + 1), (int)LOCAL_ARRAY_SIZE);

Luego calcularemos el número de elementos de cada filtro en el búfer de resultados y determinaremos los desplazamientos en los búferes de datos.

   const int shift_w = (out + v * window_out) * (window_in + 1) + inp;
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_out = v * total * window_out + out;
   const int shift_in = v * inputs + inp;
   const float w = IsNaNOrInf(matrix_w[shift_w], 0);

Aquí guardaremos el valor actual del parámetro analizado en una variable local, lo cual nos permitirá reducir aún más el número de operaciones de acceso global a la memoria.

En el siguiente paso, recopilaremos el gradiente de error de todos los elementos del búfer de resultados que se hayan visto afectados por el parámetro analizado.

   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(inp != window_in && (inp + t * step) >= inputs)
         break;
      float g = IsNaNOrInf(matrix_g[t * window_out + shift_out],0);
      float i = IsNaNOrInf(inp == window_in ? 1.0f : matrix_i[t * step + shift_in],0);
      grad += IsNaNOrInf(g * i,0);
     }

Lo ajustaremos según el valor absoluto de nuestro parámetro.

   grad *= fabs(w);

Y utilizaremos el algoritmo de dos ciclos consecutivos presentado anteriormente para sumar los cuadrados de los valores obtenidos dentro de un grupo de trabajo.

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

La raíz cuadrada de la suma resultante será la norma deseada de los gradientes de error.

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7),w);
//---
   matrix_epsw[shift_w] = epsw;
  }

Después calcularemos el valor del parámetro corregido y lo almacenaremos en el elemento correspondiente del búfer de resultados.

Con esto daremos por completo el trabajo en el lado del programa OpenCL. Podrá ver su código completo en el archivo adjunto.

2.2 Capa de optimización SAM completamente conectada

Una vez completado el trabajo en la parte del programa OpenCL, pasaremos a nuestra biblioteca, donde crearemos un objeto de capa completamente conectada con la funcionalidad de optimización SAM CNeuronBaseSAMOCL. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronBaseSAMOCL  :  public CNeuronBaseOCL
  {
protected:
   float             fRho;
   CBufferFloat      cWeightsSAM;
   //---
   virtual bool      calcEpsilonWeights(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      feedForwardSAM(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronBaseSAMOCL(void) {};
                    ~CNeuronBaseSAMOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint numNeurons, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const    {  return defNeuronBaseSAMOCL;      }
   virtual int       Activation(void)  const    {  return (fRho == 0 ? (int)None : (int)activation);   }
   virtual int       getWeightsSAMIndex(void)   {  return cWeightsSAM.GetIndex();   }
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Como puede ver en la estructura del nuevo objeto presentada anteriormente, heredaremos la funcionalidad principal de la capa básica completamente conectada. Básicamente, lo que tiene delante es una copia de la capa básica completamente conectada en la que redefiniremos el método de actualización de parámetros para considerar la funcionalidad de optimización SAM.

No obstante, hemos añadido el método de envoltorio calcEpsilonWeights para el kernel homónimo descrito anteriormente, y hemos hecho una copia del método de pasada directa en el que modificamos el búfer de coeficientes de peso feedForwardSAM.

Aquí debemos decir que los autores del framework SAMformer primero añaden ε a los parámetros del modelo y luego lo restan, devolviendo los parámetros del modelo a su estado original. Nosotros hemos hecho las cosas de forma un poco diferente. Y hemos guardado los parámetros corregidos en un búfer aparte. Esto nos permitió suprimir la operación de resta ε y reducir así el tiempo total de ejecución de las operaciones. Pero lo primero es lo primero.

Ahora declararemos estáticamente el búfer de parámetros del modelo ajustado, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos declarados y heredados se realizará en el método Init.

bool CNeuronBaseSAMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, 
                             float rho, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

En los parámetros del método obtendremos las constantes básicas que definirán la arquitectura del objeto a crear. Y en el cuerpo del método llamaremos directamente al método homónimo de la clase padre que controla los parámetros recibidos y la inicialización de los objetos heredados.

Una vez ejecutado con éxito el método de la clase padre, almacenaremos el coeficiente del área de dispersión en una variable interna.

   fRho = fabs(rho);
   if(fRho == 0 || !Weights)
      return true;

Y a continuación comprobaremos el valor del coeficiente de dispersión obtenido y la existencia del array de parámetros. Si el coeficiente de dispersión es "0" o no hay array de parámetros (la capa no contiene enlaces salientes), finalizaremos el método con un resultado positivo. De lo contrario, tendremos que crear un búfer de parámetros alternativos. Lo crearemos igual que el búfer de parámetros principal, pero lo rellenaremos con valores nulos en esta etapa.

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Luego finalizaremos el método.

Le sugiero que se familiarice con los métodos de envoltorio de colocación de los kernels en la cola. Su código figura en el anexo. Ahora pasaremos al método de actualización de parámetros updateInputWeights.

bool CNeuronBaseSAMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(NeuronOCL.Type() != Type() || fRho == 0)
      return CNeuronBaseOCL::updateInputWeights(NeuronOCL);

En los parámetros del método, como siempre, obtendremos el puntero al objeto de datos de origen. Y en el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido. Sin un puntero actualizado a la capa de datos de origen, no podremos seguir utilizando el método, ya que se producirían errores críticos.

También comprobaremos el tipo del objeto de datos de origen, ya que es importante en este caso. Además, el factor de disipación deberá ser superior a "0". De lo contrario, el SAM degenerará en una capa de optimización básica. Y llamaremos al método correspondiente de la clase padre.

Una vez superado con éxito el bloque de comprobación anterior, realizaremos directamente las operaciones del método SAM. Y aquí deberemos recordar que el algoritmo SAM implica una pasada completa directa y inversa con distribuciones del gradiente de error hasta los parámetros del modelo después de añadirles ε. Sin embargo, antes ya hemos decidido que la organización del algoritmo SAM se dará dentro de una capa individual. Así que resulta bastante razonable preguntarse de dónde sacaremos los valores objetivo para cada capa.

A primera vista, la respuesta es obvia: bastará con sumar el último resultado de la pasada directa y el gradiente de error. Pero hay un matiz a considerar. Al transferir el gradiente de error de una capa posterior, lo corregiremos mediante la derivada de la función de activación, lo cual significa que la suma simple de los datos sesgará el resultado. Y aquí parecería necesario crear un mecanismo para hacer retroceder el ajuste del gradiente de error a la derivada de la función de activación, pero hemos encontrado una solución más sencilla. Simplemente redefiniremos el método de retorno de la función de activación, que devolverá None cuando el factor de disipación sea cero. Así, obtendremos de la capa posterior el gradiente de error sin corregir por la función de activación derivada. En consecuencia, podremos sumar los resultados de la pasada directa y el gradiente de error obtenido, lo que en total nos dará el objetivo de la capa neuronal analizada.

   if(!SumAndNormilize(Gradient, Output, Gradient, 1, false, 0, 0, 0, 1))
      return false;

A continuación, llamaremos al método de envoltorio para obtener los parámetros ajustados del modelo.

   if(!calcEpsilonWeights(NeuronOCL))
      return false;

Y realizaremos un pasada directa con los parámetros modificados.

   if(!feedForwardSAM(NeuronOCL))
      return false;

Ahora tendremos los valores objetivo en el búfer de gradiente de error, mientras que en el búfer de resultados tendremos un vector a dónde nos llevarán los parámetros corregidos. Para determinar la desviación entre estos valores, solo tendremos que llamar al método de la clase padre para determinar la desviación respecto a los resultados objetivo.

   float error = 1;
   if(!calcOutputGradients(Gradient, error))
      return false;

Y ahora solo nos quedará ajustar los parámetros del modelo para considerar el gradiente de error actualizado. Para ello, bastará con llamar al método homónimo de la clase padre.

   return CNeuronBaseOCL::updateInputWeights(NeuronOCL);
  }

Conviene decir unas palabras sobre los métodos de trabajo con archivos. Para ahorrar espacio en disco, no guardaremos el búfer de parámetros ajustados cWeightsSAM. Guardar sus datos no tendrá ningún valor práctico, ya que el contenido de este búfer solo resultará relevante en el ámbito del método de actualización de parámetros. Y la próxima vez que se llame el método, se sobrescribirá. Así, la cantidad de datos almacenados ha aumentado en un solo elemento de tipo float (el coeficiente del área de dispersión).

bool CNeuronBaseSAMOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, fRho) < INT_VALUE)
      return false;
//---
   return true;
  }

Por otro lado, para implementar la funcionalidad dada, necesitaremos el búfer cWeightsSAM. Su tamaño resulta crítico para nosotros: debe ser lo suficientemente grande como para guardar todos los parámetros de la capa actual. Por lo tanto, tendremos que recuperarlo al leer un modelo previamente guardado. En el método de carga de datos, primero realizaremos las operaciones del método homónimo de la clase padre.

bool CNeuronBaseSAMOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

A continuación, comprobaremos el final del archivo y, si hay datos disponibles, leeremos el coeficiente del área de dispersión.

   if(FileIsEnding(file_handle))
      return false;
   fRho = FileReadFloat(file_handle);

Y comprobaremos la diferencia del coeficiente de dispersión respecto a cero, así como la presencia del array de parámetros (su puntero puede ser irrelevante si no hay enlaces salientes de la capa de neuronas).

   if(fRho == 0 || !Weights)
      return true;

Si encontramos al menos un desajuste, la optimización de parámetros regresará en los métodos básicos y no necesitaremos crear un búfer de parámetros corregidos. Por lo tanto, finalizaremos el método con un resultado positivo.

Aquí vale la pena señalar que el fallo de este bloque de controles resulta crítico para la optimización de SAM, pero no es crítico para el rendimiento del modelo. Por ello, seguiremos trabajando con técnicas básicas de optimización.

Si necesitamos crear un búfer, primero borraremos el búfer existente. Al hacerlo esto, además, no comprobaremos conscientemente el resultado de las operaciones. Después de todo, puede haber situaciones en las que dicho búfer no exista al momento de cargar los datos. 

   cWeightsSAM.BufferFree();

A continuación, inicializaremos un búfer de tamaño suficiente con valores nulos y crearemos una copia del mismo en el contexto OpenCL.

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Esta vez controlaremos la ejecución de las operaciones, ya que su correcta ejecución resulta crítica para el posterior funcionamiento del modelo. Y una vez realizadas las operaciones, finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluirá nuestra revisión de los algoritmos para construir los métodos de los objetos de capa completamente conectada con la funcionalidad de optimización SAM CNeuronBaseSAMOCL. Podrá leer el código completo de esta clase y todos sus métodos en el archivo adjunto.

Por desgracia, casi hemos agotado la extensión del artículo y aún no hemos terminado el trabajo. En el próximo artículo continuaremos lo empezado y veremos la implementación de la capa de convolución con la realización de la funcionalidad SAM. Asimismo, veremos la implementación de las tecnologías propuestas en la arquitectura del Transformer y, por supuesto, probaremos la eficacia de los enfoques propuestos con datos históricos reales

Conclusión

El SAMformer ofrece una solución eficaz a los problemas clave del Transformer en la previsión de series temporales multidimensionales a largo plazo, como la complejidad del entrenamiento y la escasa capacidad de generalización en muestras pequeñas. Con una arquitectura poco profunda y un mecanismo de optimización que tiene en cuenta la nitidez, el SAMformer no solo evita los malos mínimos locales, sino que también demuestra superioridad sobre los métodos más avanzados con menos parámetros. Los resultados presentados en el trabajo del autor confirman su potencial como herramienta universal para los problemas de series temporales.

En la parte práctica de nuestro artículo, hemos empezado a trabajar en la implementación de los enfoques propuestos utilizando herramientas MQL5. Pero nuestro trabajo sigue en marcha. En el próximo artículo evaluaremos el valor práctico de los enfoques propuestos para resolver nuestros problemas.

Enlaces

SAMformer: Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention

Sharpness-Aware Minimization for Efficiently Improving Generalization

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL