Asesor experto basado en un aproximador MLP universal

Contenido

1. Introducción
2. Inmersión en los problemas de aprendizaje
   
3. El aproximador universal
4. La implantación del MLP como parte de un asesor comercial

Introducción

Al hablar de redes neuronales, mucha gente imagina algoritmos complejos y engorrosos detalles técnicos. En esencia, una red neuronal es un compuesto de características, donde cada capa consta de una combinación de una transformación lineal y de una función de activación no lineal. Si visualizamos esto en forma de fórmula, podemos escribirlo como:

F(x) = f2(f1(x))

donde f1 es una función de la primera capa, mientras que f2 es una función de la segunda capa.

Mucha gente considera que las redes neuronales son algo inimaginablemente complejo y difícil de entender, sin embargo, hoy las explicaremos con palabras sencillas para que todo el mundo pueda verlas desde una perspectiva diferente. Existen muchas arquitecturas de redes neuronales, cada una diseñada para realizar tareas específicas. En este artículo, nos centramos en el perceptrón multicapa (MLP) más sencillo, que lleva a cabo la transformación de la información entrante usando funciones no lineales. Conociendo la arquitectura de la red, podemos escribirla de forma analítica, es decir, de manera que cada función de activación en las neuronas sirva como un transformador no lineal.

Cada capa de la red contiene un grupo de neuronas que procesarán la información que pasa por un conjunto de transformaciones no lineales. Un perceptrón multicapa es capaz de realizar tareas como la aproximación, la clasificación y la extrapolación. La fórmula general que describe el funcionamiento del perceptrón se regula con la ayuda de pesos, lo cual nos permite adaptarla a diferentes tareas.

Curiosamente, podemos integrar este aproximador en cualquier sistema comercial. Si consideramos una red neuronal sin mencionar optimizadores como SGD o ADAM, el MLP se puede utilizar como transformador de información. Por ejemplo, podemos analizar las condiciones del mercado -ya sea plano, de tendencia o un estado transitorio- y aplicar distintas estrategias comerciales en función de estas. También podemos usar una red neuronal para convertir los datos de los indicadores en señales comerciales.

En este artículo, pretendemos disipar el mito sobre la complejidad del uso de las redes neuronales y mostrar cómo, dejando a un lado los intrincados detalles de la configuración de los pesos y la optimización, se puede crear un asesor comercial basado en una red neuronal sin tener conocimientos profundos de aprendizaje automático. Iremos a través del proceso de creación del EA paso a paso, desde la recogida y preparación de datos hasta el entrenamiento del modelo y su integración en una estrategia comercial.

Inmersión en los problemas de aprendizaje

Existen tres tipos principales de aprendizaje. A nosotros nos interesan los matices de estos tipos aplicados al análisis de datos de mercado. El enfoque que se presenta en este artículo está pensado para considerar las deficiencias de estos tipos de aprendizaje.

Aprendizaje supervisado. El modelo se entrena con datos etiquetados y realiza sus predicciones basándose en ejemplos. Función objetivo: minimización del error de previsión que se corresponde con el valor objetivo (por ejemplo, error MSE). No obstante, este enfoque presenta una serie de desventajas. Requiere una cantidad significativa de datos etiquetados de alta calidad, lo cual supone un gran reto en el contexto de las series temporales. Si tenemos ejemplos claros y válidos para el aprendizaje, por ejemplo, como en las tareas de reconocimiento de escritura a mano o de contenido de imágenes, el proceso de aprendizaje será fluido. La red neuronal aprende a reconocer exactamente aquello para lo que ha sido entrenada.

En el caso de las series temporales, la situación es distinta: resulta extremadamente difícil marcar los datos de tal manera que se pueda estar seguro de su fiabilidad y pertinencia. En la práctica, resulta que la red aprende lo que suponemos, en lugar de lo realmente relevante para el proceso investigado. Muchos autores insisten en la necesidad de usar etiquetas "buenas" para que el aprendizaje supervisado tenga éxito, pero el alcance de su calidad en el contexto de las series temporales suele ser difícil de determinar de antemano.

Como resultado, surgen otras evaluaciones subjetivas de la calidad del aprendizaje, como el "sobreentrenamiento", además de introducirse la noción artificial de "ruido", lo cual implica que una red excesivamente "sobreentrenada" puede memorizar datos de ruido en lugar de los patrones subyacentes. No encontrará definiciones claras ni una cuantificación del "ruido" y el "sobreentrenamiento" en ningún sitio, precisamente porque son conceptos subjetivos al trabajar con el análisis de series temporales. Por consiguiente, debemos reconocer que aplicar el aprendizaje supervisado a las series temporales exige tener en cuenta muchos matices difíciles de "algoritmizar" que afectan significativamente a la robustez del modelo sobre nuevos datos.

Aprendizaje no supervisado. El propio modelo busca estructuras ocultas en datos no etiquetados. Función objetivo: distinta según los métodos. Resulta difícil evaluar la calidad de los resultados obtenidos, ya que no hay marcadores claros que comprobar. El modelo puede no encontrar patrones útiles si los datos no están claramente estructurados, y no se sabe si realmente se han hallado estructuras en los datos que sean directamente relevantes para el "proceso portador".

Métodos que tradicionalmente se clasifican como aprendizaje no supervisado: K-means, mapas autoorganizativos (SOM) y otros. Todos estos métodos se entrenan usando funciones objetivo específicas para ellos.

Aquí tenemos algunos ejemplos relevantes:

• K-medias (K-means). Minimización de la varianza intraclúster, que se define como la suma de los cuadrados de las distancias entre cada punto y el centro de su clúster.
• Método de componentes principales (PCA). Maximización de la varianza de las proyecciones de los datos sobre nuevos ejes (componentes principales).
• Árboles de decisión (DT). Minimización de la entropía, índice de Gini, varianza y otros.
  

Aprendizaje por refuerzo. Función objetivo: recompensa total. Es una técnica de aprendizaje automático en la que un agente (un programa o un robot, por ejemplo) aprende a tomar decisiones interactuando con el entorno. El agente es recompensado o penalizado según sus acciones. El objetivo del agente consiste en maximizar la recompensa total aprendiendo de la experiencia.

Los resultados pueden ser inestables debido a la naturaleza aleatoria del aprendizaje, lo cual dificulta la predicción del comportamiento del modelo, y no siempre resulta adecuado para tareas en las que no existe un sistema claro de recompensa y penalización, lo que puede restar eficacia al entrenamiento. El aprendizaje por refuerzo suele asociarse a numerosos problemas prácticos, como la dificultad de representar la función objetivo de refuerzo cuando se utilizan algoritmos de aprendizaje de redes neuronales como ADAM y similares, ya que debemos normalizar los valores de la función objetivo en un rango cercano a [-1;1]. Esto implica computar las derivadas de la función de activación en las neuronas y realizar la pasada inversa del error a través de la red para ajustar los pesos con el fin de evitar la "explosión de pesos" y efectos similares que provocan el estupor de la red neuronal.

Más arriba hemos considerado la clasificación clásica de los tipos de aprendizaje. Como podemos ver, todos se basan en la minimización/maximización de una cierta función objetivo. Entonces se hace evidente que la principal diferencia entre ellos es cosa simple: la ausencia o presencia de un "supervisor"; en ausencia de este, la división de los tipos de aprendizaje se reduce a las especificidades de la función objetivo a optimizar.

Así, en mi opinión, la clasificación de los tipos de aprendizaje puede presentarse como aprendizaje supervisado, cuando hay valores objetivo (minimización del error de predicción con respecto al objetivo) y aprendizaje no supervisado, cuando no tenemos valores objetivo. Luego tenemos subespecies de aprendizaje no supervisado según el tipo de función objetivo basada en las propiedades de los datos (distancias, densidades, etc.), los resultados del sistema (métricas integrales como beneficios, productividad, etc.), las distribuciones (para modelos generativos) y otros criterios de evaluación.

El aproximador universal

El enfoque que he proponemos es del segundo tipo: aprendizaje no supervisado. En este método, no intentaremos "enseñar" a la red neuronal cómo operar correctamente, ni le diremos dónde abrir o cerrar posiciones, porque nosotros mismos no conocemos la respuesta a estas preguntas. En su lugar, permitiremos que la red tome sus propias decisiones comerciales, y nuestro trabajo consistirá en evaluar su rendimiento comercial conjunto.

Al hacerlo, no necesitaremos normalizar la función de evaluación ni preocuparnos por problemas como las "explosión de pesos" y el "estupor de la red", ya que estarán ausentes en este enfoque. Luego separaremos lógicamente la red neuronal del algoritmo de optimización y le encomendaremos únicamente la tarea de convertir los datos de entrada en un nuevo tipo de información que refleje las habilidades del tráder. En esencia, nos limitaremos a convertir un tipo de información en otro, sin tener ni idea de los patrones de las series temporales ni de cómo operar para obtener beneficios.

Un tipo de red neuronal como MLP (perceptrón multicapa) será ideal para esta función, que queda demostrada por el teorema de aproximación universal. Este teorema afirma que las redes neuronales pueden aproximar cualquier función continua. En nuestro caso, por "función continua" entenderemos un proceso que se produce en la serie temporal analizada. En este enfoque, no será necesario recurrir a conceptos artificiales y subjetivos como "ruido" y "sobreentrenamiento", no cuantificables.

Para hacerse una idea de cómo funciona, bastará con consultar la figura 1. Suministraremos al MLP cierta información relacionada con los datos de mercado en el momento actual (pueden ser precios de barras OHLC, valores de indicadores, etc.), y la salida obtendremos señales comerciales listas para usar. Tras recorrer la historia de símbolos comerciales, podemos calcular la función objetivo, que será una puntuación integral (o conjunto de puntuaciones) de los resultados comerciales, y ajustar los pesos de la red mediante un algoritmo de optimización externo, maximizando la función objetivo que describe la calidad de los resultados comerciales de la red neuronal.

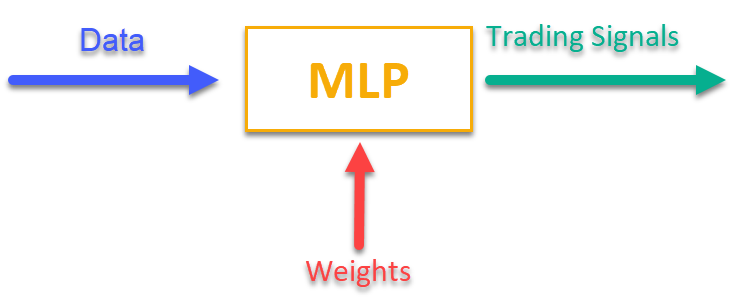
Figura 1. Transformación de un tipo de información en otro

La implantación del MLP como parte de un asesor comercial

Primero escribiremos la clase de MLP y luego la incluiremos en el EA. Existen muchas implementaciones de redes de diferentes arquitecturas en diferentes artículos, pero mostraremos nuestra variante de MLP, que es exactamente una red neuronal, sin optimizador.

Vamos a declarar ahora la clase "C_MLP" que implementará un perceptrón multicapa (MLP). Funciones principales:

1. Init () — inicialización, configura la red según el número requerido de capas y el número de neuronas en cada capa y retorna el número total de pesos.

2. ANN ()  — pasada directa de la primera capa de entrada a la última capa de salida; el método acepta los datos de entrada y los pesos, y calcula los valores de salida de la red (ver figura 1).

3. GetWcount () — método que devuelve el número total de pesos de la red.

4. LayerCalc () — realiza el cálculo de la capa de red.

Elementos internos:

• layers — almacenan los valores de las neuronas
• weightsCNT — número total de pesos
• layersCNT — número total de capas

La clase permite crear una red neuronal MLP con cualquier número de capas ocultas y cualquier número de neuronas en estas.

//+----------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                          |
//| Implement a forward pass through a fully connected neural network          |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                            |
//+----------------------------------------------------------------------------+
class C_MLP
{
  public: //--------------------------------------------------------------------

  // Initialize the network with the given configuration
  // Return the total number of weights in the network, or 0 in case of an error
  int Init (int &layerConfig []);

  // Calculate the values of all layers sequentially from input to output
  void ANN (double &inLayer  [],  // input values
            double &weights  [],  // network weights (including biases)
            double &outLayer []); // output layer values

  // Get the total number of weights in the network
  int GetWcount () { return weightsCNT; }

  int layerConf []; // Network configuration - number of neurons in each layer

  private: //-------------------------------------------------------------------
  // Structure for storing the neural network layer
  struct S_Layer
  {
      double l [];     // Neuron values
  };

  S_Layer layers [];    // Array of all network layers
  int     weightsCNT;   // Total number of weights in the network (including biases)
  int     layersCNT;    // Total number of layers (including input and output ones)
  int     cnt_W;        // Current index in the weights array when traversing the network
  double  temp;         // Temporary variable to store the sum of the weighted inputs

  // Calculate values of one layer of the network
  void LayerCalc (double   &inLayer  [], // values of neurons of the previous layer
                  double   &weights  [], // array of weights and biases of the entire network
                  double   &outLayer [], // array for writing values of the current layer
                  const int inSize,      // number of neurons in the input layer
                  const int outSize);    // outSize  - number of neurons in the output layer
};

Se inicializa un perceptrón multicapa (MLP) con la configuración de capas especificada. Pasos básicos:

1. Comprobación de la configuración:

• Se comprueba que la red tenga al menos 2 capas (entrada y salida).
• Se comprueba que haya al menos 1 neurona en cada capa. Si no se cumplen las condiciones, se imprime un mensaje de error y la función devuelve 0.

2. Se guarda la configuración de cada capa para un acceso rápido al array "layerConf".

3. Se crean los arrays de capas: se asigna la memoria para almacenar las neuronas de cada capa.

4. Se recuentan los pesos: se calcula el número total de pesos de la red, incluidos los desplazamientos de cada neurona.

La función retorna el número total de pesos o 0 en caso de error.

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLP::Init (int &layerConfig [])
{
  // Check that the network has at least 2 layers (input and output)
  layersCNT = ArraySize (layerConfig);
  if (layersCNT < 2)
  {
    Print ("Error Net config! Layers less than 2!");
    return 0;
  }

  // Check that each layer has at least 1 neuron
  for (int i = 0; i < layersCNT; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Error Net config! Layer No." + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  // Save network configuration
  ArrayCopy (layerConf, layerConfig, 0, 0, WHOLE_ARRAY);

  // Create an array of layers
  ArrayResize (layers, layersCNT);

  // Allocate memory for neurons of each layer
  for (int i = 0; i < layersCNT; i++)
  {
    ArrayResize (layers [i].l, layerConfig [i]);
  }

  // Calculate the total number of weights in the network
  weightsCNT = 0;
  for (int i = 0; i < layersCNT - 1; i++)
  {
    // For each neuron of the next layer we need:
    // - one bias value
    // - weights for connections with all neurons of the current layer
    weightsCNT += layerConf [i] * layerConf [i + 1] + layerConf [i + 1];
  }

  return weightsCNT;
}

El método "LayerCalc" realiza los cálculos para una sola capa de una red neuronal usando una tangente hiperbólica como función de activación. Pasos básicos:

1. Parámetros de entrada y salida:

• inLayer []  — array de valores de entrada de la capa anterior
• weights [] — el array de pesos contiene los desplazamientos y los pesos de los enlaces
• outLayer [] — array para almacenar los valores de salida de la capa actual
• inSize — número de neuronas en la capa de entrada
• outSize — número de neuronas en la capa de salida

2. Ciclo por las neuronas de la capa de salida. Para cada neurona en la capa de salida:

• comienza con el valor de desplazamiento
• añade valores de entrada ponderados (cada valor de entrada se multiplica por el peso correspondiente)
• se considera el valor de la función de activación para la neurona

3. Aplicación de la función de activación:

• usa una tangente hiperbólica para transformar no linealmente el valor a un rango de -1 a 1
• el resultado se escribe en el array de valores de salida "outLayer []"

//+----------------------------------------------------------------------------+
//| Calculate values of one layer of the network                               |
//| Implement the equation: y = tanh(bias + w1*x1 + w2*x2 + ... + wn*xn)       |
//+----------------------------------------------------------------------------+
void C_MLP::LayerCalc (double    &inLayer  [],
                       double    &weights  [],
                       double    &outLayer [],
                       const int  inSize,
                       const int  outSize)
{
  // Calculate the value for each neuron in the output layer
  for (int i = 0; i < outSize; i++)
  {
    // Start with the bias value for the current neuron
    temp = weights [cnt_W];
    cnt_W++;

    // Add weighted inputs from each neuron in the previous layer
    for (int u = 0; u < inSize; u++)
    {
      temp += inLayer [u] * weights [cnt_W];
      cnt_W++;
    }

    // Apply the "hyperbolic tangent" activation function
    // f(x) = 2/(1 + e^(-x)) - 1
    // Range of values f(x): [-1, 1]
    outLayer [i] = 2.0 / (1.0 + exp (-temp)) - 1.0;
  }
}

Implementaremos el funcionamiento de la red neuronal artificial calculando secuencialmente los valores de todas las capas, desde la entrada hasta la salida. 

1. Parámetros de entrada y salida:

• inLayer []  — array de valores de entrada que se introducen en la red neuronal
• weights []  — array de pesos que incluye tanto los pesos de las conexiones entre neuronas como los desplazamientos
• outLayer []  — array donde se almacenarán los valores de salida de la última capa de la red neuronal

2. Puesta a cero del contador de pesos: la variable "cnt_W", que lleva la cuenta de la posición actual en el array de pesos, se pone a cero antes de comenzar los cálculos.

3. Copiado de los datos de entrada: los datos de entrada de "inLayer" se copian en la primera capa de la red usando la función "ArrayCopy".

4. Ciclo por las capas:

• ciclo por todas las capas de la red neuronal.
• para cada capa se llama a la función "LayerCalc", que calcula los valores de la capa actual partiendo de los valores de salida de la capa anterior, los pesos y el tamaño de las capas.

5. Una vez finalizados los cálculos de todas las capas, los valores de salida de la última capa se copiarán en el array "outLayer" usando la función "ArrayCopy".

//+----------------------------------------------------------------------------+
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLP::ANN (double &inLayer  [],  // input values
                 double &weights  [],  // network weights (including biases)
                 double &outLayer [])  // output layer values
{
  // Reset the weight counter before starting the pass
  cnt_W = 0;

  // Copy the input data to the first layer of the network
  ArrayCopy (layers [0].l, inLayer, 0, 0, WHOLE_ARRAY);

  // Calculate the values of each layer sequentially
  for (int i = 0; i < layersCNT - 1; i++)
  {
    LayerCalc (layers    [i].l,     // output of the previous layer
               weights,             // network weights (including bias)
               layers    [i + 1].l, // next layer
               layerConf [i],       // size of current layer
               layerConf [i + 1]);  // size of the next layer
  }

  // Copy the values of the last layer to the output array
  ArrayCopy (outLayer, layers [layersCNT - 1].l, 0, 0, WHOLE_ARRAY);
}

Ahora nos toca a nosotros escribir un asesor experto para una estrategia comercial automatizada utilizando aprendizaje automático basado en una red neuronal MLP.

1. Primero conectaremos las bibliotecas para las transacciones comerciales, el procesamiento de información sobre símbolos comerciales, las funciones matemáticas, los perceptrones multicapa (MLP) y los algoritmos de optimización.

2. Parámetros comerciales: volumen de posiciones, horas de inicio y fin de la negociación. Parámetros de entrenamiento: selección del optimizador, la estructura de la red neuronal, el número de barras para el análisis, la profundidad de la historia para el entrenamiento, el periodo de relevancia del modelo y el umbral de la señal.

3. Declaración de clases y variables: objetos de clase para las utilidades, la red neuronal, y las variables para almacenar los datos de entrada, los pesos y el último tiempo de entrenamiento.

#include "#Symbol.mqh"
#include <Math\AOs\Utilities.mqh>
#include <Math\AOs\NeuroNets\MLP.mqh>
#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>

//------------------------------------------------------------------------------
input group    "---Trade parameters-------------------";
input double   Lot_P              = 0.01;   // Position volume
input int      StartTradeH_P      = 3;      // Trading start time
input int      EndTradeH_P        = 12;     // Trading end time

input group    "---Training parameters----------------";
input E_AO     OptimizerSelect_P  = AO_CLA; // Select optimizer
input int      NumbTestFuncRuns_P = 5000;   // Total number of function runs
input string   MLPstructure_P     = "1|1";  // Hidden layers, <4|6|2> - three hidden layers
input int      BarsAnalysis_P     = 3;      // Number of bars to analyze
input int      DepthHistoryBars_P = 10000;  // History depth for training in bars 
input int      RetrainingPeriod_P = 12;     // Duration in hours of the model's relevance
input double   SigThr_P           = 0.5;    // Signal threshold

//------------------------------------------------------------------------------
C_AO_Utilities U;
C_MLP          NN;
int            InpSigNumber;
int            WeightsNumber;
double         Inputs  [];
double         Weights [];
double         Outs    [1];
datetime       LastTrainingTime = 0;

C_Symbol       S;
C_NewBar       B;
int            HandleS;
int            HandleR;

Elegí lo primero que me vino a la mente como la información que llega a la red neuronal para ser procesada: OHLC: precios de las barras (por defecto en la configuración 3 barras anteriores a la actual) y valores de los indicadores RSI y Stochastic en estas barras. La función "OnInit ()" inicializa una estrategia comercial utilizando una red neuronal. 

1. Inicialización de los indicadores: se crean los objetos RSI y Stochastic.

2. Cálculo del número de señales de entrada para la red según el parámetro de entrada "BarsAnalysis_P".

3. Configuración de la estructura de la red neuronal: se divide la cadena de parámetros de entrada con la configuración de la red, y se comprueba que el número de capas y neuronas sea correcto. El parámetro de cadena de entrada especifica el número de capas ocultas de la red y las neuronas en ellas, por defecto el parámetro será "1|1", lo que indicará 2 capas ocultas en la red con una neurona en cada una.

4. Inicialización de la red neuronal: se llama al método para inicializar la red, se crean los arrays para los pesos y los datos de entrada.

5. Muestra de información: se imprimen el número de capas y los parámetros de la red.

6. Luego se devuelve el estado de inicialización exitosa.

La función posibilita la preparación de todos los componentes necesarios para el funcionamiento de la estrategia comercial.

//——————————————————————————————————————————————————————————————————————————————
int OnInit ()
{
  //----------------------------------------------------------------------------
  // Initializing indicators: Stochastic and RSI
  HandleS = iStochastic (_Symbol, PERIOD_CURRENT, 5, 3, 3, MODE_EMA, STO_LOWHIGH);
  HandleR = iRSI        (_Symbol, PERIOD_CURRENT, 14, PRICE_TYPICAL);

  // Calculate the number of inputs to the neural network based on the number of bars to analyze
  InpSigNumber = BarsAnalysis_P * 2 + BarsAnalysis_P * 4;

  // Display information about the number of inputs
  Print ("Number of network logins  : ", InpSigNumber);

  //----------------------------------------------------------------------------
  // Initialize the structure of the multilayer MLP
  string sepResult [];
  int layersNumb = StringSplit (MLPstructure_P, StringGetCharacter ("|", 0), sepResult);

  // Check if the number of hidden layers is greater than 0
  if (layersNumb < 1)
  {
    Print ("Network configuration error, hidden layers < 1...");
    return INIT_FAILED; // Return initialization error
  }

  // Increase the number of layers by 2 (input and output)
  layersNumb += 2;

  // Initialize array for neural network configuration
  int nnConf [];
  ArrayResize (nnConf, layersNumb);

  // Set the number of inputs and outputs in the network configuration
  nnConf [0] = InpSigNumber;   // Input layer
  nnConf [layersNumb - 1] = 1; // Output layer

  // Filling the hidden layers configuration
  for (int i = 1; i < layersNumb - 1; i++)
  {
    nnConf [i] = (int)StringToInteger (sepResult [i - 1]); // Convert a string value to an integer

    // Check that the number of neurons in a layer is greater than 0
    if (nnConf [i] < 1)
    {
      Print ("Network configuration error, in layer ", i, " <= 0 neurons...");
      return INIT_FAILED; // Return initialization error
    }
  }

  // Initialize the neural network and get the number of weights
  WeightsNumber = NN.Init (nnConf);
  if (WeightsNumber <= 0)
  {
    Print ("Error initializing MLP network...");
    return INIT_FAILED; // Return initialization error
  }

  // Resize the input array and weights
  ArrayResize (Inputs,  InpSigNumber);
  ArrayResize (Weights, WeightsNumber);

  // Initialize weights with random values in the range [-1, 1] (for debugging)
  for (int i = 0; i < WeightsNumber; i++)
      Weights [i] = 2 * (rand () / 32767.0) - 1;

  // Output network configuration information
  Print ("Number of all layers     : ", layersNumb);
  Print ("Number of network parameters: ", WeightsNumber);

  //----------------------------------------------------------------------------
  // Initialize the trade and bar classes
  S.Init (_Symbol);
  B.Init (_Symbol, PERIOD_CURRENT);

  return (INIT_SUCCEEDED); // Return successful initialization result
}
//——————————————————————————————————————————————————————————————————————————————

La lógica principal de la estrategia comercial se implementa en la función "OnTick ()". La estrategia es sencilla: si la señal de la neurona de la capa de salida supera el umbral establecido en los parámetros, la señal se interpretará como correspondiente a la dirección de compra/venta, y si no hay posiciones abiertas y la hora actual está permitida para la negociación, abriremos una posición. La posición se cerrará si se recibe una señal contraria de la red neuronal; o bien se cerrará forzosamente, en caso de que se acabe el tiempo permitido para negociar. Repasemos los pasos básicos de la estrategia:

1. Comprobación de la necesidad de nuevo entrenamiento. Si ha transcurrido suficiente tiempo desde el último entrenamiento, se iniciará el proceso de entrenamiento de la red neuronal. En caso de error, se mostrará un mensaje.

2. Comprobación de una nueva barra. Si el tick actual no supone el comienzo de una nueva barra, la función finalizará.

3. Obtención de datos. El código solicita los datos de precios (apertura, cierre, máximo, mínimo) y los valores de los indicadores (RSI y Stochastic).

4. Normalización de datos. Se encuentran los máximos y mínimos entre los datos de precios de los símbolos obtenidos; a continuación, todos los datos se normalizarán entre -1 y 1.

5. Predicción. Los datos normalizados se introducen en la red neuronal para producir señales de salida.

6. Generación de señales comerciales. Según los datos de salida, se generará una señal de compra (1) o de venta (-1).

7. Gestión de las posiciones. Si la posición actual contradice la señal, se cerrará. Si la señal para abrir una nueva posición coincide con el tiempo permitido, se abrirá una posición. En caso contrario, si hay una posición abierta, se cerrará.

Así, la lógica de OnTick () implementará el ciclo completo de la negociación automatizada, incluido el aprendizaje, la adquisición de datos, la normalización, la previsión y la gestión de posiciones.

//——————————————————————————————————————————————————————————————————————————————
void OnTick ()
{
  // Check if the neural network needs to be retrained
  if (TimeCurrent () - LastTrainingTime >= RetrainingPeriod_P * 3600)
  {
    // Start the neural network training
    if (Training ()) LastTrainingTime = TimeCurrent (); // Update last training time
    else             Print ("Training error...");      // Display an error message

    return; // Complete function execution
  }

  //----------------------------------------------------------------------------
  // Check if the current tick is the start of a new bar
  if (!B.IsNewBar ()) return;

  //----------------------------------------------------------------------------
  // Declare arrays to store price and indicator data
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  // Get price data
  if (CopyRates (_Symbol, PERIOD_CURRENT, 1, BarsAnalysis_P, rates) != BarsAnalysis_P) return;

  // Get Stochastic values
  if (CopyBuffer (HandleS, 0, 1, BarsAnalysis_P, sto) != BarsAnalysis_P) return;
  // Get RSI values
  if (CopyBuffer (HandleR, 0, 1, BarsAnalysis_P, rsi) != BarsAnalysis_P) return;

  // Initialize variables to normalize data
  int wCNT   = 0;
  double max = -DBL_MAX; // Initial value for maximum
  double min =  DBL_MAX; // Initial value for minimum

  // Find the maximum and minimum among high and low
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    if (rates [b].high > max) max = rates [b].high; // Update the maximum
    if (rates [b].low  < min) min = rates [b].low;  // Update the minimum
  }

  // Normalization of input data for neural network
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    Inputs [wCNT] = U.Scale (rates [b].high,  min, max, -1, 1); wCNT++; // Normalizing high
    Inputs [wCNT] = U.Scale (rates [b].low,   min, max, -1, 1); wCNT++; // Normalizing low
    Inputs [wCNT] = U.Scale (rates [b].open,  min, max, -1, 1); wCNT++; // Normalizing open
    Inputs [wCNT] = U.Scale (rates [b].close, min, max, -1, 1); wCNT++; // Normalizing close

    Inputs [wCNT] = U.Scale (sto   [b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
    Inputs [wCNT] = U.Scale (rsi   [b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
  }

  // Convert data from Inputs to Outs
  NN.ANN (Inputs, Weights, Outs);

  //----------------------------------------------------------------------------
  // Generate a trading signal based on the output of a neural network
  int signal = 0;
  if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
  if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

  // Get the type of open position
  int posType = S.GetPosType ();
  S.GetTick ();

  if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
  {
    if (!S.PosClose ("", ORDER_FILLING_FOK) != 0) posType = 0;
    else return;
  }

  MqlDateTime time;
  TimeToStruct (TimeCurrent (), time);

  // Check the allowed time for trading
  if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P)
  {
    // Open a new position depending on the signal
    if (posType == 0 && signal != 0) S.PosOpen (signal, Lot_P, "", ORDER_FILLING_FOK, 0, 0.0, 0.0, 1);
  }
  else
  {
    if (posType != 0) S.PosClose ("", ORDER_FILLING_FOK);
  }
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, analizaremos el entrenamiento de una red neuronal con datos históricos:

1. Obtención de datos. Se descargan los datos históricos de las cotizaciones, además de los valores de los indicadores RSI y Stochastic.

2. Definición del horario comercial. Se crea un array que marcará qué barras entran dentro del tiempo permitido para negociar.

3. Ajuste de los parámetros de optimización. Se inicializan los límites de los parámetros y los pasos para la optimización.

4. Selección del algoritmo de optimización. Se define el algoritmo de optimización y se establece el tamaño de la población.

5. Ciclo básico de optimización de los pesos de la red neuronal: 

• para cada solución de la población se calculará el valor de la función objetivo que evalúa su calidad.
• La población de soluciones se actualizará en función de los resultados.

6. Muestra de resultados. Se imprime el nombre del algoritmo, el mejor resultado y se copian los mejores parámetros al array de pesos.

7. Se libera la memoria ocupada por el objeto de algoritmo de optimización.

La función realizará el proceso de entrenamiento de la red neuronal para encontrar los mejores parámetros a partir de los datos históricos.

//——————————————————————————————————————————————————————————————————————————————
bool Training ()
{
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  int bars = CopyRates (_Symbol, PERIOD_CURRENT, 1, DepthHistoryBars_P, rates);
  Print ("Training on history of ", bars, " bars");
  if (CopyBuffer (HandleS, 0, 1, DepthHistoryBars_P, sto) != bars) return false;
  if (CopyBuffer (HandleR, 0, 1, DepthHistoryBars_P, rsi) != bars) return false;

  MqlDateTime time;
  bool truTradeTime []; ArrayResize (truTradeTime, bars); ArrayInitialize (truTradeTime, false);
  for (int i = 0; i < bars; i++)
  {
    TimeToStruct (rates [i].time, time);
    if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P) truTradeTime [i] = true;
  }

  //----------------------------------------------------------------------------
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = NumbTestFuncRuns_P / popSize; // Total number of epochs (iterations) for optimization

  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps

  ArrayResize (rangeMin,  WeightsNumber);              // Resize 'min' borders array
  ArrayResize (rangeMax,  WeightsNumber);              // Resize 'max' borders array
  ArrayResize (rangeStep, WeightsNumber);              // Resize the steps array

  for (int i = 0; i < WeightsNumber; i++)
  {
    rangeMax  [i] =  5.0;
    rangeMin  [i] = -5.0;
    rangeStep [i] = 0.01;
  }

  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (OptimizerSelect_P);             // Select an optimization algorithm

  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)

  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs

  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = TargetFunction (ao.a [set].c, rates, rsi, sto, truTradeTime); //FF.CalcFunc (ao.a [set].c); //ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }

  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB);
  ArrayCopy (Weights, ao.cB);
  delete ao;                                           // Release the memory occupied by the algorithm object

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Luego implementaremos la función objetivo para evaluar la eficacia de la estrategia comercial mediante una red neuronal.

1. Inicialización de variables. Se establecen las variables para controlar los beneficios, las pérdidas, el número de operaciones y otros parámetros.

2. Procesamiento de datos históricos. El ciclo recorre los datos históricos y comprueba si está permitido abrir posiciones en la barra actual.

3. Normalización de datos. Para cada barra, se normalizan los valores de los precios (high, low, open, close) y de los indicadores (RSI y Stochastic) para su posterior transmisión a la red neuronal.

4. Predicción de las señales. Los datos normalizados se introducen en una red neuronal que genera señales comerciales (de compra o venta).

5. Las posiciones virtuales se gestionan según la estrategia comercial en OnTick ().

6. Cálculo del resultado. Al final de la función, se calcula el ratio total de beneficios/pérdidas multiplicado por el número de operaciones, considerando el factor de reducción del desequilibrio entre compra y venta.

La función evalúa la eficacia de la estrategia comercial analizando los beneficios y las pérdidas a partir de las señales generadas por la red neuronal y devuelve un valor numérico que refleja su calidad (de hecho, la función realiza una pasada por la historia hacia atrás desde la posición actual en el tiempo del asesor experto).

//——————————————————————————————————————————————————————————————————————————————
double TargetFunction (double &weights [], MqlRates &rates [], double &rsi [], double &sto [], bool &truTradeTime [])
{
  int bars = ArraySize (rates);

  // Initialize variables to normalize data
  int    wCNT       = 0;
  double max        = 0.0;
  double min        = 0.0;
  int    signal     = 0;
  double profit     = 0.0;
  double allProfit  = 0.0;
  double allLoss    = 0.0;
  int    dealsNumb  = 0;
  int    sells      = 0;
  int    buys       = 0;
  int    posType    = 0;
  double posOpPrice = 0.0;
  double posClPrice = 0.0;

  // Run through history
  for (int h = BarsAnalysis_P; h < bars - 1; h++)
  {
    if (!truTradeTime [h])
    {
      if (posType != 0)
      {
        posClPrice = rates [h].open;
        profit = (posClPrice - posOpPrice) * signal - 0.00003;

        if (profit > 0.0) allProfit += profit;
        else              allLoss   += -profit;

        if (posType == 1) buys++;
        else              sells++;

        allProfit += profit;
        posType = 0;
      }

      continue;
    }

    max  = -DBL_MAX; // Initial value for maximum
    min  =  DBL_MAX; // Initial value for minimum

    // Find the maximum and minimum among high and low
    for (int b = 1; b <= BarsAnalysis_P; b++)
    {
      if (rates [h - b].high > max) max = rates [h - b].high; // Update maximum
      if (rates [h - b].low  < min) min = rates [h - b].low;  // Update minimum
    }

    // Normalization of input data for neural network
    wCNT = 0;
    for (int b = BarsAnalysis_P; b >= 1; b--)
    {
      Inputs [wCNT] = U.Scale (rates [h - b].high,  min, max, -1, 1); wCNT++; // Normalizing high
      Inputs [wCNT] = U.Scale (rates [h - b].low,   min, max, -1, 1); wCNT++; // Normalizing low
      Inputs [wCNT] = U.Scale (rates [h - b].open,  min, max, -1, 1); wCNT++; // Normalizing open
      Inputs [wCNT] = U.Scale (rates [h - b].close, min, max, -1, 1); wCNT++; // Normalizing close

      Inputs [wCNT] = U.Scale (sto   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
      Inputs [wCNT] = U.Scale (rsi   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
    }

    // Convert data from Inputs to Outs
    NN.ANN (Inputs, weights, Outs);

    //----------------------------------------------------------------------------
    // Generate a trading signal based on the output of a neural network
    signal = 0;
    if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
    if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

    if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
    {
      posClPrice = rates [h].open;
      profit = (posClPrice - posOpPrice) * signal - 0.00003;

      if (profit > 0.0) allProfit += profit;
      else              allLoss   += -profit;

      if (posType == 1) buys++;
      else              sells++;

      allProfit += profit;
      posType = 0;
    }

    if (posType == 0 && signal != 0)
    {
      posType = signal;
      posOpPrice = rates [h].open;
    }
  }

  dealsNumb = buys + sells;

  double ko = 1.0;
  if (sells == 0 || buys == 0) return -DBL_MAX;
  if (sells / buys > 1.5 || buys / sells > 1.5) ko = 0.001;

  return (allProfit / (allLoss + DBL_EPSILON)) * dealsNumb;
}
//——————————————————————————————————————————————————————————————————————————————

La figura 2 muestra el gráfico del balance de los resultados comerciales obtenidos utilizando el EA basado en MLP sobre datos nuevos y desconocidos para la red neuronal. Luego se introducen los valores de precio OHLC normalizados, así como los indicadores RSI y Stochastic calculados a partir del número de barras especificado. El asesor negocia mientras la red neuronal siga actualizada; de lo contrario, entrenará la red y luego seguirá negociando. Así pues, los resultados mostrados en la figura 2 reflejan el rendimiento en OOS (out of sample).

Figura 2. Resultado del funcionamiento del asesor experto sobre datos desconocidos para los MLP

Conclusiones

El artículo presenta una forma sencilla y asequible de usar redes neuronales en un asesor comercial que resulta cómodo para una amplia gama de tráders y no requiere conocimientos profundos en el campo del aprendizaje automático. Este método nos ahorra la necesidad de normalizar los valores de la función objetivo para introducirlos luego en la red neuronal como error, y también elimina la necesidad de otros métodos para evitar la "explosión de pesos". Asimismo, resuelve el problema del "estupor de la red" y ofrece un entrenamiento intuitivo con seguimiento visual de los resultados.

Eso sí, debemos considerar que el asesor experto no contiene las comprobaciones necesarias para realizar operaciones comerciales y está pensado únicamente con fines introductorios.

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de optimización basados en la población
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	Utilities.mqh	Archivo de inclusión	Biblioteca de funciones auxiliares
4	#Symbol.mqh	Archivo de inclusión	Biblioteca de funciones comerciales y auxiliares
5	ANN EA.mq5	Asesor	Asesor basado en la red neuronal de MLP