
Neuronale Netze im Handel: Zweidimensionale Verbindungsraummodelle (Chimera)
Einführung
Die Modellierung von Zeitreihen ist eine komplexe Aufgabe mit einem breiten Anwendungsspektrum in verschiedenen Bereichen, darunter Medizin, Finanzmärkte und Energiesysteme. Die größten Herausforderungen bei der Entwicklung universeller Zeitreihenmodelle sind damit verbunden:
- Berücksichtigung mehrskaliger Abhängigkeiten, einschließlich kurzfristiger Autokorrelationen, Saisonalität und langfristiger Trends. Dies erfordert den Einsatz flexibler und leistungsfähiger Architekturen.
- Adaptiver Umgang mit multivariaten Zeitreihen, bei denen die Beziehungen zwischen den Variablen dynamisch und nichtlinear sein können. Dies erfordert Mechanismen, die kontextabhängige Wechselwirkungen berücksichtigen.
- Minimierung der Notwendigkeit einer manuellen Datenvorverarbeitung, um eine automatische Identifizierung von Strukturmustern ohne umfangreiche Parametereinstellungen zu gewährleisten.
- Recheneffizienz, insbesondere bei der Verarbeitung langer Sequenzen, die eine Optimierung der Modellarchitektur für eine effiziente Nutzung der Rechenressourcen und geringere Ausbildungskosten erfordert.
Klassische statistische Methoden erfordern eine umfangreiche Vorverarbeitung der Rohdaten und können komplexe nichtlineare Abhängigkeiten oft nicht angemessen erfassen. Tiefe neuronale Netzwerkarchitekturen haben eine hohe Ausdruckskraft bewiesen, aber die quadratische Rechenkomplexität von Transformer-basierten Modellen macht es schwierig, sie auf multivariate Zeitreihen mit einer großen Anzahl von Merkmalen anzuwenden. Darüber hinaus unterscheiden solche Modelle häufig nicht zwischen saisonalen und langfristigen Komponenten oder beruhen auf starren A-priori-Annahmen, was ihre Anpassungsfähigkeit an verschiedene praktische Szenarien einschränkt.
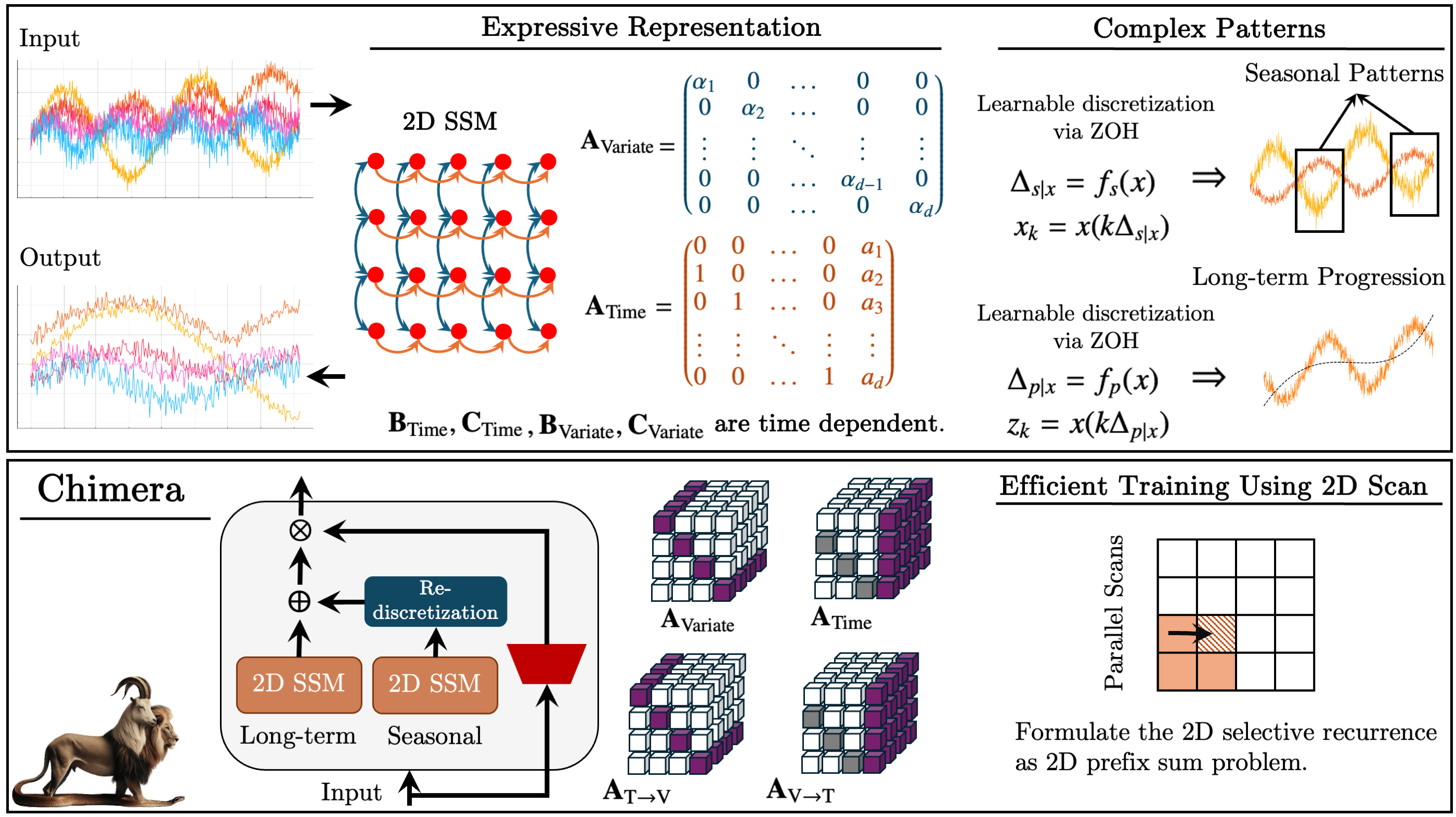
Ein Ansatz, der diese Probleme angeht, wurde in dem Papier „Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models“ vorgeschlagen. Der Chimera-Rahmen ist ein zweidimensionales Zustandsraummodell (2D-SSM), das lineare Transformationen sowohl entlang der zeitlichen als auch der variablen Achse vornimmt. Chimera umfasst drei Hauptkomponenten: Zustandsraummodelle entlang der Zeitdimension, entlang der Variablendimension und dimensionsübergreifende Übergänge. Die Parametrisierung basiert auf kompakten diagonalen Matrizen, sodass sowohl klassische statistische Methoden als auch moderne SSM-Architekturen nachgebildet werden können.
Darüber hinaus beinhaltet Chimera eine adaptive Diskretisierung, um saisonale Muster und Merkmale dynamischer Systeme zu berücksichtigen.
Die Autoren von Chimera haben die Leistung des Frameworks für verschiedene multivariate Zeitreihenaufgaben bewertet, darunter Klassifizierung, Vorhersage und Erkennung von Anomalien. Experimentelle Ergebnisse zeigen, dass Chimera eine Genauigkeit erreicht, die mit den modernsten Methoden vergleichbar ist oder diese sogar übertrifft, während gleichzeitig die Gesamtkosten für die Berechnung reduziert werden.
Der Chimera-Algorithmus
Zustandsraummodelle (State Space Models, SSM) spielen aufgrund ihrer Einfachheit und Aussagekraft bei der Modellierung komplexer Abhängigkeiten, einschließlich autoregressiver Beziehungen, eine wichtige Rolle in der Zeitreihenanalyse. Diese Modelle stellen Systeme dar, bei denen der aktuelle Zustand vom vorherigen Zustand der beobachteten Umgebung abhängt. Traditionell beschreiben SSMs jedoch Systeme, bei denen der Zustand von einer einzigen Variable (z. B. der Zeit) abhängt. Dies schränkt ihre Anwendbarkeit auf multivariate Zeitreihen ein, bei denen Abhängigkeiten sowohl zeitlich als auch zwischen den Variablen erfasst werden müssen.
Multivariate Zeitreihen sind von Natur aus komplexer und erfordern Methoden, die in der Lage sind, Interdependenzen zwischen mehreren Variablen gleichzeitig zu modellieren. Klassische zweidimensionale Zustandsraummodelle (2D-SSMs), die für solche Aufgaben verwendet werden, unterliegen im Vergleich zu modernen Deep-Learning-Methoden mehreren Einschränkungen. Die folgenden Punkte können hier hervorgehoben werden:
- Beschränkung auf lineare Abhängigkeiten. Traditionelle 2D-SSMs können nur lineare Beziehungen modellieren, was ihre Fähigkeit einschränkt, die komplexen, nichtlinearen Abhängigkeiten darzustellen, die für reale multivariate Zeitreihen charakteristisch sind.
- Diskrete Modellauflösung. Diese Modelle haben oft eine vordefinierte Auflösung und können sich nicht automatisch an Änderungen der Datenmerkmale anpassen, was ihre Effektivität bei der Modellierung von saisonalen oder variablen Auflösungsmustern verringert.
- Schwierigkeiten mit großen Datensätzen. In der Praxis sind 2D-SSMs oft ineffizient bei der Verarbeitung großer Datenmengen, was ihren praktischen Nutzen einschränkt.
- Aktualisierung der statischen Parameter. Klassische Aktualisierungsmechanismen sind starr und berücksichtigen nicht die dynamischen Abhängigkeiten, die sich im Laufe der Zeit entwickeln. Dies ist eine erhebliche Einschränkung bei Anwendungen, bei denen sich die Daten weiterentwickeln und adaptive Ansätze erfordern.
Im Gegensatz dazu bieten Deep-Learning-Methoden, die sich in den letzten Jahren rasant entwickelt haben, das Potenzial, viele dieser Einschränkungen zu überwinden. Sie ermöglichen die Modellierung komplexer nichtlinearer Abhängigkeiten und zeitlicher Dynamik, was sie für die multivariate Zeitreihenanalyse vielversprechend macht.
In Chimera werden 2D-SSMs zur Modellierung multivariater Zeitreihen verwendet, wobei die erste Achse der Zeit und die zweite Achse den Variablen entspricht. Jeder Zustand hängt sowohl von der Zeit als auch von den Variablen ab. Der erste Schritt besteht darin, das kontinuierliche 2D-SSM in eine diskrete Form umzuwandeln, wobei die Schrittgrößen Δ1 und Δ2 berücksichtigt werden, die die Signalauflösung entlang jeder Achse darstellen. Mit Hilfe der Methode Zero-Order-Hold (ZOH) können die ursprünglichen Daten diskretisiert werden als:
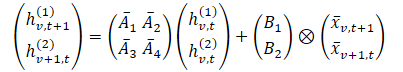
wobei t und v Indizes entlang der zeitlichen bzw. variablen Dimension bezeichnen. Dieser Ausdruck kann in einer einfacheren Form dargestellt werden.
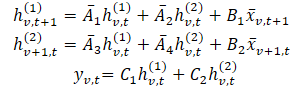
In dieser Formulierung: hv,t(1) – ist ein verborgener Zustand, der zeitliche Informationen trägt (jeder Zustand hängt vom vorhergehenden Zeitschritt für dieselbe Variable ab), wobei A1 und A2 die Betonung vergangener zeit- bzw. variantenübergreifender Informationen steuern. Dann ist hv,t(2) ein verborgener Zustand, der variablenübergreifende Informationen enthält (jeder Zustand hängt von anderen Variablen im gleichen Zeitschritt ab).
Zeitreihendaten werden häufig aus einem zugrunde liegenden kontinuierlichen Prozess abgetastet. In solchen Fällen kann Δ1 als die zeitliche Auflösung oder die Abtastfrequenz interpretiert werden. Die Diskretisierung entlang der variablen Achse, die von Natur aus diskret ist, ist weniger intuitiv, aber unerlässlich. In 1D-SSMs ist die Diskretisierung eng mit den RNN-Gate-Mechanismen verknüpft, die eine Modellnormalisierung und gewünschte Eigenschaften wie Auflösungsinvarianz ermöglichen.
Ein 2D diskretes SSM mit Parametern ({Ai}, {Bi}, {Ci}, kΔ1, ℓΔ2) entwickelt sich k-mal schneller entlang der Zeit als ein 2D diskretes SSM mit Parametern ({Ai}, {Bi}, {Ci}, Δ1ℓΔ2), und ℓ-mal schneller ({Ai}, {Bi}, {Ci}, kΔ1, Δ2).. Daher kann Δ1 als Regler der vom Modell erfassten Abhängigkeitslänge betrachtet werden. Ausgehend von der obigen Beschreibung verstehen wir die Diskretisierung entlang der Zeitachse als Einstellung der Auflösung oder der Abtastfrequenz. Das kleinere Δ1 erfasst die langfristige Entwicklung, während das größere Δ1 die saisonalen Muster erfasst.
Die Diskretisierung entlang der Variablenachse erfolgt analog zu den RNN-Gates, wobei Δ2 die Kontextlänge des Modells steuert. Größere Werte von Δ2 führen zu kleineren Kontextfenstern und reduzieren die Wechselwirkungen zwischen den Variablen, während kleinere Δ2 die Abhängigkeiten zwischen den Variablen betonen.
Um die Aussagekraft zu erhöhen und eine autoregressive Rückgewinnung zu ermöglichen, enthalten die verborgenen Zustände hv,t(1) zeitliche Informationen aus der Vergangenheit. Die Autoren beschränken die Matrizen A1 und A2 auf strukturierte Formen. Und selbst einfache diagonale Matrizen für A3 and A4 führen variablenübergreifende Informationen effektiv zusammen.
Da 2D-SSMs entlang der Variablendimension kausal sind (der es an intrinsischer Ordnung mangelt), verwendet Chimera getrennte Vorwärts- und Rückwärtsmodule entlang der Merkmalsdimension, um Beschränkungen des Informationsflusses anzugehen.
Ähnlich wie bei effektiven 1D-SSMs kann eine datenunabhängige Formulierung als eine Faltung mit Kernel K interpretiert werden. Dies ermöglicht schnelleres Training durch Parallelisierung und verbindet Chimera mit neueren faltungsbasierten Architekturen für Zeitreihen.
Wie bereits erörtert, steuern die Parameter A1 and A2 die Gewichtung der zeit- und variantenübergreifenden Informationen der Vergangenheit. In ähnlicher Weise regeln Δ1 und B1 die Betonung des aktuellen und des historischen Inputs. Diese datenunabhängigen Parameter stellen globale Systemmerkmale dar. In komplexen Systemen hängt der Schwerpunkt jedoch von der aktuellen Eingabe ab. Daher ist es notwendig, dass diese Parameter eine Funktion der ursprünglichen Daten sind. Die analysierte Parameterabhängigkeit bietet analog zu Transformeren einen Mechanismus zur adaptiven Auswahl relevanter und Filterung irrelevanter Informationen für jeden Eingabesatz. Darüber hinaus sollte das Modell je nach Datenlage adaptiv lernen, Informationen über verschiedene Varianten hinweg zu mischen. Die Abhängigkeit der Parameter von den Eingabedaten trägt diesem Problem Rechnung und ermöglicht es dem Modell, relevante Parameter zu mischen und irrelevante Parameter herauszufiltern, um die Variable von Interesse zu modellieren. Einer der technischen Beiträge von Chimera ist die Konstruktion von Bi, Ci and Δi durch eine Funktion der Eingabe𝐱v,t.
Chimera stapelt 2D-SSMs mit Nichtlinearitäten zwischen den Schichten. Um die Aussagekraft und die Möglichkeiten der oben genannten 2D-SSMs zu verbessern, können ähnlich wie bei tiefen SSM-Modellen alle Parameter trainiert werden, und in jeder Schicht werden mehrere 2D-SSMs verwendet, von denen jede ihre eigene Verantwortung hat.
Chimera folgt der üblichen Zeitreihenzerlegung und trennt Trends und saisonale Muster. Außerdem nutzt es die einzigartigen Eigenschaften von 2D-SSMs, um diese Komponenten effektiv zu erfassen.
Die ursprüngliche Visualisierung der Chimera ist unten angeführt.
Implementierung in MQL5
Nachdem wir die theoretischen Aspekte des Chimera-Rahmens erläutert haben, gehen wir zur praktischen Umsetzung unserer eigenen Interpretation der vorgeschlagenen Ansätze über. In diesem Abschnitt untersuchen wir die Interpretation des Chimera-Konzepts mit Hilfe der Möglichkeiten der Programmiersprache MQL5. Bevor wir jedoch mit der Codierung beginnen, müssen wir die Modellarchitektur sorgfältig entwerfen, um ihre Flexibilität, Effizienz und Anpassungsfähigkeit an verschiedene Datentypen zu gewährleisten.
Architektonische Lösungen
Eine der Schlüsselkomponenten des Chimera-Rahmens ist die Menge der verborgenen Zustandsaufmerksamkeitsmatrizen A{1,...,4}. Die Autoren schlugen vor, diagonale Matrizen mit Augmentierung zu verwenden, was die Anzahl der lernbaren Parameter reduziert und die Rechenkomplexität verringert. Dieser Ansatz verringert den Ressourcenverbrauch erheblich und beschleunigt das Modelltraining.
Diese Lösung hat jedoch ihre Grenzen. Die Verwendung diagonaler Matrizen schränkt das Modell ein, da es nur lokale Abhängigkeiten zwischen aufeinanderfolgenden Elementen der Sequenz analysieren kann. Dies schränkt ihre Ausdruckskraft und ihre Fähigkeit, komplexe Muster zu erfassen, ein. Daher verwenden wir in unserer Interpretation vollständig trainierbare Matrizen. Dadurch erhöht sich zwar die Zahl der Parameter, aber auch die Anpassungsfähigkeit des Modells, da es komplexere Abhängigkeiten in den Daten erfassen kann.
Gleichzeitig bewahrt unser Matrixansatz das Schlüsselkonzept des ursprünglichen Entwurfs – die Matrizen sind trainierbar, aber nicht direkt von den Eingabedaten abhängig. Dadurch bleibt das Modell universeller, was besonders für multivariate Zeitreihenanalysen wichtig ist.
Ein weiterer kritischer Aspekt ist die Integration dieser Matrizen in den Berechnungsprozess. Wie im theoretischen Teil erläutert, werden die Aufmerksamkeitsmatrizen mit den versteckten Zuständen des Modells multipliziert, wobei ähnliche Prinzipien wie bei neuronalen Schichten gelten. Wir schlagen vor, sie als eine Faltungsschicht eines neuronalen Netzes zu implementieren, wobei jede Aufmerksamkeitsmatrix als trainierbarer Tensor von Parametern dargestellt wird. Die Integration in standardmäßige neuronale Architekturen ermöglicht die Nutzung bereits vorhandener Optimierungsalgorithmen.
Um die parallele Berechnung aller vier Aufmerksamkeitsmatrizen gleichzeitig zu ermöglichen, fügen wir sie zu einem einzigen verketteten Tensor zusammen, was auch die Kombination zweier verborgener Zustandsmatrizen zu einem einzigen Tensor erfordert.
Trotz der Vorteile ist dieser Ansatz nicht universell auf andere parametrische Matrizen in 2D-SSM anwendbar. Eine Einschränkung ist die feste Matrixstruktur, die die Flexibilität bei der Verarbeitung komplexer multivariater Daten verringert. Um die Aussagekraft des Modells zu erhöhen, verwenden wir kontextabhängige Matrizen Bi, Ci und Δi, die sich dynamisch an die Eingabedaten anpassen und eine tiefere Analyse der zeitlichen Abhängigkeiten ermöglichen.
Aus den Eingabedaten werden kontextabhängige Matrizen generiert, die es dem Modell ermöglichen, die Datenstruktur zu berücksichtigen und die Parameter entsprechend der Sequenzmerkmale anzupassen. Dieser Ansatz ermöglicht es dem Modell, nicht nur lokale Abhängigkeiten, sondern auch globale Trends zu analysieren, was für Prognosen und Zeitreihen entscheidend ist.
Den Empfehlungen der Autoren des Frameworks folgend, werden diese Matrizen mit Hilfe spezieller neuronaler Schichten implementiert, die für die kontextabhängige Anpassung der Parameter verantwortlich sind.
Der nächste Schritt besteht darin, komplexe Dateninteraktionen innerhalb des 2D-SSM-Modells zu organisieren. Da multivariate Datenstrukturen eine optimierte Verarbeitung erfordern, ist eine effiziente Ressourcenverwaltung erforderlich. Um die Anforderungen an die Recheneffizienz und die Leistung zu erfüllen, haben wir beschlossen, diesen Vorgang als separaten OpenCL-Kernel zu implementieren.
Dieser Ansatz bietet mehrere Vorteile. Erstens beschleunigt die parallele Ausführung auf dem Grafikprozessor die Datenverarbeitung erheblich und verringert die Latenzzeit. Dies ist entscheidend für große Datensätze, bei denen eine sequenzielle Berechnung zu langsam wäre. Zweitens ermöglicht OpenCL aufgrund der Hardwarebeschleunigung eine effiziente Parallelisierung und damit die Echtzeitverarbeitung komplexer Zeitreihen.
Ausweitung des OpenCL-Programms
Nach dem Entwurf der Architektur ist der nächste Schritt ihre Implementierung in Code. Zunächst müssen wir das OpenCL-Programm modifizieren, um die Berechnungsvorgänge zu optimieren und eine effektive Interaktion mit den Modellkomponenten zu gewährleisten. Wir erstellen einen Kernel, SSM2D_FeedForward, der komplexe Interaktionen zwischen trainierbaren 2D-SSM-Parametern und Eingabedaten verarbeitet.
Die Methode erhält Zeiger auf Datenpuffer, die alle Modellparameter und Eingabeprojektionen im Kontext von Zeit und Variablen enthalten.
__kernel void SSM2D_FeedForward(__global const float *ah, __global const float *b_time, __global const float *b_var, __global const float *px_time, __global const float *px_var, __global const float *c_time, __global const float *c_var, __global const float *delta_time, __global const float *delta_var, __global float *hidden, __global float *y ) { const size_t n = get_local_id(0); const size_t d = get_global_id(1); const size_t n_total = get_local_size(0); const size_t d_total = get_global_size(1);
Innerhalb des Kernels identifizieren wir zunächst den aktuellen Thread in einem zweidimensionalen Aufgabenraum. Die erste Dimension entspricht der Länge der Sequenz und die zweite der Dimensionalität der Merkmale. Alle Sequenzelemente für ein einzelnes Merkmal werden in Arbeitsgruppen gruppiert.
Es ist wichtig, dass die Projektionen der trainierbaren Parameter und der Eingabedaten während der Datenaufbereitung abgeglichen werden, bevor sie an den Kernel übergeben werden.
Als Nächstes berechnen wir den verborgenen Zustand in beiden Kontexten unter Verwendung der aktualisierten Informationen. WE speichert die Ergebnisse in dem entsprechenden Datenpuffer.
//--- Hidden state for(int h = 0; h < 2; h++) { float new_h = ah[(2 * n + h) * d_total + d] + ah[(2 * n_total + 2 * n + h) * d_total + d]; if(h == 0) new_h += b_time[n] * px_time[n * d_total + d]; else new_h += b_var[n] * px_var[n * d_total + d]; hidden[(h * n_total + n)*d_total + d] = IsNaNOrInf(new_h, 0); } barrier(CLK_LOCAL_MEM_FENCE);
Danach synchronisieren wir die Arbeitsgruppen-Threads, da die nachfolgenden Operationen die Ergebnisse der gesamten Gruppe benötigen.
Anschließend berechnen wir die Modellleistung. Dazu multiplizieren wir Kontext- und Diskretisierungsmatrizen mit dem berechneten verborgenen Zustand. Um diese Operation durchzuführen, organisieren wir eine Schleife, in der wir die entsprechenden Elemente der Matrizen im Zeit- und Variablenkontext multiplizieren. Dann addieren wir die Ergebnisse aus beiden Kontexten.
//--- Output uint shift_c = n; uint shift_h1 = d; uint shift_h2 = shift_h1 + n_total * d_total; float value = 0; for(int i = 0; i < n_total; i++) { value += IsNaNOrInf(c_time[shift_c] * delta_time[shift_c] * hidden[shift_h1], 0); value += IsNaNOrInf(c_var[shift_c] * delta_var[shift_c] * hidden[shift_h2], 0); shift_c += n_total; shift_h1 += d_total; shift_h2 += d_total; }
Jetzt müssen wir nur noch den empfangenen Wert in das entsprechende Element des Ergebnispuffers speichern.
//--- y[n * d_total + d] = IsNaNOrInf(value, 0); }
Als Nächstes müssen wir das Verfahren des Rückwärtsdurchgangs einrichten. Wir werden die Parameter mit Hilfe der entsprechenden neuronalen Schichten optimieren. Um dann den Fehlergradienten zwischen ihnen zu verteilen, erstellen wir den Kernel SSM2D_CalcHiddenGradient – in seinem Hauptteil implementieren wir einen Algorithmus, der umgekehrt zu dem oben beschriebenen ist.
Die Kernel-Parameter enthalten Zeiger auf denselben Satz von Matrizen, ergänzt durch Puffer für Fehlergradienten. Um Verwechslungen bei der großen Anzahl von Puffern zu vermeiden, verwenden wir das Präfix grad_ für Puffer, die Fehlergradienten entsprechen.
__kernel void SSM2D_CalcHiddenGradient(__global const float *ah, __global float *grad_ah, __global const float *b_time, __global float *grad_b_time, __global const float *b_var, __global float *grad_b_var, __global const float *px_time, __global float *grad_px_time, __global const float *px_var, __global float *grad_px_var, __global const float *c_time, __global float *grad_c_time, __global const float *c_var, __global float *grad_c_var, __global const float *delta_time, __global float *grad_delta_time, __global const float *delta_var, __global float *grad_delta_var, __global const float *hidden, __global const float *grad_y ) { //--- const size_t n = get_global_id(0); const size_t d = get_local_id(1); const size_t n_total = get_global_size(0); const size_t d_total = get_local_size(1);
Dieser Kernel wird im gleichen Aufgabenraum wie der Forward-Pass-Kernel ausgeführt. In diesem Fall werden die Threads jedoch entlang der Merkmalsdimension in Arbeitsgruppen gruppiert.
Bevor wir mit der Berechnung beginnen, initialisieren wir mehrere lokale Variablen, um Zwischenwerte und Offsets in den Datenpuffern zu speichern.
//--- Initialize indices for data access uint shift_c = n; uint shift_h1 = d; uint shift_h2 = shift_h1 + n_total * d_total; float grad_hidden1 = 0; float grad_hidden2 = 0;
Als Nächstes organisieren wir eine Schleife, um den Fehlergradienten vom Ausgabepuffer auf den verborgenen Zustand sowie auf die Kontext- und Diskretisierungsmatrizen zu verteilen, und zwar entsprechend ihrem Beitrag zur endgültigen Ausgabe des Modells. Gleichzeitig wird der Fehlergradient über die Zeit und den variablen Kontext verteilt.
//--- Backpropagation: compute hidden gradients from y for(int i = 0; i < n_total; i++) { float grad = grad_y[i * d_total + d]; float c_t = c_time[shift_c]; float c_v = c_var[shift_c]; float delta_t = delta_time[shift_c]; float delta_v = delta_var[shift_c]; float h1 = hidden[shift_h1]; float h2 = hidden[shift_h2]; //-- Accumulate gradients for hidden states grad_hidden1 += IsNaNOrInf(grad * c_t * delta_t, 0); grad_hidden2 += IsNaNOrInf(grad * c_v * delta_v, 0); //--- Compute gradients for c_time, c_var, delta_time, delta_var grad_c_time[shift_c] += grad * delta_t * h1; grad_c_var[shift_c] += grad * delta_v * h2; grad_delta_time[shift_c] += grad * c_t * h1; grad_delta_var[shift_c] += grad * c_v * h2; //--- Update indices for the next element shift_c += n_total; shift_h1 += d_total; shift_h2 += d_total; }
Dann verteilen wir den Fehlergradienten auf die Aufmerksamkeitsmatrizen
//--- Backpropagate through hidden -> ah, b_time, px_time for(int h = 0; h < 2; h++) { float grad_h = (h == 0) ? grad_hidden1 : grad_hidden2; //--- Store gradients in ah (considering its influence on two elements) grad_ah[(2 * n + h) * d_total + d] = grad_h; grad_ah[(2 * (n_total + n) + h) * d_total + d] = grad_h; }
und leiten sie an die Projektionen der Eingangsdaten weiter.
//--- Backpropagate through px_time and px_var (influenced by b_time and b_var)
grad_px_time[n * d_total + d] = grad_hidden1 * b_time[n];
grad_px_var[n * d_total + d] = grad_hidden2 * b_var[n];
Der Fehlergradient für die Matrix Bi muss über alle Dimensionen hinweg aggregiert werden. Daher setzen wir zunächst den entsprechenden Fehlergradientenpuffer auf Null und synchronisieren die Threads der Arbeitsgruppe.
if(d == 0) { grad_b_time[n] = 0; grad_b_var[n] = 0; } barrier(CLK_LOCAL_MEM_FENCE);
Dann addieren wir die Werte der einzelnen Threads der Arbeitsgruppe.
//--- Sum gradients over all d for b_time and b_var
grad_b_time[n] += grad_hidden1 * px_time[n * d_total + d];
grad_b_var[n] += grad_hidden2 * px_var[n * d_total + d];
}
Die Ergebnisse dieser Operationen werden in die entsprechenden globalen Datenpuffer geschrieben, womit die Kernelausführung abgeschlossen ist.
Damit ist unsere Implementierungs-Arbeit auf Seiten von OpenCL abgeschlossen. Der vollständige Quellcode ist im Anhang enthalten.
2D-SSM Objekt
Nach Abschluss der Operationen auf Seiten von OpenCL besteht der nächste Schritt darin, die 2D-SSM-Struktur im Hauptprogramm zu konstruieren. Wir erstellen die Klasse CNeuron2DSSMOCL, in der die notwendigen Algorithmen implementiert sind. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuron2DSSMOCL : public CNeuronBaseOCL { protected: uint iWindowOut; uint iUnitsOut; CNeuronBaseOCL cHiddenStates; CLayer cProjectionX_Time; CLayer cProjectionX_Variable; CNeuronConvOCL cA; CNeuronConvOCL cB_Time; CNeuronConvOCL cB_Variable; CNeuronConvOCL cC_Time; CNeuronConvOCL cC_Variable; CNeuronConvOCL cDelta_Time; CNeuronConvOCL cDelta_Variable; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForwardSSM2D(void); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradientsSSM2D(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuron2DSSMOCL(void) {}; ~CNeuron2DSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuron2DSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
In dieser Objektstruktur sehen wir eine vertraute Reihe von virtuellen Überschreibungsmethoden und eine relativ große Anzahl von internen Objekten. Die Anzahl der Objekte ist nicht unerwartet. Sie wird durch die Modellarchitektur bestimmt. Zum Teil lässt sich der Zweck der Objekte aus ihren Namen ableiten. Eine genauere Beschreibung der Funktionen der einzelnen Objekte wird bei der Implementierung der Klassenmethoden gegeben.
Alle internen Objekte werden als statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Vorteile dieses Ansatzes wurden bereits erörtert. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.
bool CNeuron2DSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_out, optimization_type, batch)) return false; SetActivationFunction(None);
Die Methode erhält eine Reihe von Konstanten als Parameter, die die Architektur des erstellten Objekts definieren. Dazu gehören die Dimensionen der Eingabedaten und der erwarteten Ausgabe: {units_in, window_in} bzw. {units_out, window_out},
Innerhalb der Methode rufen wir zunächst die Methode der übergeordneten Klasse mit den erwarteten Ausgabedimensionen auf. Die Methode der Elternklasse implementiert bereits die notwendigen Kontrollblock- und Initialisierungsalgorithmen für geerbte Objekte und Schnittstellen. Nach erfolgreicher Ausführung speichern wir die Tensordimensionen des Ergebnisses in internen Variablen.
iWindowOut = window_out; iUnitsOut = units_out;
Wie bereits erwähnt, müssen bei der Konstruktion von Kerneln auf der OpenCL-Seite die Eingabeprojektionen für beide Kontexte eine vergleichbare Form haben. In unserer Implementierung richten wir sie an den Dimensionen des Ergebnistensors aus. Zunächst erstellen wir das Projektionsmodell für den Zeitkontext.
Um die Informationen in den Einheitsfolgen der multivariaten Zeitreihen zu erhalten, führen wir eine unabhängige Projektion der eindimensionalen Folgen auf die Zielgröße durch. Es ist wichtig zu beachten, dass die Eingabedaten als Matrix empfangen werden, wobei die Zeilen den Zeitschritten entsprechen. Daher transponieren wir zunächst die Eingabematrix, um die Handhabung von Einheitsfolgen zu erleichtern.
//--- int index = 0; CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL; //--- Projection Time cProjectionX_Time.Clear(); cProjectionX_Time.SetOpenCL(OpenCL); transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) || !cProjectionX_Time.Add(transp)) { delete transp; return false; }
Erst dann wird die Faltungsschicht angewendet, um die Dimensionalität der univariaten Sequenzen anzupassen.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, iUnitsOut, window_in, 1, optimization, iBatch) || !cProjectionX_Time.Add(conv)) { delete conv; return false; }
Als Nächstes projizieren wir die Daten entlang der Merkmalsdimension. Dazu führen wir die inverse Transponierung durch
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_in, iUnitsOut, optimization, iBatch) || !cProjectionX_Time.Add(transp)) { delete transp; return false; }
und wenden eine Faltungsprojektionsschicht an.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, iWindowOut, iUnitsOut, 1, optimization, iBatch) || !cProjectionX_Time.Add(conv)) { delete conv; return false; }
In ähnlicher Weise erstellen wir die Projektionen der Merkmalskontexteingabe, indem wir zunächst entlang der Variablenachse projizieren, dann transponieren und entlang der Zeitachse projizieren.
//--- Projection Variables cProjectionX_Variable.Clear(); cProjectionX_Variable.SetOpenCL(OpenCL); index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, iUnitsOut, units_in, 1, optimization, iBatch) || !cProjectionX_Variable.Add(conv)) { delete conv; return false; }
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, iUnitsOut, optimization, iBatch) || !cProjectionX_Variable.Add(transp)) { delete transp; return false; }
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, iWindowOut, iUnitsOut, 1, optimization, iBatch) || !cProjectionX_Variable.Add(conv)) { delete conv; return false; }
Nach der Initialisierung der Eingabeprojektionsmodelle gehen wir zu anderen internen Objekten über. Zunächst initialisieren wir das versteckte Zustandsobjekt. Dieses Objekt dient lediglich als Datencontainer und enthält keine trainierbaren Parameter. Sie muss jedoch ausreichend groß sein, um die verborgenen Zustandsdaten für beide Kontexte zu speichern.
//--- HiddenState index++; if(!cHiddenStates.Init(0, index, OpenCL, 2 * iUnitsOut * iWindowOut, optimization, iBatch)) return false;
Als Nächstes initialisieren wir die versteckten Aufmerksamkeitsmatrizen. Wie bereits erwähnt, werden alle vier Matrizen in einer einzigen Faltungsschicht implementiert. Dies ermöglicht eine parallele Ausführung.
Es ist wichtig zu beachten, dass die Ausgabe dieser Schicht Multiplikationen des verborgenen Zustands mit vier unabhängigen Matrizen liefern sollte: zwei im zeitlichen Kontext und zwei im Merkmalskontext. Um dies zu erreichen, definieren wir die Faltungsschicht mit der doppelten Anzahl von Filtern wie das Eingabefenster, was zwei Aufmerksamkeitsmatrizen entspricht. Und wir geben an, dass die Ebene zwei unabhängige Sequenzen verarbeiten soll, die dem Zeit- und dem Merkmalskontext entsprechen. Erinnern Sie sich, dass die Faltungsschicht separate Filtermatrizen für unabhängige Sequenzen verwendet. Daraus ergeben sich vier Aufmerksamkeitsmatrizen, wobei jedes Paar in unterschiedlichen Kontexten funktioniert.
//--- A*H index++; if(!cA.Init(0, index, OpenCL, iWindowOut, iWindowOut, 2 * iWindowOut, iUnitsOut, 2, optimization, iBatch)) return false;
Große Aufmerksamkeitsparameter können zu einer Gradientenexplosion führen. Wir verkleinern also die Parameter nach der zufälligen Initialisierung um das Zehnfache.
if(!SumAndNormilize(cA.GetWeightsConv(), cA.GetWeightsConv(), cA.GetWeightsConv(), iWindowOut, false, 0, 0, 0, 0.05f)) return false;
Der nächste Schritt ist die Erstellung von adaptiven kontextabhängigen Matrizen Bi, Ci and Δi, die in unserer Implementierung Funktionen der Eingabedaten sind. Diese Matrizen werden mit Hilfe von Faltungsschichten erzeugt, die die Eingabeprojektionen für den entsprechenden Kontext nehmen und die erforderliche Matrix ausgeben.
//--- B index++; if(!cB_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, optimization, iBatch)) return false; cB_Time.SetActivationFunction(TANH); index++; if(!cB_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, optimization, iBatch)) return false; cB_Variable.SetActivationFunction(TANH);
Dieser Ansatz ist analog zu den RNN-Gates. Wir verwenden den hyperbolischen Tangens als Aktivierungsfunktion für Bi und Ci, wobei sowohl positive als auch negative Abhängigkeiten berücksichtigt werden.
//--- C index++; if(!cC_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cC_Time.SetActivationFunction(TANH); index++; if(!cC_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cC_Variable.SetActivationFunction(TANH);
Die Δi Matrix implementiert eine trainierbare Diskretisierung und darf keine negativen Werte enthalten. Dazu verwenden wir SoftPlus als Aktivierungsfunktion, ein glattes Analogon von ReLU.
//--- Delta index++; if(!cDelta_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cDelta_Time.SetActivationFunction(SoftPlus); index++; if(!cDelta_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cDelta_Variable.SetActivationFunction(SoftPlus); //--- return true; }
Nachdem alle internen Objekte initialisiert sind, gibt die Methode ein logisches Ergebnis an das aufrufende Programm zurück.
Wir haben heute bedeutende Fortschritte gemacht, aber unsere Arbeit ist noch nicht abgeschlossen. Es empfiehlt sich, eine kurze Pause einzulegen, bevor es im nächsten Artikel weitergeht. Dort werden wir die Konstruktion der notwendigen Objekte abschließen, sie in das Modell integrieren und die Wirksamkeit der implementierten Ansätze an realen historischen Daten testen.
Schlussfolgerung
In diesem Artikel haben wir das 2D-Zustandsraummodell Chimera untersucht, das neue Ansätze für die Modellierung multivariater Zeitreihen mit Abhängigkeiten über Zeit- und Merkmalsdimensionen hinweg bietet. Chimera verwendet zweidimensionale Zustandsraummodelle (2D-SSM), mit denen sich sowohl langfristige Trends als auch saisonale Muster effizient erfassen lassen.
Im praktischen Teil haben wir begonnen, unsere Interpretation des Rahmens mit MQL5 umzusetzen. Es wurden zwar Fortschritte erzielt, aber die Umsetzung ist noch nicht abgeschlossen. Im nächsten Artikel werden wir die vorgeschlagenen Ansätze weiter ausbauen und die Wirksamkeit der implementierten Lösungen an realen historischen Datensätzen validieren.
Referenzen
- Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models
- Andere Artikel aus dieser Reihe
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor für die Probenahme |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit dem Real-ORL Methode |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor für das Modelltraining |
| 4 | Test.mq5 | Expert Advisor | Modellprüfung Expert Advisor |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17210
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Billard-Optimierungsalgorithmus (BOA)
Billard-Optimierungsalgorithmus (BOA)
 Analyse aller Preisbewegungsoptionen auf dem IBM-Quantencomputer
Analyse aller Preisbewegungsoptionen auf dem IBM-Quantencomputer
 Eine alternative Log-datei mit der Verwendung der HTML und CSS
Eine alternative Log-datei mit der Verwendung der HTML und CSS
 Kapitalmanagement im Handel und das Buchhaltungsprogramm des Händlers zu Hause mit einer Datenbank
Kapitalmanagement im Handel und das Buchhaltungsprogramm des Händlers zu Hause mit einer Datenbank
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.