Neuronale Netze im Handel: Hyperbolisches latentes Diffusionsmodell (HypDiff)
Einführung
Diagramme enthalten die Vielfalt und Bedeutung der topologischen Strukturen von Rohdaten. Diese topologischen Merkmale spiegeln häufig die zugrunde liegenden physikalischen Prinzipien und Entwicklungsmuster wider. Herkömmliche Zufallsgraphenmodelle, die auf der klassischen Graphentheorie basieren, stützen sich stark auf künstliche Heuristiken, um Algorithmen für bestimmte Topologien zu entwerfen, und sind nicht flexibel genug, um vielfältige und komplexe Graphenstrukturen effektiv zu modellieren. Um diese Einschränkungen zu überwinden, wurden zahlreiche Deep-Learning-Modelle für die Graphenerzeugung entwickelt. Probabilistische Diffusionsmodelle mit Rauschunterdrückungsfunktionen haben sich als sehr leistungsfähig erwiesen, insbesondere bei Visualisierungsaufgaben.
Aufgrund der unregelmäßigen und nicht-euklidischen Natur von Graphenstrukturen unterliegt die Anwendung von Diffusionsmodellen in diesem Zusammenhang jedoch zwei wesentlichen Einschränkungen:
- Hohe Computerkomplexität. Die Generierung von Graphen beinhaltet naturgemäß die Verarbeitung diskreter, spärlicher und anderer nicht-euklidischer topologischer Merkmale. Die in einfachen Diffusionsmodellen verwendete Gaußsche Rauschstörung ist für diskrete Daten nicht gut geeignet. Diskrete Graphen-Diffusionsmodelle weisen daher in der Regel eine hohe zeitliche und räumliche Komplexität auf, die auf strukturelle Sparsamkeit zurückzuführen ist. Darüber hinaus stützen sich solche Modelle auf kontinuierliche Gaußsche Rauschprozesse, um vollständig verbundene, verrauschte Graphen zu erzeugen, was häufig zu einem Verlust an struktureller Information und den zugrunde liegenden topologischen Eigenschaften führt.
- Anisotropie von nicht-euklidischen Strukturen. Im Gegensatz zu Daten mit regulärer Struktur sind die Einbettungen von Graphenknoten im nicht-euklidischen Raum anisotrop im kontinuierlichen latenten Raum. Wenn Knoteneinbettungen in den euklidischen Raum abgebildet werden, weisen sie eine ausgeprägte Anisotropie entlang bestimmter Richtungen auf. Ein isotroper Diffusionsprozess im latenten Raum neigt dazu, diese anisotrope Strukturinformation als Rauschen zu behandeln, was zu ihrem Verlust in der Rauschunterdrückungsphase führt.
Der hyperbolische geometrische Raum ist weithin als ideale kontinuierliche Mannigfaltigkeit für die Darstellung diskreter baumartiger oder hierarchischer Strukturen anerkannt und wird bei verschiedenen Graphenlernaufgaben eingesetzt. Die Autoren der Arbeit „Hyperbolic Geometric Latent Diffusion Model for Graph Generation“ behaupten, dass die hyperbolische Geometrie ein großes Potenzial hat, um das Problem der nicht-euklidischen strukturellen Anisotropie in latenten Diffusionsprozessen für Graphen anzugehen. Im hyperbolischen Raum ist die Verteilung der Knoteneinbettungen tendenziell global isotrop. Gleichzeitig bleibt die Anisotropie lokal erhalten. Darüber hinaus vereinigt die hyperbolische Geometrie Winkel- und Radialmessungen in Polarkoordinaten und bietet geometrische Dimensionen mit physikalischer Semantik und Interpretierbarkeit. Insbesondere kann die hyperbolische Geometrie den latenten Raum mit geometrischen Prioritäten ausstatten, die die intrinsische Struktur der Graphen widerspiegeln.
Basierend auf diesen Erkenntnissen zielen die Autoren darauf ab, einen geeigneten latenten Raum zu entwerfen, der auf hyperbolischer Geometrie basiert, um einen effizienten Diffusionsprozess über nicht-euklidische Strukturen für die Graphengenerierung zu ermöglichen und dabei die topologische Integrität zu erhalten. Auf diese Weise versuchen sie, zwei Kernprobleme zu lösen:
- Die additive Natur der kontinuierlichen Gaußschen Verteilungen ist im hyperbolischen latenten Raum undefiniert.
- Entwicklung eines wirksamen anisotropen Diffusionsverfahrens, das auf nicht-euklidische Strukturen zugeschnitten ist.
Um diese Probleme zu überwinden, schlagen die Autoren ein hyperbolisches latentes Diffusionsmodell (HypDiff) vor. Für das Problem der Additivität von Gaußverteilungen im hyperbolischen Raum wird ein Diffusionsprozess auf der Grundlage von Radialmaßen eingeführt. Zusätzlich werden Winkelbeschränkungen angewandt, um anisotropes Rauschen zu begrenzen, wodurch strukturelle Prioritäten erhalten bleiben und das Diffusionsmodell auf feinere strukturelle Details innerhalb des Graphen ausgerichtet wird.
1. Der Algorithmus HypDiff
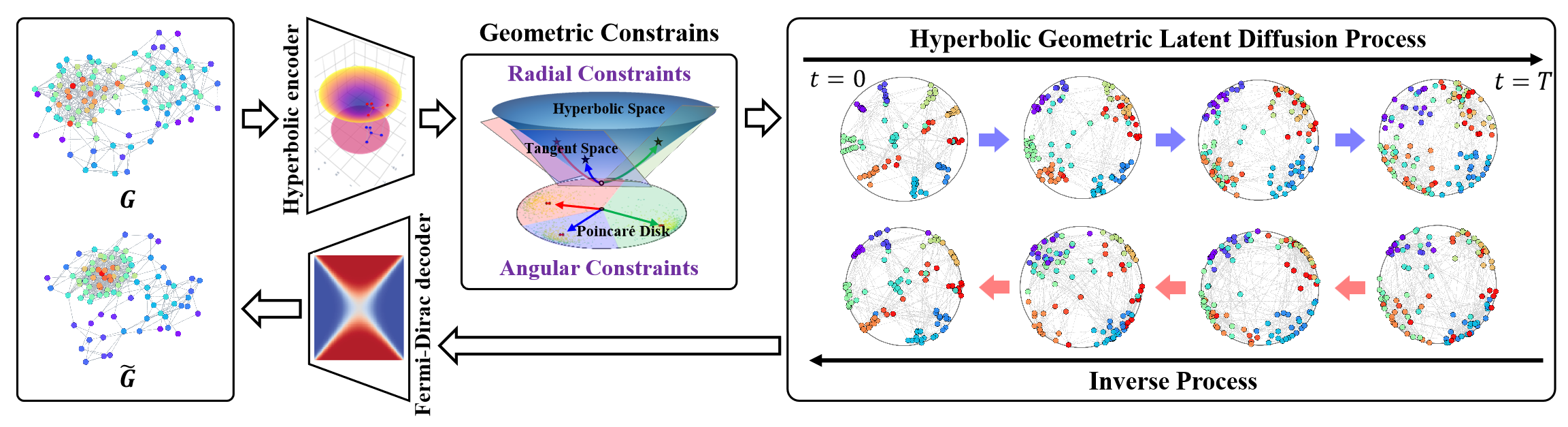
Das Hyperbolische Latente Diffusionsmodell (HypDiff) befasst sich mit zwei zentralen Herausforderungen bei der Erstellung von Graphen. Es nutzt die hyperbolische Geometrie zur Abstraktion der impliziten Hierarchie der Graphenknoten und führt zwei geometrische Beschränkungen ein, um wesentliche topologische Eigenschaften zu erhalten. Die Autoren verwenden eine zweistufige Trainingsstrategie. Erstens wird ein hyperbolischer Autoencoder trainiert, um vortrainierte Knoteneinbettungen zu erhalten, und zweitens wird ein hyperbolischer geometrischer latenter Diffusionsprozess trainiert.
In einem ersten Schritt werden die Graphdaten 𝒢 = (𝐗, A) in einen niedrigdimensionalen hyperbolischen Raum eingebettet, was den latenten Diffusionsprozess des Graphen verbessert.
Der vorgeschlagene hyperbolische Autoencoder umfasst einen hyperbolischen geometrischen Encoder und einen Fermi-Dirac-Decoder. Der Kodierer bildet den Graphen 𝒢 = (𝐗, A) in einen hyperbolischen geometrischen Raum ab, um eine geeignete hyperbolische Darstellung zu erhalten, während der Fermi-Dirac-Dekodierer die Darstellung zurück in den Graphen-Datenbereich rekonstruiert. Die hyperbolische Mannigfaltigkeit ℍᵈ Hd und ihr Tangentenraum 𝒯x können durch exponentielle und logarithmische Abbildungen ineinander überführt werden. Mehrschichtige Perceptrons (MLPs) oder graphische neuronale Netze (GNNs) können verwendet werden, um mit diesen exponentiellen/logarithmischen Darstellungen zu arbeiten. In ihrer Implementierung verwenden die Autoren Hyperbolic Graph Convolutional Networks (HGCNs) als hyperbolischen geometrischen Kodierer.
Aufgrund des Versagens der Additivität der Gaußschen Verteilung im hyperbolischen Raum können die traditionellen riemannschen Normal- oder gewickelten Normalverteilungen nicht direkt angewendet werden. Anstatt Einbettungen direkt in den hyperbolischen Raum zu diffundieren, schlagen die Autoren vor, einen Produktraum aus mehreren Mannigfaltigkeiten zu verwenden. Um dieses Problem zu lösen, führen die Autoren von HypDiff einen neuartigen Diffusionsprozess im hyperbolischen Raum ein. Aus Gründen der Berechnungseffizienz wird die Gauß-Verteilung des hyperbolischen Raums durch die Gauß-Verteilung der Tangentialebene 𝒯μ angenähert.
Im Gegensatz zum euklidischen Raum, der lineare Addition unterstützt, verwendet der hyperbolische Raum Möbius-Addition. Dies stellt eine Herausforderung für die Diffusion auf der Grundlage vielfältiger Daten dar. Außerdem verringert isotropes Rauschen schnell das Signal-Rausch-Verhältnis, sodass es schwierig ist, topologische Informationen zu erhalten.
Die Anisotropie von Graphen im latenten Raum ist von Natur aus mit einer induktiven Verzerrung der Graphenstruktur verbunden. Ein zentrales Problem ist die Identifizierung der dominanten Richtungen dieser Anisotropie. Um dieses Problem zu lösen, schlagen die Autoren der Methode HypDiff einen Rahmen für hyperbolische anisotrope Diffusion vor. Der Kerngedanke hierbei ist die Auswahl einer primären Diffusionsrichtung (d. h. eines Winkels) auf der Grundlage der Clusterbildung von Knoten durch Ähnlichkeit. Dadurch kann der hyperbolische latente Raum effektiv in mehrere Sektoren unterteilt werden. Die Knoten jedes Clusters werden dann auf die Tangentialebene ihres Schwerpunkts projiziert, um die Diffusion zu ermöglichen.
Diese Cluster können mit einem beliebigen, auf Ähnlichkeit basierenden Clustering-Algorithmus während der Vorverarbeitung gebildet werden.
Der hyperbolische Clustering-Parameter k ∈ [1, n] definiert die Anzahl der Sektoren, die den hyperbolischen Raum unterteilen. Die hyperbolische anisotrope Diffusion ist äquivalent zur gerichteten Diffusion im Rahmen des Modells Klein 𝕂c,n mit mehrfachen Krümmungen Ci ∈|k| , approximiert als Projektionen auf die Menge der Tangentialebenen 𝒯𝐨i∈{|k|} an den Clusterschwerpunkten Oi∈{|k|}.
Diese Eigenschaft stellt auf elegante Weise eine Verbindung zwischen dem Annäherungsalgorithmus der Autoren von HypDiff und dem mehrfach gekrümmten Modell von Klein her.
Das Verhalten des vorgeschlagenen Algorithmus variiert je nach dem Wert von k. Dies ermöglicht eine flexiblere und feinkörnigere Darstellung der Anisotropie in der hyperbolischen Geometrie, was die Genauigkeit und Effizienz sowohl bei der Rauschinjektion als auch beim Modelltraining verbessert.
Die hyperbolische Geometrie kann die Konnektivität von Knoten während des Graphenwachstums natürlich und geometrisch beschreiben. Die Beliebtheit eines Knotens kann durch seine radiale Koordinate abstrahiert werden, während die Ähnlichkeit durch Winkelabstände im hyperbolischen Raum ausgedrückt werden kann.
Das Hauptziel ist die Modellierung von Diffusion mit geometrischem Radialwachstum, das mit den Eigenschaften des hyperbolischen Raums in Einklang steht.
Der Hauptgrund, warum Standard-Diffusionsmodelle in Diagrammen unterdurchschnittlich abschneiden, ist der schnelle Rückgang des Signal-Rausch-Verhältnisses. In HypDiff wird die geodätische Richtung vom Zentrum jedes Clusters zum Nordpol O als Ziel-Diffusionsrichtung verwendet, um den Vorwärtsdiffusionsprozess unter geometrischen Einschränkungen zu steuern.
In Anlehnung an das Standardverfahren zur Rauschunterdrückung und Reverse-Diffusion-Modellierung verwenden die Autoren von HypDiff ein UNet-basiertes Rauschunterdrückungs-Diffusion-Modell (DDM), um die Vorhersage von X0 zu trainieren.
Darüber hinaus zeigen die HypDiff-Autoren, dass das Sampling gemeinsam in einem einzigen Tangentenraum und nicht in mehreren Tangentenräumen von Clusterzentren durchgeführt werden kann, um die Effizienz zu verbessern.
Die Autoren stellen im Folgenden die Visualisierung des Rahmens von HypDiff vor.
2. Die Implementation in MQL5
Nachdem wir die theoretischen Aspekte der Methode HypDiff erläutert haben, gehen wir nun zum praktischen Teil des Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen. Es sei gleich zu Beginn darauf hingewiesen, dass die Umsetzung recht langwierig und schwierig sein wird. Stellen Sie sich also auf ein erhebliches Arbeitsvolumen ein.
2.1 Erweitern des OpenCL-Programms
Wir beginnen unsere praktische Implementierung, indem wir unser bestehendes OpenCL-Programm modifizieren. Der erste Schritt besteht in der Projektion der Eingabedaten in den hyperbolischen Raum. Bei dieser Transformation ist es entscheidend, jede Position eines Elements in der Sequenz zu berücksichtigen, da der hyperbolische Raum euklidische Raumparameter mit zeitlichen Aspekten kombiniert. In Anlehnung an die ursprüngliche Methodik wenden wir das Lorentz-Modell an. Diese Projektion ist im HyperProjection-Kernel implementiert.
__kernel void HyperProjection(__global const float *inputs, __global float *outputs ) { const size_t pos = get_global_id(0); const size_t d = get_local_id(1); const size_t total = get_global_size(0); const size_t dimension = get_local_size(1);
Der Kernel erhält Zeiger auf Datenpuffer als Parameter: die zu analysierende Sequenz und die Transformationsergebnisse. Die Eigenschaften dieser Datenpuffer werden durch den Arbeitsbereich definiert. Die erste Dimension entspricht der Länge der Sequenz, während die zweite Dimension die Größe des Merkmalsvektors angibt, der jedes einzelne Element der Sequenz beschreibt. Die Arbeitsaufgaben werden auf der Grundlage der endgültigen Dimension in Arbeitsgruppen gruppiert.
Beachten Sie, dass der Merkmalsvektor für jedes Sequenzelement 1 zusätzliche Komponente enthält.
Als Nächstes deklarieren wir ein lokales Array für den Datenaustausch zwischen Threads innerhalb einer Arbeitsgruppe.
__local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Wir definieren die Offset-Konstanten in den Datenpuffern.
const int shift_in = pos * dimension + d; const int shift_out = pos * (dimension + 1) + d + 1;
Laden wir die Eingabedaten aus dem globalen Puffer in die lokalen Elemente des entsprechenden Workflows und berechnen wir die quadratischen Werte. Wir sollten auch darauf achten, das Ergebnis der Ausführung der Operation zu überprüfen.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; //--- float v2 = v * v; if(isinf(v2) || isnan(v2)) v2 = 0;
Als Nächstes müssen wir die Norm des Eingangsdatenvektors berechnen. Dazu addieren wir das Quadrat seiner Werte mit Hilfe unseres lokalen Arrays. Das liegt daran, dass jeder Arbeitsgruppenfaden 1 Element enthält.
//--- if(d < ls) temp[d] = v2; barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += v2; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
An dieser Stelle sei angemerkt, dass wir die Vektornorm nur benötigen, um den Wert des ersten Elements in unserem Vektor zu berechnen, der die hyperbolischen Koordinaten des Elements der zu analysierenden Folge beschreibt. Alle anderen Elemente verschieben wir ohne Änderungen, aber mit einer Positionsverschiebung.
outputs[shift_out] = v;
Um zusätzliche Operationen zu vermeiden, bestimmen wir den Wert des ersten Elements des hyperbolischen Vektors nur im ersten Thread jeder Arbeitsgruppe.
Hier berechnen wir zunächst den Anteil des Versatzes des analysierten Elements in der ursprünglichen Sequenz. Dann subtrahieren wir das Quadrat des erhaltenen Normwertes des oben berechneten ursprünglichen Repräsentationsvektors. Schließlich berechnen wir die Quadratwurzel aus dem erhaltenen Wert.
if(d == 0) { v = ((float)pos) / ((float)total); if(isinf(v) || isnan(v)) v = 0; outputs[shift_out - 1] = sqrt(fmax(temp[0] - v * v, 1.2e-07f)); } }
Beachten Sie, dass wir beim Extrahieren von Quadratwurzeln ausdrücklich sicherstellen, dass nur Werte größer als Null verwendet werden. Dadurch wird das Risiko von Laufzeitfehlern und ungültigen Ergebnissen während der Berechnung ausgeschlossen.
Um die Algorithmen der Backpropagation zu implementieren, werden wir sofort den HyperProjectionGrad-Kernel erstellen, der die Fehlergradientenfortpflanzung durch die zuvor definierten Feedforward-Operationen implementiert. Bitte beachten Sie die folgenden beiden Punkte. Erstens ist die Position eines Elements innerhalb der Sequenz statisch und nicht parametrisch. Das bedeutet, dass kein Gradient auf ihn übertragen wird.
Zweitens wird die Steigung der verbleibenden Elemente durch zwei separate Informationsstränge weitergegeben. Die eine ist die direkte Gradientenausbreitung. Gleichzeitig wurden alle Komponenten des ursprünglichen Merkmalsvektors für die Berechnung der Vektornorm verwendet, die wiederum das erste Element der hyperbolischen Darstellung bestimmt. Daher muss jedes Merkmal einen proportionalen Anteil des Fehlergradienten aus dem ersten Element des hyperbolischen Vektors erhalten.
Untersuchen wir nun, wie diese Ansätze in Code umgesetzt werden. Der HyperProjectionGrad-Kernel benötigt 3 Datenpuffer-Zeiger als Parameter. Ein neuer Eingabe-Gradientenpuffer (inputs_gr) wird eingeführt. Der Puffer, der die hyperbolische Darstellung der ursprünglichen Sequenz enthält, wird durch den entsprechenden Fehlergradientenpuffer (outputs_gr) ersetzt.
__kernel void HyperProjectionGrad(__global const float *inputs, __global float *inputs_gr, __global const float *outputs_gr ) { const size_t pos = get_global_id(0); const size_t d = get_global_id(1); const size_t total = get_global_size(0); const size_t dimension = get_global_size(1);
Wir belassen den Kernel des Aufgabenraums gleich dem Vorwärtsdurchlauf, fassen die Threads aber nicht mehr in Arbeitsgruppen zusammen. Im Kernelkörper identifizieren wir zunächst den aktuellen Thread im Aufgabenraums. Anhand der ermittelten Werte wird der Offset in den Datenpuffern bestimmt.
const int shift_in = pos * dimension + d; const int shift_start_out = pos * (dimension + 1); const int shift_out = shift_start_out + d + 1;
In dem Block, der die Daten aus den globalen Puffern lädt, wird der Wert des analysierten Elements aus der ursprünglichen Darstellung und sein Fehlergradient auf der Ebene der hyperbolischen Darstellung berechnet.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0;
Anschließend wird der Anteil des Fehlergradienten des ersten Elements der hyperbolischen Darstellung bestimmt, der als Produkt aus seinem Fehlergradienten und dem Eingangswert des analysierten Elements definiert ist.
v = v * outputs_gr[shift_start_out]; if(isinf(v) || isnan(v)) v = 0;
Vergessen Sie auch nicht, den Prozess in jeder Phase zu kontrollieren.
Wir speichern den Gesamtfehlergradienten in dem entsprechenden globalen Datenpuffer.
//---
inputs_gr[shift_in] = v + grad;
}
In diesem Stadium haben wir die Projektion der Eingabedaten in den hyperbolischen Raum implementiert. Die Autoren der Methode HypDiff schlagen jedoch vor, dass der Diffusionsprozess in den Projektionen des hyperbolischen Raums auf Tangentialebenen durchgeführt wird.
Auf den ersten Blick mag es seltsam erscheinen, Daten aus einem flachen Raum in den hyperbolischen Raum und dann wieder zurück zu projizieren, nur um ein Rauschen einzuführen. Der springende Punkt ist jedoch, dass die ursprüngliche flache Darstellung wahrscheinlich erheblich von der endgültigen Projektion abweichen wird. Denn die ursprüngliche Datenebene und die für die Projektion hyperbolischer Darstellungen verwendeten Tangentialebenen sind nicht dieselben Ebenen.
Dieses Konzept ist vergleichbar mit dem Entwurf einer technischen Zeichnung anhand eines Fotos. Zunächst rekonstruieren wir auf der Grundlage unseres Vorwissens und unserer Erfahrung gedanklich eine dreidimensionale Darstellung des auf dem Foto abgebildeten Objekts. Dann übersetzen wir dieses mentale Bild in eine zweidimensionale technische Zeichnung mit Seiten-, Front- und Draufsicht. In ähnlicher Weise projiziert HypDiff Daten auf mehrere Tangentialebenen, die jeweils um einen anderen Punkt im hyperbolischen Raum zentriert sind.
Um diese Funktionalität zu implementieren, werden wir den Kernel LogMap erstellen. Dieser Kernel akzeptiert sieben Datenpuffer-Zeiger als Parameter, was zugegebenermaßen ziemlich viel ist. Darunter befinden sich drei Eingangsdatenpuffer:
- Der Puffer features enthält den Tensor der hyperbolischen Einbettungen, die die Eingabedaten darstellen.
- Der Puffer „centroids“ enthält die Koordinaten der Zentroiden. Sie dienen als Basispunkte für die Tangentialebenen, auf die die Projektionen durchgeführt werden sollen.
- Der Puffer curvatures definiert die Krümmungsparameter, die mit jedem Schwerpunkt verbunden sind.
Der Puffer outputs speichert die Ergebnisse der Projektionsoperationen. In drei weiteren Puffern werden Zwischenergebnisse gespeichert, die bei den Berechnungen der Rückwärtsdurchläufe verwendet werden.
An dieser Stelle ist anzumerken, dass wir bei unserer Implementierung leicht vom ursprünglichen Rahmen abgewichen sind. Bei der ursprünglichen Methode HypDiff haben die Autoren die Sequenzelemente in der Phase der Datenvorverarbeitung vorgeclustert. Sie projizierten nur die Mitglieder der jeweiligen Gruppe auf die Tangentialebene. In unserem Ansatz haben wir uns jedoch dafür entschieden, die Sequenzelemente nicht vorzugruppieren. Stattdessen projizieren wir jedes Element auf jede Tangentialebene. Dadurch erhöht sich natürlich die Zahl der Operationen. Auf der anderen Seite wird es das Verständnis des Modells für die analysierte Sequenz bereichern.
__kernel void LogMap(__global const float *features, __global const float *centroids, __global const float *curvatures, __global float *outputs, __global float *product, __global float *distance, __global float *norma ) { //--- identify const size_t f = get_global_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_global_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
Im Hauptteil der Methode wird der aktuelle Handlungsstrang im dreidimensionalen Aufgabenraum festgelegt. Die erste Dimension verweist auf ein Element der ursprünglichen Sequenz. Der zweite zeigt auf den Schwerpunkt. Der dritte verweist auf die Position im Beschreibungsvektor des analysierten Sequenzelements. In diesem Fall fassen wir die Threads entsprechend der letzten Dimension in Arbeitsgruppen zusammen.
Als Nächstes deklarieren wir ein lokales Datenaustausch-Array innerhalb der Arbeitsgruppe.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Wir definieren die Offset-Konstanten in den Datenpuffern.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
Danach laden wir die Eingabedaten aus den globalen Puffern und überprüfen die Gültigkeit der erhaltenen Werte.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7;
Als Nächstes müssen wir die Produkte der Tensoren der Eingabedaten und der Zentroiden berechnen. Da wir jedoch mit einer hyperbolischen Darstellung arbeiten, werden wir das Minkowski-Produkt verwenden. Zur Berechnung führen wir zunächst die Multiplikation der entsprechenden Einzelwerte durch.
//--- dot(features, centroids) float fc = feature * centroid; if(isnan(fc) || isinf(fc)) fc = 0;
Dann summieren wir die erhaltenen Werte innerhalb der Arbeitsgruppe.
//--- if(d < ls) temp[d] = (d > 0 ? fc : -fc); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += fc; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float prod = temp[0]; if(isinf(prod) || isnan(prod)) prod = 0;
Anders als bei der üblichen Multiplikation von Vektoren im euklidischen Raum nehmen wir das Produkt der ersten Elemente der Vektoren mit dem Kehrwert.
Wir überprüfen die Gültigkeit des Ergebnisses der Operation und speichern den erhaltenen Wert im entsprechenden Element des globalen Zwischenspeichers. Wir benötigen diesen Wert während des Rückwärtsdurchlaufs.
product[shift_temporal] = prod;
Auf diese Weise lässt sich feststellen, um wie viel und in welche Richtung das analysierte Element gegenüber dem Schwerpunkt verschoben ist.
//--- project float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
Wir bestimmen die Minkowski-Norm des erhaltenen Verschiebungsvektors. Wie zuvor nehmen wir das Quadrat jedes Elements.
//--- norm(u) float u2 = u * u; if(isinf(u2) || isnan(u2)) u2 = 0;
Und wir addieren die erhaltenen Werte innerhalb der Arbeitsgruppe, wobei wir das Quadrat des ersten Elements mit umgekehrtem Vorzeichen nehmen.
if(d < ls) temp[d] = (d > 0 ? u2 : -u2); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += u2; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float normu = temp[0]; if(isinf(normu) || isnan(normu) || normu <= 0) normu = 1.0e-7f; normu = sqrt(normu);
Auch hier werden wir den erhaltenen Wert als Teil des Rückwärtsdurchlaufs verwenden. Deshalb speichern wir sie in einem temporären Datenspeicher.
norma[shift_temporal] = normu;
Im nächsten Schritt bestimmen wir den Abstand vom untersuchten Punkt zum Schwerpunkt im hyperbolischen Raum mit den Parametern der Schwerpunktskrümmung. In diesem Fall wird das Produkt der Vektoren nicht neu berechnet, sondern der zuvor ermittelte Wert verwendet.
//--- distance features to centroid float theta = -prod * curv; if(isinf(theta) || isnan(theta)) theta = 0; theta = fmax(theta, 1.0f + 1.2e-07f); float dist = sqrt(clamp(pow(acosh(theta), 2.0f) / curv, 0.0f, 50.0f)); if(isinf(dist) || isnan(dist)) dist = 0;
Wir überprüfen die Gültigkeit des erhaltenen Wertes und speichern das Ergebnis im globalen temporären Datenspeicher.
distance[shift_temporal] = dist;
Wir passen die Werte des Offset-Vektors an.
float proj_u = dist * u / normu;
Und dann müssen wir die erhaltenen Werte nur noch auf die Tangentialebene projizieren. Ähnlich wie bei der Lorentz-Projektion oben müssen wir hier das erste Element des Projektionsvektors anpassen. Dazu berechnen wir das Produkt aus Projektions- und Schwerpunktvektor, ohne die ersten Elemente zu berücksichtigen.
if(d < ls) temp[d] = (d > 0 ? proj_u * centroid : 0); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += proj_u * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Passen Sie den Wert des ersten Projektionselements an.
//--- if(d == 0) { proj_u = temp[0] / centroid; if(isinf(proj_u) || isnan(proj_u)) proj_u = 0; proj_u = fmax(u, 1.2e-7f); }
Speichern Sie das Ergebnis.
//---
outputs[shift_out] = proj_u;
}
Wie Sie sehen können, ist der Kernel-Algorithmus bei einer großen Anzahl komplexer Verbindungen ziemlich schwerfällig. Das macht es ziemlich schwierig, den Weg zu verstehen, den der Fehlergradient während des Rückwärtsdurchlaufs nimmt. Wie auch immer, wir müssen dieses Wirrwarr entwirren. Achten Sie bitte auf die Details. Der Algorithmus des Rückwärtsdurchlaufs ist im LogMapGrad-Kernel implementiert.
__kernel void LogMapGrad(__global const float *features, __global float *features_gr, __global const float *centroids, __global float *centroids_gr, __global const float *curvatures, __global float *curvatures_gr, __global const float *outputs, __global const float *outputs_gr, __global const float *product, __global const float *distance, __global const float *norma ) { //--- identify const size_t f = get_local_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_local_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
In den Kernelparametern haben wir Fehlergradientenpuffer auf der Quell- und der Ausgangsebene hinzugefügt. Damit haben wir 4 zusätzliche Datenpuffer.
Wir haben den Aufgabenraum des Kernels ähnlich belassen wie beim Vorwärtsdurchlauf, jedoch das Prinzip der Gruppierung in Arbeitsgruppen geändert. Denn nun müssen wir nicht nur Werte innerhalb der Vektoren der einzelnen Elemente der Sequenz sammeln, sondern auch Gradienten für die Zentren. Jeder Zentroid arbeitet mit allen Elementen der analysierten Sequenz. Dementsprechend sollte der Fehlergradient von jedem empfangen werden.
Im Kernelkörper wird der Ablauf der Operationen in allen Dimensionen des Aufgabenraums festgelegt. Danach erstellen wir ein lokales Array für den Datenaustausch zwischen den Elementen der Arbeitsgruppe.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Wir definieren die Offset-Konstanten in den globalen Datenpuffern.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
Danach laden wir Daten aus globalen Puffern. Zunächst extrahieren wir die Eingabedaten und Zwischenwerte.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float centroid0 = (d > 0 ? centroids[shift_cent - d] : centroid); if(isinf(centroid0) || isnan(centroid0) || centroid0 == 0) centroid0 = 1.2e-7f; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7; float prod = product[shift_temporal]; float dist = distance[shift_temporal]; float normu = norma[shift_temporal];
Dann berechnen wir die Werte des Vektors, der den Abstand des analysierten Sequenzelements vom Schwerpunkt enthält. Im Gegensatz zu den Operationen der Vorwärtsdurchläufe verfügen wir bereits über alle erforderlichen Daten.
float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
Wir laden den vorhandenen Fehlergradienten auf die Ergebnisebene.
float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0; float grad0 = (d>0 ? outputs_gr[shift_out - d] : grad); if(isinf(grad0) || isnan(grad0)) grad0 = 0;
Bitte beachten Sie, dass wir den Fehlergradienten nicht nur für das analysierte Element, sondern auch für das erste Element im Beschreibungsvektor des analysierten Sequenzelements laden. Der Grund hierfür ist ähnlich wie oben für den Kernel HyperProjectionGrad beschrieben.
Als Nächstes initialisieren wir lokale Variablen für die Akkumulation von Fehlergradienten.
float feature_gr = 0; float centroid_gr = 0; float curv_gr = 0; float prod_gr = 0; float normu_gr = 0; float dist_gr = 0;
Zunächst propagieren wir den Fehlergradienten von der Projektion der Daten auf die Tangentialebene zum Offset-Vektor.
float proj_u_gr = (d > 0 ? grad + grad0 / centroid0 * centroid : 0);
Dabei ist zu beachten, dass das erste Element des Offset-Vektors keinen Einfluss auf das Ergebnis hat. Daher ist die Steigung „0“. Andere Elemente erhielten sowohl einen direkten Fehlergradienten als auch einen Anteil am ersten Element der Ergebnisse.
Dann bestimmen wir die ersten Werte der Fehlergradienten für die Zentroiden. Wir berechnen sie in einer Schleife und sammeln die Werte aller Elemente der Sequenz.
for(int id = 0; id < dimension; id += ls) { if(d >= id && d < (id + ls)) { int t = d % ls; for(int ifeat = 0; ifeat < total_f; ifeat++) { if(f == ifeat) { if(d == 0) temp[t] = (f > 0 ? temp[t] : 0) + outputs[shift_out] / centroid * grad; else temp[t] = (f > 0 ? temp[t] : 0) + grad0 / centroid0 * outputs[shift_out]; } barrier(CLK_LOCAL_MEM_FENCE); }
Nach dem Sammeln der Fehlergradienten aus allen Elementen der Sequenz innerhalb des lokalen Arrays verwenden wir einen Thread und übertragen die gesammelten Werte in eine lokale Variable.
if(f == 0) { if(isnan(temp[t]) || isinf(temp[t])) temp[t] = 0; centroid_gr += temp[0]; } } barrier(CLK_LOCAL_MEM_FENCE); }
Wir müssen auch sicherstellen, dass die Barrieren ausnahmslos von allen Operationsthreads besucht werden.
Als Nächstes berechnen wir den Fehlergradienten für die Vektoren Abstand, Norm und Offset.
dist_gr = u / normu * proj_u_gr;
float u_gr = dist / normu * proj_u_gr;
normu_gr = dist * u / (normu * normu) * proj_u_gr;
Bitte beachten Sie, dass die Elemente des Offset-Vektors in jedem Thread individuell sind. Die Vektornorm und der Abstand sind jedoch diskrete Werte. Daher müssen wir die entsprechenden Fehlergradienten innerhalb eines Elements der analysierten Sequenz summieren. Zunächst sammeln wir die Fehlergradienten für die Entfernung. Wir summieren die Werte über ein lokales Array.
for(int ifeat = 0; ifeat < total_f; ifeat++) { if(d < ls && f == ifeat) temp[d] = dist_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += dist_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; dist_gr = temp[0];
Unmittelbar danach bestimmen wir den Fehlergradienten für den Krümmungsparameter des entsprechenden Schwerpunkts und das Produkt der Vektoren.
if(d == 0) { float theta = -prod * curv; float theta_gr = 1.0f / sqrt(curv * (theta * theta - 1)) * dist_gr; if(isinf(theta_gr) || isnan(theta_gr)) theta_gr = 0; curv_gr += -pow(acosh(theta), 2.0f) / (2 * sqrt(pow(curv, 3.0f))) * dist_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = -curv * theta_gr; if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; curv_gr += -prod * theta_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; } } barrier(CLK_LOCAL_MEM_FENCE);
Beachten Sie jedoch, dass die Steigung des Krümmungsparameterfehlers nur akkumuliert wird, um im globalen Datenpuffer gespeichert zu werden. Im Gegensatz dazu ist der Vektorprodukt-Fehlergradient ein Zwischenwert für die spätere Verteilung auf die beeinflussenden Elemente. Deshalb ist es wichtig, dass wir sie innerhalb der Arbeitsgruppe synchronisieren. In diesem Stadium speichern wir sie also in einem lokalen Array-Element. Später werden wir sie in eine lokale Variable verschieben.
if(f == ifeat) prod_gr += temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Ich glaube, Sie haben eine große Anzahl von sich wiederholenden Kontrollen bemerkt. Dies verkompliziert den Code, ist aber notwendig, um den korrekten Durchgang von Synchronisationsbarrieren von Workgroup-Threads zu organisieren.
Als Nächstes summieren wir auf ähnliche Weise den Fehlergradienten der Norm des Offset-Vektors.
if(d < ls && f == ifeat) temp[d] = normu_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += normu_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { normu_gr = temp[0]; if(isinf(normu_gr) || isnan(normu_gr)) normu_gr = 1.2e-7;
Anschließend wird der Fehlergradient des Offsetvektors angepasst.
u_gr += u / normu * normu_gr; if(isnan(u_gr) || isinf(u_gr)) u_gr = 0;
Und wir verteilen sie auf die Eingabedaten und den Schwerpunkt.
feature_gr += u_gr; centroid_gr += prod * curv * u_gr; } barrier(CLK_LOCAL_MEM_FENCE);
Dabei ist zu beachten, dass der Fehlergradient des Offset-Vektors sowohl auf die Ebene des Vektorprodukts als auch auf den Krümmungsparameter verteilt sein muss. Bei diesen Entitäten handelt es sich jedoch um skalare Werte. Das bedeutet, dass wir die Werte innerhalb jedes Elements der analysierten Sequenz aggregieren müssen. In diesem Stadium führen wir die Summierung der Produkte der entsprechenden Fehlergradienten des Verschiebungsvektors mit den Elementen der Zentroide durch. Im Wesentlichen ist diese Operation gleichbedeutend mit der Berechnung des Punktprodukts dieser Vektoren.
//--- dot (u_gr * centroid) if(d < ls && f == ifeat) temp[d] = u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Wir verwenden die erhaltenen Werte, um den Fehlergradienten auf die entsprechenden Entitäten zu verteilen.
if(f == ifeat && d == 0) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; prod_gr += temp[0] * curv; if(isinf(prod_gr) || isnan(prod_gr)) prod_gr = 0; curv_gr += temp[0] * prod; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = prod_gr; } barrier(CLK_LOCAL_MEM_FENCE);
Als Nächstes synchronisieren wir den Fehlergradientenwert auf der Ebene des Vektorprodukts innerhalb der Arbeitsgruppe.
if(f == ifeat) { prod_gr = temp[0];
Und wir verteilen den erhaltenen Wert auf die Eingabedaten.
feature_gr += prod_gr * centroid * (d > 0 ? 1 : -1); centroid_gr += prod_gr * feature * (d > 0 ? 1 : -1); } barrier(CLK_LOCAL_MEM_FENCE); }
Nachdem alle Operationen erfolgreich abgeschlossen wurden und die Fehlergradienten vollständig in lokalen Variablen gesammelt wurden, werden die erhaltenen Werte in globale Datenpuffer übertragen.
//--- result features_gr[shift_f] = feature_gr; centroids_gr[shift_cent] = centroid_gr; if(f == 0 && d == 0) curvatures_gr[cent] = curv; }
Und damit ist die Kernel-Implementierung abgeschlossen.
Wie Sie vielleicht schon bemerkt haben, ist der Algorithmus recht komplex, aber dennoch interessant. Um sie zu verstehen, muss man genau hinschauen.
Wie bereits erwähnt, ist die Implementierung des Rahmens von HypDiff mit einem erheblichen Arbeitsaufwand verbunden. In diesem Artikel haben wir uns ausschließlich auf die Implementierung der Algorithmen innerhalb des OpenCL-Programms konzentriert. Der vollständige Quellcode ist im Anhang enthalten. Allerdings ist die Länge des Artikels fast erschöpft. Daher schlage ich vor, die Erforschung der algorithmischen Implementierung des Rahmens auf der Seite des Hauptprogramms im nächsten Artikel fortzusetzen. Dieser Ansatz ermöglicht es uns, die Gesamtarbeit logisch in zwei Teile zu unterteilen.
Schlussfolgerung
Durch die Verwendung der hyperbolischen Geometrie werden die Herausforderungen, die sich aus der Diskrepanz zwischen diskreten Graphdaten und kontinuierlichen Diffusionsmodellen ergeben, wirksam angegangen. Mit HypDiff wird eine fortschrittliche Methode zur Erzeugung von hyperbolischem Gauß-Rauschen eingeführt. Es zielt darauf ab, das Problem des additiven Versagens in Gaußschen Verteilungen im hyperbolischen Raum anzugehen. Geometrische Beschränkungen, die auf der Winkelähnlichkeit basieren, werden auf den anisotropen Diffusionsprozess angewendet, um die lokale Graphenstruktur zu erhalten.
Im praktischen Teil dieses Artikels haben wir mit der Implementierung der vorgeschlagenen Ansätze unter MQL5 begonnen. Der Umfang der Arbeit geht jedoch über die Grenzen eines einzelnen Artikels hinaus. Wir werden den vorgeschlagenen Rahmen im nächsten Artikel weiterentwickeln.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16306
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Nichtlineare Regressionsmodelle an der Börse
Nichtlineare Regressionsmodelle an der Börse
 Arithmetischer Optimierungsalgorithmus (AOA): Von AOA zu SOA (Simpler Optimierungsalgorithmus)
Arithmetischer Optimierungsalgorithmus (AOA): Von AOA zu SOA (Simpler Optimierungsalgorithmus)
 Von der Grundstufe bis zur Mittelstufe: Union (II)
Von der Grundstufe bis zur Mittelstufe: Union (II)
 Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends
Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.