取引におけるニューラルネットワーク:二重アテンションベースのトレンド予測モデル
はじめに
金融商品の価格は、金利、インフレ、金融政策、投資家心理など、さまざまな要因の影響を受ける非常に変動の激しい時系列データです。金融商品の価格とこれらの要因との関係をモデル化し、その動向を予測することは、研究者や投資家にとって重要な課題となっています。
金融時系列の予測と分析に関する研究は数多くおこなわれてきました。従来の統計手法では、時系列が線形プロセスによって生成されると仮定されることが多く、非線形な動きを捉えるには限界があります。一方、機械学習やディープラーニングの手法は、非線形な関係を捉える能力に優れているため、金融時系列のモデリングにおいて高い成功を収めています。多くの研究では、特定の時点における特徴量を抽出し、それをモデリングや予測に活用するアプローチが取られています。しかし、このような手法では、データ間の相互作用や短期的な変動の継続性が見落とされがちです。
こうした課題を克服するため、研究「A Dual-Attention-Based Stock Price Trend Prediction Model With Dual Features」では、二重特徴量抽出手法を提案しています。この手法では、個々の時点だけでなく、複数の時間範囲にわたる情報を活用します。市場の短期特徴量と時間的長期特徴量を統合することで、予測精度の向上を図ります。本モデルは、エンコーダー-デコーダーアーキテクチャを基盤としており、エンコーダーとデコーダーの両ステージにアテンションメカニズムを導入することで、長い時系列データの中から最も関連性の高い特徴量を抽出できるよう設計されています。
本研究では、二重特徴量抽出と二重アテンションメカニズムを用いた新しい株価トレンド予測モデル (TPM: Trend Prediction Model) を提案します。TPMは、株価の変動方向と持続期間の両方を予測することを目的としています。提案手法の主な貢献は以下のとおりです。
- 異なる時間範囲を活用した新しい二重特徴量抽出手法:重要な市場情報を効果的に抽出し、予測の精度を向上させます。TPMでは、区分線形回帰と畳み込みニューラルネットワークを組み合わせることで、金融時系列データから長期および短期の市場特徴量をそれぞれ抽出します。市場情報を二重の特徴量として表現することで、モデルの予測性能を大幅に向上させています。
- エンコーダー-デコーダー構造と二重アテンションメカニズムを使用した株価トレンド予測モデル(TPM):エンコーダーおよびデコーダーステージの両方にアテンションメカニズムを導入することで、最も関連性の高い短期的な市場特徴量を適応的に選択し、長期的な時間的特徴量と統合することで予測精度を向上させます。
1. TPMアルゴリズム
既存の時系列予測手法を分析した結果、TPMの著者は以下の結論に達しました。
- 単変量の金融時系列データでは、将来の価格変動を確実に予測するのに十分な情報を得ることができない。
- 従来の特徴量抽出手法では、複雑な市場の動きを捉えるのに限界がある。
- 単一のニューラルネットワークを用いた時系列分析は不完全である。
TPMは、二重特徴量抽出と二重アテンションメカニズムを採用することで、これらの問題に対処します。提案されたアルゴリズムは2つのフェーズで構成されています。まず、区分線形回帰法を用いて金融時系列データをセグメント化し、異なる時間間隔のサブシーケンスに基づいて過去の長期的な時間的特徴量を抽出します。また、畳み込みニューラルネットワークを用いて、個々の時点から短期的な空間的市場特徴量を抽出します。
次に、TPM第2フェーズでは、先に抽出された二重特徴量を、二重アテンションメカニズムを組み込んだトレンド予測モデルで分析します。提案されたモデルは、エンコーダー-デコーダーアーキテクチャに基づいて構築されています。
エンコーダーは、再帰型LSTMブロックを基盤とし、最も関連性の高い短期的な市場特徴量を適応的に抽出するためにアテンションメカニズムを導入しています。
デコーダーもLSTMブロックとアテンションメカニズムを用いて構築されており、最も関連性の高い統合特徴量を選択・デコードし、株価の動向を予測します。
1次元の金融時系列データだけでは情報が不十分であるため、そのようなデータを基に株価の動向をモデル化・予測するのは困難です。そのため、TPMの著者はバーの始値・終値・最高値・最低値・取引量などの基本的な市場データを分析し、それらを一連のテクニカル指標に変換しています。
データの継続的な変化を考慮し、TPMは区分線形回帰(PLR)を用いて長期的な時間的特徴量を抽出します。PLRは短期的な変動ノイズを平滑化し、データの次元を削減することで計算効率を向上させます。
時系列のセグメンテーションは、最大誤差閾値δに依存します。CSI 300データを例に取ると、著者らはPLRを用いて過去の終値をセグメント化しています。δ=2.0の場合、時系列は16のサブシーケンスに分割できます。一方、閾値δ=4.0では、同じ時系列が4つのサブシーケンスにのみ分割されます。つまり、閾値が大きくなるほど、より多くのデータ変動が無視され、形成されるサブシーケンスの数が減少します。閾値の設定は、過去の時系列データから抽出される特徴量の信頼性に影響を及ぼします。各サブシーケンスは、特定の期間におけるデータの変動を表し、それぞれの傾きsmと持続時間dmが、トレンド予測のための長期的な時間的特徴量として生成されます。
同じ時点における異なるデータの相互作用を考慮し、各時間ステップの短期的で空間的な市場特徴量を畳み込みニューラルネットワーク(CNN)を用いて抽出します。分析対象の金融時系列データに対して市場行列を構築し、各行はデータの1次元を、行数nはその次元の数を示します。一方、各列は時点を表します。CNNは元のデータの近隣関係や空間的な特徴量を保持するため、市場行列と株価動向の間にある非線形な関係を捉えることができます。これにより、短期的な過去の時系列データから空間的特徴量を抽出することが可能になります。
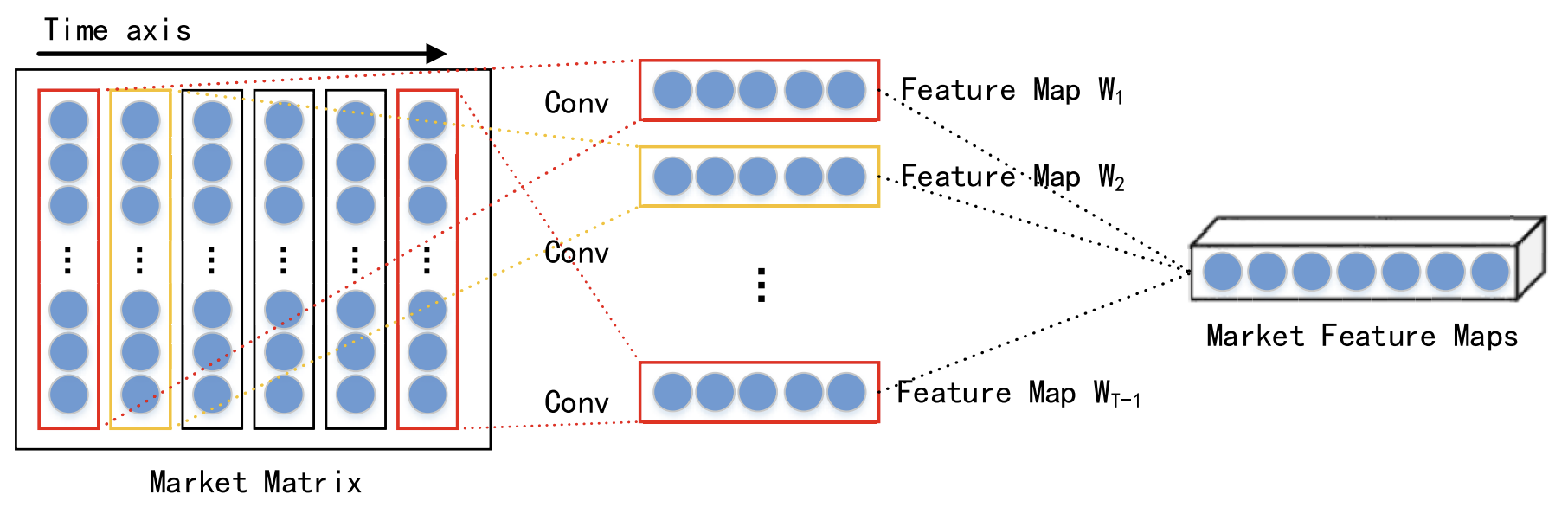
著者は、本研究において、1 × 3から1 × 5などの異なるカーネルサイズを持つ畳み込み層を使用し、抽象的かつ多層的な空間市場の特徴量を抽出しています。非線形活性化関数としてReLU関数が採用されています。
畳み込み層の後には、最大プーリング層が適用されます。これにより、特徴量マップの次元が削減され、過学習の防止に寄与します。
複数の畳み込み層および最大プーリング層からの出力は、さらなる処理のために投影層へと渡されます。
前述の通り、抽出された短期および長期の特徴量は、エンコーダー-デコーダーアーキテクチャ内で処理されます。この構造では、エンコーダーが入力情報を固定サイズのベクトルに圧縮し、デコーダーがこれらのベクトルを処理して最終的な出力を生成します。しかし、入力データが大量になると、エンコーダーがすべての関連情報を効果的に捉えきれず、モデルの性能が低下する可能性があります。この課題に対処するため、アテンションメカニズムが導入され、関連するニューロンの隠れ状態を解読することで情報の抽出精度を向上させます。
ただし、アテンションメカニズムを搭載したデコーダーには、最も関連性の高い入力特徴量を明示的に選択する機能がない点に注意が必要です。この問題を克服するため、TPM手法の著者らは、エンコーダーとデコーダーの両段階にアテンションメカニズムを組み込んでいます。
TPMアルゴリズムの第2フェーズは、二重アテンションメカニズムに基づいています。エンコーダー-デコーダー構造は2つの段階に分かれており、第1段階では、アテンションメカニズムを備えたLSTMベースのエンコーダーが、CNNによって抽出された短期的な空間市場の特徴量を解析します。各時点において、適応的に選択された短期特徴量がベクトルへとエンコードされます。
第2段階では、PLRによって抽出されたエンコード済みベクトルと長期的な時間的特徴量がLSTMベースのデコーダーに入力され、アテンションメカニズムに基づいて対応するベクトルと特徴量がデコードされ、株式市場のトレンドが予測されます。二重アテンションメカニズムを活用することで、TPMモデルはトレンドのモデリングと予測において、最も重要な空間市場および時間的特徴量を適応的に識別することが可能となります。
各時点tにおいて、エンコーダーは入力特徴量Wtと隠れ状態Htの関係を学習します。
![]()
ここで、Htは時刻tにおけるエンコーダーの隠れ状態、fen(•)は非線形関数、ʘenはエンコーダーのパラメータを表します。
本手法の著者らは、時間依存関係を捉え、短期特徴量エンコーダーを構築するために、非線形関数fenとしてLSTMを採用しています。LSTMは、時系列データの動的な時間変化を効果的にモデル化し、RNNにおける勾配消失や勾配爆発の問題を回避することができます。
また、著者らはエンコーダーの段階でアテンションメカニズムを導入し、初期特徴量WMarketをその次元数mに応じて分割しています。時間ステップt-1で計算された隠れ状態Ht-1とセル状態(コンテキスト)Ct-1は、入力特徴量の次元に対応する形で識別され、次の時刻tにおいて元の特徴量を更新するために使用されます。
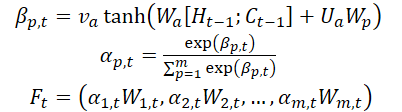
ここで、va、Wa、Uaはパラメータであり、SoftMax関数は各特徴量次元の重要度αm,tを計算するために使用されます。
すべての次元WtはFtに更新され、エンコーダーに入力されます。その後、時刻tの隠れ状態が更新されます。
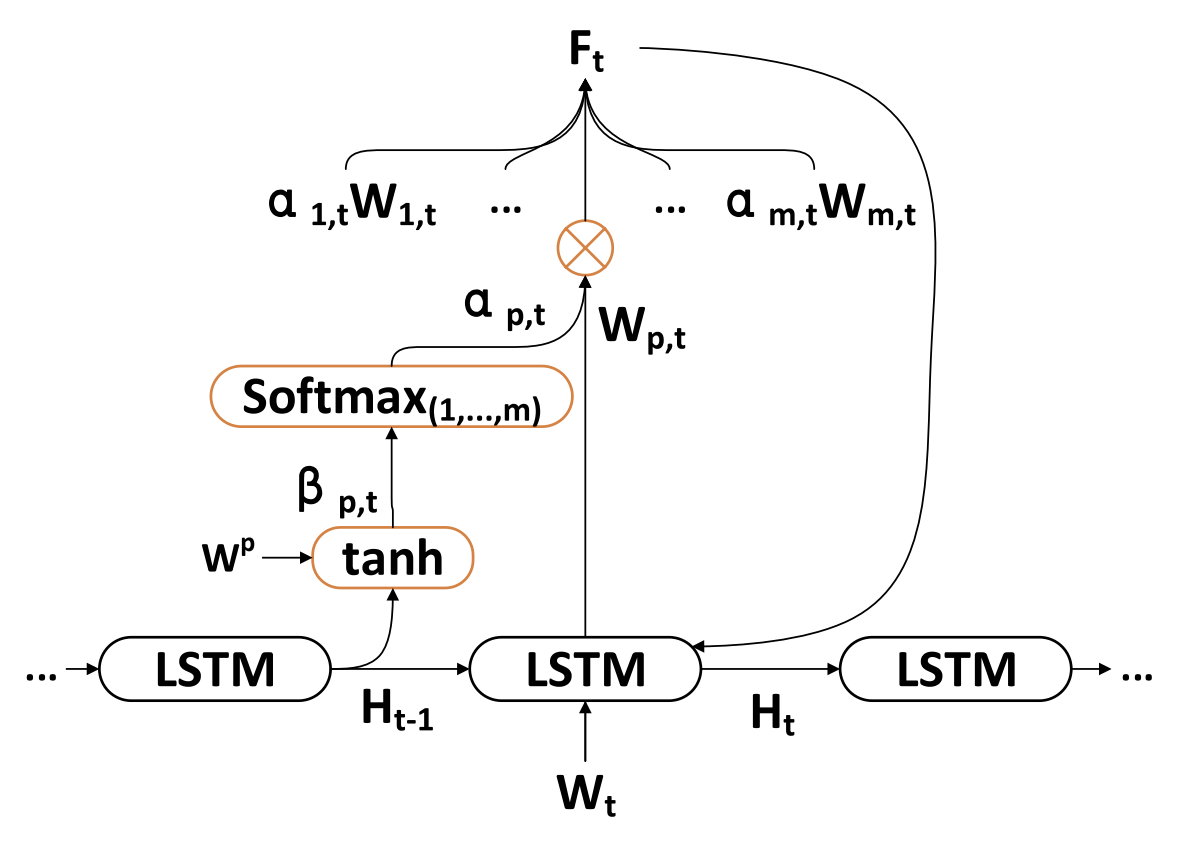
したがって、各時間ステップtにおいて、空間市場の特徴量の関連する次元を選択し、元の特徴量とエンコーダーの隠れ状態を反復的に更新することで、短期的な特徴量に最も関連性の高いエンコーディングベクトルを生成することができます。
デコーダーは、株式市場のトレンドを予測するために設計されたLSTMブロックです。長期的な時間的特徴量ZT-1はPLR法によって抽出されます。
各時間ステップtにおいて、デコーダーはエンコードベクトルWt、長期特徴量Lt、および隠れ状態Htの関係を学習します。
![]()
ここで、H'tは時間ステップtにおけるデコーダーの隠れ状態、fde(•)は非線形関数、ʘdeはデコーダーのパラメータを表します。
TPMの著者らは、時間的な依存関係を捉え、Long-Term Feature Decoderを構築するために、非線形関数fdeとしてLSTMを使用しています。計算手順はエンコーダーのステージと同様です。
また、TPMの著者は、すべての時間ステップにおけるエンコーダーの関連する隠れ状態を取得するために、デコーダーの段階でアテンションメカニズムを導入しています。
デコーダーに入力されるコンテキストベクトルは、エンコーダーのすべての隠れ状態をもとに取得されます。
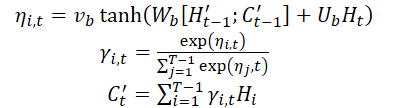
コンテキストベクトルC'tが取得されると、それは長期の一時的特徴量Ltと結合され、混合特徴量ytが生成されます。
![]()
上記の式を用いて、各時間ステップtにおいて、アルゴリズムは全時間ステップにおけるエンコーダの最も関連性の高い隠れ状態と長期的な時間的特徴量を選択し、混合特徴量ベクトルを生成します。
次に、株式市場のトレンドと二重特徴量の間の非線形マッピング関数F(•)について検討します。最後に、線形関数を適用し、時刻Tにおける株式市場のトレンド予測を生成します。
本モデルは、確率的勾配降下法(SGD)とモメンタム最適化法を用いて訓練されました。訓練時のバッチサイズは64、学習率は0.001です。
損失関数として、正則化項を含む二次誤差関数が使用されます。
著者によるTPM法の視覚的表現を以下に示します。
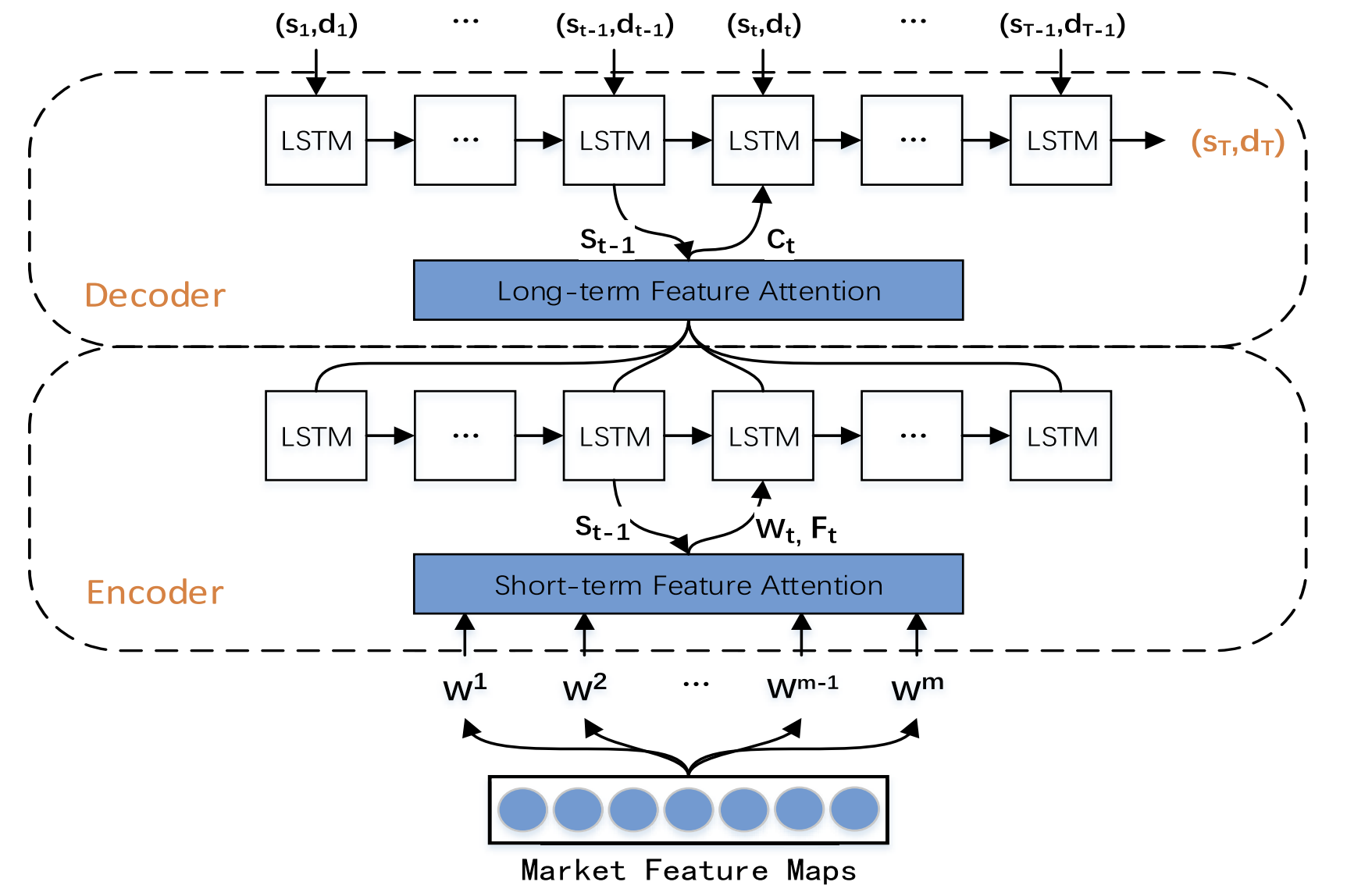
2. MQL5での実装
提案されたTPM法の理論的側面を検討した後、本章ではその実際の実装に移り、提案手法の解釈を示します。従来どおり、提案された方法論の全体的なフレームワークは維持しつつ、実装の詳細にはいくつかの変更を加えています。もちろん、これらの調整はモデルの最終的なパフォーマンスにさまざまな影響を及ぼす可能性があります。
まずエンコーダの構築から始めます。
2.1 TPMエンコーダ
以前に作成したLSTMブロックCNeuronLSTMOCLから基本機能を継承するCNeuronTPMEncoderクラス内で、モデルのエンコーダを実装します。この親クラスを選択したのは意図的です。ご存知のとおり、TPM法のエンコーダーは、アテンションメカニズムを追加したLSTMブロックに基づいています。
さらに、短期的な特徴量の抽出プロセスをエンコーダーに直接組み込むことにしました。特徴量抽出には、以前に開発したデータピラミッド構造ビルダーCSCMを使用します。ただし、重要な点として、これまでCSCMブロックは単変量時系列データから特徴量を抽出するために用いられていました。しかし今回は、個々の時点ごとに特徴量を抽出する必要があるため、データフローを若干調整する必要があります。
エンコーダーの全体構造体を以下に示します。
class CNeuronTPMEncoder : public CNeuronLSTMOCL { protected: bool bTSinRow; //--- CNeuronCSCMOCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronTransposeOCL cTranspose; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPMEncoder(void){}; ~CNeuronTPMEncoder(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPMEncoder; } virtual void SetOpenCL(COpenCLMy *obj); };
ここでは、オーバーライドされたメソッドの馴染みのあるセットと、いくつかのネストされたオブジェクトが登場します。これらの目的は、実装を進めるにつれて明らかになっていきます。
以前と同様に、すべてのネストされたオブジェクトはstaticとして宣言されます。このアプローチにより、クラスのコンストラクタとデストラクタは「空」のままとすることが可能になります。新しいクラスのインスタンスの実際の初期化は、Initメソッド内でおこなわれます。
bool CNeuronTPMEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(variables * lenth)) return false;
このメソッドは、引数として作成されたオブジェクトの主要なパラメータを受け取ります。本ケースでは、以下の3つのパラメータが含まれます。
- variables:分析対象の多峰性時系列データに含まれる単変量シーケンスの数
- lenth:分析対象のシーケンスの長さ(履歴の深さ)
- hidden_size:LSTMブロック内の隠れ層のサイズ
さらに、入力データテンソル内で各単変量シーケンスが行として配置されていることを示すフラグts_in_rowを追加しました。
メソッド本体では、親クラスの同名メソッドを呼び出します。このメソッドは、作成された層のパラメータを検証し、継承されたオブジェクトを初期化するために必要な制御ブロックを提供します。
また、親クラスの入力テンソルのサイズも渡します。このサイズは、単変量シーケンスのサイズと、入力データ内の単変量シーケンスの数の積に等しくなります。
なお、LSTMブロック内では全結合層を使用していますが、本ケースでは入力データテンソルの形状は影響しない点に注意してください。
次のステップでは、短期特徴量抽出ブロックを初期化します。
uint windows[] = {variables, 6, 5, 4}; if(!cFeatureExtraction.Init(0, 0, OpenCL, windows, lenth, variables, ts_in_row, optimization, batch)) return false;
これをおこなうには、まず畳み込み特徴量抽出層のウィンドウサイズを設定し、CSCMブロックの初期化メソッドを呼び出します。
CSCMブロックの初期化メソッドを呼び出す際、単変量シーケンスのサイズと数のパラメータを再配置している点に注意してください。これは、MSFformerメソッドのように単変量シーケンス全体から特徴量を抽出するのではなく、各時間ステップ(バー)ごとに特徴量を抽出する必要があるためです。
次に、アテンションブロックのネストされたオブジェクトを初期化します。ここでは、まず新たな層を作成し、そのバッファ内で前のステップのLSTMブロックの隠れ状態とコンテキストを連結します。
if(!cMemAndHidden.Init(0, 1, OpenCL, hidden_size * 2, optimization, batch)) return false;
個々の特徴量の重要度係数を計算するために、連結層を使用し、その出力をSoftMax関数で正規化します。
if(!cConcatenated.Init(0, 2, OpenCL, variables * lenth, variables * lenth, hidden_size * 2, optimization, batch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 3, OpenCL, variables * lenth, optimization, batch)) return false; cSoftMax.SetHeads(variables);
この段階では、データの正規化は単変量シーケンス内で実行されることに注意してください。
次に、アテンションの出力を記録する層を追加します。
if(!cAttentionOut.Init(0, 4, OpenCL, variables * lenth, optimization, batch)) return false;
必要に応じて、データ転置層を初期化します。
bTSinRow = ts_in_row; if(!bTSinRow) { if(!cTranspose.Init(0, 5, OpenCL, variables, lenth, optimization, iBatch)) return false; }
中間値を記録するための補助バッファも追加します。
//--- if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
すべてのネストされたオブジェクトの初期化が正常に完了したら、実行された処理の論理結果を呼び出し元に渡し、メソッドを終了します。
オブジェクトの初期化が完了したら、新しいクラスのフィードフォワードパスアルゴリズムの構築に進みます。このアルゴリズムはfeedForwardメソッド内で実装されます。
bool CNeuronTPMEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
いつものように、このメソッドのパラメータには、前のニューラル層のオブジェクトへのポインタを受け取ります。ただし、この場合、受け取ったポインタのチェックはおこなわず、そのまま内部の短期特徴量抽出層のフィードフォワードメソッドに渡します。呼び出されたメソッド本体の中で、受け取ったポインタの制御が実装されています。
次のステップで、前のフィードフォワードパスから保存されたオブジェクトの隠れ状態とコンテキストを組み合わせます。
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false;
これで準備作業は終了です。次に、アテンションブロックに移りましょう。このブロックでは、個々の特徴量の重要度係数を計算します。
if(!cConcatenated.FeedForward(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false; int map = cSoftMax.getOutputIndex();
必要に応じて、重要度係数テンソルを転置します。
if(!bTSinRow) { if(!cTranspose.FeedForward(cSoftMax.AsObject())) return false; map = cTranspose.getOutputIndex(); }
次に、得られた係数を対応する短期特徴量で要素ごとに乗算する必要があります。2つのテンソルの要素ごとの乗算には、ドロップアウト層のフィードフォワードパスカーネルを使用します。
このカーネルは、本来入力データにニューロン除外マスクを適用するために作成しましたが、今回は重要度係数をマスクとして使用します。
タスク空間の次元を定義しましょう。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;
カーネルにパラメータを渡します。
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, map)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
その後、実行キューに入れます。
if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
AttentionOut層のバッファでカーネルを実行すると、重要度係数を考慮した短期的な特徴量を取得できます。これで、エンコーダーの出力において特徴量テンソルを表現するために、LSTMブロックの基本機能を使用できるようになりました。
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttentionOut.AsObject())) return false; //--- return true; }
各段階での作動プロセスの監視を忘れないでください。処理が正常に完了したら、実行された操作の論理結果を呼び出し元に渡し、メソッドを終了します。
フィードフォワードパスの実装後、通常はバックプロパゲーションメソッドの構築に進みます。このクラスも例外ではありません。次のステップでは、モデルの最終結果への影響に応じて、すべてのネストされたオブジェクトと入力データテンソルに誤差勾配伝播を実装します。この機能はcalcInputGradientsメソッドに実装します。
また、このメソッドのパラメータでは、前のニューラル層のオブジェクトへのポインタを受け取ります。これは、先ほど説明した方法と同様です。
bool CNeuronTPMEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
メソッド本体では、まず受け取ったポインタの妥当性を確認します。
次に、継承された機能を活用し、LSTMブロックのアルゴリズムを通じて誤差勾配をアテンションブロックの出力レベルまで伝播します。
if(!CNeuronLSTMOCL::calcInputGradients(cAttentionOut.AsObject())) return false;
その後、誤差勾配を特徴量の重要度係数と特徴量そのものの2つの方向へ分配します。カーネルをキューに配置するアルゴリズムは、前述のものと同様です。
//--- uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = cSoftMax.Neurons(); ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cTemp.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, (bTSinRow ? cSoftMax.getOutputIndex() : cTranspose.getOutputIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, (bTSinRow ? cSoftMax.getGradientIndex() : cTranspose.getGradientIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, NeuronOCL.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
ここで、2つの重要なポイントに注意する必要があります。まず、誤差勾配の伝播バッファは、重要度係数の転置層が必要かどうかによって影響を受けます。第二に、短期的な特徴量は、重要度係数の乗算時と、これらの係数の計算時の両方で使用されます。そのため、この段階では、短期的な特徴量の誤差勾配を一時データバッファに保存します。
次のステップでは、必要に応じて、個々の特徴量の重要度係数の誤差勾配を転置します。
if(bTSinRow) { if(!cSoftMax.calcHiddenGradients(cTranspose.AsObject())) return false; }
その後、アテンションブロックアルゴリズムを通じて誤差勾配を短期特徴量のレベルまで伝播します。
if(!cConcatenated.calcHiddenGradients((CObject*)cSoftMax.AsObject(),(CBufferFloat *)NULL,(CBufferFloat *)NULL) || !DeActivation(cConcatenated.getOutput(), cConcatenated.getGradient(), cConcatenated.getGradient(), cConcatenated.Activation())) return false; if(!cFeatureExtraction.calcHiddenGradients(cConcatenated.AsObject(), cMemAndHidden.getOutput(), cMemAndHidden.getGradient())) return false;
次に、2つの情報スレッドから短期特徴量のレベルで誤差勾配を合計します。
if(!DeActivation(cFeatureExtraction.getOutput(), GetPointer(cTemp), GetPointer(cTemp), NeuronOCL.Activation()) || !SumAndNormilize(cFeatureExtraction.getGradient(), GetPointer(cTemp), cFeatureExtraction.getGradient(), 1, false)) return false;
メソッドの最後に、誤差勾配を前の層のレベルまで伝播し、操作の論理結果を呼び出し元に渡します。
if(!NeuronOCL.calcHiddenGradients(cFeatureExtraction.AsObject())) return false; //--- return true; }
誤差勾配を分配した後は、モデルのパラメータを最適化し、全体的な誤差を最小化するだけです。この機能は、updateInputWeightsメソッドに実装されており、訓練可能なパラメータを含むネストされたオブジェクトの同名メソッドを呼び出すことで実行されます。
bool CNeuronTPMEncoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronLSTMOCL::updateInputWeights(cAttentionOut.AsObject())) return false; if(!cFeatureExtraction.UpdateInputWeights(NeuronOCL)) return false; if(!cConcatenated.UpdateInputWeights(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; //--- return true; }
これで、エンコーダーの主な機能を実装するためのアルゴリズムの説明は終わりです。このクラスのすべてのメソッドの完全なコードは、この記事の作成に使用されたすべてのプログラムの完全なコードとともに、添付ファイルで入手可能です。
2.2 TPMデコーダー
TPMエンコーダのアルゴリズムを実装した後、次のステップとしてデコーダの構築に進みます。TPMメソッドの理論的な側面を確認した際、エンコーダーとデコーダーのアルゴリズムには多くの共通点があることに気づいたかもしれません。ただし、わずかな違いがある場合でも、新しいクラスを開発する必要があります。
エンコーダーと同様に、新しいデコーダークラスCNeuronTPMDecoderはLSTMブロッククラスから派生しています。以下に新しいクラスの構造を示します。
class CNeuronTPM : public CNeuronLSTMOCL { protected: CNeuronTPMEncoder cEncoder; CNeuronPLROCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronConcatenate cAttAndFeature; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPM(void){}; ~CNeuronTPM(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPM; } virtual void SetOpenCL(COpenCLMy *obj); };
上で説明したエンコーダークラスとの類似点は簡単にわかります。追加されたネストオブジェクトは2つのみであり、特徴量抽出層の種類が変更されている点にも気づくでしょう。デコーダーでは、長期的な特徴量を抽出するためにPLRを使用しています。
また、エンコーダークラスには「所有権の指定」が含まれていますが、デコーダーには存在しないことに気づいたかもしれません。この区別には理由があります。エンコーダーとデコーダーは同じ入力データに対して動作しますが、異なる抽象化レベルで特徴量を抽出します。上位レベルのモデル構造を複雑にしないように、エンコーダーとデコーダーを1つの統合ブロックにしました。その結果、従来のエンコーダークラスは新しいクラスの内部層として組み込まれ、TPMアルゴリズム全体が単一のエンティティとして統合されました。この決定は新しいクラスの名前に反映されています。CNeuronTPM。
新しいクラスの初期化メソッドのパラメータは、エンコーダーの初期化メソッドと完全に同一です。
bool CNeuronTPM::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(hidden_size)) return false;
メソッドの本体では、親クラスの初期化メソッドも呼び出します。ただし、入力データテンソルのサイズは、エンコーダーの隠れ状態のサイズにすでに対応しています。これは、デコーダーにエンコーダーから受信した特徴量の加重ベクトルが供給されるためです。
エンコーダーオブジェクトを初期化します。
if(!cEncoder.Init(0, 0, OpenCL, variables, lenth, hidden_size, ts_in_row, optimization, iBatch)) return false;
特徴量抽出層を初期化します。
if(!cFeatureExtraction.Init(0, 1, OpenCL, variables, lenth, !ts_in_row, optimization, iBatch)) return false;
アテンションブロックの初期化アルゴリズムは、エンコーダーの初期化時の操作と似ています。しかし、入力データテンソルのサイズに違いがある点が特徴です。
if(!cMemAndHidden.Init(0, 2, OpenCL, hidden_size * 2, optimization, iBatch)) return false; if(!cConcatenated.Init(0, 3, OpenCL, hidden_size, hidden_size, hidden_size * 2, optimization, iBatch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 4, OpenCL, hidden_size, optimization, iBatch)) return false; cSoftMax.SetHeads(1); if(!cAttentionOut.Init(0, 5, OpenCL, hidden_size, optimization, iBatch)) return false;
前述したように、LSTMブロックは全結合層を使用します。したがって、エンコーダーから取得された短期特徴量のテンソルは、マルチモーダル時系列の単変量シーケンスのコンテキストでは「匿名」と見なすことができます。これにより、テンソル全体を対象に重要度係数を正規化できます。この段階では、入力テンソルの向きは重要ではありません。
分析された時系列の重み付けされた短期および長期特徴量の投影層を追加し、これをLSTMブロックに入力しましょう。
if(!cAttAndFeature.Init(0, 6, OpenCL, hidden_size, hidden_size, variables * lenth, optimization, iBatch)) return false;
クラスの初期化操作の最後に、一時データを格納するためのバッファを追加します。
if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
ネストされたオブジェクトを初期化した論理結果を呼び出し元に返します。
ネストされたオブジェクトを初期化した後、feedForwardメソッドでフィードフォワードアルゴリズムの実装に進みます。他の同じ名前のメソッドと同様に、パラメータとして前のニューラル層のオブジェクトへのポインタを受け取ります。
bool CNeuronTPM::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Encoder if(!cEncoder.FeedForward(NeuronOCL)) return false;
次に、受信したポインタをエンコーダーのフィードフォワードメソッドに渡します。
次に、同じポインタを渡して、分析された時系列の長期特徴量を抽出します。
//--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
アテンションブロックの動作は、上で説明したエンコーダーブロックと同様です。
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false; //--- Attention if(!cConcatenated.FeedForward(cEncoder.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false;
重要度係数をエンコーダーの短期特徴量のベクトルに掛けます。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cEncoder.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cSoftMax.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
短期特徴量の加重ベクトルと長期特徴量を連結層で組み合わせます。
//--- Attention and Features if(!cAttAndFeature.FeedForward(cAttentionOut.AsObject(), cFeatureExtraction.getOutput())) return false;
次に、この準備されたデータをLSTMブロックに入力します。
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttAndFeature.AsObject())) return false; //--- return true; }
操作の論理結果を検証し、呼び出し元のプログラムに返します。
次に、通常はバックプロパゲーション法の構築に進みます。ただし、エンコーダーとデコーダーのフォワードパス方式の類似点に気付いたと思います。もちろん、いくつかのニュアンスはあります。バックプロパゲーション法にも同様のニュアンスが存在します。それでも、アルゴリズムは全体的に非常に似ています。したがって、添付の資料でご自身で調べてみることをお勧めします。
2.3 学習可能なモデルのアーキテクチャ
MQL5を使用したTPM法の実装を検討しました。この手法は株価の動向を予測するために開発されました。当然、これを環境状態エンコーダーに統合します。そのアーキテクチャはCreateEncoderDescriptionsメソッドで説明されています。
パラメータでは、メソッドは埋め込みモデルアーキテクチャを保存する動的配列へのポインタを受け取ります。
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
メソッド本体では、受け取ったポインタの妥当性を確認し、必要であれば動的配列オブジェクトの新しいインスタンスを作成します。
いつものように、環境の状態を記述する生データをモデルに入力します。初期データを記録するために、分析されたテンソルを書き込むのに十分なサイズの基本的な全結合層を使用します。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
取得された初期データはバッチ正規化層で前処理されます。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
前処理されたデータはTPMモジュールに渡されます。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTPM; descr.count = LatentCount; descr.window = BarDescr; descr.window_out = HistoryBars; descr.step = int(false); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
TPMモジュールから取得されたデータは3層MLPを介して伝播され、その出力で分析された時系列の予測値が得られることが期待されます。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = BarDescr * NForecast; descr.optimization = ADAM; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
予測値には、以前にバッチ正規化層で削除された元の時系列の統計変数を追加します。
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
次に、得られた予測出力を周波数表現で整列させます。
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
ActorおよびCriticモデルは、以前の作業から変更なくコピーされています。これらは添付ファイルで確認できます。
2.4 モデル訓練EA
モデルを訓練する際は、再帰型モデルの訓練に特有の課題を考慮することが重要です。ご存知のように、再帰型モデルの主な特徴量は、入力データのシーケンスに対する感度です。そのため、訓練プロセスでは、訓練データセットのデータを履歴順に保持したまま使用する必要があります。しかし、このアプローチは、多くのモデルにおいて訓練効率を低下させる可能性があります。短い時間間隔内での過剰適合を引き起こしやすく、訓練期間全体への一般化が困難になるためです。
これらの負の影響を最小限に抑えるために、訓練プロセスでは、履歴順を維持しながらエクスペリエンスリプレイバッファから小さなサブセットをランダムに抽出します。その後、新しい訓練バッチをサンプリングします。環境状態エンコーダーの訓練方法を例に、このアプローチの実装を詳しく見ていきましょう。エキスパートアドバイザーファイル「...\Experts\TPM\StudyEncoder.mq5」も以下に添付されています。
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
メソッドの本体では、まず、パスの収益性によってランク付けされた、訓練セットからパスを選択する確率のベクトルを生成します。その後、必要なローカル変数を宣言します。
vector<float> result, target, state; bool Stop = false;
次に、1つのサブセット訓練バッチのサイズを示す変数を追加します。
int Batch = 100;
次に、ネストされたループのシステムを作成します。外側のループでは、訓練セットから軌跡をサンプリングし、サンプリングした軌跡上の訓練サブセットの開始状態をサンプリングします。
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch) { int tr = SampleTrajectory(probability); int st = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(st <= 0) { iter -= Batch; continue; }
LSTMブロックの隠れ状態とコンテキストバッファをクリアします。
Encoder.Clear();
その後、ネストされたループを実行して、環境の選択された状態から、履歴シーケンス内の状態を順番に反復します。
for(int i = st; (i < MathMin(st + Batch, Buffer[tr].Total - NForecast) && !IsStopped() && !Stop); i++) { state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter += i - st - Batch; break; } bState.AssignArray(state);
ネストされたループの本体では、環境の分析された状態をデータバッファに転送します。得られたデータに基づいて、次の価格変動の軌道を予測します。
//--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
次に、経験再生バッファから次の軌道のターゲット値を読み込みます。
//--- Collect target data if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!Result.Resize(BarDescr * NForecast)) continue;
次に、予測の精度を確認します。バックプロパゲーションパス中に、次の動きを予測する際の誤差を最小限に抑えるようにモデルパラメータを調整します。
if(!Encoder.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
学習過程の進捗状況をユーザーに知らせ、ループの次の反復に移ります。
if(GetTickCount() - ticks > 500) { double percent = double(iter + i - st) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
ループシステムのすべての反復が正常に完了したら、銘柄チャートのコメントフィールドをクリアします。訓練結果をターミナルログに出力し、エキスパートアドバイザー(EA)のシャットダウンを初期化します。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
ActorおよびCriticの訓練EAにも同様の編集がおこなわれました。これらのモデルには再帰ブロックは追加されていませんが、環境状態エンコーダーが正しく動作することを保証するには、これらの編集をおこなう必要がありました。これは、ActorとCriticの両方がそれを入力データとして使用するためです。
モデル訓練EAの完全なコードは添付ファイルにあります。添付ファイルには、この記事で使用されているすべてのプログラム、クラス、メソッドの完全なコードも含まれています。
3.テスト
この記事では、TPMを使用して今後の株価の軌道を予測する方法を検討し、提案されたアプローチの解釈を実装しました。次に、実際のデータを使用して作業の結果をテストします。いつものように、提示されたモデルを2023年のEURUSD H1時間枠の履歴データで訓練します。
まず、Actorの行動を評価せずに過去の価格変動データを分析する環境エンコーダーモデルの訓練から始めます。このアプローチにより、頻繁な更新を必要とせずに、初期データセットでモデルを完全に訓練できます。訓練プロセスは比較的速く、良好な結果が得られました。以下は、予測された価格変動の軌跡と実際の価格変動の軌跡を比較したグラフです。
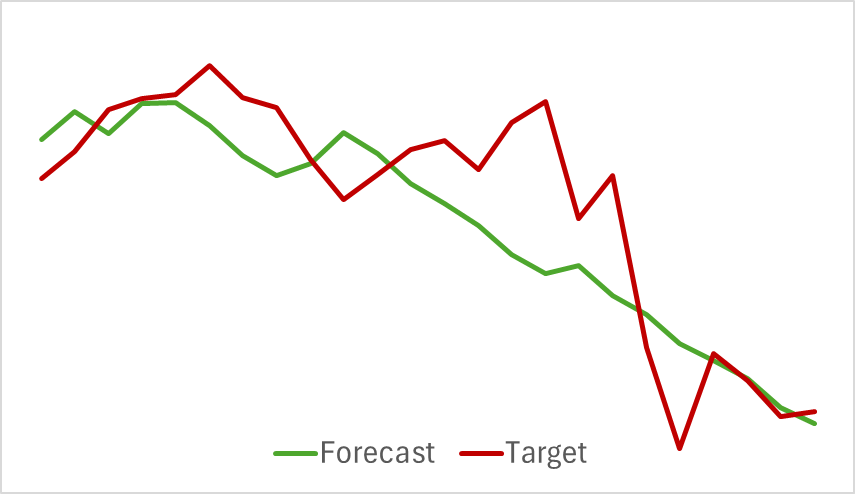
グラフでは2つの線が密接に重なり合っており、予測される軌道はより滑らかに見えます。このスムージング効果により、Actorの訓練の安定性が向上する可能性があります。
ご存知のとおり、私たちの主な目的は、Actorの方策を最適化することです。環境エンコーダーを訓練した後、訓練プロセスの第2段階であるActor方策訓練に進みます。このプロセスは本質的に反復的です。Actorの行動はシフトされ、以前に収集された訓練データの範囲を超えて移動する可能性があるため、Actorの現在の方策行動に近い状態と報酬を入力して、経験再生バッファを定期的に更新する必要があります。
ActorモデルとCriticモデルの訓練を交互に繰り返し、訓練データセットを更新した後、過去の訓練データで利益を生み出すことができる方策を開発しました。
訓練データセット外でのモデルのパフォーマンスを評価するために、他の条件を同じに保ちながら、2024年1月の履歴データを使用してテストします。
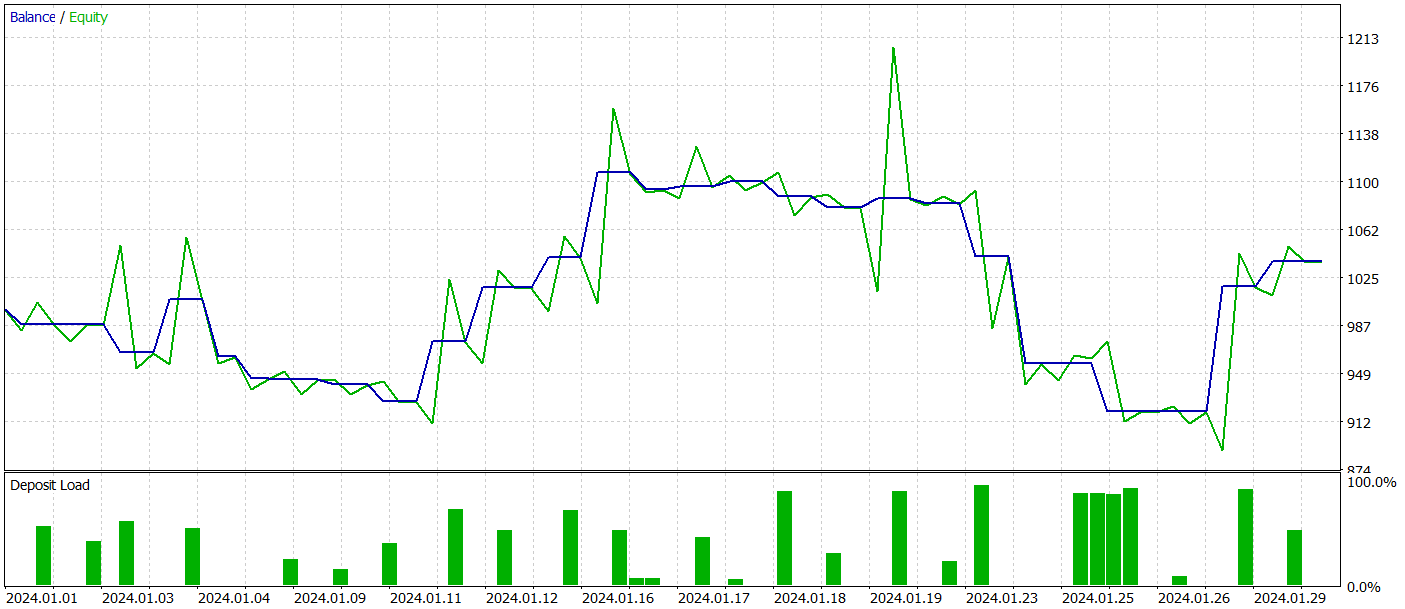
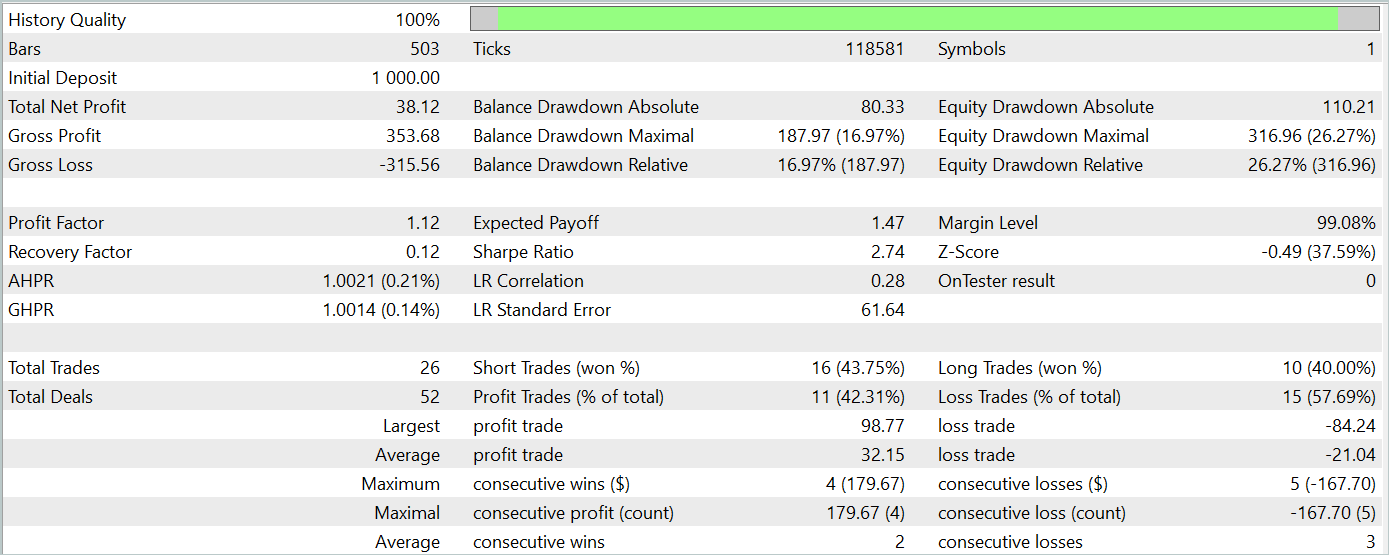
テスト期間中、モデルは26件の取引を実行しましたが、そのうち利益が出たのは11件だけで、42%強でした。ただし、取引あたりの最大利益と平均利益の両方が対応する損失指標を上回ったため、テスト期間全体では利益となりました。テスト期間のプロフィットファクターは1.12でした。
それにもかかわらず、残高チャートを見ると、その月の30年目の前半に大幅な下落があったことがわかります。これは懸念を引き起こします。利益は生み出されているものの、モデルにはさらなる改良が必要です。
結論
この記事では、TPMを用いた価格変動予測の興味深い手法について検討しました。この手法は、短期的な依存関係を分析する畳み込みモデルの強みと、長期的な傾向を識別するPLRの特長を効果的に組み合わせたものです。
実践セクションでは、MQL5を使用して提案手法の実装を行い、モデルの訓練とテストを実施しました。その結果、訓練済みモデルが訓練データセット外のデータでも利益を生み出せることが確認されました。しかし、残高チャートには期待通りの一貫した上昇傾向が見られず、ドローダウンも発生しました。
総じて、本手法は有望であるものの、開発したモデルにはさらなる改良の余地があると言えます。
参照文献
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | StudyEncoder.mq5 | EA | エンコーダー訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15255
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 取引におけるニューラルネットワーク:時空間ニューラルネットワーク(STNN)
取引におけるニューラルネットワーク:時空間ニューラルネットワーク(STNN)
 ボラティリティを予測するための計量経済学ツール:GARCHモデル
ボラティリティを予測するための計量経済学ツール:GARCHモデル
 人工電界アルゴリズム(AEFA)
人工電界アルゴリズム(AEFA)
 取引におけるニューラルネットワーク:時系列の区分線形表現
取引におけるニューラルネットワーク:時系列の区分線形表現
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索