MetaTrader 5 / 例
English Deutsch
preview
受信者動作特性曲線の紹介

受信者動作特性曲線の紹介

MetaTrader 5 — 例 | 27 6月 2025, 07:41
42 0
Francis Dube
Francis Dube

はじめに

受信者操作特性(ROC、Receiver Operating Characteristic)グラフは、分類器の性能に基づいてそれらを視覚化・整理・選択するための手法です。ROC曲線は信号検出理論に起源を持ち、分類器の真陽性率と偽陽性率のトレードオフを示すために使用されてきました。ROC曲線は、単なる性能可視化ツールとしての有用性にとどまらず、クラス分布に偏りがある場合や、誤分類のコストが異なるドメインにおいて特に有効です。これは、金融時系列データセットに適用される分類器にとって特に関連性が高いといえます。

ROC曲線の概念的な枠組みは比較的シンプルですが、実際の応用では注意すべき複雑な側面が存在します。また、実務においては誤解されやすい点や陥りやすい罠もあります。この記事では、ROC曲線の基礎を紹介し、分類器の性能を評価するうえでの実用的な指針を提供することを目的とします。


二値分類の定式化

現実の多くの応用分野では、サンプルが2つの相互に排他的かつ包括的なクラスのいずれかに分類される「二値分類」問題が発生します。このようなシナリオでは、単一のターゲットクラスを定義し、各サンプルがそのクラスのメンバーか、またはその補集合（非ターゲットクラス）に分類されるケースがあります。  たとえば、レーダーシステムにより画面上に検出された輪郭を、「戦車（ターゲットクラス）」または「非戦車オブジェクト」として分類するタスクが挙げられます。  同様に、クレジットカードの取引を「不正（ターゲットクラス）」か「正当な取引」として判定するタスクも、典型的な二値分類問題です。

ターゲットか否か？

単一のターゲットクラスを識別するというこの二値分類問題の定式化は、以降の分析の基礎となります。  サンプルを明示的に2つの異なるクラスに分類するのではなく、本稿で採用するアプローチでは、あるサンプルが指定されたターゲットクラスに属するかどうかの判断に焦点を当てます。  「ターゲット」とその補集合という用語は、軍事的なニュアンスを想起させるかもしれませんが、この概念自体はさまざまな分野に幅広く適用可能です。  ターゲットクラスは、悪性腫瘍、成功した金融取引、あるいは前述のような不正なクレジットカード取引など、さまざまな対象を表すことができます。  ここで重要なのは、「関心のある特定のクラス」と「それ以外のすべてのクラス」という二分法的な構造です。


混同行列

ある分類器をテストデータセットに適用した場合、分類結果として4つの異なる結果が得られます。正例（ターゲットクラスに属するサンプル）のサンプルが正しく正例として分類された場合は「真陽性(TP: True Positive)」と呼ばれます。反対に、正例のサンプルが誤って負例（非ターゲットクラスに属するサンプル）として分類された場合は「偽陰性(FN: False Negative)」と呼ばれます。同様に、負例のサンプルが正しく負例として分類された場合は「真陰性(TN: True Negative)」、誤って正例として分類された場合は「偽陽性(FP: False Positive)」と呼ばれます。これらの4つの分類結果は、いわゆる「2×2の混同行列（別名：分割表）」を構成します。

混同行列

この混同行列は、これら4つの分類結果に対するサンプルの分布を示しており、多くの一般的に使用される性能指標の基礎となります。代表的な指標には以下のようなものがあります。

  • 再現率(Recall)（別名：感度(Sensitivity)、Hit Rate）ターゲットに属するサンプル（正例）のうち、正しくターゲットとして分類された割合で、計算式は「TP / (TP + FN)」です。
  • 誤警報率（False Alarm Rate、第I種過誤率）：ターゲットに属さないサンプル（負例）のうち、誤ってターゲットとして分類された割合で、計算式は「FP / (TN + FP)」です。
  • Miss Rate（第II種過誤率）：ターゲットに属するサンプル（正例）のうち、誤って非ターゲットとして分類された割合で、計算式は「FN / (TP + FN)」です。
  • 特異性(Specificity)：ターゲットに属さないサンプル（負例）のうち、正しく非ターゲットとして分類された割合で、計算式は「TN / (TN + FP)」です。

英語版Wikipediaには、混同行列から得られた性能指標の広範なリストを表示する便利なグラフィックがあります（日本語ではhttps://ja.wikipedia.org/wiki/%E7%B5%B1%E8%A8%88%E5%AD%A6%E3%81%8A%E3%82%88%E3%81%B3%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%81%AE%E8%A9%95%E4%BE%A1%E6%8C%87%E6%A8%99）。

混同行列の表


ROC曲線

ほとんどの二値分類モデルの内部では、まず数値的な予測値が生成され、それがあらかじめ定められた閾値と比較されることで、分類がおこなわれます。予測値がこの閾値以上であればサンプルはターゲットとして分類され、閾値未満であれば非ターゲットと見なされます。このように、すべての性能指標は閾値の設定によって大きく影響を受けることが明らかです。たとえば、閾値を予測値の最小値以下に設定すると、すべてのサンプルがターゲットとして分類されることになり、再現率は完全(1.0)となりますが、その代償として誤警報率も非常に高くなり、性能評価としては望ましくない結果となります。

意思決定メカニズム

一方、閾値を予測値の最大値よりも高く設定すると、すべてのサンプルが非ターゲットとして分類されることになり、再現率は0となり、誤警報率は完全に0となります。実際のところ、最適な閾値はこの両極端の中間に存在します。閾値をその全範囲にわたって系統的に変化させることで、再現率と誤警報率の両方が0から1の範囲を移動し、一方が改善すれば他方が犠牲になるという関係が現れます。これら2つの指標をそれぞれ縦軸と横軸にプロットすることで生成される曲線（閾値を潜在パラメータとして）は、受信者動作特性曲線(ROC: Receiver Operating Characteristic curve)と呼ばれます。

ROC曲線は通常、横軸に誤警報率、縦軸に再現率をとって描画されます。たとえば、分類モデルがランダムな数値予測を出力し、その予測がケースの真のクラスと無関係であるような状況を考えてみましょう。

ランダム性能

このような状況では、すべての閾値においてヒット率と誤警報率が平均的に等しくなり、ROC曲線はグラフの左下から右上に伸びる対角線に近い形になります。たとえば、サンプルを50％の確率でランダムに正例として割り当てる分類器は、正例および負例のサンプルをそれぞれ50％の確率で正しく分類すると期待されます。このとき、ROC空間上の位置は座標点 (0.5, 0.5) となります。

同様に、その分類器が分類器がサンプルをランダムに90%の確率で正例として分類する場合、正例の90%を正しく分類できると期待されますが、それに伴い偽陽性率も90%に増加し、ROC空間上では座標点(0.9, 0.9)に対応します。このように、ランダム分類器はROC空間において対角線上の点をたどることになり、その位置は正例として分類する頻度によって決定されます。ランダムな推測を超える性能を達成するためには、分類器はROC空間の上三角領域（対角線の上側の三角形部分）に位置する必要があり、そのためにデータ内に存在する有用なパターンを活用しなければなりません。

完璧な性能

逆に、予測値が閾値以上であればターゲット、閾値未満であれば非ターゲットとして正確に区別できる閾値が存在する完全なモデルは、特徴的なROC曲線を示します。パラメトリックな閾値が最小値から最適閾値へと移動する間、誤警報率は1から0へ減少し、一方でヒット率は常に1を維持します。その後、パラメトリックな閾値がさらに増加すると、ヒット率は1から0へと低下し、誤警報率は0のままとなります。この結果、ROC曲線は右上の点から左上の点を経て左下の点へと移動する経路を形成します。

中間的な性能

中間的な性能を示すモデルは、これらの極端な例の間に位置し、ROC曲線は対角線と左上隅の間に描かれます。ROC曲線が対角線から左上隅にどれだけ離れているかが、そのモデルの性能の指標となります。一般的に、ROCプロット上のある点が別の点より優れているとは、真陽性率が高いか、偽陽性率が低いか、またはその両方である場合を指します。ROCプロットの左側、横軸に近い位置に存在する分類器は保守的であると特徴付けられます。

これらの分類器は、十分な証拠がある場合にのみ正例と分類する傾向があり、その結果、偽陽性率は低く抑えられますが、真陽性率はしばしば低下します。一方、ROC曲線の右上側に位置する分類器は保守的でないとされ、わずかな証拠でも正例と分類する傾向があり、真陽性率は高いものの偽陽性率も高くなることが多いです。実際の多くの領域では、負例が多数を占めるため、ROCプロットの左側領域に位置する分類器の性能が特に重要となります。

ROC空間の右下の三角領域に位置する分類器は、ランダム推測よりも性能が劣ることを示します。そのため、この領域には通常ROC曲線上に点は存在しません。分類器の否定（すなわち、すべてのサンプルに対する分類結果を逆転させる操作）は、真陽性を偽陰性に、偽陽性を真陰性に変換します。したがって、右下三角領域に点を持つ分類器は、その否定を取ることで左上三角領域に対応する点を持つ分類器に変換可能です。対角線上に位置する分類器は、正例と負例の区別に関して判別能力を持たないものとみなすことができます。一方、対角線の下に位置する分類器は、有用なパターンを持ちながらもそれを誤った方法で適用していると解釈できます。


ROCの性能指標

ROC曲線のプロットを視覚的に確認することで初歩的な洞察を得ることは可能ですが、モデル性能をより包括的に理解するためには、関連する性能指標の分析が必要です。詳細な分析に先立ち、ROC曲線を特徴付けるデータ構造について明確にすることが重要です。理解を促進するために、説明的な例を示します。

以下の表は、分類モデルから得られたROC性能指標の仮想的なサンプルを示しています。この例では、PythonのSklearnライブラリで利用可能なアヤメの花データセットを使用しています。ターゲット（正例）/非ターゲット（負例）のパラダイムに従い、分類の目的は単一のアヤメ品種の識別に限定しました。具体的には、setosaをターゲットとして指定し、それ以外の品種を非ターゲットとして分類しています。一般的な分類手法と同様に、モデルは非ターゲットに対して0、ターゲットに対して1の出力を生成するよう学習しており、サンプルのラベルもそれに合わせて変換されています。なお、他のラベリング方法も可能であることに留意してください。

決定閾値の範囲内の各閾値について、混同行列が作成され、真陽性率と偽陽性率が計算されます。これらの計算は、学習済みの予測モデルから得られた確率値または決定関数の値を用い、対応する閾値によってサンプルのクラスが判定されます。ここに示す表は、スクリプト「ROC_curves_table_demo.mq5」を用いて生成されました。

KG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH
NF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195
DI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708
OI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556
GI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334
GH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221
RH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211
IK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935
CK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736
NK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715
EJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645
DJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552
HJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534
NM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417
GM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155
CL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943
LL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699
NL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593
KO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258
NO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660
CN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489
OQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420
NQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619
GQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375
PP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087
OP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257
RP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124
RS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349
KS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502
KR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523
JR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147
HE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841
QE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488
DE      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195
PD      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058
MG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819
JG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744
EG      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683
LF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635
CF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589
KF      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556
JI      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494
NH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416
PH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347
LH      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244
KK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238
HK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225
LK      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213
PJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192
CJ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189
EM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177
IM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157
HM      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132
EL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127
DL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119
KL      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104
DO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102
RO      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085
DN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082
EN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069
HN      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062
HQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052
DQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048
FQ      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044
MP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028
LP      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026
NS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015
ES      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012
MS      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007
QR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004
CR      0       17:13:16.458    ROC_curves_table_demo (Crash 1000 Index,M5)     1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002

表形式のROC曲線データを検証すると、明確な傾向が見られます。決定閾値の増加に伴い、真陽性率(TPR)と偽陽性率(FPR)の両方が1から0へと減少します。モデルの予測能力により、FPRはTPRよりも速く減少する傾向があり、FPRが0に達している一方でTPRは1を維持しています。そのため、第I種過誤（偽陽性）と第II種過誤（偽陰性）の相対的なコストに大きな差がなければ、最適な閾値はこれらの極値の間に存在すると考えられます。また、表には特異性も含まれており、これは真陰性率(TNR: True Negative Rate)に相当し、FPRの補数であることに注意してください。

多くの場合、最適な閾値は真陽性率と偽陽性率の列を直接確認することで決定可能です。ターゲットおよび非ターゲットのサンプルサイズが示されているため、この判断はより理解しやすくなっています。第I種過誤と第II種過誤のコストがほぼ同等である場合、平均誤差が適切な単一の性能指標として機能します。表中のM_Eは誤警報率とMiss Rateの算術平均として計算されています。

しかし、これらの過誤コストが大きく異なる場合、平均誤差の指標としての有用性は低下します。特に適合率(precision)は多くの応用分野で重要な性能指標です。通常、ターゲットに対する適合率が主な関心対象となりますが、文脈によっては、非ターゲットを正しく認識する能力も要視されることもあります。ターゲットの検出精度に関しては、表中のPREC列が該当し、非ターゲットの識別精度についてはNPREC列が関連します。

表にはさらに、正解率(ACC: accuracy、別名「精度」)およびバランス精度(B_ACC: balanced accuracy)の性能指標が示されています。正解率は、全データセット中で真陽性と真陰性の両方に該当する正しく分類されたサンプルの割合を示します。バランス精度は感度と特異性の算術平均として計算され、ターゲットと非ターゲットのサンプル数に大きな偏りがあるクラス不均衡の影響を緩和するために用いられます。ROC曲線下面積(AUC: Area Under the ROC Curve)について説明する前に、前述のROC指標の表を生成するために使用された計算手順を調べる必要があります。具体的には、これらのROC関連指標の計算を担当するコードを分析します。

関連するコードはヘッダーファイル「roc_curves.mqh」にまとめられており、一連の関数群とデータ構造体「conf_stats」が定義されています。このconf_stats構造体は混同行列から導出される様々なパラメータを格納するコンテナとして機能します。

//+------------------------------------------------------------------+
//|  confusion matrix stats                                          |
//+------------------------------------------------------------------+
struct conf_stats
  {
   double              tn;                //true negatives
   double              tp;                //true positives
   double              fn;                //false negatives
   double              fp;                //false positives
   double              num_targets;       //number of actual positive labels(target)
   double              num_non_targets;   //number of acutal negative labels(non targets)
   double            tp_rate;             //true positives rate - hit rate -  recall - sensitivity
   double            fp_rate;             //false positives rate - fall out - type 1 error
   double            fn_rate;             //false negatives rate - miss rate - type 2 error
   double            tn_rate;             //true negatives rate - specificity
   double            precision;           //precision - positive predictve value
   double            null_precision;      //null precision - false discovery rate
   double            prevalence;          //prevalence
   double            lr_plus;             //positive likelihood ratio
   double            lr_neg;              //negative likelihood ratio
   double            for_rate;            //false omission rate
   double            npv;                 //negative predictive value
   double            acc;                 //accuracy
   double            b_acc;               //balanced accuracy
   double            f1_score;            //f1 score
   double            mean_error;          //mean error
  };

conf_stats構造体は、関数「roc_stats」における主要なパラメータとして機能し、混同行列に基づいて得られた評価結果を格納する役割を果たします。この評価は、真のラベル、対応する予測値、および指定された閾値から構成されるデータセットに対して実行されます。真のラベルはtargetsと呼ばれるベクトルとして提供され、関数の第2引数として渡されます。第3引数であるprobasは、予測確率または決定関数の出力を表すベクトルです。

//+------------------------------------------------------------------+
//| defines                                                          |
//+------------------------------------------------------------------+
bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0)
  {
   vector all_labels = np::unique(targets);

   if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return false;
     }
//---
   cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0;
//---
   for(ulong i = 0; i<targets.Size(); i++)
     {
      if(probas[i]>=threshold && long(targets[i]) == target_label)
         cmat.tp++;
      else
         if(probas[i]>=threshold && long(targets[i]) == non_target_label)
            cmat.fp++;
         else
            if(probas[i]<threshold && long(targets[i]) == target_label)
               cmat.fn++;
            else
               cmat.tn++;
     }
//---
   cmat.num_targets = cmat.tp+cmat.fn;
   cmat.num_non_targets = cmat.fp+cmat.tn;
//---
   cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na");
   cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na");
   cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na");
   cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na");
   cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na");
   cmat.null_precision = 1.0 - cmat.precision;
   cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na");
   cmat.npv = 1.0 - cmat.for_rate;
   cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na");
   cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na");
   cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na");
   cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0);
   cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na");
   cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0);
//---
   return true;
//---
  }

thresholdパラメータは、クラスの所属を区別するために使用される臨界値（閾値）を定義します。最後の2つのパラメータは、それぞれターゲットラベルと非ターゲットラベルを明示的に指定するためのものです。この関数はbool型の値を返し、正常に実行された場合はtrueを、エラーが発生した場合はfalseを返します。

//+------------------------------------------------------------------+
//| roc table                                                        |
//+------------------------------------------------------------------+
matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0)
  {
   matrix roctable(probas.Rows(),10);

   conf_stats mts;

   vector probs = probas.Col(target_probs_col);

   if(!np::quickSort(probs,false,0,probs.Size()-1))
      return matrix::Zeros(1,1);

   for(ulong i = 0; i<roctable.Rows(); i++)
     {
      if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label))
         return matrix::Zeros(1,1);
      roctable[i][0] = mts.tp_rate;
      roctable[i][1] = mts.fp_rate;
      roctable[i][2] = mts.fn_rate;
      roctable[i][3] = mts.tn_rate;
      roctable[i][4] = mts.precision;
      roctable[i][5] = mts.null_precision;
      roctable[i][6] = mts.mean_error;
      roctable[i][7] = mts.acc;
      roctable[i][8] = mts.b_acc;
      roctable[i][9] = probs[i];
     }
//---
   return roctable;
  }

roc_table関数は、ROC曲線データを含む行列を生成します。入力パラメータには、真のクラスラベルのベクトル、予測確率または決定関数の値を含む行列、そして多列の行列においてクラス判定に使用する列インデックスを指定するunsigned long型の整数が含まれます。最後の2つのパラメータは、ターゲットおよび非ターゲットのラベルを定義します。エラーが発生した場合、この関数は1×1のゼロ行列を返します。roc_statsおよびroc_tableの両関数は、二値分類モデル専用に設計されていることに注意が必要です。この要件を満たさない入力が与えられた場合、エラーメッセージが返されます。

//+------------------------------------------------------------------+
//| roc curve table display                                          |
//+------------------------------------------------------------------+
string roc_table_display(matrix &out)
  {
   string output,temp;

   if(out.Rows()>=10)
     {
      output = "TPR   FPR   FNR   TNR   PREC  NPREC  M_E   ACC   B_ACC THRESH";
      for(ulong i = 0; i<out.Rows(); i++)
        {
         temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf",
                             out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]);
         StringAdd(output,temp);
        }
     }
   return output;
  }

roc_table_display関数は、1つの行列パラメータを受け取ります。理想的には、これは先に実行されたroc_table関数の出力であることが望ましく、そのデータを表形式の文字列として整形します。


ROC曲線下面積(AUC)

AUC (Area Under the ROC Curve)は、分類器の性能を要約するための簡潔な単一の指標を提供し、詳細すぎるROC曲線の代替として機能します。ROC曲線が真陽性率と偽陽性率のトレードオフを視覚的に表現するのに対し、AUCはモデルがクラスを識別する能力を定量的に評価する指標です。ROC曲線上で対角線（ランダムな分類）を示す無意味なモデルは、AUC = 0.5を持ち、分類性能がランダムと等しいことを示します。一方、ROC曲線が左上隅に張り付くような完全なモデルでは、AUC = 1.0となり、完全な分類性能を示します。したがって、AUCの値が高いほど、モデル性能は優れていると判断されます。AUCの計算はROC曲線下面積を求めることでおこなわれます。テストデータにおける統計的変動を考慮しても、通常は単純な数値積分（台形則）で十分な精度が得られるため、複雑な数値積分をおこなう必要はありません。

AUCには重要な統計的解釈があります。それは、ランダムに選ばれた正例が、ランダムに選ばれた負例よりも高いスコアを与えられる確率を表しており、この特性によりAUCとウィルコクソンの順位和検定（マン・ホイットニーのU検定）が統計的に同値であることが示されます。

ウィルコクソンの順位和検定は、正規分布を仮定せずに2つの独立した群の差を評価するノンパラメトリックな手法です。この検定はすべての観測値を順位付けし、それぞれの群の順位和を比較することで、中央値の差異を評価します。

さらに、AUCはジニ係数と本質的に関連しています。ジニ係数は、ランダム分類の対角線とROC曲線との間の面積の2倍として定義されます。ジニ係数は分布の不平等の度合いを定量化する指標で、0（完全平等）から1（最大不平等）の範囲を取ります。所得分布の文脈では、収入の格差を反映します。グラフ上では、ジニ係数はローレンツ曲線と完全平等線との間の面積の比率として定義されます。

roc_auc関数（roc_curves.mqhに定義）は、二値分類問題に対するAUCを計算します。この関数は、最大FPRを指定することで、計算範囲を制限するオプションを備えています。引数として、真のクラスラベルと予測確率に加え、オプションでターゲットラベルと最大FPRを受け取ります。最大FPRが1.0に設定された場合、標準のAUCが計算されます。それ以外の場合、ROC曲線を計算し、searchsortedによって指定された最大FPRに対応する点を見つけ、そこでTPRを補間し、台形則によりその範囲内での部分AUCを算出します。最後に、この部分AUCを0.5から1.0の範囲に正規化し、指定されたFPR範囲における分類器性能を示す指標として提供します。

//+------------------------------------------------------------------+
//|  area under the curve                                            |
//+------------------------------------------------------------------+
double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0)
  {
   vector all_labels = np::unique(true_classes);

   if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0)
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   if(max_fpr == 1.0)
     {
      vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
      return auc[0];
     }

   matrix tpr,fpr,threshs;

   if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs))
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid inputs ");
      return EMPTY_VALUE;
     }

   vector xp(1);
   xp[0] = max_fpr;
   vector stop;

   if(!np::searchsorted(fpr.Row(0),xp,true,stop))
     {
      Print(__FUNCTION__, " ", __LINE__, " searchsorted failed ");
      return EMPTY_VALUE;
     }

   vector xpts(2);
   vector ypts(2);

   xpts[0] = fpr[0][long(stop[0])-1];
   xpts[1] = fpr[0][long(stop[0])];
   ypts[0] = tpr[0][long(stop[0])-1];
   ypts[1] = tpr[0][long(stop[0])];

   vector vtpr = tpr.Row(0);
   vtpr = np::sliceVector(vtpr,0,long(stop[0]));
   vector vfpr = fpr.Row(0);
   vfpr = np::sliceVector(vfpr,0,long(stop[0]));

   if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1))
     {
      Print(__FUNCTION__, " ", __LINE__, " error  ", GetLastError());
      return EMPTY_VALUE;
     }

   vfpr[vfpr.Size()-1] = max_fpr;

   vector yint = np::interp(xp,xpts,ypts);


   vtpr[vtpr.Size()-1] = yint[0];

   double direction = 1.0;

   vector dx = np::diff(vfpr);

   if(dx[dx.ArgMin()]<0.0)
      direction = -1.0;

   double partial_auc = direction*np::trapezoid(vtpr,vfpr);

   if(partial_auc == EMPTY_VALUE)
     {
      Print(__FUNCTION__, " ", __LINE__, " trapz failed ");
      return EMPTY_VALUE;
     }

   double minarea = 0.5*(max_fpr*max_fpr);
   double maxarea = max_fpr;

   return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea));
  }

max_fprパラメータは、ROC曲線の一部の領域に限定した部分AUCの計算を可能にし、特定のFPRの範囲内での分類器の性能評価を実現します。この機能は、特に低いFPRの閾値に重点を置くシナリオにおいて有用です。また、多数の真陰性が存在する不均衡データセットを分析する際にも有利であり、ROC曲線が真陰性の影響で過度に左右されることを避け、関心のある領域に焦点を当てた評価を可能にします。

ROC曲線は分類器の評価における有効な枠組みを提供しますが、分類器の優劣を最終的に決定するための基準として用いる際には慎重な検討が必要です。特に誤分類にかかるコストを考慮する場合、その重要性が増します。AUCは分類器の品質を評価するための指標を提供しますが、比較評価をおこなう際にはより精緻なアプローチが求められます。このようなコストの問題に適切に対応するためには、出発点である混同行列に立ち戻る必要があります。

従来の分類モデルでは、しばしば正解率の最大化が重視され、すべての誤分類に対して等しいコストがかかるという仮定が暗黙的に存在します。これに対してコスト考慮型(Cost-Sensitive)分類では、誤分類の種類ごとに異なるコストが存在することを考慮し、単に正解率を最大化するのではなく、誤分類による総コストの最小化を目指します。たとえば、有望な投資銘柄を識別する分類器においては、見逃し（偽陰性）のコストは、誤って選定すること（偽陽性）のコストよりも小さいと見なされる場合があります。各種の誤分類タイプにコストを割り当てることで、コスト行列が構成されます。この行列は、誤った予測（偽陽性や偽陰性）によって生じる損失やペナルティ、さらには必要に応じて正しい予測にもコストを割り当てて、各予測結果に対応するコストを明示します。以下に、仮想的な混同行列とそれに対応するコスト行列の一例を示します。

コスト行列

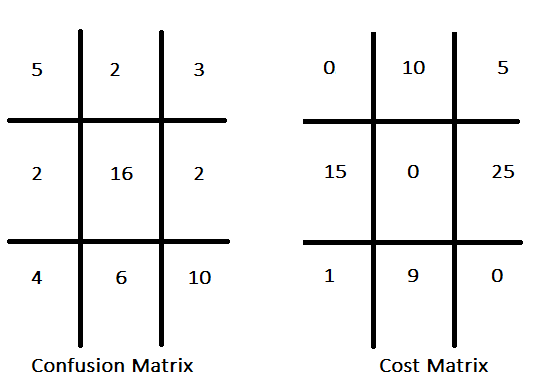
コスト行列では、通常、対角要素にゼロが配置されます。これは、正しい予測にはコストが発生しないという前提を意味します。この慣習は広く用いられていますが、必ずしも強制されるものではありません。すべての誤分類タイプに対してコスト構造が定義されている場合、混同行列に含まれる情報を集約して単一の性能指標に変換することが可能です。最も基本的な方法は、各誤分類の発生頻度に対応するコストを掛け、その積をすべて合計することです。ただし、この方法による評価の妥当性は、データセット内のクラス比率が実際の運用環境におけるクラス分布を正確に反映していることを前提としています。

より堅牢なコスト考慮型性能評価指標としては、1サンプルあたりの期待コストが挙げられます。この指標では、まず混同行列における各クラスのサンプル数を行ごとに正規化して、真のクラスが与えられた場合に分類器が出力するクラスの条件付き確率を求めます。これに、コスト行列に定義されたそれぞれの予測結果に対するコストを掛け、それらの積を各行に対して合計することで、各クラスに属するサンプルの期待コストを算出します。その後、これらのクラスごとの期待コストに、各クラスにおけるサンプルの出現比率、すなわち事前確率を掛け合わせ、全体としての期待コストを求めます。現実の運用環境におけるクラスの出現比率を推定するためには、データの背後にある分布に関する深い理解が必要です。この推定のための方法論には、以下が含まれます。

  • 過去のデータの分析：既存の記録を調査することで、クラスの比率に関する信頼性の高い推定が可能になります。たとえば、医療診断においては、患者の記録を分析することで有病率を明らかにできます。
  • 専門家への相談：専門的な知識を持つドメインの専門家に意見を求めることで、他の手法で得られた推定結果を精緻化または検証することができます。
  • 代表的なサンプリング手法の実施：新たなデータ収集が可能な場合には、サンプルが実世界の分布を正確に反映するように設計します。特に不均衡なデータセットにおいては、層化抽出法を用いることで、すべてのクラスが十分に代表されるようにすることができます。

あるクラス内のサンプルの期待される割合は、形式的には事前確率と同等です。特に二値分類の文脈では、
qをターゲットクラスに属するサンプルの事前確率とします。さらに、p₁は第I種過誤、すなわち偽陽性の確率であり、その誤りに伴うコストをc₁とします。一方、p₂は第II種過誤、すなわち偽陰性の確率であり、これに対応するコストをc₂とします。多くの応用において、qは理論的あるいは経験的手法によって特定可能であり、c₁およびc₂は正確に、または合理的な近似として把握されていることが一般的です。したがって、これら3つの量(q, c₁, c₂)は固定されたパラメータとして扱うことができます。一方、誤り確率であるp₁とp₂は分類の閾値によって決定されます。このとき、期待コストは次の式によって表されます。

コスト計算式

この式を変形すると次のようになります。

コスト計算式を再構成

任意の期待コストに対して、p₁（偽陽性率）とp₂（偽陰性率）の間には線形関係が存在することが示されます。この線形関係をROC曲線上に図示すると、その傾きは事前確率qとコスト比c₂ / c₁によって決定されます。期待コストの値を変化させることで、一連の平行な直線が生成されます。これらの直線のうち、右下に位置するものほど、より高いコストを意味します。この直線がROC曲線と2点で交わる場合、それらの点は等しい（ただし最適ではない）期待コストをもたらす2つの異なる閾値を示します。一方、ROC曲線よりも完全に上方かつ左方に位置する直線は、その分類モデルでは達成不可能な性能を表しています。ROC曲線に接する直線は、モデルが実現可能な中で最小の期待コスト、すなわち最適なコストを表します。

この分析から分かるように、AUC（曲線下面積）は分類モデルの実用的な性能を必ずしも正確に反映する指標ではありません。AUCは全体的な品質を評価するための有効な指標ではありますが、運用上のコストが関与する状況では、コスト感度のある応用において誤解を招く結論を導く可能性があるため、その有用性は限定的です。


2クラスを超える意思決定問題

ROC曲線の枠組みを多クラス分類に拡張するには、特定の適応戦略を採用する必要があります。主に用いられるのは、One-vs-Rest (OvR)（またはOne-vs-All (OvA)）戦略と、One-vs-One (OvO)戦略の2つです。OvR戦略では、各クラスを正例として扱い、それ以外のすべてのクラスを負例として扱うことで、多クラス問題を複数の二値分類問題に変換します。その結果、n個のクラスに対してn本のROC曲線が得られます。一方、OvO戦略では、すべてのクラスのペアに対して二値分類問題を構築します。そのため、n(n−1)/2本のROC曲線が生成されます。 

これらの二値分類から得られた性能指標を統合するには、平均化手法が使用されます。マイクロ平均(micro-averaging)では、すべてのクラスにわたる個々のサンプルを考慮して、全体のTPRとFPRを計算します。これにより、各サンプルに等しい重みが与えられます。これに対して、マクロ平均(macro-averaging)は、各クラスごとにTPRとFPRを個別に算出し、それらを平均します。この方法では各クラスに等しい重みが与えられ、特にクラスごとの性能評価が重要な場合に有用です。したがって、多クラスROC曲線の解釈は、採用された分解戦略（OvRまたはOvO）と平均化手法（マイクロまたはマクロ）に大きく依存します。これらの選択が、最終的な性能評価に与える影響は非常に大きいため、目的に応じて慎重に選ぶ必要があります。


MQL5におけるROC曲線およびAUCの組み込み関数

MQL5では、ROC（受信者動作特性）曲線およびAUC（曲線下面積）の計算が、専用の機能を通じて可能となっています。

ROC曲線の可視化に必要な値を生成するには、ReceiverOperatingCharacteristicベクトルメソッドが使用されます。このメソッドは、真のクラスラベルを表すベクトルに対して呼び出されます。第1引数には、クラス数に対応する列を持つ確率または判定値の行列を指定します。第2引数には、平均化手法を指定するENUM_AVERAGE_MODE列挙型の変数を渡します。対応しているのは、AVERAGE_NONE、AVERAGE_BINARY、AVERAGE_MICROのみです。正常に実行されると、偽陽性率(FPR)、真陽性率(TPR)、および対応する閾値が、後続の3つの引数として渡された行列に書き込まれます。メソッドは、成功可否を示すブール値を返します。

AUCの計算には、ClassificationScoreベクトルメソッドが使用されます。こちらも、真のクラスラベルのベクトルに対して呼び出され、予測確率または判定値の行列を第1引数に取ります。第2引数には、ENUM_CLASSIFICATION_METRIC列挙型のCLASSIFICATION_ROC_AUCを指定することで、AUC計算を実行します。ROCメソッドと異なり、この関数はENUM_AVERAGE_MODEのすべての値に対応しています。メソッドは、計算されたAUC値のベクトルを返します。ベクトルの要素数は、選択された平均化モードおよびデータセット内のクラス数に依存します。

さまざまな平均化モードがモデル評価に与える影響を明示するため、ROC_Demo.mq5スクリプトが開発されました。このスクリプトでは、アヤメの花データセットとロジスティック回帰モデルを用いて、ユーザーが設定可能な二値分類問題または多クラス分類問題に対応しています。完全なスクリプトコードを以下に示します。

//+------------------------------------------------------------------+
//|                                                     ROC_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<logistic.mqh>
#include<ErrorDescription.mqh>
#include<Generic/SortedSet.mqh>
//---
enum CLASSIFICATION_TYPE
  {
   BINARY_CLASS = 0,//binary classification problem
   MULITI_CLASS//multiclass classification problem
  };
//--- input parameters
input double   Train_Test_Split = 0.5;
input int      Random_Seed = 125;
input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS;
input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj());
//---
   matrix data = np::readcsv("iris.csv");
   data = np::sliceMatrixCols(data,1);
//---
   if(classification_problem == BINARY_CLASS)
      data = np::sliceMatrixRows(data,0,100);
//---
   ulong rindices[],trainset[],testset[];
   np::arange(rindices,int(data.Rows()));
//---
//---
   if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset))
     {
      Print(__LINE__, "  error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   CSortedSet<ulong> test_set(rindices);
//---
   test_set.ExceptWith(trainset);
//---
   test_set.CopyTo(testset);
//---
   matrix testdata = np::selectMatrixRows(data,testset);
   matrix test_predictors = np::sliceMatrixCols(testdata,0,4);
   vector test_targets = testdata.Col(4);
   matrix traindata = np::selectMatrixRows(data,trainset);
   matrix train_preditors = np::sliceMatrixCols(traindata,0,4);
   vector train_targets = traindata.Col(4);
//---
   logistic::Clogit logit;
//--
   if(!logit.fit(train_preditors,train_targets))
     {
      Print(" error training logistic model ");
      return;
     }
//---
   matrix y_probas = logit.probas(test_predictors);
   vector y_preds = logit.predict(test_predictors);
//---
   vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode);
//---
   if(auc.Size()>0)
      Print(" AUC ", auc);
   else
      Print(" AUC error ", ErrorDescription(GetLastError()));
//---
   matrix fpr,tpr,threshs;
   if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs))
     {
      Print(" ROC error ", ErrorDescription(GetLastError()));
      return;
     }
//---
   string legend;
   for(ulong i = 0; i<auc.Size(); i++)
     {
      string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]);
      StringAdd(legend,temp);
     }

   CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500);
   if(CheckPointer(roc)!=POINTER_INVALID)
     {
      Sleep(7000);
      roc.Destroy();
      delete roc;
      ChartRedraw();
     }
  }
//+------------------------------------------------------------------+

最初に、二値分類問題を対象として検討し、平均化モードにはAVERAGE_BINARYが設定されます。このモードでは、ROC曲線およびAUCの計算において、ターゲットクラスが1にラベリングされているという前提のもとで、ROC曲線生成における基本的な「ターゲット/非ターゲット」パラダイムに従います。この設定でスクリプトを実行した結果として出力される内容を見ると、AUCの値は1つの要素を持つベクトルとして返されることが確認できます。さらに、FPR・TPR・閾値の各行列も、それぞれ1行のみを含んでいることが分かります。

ROCデモスクリプト出力二値分類

MK      0       12:45:28.930    ROC_Demo (Crash 1000 Index,M5)   AUC [1]

ラベル1以外のターゲットクラスについてROC曲線および対応するAUCを調べるには、平均化モードをAVERAGE_NONEに設定する必要があります。このモードでは、ReceiverOperatingCharacteristicとClassificationScoreの両関数が各クラスを独立してターゲットとして評価し、それぞれに対応する結果を返します。AVERAGE_NONEを設定して二値分類問題のスクリプトを実行すると、以下のような出力が得られます。この場合、ROC曲線には2本の曲線が表示され、これはFPR行列およびTPR行列の各行に対応するプロットです。また、2つのAUC値も計算されます。

ROCデモ二値分類-平均化なし

CK      0       16:42:43.249    ROC_Demo (Crash 1000 Index,M5)   AUC [1,1]

結果はクラスラベルの順序に対応して提示されます。たとえば、前述のスクリプトで示された二値分類問題（ラベルが0と1の場合）では、TPR、FPR、および閾値行列の第1行がラベル0をターゲットクラスとした場合のROC曲線の値を表し、第2行はラベル1をターゲットとした場合に対応します。この順序付けはAUCの値にも同様に適用されます。この結果形式は、多クラスデータセットから計算されたROC統計においても一貫しています。二値分類の場合、AVERAGE_NONEおよびAVERAGE_BINARY以外の平均化オプションを使用すると、多クラスデータセットの処理に対応した計算手法が呼び出されます。一方、多クラス分類においては、AVERAGE_BINARYを使用するとエラーが発生します。しかし、AVERAGE_MICRO、AVERAGE_MACRO、AVERAGE_WEIGHTEDの各モードでは、単一の集約されたAUC値が得られます。

ROCデモ多クラス-平均化なし

LL      0       17:27:13.673    ROC_Demo (Crash 1000 Index,M5)   AUC [1,0.9965694682675815,0.9969135802469137]

AVERAGE_MICRO 平均化モードは、One-Hotエンコードされた真のクラス行列の各要素を個別のラベルとして扱うことで、ROC曲線およびAUCをグローバルに計算します。この手法では、まず真のクラスラベルをワンホットエンコードすることで多クラス問題を二値分類問題に変換し、クラス数に対応する列を持つ行列を生成します。この行列と、予測された判定値または確率の行列を、それぞれ単一の列構造に平坦化します。その後、これらの平坦化されたデータを用いてROC曲線およびAUCの計算がおこなわれます。この方法により、すべてのクラスを網羅する包括的な性能指標が得られ、各サンプルに等しい重みが割り当てられます。特にクラス間の不均衡が大きい場合に有効で、多数派クラスへのバイアスを軽減する効果があります。デモスクリプトによる実証結果も、この挙動を示しています。

ROCデモ多クラス-マイクロ平均化

RG      0       17:26:51.955    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9984000000000001]

AVERAGE_MACRO平均化モードは、クラスの不均衡に対応するために異なるアプローチを採用しています。各クラスを独立して評価し、それぞれのクラス確率に基づいてAUCを計算します。最終的なAUCは、これら個別のAUC値の算術平均として求められます。なお、MQL5のドキュメントによると、ReceiverOperatingCharacteristicメソッドはAVERAGE_MACROをサポートしていません。一方で、ClassificationScoreメソッドは多クラスデータセットのAUC計算においてOvR (One-vs-Rest)手法を実装しています。スクリプトをAVERAGE_MACROで実行した結果、AUCの計算は正常におこなわれる一方、ROC曲線の生成は予想通り失敗することが確認されています。

ER      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   AUC [0.997827682838166]
NF      0       17:26:09.341    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function

AVERAGE_WEIGHTED平均化モードは、基本的にはAVERAGE_MACROと同様の動作をしますが、最終的な集約方法が異なります。単純な算術平均ではなく、真のクラスラベルの分布に基づいて重み付けされた加重平均を計算します。この方法により、データセット内で優勢なクラスを考慮した最終的なAUC値が得られます。AVERAGE_MACROと同様に、ReceiverOperatingCharacteristicメソッドはAVERAGE_WEIGHTEDをサポートしていません。スクリプトの実行結果も、この挙動を示しています。

IN      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   AUC [0.9978825995807129]
HO      0       17:26:28.465    ROC_Demo (Crash 1000 Index,M5)   ROC error Wrong parameter when calling the system function


結論

ROC曲線は、分類器の可視化および評価において非常に有効なツールです。精度や誤分類率、誤分類コストなどの単一の指標と比較して、分類性能をより包括的に評価することが可能です。ROC曲線は、分類器の性能をクラスの偏りや誤分類コストから切り離して評価できるため、適合率や再現率の曲線など他の評価手法に比べて優れた利点を提供します。しかしながら、どの評価指標にも言えることですが、ROC曲線を適切に活用するためには、その本質的な特性や制約を十分に理解することが必要です。本記事がROC曲線に関する一般的な知識の向上に寄与し、コミュニティにおける評価手法の改善と普及に繋がることを期待しています。


ファイル名 
ファイルの説明
MQL5/Scripts/ROC_Demo.mq5 ROC曲線に関連する組み込みMQL5関数を示すスクリプト
MQL5/Scripts/ROC_curves_table_demo.mq5 さまざまなROCベースの性能指標の生成を示すスクリプト
MQL5/Include/logisitc.mqh
ロジスティック回帰を実装するClogitクラスの定義を含むヘッダーファイル
MQL5/Include/roc_curves.mqh
二値分類の性能評価のためのさまざまなユーティリティを実装するカスタム関数のヘッダー
MQL5/Include/np.mqh
様々なベクトルおよび行列ユーティリティ関数のヘッダファイル
MQL5/Files/iris.csv アヤメの花データセットのCSVファイル

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/17390

添付されたファイル |
ZIPをダウンロード
iris.csv (3.29 KB)
np.mqh (90.9 KB)
logistic.mqh (16.16 KB)
roc_curves.mqh (8.92 KB)
ROC_curves_table_demo.mq5 (2.81 KB)
ROC_Demo.mq5 (3.56 KB)
Mql5.zip (22.86 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
最適化におけるカスタム基準への新しいアプローチ（第1回）:活性化関数の例 最適化におけるカスタム基準への新しいアプローチ（第1回）:活性化関数の例
これは、カスタム基準に関する数学的考察をおこなう連載記事の第1回目です。特に、ニューラルネットワークで使用される非線形関数、実装用のMQL5コード、さらにターゲットオフセットや補正オフセットの活用に焦点を当てています。
MQL5で取引管理者パネルを作成する（第9回）：コード編成(III)コミュニケーションモジュール MQL5で取引管理者パネルを作成する（第9回）：コード編成(III)コミュニケーションモジュール
MQL5インターフェイス設計における最新の進展を、再設計されたコミュニケーションパネルの公開とともに詳しく解説します。また、モジュール化の原則に基づいて新しい管理パネルを構築するシリーズも引き続き展開していきます。この記事では、CommunicationsDialogクラスを段階的に開発し、それをDialogクラスから継承する方法を丁寧に解説します。さらに、開発には配列およびListViewクラスを活用します。MQL5開発スキルを高めるための実用的な知見を得るために、ぜひ記事を読み、コメント欄でディスカッションにご参加ください。
初心者からエキスパートへ：サポートとレジスタンスの強度指標(SRSI) 初心者からエキスパートへ：サポートとレジスタンスの強度指標(SRSI)
本記事では、MQL5プログラミングを活用して市場の価格レベルを正確に特定し、弱いレベルと強いレベルを見分ける方法についての知見を共有します。さらに、実用的なサポートおよびレジスタンス強度インジケーター(SRSI)を完全に開発していきます。
データサイエンスとML（第34回）：時系列分解、株式市場を核心にまで分解 データサイエンスとML（第34回）：時系列分解、株式市場を核心にまで分解
ノイズが多く、予測が難しいデータで溢れる世界では、意味のあるパターンを特定するのは困難です。この記事では、データをトレンド、季節パターン、ノイズといった主要な要素に分解する強力な分析手法「季節分解」について解説します。こうしてデータを分解することで、隠れた洞察を見つけ、より明確で解釈しやすい情報を得ることが可能になります。