MQL5における予測および分類評価のためのリサンプリング手法

はじめに

機械学習モデルの性能評価は通常、1つのデータセットで訓練（学習）をおこない、別のデータセットで検証をおこなうという2つの異なる段階を経て実施されます。しかし、リソースの制約や実務上の制限により、複数のデータセットを用意することが難しい場合には、代替的な手法を採用する必要があります。

そのような手法の1つが、リサンプリング技術を用いた予測または分類モデルの評価です。このアプローチは、いくつかの潜在的な欠点があるものの、信頼性のある結果を提供することが示されています。本記事では、1つのデータセットを訓練（学習）と検証の両方に活用する、新しいモデル品質評価の手法について検討します。こうした手法を用いる主な理由は、検証用データの入手が限られている点にあります。

そのため、実務においては、より高度なリサンプリングアルゴリズムを用いて、一般的な評価手法と同等の性能指標を得る必要があります。これらの手法は計算資源を多く消費し、モデル開発プロセスに複雑さを加える可能性があります。しかし、このようなトレードオフがある一方で、特定の状況下では、その利点がコストを上回ることから、リサンプリングに基づく評価戦略は非常に有用となり得ます。

誤差の分解

本稿で提示するアルゴリズム概念を明確に説明するため、ここでは記法体系を導入します。この記法の枠組みは主に、モデル誤差をその構成要素に分解することを目的としています。まず、未知の分布Fに従う母集団から得られたデータセットTを考えます。このデータセットはn個の観測値から構成されており、各観測には予測変数x（スカラーまたはベクトル）と、目的変数y（スカラー）が含まれます。予測変数と目的変数の間の本質的な関係性を強調するため、トレーニングデータを表す複合的な表現として、ペアt=(x, y)を用います。したがって、データセットにおける第iの観測値はt_i = (x_i, y_i)として表されます。この記法は数値予測を前提としていますが、分類問題にも対応可能であり、その場合はy_iを第iの観測におけるクラス所属と解釈します。

完全なデータセットをTと表記し、これをトレーニングセットとして用いて学習させたモデルをM_Tと記します。学習済みモデルM_Tに予測変数xの値を入力することで、対応する目的変数の予測値M_T(x)が得られます。簡略化のため、汎用的な予測出力を単にMと表記することもあります。予測モデルの有効性を評価する際には、モデルの予測値Mと実際の観測値yとの間の差異を定量化する必要があります。この差異は誤差の尺度として厳密に定義されており、Ef[y,M]と表されます。回帰問題において一般的に用いられる誤差指標は平均二乗誤差(MSE)であり、次の式のような二乗差が使われます。一方、分類問題においては、Ef[y, M]を二変数関数として定義し、yがMに等しい場合は0を、そうでない場合は1を割り当てます。

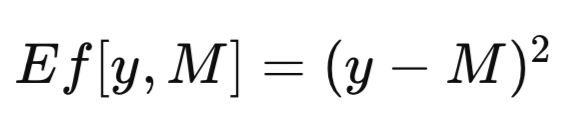
学習済みモデルを、その学習に使用したのと同じデータセットに適用した場合、すべての学習データに対する平均誤差は「見かけの誤差」(apparent error)と呼ばれます。従来の手法では、この見かけの誤差を最小化するようにモデルを学習させますが、本稿で紹介する方法論ではそのような制約は課しません。任意の評価指標を最適化した後で、異なる基準を用いて学習済みモデルの品質を評価することが許容されます。以下で定義する見かけの誤差は、あくまで学習データ上のモデルの予測結果に対してEf[]関数を適用した値の平均であり、学習手法自体には依存しません。

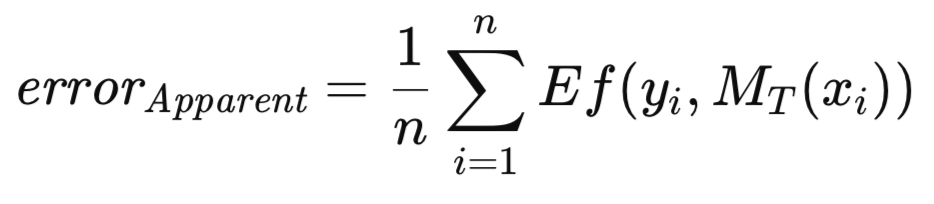
見かけの誤差は、モデルの評価に学習時に用いた同一データを使うため、楽観的なバイアス（トレーニングバイアスとも呼ばれる）が生じることは周知の事実です。このバイアスを軽減するために、十分なデータがある場合は、学習済みモデルを独立した別のデータセットで評価します。これにより、トレーニングセットで学習させたモデルが母集団全体に適用された場合の期待誤差を推定することが可能となります。トレーニングセットで学習させたモデルに条件付けられた期待誤差が、「予測誤差」と呼ばれます。ここでの重点は、特定の学習済みモデルの将来の予想される性能の評価にあります。予測誤差は、以下の式で厳密に表されます。

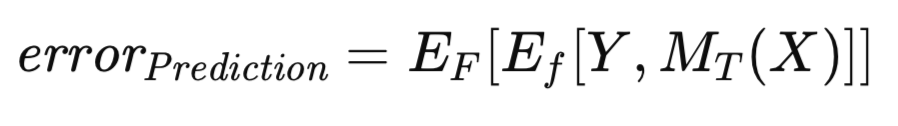
これまで定義してきた予測誤差とは異なるが、関連性のある概念として、考慮すべき誤差指標が存在します。予測誤差は、特定のトレーニングセットで学習された、特定の実現済みモデルに条件付けられた期待誤差です。しかし、この期待値の範囲を、考えうるすべてのトレーニングセットにまで拡張することも可能です。具体的には、トレーニングセットが未知の分布から抽出されたn個の観測値で構成されていると仮定したとき、そのトレーニングセットを用いて学習させたモデルに関する予測誤差を、独立した検証データで近似的に評価することができます。ここで、新たなトレーニングセットが再び抽出され、同じトレーニング手順が繰り返された場合を考えると、当然ながら、やや異なる予測誤差が得られることになります。したがって、あらゆる可能なトレーニングセットにわたる予測誤差の期待値を捉える指標が必要になります。この指標は「母集団誤差」(population error)と呼ばれ、以下の式で厳密に表されます。

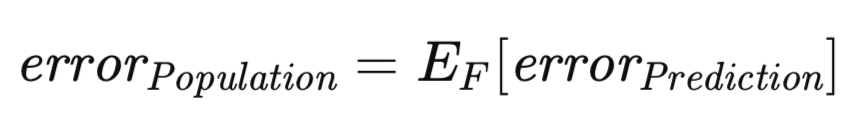
任意のトレーニングセットに対して、見かけの誤差は高い確率で予測誤差を過小評価するという原則は、よく知られた事実です。この乖離は、モデルがトレーニングデータの特性に過剰適合し、結果として母集団全体への汎化性能が損なわれることに起因します。予測誤差と見かけの誤差の差の大きさは、「過剰誤差」(excess error)と定義されます。

この文脈において特に重要なのが、「期待過剰誤差」です。予測誤差と見かけの誤差の双方が、特定のトレーニングセットに依存して定義されるものであることを踏まえると、母集団誤差の導出と同様に、考えうるすべてのトレーニングセットにわたる過剰誤差の期待値を考慮する必要があります。これは以下の式で厳密に表されます。

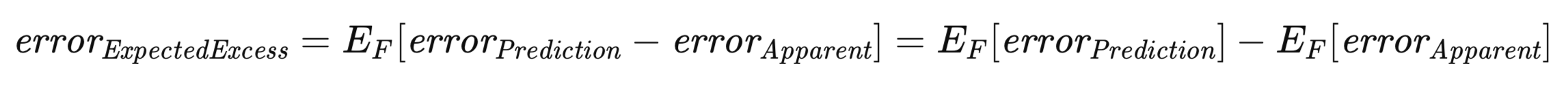
上記の式は、「期待過剰誤差」という概念を捉えるうえでの二重性を強調しています。すなわち、各トレーニングセットにおける予測誤差と見かけの誤差の差について、すべての可能なトレーニングセットにわたってその期待値を取るものとして解釈することができます。この解釈は、概念の直感的な理解と一致しています。あるいは、期待過剰誤差は「母集団誤差」と「期待見かけ誤差」との差としても表すことが可能です。

交差検証：方法論と限界

交差検証は、研究コミュニティにおいて広く確立された手法です。本稿で扱うアルゴリズムの中でも、交差検証は概念的にシンプルで実装も容易であり、計算効率も比較的高いという特徴を持っています。さらに、将来のモデル性能の期待値に対して、ほぼバイアスのない推定を提供できるという利点もあります。

また、この手法は非常に広範なモデル学習アルゴリズムに適用可能であり、これは他の手法には見られない汎用性です。ただし、交差検証には重大な制約もあります。それは、ばらつき（分散）が大きくなる傾向があるという点であり、場合によっては実用上容認できないレベルになることもあります。これは、元のデータセットからランダムにサンプリングを行う際に生じる確率的な変動に対して、非常に敏感であることを意味します。

具体的には、ある実験者がデータを収集し、モデルを学習させた後、交差検証によって将来の性能を評価したとしても、別の独立したデータサンプルで同じ手順を繰り返すと、結果が大きく異なる可能性があります。推定値がほぼバイアスのない点は望ましい特性ではありますが、その分散の大きさがその利点を打ち消す場合も少なくありません。そして重要なことに、この分散の影響は過小評価されがちです。

同様の目的に対して、より優れた手法が存在することは事実ですが、交差検証はそのシンプルさや、他の手法が適用できない状況でも利用可能であることから、依然として広く使用されています。したがって、その使用頻度と重要性を踏まえ、交差検証手法の詳細な解説が求められます。

交差検証の基本的な考え方は非常に単純です。まず、データセットを2つの異なる部分に分割します。一方をモデルのパラメータ推定のためのトレーニングセットとして用い、もう一方を検証セットとしてモデルの性能を独立に評価します。この手順は、十分なデータ量がある場合に通常おこなわれる、汎化性能評価の方法と一致します。

しかし、交差検証では性能評価のために大量のデータを検証セットに割り当てるのではなく、逆にごく少数の観測値を検証セットにし、残りをトレーニングに用いるというアプローチを取ります。具体的には、1つの観測値を検証セットとして使用するのが一般的です。

その後、その検証データに対して性能を評価します。そして次に、元のデータセットにその検証セットを戻し、別の観測値を検証セットとして選び直します。この手順を、すべての観測値が一度ずつ検証セットとして使われるまで繰り返します。最終的に、すべての反復における検証誤差の平均値をとることで、交差検証誤差推定値が得られます。

最も一般的な交差検証の形式は、1つの観測値を順番に除外する方式です。これを複数の観測値を除外する方式に拡張するのは比較的容易です。ここで、M_Tを完全なデータセットTに対して学習させたモデルとし、M_T(i)を、データセットTからi番目の観測値を除外して学習させたモデルと定義します。このとき、モデルの将来の期待誤差に対す交差検証推定値は、次のように厳密に表されます。

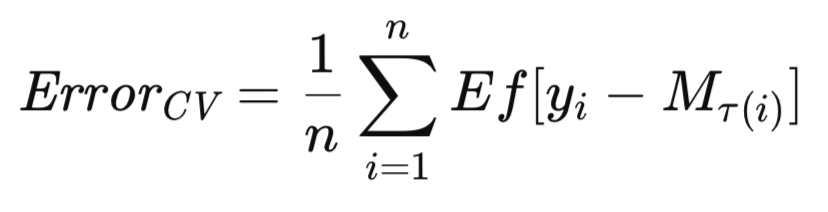
このセクションでは、交差検証アルゴリズムの実装と、その説明を提示します。記事の後半では、他の手法との比較評価も掲載しています。期待誤差を推定するために使用されるすべてのアルゴリズムは、ヘッダファイル「error_variance_estimation.mqh」にまとめられています。交差検証のアルゴリズムは、cross_validationメソッドとして実装されています。このルーチンおよび他の誤差推定アルゴリズムを実装する関数は、構造やパラメータの使い方が共通しています。各関数のパラメータは以下のとおりです。

• 最初の2つの引数は、トレーニングデータセットの行列です。1つ目の行列には予測変数、2つ目には対応する目標変数が格納されます。
  
• 3つ目の引数には、IModelインターフェイスを実装したモデルのインスタンスを渡します。これは評価対象となる予測モデルを表します。
• 最後の引数には、計算によって得られた誤差指標の最終結果が格納されます。なお、処理中にエラーが発生した場合、このメソッドはブール値falseを返します。

//+------------------------------------------------------------------+
//| estimate error variance using cross validation testing           |
//+------------------------------------------------------------------+
bool CErrorVar::cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   vector test;
   double test_target;
   matrix preds,targs;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      test = predictors.Row(i);
      test_target = targets[i][0];
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
      
      preds = np::sliceMatrixRows(predictors,0,long(predictors.Rows()-1));
      targs = np::sliceMatrixRows(targets,0,long(targets.Rows()-1));

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ");
         return false;
        }

      out_err += error_fun(test_target,model.forecast(test));
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
     }

   out_err/=double(predictors.Rows());

   return true;
  }

cross_validation関数を呼び出すと、トレーニングデータセットを走査するループ処理が開始されます。このループでは、常にデータセットの最後の位置が検証用のサンプルとして使用されます。他のサンプルは、予測変数および目標変数の行列内でこの位置に1つずつ順番に入れ替えられます。トレーニングデータセットの最後の位置は常にテストスポットとして使用されます。そのエラーは累積され、最終的にはループ全体を実行した結果として返されます。

母集団誤差のブートストラップ推定

このセクションでは、母集団誤差を推定するための基本的なブートストラップアルゴリズムを説明します。このアルゴリズムは実用上あまり推奨されていないことに注意が必要です。というのも、後のセクションで説明するE0アルゴリズムやE632アルゴリズムの方が通常は性能が優れているからです。それでもなお、ここで紹介する直接的なブートストラップ法は、より高度なアルゴリズムの基礎原理となっており、それらを正しく理解するためには本手法の動作原理をしっかり把握しておくことが不可欠です。

本節では、母集団Fが存在し、そのFからトレーニングデータセットの観測値がランダムに抽出されると仮定します。モデルはこのトレーニングデータT上で学習し、評価され、「見かけの誤差」が得られます。しかしこの誤差は本質的に楽観的なものであり、実際の母集団誤差はこれよりも大きいと考えられます。見かけの誤差に対して母集団誤差がどれだけ上回るか、その差分が「超過誤差」です。ただし、独立した検証セットが存在しない場合には、我々が最も知りたい超過誤差や母集団誤差は直接観測することができず、楽観的な見かけの誤差しか手元にありません。このような状況でも、ブートストラップ法を用いれば超過誤差を推定することが可能です。そして、この推定された超過誤差を見かけの誤差に加えることで、母集団誤差のおおよその推定値を得ることができます。

超過誤差のブートストラップ推定は、パラメータのバイアス推定と似た手順でおこなわれます。まず、未知の母集団分布の代わりに経験分布関数を用い、そこから多数のブートストラップサンプルを生成します。各ブートストラップサンプルを用いてモデルを学習させます。モデルのそのブートストラップサンプルに対する誤差は、そのサンプルにおける見かけの誤差を表します。モデルの全データセットに対する誤差は予測誤差を表し、経験分布は実質的に母集団として機能します。この2つの誤差の差分が、そのブートストラップサンプルにおける超過誤差になります。多数のブートストラップ反復にわたるこの超過誤差の平均が、期待超過誤差の推定値となります。

前述のアルゴリズムの厳密さを高めるために、一連の定義と数式を導入します。Bは、元のデータセットからブートストラップサンプリングによって生成されたトレーニングセットを表します。具体的には、BはTからn個の観測値を復元抽出でランダムに選択することで構成されます。モデルはこのBを用いて学習します。モデルの予測誤差は、ブートストラップサンプルが抽出された母集団、すなわちこの文脈では元のデータセットに含まれるすべての観測値に対する誤差を平均することで求められます。これは以下の式で厳密に表されます。

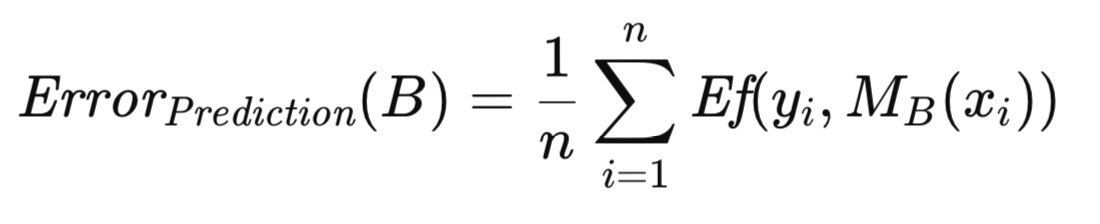
k_iは、Tに含まれる第i番目の観測値がBに出現する回数を表すものとします。Bに関連付けられる見かけの誤差は、Bを構成する観測値に対するモデルの誤差を平均することによって計算されます。これは、以下の式で示されます。

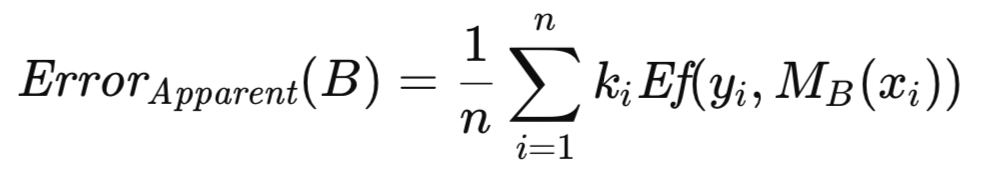
Bに関連付けられる超過誤差は、その予測誤差と見かけの誤差の差として定義されます。ただし、これらを個別に計算してから差を取ると、誤差項に重複があるため、計算が冗長になります。そこで、共通項を因数としてまとめることで、より効率的な形式を得ることができます。この結果得られる式は、数百から数千回に及ぶ多数のブートストラップ反復に対して評価する必要があります。これらの反復における超過誤差の平均は、期待超過誤差の推定値となり、これを元の全サンプルにおける見かけの誤差に加えることで、母集団誤差のおおよその推定値が得られます。

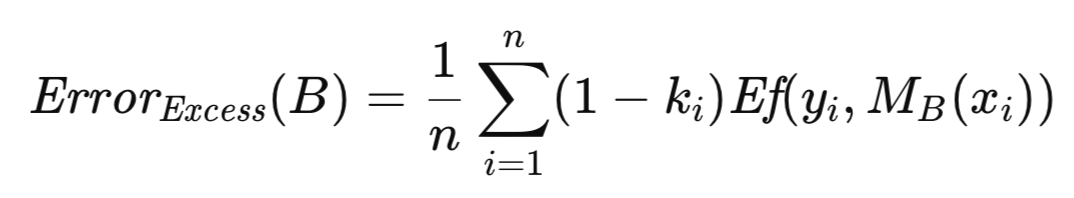
誤差推定のためのブートストラップ手法は、boot_strapというメソッドとして実装されています。交差検証の実装で使用されるパラメータに加えて、このメソッドにはブートストラップ反復回数を指定する追加のパラメータが含まれます。このルーチンは、AlglibライブラリのMQL5実装によって提供される乱数生成器のインスタンスを初期化することから始まります。この乱数生成器を使用して、トレーニングデータセットからランダムに行のインデックスを選び、それをブートストラップサンプルとして、行列変数predsおよびtargsに格納します。このブートストラップサンプル集合を用いてモデルを学習させ、その後検証することで、超過誤差を蓄積していきます。

//+------------------------------------------------------------------+
//| estimate error variance using ordinary bootstrap                 |
//+------------------------------------------------------------------+
bool CErrorVar::boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double err,apparent,excess;
   excess = 0.0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         predicted[i] = model.forecast(predictors.Row(i));
         err = error_fun(targets[i][0],predicted[i]);
         excess+=(1.0 - double(count[i]))*err;
        }
     }

   excess/=double(nsize*nboot);

ブートストラップ処理が完了したら、元のトレーニングデータセットを使用して見かけの誤差を計算します。最終的な誤差の推定値は、超過誤差と見かけの誤差を合算した値となります。

if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }
   apparent = 0.0;
   for(ulong i=0; i<nsize; i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      err = error_fun(targets[i][0],predicted[i]);
      apparent+=err;
     }
   apparent/=double(nsize);
   out_err = apparent+excess;
   return true;
  }

EfronによるE0推定量による母集団誤差の推定

ブートストラップサンプル内でトレーニングデータが重複することにより生じる顕著な課題の一つは、特定のモデルクラスが正常に機能しなくなる可能性がある点です。特に、確率的モデルや一般化回帰型のニューラルネットワークはこの問題の影響を受けやすいです。平滑化定数が十分に大きくない場合、テストケースが訓練ケースと完全に一致すると、ほぼ完全な予測が得られ、楽観的なバイアスがさらに悪化します。この問題を軽減するために、Bradley Efronは重複によるアーティファクトを防ぐという単純な解決策を提案しました。これは、通常の再サンプリング手順によってブートストラップトレーニングセットを生成する一方で、各ブートストラップ反復においては、そのトレーニングセットに含まれていない元の観測値に対してのみモデルを評価する、という方法です。そして、これらの除外された観測値における誤差の平均値を、母集団誤差の推定量として用います。この手法はE0推定量と呼ばれます。

学術文献では、E0を計算するための2つの異なる手法が提示されています。元々の方法では、評価対象となったすべての誤差を合計し、それを評価したケースの総数で割って算出します。本実装ではこの方法を採用しています。その後の理論的研究では、E0の性質に関する考察から、平均化処理を2段階に分解する代替アルゴリズムが提案されています。まず、各元の観測値に対して、その観測値を含まないすべてのブートストラップ反復での誤差を合計し、それをそのような反復の回数で割ることで、その観測値に対する平均誤差を求めます。次に、すべての観測値におけるこの平均誤差を合計し、観測値の総数で割ることで、全体の平均を算出します。この後者の手法は計算量が増えるものの、理論的（漸近的）には前者と等価であり、実証的な評価においても性能差はほとんど見られないとされています。そのため、本手法では簡便さを重視して、元々の方法を採用しています。

アルゴリズムの説明をより明確にするために、追加の記法を導入します。これまでと同様に、Tは元のデータセットを表し、Bはブートストラップサンプルを表します。Cを、Tに含まれるがBには含まれない観測値の集合とします。count(C)はCの要素数（観測値の数）を表します。すると、Efronの元々のE0による母集団誤差の推定値は、以下の式で厳密に表されます。

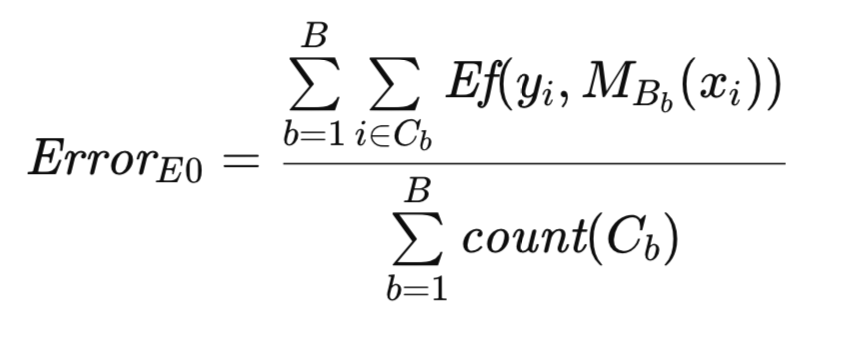
E0推定量のアルゴリズム実装は、前述のブートストラップ処理と類似しています。モデルの学習に用いるブートストラップサンプルの生成および利用は両者で共通しています。ただし、本手法においては、カウント配列は前述の処理での頻度カウンタとしてではなく、観測値の有無を示す二値指標として機能します。アルゴリズムはefrons_0メソッドとして実装されています。 

//+------------------------------------------------------------------+
//| estimate error variance using efron's E0 bootstrap               |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   ulong tot = 0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         continue;//return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         if(count[i])
            continue;
         predicted[i] = model.forecast(predictors.Row(i));
         out_err+= error_fun(targets[i][0],predicted[i]);
         ++tot;
        }
     }

   if(tot)
      out_err/=double(tot);
   else
     {
      Print(__FUNCTION__, " zero denominator ");
      return false;
     }
   return true;
  }

EfronのE632推定量による母集団誤差の推定

前述のE0推定量は望ましい性質を備えており、実務的な応用において一般的に推奨されます。トレーニングセットに含まれる観測値の評価を避けることで、多様なモデルクラスに対して適用可能であることが保証されます。さらに、その分散は比較的抑えられており、現時点の方法論の発展段階を反映しています。

しかしながら、E0推定量にはやや保守的なバイアスがあり、実際の母集団誤差を過大評価しがちです。ただし、このバイアスが過度でない限り、過大評価は一般的に過小評価よりも問題視されにくいことに留意が必要です。通常のブートストラップで観察される過小評価は、不適切な楽観主義を助長する傾向があるため、より有害とされています。E0法を利用することで、実際の母集団誤差が計算値よりも低い可能性が高いという安心感を得られます。この内在する保守性は概ね有利ですが、過度の悲観的評価によりモデルを誤って棄却してしまう可能性もあります。E632推定量は、E0に内在するこの保守的バイアスを緩和することを目的として設計されています。

トレーニングセットを用いた評価（見かけの誤差）を母集団誤差の推定に用いることの本質的な限界を考えてみましょう。この評価手法は、本質的にバイアスを含んでいます。なぜなら、評価対象が学習に使用された観測値のみに限定されており、この部分集合は母集団全体を代表していないためです。トレーニングセットに過度に類似しているため、楽観的なバイアスが生じます。

これに対し、E0推定量は逆のバイアスを示します。学習に使用された観測値を意図的に評価から除外することで、テストセットが母集団を代表せず、トレーニングセットと過度に異なるものとなります。現実の状況では、学習データの観測値と同一またはほぼ同一の観測値が必ず存在します。E0がこれらを除外することにより、悲観的なバイアスが生じるのです。

E632アルゴリズムは、これら二つの極端な値の間で妥協点を見出すことを目指しています。より公平な方法としては、実際の発生頻度を反映した確率でトレーニングセット内外の両方からサンプリングし、モデルを評価する方法が考えられます。または、サンプリングの不均衡を補正する調整を加えることも可能です。サンプルサイズが大きくなるにつれて、任意の観測値がブートストラップサンプルに含まれる確率は、1 − 1/e ≈ 0.632に収束します。Efronの経験則では、母集団誤差をE0と見かけの誤差の加重和として推定し、その重みはこれらのサンプリング確率によって決定されます。彼の推定量であるE632は、以下の式で厳密に表されます。

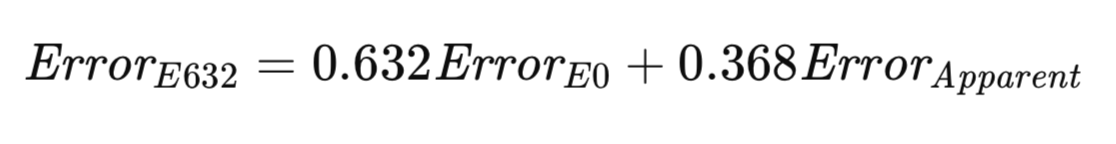
E632アルゴリズムの実装は、次に示すefrons_632メソッドとして提供されます。

//+------------------------------------------------------------------+
//| estimate error variance using efron's E632 bootstrap             |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double apparent;

   if(!efrons_0(nboot,predictors,targets,model,out_err))
      return false;


   if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }

   apparent = 0.0;
   
   vector predicted(predictors.Rows());

   for(ulong i=0; i<predictors.Rows(); i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      apparent+= error_fun(targets[i][0],predicted[i]);
     }

   apparent/=double(predictors.Rows());

   out_err = 0.632*out_err + 0.368*apparent;

   return true;
  }

これまで本稿で説明してきたすべてのアルゴリズムは、CErrorVarクラスのメンバーとして実装されています。このクラスでは、予測値（メソッドの第2引数として渡される）と対応する目標値（メソッドの第1引数として渡される）との誤差を計算するためのerror_funメソッドも定義されています。

//+------------------------------------------------------------------+
//|  class for estimating error variance                             |
//+------------------------------------------------------------------+
class CErrorVar
  {
public:
                     CErrorVar(void);
                    ~CErrorVar(void);

   virtual double    error_fun(const double truevalue,const double predictedvalue);
   virtual bool      cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CErrorVar::CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CErrorVar::~CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| calculate the error                                              |
//+------------------------------------------------------------------+
double CErrorVar::error_fun(const double truevalue,const double predictedvalue)
  {
   return pow(truevalue-predictedvalue,2.0);
  }

次のセクションでは、学習済みモデルの誤差をトレーニングデータセットのみを用いて推定するこれらのアルゴリズムの実演を紹介します。

予測誤差推定値の比較分析

本稿では、予測モデルの母集団誤差を推定するための一連の手法を紹介しました。以下の重要なポイントに留意してください。

• 交差検証：この手法は実装の容易さと計算効率の良さが特徴です。多様なモデルクラスに広く適用でき、ほぼバイアスのない推定を提供します。ただし、不安定な学習手順を伴う場合には分散が大きくなる傾向があり、そのため代替手法が利用できない場合を除いて、主な手法としての推奨は一般的にされません。効果的ではあるものの、最適とは考えられていません。
• 単純ブートストラップ：この方法は一般的に最も望ましくない選択肢とされています。重複した学習データの観測値を扱えないモデルや、トレーニングセット内にテスト観測値が含まれることで性能が損なわれるモデルとは相性が悪いです。さらに、実際の母集団誤差を過小評価する傾向が顕著であり、これといった利点はほとんどありません。
• E0推定値：学習過程で重複観測値を許容するモデルの場合、一般的にE0推定量が推奨されます。学習データの観測値を評価から除外するため、多くのモデルに適用可能で、不安定な学習条件下でも頑健です（たとえば確率的な学習手順を持つモデルなど）。実証的には、安定した学習環境では交差検証と同程度の分散を示し、不安定環境では大幅に分散が低減します。さらに、E632推定量に必要な見かけの誤差をE0推定量と同時に計算できるため、計算効率も良好です。ただし、実務者の中には、より保守的なバイアスを持つE0を、バイアスは低いが分散がやや大きいE632よりも重視する傾向があることも重要です。

これらの推定量を実証的に評価するために、本稿で紹介したアルゴリズムを用いて、モデルy = x_1 - x_2 + errorに基づく人工データを用いたシミュレーション研究をおこないました。このモデルでは、予測変数x_1およびx_2は標準正規分布に従い、誤差項は平均ゼロ、分散はユーザー指定の正規分布に従います。普通の線形モデルをデータセットに適合させ、ここで示したアルゴリズムを用いて母集団平均二乗誤差を推定しました。また、独立したテストデータで適合モデルを評価し、真の誤差を測定しました。この一連の過程をユーザー指定の試行回数繰り返し、誤差推定の平均値と標準偏差を算出しました。この処理は、スクリプトErrorVarianceEstimation_NumericalPredictionDemo.mq5として実装されています。

//+------------------------------------------------------------------+
//|              ErrorVarianceEstimation_NumericalPredictionDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     Variance = 1.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = Variance ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVar errorvar;
   COrdReg regmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = normal(rngstate);
         xdata[i][2] = xdata[i][0] - xdata[i][1] + std * normal(rngstate);
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = normal(rngstate);
         testdata[j][2] = testdata[j][0] - testdata[j][1] + std *normal(rngstate);
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!regmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = regmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,regmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,regmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,regmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,regmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
      //---
     }
//---
   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf      std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+------------------------------------------------------------------+

分散を1.0、サンプルサイズを15観測値、ブートストラップ反復回数を1,000回として実施しました。結果は次のとおりです。

MJ      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    Number of Iterations 100   Observed error = 1.18380
RF      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.18825      std=   0.53117
PK      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.12521      std=   0.48780
IR      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.38168      std=   0.63579
NO      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.18647      std=   0.52380

予想どおり、標準的なブートストラップ法は真の誤差を過小評価する結果となりました。一方で、E0推定量は誤差を大きく過大評価しました。この過大評価は一見すると欠点のように見えるかもしれませんが、E0推定量は同時に最も高い標準偏差を示していたことにも注目すべきです。この程度の過大評価は、主にサンプルサイズが極端に小さいことに起因しています。ただし、それが許容されるかどうかは主観的な判断に依存します。誤差推定量の性能をさらに評価するために、サンプルサイズを100観測値に増やしてシミュレーションを再実行しました。これは、実務的な用途においてより代表的なシナリオといえます。以下にその結果を示します。

KG      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.01810      std=   0.24132
LH      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.01672      std=   0.14194
PS      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.01989      std=   0.14441
IP      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.01855      std=   0.14099

この実験の結果から、4つの手法すべてにおいて満足のいく性能が示されました。特に、E0推定量はわずかに誤差を過大評価する傾向を示しました。他の3つのアルゴリズムは、誤差をわずかに過小評価しましたが、その程度はほとんど無視できるレベルでした。E0推定量は引き続き最も高い標準偏差を示しましたが、その差はごくわずかでした。全体的に推定精度が高い状況においては、E0推定量によるわずかな過大評価のほうが、他の手法で見られる取るに足らない過小評価よりも好ましいと考えられます。特に、過小評価がモデル選択や評価に与える影響を考慮するとその傾向が強まります。

前述の例では、母集団誤差を推定するさまざまな手法の違いをいくつか示しました。しかしながら、交差検証が他の手法と常に同等に効果的であるかのような印象を与えてしまった可能性があります。この印象は、滑らかな誤差関数、すなわち単純なモデルの平均二乗誤差を用いたことに起因しています。このような構成は安定した学習環境を形成するため、交差検証が有効に機能します。

一方、分類タスクは本質的に不安定であることが多いです。データに対するわずかな変化が、誤分類率に急激かつ大きな変動をもたらすことがあります。本セクションでは、このような現象を検証するための例を紹介します。母集団誤差を推定するためのアルゴリズムは前節と同様ですが、誤差関数の定義と、比較評価のために使用されるメインプログラムの構造に変更が加えられています。

テストスクリプト「ErrorVarianceEstimation_ClassificationDemo.mq5」では、適度な正の相関を持つ二変量データを生成します。

//+------------------------------------------------------------------+
//|                   ErrorVarianceEstimation_ClassificationDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     PredictionDifficultyLevel = 0.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//+------------------------------------------------------------------+
//| error variance for classification models                         |
//+------------------------------------------------------------------+
class CErrorVarC:public CErrorVar
  {
public:
                     CErrorVarC(void)
     {
     }
                    ~CErrorVarC(void)
     {
     }

   virtual double    error_fun(const double truevalue,const double predictedvalue)
     {
      if(truevalue*predictedvalue>0.0)
         return 0.0;
      else
         return 1.0;
     }


  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = PredictionDifficultyLevel ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVarC errorvar;
   COrdReg olsmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = 0.7071 * xdata[i][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            xdata[i][0] -=dfactor;
            xdata[i][1] +=dfactor;
            xdata[i][2] = 1.0;
           }
         else
           {
            xdata[i][0] +=dfactor;
            xdata[i][1] -=dfactor;
            xdata[i][2] = -1.0;
           }
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = 0.7071 * testdata[j][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            testdata[j][0] -=dfactor;
            testdata[j][1] +=dfactor;
            testdata[j][2] = 1.0;
           }
         else
           {
            testdata[j][0] +=dfactor;
            testdata[j][1] -=dfactor;
            testdata[j][2] = -1.0;
           }
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!olsmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = olsmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,olsmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,olsmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,olsmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,olsmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
     }

   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf    std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf    std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+--------------------------------------------------------------------+

PredictionDifficultyLevelが1.0に設定された場合のデータの散布図は、右上がりの対角方向に主軸を持つ楕円形の分布を示します。スクリプト内のPredictionDifficultyLevelパラメータは、クラスタ間の分離度を制御する役割を果たし、それによって分類のしやすさが変化します。この値が小さいほど、クラスの判別が難しくなり、モデルにとって正しいクラスを推定するのがより困難になります。

2つの異なるクラスが生成され、それぞれのデータ分布は、主軸に対してほぼ垂直な方向に、ユーザー指定の大きさでシフトされます。データには線形モデルが適合され、予測変数には、一方のクラスには−1.0、もう一方のクラスには+1.0が割り当てられます。予測誤差は、真の値と予測値が同じ符号を持つ場合は0.0、異なる符号を持つ場合は1.0と定義されます。このバイナリ型の誤差指標は、分類問題の本質的な特性を反映しています。

2つの実験的評価が実施されました。最初の実験では、サンプルサイズ15、ブートストラップ反復回数1,000回、試行回数100回、クラス間の分離度0という設定を用いました。この構成では、2つのクラスの分布が完全に一致しているため、識別に関する情報が一切存在しない状況を効果的にシミュレートしています。予想された通り、観測された平均誤差は約0.5となりました。この実験の結果を以下に示します。

OO      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.50267
PS      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.50267      std=   0.18389
KM      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.45214    std=   0.11748
EQ      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.50517      std=   0.10845
RF      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.45196    std=   0.09941

交差検証は、今回もほぼ偏りのない性質を示しました。この結果は、今回のシナリオにおいては予想通りです。というのも、このモデルには予測能力がないため、任意の観測値が誤分類される確率は50%となり、それが誤差推定に反映されるからです。同様の理屈はE0推定量にも当てはまります。通常、E0は悲観的なバイアスを示すとされていますが、この特性が現れるのは、モデルがある程度の予測力を持つ場合に限られます。今回のようにモデルに予測力がまったくない状況では、E0が検証用観測値をトレーニングセットから強制的に除外しても、その影響は中立的です。

しかし、この中立性はE632推定量には当てはまりません。E632は、実際にはバイアスのない成分と、強い楽観的バイアスを持つ成分の加重平均として構成されるため、結果として大きな楽観的バイアスを示します。このようなバイアスの可能性は、慎重に考慮する必要があります。また、この実験では、交差検証の最大の欠点である分散の大きさも明らかになりました。交差検証による推定値の標準偏差は、E0推定量に比べてかなり高くなっています。よく見られるように、E632推定量は最も低い標準偏差を示しましたが、このメリットはE632が持つ強い楽観的バイアスによって相殺されています。

続いて、モデルにある程度の予測能力を持たせた状態で、2回目の実験をおこないました（PredictionDifficultyLevelパラメータを1.0に設定）。この実験結果を以下に示します。

GM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.00747
NM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.00533      std=   0.01909
RO      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.00716    std=   0.01766
OG      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.01012      std=   0.01878
FD      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.00820    std=   0.01869

この実験では、E632推定量が最も効果的であることが示されました。E632はバイアスが小さく、標準偏差も最も低くなっています。一方で、E0推定量は、標準偏差がやや高めであるものの、特有の（そして多くの場合で望ましい）悲観的バイアスを示しています。前の実験結果を踏まえると、E0とE632のいずれを選ぶかについては、このバイアスの性質を慎重に評価する必要があります。今回も、交差検証は最も高い標準偏差を示し、単純ブートストラップは危険性のある楽観的バイアスを示しました。

本稿で紹介したアルゴリズムを分類性能の推定に用いる際には、いくつか注意すべき点があります。ここで紹介したアルゴリズムを分類問題の誤差推定に用いる場合、重要な制約が存在します。ブートストラップ法で分類用のデータセットを生成する際に、ブートストラップサンプルが単一クラスのデータのみを含むことがあるという問題です。こうした場合、分類アルゴリズムが適切に動作しない、あるいは完全に失敗してしまう可能性があります。

結論

本記事の内容をざっと眺めると、モデルの母集団誤差を推定するためのリサンプリング技術は概念的には興味深いものの、複雑すぎて実用性が限られていると感じられるかもしれません。しかし、そのような結論は非常に残念なことです。本稿で紹介したリサンプリング手法は多くの利点を持ち、真剣に検討される価値があります。

具体的には、これらの手法はモデル評価における根本的な課題である「独立したデータセットの必要性」に対応しています。従来の方法では、独立した別のデータセットを用意しなければならず、その取得はしばしば手間がかかり、場合によっては実現が困難です。

本稿で取り上げたリサンプリング技術はこの問題を解消します。データセット全体をモデルの学習と将来の性能推定の両方に活用できるため、データの有効活用が最大化されます。この能力は大きな方法論的進歩を示しており、軽視されるべきではありません。

ファイル名	ファイルの説明
MQL5/include/error_variance_estimation.mqh	この記事で説明されている誤差推定アルゴリズムの定義を含むヘッダーファイル
MQL5/include/imodel.mqh	機械学習モデルと対話するために使用されるインターフェイスの定義を含むヘッダーファイル
MQL5/include/np.mqh	さまざまなベクトルおよび行列ユーティリティ関数を含むヘッダーファイル
MQL5/include/OLS.mqh	通常の最小二乗モデルを実装するOLSクラスを定義するインクルードファイル
MQL5/スクリプト/ErrorVarianceEstimation_NumericalPredictionDemo.mq5	数値予測における誤差推定アルゴリズムの有用性を示すデモスクリプト
MQL5/スクリプト/ErrorVarianceEstimation_ClassificationDemo.mq5	データ分類における誤差推定アルゴリズムの有用性を示すデモスクリプト