母集団最適化アルゴリズム：2進数遺伝的アルゴリズム(BGA)（第2回）

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

前回の記事では、遺伝的アルゴリズムだけでなく、あらゆる集団最適化アルゴリズムで使用される重要な基本概念と手法のすべてを知ることができました。さて、この知識をもとに、今回の「2巻本」のメインテーマである2進数遺伝的アルゴリズム(BGA)について詳しく考えてみましょう。一般的な情報から始めて、この注目すべき検索戦略のコードに移り、最後にテスト結果を見てみましょう。

遺伝的アルゴリズム(GA)とは進化的アルゴリズムのことで、遺伝的アルゴリズム、遺伝的プログラミング、進化戦略など様々なアプローチがあります。遺伝的アルゴリズムは進化と遺伝の考え方に基づいており、解は集団として表現され、遺伝的演算子（交叉や突然変異など）が新しい世代の解を作り出すために適用されます。

遺伝的アルゴリズムは、自然淘汰と遺伝学の原理を利用して最適化問題を解きます。この記事で取り上げた2進数遺伝的アルゴリズム(BGA)は、遺伝的アルゴリズムの中で最初のものです。したがって、BGAは進化的アルゴリズムのクラスに属し、データの2進表現を使用する遺伝的アルゴリズムの特定の変種です。

遺伝的アルゴリズムの開発は20世紀半ばに始まりました。創設者の1人はジョン・ホランドで、彼は1975年に著書『Adaptation in Natural and Artificial Systems』を出版し、最適化問題を解くためのアプローチの方向性として遺伝的アルゴリズムを紹介しました。

遺伝的2進数アルゴリズムの開発は、いくつかの要因とアイデアに触発されました。主なものは、以下の通りです。

• 自然淘汰と進化の原理：BGAは、チャールズ・ダーウィンが提唱した自然淘汰と進化の原理に基づいています。集団には多様な解決策が存在し、より環境に適応したものが生き残り、次の世代にその特徴を引き継ぐ可能性が高いという考え方です。
• 遺伝と遺伝性：BGAはまた、遺伝子、染色体、遺伝といった遺伝学の概念も用いています。BGAの解は2進数文字列として表現され、個々のビット群は特定の遺伝子を表し、遺伝子は最適化されるパラメータを表す。交叉や突然変異のような遺伝的演算子は、新しい世代の解を作成するために2進数文字列に適用されます。

全体として、BGAの開発は、進化的アルゴリズム、遺伝学、最適化の分野からのアイデアの組み合わせの結果でした。BGAは自然淘汰と遺伝学の原理を利用して最適化問題を解くために作られ、その発展は今日まで続いています。膨大な数のGAオプションが作られただけでなく、非常に複雑なものを含むハイブリッドアルゴリズムの一部として遺伝的アルゴリズムのアイデアやアプローチが広く利用されています。

2進数遺伝的アルゴリズム(BGA)は、データの2進表現を使用します。つまり、各個体（解）はビット列（0と1）として表現されます。交叉や突然変異といった遺伝的演算子をビット列に適用し、新しい世代の解を作り出します。

興味深い事実：BGAを含む遺伝的アルゴリズムは、人工知能の作成と改良に使用できます。例えば、ニューラルネットワークを進化させ、より効率的な機械学習モデルを作ることができます。

一般に遺伝的アルゴリズム、特にBGAは、解析的な解がないために従来の手法では十分な効果が得られないような複雑な最適化問題を解くための強力なツールです。MetaTrader 5は2進数GAを使用しているため、この注目すべきアルゴリズムの動作原理を研究することはさらにエキサイティングです。

2.アルゴリズム

2進数遺伝的アルゴリズムには以下のステップがあります。

1. 母集団の初期化：ランダムな2進数値を持つ染色体からなる初期母集団を作成します。
2. 適合度評価：娘集団の各個体（染色体）の適合度を評価します。
3. 選択：ルーレット方式で親を選び、子孫を残します。
4. 交叉：親染色体を分割し、両方の親染色体の一部を持つ新しい娘染色体を作ります。
5. 反転：娘個体の染色体を無作為に選択した箇所で分割し、その結果生じた部分を入れ替えます。
   
6. 突然変異：ある確率で子孫の遺伝子のビットをランダムに変化させます。
7. 子孫の適合度の評価：それぞれの新しい子孫の適合度を評価します。
8. 新しい母集団の形成：子の母集団を全母集団の最後に置き、適合度値で並び替えます。
9. 停止基準：停止基準に達するまで、ステップ3からのプロセスを繰り返します。

最適化されたパラメータの「最大値」と「最小値」の間の距離を使用して、BGAが正数のみで動作するようにし、2進文字列の操作を簡素化し、計算速度を向上させます。このようにして得られた正の距離値を2値のグレイコードの形で表し、図1に示すように、染色体記号の1つの共通配列に順次配置します。交叉法を実行する場合、染色体上の切断点は染色体上のランダムな場所に配置され、必ずしも遺伝子の結合点に配置されるとは限りません。切断点は遺伝子空間の中に置くこともできます。

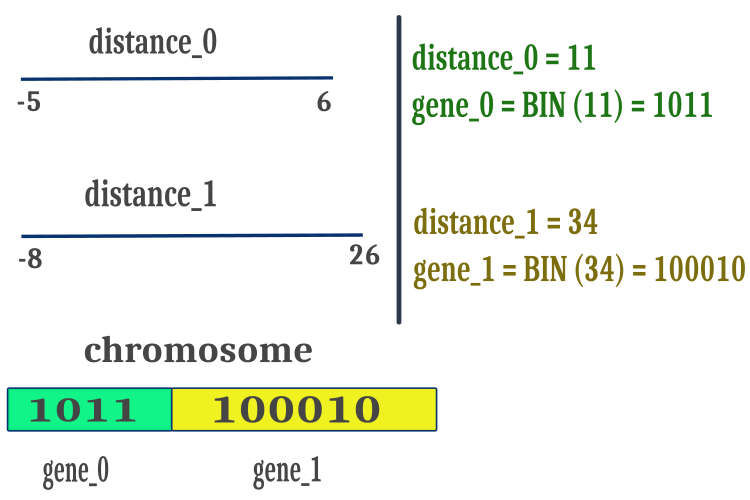
図1：個体の特性（最適化されたパラメータ）を染色体に配置します。

遺伝的アルゴリズムにはかなりの数の外部パラメータがあるので、それらをより詳細に検討することは合理的です。デフォルトの設定は、科学出版物の多くの著者が推奨する設定とほぼ一致しています。私は、ほとんどの種類の作業で最大限の効率を発揮するようにテストし、選択しました。しかし、これらのパラメータからいかなる方向に逸脱しても、個々の関数について最適化されたパラメータが10個、あるいは50個のテストでは100%の収束を達成することができますが、同時に他のタスクの効率は著しく低下します。したがって、ほとんどの実用的なケースでは、デフォルトの設定が最適です。

• Population_P（母集団の大きさ = 50）：母集団の各世代における娘個体の数。この母集団サイズは、テストで取り上げたアルゴリズムのほとんどで使用されており、解の多様性と収束速度の残高を提供します。
  

• ParentPopulation_P（親集団のサイズ = 50）：繁殖のために選択され、次の世代を作成する親の数。このパラメータの値を小さくすると、滑らかな関数での収束性が向上し（精度が向上し）、値を大きくすると、離散関数での収束性が向上します（遺伝物質の多様性が向上する）。
  

• CrossoverProbab_P（交叉確率 = 1.0）：選択された2つの親の間で交叉操作が実行される確率。交叉の確率が高いほど、アルゴリズムの組み合わせ能力が高まります。値を小さくすると収束のスピードは上がりますが、行き詰まる確率は高くなります。
  

• CrossoverPoints_P（交叉ポイント数 = 3）：2つの親染色体間で交叉が発生するポイントの数。ポイントを増やすと、パラメータ同士の混合が激しくなり、極限ではアルゴリズムのランダムな行動になります。
  

• MutationProbab_P（変異確率 = 0.001）：染色体遺伝子型の各ビットの変異確率。突然変異は遺伝物質にランダムな変化を与え、集団に新しい解を加えます。確率が低いとアルゴリズムの収束率は上がりますが多様性は低下し、逆に高すぎると有用な情報が失われます。

• InversionProbab_P（反転確率 = 0.7）：染色体に反転操作をおこなう確率。反転の確率が高いほど遺伝物質の多様性が高まりますが、高すぎるとアルゴリズムがランダムになります。

• DoubleDigitsInChromo_P（遺伝子の小数点以下の桁数）：染色体の2進数で表現される実数（最適化されたパラメータ）の小数点以下の桁数。値を大きくすると、計算が複雑になり、最適化時間が長くなります（問題を解く際に2進数形式を直接使用しない場合、16以上の値を設定する意味はありません。出力ビットはdoubleに変換する際に失われます）。

コードの確認に移りましょう。

エージェントを初期化する際には、最適化されるパラメータの2進表現のビット数を決定する必要があります。あるグレイコードの長さに相当する小数点以下5桁を考慮する必要があるとしましょう。ただし、このコードには、必要な数以上をエンコードすることができます。したがって、2進数形式でエンコードできる最大の実数を決定する必要があります。将来的には、エンコードされた数値を最適化された出力パラメータの必要な範囲にスケーリングすることができます。実数の小数部には（パラメータで指定された）指定された桁数を使用し、整数部には2進数形式で必要な桁数を使用します。

例えば、digitsInGrayCode関数の入力パラメータが3の場合、関数は3ビットのグレイコードを使用したulong型の最大値、つまり7（2進数で111）を返します。

実数の小数部と整数部について、与えられたビット数でエンコード可能な最大数を求めるには、GetMaxDecimalFromGray関数を使用します。

//——————————————————————————————————————————————————————————————————————————————
//Calculation of the maximum possible ulong number using the Gray code for a given number of bits
ulong GetMaxDecimalFromGray (int digitsInGrayCode)
{
  ulong maxValue = 1;

  for (int i = 1; i < digitsInGrayCode; i++)
  {
    maxValue <<= 1;
    maxValue |= 1;
  }

  return maxValue;
}
//——————————————————————————————————————————————————————————————————————————————

染色体の各遺伝子（染色体上の遺伝子の位置）を表現するために、2進数形式で遺伝子を扱うためのフィールドとメソッドを含むS_BinaryGene構造体を使用します。

• gene：遺伝子を表す文字配列
• integPart：整数遺伝子部分の文字配列
• fractPart：分数遺伝子部分の文字配列
• integGrayDigits：遺伝子の整数部分のグレイの桁数
• fractGrayDigits：遺伝子の分数部分のグレイの桁数
• length：遺伝子の全長
• minDoubleRange：実数値範囲の最小値
• maxDoubleRange：実数値範囲の最大値
• maxDoubleNumber：遺伝子を用いて表現できる最大の実数
• doubleFract：遺伝子の小数部分を実数に変換する値

構造体メソッド

• Init：構造体フィールドを初期化します。実数の範囲の最小値と最大値、および遺伝子の小数部の桁数を受け取ります。このメソッドでは、遺伝子のコード部分の最大実数の値がグレイコードを使用して計算されます。
  

• ToDouble：遺伝子を実数に変換します。グレイコード文字の配列chromoと遺伝子開始インデックスindChrを受け取ります。このメソッドは染色体の領域を読み取り、読み取った遺伝子を10進数に変換し、指定した実数の範囲にスケーリングします。

• Scale：In入力値をInMINとInMAXの範囲からOutMINとOutMAXの出力範囲にスケーリングします。これはToDoubleで使用される補助メソッドです。

//——————————————————————————————————————————————————————————————————————————————
struct S_BinaryGene
{
  char   gene      [];
  char   integPart [];
  char   fractPart [];

  uint   integGrayDigits;
  uint   fractGrayDigits;
  uint   length;

  double minDoubleRange;
  double maxDoubleRange;
  double maxDoubleNumber;
  double doubleFract;

  //----------------------------------------------------------------------------
  void Init (double min, double max, int doubleDigitsInChromo)
  {
    doubleFract = pow (0.1, doubleDigitsInChromo);
    
    minDoubleRange = min;
    maxDoubleRange = max - min;

    ulong decInfr = 0;

    for (int i = 0; i < doubleDigitsInChromo; i++)
    {
      decInfr += 9 * (ulong)pow (10, i);
    }
    
    //----------------------------------------
    DecimalToGray (decInfr, fractPart);
    
    ulong maxDecInFr = GetMaxDecimalFromGray (ArraySize (fractPart));
    double maxDoubFr = maxDecInFr * doubleFract;
    
    
    //----------------------------------------
    DecimalToGray ((ulong)maxDoubleRange, integPart);
    
    ulong  maxDecInInteg = GetMaxDecimalFromGray (ArraySize (integPart));
    double maxDoubInteg  = (double)maxDecInInteg + maxDoubFr;

    maxDoubleNumber = maxDoubInteg;

    ArrayResize (gene, 0, 1000);
    integGrayDigits = ArraySize (integPart);
    fractGrayDigits = ArraySize (fractPart);
    length          = integGrayDigits + fractGrayDigits;

    ArrayCopy (gene, integPart, 0,                0, WHOLE_ARRAY);
    ArrayCopy (gene, fractPart, ArraySize (gene), 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double ToDouble (const char &chromo [], const int indChr)
  {
    double d;
    if(integGrayDigits > 0)d = (double)GrayToDecimal(chromo, indChr, indChr + integGrayDigits - 1);
    else                   d = 0.0;

    d +=(double)GrayToDecimal(chromo, indChr + integGrayDigits, indChr + integGrayDigits + fractGrayDigits - 1) * doubleFract;

    return minDoubleRange + Scale(d, 0.0, maxDoubleNumber, 0.0, maxDoubleRange);
  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

エージェントを記述するにはS_Agent構造体が必要です。これはエージェントを表し、染色体に加えて以下のデータを含みます。

• c：実数としてのエージェント座標値の配列 
• f：エージェントの適合度値
• genes：S_BinaryGene構造体の配列。染色体における各遺伝子の位置と、2進数コードを実数に変換するルールを記述します。
• chromosome：エージェントの染色体文字の配列
• calculated：エージェントの値が計算されているかどうかを示すブール値（フィールドは存在しますが、コードでは使用されない）。

構造体メソッド

• Init：構造体フィールドを初期化します。coords（座標の数）、各最適化パラメータの最小値と最大値を含むminおよびmax配列、doubleDigitsInChromo (遺伝子の小数部分の実数の桁数) を受け入れます。このメソッドは、各座標の遺伝子を作成して初期化し、また初期適合度値とcalculatedフラグを設定します。

• ExtractGenes：染色体から遺伝子の値を抽出し、c配列に格納します。S_BinaryGene構造体のToDoubleメソッドを使用して、染色体の遺伝子を実数に変換します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }

    calculated = false;
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  double c []; //coordinates
  double f;    //fitness

  S_BinaryGene genes [];
  char chromosome    [];
  bool calculated;
};
//——————————————————————————————————————————————————————————————————————————————

次のコードは、ルーレットセグメントを表すS_Roulette構造体の定義です。

構造体フィールド

• start：ルーレットのセグメント開始点の値
• end：ルーレットのセグメント終了点

//——————————————————————————————————————————————————————————————————————————————
struct S_Roulette
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

遺伝的アルゴリズムを実装するC_AO_BGAクラスを宣言します。

• cB：最適な座標値の配列
• fB：最良の座標の適合度値
• a：エージェントを表すS_Agent構造体の配列
• rangeMax：検索範囲の最大値の配列
• rangeMin：検索範囲の最小値の配列
• rangeStep：検索ステップを表す値の配列

クラスのメソッド

• Init：クラスフィールドを初期化します。coordsP：座標の数、popSizeP：母集団のサイズ、parentPopSizeP：親母集団のサイズ、crossoverProbabP：交叉確率、crossoverPointsP：交叉点の数、mutationProbabP：変異確率、inversionProbabP：反転確率、doubleDigitsInChromoP：反転点の数交叉点の数、mutationProbabP：変異確率、inversionProbabP：反転確率、doubleDigitsInChromoP：遺伝子の小数点以下の桁数の各パラメータを受け付けます。このメソッドは、遺伝的アルゴリズムの動作に必要な内部変数と配列を初期化します。

• Moving：遺伝的アルゴリズムの主な手法で、交叉、突然変異、反転、適性評価などの操作を集団に対しておこないます。

• Revision：このメソッドは、エージェントをソートし、最適なものを選択する、母集団の改訂を実行します。

このクラスのprivateフィールドとメソッドは、ルーレット操作、値のスケーリング、ソート、その他の操作を含む遺伝的アルゴリズムを内部的に実装するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BGA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP);//number of decimal places in the gene

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;               //coordinates number
  private: int    popSize;              //population size
  private: int    parentPopSize;        //parent population size
  private: double crossoverProbab;      //crossover probability
  private: int    crossoverPoints;      //crossover points
  private: double mutationProbab;       //mutation probability
  private: double inversionProbab;      //inversion probability
  private: int    doubleDigitsInChromo; //number of decimal places in the gene
  private: bool   revision;

  private: S_Agent    parents    [];  //parents
  private: int        ind        [];  //temporary array for sorting the population
  private: double     val        [];  //temporary array for sorting the population
  private: S_Agent    pTemp      [];  //temporary array for sorting the population
  private: char       tempChrome [];  //temporary chromosome for inversion surgery
  private: uint       lengthChrome;   //length of the chromosome (the length of the string of characters according to the Gray code)
  private: int        pCount;         //indices of chromosome break points
  private: uint       poRND      [];  //temporal indices of chromosome break points
  private: uint       points     [];  //final indices of chromosome break points
  private: S_Roulette roulette   [];  //roulette

  private: void   PreCalcRoulette ();
  private: int    SpinRoulette    ();
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: void   Sorting   (S_Agent &p [], int size);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
};
//——————————————————————————————————————————————————————————————————————————————

次のコードは、C_AO_BGAクラスのInitメソッドの実装を表しています。このメソッドは、遺伝的アルゴリズムが動作するために必要なクラスのフィールドと配列を初期化します。

メソッドの入力

• coordsP：座標の数
• popSizeP：母集団のサイズ
• parentPopSizeP：親の母集団のサイズ
• crossoverProbabP：交叉の確率
• crossoverPointsP：交叉ポイントの数
• mutationProbabP：突然変異の確率
• inversionProbabP：逆転確率
• doubleDigitsInChromoP：遺伝子の小数点以下の桁数

Initメソッドは、遺伝的アルゴリズムを実行する前に、クラスのフィールドと配列を初期化するために使用されます。クラスフィールドの値を設定し、いくつかのパラメータの値を確認して調整し、また、メモリを確保して配列のサイズを変更します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP) //number of decimal places in the gene
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords               = coordsP;
  popSize              = popSizeP;
  parentPopSize        = parentPopSizeP;
  crossoverProbab      = crossoverProbabP;
  crossoverPoints      = crossoverPointsP;
  pCount               = crossoverPointsP;
  mutationProbab       = mutationProbabP;
  inversionProbab      = inversionProbabP;
  doubleDigitsInChromo = doubleDigitsInChromoP;

  if (crossoverPoints < 1) crossoverPoints = 1;
  if (pCount < 1) pCount = 1;

  ArrayResize (poRND,  pCount);
  ArrayResize (points, pCount + 2);

  ArrayResize (ind,   parentPopSize + popSize);
  ArrayResize (val,   parentPopSize + popSize);
  ArrayResize (pTemp, parentPopSize + popSize);
  ArrayResize (a,     popSize);

  ArrayResize (parents,  parentPopSize + popSize);
  ArrayResize (roulette, parentPopSize);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

エージェントの遺伝物質を操作するための基本的な操作はすべて、C_AO_BGAクラスのMovingメソッドを使用しておこなわれます。Movingメソッドは遺伝的アルゴリズムステップを実行し、親の選択、交叉、反転、染色体の突然変異、遺伝子と個体の座標への操作を含みます。

このメソッドは論理的にいくつかの部分に分かれています。

1. if (!revision)：revisionがfalseの場合、個体群が初期化されます。

• Initメソッドは、与えられたパラメータで個体を初期化するために呼ばれます。
• 各遺伝子を0か1のランダムな値で埋めることにより、ランダムな染色体が生成されます。
• ExtractGenesメソッドは、染色体から遺伝子を抽出するために呼び出されます。
• c個の座標は、SeInDiSp関数を使用して範囲に縮小されます。
• 各個体の適合度値fは-DBL_MAXに設定されます。
• lengthChrome = ArraySize (a [0].chromosome)：個体の染色体の長さ（すべての個体が同じ長さ）
• ArrayResize (tempChrome, lengthChrome)：tempChrome一時配列のサイズをlengthChromeで置き換えます

2.母集団の各個体について

• PreCalcRouletteメソッドを使用して、親選択ルーレットの予備計算がおこなわれます。
• 親はスピンルーレット方式で選ばれます。
• 選択された親個体の染色体が、現在の個体の染色体にコピーされます。
• 交叉操作はcrossoverProbabの確率でおこなわれます。
• 2番目の親が選ばれます。
• 染色体切断点が決定されます。
• 親個体の染色体を交配します。
• 反転操作はinversionProbabの確率でおこなわれます。
• ランダムな染色体切断点が決定されます。
• 染色体の一部が場所を変えます。
• 突然変異操作は、各染色体遺伝子に対してmutationProbabの確率で実行されます。
• ExtractGenesメソッドは、染色体から遺伝子を抽出するために呼び出されます。
• c個の座標は、SeInDiSp関数を使用して範囲に縮小されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      a [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);

      int r = 0;

      for (int len = 0; len < ArraySize (a [i].chromosome); len++)
      {
        r  = MathRand (); //[0,32767]

        if (r > 16384) a [i].chromosome [len] = 1;
        else           a [i].chromosome [len] = 0;
      }

      a [i].ExtractGenes ();

      for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].f = -DBL_MAX;
      a [i].calculated = true;
    }

    lengthChrome = ArraySize (a [0].chromosome);
    ArrayResize (tempChrome, lengthChrome);

    for (int i = 0; i < parentPopSize + popSize; i++)
    {
      parents [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);
      parents [i].f = -DBL_MAX;
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    pos       = 0;
  double r         = 0;
  uint   p1        = 0;
  uint   p2        = 0;
  uint   p3        = 0;
  uint   temp      = 0;

  for (int i = 0; i < popSize; i++)
  {
    PreCalcRoulette ();

    //selection, select and copy the parent to the child------------------------
    pos = SpinRoulette ();

    ArrayCopy (a [i].chromosome, parents [pos].chromosome, 0, 0, WHOLE_ARRAY);

    //crossover-----------------------------------------------------------------
    r = RNDfromCI (0.0, 1.0);

    if (r < crossoverProbab)
    {
      //choose a second parent to breed with------------------------------------
      pos = SpinRoulette ();

      //determination of chromosome break points--------------------------------
      for (int p = 0; p < pCount; p++)
      {
        poRND [p] = (int)RNDfromCI (0.0, lengthChrome);
        if (poRND [p] >= lengthChrome) poRND [p] = lengthChrome - 1;
      }
      ArraySort (poRND);
      ArrayCopy (points, poRND, 1, 0, WHOLE_ARRAY);
      points [0] = 0;
      points [pCount + 1] = lengthChrome - 1;

      r = RNDfromCI (0.0, 1.0);

      int startPoint = r > 0.5 ? 0 : 1;

      for (int p = startPoint; p < pCount + 2; p += 2)
      {
        if (p < pCount + 1)
        {
          for (uint len = points [p]; len < points [p + 1]; len++) a [i].chromosome [len] = parents [pos].chromosome [len];
        }
      }
    }

    //perform an inversion------------------------------------------------------
    //(break the chromosome, swap the received parts, connect them together)
    r = RNDfromCI (0.0, 1.0);

    if (r < inversionProbab)
    {
      p1 = (int)RNDfromCI (0.0, lengthChrome);
      if (p1 >= lengthChrome) p1 = lengthChrome - 1;

      //copying the second part to the beginning of the temporary array
      for (uint len = p1; len < lengthChrome; len++) tempChrome [len - p1] = a [i].chromosome [len];

      //copying the first part to the end of the temporary array
      for (uint len = 0; len < p1; len++)       tempChrome [lengthChrome - p1 + len] = a [i].chromosome [len];

      //copying a temporary array back
      for (uint len = 0; len < lengthChrome; len++)   a [i].chromosome [len] = tempChrome [len];
    }

    //perform mutation---------------------------------------------------------
    for (uint len = 0; len < lengthChrome; len++)
    {
      r = RNDfromCI (0.0, 1.0);
      if (r < mutationProbab) a [i].chromosome [len] = a [i].chromosome [len] == 1 ? 0 : 1;
    }

    a [i].ExtractGenes ();

    for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

    a [i].calculated = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは母集団の修正をおこない、個体の適合度関数の値で並び替え、最適解の適合度fBと最適解の座標cBを更新します。母集団を並び替える前に、子母集団が総母集団の最後にコピーされます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = a [i - parentPopSize];
  }

  Sorting (parents, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

予備ルーレットレイアウトコードはPreCalcRouletteメソッドを表しています。この手法は、適性関数に基づいて個体のルーレット選択の範囲値を事前に計算します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::PreCalcRoulette ()
{
  roulette [0].start = parents [0].f;
  roulette [0].end   = roulette [0].start + (parents [0].f - parents [parentPopSize - 1].f);

  for (int s = 1; s < parentPopSize; s++)
  {
    if (s != parentPopSize - 1)
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s].f - parents [parentPopSize - 1].f);
    }
    else
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s - 1].f - parents [s].f) * 0.1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

SpinRouletteメソッドは、親個体の位置を確実に選択します。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BGA::SpinRoulette ()
{
  double r = RNDfromCI (roulette [0].start, roulette [parentPopSize - 1].end);

  for (int s = 0; s < parentPopSize; s++)
  {
    if (roulette [s].start <= r && r < roulette [s].end) return s;
  }

  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

BGAテストスタンドの結果：

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs:10000; result:0.9999191151339382
25 Hilly's; Func runs:10000; result:0.994841435673127
500 Hilly's; Func runs:10000; result:0.5048331764136147
=============================
5 Forest's; Func runs:10000; result:1.0
25 Forest's; Func runs:10000; result:0.9997457419655973
500 Forest's; Func runs:10000; result:0.32054251149158375
=============================
5 Megacity's; Func runs:10000; result:0.9066666666666668
25 Megacity's; Func runs:10000; result:0.9640000000000001
500 Megacity's; Func runs:10000; result:0.23034999999999997
=============================
All score:6.92090 (76.90%)

BGA最適化の可視化は、アルゴリズムの高い収束性を明確に示しています。興味深いことに、最適化プロセスの間、母集団の一部は大域的極値から離れたままです。これは、母集団内の解の多様性を維持しながら、探索空間の新しい未知の領域を探索していることを示しています。ただし、Megacity離散関数を扱うとき、このアルゴリズムはある困難に直面します。この複雑な関数を扱った場合、結果に多少のばらつきはあるものの、BGAは他のアルゴリズムよりも大幅に優れた性能を発揮します。

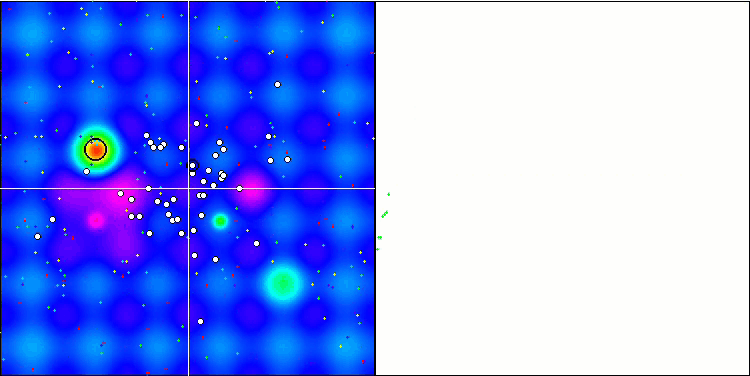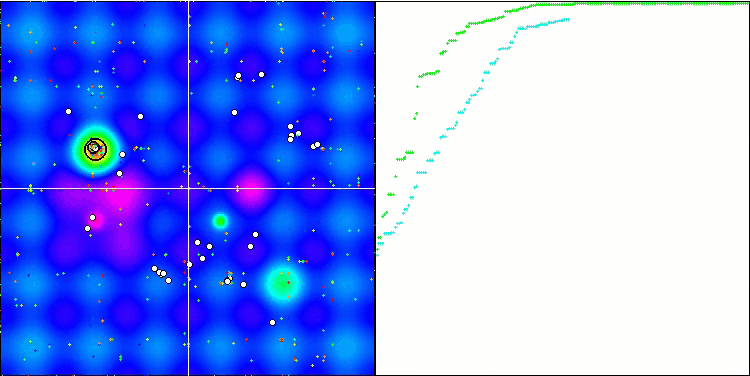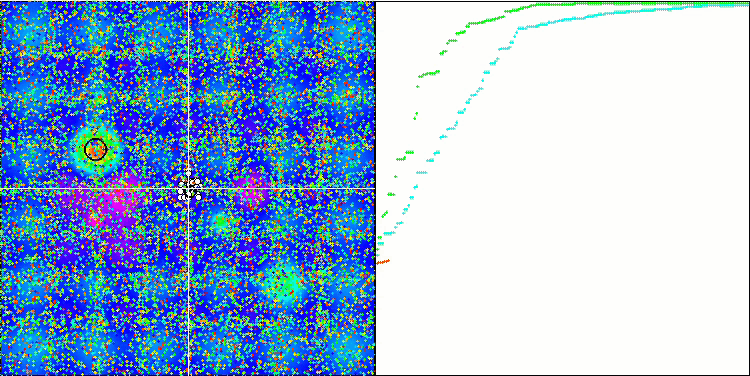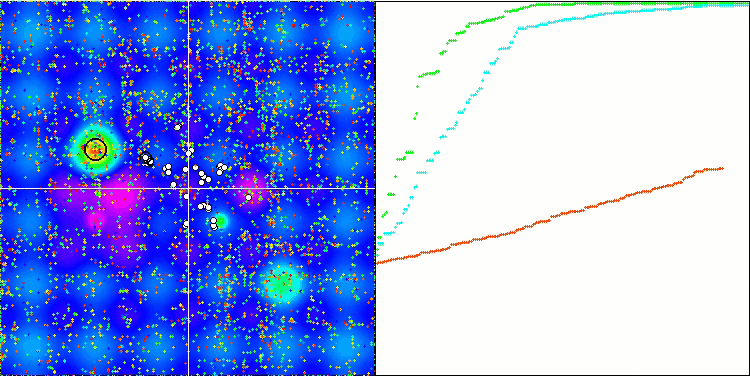
Hillyテスト関数のBGA

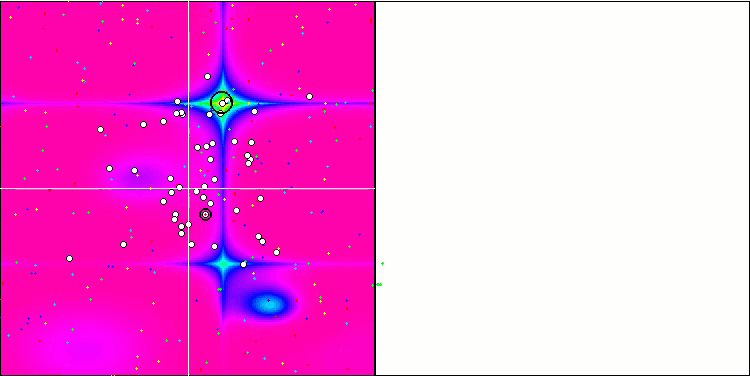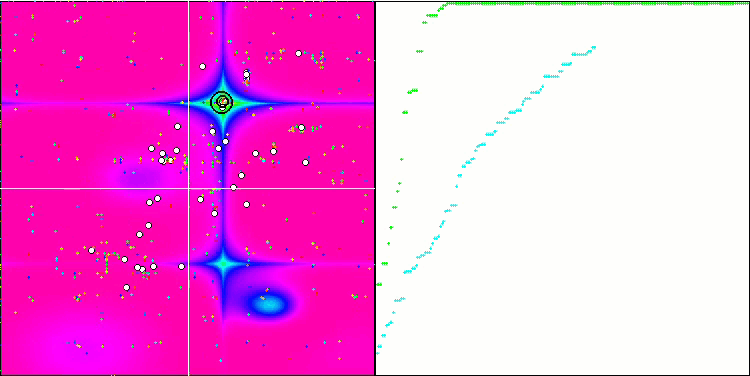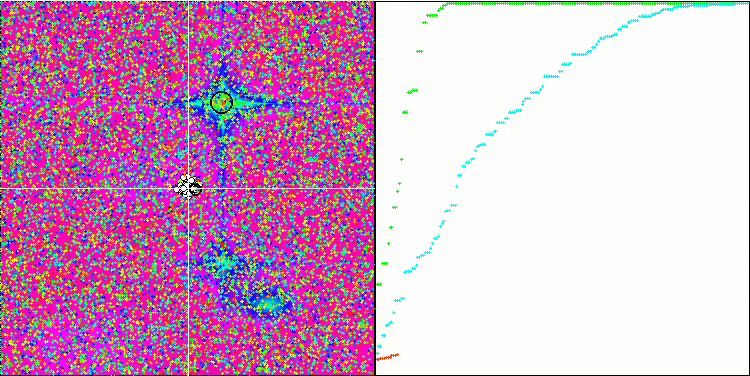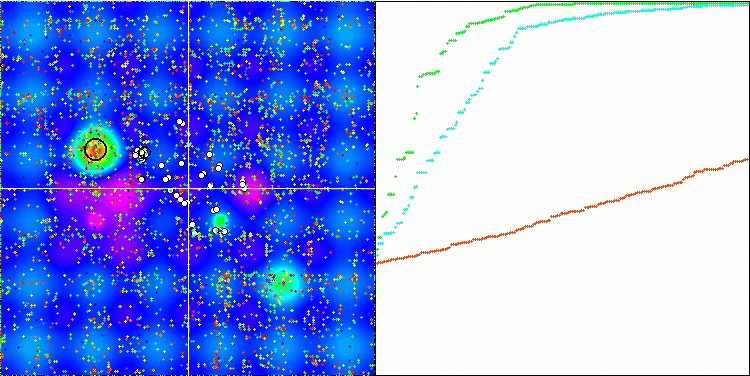
Forestテスト関数のBGA

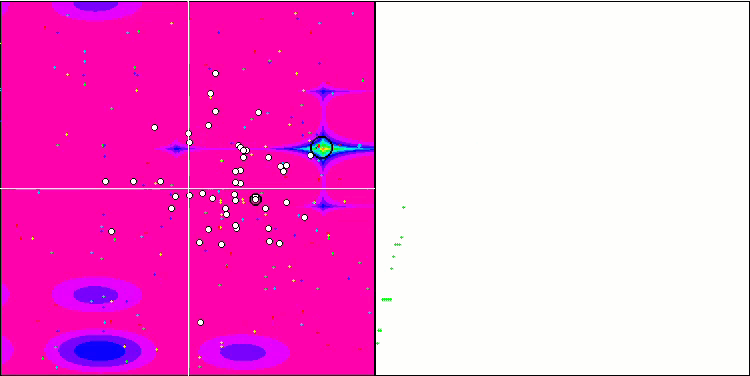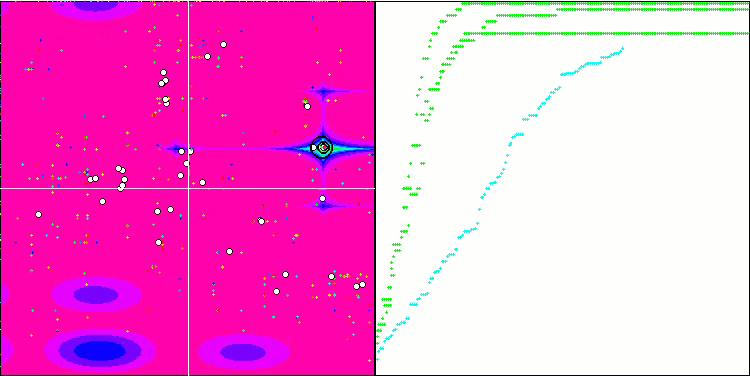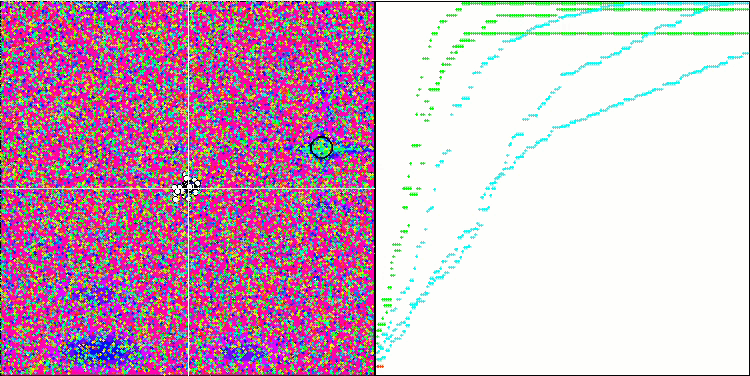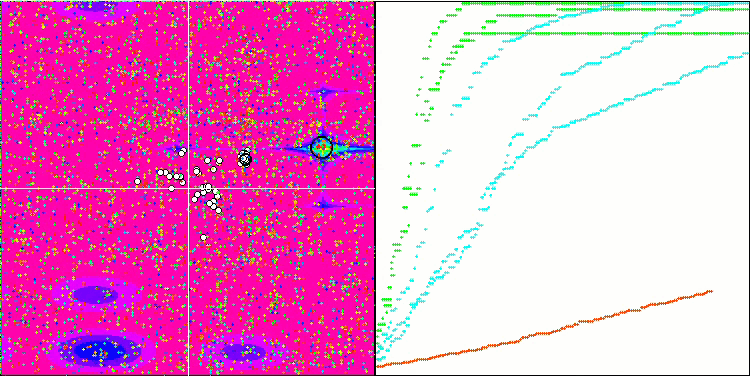
Megacityテスト関数のBGA

BGAは、3つのテスト関数すべてにおいて、ほとんどのテストで最高のパフォーマンスを示し、表のトップに立ちました。BGAはMegacity離散関数で特に素晴らしい結果を示し、他のアルゴリズムを凌駕しました。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの% 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 1 BGA 2進数遺伝的アルゴリズム 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90 2 (P+O)ES (P+O）進化戦略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18 3 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44 4 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76 5 DE 微分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06 6 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79 7 SSG 苗木の種まきと成長 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95 8 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22 9 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31 10 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93 11 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55 12 IWO 侵入雑草の最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81 13 Micro-AIS マイクロ人工免疫システム 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54 14 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21 15 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44 16 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92 17 FAm ホタルアルゴリズム M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87 18 GSA 重力探索アルゴリズム 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34 19 BFO 細菌採食の最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72 20 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06 21 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93 22 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43 23 IWDm インテリジェント水滴M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06 24 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77 25 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40 26 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38 27 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84 28 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37 29 GWO 灰色オオカミオプティマイザー 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32 30 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46 31 EM 電磁気的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85

まとめ

この記事では、GA遺伝的アルゴリズムの一般的なクラスの特別なケースであるBGAの古典的なバージョンについて検討しました。解を2進数で表現するという考えは長年あるにもかかわらず、2進コードを使ったアプローチは今日に至るまで有効です。このアルゴリズムは、従来の実数値特徴エンコーディングでは実現が困難であった、最適化問題の独立した空間次元の情報を1つの染色体にエンコードすることにより、最適化問題の全体像を1つにまとめるものであり、他の最適化アルゴリズムの中でも際立っています。

BGA戦略の数学と論理は私にとって完全に明確なのですが、それでも私は染色体で何が起こっているのかに魅了されています。それは魔法の万華鏡に例えられます。万華鏡を回すと、さまざまな形や色がユニークなパターンに組み合わされ、壮大な絵ができあがります。同様に、BGAの交叉演算子は、染色体を 内部パラメータ領域を含むいくつかの部分にランダムに切断します。これらのピースは、万華鏡のピースをシャッフルするように組み合わされます。これにより、さまざまなソリューションの長所を組み合わせ、より最適な組み合わせを新たに作り出すことができます。万華鏡のように、BGAの交叉の結果は、単純な染色体を最適解の真の「ダイヤモンド」に変える、驚きと予期せぬものになります。

遺伝的アルゴリズムで使用される手法とツールに関するこの2部構成の記事の情報が、読者の知識を広げ、仕事や研究で新たな高みに到達する助けになると確信しています。進化の力は、自然、テクノロジー、そして人間の心の中に絶えず現れており、BGAは、私たちが新たな高みへと到達し、達成するのを助けてくれる数多くの驚くべきアルゴリズムの1つです。

BGAは、滑らかな曲面、離散的な問題、あるいは確率論的なアプローチを含む大規模な問題など、さまざまな問題を効果的に解決し、解析的な解決法では限界がある新たな可能性を切り開きます。

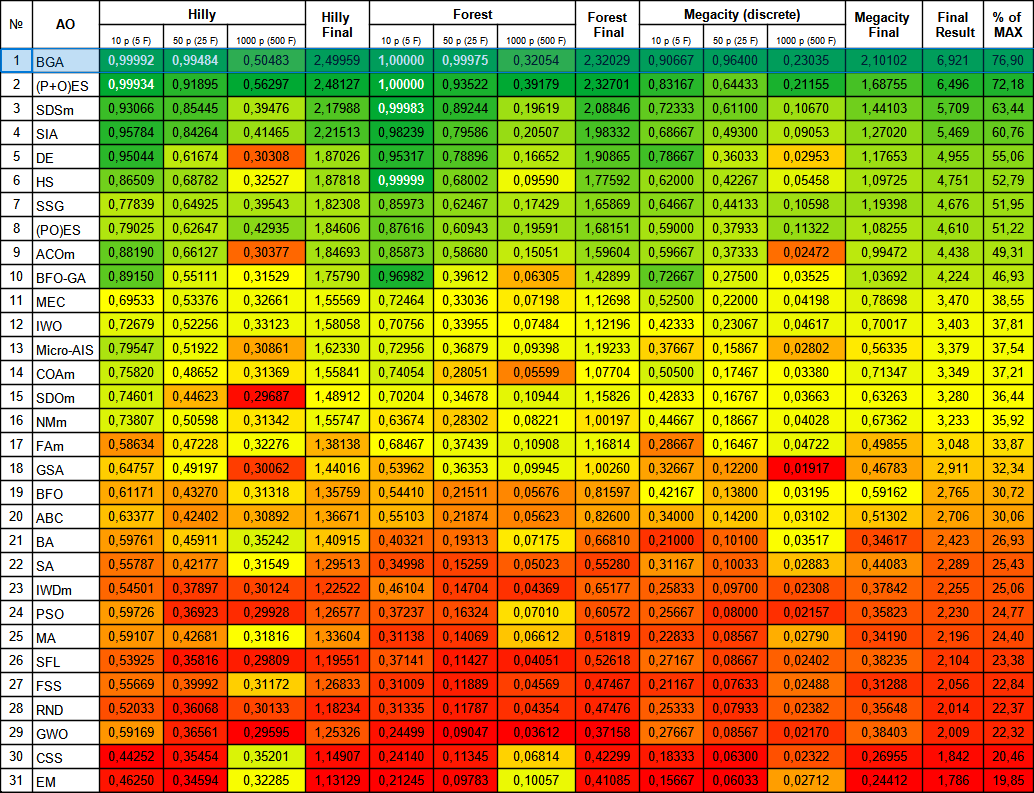
図2：関連テストに応じたアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示

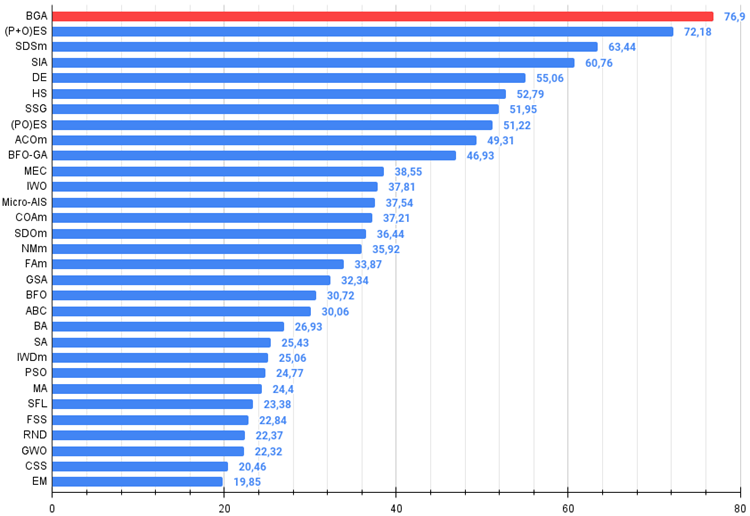
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果であり、アーカイブには格付け表を計算するスクリプトが含まれています)

2進数遺伝的アルゴリズム(BGA)の長所と短所は、今回紹介する実装にのみ適用されます。

長所

1. 様々な問題を高い効率で解決
2. 行き詰まりにくい
3. 平滑離散関数と複雑な離散関数の両方で有望な結果
4. 収束性が高い

短所

1. 多数の外部パラメータ
   
2. 実装がかなり複雑
   
3. 計算量が多い
   

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。