取引におけるニューラルネットワーク：時空間ニューラルネットワーク(STNN)

はじめに

時系列予測は、金融を含むさまざまな分野で重要な役割を果たしています。私たちは、多くの実世界のシステムにおいて、目標変数の動態に関する豊富な情報を含む多次元データを測定できることにすでに慣れています。しかし、多変量時系列データの効果的な分析と予測は、「次元の呪い」によってしばしば困難になります。そのため、分析対象とする過去データのウィンドウを適切に選択することが重要な要素となります。分析対象のデータ範囲が不十分である場合、予測モデルのパフォーマンスが低下し、適切な予測ができなくなることがあります。 

この多変量データの複雑性に対処するため、遅延埋め込み定理に基づいた時空間情報(STI)変換方程式が開発されました。STI方程式は、多変量データの空間情報を目標変数の時間的ダイナミクスへと変換します。これにより、実質的にサンプルサイズが増加し、短期間のデータによる制約を軽減することができます。

Transformerベースのモデルは、すでにデータシーケンスの処理に広く用いられており、自己アテンション（Self-Attention）メカニズムを活用して変数間の関係を分析します。この手法では、変数間の相対的な距離を考慮せず、大域的な情報を捉え、最も重要な特徴に焦点を当てることが可能となり、「次元の呪い」を緩和する効果があります。

研究「Spatiotemporal Transformer Neural Network for Time-Series Forecasting」では、多変量短期時系列の効率的な多段階予測を実現するため、時空間Transformerニューラルネットワーク(STNN: Spatiotemporal Transformer Neural Network)が提案されました。このアプローチは、STI方程式とTransformerフレームワークの利点を組み合わせたものです。

著者は、この手法の主な利点として、以下を強調しています。

1. STNNは、STI方程式を利用して、多変量データの空間情報を目標変数の時間発展へと変換し、サンプルサイズを効果的に増加させる。
2. 数値予測精度を向上させるために、連続アテンションメカニズムを導入。
3. STNNの空間的自己アテンション機構は、多変量データから効率的に空間情報を抽出し、一方で時間的自己アテンション機構は時間発展に関する情報を収集。Transformer構造により、これらの空間情報と時間情報を統合する。
4. STNNモデルは、時系列予測のために力学系の位相空間を再構成できる。

1. STNNアルゴリズム

STNNモデルの目的は、Transformerを用いた学習を通じて非線形変換方程式STIを効果的に解くことです。

STNNモデルは変換方程式STIを活用し、多段階先読み予測をおこなうための2つの専用のアテンションモジュールを備えています。上記の式からも分かるように、時刻tにおけるD-次元の入力データXtはエンコーダーに入力され、エンコーダーは入力変数から有効な空間情報を抽出します。

その後、抽出された空間情報はデコーダーへと送られます。デコーダーは目標変数Y (𝐘t)から長さL-1の時系列を導入し、目標変数の時間発展に関する情報を抽出します。そして、入力変数の空間情報𝐗tと目標変数の時間情報𝐘tを組み合わせることで、目標変数の将来の値を予測します。

目標変数は、多変量入力データXの一部であることに注意してください。

STIの非線形変換はエンコーダーとデコーダーのペアによって解決されます。エンコーダーは2層で構成されています。1つ目は全結合層で、2つ目は連続空間自己アテンション層です。STNN手法の著者は、多変量入力データ𝐗tから効果的な空間情報を抽出するために、連続空間自己アテンション層を活用しています。

全結合層は、入力された多変量時系列データ𝐗tを平滑化し、ノイズを除去する役割を担います。次の図に、単層ニューラルネットワークの構造を示します。

ここで、WFFNは係数の行列
      bFFNはバイアス
      ELUは活性化関数

連続空間自己アテンション層は、入力データとして𝐗t,FFNを受け取ります。自己アテンション層は多変量時系列データを処理できるため、エンコーダーは入力データから空間情報を抽出することが可能です。効果的な空間情報(SSAt)を得るために、連続空間自己アテンション層における継続的アテンションのメカニズムが提案されています。その動作は次のように説明できます。

まず、訓練可能なパラメータを持つ3つの行列（WQE、WKE、WVE）を生成し、これらを連続空間自己アテンション層で使用します。

次に、入力データ𝐗t,FFNにこれらの重み行列を乗じることで、連続空間自己アテンション層のQuery、Key、Valueの各エンティティを生成します。

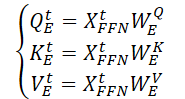
行列のスカラー積を実行することで、入力データ𝐗tに対する重要な空間情報(SSAt)の式が得られます。

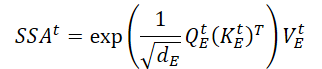
ここで、dEはQuery行列、Key行列、Value行列の次元です。

STNN法の著者は、古典的な離散確率的アテンションのメカニズムとは異なり、提案された連続アテンションのメカニズムがエンコーダーのデータを中断なく伝達できることを強調しています。

エンコーダーの出力では、主要な空間情報テンソルを平滑化された入力データと加算し、その後データを正規化することで、急激な勾配消失を防ぎ、モデルの収束速度を向上させます。

デコーダーは、有効な空間情報と目標変数の時間的進化を組み合わせます。そのアーキテクチャには、2つの全結合層、連続時間自己アテンション層、およびTransformerアテンション層が含まれます。

デコーダーには、目標変数の履歴シーケンスを入力データとして与えます。エンコーダーの場合と同様に、入力データ(𝐘t,FFN)は、全結合層でノイズを除去した後に効率的な表現が得られます。

次に、このデータは連続時間自己アテンション層に送られます。この層は、目標変数の異なる時間ステップ間における時間的変化の履歴情報に焦点を当てます。時間の影響は不可逆であるため、我々は過去の情報を用いて時系列の現在の状態を決定しますが、未来の情報は使用しません。そのため、連続時間アテンション層では、未来の情報をフィルタリングするためにマスクドアテンション機構を使用します。この処理を詳しく見ていきましょう。

まず、時空間自己アテンションのために、訓練可能なパラメータを持つ3つの行列(WQD、WKD、WVD)を生成します。次に、対応するQuery、Key、Valueのエンティティ行列を計算します。

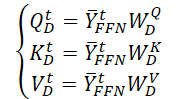
行列スカラー積を実行し、分析目標変数の分析期間中の時間発展に関する情報を得ます。

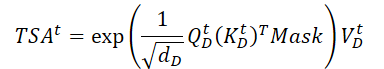
エンコーダーとは異なり、ここでは分析データの後続要素の影響を除去するマスキングを追加します。これにより、目標変数の時間的進化関数を構築する際に、モデルが「未来を参照する」ことを防ぎます。

次に、残差接続を適用し、目標変数の時間的進化に関する情報を正規化します。

目標変数の将来値を予測するために、連続Transformerアテンション層は、空間依存情報(SSAt)と目標変数の時間発展に関するデータ(TSAt)を統合します。

残差関係とデータの正規化もここで使用されます。

デコーダーの出力で、このメソッドの著者は、目標変数の値を予測するために第2の全結合層を使用します。

STNNモデルを訓練する際、この手法の著者は損失関数としてMSEを用い、パラメータにL2正則化を適用しました。

以下は、著者によるこの手法の視覚化です。

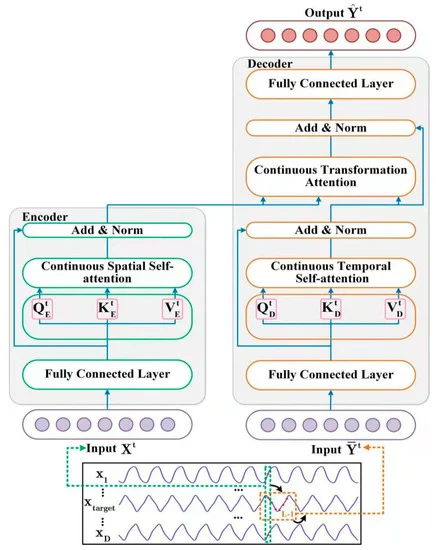
2. MQL5での実装

STNN法の理論的側面を考察した後、本稿の実践的な部分に移り、提案されたアプローチをMQL5で実装します。

本記事では、オリジナルの実装とは異なる可能性がありますが、私たち独自の視点から実装方法を紹介します。また、この実装においては、既存の開発資産を最大限に活用することを試みたため、その影響が結果にも反映されています。この点については、実装を進めながら詳しく説明していきます。

上記のSTNNアルゴリズムの理論的な説明からもわかるように、STNNには2つの主要なブロック（エンコーダーとデコーダー）があります。したがって、私たちの実装も、それぞれのクラスに分けて構築していきます。まずは、エンコーダーの実装から始めましょう。

2.1 STNNエンコーダー

エンコーダーアルゴリズムは、CNeuronSTNNEncoderクラス内で実装します。本手法の著者は、自己アテンションアルゴリズムにいくつかの調整を加えていますが、基本的な構造は従来のアプローチと変わらず、十分に理解しやすいものとなっています。したがって、新しいクラスの実装には既存のコードを活用し、基本的な自己アテンションアルゴリズムの主要機能をCNeuronMLMHAttentionMLKVクラスから継承します。以下に、新クラスの全体構造を示します。

class CNeuronSTNNEncoder  :  public CNeuronMLMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronSTNNEncoder(void)  {};
                    ~CNeuronSTNNEncoder(void)  {};
   //---
   virtual int       Type(void)   override const   {  return defNeuronSTNNEncoder;   }
  };

ご覧のとおり、新しいクラス内には新しい変数やオブジェクトの宣言がありません。さらに、この構造にはオブジェクトの初期化メソッドのオーバーライドすら含まれていません。これには理由があります。前述のとおり、既存の開発を最大限に活用する方針を取っているためです。

まず、提案されたアプローチと、これまでに実装した手法の違いを確認してみましょう。最も大きな違いのひとつは、STNN法では、自己アテンションブロックの前に全結合層が配置されている点です。技術的には、この追加によってフィードフォワードおよびバックプロパゲーションの計算処理が変わるだけで、オブジェクトの宣言自体には影響しません。つまり、この変更が初期化メソッドのアルゴリズムに影響を及ぼすことはありません。

次に、STNN法では全結合層が1層のみとなっています。一方で、従来のアプローチでは、通常2層の全結合層を使用します。私個人の意見としては、全結合層を2層にすると計算コストは増加するものの、モデルの精度が著しく低下することはないと考えています。そのため、既存の実装を最大限活用する観点から、今回は1層ではなく2層の完全連結層を試験的に使用してみます。

さらに、STNN手法の著者は、自己アテンションのスコアを正規化する際にSoftMax関数を使用していません。代わりに、単純にQueryとKeyの内積を指数関数に適用する手法を採用しています。私の考えでは、SoftMaxの主な役割はデータの正規化と、より複雑なスコア計算をおこなうことにあります。したがって、今回の実装では、従来どおりSoftMaxを使用した手法を採用することにします。   

続いて、フィードフォワードアルゴリズムの実装に移ります。ここで気づいた点として、STNN手法の著者は、デコーダー部分にのみマスキングを適用している点が挙げられます。通常、エンコーダーの入力データにも目的変数が含まれる可能性があるため、エンコーダー側でのマスキングがないのはやや不自然に思えました。しかし、著者が示した可視化図を詳しく分析すると、その意図が明確になりました。

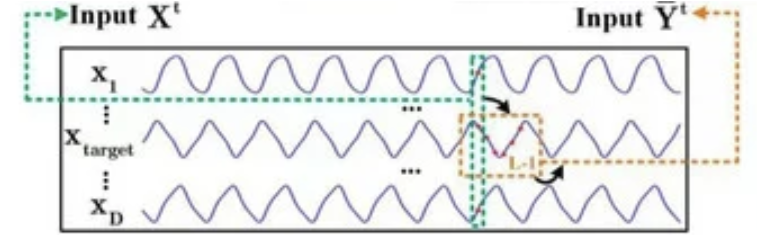
エンコーダーの入力データは、解析対象の状態よりも過去の地点に位置しています。なぜ著者がこのような実装を選択したのかは判断できません。しかし、個人的には、データ分析時点で利用可能な全情報を活用することで、より多くの情報が得られ、予測精度が向上する可能性があると考えています。そこで私の実装では、エンコーダーの入力データを現在の時点にシフトし、初期データにマスクを適用することで、過去のデータのみを考慮して依存関係を分析できるようにしました。

データマスキングを実装するには、OpenCLプログラムに変更を加える必要があります。ただし、ここではMH2AttentionOutカーネルに最小限の変更を加えるだけです。追加のマスキング用バッファは使用せず、よりシンプルな方法を採用します。具体的には、マスキングの有無を制御する定数を1つ追加し、カーネルアルゴリズム内で直接マスキングを適用する形にします。 

__kernel void MH2AttentionOut(__global float *q,
                              __global float *kv,
                              __global float *score,
                              __global float *out,
                              int dimension,
                              int heads_kv,
                              int mask ///< 1 - calc only previous units, 0 - calc all
                             )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);
   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   __local float temp[LOCAL_ARRAY_SIZE];

カーネル本体では、指数の和を計算する際に微調整をするだけです。 

//--- sum of exp
   uint count = 0;
   if(k < ls)
     {
      temp[k] = 0;
      do
        {
         if(mask == 0 || q_id <= (count * ls + k))
            if((count * ls) < (kunits - k))
              {
               float sum = 0;
               int sh_k = 2 * dimension * heads_kv * count * ls;
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * kv[shift_k + d + sh_k];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
               temp[k] = temp[k] + sum;
              }
         count++;
        }
      while((count * ls + k) < kunits);
     }
   barrier(CLK_LOCAL_MEM_FENCE);
   count = min(ls, (uint)kunits);

ここでは条件を追加し、過去の要素に対してのみ指数を計算するようにします。モデルの入力データを作成する際、過去の価格データとインジケーターの時系列データから構成されることに注意してください。時系列データにおいて、現在のバーのインデックスは0です。そのため、過去のデータに対するマスキングを適用するには、現在のQueryよりもインデックスが小さいすべての要素の依存係数をリセットする必要があります。指数の合計や依存係数の計算時（コード内の該当部分で下線が引かれている箇所）に、この処理が反映されているのが確認できます。

//---
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
//--- score
   float sum = temp[0];
   float sc = 0;
   if(mask == 0 || q_id >= (count * ls + k))
      if(sum != 0)
        {
         for(int d = 0; d < dimension; d++)
            sc = q[shift_q + d] * kv[shift_k + d];
         sc = exp(sc / koef) / sum;
         if(isnan(sc))
            sc = 0;
        }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

残りのカーネルコードに変更はありません。

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum =
                  kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

この実装では、単純に次の要素の依存係数をゼロにしています。これにより、フィードフォワードパスのカーネルに最小限の修正を加えるだけで、マスキングを実装できました。さらに、このアプローチではバックプロパゲーションのカーネルを調整する必要がありません。なぜなら、依存係数が0である要素に対しては、誤差勾配が自動的にゼロになるためです。

これでOpenCLプログラム側の修正は完了です。次に、メインプログラムの作業に移ります。

ここではまず、CNeuronSTNNEncoder::AttentionOutメソッド内で、先ほどのカーネルを呼び出す処理を追加します。カーネルの実行キューへの登録アルゴリズムは変更されていません。添付ファイルにあるコードをご自身で勉強してください。ただし、データマスキングを適用するために、def_k_mh2ao_maskパラメータが1に設定されている点に注目してください。

次に、新しいクラスのフィードフォワードパスの実装に移ります。このメソッドをオーバーライドすることで、FeedForwardブロックをSelf-Attentionより前に配置できるようにします。また、従来のTransformerとは異なり、FeedForwardブロックには残差関係やデータの正規化がないことにも注意すべきです。

アルゴリズムを実装する前に、親クラスの初期化時に不要なデータコピーを防ぐための工夫を思い出してください。 具体的には、この層の結果バッファと誤差勾配バッファのポインタを、FeedForwardブロックの最後の層のバッファと共有する形にしました。このアプローチは、アテンションブロックとFeedForwardブロックの結果バッファサイズが同一であることを利用しています。そのため、アクセス時のインデックス調整をおこなうだけで、データの整合性を保つことができます。

では、実装を見ていきましょう。従来と同様に、このメソッドのパラメータには、入力データを提供する前の層のオブジェクトへのポインタが含まれています。

bool CNeuronSTNNEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

メソッドの冒頭で、受け取ったポインタが有効かどうかを検証します。この検証が完了したら、そのままフィードフォワードアルゴリズムの構築に進みます。ここで、本実装とSTNN法のオリジナル実装との重要な違いをもう一つ強調しておきます。STNN法の著者は、エンコーダー層の数やアテンションヘッドの数を明示していません。先に示した手法の視覚化や説明から推測すると、1つのエンコーダー層には1つのアテンションヘッドのみが存在する可能性があります。しかし、本実装では従来のTransformerのアプローチを採用し、マルチヘッドアテンションを用いた多層アーキテクチャを構築します。この設計に基づき、ネストされたエンコーダー層を順番に処理するためのループを構成します。

ループ内では、前述のとおり、入力データはまずFeedForwardブロックを通過します。 ここで、データの平滑化とフィルタリングがおこなわれます。

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Feed Forward
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
      CBufferFloat *temp = FF_Tensors.At(i * 6 + 1);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, 
                                                                      iWindow, 4 * iWindow, LReLU))
         return false;
      inputs = FF_Tensors.At(i * 6);
      if(IsStopped() ||
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, inputs, 
                                                                       4 * iWindow, iWindow, None))
         return false;

その後、Query、Key、Value各エンティティの行列を定義します。

      //--- Calculate Queries, Keys, Values
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
        !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                          iWindow, iWindowKey * iHeads, None))
         return false;
      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, 
                                                      iWindow, 2 * iWindowKey * iHeadsKV, None))
            return false;
        }

なお、本実装では親クラスから継承されたMLKVメソッドのアプローチを使用している点に注意してください。このアプローチにより、複数のアテンションヘッドおよび自己アテンション層で、1つのKey-Valueバッファを共有することが可能になります。

次に、得られたデータを基に、マスキングを考慮した依存係数を計算します。

      //--- Score calculation and Multi-heads attention calculation
      temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

次に、残差接続とデータの正規化を考慮して、注目層の結果を計算します。

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 6 + 2);
      if(IsStopped() || 
        !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                      iWindowKey * iHeads, iWindow, None))
         return false;
      //--- Sum and normilize attention
      if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true))
         return false;
     }
//---
   return true;
  }

そして、次のネストされた層へと処理を進めます。すべての層の処理が完了したら、メソッドを終了します。

同様の方法で、ただし処理の順序を逆にして、誤差勾配の伝播をおこなうメソッドCNeuronSTNNEncoder::calcInputGradientsのアルゴリズムを構築します。このメソッドはパラメータとして、前の層のオブジェクトへのポインタを受け取る点は同じですが、今回はモデルの出力に対する入力の影響を考慮した誤差勾配を渡す必要があります。

bool CNeuronSTNNEncoder::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(CheckPointer(prevLayer) == POINTER_INVALID)
      return false;
//---
   CBufferFloat *out_grad = Gradient;
   CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);

メソッド本体では、前回と同様、受け取ったポインタの正しさを確認します。また、データバッファのオブジェクトへのポインタを一時的に格納するためのローカル変数も宣言します。

次に、エンコーダーのネストした層を反復するループを宣言します。

   for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--)
     {
      if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0)
         kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1);
      //--- Split gradient to multi-heads
      if(IsStopped() ||
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, 
                                   AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None))
         return false;

ループ本体では、まず、後続層で得られた誤差勾配を注目ヘッド間に分配します。その後、Query、Key、Value各エンティティレベルで誤差を判断します。

      //--- Passing gradient to query, key and value
      if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0)
        {
         if(IsStopped() ||
           !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), 
                                     KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, 
                                     S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1)))
            return false;
        }
      else
        {
         if(IsStopped() || 
           !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), 
                                     KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), 
                                     S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1)))
            return false;
         if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1))
            return false;
        }

これは、現在の層によって、Key-Valueテンソルへの誤差勾配の分配方法が異なるために発生します。

次に、残差接続を考慮しながら、QueryエンティティからFeedForwardブロックへ誤差勾配を伝播させます。

      CBufferFloat *inp = FF_Tensors.At(i * 6);
      CBufferFloat *temp = FF_Tensors.At(i * 6 + 3);
      if(IsStopped() || 
        !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), 
                                                                  inp, temp, iWindow, iWindowKey * iHeads, None))
         return false;
      //--- Sum and normilize gradients
      if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1))
         return false;

必要に応じて、KeyおよびValueエンティティへの影響に対する誤差を追加します。

      if((i % iLayersToOneKV) == 0)
        {
         if(IsStopped() || 
           !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, 
                                                         GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1))
            return false;
        }

次に、FeedForwardブロックを通して誤差勾配を伝播させます。

      //--- Passing gradient through feed forward layers
      if(IsStopped() ||
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, 
                                   FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None))
         return false;
      inp = (i > 0 ? FF_Tensors.At(i * 6 - 4) : prevLayer.getOutput());
      temp = (i > 0 ? FF_Tensors.At(i * 6 - 1) : prevLayer.getGradient());
      if(IsStopped() || 
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), 
                                                                           inp, temp, iWindow, 4 * iWindow, LReLU))
         return false;
      out_grad = temp;
     }
//---
   return true;
  }

ループの反復は、すべてのネストされた層が処理され、最終的に誤差勾配が前の層へ伝播されるまで続きます。

誤差勾配が分配された後の次のステップは、モデルのパラメータを最適化し、全体の予測誤差を最小限に抑えることです。これらの操作は、CNeuronSTNNEncoder::updateInputWeightsメソッドに実装されています。このメソッドのアルゴリズムは、親クラスの同様のメソッドとほぼ同じで、唯一の違いはデータバッファの指定方法です。そのため、ここでは詳しく説明しません。興味がある方は、添付資料を参考にしてください。また、エンコーダークラスの完全なコードとすべてのメソッドもそちらに含まれています。

2.2 STNNデコーダー

エンコーダーの実装が完了したら、次の作業として、STNN法のデコーダーアルゴリズムの開発に移ります。ここでも、エンコーダーの構築時と同じ原則に従い、可能な限り既存のコードを再利用する方針で進めます。

デコーダーアルゴリズムの実装を開始するにあたり、エンコーダーとの重要な違いを理解しておくことが重要です。特に、新しいクラスはクロスアテンションオブジェクトを継承する点が大きな違いとなります。これは、デコーダーが空間情報と時間情報のマッピングをおこなうために必要な構造です。新しいクラスの全体構造を以下に示します。

class CNeuronSTNNDecoder   :  public CNeuronMLCrossAttentionMLKV
  {
protected:
   CNeuronSTNNEncoder      cEncoder;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override;
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                       CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override;

public:
                     CNeuronSTNNDecoder(void) {};
                    ~CNeuronSTNNDecoder(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, 
                          uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, 
                          uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronSTNNDecoder;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

このクラスでは、以前作成したエンコーダーのネストされたオブジェクトを宣言しています。ただし、この場合、それは少し異なる目的で使用される点に注意が必要です。

第1回の記事で説明した理論的な背景に立ち返ると、空間的依存関係と時間的依存関係を特定するブロックには共通点があることが分かります。両者の違いは、分析対象となる入力データの種類にあります。空間的依存関係のブロックでは、短い時間間隔の中で多数のパラメータを分析するのに対し、時間的依存関係のブロックでは、特定の過去の期間にわたって目的変数を分析します。このような違いはあるものの、アルゴリズム自体は非常に類似しています。したがって、本ケースではネストされたエンコーダーを活用し、目的変数の時間的依存関係を特定します。

では、メソッドのアルゴリズムの説明に戻りましょう。たとえ静的なオブジェクトであっても、追加のネストオブジェクトを宣言する場合は、クラスの初期化メソッドInitをオーバーライドする必要があります。しかし、これまで開発してきたコンポーネントの再利用を重視した結果、新しい初期化メソッドは非常にシンプルなものとなりました。

bool CNeuronSTNNDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, 
                              uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, 
                              uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!cEncoder.Init(0, 0, open_cl, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, 
                                                                                        optimization_type, batch))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::Init(numOutputs, myIndex, open_cl, window, window_key, heads, window_kv, heads_kv, 
                                        units_count, units_count_kv, layers, layers_to_one_kv, optimization_type, batch))
      return false;
//---
   return true;
  }

こここでは、ネストされたエンコーダーと親クラスのメソッドを、それぞれの引数に同じパラメータ値を指定して単純に呼び出します。私たちの役割は、演算結果を検証し、得られたブール値を呼び出し元のプログラムへ返すことに限られます。

同様のアプローチは、フィードフォワードやバックプロパゲーションの処理にも見られます。例えば、フォワードパスのメソッドでは、まず関連するエンコーダーのメソッドを呼び出し、目標変数の値における時間的依存関係を特定します。次に、特定された時間的依存関係を、STNNモデルのエンコーダーから取得した空間的依存関係と統合します。この統合は、本メソッドのコンテキストパラメータを介しておこなわれ、親クラスから継承されたフィードフォワードのメカニズムを用いて実行されます。

bool CNeuronSTNNDecoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.FeedForward(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::feedForward(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

STNN法の著者が提案したアルゴリズムから逸脱した点をいくつか挙げておきます。私たちは全体的なコンセプトを維持しつつも、具体的な実装方法においては大きな自由を取り入れました。

保持した要素

• 時間的依存関係の特定
• 目標変数の値を予測するための時間的・空間的依存関係の調整

しかし、エンコーダーと同様に、著者が提案した単一層のアーキテクチャではなく、2つの全結合層からなるFeedForwardブロックを使用しています。これは、時間依存性を特定する前のデータフィルタリングと、デコーダー出力での目標変数値の予測の両方に適用されます。

さらに、クロスアテンションの実装には親クラスのフィードフォワードパスを使用しました。これにより、アテンションブロックとFeedForwardブロックの間に残差接続を持つ、クラシックな多層クロスアテンションアルゴリズムを適用しています。これは、STNN法の著者が提案したクロスアテンションアルゴリズムとは異なるアプローチです。

とはいえ、特に「過去に開発したコンポーネントを最大限に再利用する」という本実験の目的を考慮すると、この実装は十分に合理的であると考えています。

また、時間依存性ブロックやクロスアテンションブロックでは多層構造を採用しているにもかかわらず、デコーダー全体のアーキテクチャは単層構造のままであることにも注目してください。言い換えれば、まずず多層のネスト化されたエンコーダーで時間的依存関係を特定し、多層のクロスアテンションブロックを使用し、時間的・空間的依存関係を比較した上で目標変数の値を予測します。

（逆伝播処理）も同様のアプローチで構築されていますが、ここでは詳しく触れません。詳細は、添付ファイルのコードを参照しながら確認してみてください。

これで、新たに導入したオブジェクトのアーキテクチャとアルゴリズムに関する説明は完了です。コンポーネントの完全なコードは、添付ファイルに含まれていますので、ご確認ください。

2.3 モデルアーキテクチャ

提案されたSTNN法の実装アルゴリズムを詳しく検討した後、次に学習可能なモデルへの実用的な応用へと進みます。ここで重要なのは、本アルゴリズムにおけるエンコーダーとデコーダーが、それぞれ異なる入力データを処理するという点です。この違いを考慮し、エンコーダーとデコーダーを別々のモデルとして実装することにしました。それぞれのモデルのアーキテクチャは、CreateStateDescriptionsメソッドで定義されています。

このメソッドのパラメータとして、2つの動的配列へのポインタが含まれており、それらを利用して各モデルのアーキテクチャを設定します。

bool CreateStateDescriptions(CArrayObj *&encoder, CArrayObj *&decoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//---
   if(!decoder)
     {
      decoder = new CArrayObj();
      if(!decoder)
         return false;
     }

メソッド本体では、受け取ったポインタを確認し、必要であれば新しいオブジェクトインスタンスを生成します。

エンコーダーに、すでにおなじみの生のデータセットを入力します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

データはバッチ正規化層で前処理されます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次にSTNNエンコーダー層が来ます。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSTNNEncoder;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = 32;
   descr.layers   =  4;
   descr.step = 2;
     {
      int ar[] = {8, 4};
      if(ArrayCopy(descr.heads, ar) < (int)ar.Size())
         return false;
     }
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

ここでは、4つのネストされたエンコーダー層を使用します。各層は、Queryエンティティの8つのアテンションヘッドと、Key-Valueテンソルの4つアテンションヘッドを使用します。さらに、1つのKey-Valueテンソルは、2つのネストされたエンコーダー層に使用されます。

これでエンコーダーモデルのアーキテクチャは完成です。その出力をデコーダーで使用します。

デコーダーに目標変数の過去の値を入力します。分析された履歴の深さは、私たちの計画期間に対応しています。

//--- Decoder
   decoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (NForecast * ForecastBarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

ここでは、バッチデータ正規化層に供給される生データも使用します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

次にSTNNデコーダー層が続きます。そのアーキテクチャには、4つのネストされた時間的アテンション層およびクロスアテンション層も含まれています。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSTNNDecoder;
     {
      int ar[] = {NForecast, HistoryBars};
      if(ArrayCopy(descr.units, ar) < (int)ar.Size())
         return false;
     }
     {
      int ar[] = {ForecastBarDescr, BarDescr};
      if(ArrayCopy(descr.windows, ar) < (int)ar.Size())
         return false;
     }
     {
      int ar[] = {8, 4};
      if(ArrayCopy(descr.heads, ar) < (int)ar.Size())
         return false;
     }
   descr.window_out = 32;
   descr.layers   =  4;
   descr.step = 2;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

デコーダーの出力では、目標変数の予測値が得られると予想されます。バッチ正規化層で抽出された統計変数をこれらに加えます。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = ForecastBarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、予測時系列の周波数特性を揃えます。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = ForecastBarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ActorモデルとCriticモデルのアーキテクチャーは、以前の記事と変更なく、本記事の添付ファイル（ファイル...\Experts\STNN\Trajectory.mqh）にあるCreateDescriptionsメソッドで示されています。

2.4 モデル訓練プログラム

環境状態エンコーダーを2つのモデルに分離したことで、それらの訓練プログラムにも変更が必要となりました。アルゴリズムを2つのモデルに分けただけでなく、入力データと目標値の準備にも修正が加えられています。これらの調整については、環境状態エンコーダーの学習用EA「...\Experts\STNN\StudyEncoder.mq5」を例に説明します。

このEAでは、特定の時点での取引判断をおこなうために十分な計画期間において、今後の価格変動を予測するモデルを訓練します。

本記事では、プログラムのすべての手順について詳細には触れず、モデルの訓練メソッドであるTrainに焦点を当てます。まず、このメソッドでは、経験生成バッファ内の軌道を、それぞれの実際の履歴データ上でのパフォーマンスに基づいて選択する確率を決定します。

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target, state;
   matrix<float> mstate = matrix<float>::Zeros(1, NForecast * ForecastBarDescr);
   bool Stop = false;

また、必要最小限のローカル変数を宣言します。その後、モデルを訓練するためのループを構成します。ループの繰り返し回数は、EAの外部パラメータでユーザーが定義します。

   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }
      state.Assign(Buffer[tr].States[i].state);
      if(MathAbs(state).Sum() == 0)
        {
         iter--;
         continue;
        }

ループ本体では、モデル最適化の反復を実行するために、軌道とその上の状態をサンプリングします。まず、エンコーダーのフィードフォワードパスメソッドを呼び出すことによって、分析された変数間の空間依存性の検出を実行します。

      bStateE.AssignArray(state);
      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bStateE), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

次にデコーダーの入力を準備します。一般的に、計画期間は分析された履歴の深さより小さいと仮定します。そこで、まず分析した環境状態の履歴データを行列に移します。行列の各行が履歴データの1バーのデータを表すようにサイズを変更します。そして、行列をトリミングします。結果の行列の行数は計画期間に対応し、列数は目標変数に対応する必要があります。

      mstate.Assign(state);
      mstate.Reshape(HistoryBars, BarDescr);
      mstate.Resize(NForecast, ForecastBarDescr);
      bStateD.AssignArray(mstate);

ここで注意すべき点は、学習データセットを準備する際に、まず各バーの値動きに関するパラメータを記録したことです。これらの値は、今後の予測対象となるものです。そのため、行列の最初の列を取り出します。

その後、得られた行列の値をデータバッファに転送し、デコーダーを通じてフィードフォワードパスを実行します。

      if(!Decoder.feedForward((CBufferFloat*)GetPointer(bStateD), 1, false, GetPointer(Encoder)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

フィードフォワードパスの実行後、モデルのパラメータを最適化する必要があります。そのためには、予測対象となる変数の目標値を準備しなければなりません。この操作はデコーダーの入力準備と似ていますが、過去の時系列データの後続の値に対して実行されます。

      //--- Collect target data
      mstate.Assign(Buffer[tr].States[i + NForecast].state);
      mstate.Reshape(HistoryBars, BarDescr);
      mstate.Resize(NForecast, ForecastBarDescr);
      if(!Result.AssignArray(mstate))
         continue;

デコーダーのバックプロパゲーションパスを実行します。ここでは、デコーダーのパラメータを最適化し、誤差勾配をエンコーダーに渡します。

      if(!Decoder.backProp(Result, GetPointer(Encoder)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

その後、エンコーダーのパラメータを最適化します。

      if(!Encoder.backPropGradient((CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

そして、学習の進捗状況をユーザーに知らせ、学習サイクルの次の反復に移ります。

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Decoder", 
                                       percent, Decoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

すべての訓練反復が正常に完了した後、モデルの訓練結果を記録し、プログラムのシャットダウン処理を初期化します。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError());
   ExpertRemove();
//---
  }

これでモデル訓練アルゴリズムの話題は終わりです。また、ここで使用されているすべてのプログラムの完全なコードは添付ファイルにあります。

3.テスト

本稿では、時空間情報STNNに基づく新しい時系列予測手法を紹介しました。MQL5を用いて提案手法の実装をおこない、いよいよその成果を評価する段階です。

いつものように、2023年通年のH1時間枠のEURUSDの履歴データを使用してモデルを訓練します。次に、2024年1月のデータを使って、MetaTrader 5のストラテジーテスターで訓練済みモデルをテストします。テスト期間が学習期間に直結していることにお気づきでしょう。この手法により、モデルが実際の市場環境でどのように動作するかを忠実に再現できます。

その後の値動きを予測するモデルの訓練には、本シリーズの過去の記事執筆時に収集した訓練用データセットを使用します。ご存じのように、このモデルの訓練は過去の価格変動データと分析対象の指標のみに基づいています。エージェントの行動が分析データに影響を与えないため、学習データセットを定期的に更新する必要はありません。そのため、一貫した環境で環境状態エンコーダーモデルを訓練できます。

学習は予測誤差が安定するまで継続しました。しかし、この段階で期待外れの結果に直面しました。私たちのモデルは、今後の値動きを正確に予測することができず、トレンドのおおよその方向を示すにとどまりました。

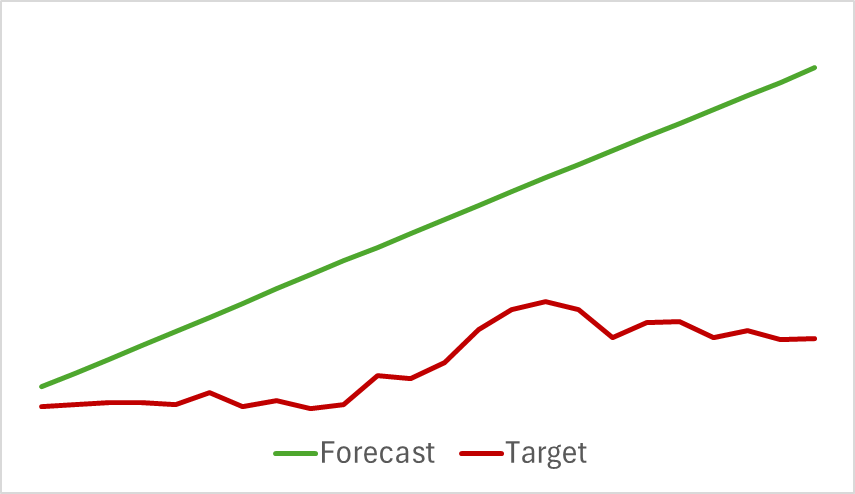
予測された値動きは直線的に見えましたが、デジタル化された数値には依然としてわずかな変動が見られました。ただし、これらの変動は極めて小さく、グラフ上では視覚的に確認することができませんでした。ここで疑問が生じます。このわずかな変動を活用して、Actorにとって利益を生み出す戦略を構築することは可能なのでしょうか。

ActorモデルとCriticは、定期的なデータセットの更新をおこないながら、反復的に訓練します。ご存じのように、Actorの方針は学習中に変化するため、その行動をより正確に評価するには、学習データセットの定期的な更新が不可欠です。

しかしながら、テストデータセット上で一貫した利益を生み出すようにActorの方針を最適化することはできませんでした。

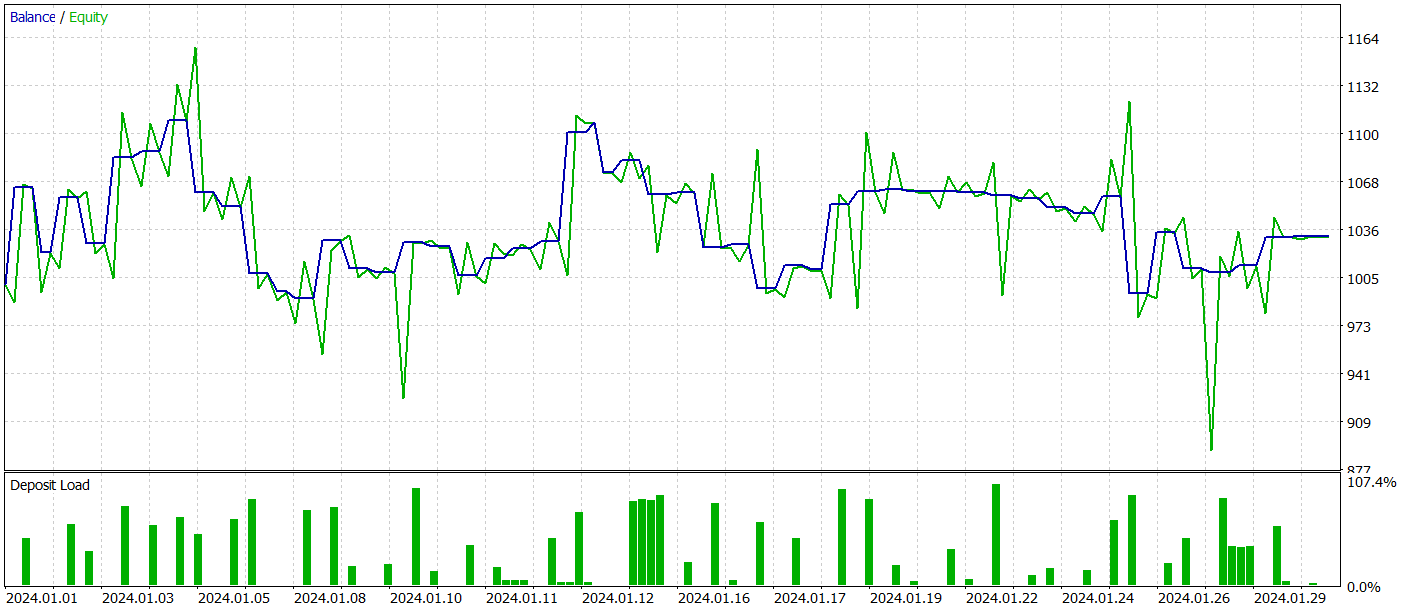
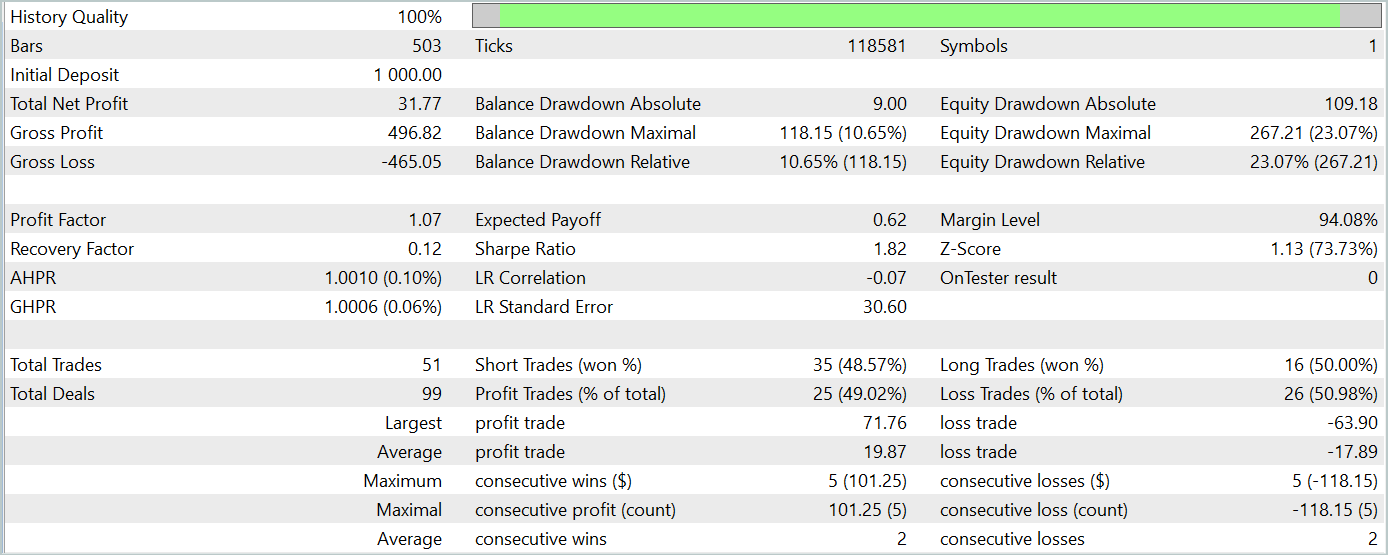
とはいえ、私たちの作業の過程で、元の手法の実装から大きく逸脱した点があり、それが得られた結果に影響を及ぼした可能性があることを認めざるを得ません。

結論

本稿では、時空間変換型ニューラルネットワーク(STNN)を用いた時系列予測の新たなアプローチを探求しました。このモデルは、時空間情報(STI)変換方程式とTransformer構造の利点を組み合わせることで、短期時系列データにおける多段階予測を効果的におこないます。

STNNは、多次元変数の空間情報を目標変数の時間情報へと変換するSTI方程式を採用しています。これは、サンプルサイズを拡張するのと同等の効果を持ち、短期間のデータ不足という課題を克服するのに役立ちます。

また、数値予測の精度を向上させるために、STNNには連続アテンションメカニズムが組み込まれています。これにより、モデルはデータの重要な側面により適切に注目し、予測の精度を向上させることができます。

実践的な部分では、MQL5言語を用いて提案手法の実装をおこないました。しかしながら、元のアルゴリズムから大きく逸脱した点があり、その影響が実験結果に表れた可能性があります。

参照文献

Spatiotemporal Transformer Neural Network for Time-Series Forecasting

Predicting future dynamics from short-term time series using an Anticipated Learning Machine

本連載の他の記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコーダー訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ