
Algoritmo de otimização caótica — Chaos optimization algorithm (COA): Continuação
Conteúdo
Introdução
No artigo anterior, nos familiarizamos com o método de otimização caótica e analisamos parte dos métodos que compõem o algoritmo. Neste artigo, finalizaremos a análise dos métodos restantes e passaremos diretamente ao teste do algoritmo em funções de teste.
O método de otimização caótica, nesta implementação, utiliza caos determinístico para explorar o espaço de soluções. O princípio-chave é a aplicação de três diferentes mapeamentos caóticos, logístico, sinusoidal e tent mapping, para a geração de sequências que possuem propriedades de pseudoaleatoriedade e ergodicidade. O algoritmo opera em três fases: busca caótica inicial, refinamento da solução pelo método do gradiente ponderado e busca local final com estreitamento adaptativo da região.
O uso de vetores de velocidade com inércia e mecanismos de detecção de estagnação permite evitar extremos locais. A adaptação dinâmica de parâmetros e diferentes tipos de mutações garantem o equilíbrio entre a exploração global e a exploração local das soluções encontradas. Isso é um resumo do principal e, agora, continuemos a analisar os métodos restantes.
Implementação do algoritmo
O método "ApplyMutation" é destinado à introdução de mutações em um agente. Sua principal tarefa é a modificação aleatória dos parâmetros de um agente específico.
O método começa com a verificação da correção do índice do agente especificado. Se o índice estiver fora do intervalo permitido, a execução do método é encerrada. Em seguida, é realizada a coleta de informações sobre o tamanho de diferentes arrays associados ao agente, como os tamanhos de seus parâmetros e das velocidades. Isso permite evitar acessos fora dos limites desses arrays durante a execução do método.
O método calcula o número máximo de coordenadas que podem ser alteradas, com base nos tamanhos dos arrays disponíveis, para garantir a segurança das operações. É selecionado um número aleatório que determina quantas coordenadas serão submetidas à mutação. Esse valor varia de 1 até 30% do número máximo de coordenadas disponíveis. Forma-se um array de índices que representa as coordenadas que podem ser alteradas. Esse array é embaralhado para garantir a seleção aleatória durante a aplicação das mutações.
No loop ocorre a seleção das coordenadas para mutação a partir do array embaralhado. Para cada coordenada selecionada, é determinado o tipo de mutação com base em um valor aleatório. Os tipos possíveis incluem mutação totalmente aleatória, na qual o novo valor é escolhido aleatoriamente dentro de um intervalo especificado, mutação em relação à melhor solução global e mutação com uso de mapeamentos caóticos.
Após a alteração do valor para cada coordenada, a velocidade do agente é redefinida, para que o novo valor não sofra influência das velocidades anteriores. Por fim, o novo valor da coordenada correspondente do agente é definido levando em conta os intervalos e os passos, o que garante que os valores permaneçam dentro dos limites permitidos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ApplyMutation (int agentIdx) { // Определяем количество координат для мутации (от 1 до 30% координат) int mutationCount = 1 + (int)(u.RNDprobab () * coords * 0.3); mutationCount = MathMin (mutationCount, coords); // Создаем массив индексов для мутации без повторений int mutationIndices []; ArrayResize (mutationIndices, coords); // Заполняем массив индексами for (int i = 0; i < coords; i++) { mutationIndices [i] = i; } // Перемешиваем индексы for (int i = coords - 1; i > 0; i--) { int j = (int)(u.RNDprobab () * (i + 1)); if (j <= i) // Дополнительная проверка для безопасности { int temp = mutationIndices [i]; mutationIndices [i] = mutationIndices [j]; mutationIndices [j] = temp; } } // Применяем мутации к выбранным координатам for (int m = 0; m < mutationCount; m++) { int c = mutationIndices [m]; // Различные типы мутаций для разнообразия double r = u.RNDprobab (); double x; if (r < 0.3) { // Полная случайная мутация x = rangeMin [c] + u.RNDprobab () * (rangeMax [c] - rangeMin [c]); } else if (r < 0.6) { // Мутация относительно глобального лучшего double offset = (u.RNDprobab () - 0.5) * (rangeMax [c] - rangeMin [c]) * 0.2; x = cB [c] + offset; } else { // Мутация с использованием хаотического отображения agent [agentIdx].gamma [c] = SelectChaosMap (agent [agentIdx].gamma [c], (epochNow + c) % 3); x = rangeMin [c] + agent [agentIdx].gamma [c] * (rangeMax [c] - rangeMin [c]); } // Сбрасываем скорость agent [agentIdx].velocity [c] = 0.0; // Применяем новое значение с проверкой диапазона a [agentIdx].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
O método "UpdateSigma" na classe é responsável pela adaptação dinâmica do parâmetro de penalização, que é utilizado no processo de otimização. Ele ajusta o valor da penalização dependendo da quantidade de soluções viáveis na população de agentes.
Se o método for chamado pela primeira vez, quando a época é igual a 1, o valor da penalização atual (currentSigma) é definido como metade do valor base (sigma). O método percorre toda a população de agentes e contabiliza o número de soluções viáveis. Para isso, é utilizada uma função auxiliar que determina se um agente é viável. Nesse ponto, é realizada a iteração por todos os agentes, o que permite determinar quantos deles atendem aos critérios estabelecidos.
Em seguida, o método calcula a proporção de soluções viáveis em relação à população total, dividindo o número de soluções viáveis pelo número total de agentes. Essa relação ajuda a compreender o quão bem a estratégia atual está funcionando. Com base na proporção calculada de soluções viáveis, o método toma decisões sobre o ajuste da penalização: se a proporção de soluções viáveis for inferior a 30%, isso indica que o algoritmo está excessivamente rigoroso, e a penalização é aumentada para forçar os agentes a apresentarem maior diversidade em suas soluções. Se, por outro lado, a proporção ultrapassar 70%, isso indica que muitos agentes encontram soluções viáveis, e a penalização é reduzida para evitar convergência prematura.
Ao final, o método garante que o valor da penalização atual permaneça dentro de limites aceitáveis. Se ele se tornar muito pequeno, inferior a 10% do valor base, a penalização é elevada até esse nível. De forma análoga, se a penalização exceder 500% do valor base, ela é limitada a esse patamar.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateSigma () { // Динамическая адаптация параметра штрафа // Начинаем с малого значения и увеличиваем его при необходимости if (epochNow == 1) { currentSigma = sigma * 0.5; return; } // Подсчет количества допустимых решений int feasibleCount = 0; for (int i = 0; i < popSize; i++) { if (IsFeasible (i)) { feasibleCount++; } } double feasibleRatio = (double)feasibleCount / MathMax (1, popSize); // Адаптация параметра штрафа в зависимости от доли допустимых решений if (feasibleRatio < 0.3) { // Слишком мало допустимых решений - увеличиваем штраф currentSigma *= 1.2; } else if (feasibleRatio > 0.7) { // Слишком много допустимых решений - уменьшаем штраф currentSigma *= 0.9; } // Ограничиваем значение sigma if (currentSigma < sigma * 0.1) currentSigma = sigma * 0.1; else if (currentSigma > sigma * 5.0) currentSigma = sigma * 5.0; } //——————————————————————————————————————————————————————————————————————————————
O método "IsFeasible" determina se uma solução específica, representada por um agente com o índice especificado "agentIdx", é viável (feasible) em relação às restrições definidas.
Primeiramente, o método verifica se o índice do agente especificado (agentIdx) está dentro do intervalo permitido, isto é, maior ou igual a 0 e menor que o tamanho da população (popSize). Se o índice for incorreto, o método retorna "false", sinalizando a inviabilidade da solução. Se o índice do agente for válido, o método prossegue para a verificação das restrições dessa solução. Ele percorre todas as coordenadas (coords) da solução e, para cada coordenada, calcula o valor de violação da restrição por meio da função "CalculateConstraintValue".
A função "CalculateConstraintValue" retorna um valor que reflete o grau de violação das restrições para uma coordenada específica da solução. Se, após a verificação de todas as coordenadas, nenhuma restrição for violada, isto é, todos os valores de violação forem menores ou iguais a "eps", a solução é considerada viável, e o método retorna "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsFeasible (int agentIdx) { // Проверяем, находится ли решение в допустимой области for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); if (violation > eps) { return false; } } return true; } //——————————————————————————————————————————————————————————————————————————————
O método "UpdateBestHistory" é necessário para armazenar o melhor valor atual no histórico da busca. Ele recebe um novo melhor valor e, inicialmente, verifica sua correção ou viabilidade. Se o valor for válido, ele é salvo no array que armazena o histórico dos melhores resultados, na posição indexada atual. Em seguida, o índice é atualizado para o próximo armazenamento, utilizando atualização cíclica por meio da operação de resto da divisão pelo tamanho do array de histórico, o que garante o preenchimento contínuo do histórico com os últimos 10 valores, sem ultrapassar os limites do array.
Esse método permite acompanhar o progresso da busca e utilizar o histórico das melhores soluções para análise.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateBestHistory (double newBest) { // Защита от некорректных значений if (!MathIsValidNumber (newBest)) return; // Обновляем историю лучших значений globalBestHistory [historyIndex] = newBest; historyIndex = (historyIndex + 1) % 10; } //——————————————————————————————————————————————————————————————————————————————
O método "IsConverged" é destinado a determinar se o algoritmo atingiu um estado de convergência. Ele analisa o histórico das melhores soluções globais para avaliar o quão significativas são as melhorias das soluções ao longo do tempo. Se as melhorias se tornarem insignificantes, considera-se que o algoritmo convergiu.
O método inicializa variáveis para contabilizar a quantidade de valores viáveis, a soma dos valores, o valor mínimo e o valor máximo a partir do histórico das melhores soluções globais (globalBestHistory). As variáveis "minVal" e "maxVal" são inicializadas, respectivamente, com o maior e o menor valor possível do tipo "double", para permitir a correta determinação dos valores mínimo e máximo posteriormente.
O método itera pelo array "globalBestHistory" e, para cada valor no histórico, realiza verificações de viabilidade dos valores, suficiência dos dados e diversidade, calcula o valor médio e a diferença relativa, e verifica a convergência. De modo geral, o método "IsConverged" fornece uma forma de determinar a convergência do algoritmo de otimização, analisando o histórico das melhores soluções e avaliando o quão significativas são as melhorias ao longo do tempo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsConverged () { // Проверка достаточного количества данных в истории int validValues = 0; double sum = 0.0; double minVal = DBL_MAX; double maxVal = -DBL_MAX; // Находим min, max и sum значений в истории for (int i = 0; i < 10; i++) { if (globalBestHistory [i] == -DBL_MAX || !MathIsValidNumber (globalBestHistory [i])) continue; minVal = MathMin (minVal, globalBestHistory [i]); maxVal = MathMax (maxVal, globalBestHistory [i]); sum += globalBestHistory [i]; validValues++; } // Если недостаточно данных или все значения одинаковые if (validValues < 5 || minVal == maxVal) return false; // Вычисляем среднее значение double average = sum / validValues; // Проверка случая, когда среднее близко к нулю if (MathAbs (average) < eps) return MathAbs (maxVal - minVal) < eps * 10.0; // Относительная разница для проверки сходимости double relDiff = MathAbs (maxVal - minVal) / MathAbs (average); return relDiff < 0.001; // Порог сходимости - 0.1% } //——————————————————————————————————————————————————————————————————————————————
O método "ResetStagnatingAgents" é destinado ao gerenciamento dos agentes no processo de otimização, especialmente para lidar com casos em que os agentes deixam de demonstrar melhorias em seus resultados. Ele monitora o estado de estagnação dos agentes e, quando necessário, aplica mutação àqueles que ficaram presos em extremos locais.
Para cada agente, é verificado se o valor atual da função de fitness (a[i].f) melhorou em comparação com o valor anterior (a[i].fB). Se o valor atual não tiver melhorado ou tiver piorado, o "stagnationCounter" desse agente é incrementado, sinalizando que o agente se encontra em estado de estagnação. Caso o valor tenha melhorado, o contador de estagnação é zerado.
Se o agente permanecer em estagnação por mais de 5 iterações, o método calcula a probabilidade de reset (resetProb). Essa probabilidade é proporcional ao valor atual do contador de estagnação, o que significa que quanto mais tempo o agente permanece estagnado, maior é a probabilidade de seu reset. A fórmula de cálculo da probabilidade considera um valor fixo (0.2) e o valor relativo do contador de estagnação. Se um valor gerado aleatoriamente for menor que a probabilidade calculada "resetProb", é aplicada uma mutação ao agente por meio da função "ApplyMutation". Após a aplicação da mutação, o contador de estagnação do agente é zerado, e o contador "resetCount" é incrementado.
O método encerra sua execução após processar todos os agentes, realizando o reset daqueles que ultrapassaram o limiar de estagnação e atenderam às condições para mutação.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ResetStagnatingAgents () { int resetCount = 0; for (int i = 0; i < popSize; i++) { // Увеличиваем счетчик стагнации, если нет улучшения if (a [i].f <= a [i].fB) { agent [i].stagnationCounter++; } else { agent [i].stagnationCounter = 0; } // Сбрасываем агента, если он находится в стагнации слишком долго if (agent [i].stagnationCounter > 5) { // Сброс только части агентов с вероятностью, зависящей от стагнации double resetProb = 0.2 * (1.0 + (double)agent [i].stagnationCounter / 10.0); if (u.RNDprobab () < resetProb) { ApplyMutation (i); agent [i].stagnationCounter = 0; resetCount++; } } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateWeightedGradient" é utilizado para avaliar o gradiente da restrição para um agente e uma coordenada específicos, levando em consideração o grau de violação dessas restrições. Ele auxilia a determinar em que direção e com que intensidade a solução deve ser ajustada para eliminar a violação, ponderando o gradiente pelo nível de violação.
Inicialmente, são verificados os índices do agente e da coordenada, para garantir que estejam dentro dos limites permitidos. Se os índices forem incorretos, é retornado um valor zero, o que indica a ausência de uma direção para correção. Em seguida, o método percorre todas as coordenadas associadas ao agente atual e calcula o valor de violação para cada uma delas. Ao longo desse processo, ele identifica a maior violação entre todas. Se a violação para a coordenada em questão for maior que o limiar "eps", considera-se que faz sentido executar ações corretivas; caso contrário, é retornado zero, pois o movimento nessa direção não faz sentido ou não é necessário.
Se a violação for significativa, para a coordenada é calculado o gradiente da restrição, que é uma medida da direção e da intensidade da mudança da restrição em relação às alterações dessa coordenada. O gradiente é multiplicado por um peso, que é definido como a razão entre a violação da coordenada atual e a violação máxima entre todas as restrições. Isso garante que uma violação maior exerça uma influência mais forte sobre a direção da correção. O valor final é o gradiente de restrição ponderado, que indica o quanto e em que direção a solução precisa ser ajustada para eliminar a violação nessa coordenada, de forma proporcional ao seu grau.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateWeightedGradient (int agentIdx, int coordIdx) { // Вычисляем максимальное значение нарушения ограничений double maxViolation = eps; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); maxViolation = MathMax (maxViolation, violation); } // Нарушение для текущей координаты double violation = CalculateConstraintValue (agentIdx, coordIdx); // Если нет значительного нарушения, возвращаем 0 if (violation <= eps) return 0.0; // Вычисляем градиент double gradient = CalculateConstraintGradient (agentIdx, coordIdx); // Нормализуем влияние в зависимости от степени нарушения double weight = violation / maxViolation; return gradient * weight; } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateConstraintValue" é utilizado para avaliar o grau de violação das restrições para uma coordenada específica de um agente específico. Ele determina o quanto o valor atual da coordenada ultrapassa os limites permitidos e retorna um valor numérico que reflete a magnitude dessa violação.
Inicialmente, o método verifica a correção dos índices do agente (agentIdx) e da coordenada (coordIdx). O método obtém o valor atual da coordenada "x" a partir do estado do agente, bem como determina os limites mínimo (min) e máximo (max) permitidos para essa coordenada, respectivamente. Em seguida, o método verifica se o valor "x" se encontra dentro do intervalo permitido, entre min e max. Ao final, o método retorna o valor "violation", que representa a magnitude total da violação das restrições para essa coordenada desse agente.
Principais características:
- O método retorna um valor positivo se a restrição for violada e 0 se ela for respeitada.
- A magnitude da violação é proporcional ao quanto o valor da coordenada ultrapassa os limites permitidos.
Em resumo, o método "CalculateConstraintValue" fornece informações importantes sobre o quanto cada agente da população atende às restrições do problema. Ele mede a magnitude da violação, o que ajuda o algoritmo a entender o quanto é necessário ajustar a posição do agente.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintValue (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженная функция нарушения ограничений с плавным переходом на границе double violation = 0.0; // Проверка нижней границы if (x < min) { violation += min - x; } // Проверка верхней границы else if (x > max) { violation += x - max; } return violation; } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateConstraintGradient" realiza o cálculo do gradiente da restrição para uma coordenada específica de um agente específico. Esse método determina em que direção e com que intensidade é necessário alterar o valor da coordenada em função da violação das restrições.
Inicialmente, o método verifica os índices de entrada do agente (agentIdx) e da coordenada (coordIdx) para garantir sua correção. Se pelo menos um dos índices estiver fora do intervalo permitido, o método retorna 0.0, o que indica a impossibilidade de calcular o gradiente. O método extrai o valor atual da coordenada do agente, bem como os limites mínimo e máximo estabelecidos para essa coordenada. Esses valores são necessários para as avaliações subsequentes. Em seguida, o método verifica se o valor atual da coordenada "x" está fora dos limites estabelecidos.
O valor final retornado pelo método reflete a direção e a necessidade de alteração do valor atual da coordenada do agente, levando em consideração as restrições definidas.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintGradient (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженный градиент для лучшей стабильности if (x < min) return -1.0; // Нужно увеличивать значение else if (x > max) return 1.0; // Нужно уменьшать значение return 0.0; } //——————————————————————————————————————————————————————————————————————————————
O método "CalculatePenaltyFunction" calcula os valores da função objetivo considerando a penalização por violação de restrições para um agente específico. Ele combina o valor base da função objetivo com uma penalização baseada na magnitude das violações das restrições.
O método inicia sua execução verificando a correção do índice do agente (agentIdx) e, se o índice for válido, obtém o valor base, não penalizado, da função objetivo desse agente (a[agentIdx].f) e o armazena na variável "baseValue". Em seguida, o método percorre todas as coordenadas (coords) de cada agente. Para cada coordenada, é calculada a magnitude da violação das restrições. Se a magnitude da violação (violation) exceder o pequeno valor especificado "eps", o quadrado da magnitude da violação é adicionado à soma das penalizações "penaltySum".
A penalização quadrática é utilizada para fornecer uma avaliação mais "suave" em casos de pequenas violações e mais "rígida" em casos de violações maiores. Após a soma de todas as penalizações por violação de restrições, é calculada a penalização total "penalty".
Por fim, o método calcula o valor "penalizado" da função objetivo subtraindo a penalização "penalty" do valor base da função objetivo "baseValue". O valor penalizado da função objetivo é então retornado.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculatePenaltyFunction (int agentIdx) { // Базовое значение целевой функции double baseValue = a [agentIdx].f; // Штрафной терм double penaltySum = 0.0; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); // Квадратичный штраф для лучшего разрешения близких к границе решений if (violation > eps) { penaltySum += violation * violation; } } // Применяем динамический коэффициент штрафа double penalty = currentSigma * penaltySum; // Для задачи максимизации: f_penalty = f - penalty return baseValue - penalty; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" é o principal procedimento de controle para o avanço da solução no processo de otimização. Ele executa etapas sequenciais voltadas à atualização do estado atual do sistema, à adaptação de parâmetros e ao gerenciamento das fases de busca.
Inicialmente, o contador da época atual é incrementado. Se este for o primeiro chamado do método, é iniciada a criação da população inicial de agentes e, em seguida, essa etapa encerra sua execução. Depois disso, ocorre a atualização dinâmica do parâmetro de penalização (sigma), o que ajuda a regular a influência das funções de penalização durante o processo de busca. Uma tarefa importante é a verificação periódica e o reset de agentes que ficaram presos ou não apresentam progresso, o que contribui para evitar estagnação em armadilhas locais.
Em seguida, a fase atual da busca é determinada com base no valor do contador de épocas, isto é, nas etapas iniciais é realizada a busca global e, posteriormente, ocorre a transição para uma busca mais restrita, de caráter local. Dependendo da fase, são chamadas as estratégias de busca correspondentes, que controlam o movimento dos agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Moving () { epochNow++; if (!revision) { InitialPopulation (); revision = true; return; } // Динамическое обновление параметра штрафа UpdateSigma (); // Сброс агентов, находящихся в стагнации if (epochNow % 5 == 0) { ResetStagnatingAgents (); } // Определяем фазу поиска if (epochNow <= S1) { FirstCarrierWaveSearch (); } else if (epochNow <= S1 + S2) { SecondCarrierWaveSearch (); } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável por aprimorar as soluções e adaptar os parâmetros de busca ao longo do processo iterativo de otimização. Ele realiza uma reavaliação do estado atual da população, atualiza as melhores soluções e ajusta os parâmetros de busca com base na eficiência das etapas mais recentes.
O método percorre todas as soluções da população, calculando seu novo valor "penalizado" por meio da função de penalização, o que permite levar em conta as violações de restrições. A correção do valor obtido é verificada e, se ele for admissível, é armazenado como o valor atual da função. Para cada agente cujo novo valor da função seja melhor que o anterior, ocorre a atualização de seus dados pessoais: o novo valor é salvo, assim como as coordenadas atuais são copiadas. Isso garante o armazenamento da melhor solução local de cada agente. Se for identificada, em um agente, uma solução melhor que a atual solução global, o melhor resultado global é atualizado e as coordenadas correspondentes são armazenadas. A história das melhores soluções também é atualizada.
Após o primeiro nível de iterações (epochNow > 1), é realizada uma avaliação do sucesso da busca, determinando-se a proporção de melhorias entre todos os agentes. Com base nessa avaliação, os parâmetros são adaptados, em especial o parâmetro "alpha", que define a área de busca para cada coordenada. Dependendo da fase atual da busca, global ou local, as regras de ajuste de "alpha" podem diferir: na fase de busca global, com baixo nível de melhorias, a área de busca é ampliada para expandir as possibilidades; na fase de busca local, em caso de falta de melhorias, a área de busca também é ampliada, enquanto que, em caso de sucessos significativos, a área de busca é reduzida, o que ajuda a localizar a solução ótima. Ao mesmo tempo, o parâmetro "alpha" é limitado por valores máximos e mínimos, com base no intervalo de valores permitidos para a coordenada.
Essa abordagem permite equilibrar dinamicamente a exploração de novas soluções e a localização das soluções ótimas, utilizando informações sobre o desempenho das iterações anteriores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Revision () { int improvementCount = 0; double bestImprovement = 0.0; // Оценка всех решений for (int i = 0; i < popSize; i++) { double newValue = CalculatePenaltyFunction (i); // Проверка на валидность нового значения if (!MathIsValidNumber (newValue)) continue; // Сохраняем текущее значение для следующей итерации a [i].f = newValue; // Обновление личного лучшего решения (перед глобальным для эффективности) if (newValue > a [i].fB) { a [i].fB = newValue; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); improvementCount++; } // Обновление глобального лучшего решения if (newValue > fB) { double improvement = newValue - fB; fB = newValue; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); // Обновляем историю лучших значений UpdateBestHistory (fB); bestImprovement = MathMax (bestImprovement, improvement); improvementCount++; } } // Адаптация параметров поиска в зависимости от фазы и успешности if (epochNow > 1) { // Коэффициент успешности поиска (предотвращение деления на ноль) double successRate = (double)improvementCount / MathMax (1, 2 * popSize); // Адаптация параметра alpha for (int c = 0; c < coords; c++) { double oldAlpha = alpha [c]; if (epochNow <= S1) { // В фазе глобального поиска if (successRate < 0.1) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate < 0.3) { // Мало улучшений - слегка увеличиваем область alpha [c] *= 1.2; } else if (successRate > 0.7) { // Много улучшений - сужаем область alpha [c] *= 0.9; } } else { // В фазе локального поиска if (successRate < 0.05) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate > 0.2) { // Достаточно улучшений - сужаем область alpha [c] *= 0.8; } } // Ограничения на диапазон alpha с безопасной проверкой границ if (c < ArraySize (rangeMax) && c < ArraySize (rangeMin)) { double maxAlpha = 0.2 * (rangeMax [c] - rangeMin [c]); double minAlpha = 0.0001 * (rangeMax [c] - rangeMin [c]); if (alpha [c] > maxAlpha) { alpha [c] = maxAlpha; } else if (alpha [c] < minAlpha) { alpha [c] = minAlpha; } } } } } //——————————————————————————————————————————————————————————————————————————————
Agora que todos os métodos foram analisados, podemos passar diretamente ao teste do algoritmo.
Resultados dos testes
De fato, o resultado fala por si só, alguns parâmetros externos foram levemente otimizados, enquanto os internos permaneceram inalterados e são apresentados exatamente como descritos anteriormente nos métodos.COA(CHAOS)|Chaos Optimization Algorithm|50.0|10.0|40.0|2.0|1.2|0.0001|
=============================
5 Hilly's; Func runs: 10000; result: 0.6083668756744218
25 Hilly's; Func runs: 10000; result: 0.4079413401686229
500 Hilly's; Func runs: 10000; result: 0.2678056430575926
=============================
5 Forest's; Func runs: 10000; result: 0.668343763134901
25 Forest's; Func runs: 10000; result: 0.38894787694645416
500 Forest's; Func runs: 10000; result: 0.2198998763835145
=============================
5 Megacity's; Func runs: 10000; result: 0.32307692307692304
25 Megacity's; Func runs: 10000; result: 0.1987692307692308
500 Megacity's; Func runs: 10000; result: 0.10598461538461638
=============================
All score: 3.18914 (35.43%)
Gostaria de chamar a atenção para a visualização do funcionamento do algoritmo: a combinação da diversidade dos métodos de busca aplicados gera um efeito visual incomum.
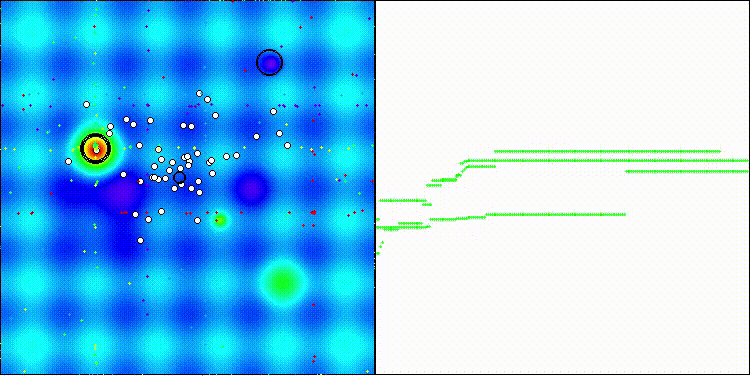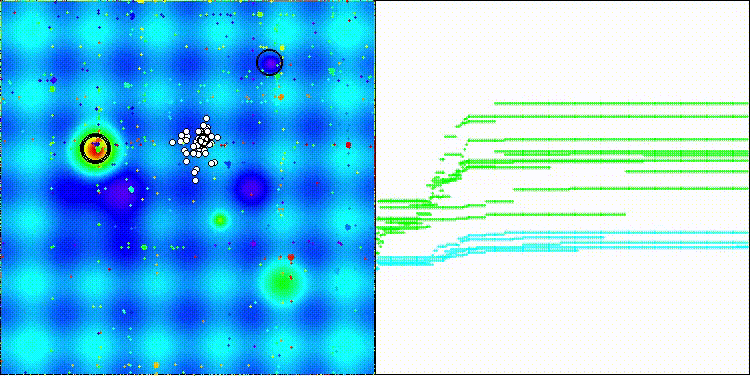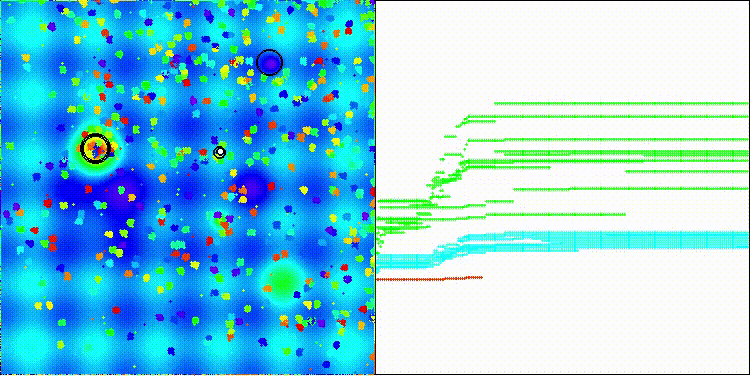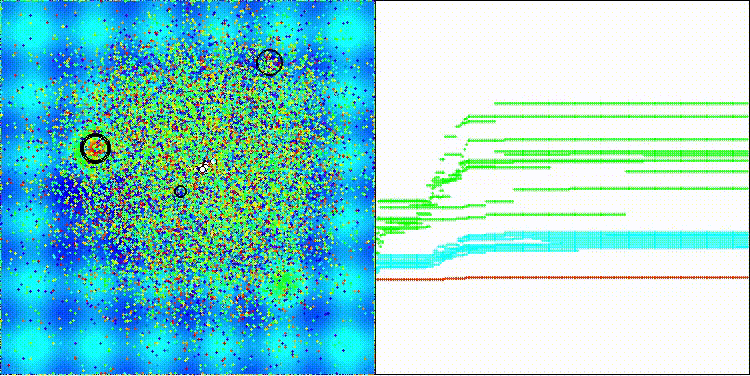
COA(CHAOS) na função de teste Hilly
COA(CHAOS) na função de teste Forest
COA(CHAOS) na função de teste Megacity
Com base nos resultados dos testes, o algoritmo COA(CHAOS) é apresentado de forma informativa em nossa tabela de classificação.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 43 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 44 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 45 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| CHAOS | chaos optimization algorithm | 0,60837 | 0,40794 | 0,26781 | 1,28412 | 0,66834 | 0,38895 | 0,21990 | 1,27719 | 0,32308 | 0,19877 | 0,10598 | 0,62783 | 3,189 | 35,43 | |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O resultado de 35% após os testes demonstra um bom potencial do algoritmo COA(CHAOS), especialmente considerando sua complexidade e a quantidade de parâmetros externos ajustáveis, incluindo os internos, que não foram otimizados. O algoritmo simplesmente ainda não demonstrou seu desempenho máximo.
Os aspectos mais interessantes e promissores do algoritmo parecem ser os seguintes: o uso de três diferentes mapeamentos, logístico, sinusoidal e tent mapping, para ampliar as capacidades de busca do algoritmo; a adição de inércia ajuda o algoritmo a manter o "impulso" do movimento, com a possibilidade de superar armadilhas locais; a alteração dinâmica dos parâmetros, dependendo do sucesso e da fase da otimização, aumenta sua flexibilidade; o acompanhamento do histórico de soluções e o reset de agentes "presos" permitem que o algoritmo não desperdice recursos computacionais em áreas sem perspectiva. Além disso, o uso do hipercubo latino e de diferentes abordagens para o posicionamento inicial dos agentes garante uma boa cobertura do espaço de busca desde o início. Para um aprimoramento adicional do algoritmo, seria recomendável realizar uma otimização mais aprofundada dos parâmetros internos.
Este algoritmo representa uma rica fonte de ideias para a melhoria de outros métodos de otimização, em particular seus mecanismos adaptativos e as formas de tratamento da estagnação poderiam ser transferidos com sucesso para outros algoritmos de aprendizado de máquina e de otimização para os mercados financeiros.
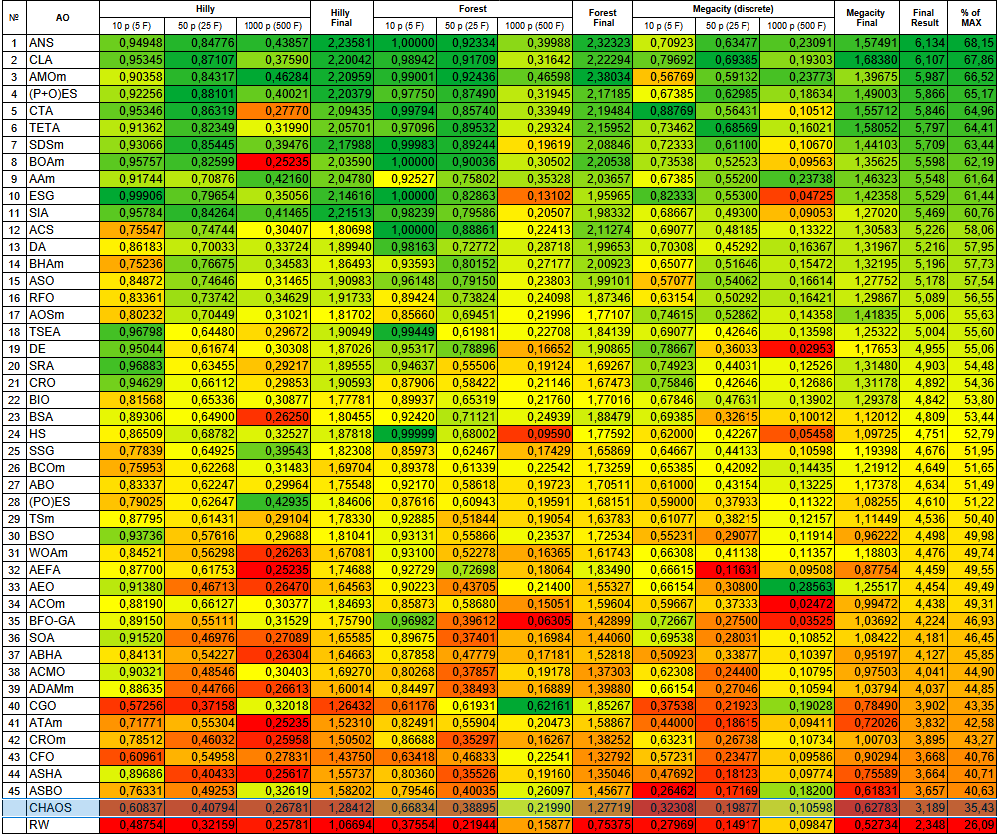
Figura 1. Graduação de cores dos algoritmos de acordo com os testes
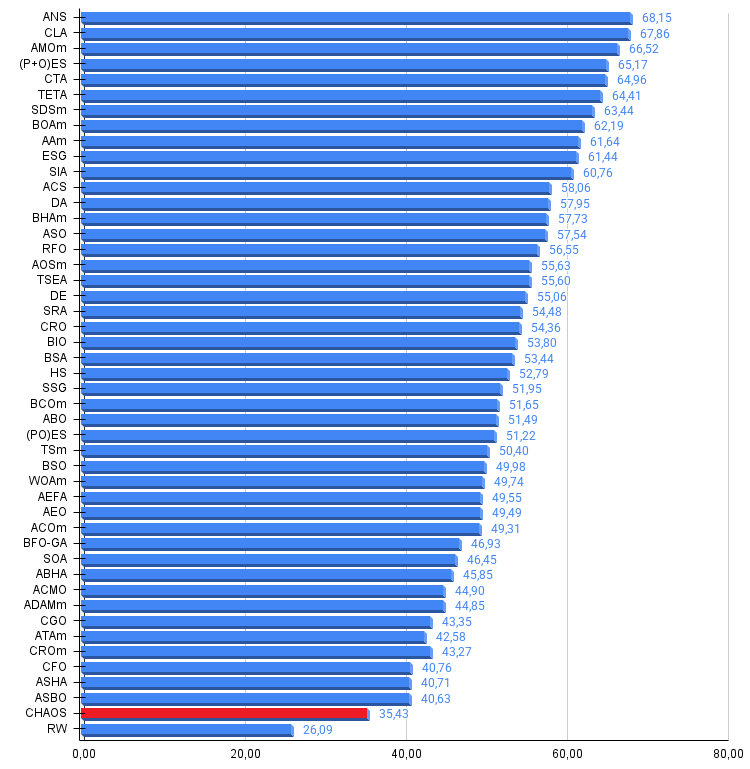
Figura 2. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para calcular a tabela de classificação)
Vantagens e contras do algoritmo COA(CHAOS):
Vantagens:
- Diversidade de métodos de busca.
- Desenvolvimento promissor.
- Resultados estáveis.
Contras:
- Grande quantidade de parâmetros externos.
- Grande quantidade de parâmetros internos não otimizáveis.
Junto ao artigo está anexado um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela absoluta precisão na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do test stand |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados em tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Test stand unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso de algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_COA_chaos.mq5 | Script | Test stand para COA(CHAOS) |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17874
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Do básico ao intermediário: Sobrecarga de operadores (IV)
Do básico ao intermediário: Sobrecarga de operadores (IV)
 Trading de arbitragem no Forex: sistema de negociação matricial para retorno ao valor justo com limitação de risco
Trading de arbitragem no Forex: sistema de negociação matricial para retorno ao valor justo com limitação de risco
 Simulação de mercado: A união faz a força (III)
Simulação de mercado: A união faz a força (III)
 Desenvolvimento do Toolkit de Análise de Price Action (Parte 8): Painel de Métricas
Desenvolvimento do Toolkit de Análise de Price Action (Parte 8): Painel de Métricas
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso