Алгоритм хаотической оптимизации — Chaos optimization algorithm (COA): Продолжение
317
0
Содержание
Введение
В предыдущей статье мы познакомились с методом хаотической оптимизации и разобрали часть методов в составе алгоритма. В данной статье мы завершим разбор оставшихся методов и перейдем непосредственно к тестированию алгоритма на тестовых функциях.
Метод хаотической оптимизации, в данной реализации, использует детерминированный хаос для исследования пространства решений. Ключевой принцип — применение трёх различных хаотических отображений (логистического, синусоидального и тент-отображения) для генерации последовательностей, обладающих свойствами псевдослучайности и эргодичности. Алгоритм работает в три фазы: начальный хаотический поиск, уточнение решения методом взвешенного градиента и финальный локальный поиск с адаптивным сужением области.
Использование векторов скорости с инерцией и механизмов обнаружения стагнации позволяет избегать локальных экстремумов. Динамическая адаптация параметров и различные типы мутаций обеспечивают баланс между глобальным исследованием и локальной эксплуатацией найденных решений. Это коротко о главном, а теперь, продолжим рассматривать оставшиеся методы.
Реализация алгоритма
Метод "ApplyMutation" предназначен для внедрения мутаций в агента. Его основной задачей является случайное изменение параметров определенного агента.
Метод начинается с проверки корректности индекса указанного агента. Если индекс выходит за пределы допустимого диапазона, выполнение метода завершается. Далее осуществляется сбор информации о размере различных массивов, связанных с агентом, таких как размеры его параметров и скорости. Это позволяет предотвратить выход за пределы этих массивов во время работы метода.
Метод рассчитывает максимальное количество координат, которые могут быть изменены, исходя из размеров доступных массивов, чтобы обеспечить безопасность операций. Выбирается случайное число, определяющее, сколько координат будет подвергнуто мутации. Это значение варьируется от 1 до 30% от максимального количества доступных координат. Формируется массив индексов, представляющий координаты, которые могут быть изменены. Этот массив перемешивается, чтобы гарантировать случайный выбор при применении мутаций.
В цикле происходит выбор координат для мутации из перемешанного массива. Для каждой выбранной координаты определяется тип мутации на основе случайного значения. Возможные типы включают полную случайную мутацию (где новое значение выбирается случайно в заданном диапазоне), мутацию относительно глобального лучшего решения, и мутацию с использованием хаотических отображений.
После изменения значения для каждой координаты, скорость агента сбрасывается, чтобы новое значение не было подвержено влиянию предыдущих скоростей. Наконец, новое значение для соответствующей координаты агента устанавливается с учетом диапазонов и шагов, что гарантирует, что значения остаются в пределах допустимого диапазона.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ApplyMutation (int agentIdx) { // Определяем количество координат для мутации (от 1 до 30% координат) int mutationCount = 1 + (int)(u.RNDprobab () * coords * 0.3); mutationCount = MathMin (mutationCount, coords); // Создаем массив индексов для мутации без повторений int mutationIndices []; ArrayResize (mutationIndices, coords); // Заполняем массив индексами for (int i = 0; i < coords; i++) { mutationIndices [i] = i; } // Перемешиваем индексы for (int i = coords - 1; i > 0; i--) { int j = (int)(u.RNDprobab () * (i + 1)); if (j <= i) // Дополнительная проверка для безопасности { int temp = mutationIndices [i]; mutationIndices [i] = mutationIndices [j]; mutationIndices [j] = temp; } } // Применяем мутации к выбранным координатам for (int m = 0; m < mutationCount; m++) { int c = mutationIndices [m]; // Различные типы мутаций для разнообразия double r = u.RNDprobab (); double x; if (r < 0.3) { // Полная случайная мутация x = rangeMin [c] + u.RNDprobab () * (rangeMax [c] - rangeMin [c]); } else if (r < 0.6) { // Мутация относительно глобального лучшего double offset = (u.RNDprobab () - 0.5) * (rangeMax [c] - rangeMin [c]) * 0.2; x = cB [c] + offset; } else { // Мутация с использованием хаотического отображения agent [agentIdx].gamma [c] = SelectChaosMap (agent [agentIdx].gamma [c], (epochNow + c) % 3); x = rangeMin [c] + agent [agentIdx].gamma [c] * (rangeMax [c] - rangeMin [c]); } // Сбрасываем скорость agent [agentIdx].velocity [c] = 0.0; // Применяем новое значение с проверкой диапазона a [agentIdx].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdateSigma" в классе отвечает за динамическую адаптацию параметра штрафа, который используется в процессе оптимизации. Он регулирует значение штрафа, в зависимости от количества допустимых решений в популяции агентов.
Если метод вызывается в первый раз (эпоха равна 1), значение текущего штрафа (currentSigma) устанавливается равным половине базового значения (sigma). Метод проходит по всей популяции агентов и подсчитывает количество допустимых решений. Для этого используется вспомогательная функция, определяющая, является ли агент допустимым. Здесь осуществляется итерация по всем агентам, что позволяет определить, сколько из них соответствуют заданным критериям.
Далее, метод вычисляет долю допустимых решений в общей популяции, деля количество допустимых решений на общее количество агентов. Это соотношение помогает понять, насколько хорошо работает текущая стратегия. На основе рассчитанного отношения допустимых решений метод принимает решения о корректировке штрафа: если доля допустимых решений составляет менее 30%, это указывает на то, что алгоритм слишком строг, и штраф увеличивается, чтобы заставить агентов проявлять больше разнообразия в своих решениях. Если же доля превышает 70%, это говорит о том, что слишком много агентов находит допустимые решения, и штраф уменьшается, чтобы избежать преждевременной конвергенции.
В конце метод гарантирует, что значение текущего штрафа остается в приемлемых пределах. Если оно становится слишком маленьким (менее 10% от базового значения), штраф увеличивается до этого уровня. Аналогично, если штраф превышает 500% от базового значения, он ограничивается до этого уровня.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateSigma () { // Динамическая адаптация параметра штрафа // Начинаем с малого значения и увеличиваем его при необходимости if (epochNow == 1) { currentSigma = sigma * 0.5; return; } // Подсчет количества допустимых решений int feasibleCount = 0; for (int i = 0; i < popSize; i++) { if (IsFeasible (i)) { feasibleCount++; } } double feasibleRatio = (double)feasibleCount / MathMax (1, popSize); // Адаптация параметра штрафа в зависимости от доли допустимых решений if (feasibleRatio < 0.3) { // Слишком мало допустимых решений - увеличиваем штраф currentSigma *= 1.2; } else if (feasibleRatio > 0.7) { // Слишком много допустимых решений - уменьшаем штраф currentSigma *= 0.9; } // Ограничиваем значение sigma if (currentSigma < sigma * 0.1) currentSigma = sigma * 0.1; else if (currentSigma > sigma * 5.0) currentSigma = sigma * 5.0; } //——————————————————————————————————————————————————————————————————————————————
Метод "IsFeasible" определяет, является ли конкретное решение, представленное агентом с заданным индексом "agentIdx", допустимым (feasible) относительно заданных ограничений.
Сначала метод проверяет, что заданный индекс агента (agentIdx) находится в пределах допустимого диапазона, то есть, больше или равен 0 и меньше размера популяции (popSize). Если индекс некорректен, метод возвращает "false", сигнализируя о недопустимости решения. Если индекс агента корректен, метод приступает к проверке ограничений для данного решения. Он проходит по всем координатам (coords) решения, и для каждой координаты вычисляет значение нарушения ограничения с помощью функции "CalculateConstraintValue".
Функция "CalculateConstraintValue" возвращает значение, которое отражает степень нарушения ограничений для конкретной координаты решения. Если после проверки всех координат, ни одно ограничение не нарушено, то есть, все значения нарушений меньше или равны "eps", то решение считается допустимым, и метод возвращает "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsFeasible (int agentIdx) { // Проверяем, находится ли решение в допустимой области for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); if (violation > eps) { return false; } } return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdateBestHistory" необходим для сохранения текущего лучшего значения в истории поиска. Он принимает новое лучшее значение и сначала проверяет его корректность или допустимость. Если значение корректное, оно сохраняется в массиве, хранящем историю лучших результатов, по текущему индексированному положению. После этого, индекс обновляется для следующего сохранения, при этом используется циклическое обновление с помощью операции взятия остатка от деления на размер массива истории, что обеспечивает постоянное заполнение истории последними 10 значениями без выхода за границы массива.
Данный метод позволяет вести учет прогресса поиска и использовать историю лучших решений для анализа.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateBestHistory (double newBest) { // Защита от некорректных значений if (!MathIsValidNumber (newBest)) return; // Обновляем историю лучших значений globalBestHistory [historyIndex] = newBest; historyIndex = (historyIndex + 1) % 10; } //——————————————————————————————————————————————————————————————————————————————
Метод "IsConverged" предназначен для определения, достиг ли алгоритм состояния сходимости. Он анализирует историю лучших глобальных решений, чтобы оценить, насколько значительно улучшаются решения с течением времени. Если улучшения становятся незначительными, считается, что алгоритм сошелся.
Метод инициализирует переменные для подсчета количества допустимых (валидных) значений, суммы значений, минимального и максимального значения из истории лучших глобальных решений (globalBestHistory). Переменные "minVal" и "maxVal" инициализируются как максимально возможное и минимально возможное значения "double" соответственно, чтобы корректно определять минимум и максимум в дальнейшем.
Метод итерируется по массиву "globalBestHistory" и для каждого значения в истории он выполняет проверки допустимости значений, достаточности данных и разнообразия, вычисляет среднее значение и относительную разницу и проверяет сходимость. В целом, метод "IsConverged" предоставляет способ определения сходимости алгоритма оптимизации, анализируя историю лучших решений и оценивая, насколько значительны улучшения с течением времени.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsConverged () { // Проверка достаточного количества данных в истории int validValues = 0; double sum = 0.0; double minVal = DBL_MAX; double maxVal = -DBL_MAX; // Находим min, max и sum значений в истории for (int i = 0; i < 10; i++) { if (globalBestHistory [i] == -DBL_MAX || !MathIsValidNumber (globalBestHistory [i])) continue; minVal = MathMin (minVal, globalBestHistory [i]); maxVal = MathMax (maxVal, globalBestHistory [i]); sum += globalBestHistory [i]; validValues++; } // Если недостаточно данных или все значения одинаковые if (validValues < 5 || minVal == maxVal) return false; // Вычисляем среднее значение double average = sum / validValues; // Проверка случая, когда среднее близко к нулю if (MathAbs (average) < eps) return MathAbs (maxVal - minVal) < eps * 10.0; // Относительная разница для проверки сходимости double relDiff = MathAbs (maxVal - minVal) / MathAbs (average); return relDiff < 0.001; // Порог сходимости - 0.1% } //——————————————————————————————————————————————————————————————————————————————
Метод "ResetStagnatingAgents" предназначен для управления агентами в процессе оптимизации, особенно для обработки случаев, когда агенты перестают демонстрировать улучшения в своих результатах. Он отслеживает состояние стагнации агентов и, при необходимости, применяет мутацию к тем из них, которые застряли в локальных экстремумах.
Для каждого агента проверяется, улучшилось ли его текущее значение фитнес-функции (a [i].f) по сравнению с предыдущим значением (a [i].fB). Если текущее значение не улучшилось, или стало хуже, увеличивается "stagnationCounter" данного агента, сигнализируя о том, что агент находится в состоянии стагнации. Если же значение улучшилось, счетчик стагнации обнуляется.
Если агент находится в стагнации более 5 итераций, метод вычисляет вероятность сброса (resetProb). Эта вероятность пропорциональна текущему значению счетчика стагнации, что означает, что чем дольше агент стагнирует, тем выше вероятность его сброса. Формула для расчета вероятности учитывает фиксированное значение (0.2) и относительное значение счетчика стагнации. Если случайно сгенерированное значение меньше рассчитанной вероятности "resetProb", к агенту применяется мутация с помощью функции "ApplyMutation". После применения мутации, счетчик стагнации агента обнуляется, а счетчик "resetCount" увеличивается.
Метод завершает свою работу после обработки всех агентов, сбрасывая тех, кто преодолел порог стагнации и выполнил условия для мутации.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ResetStagnatingAgents () { int resetCount = 0; for (int i = 0; i < popSize; i++) { // Увеличиваем счетчик стагнации, если нет улучшения if (a [i].f <= a [i].fB) { agent [i].stagnationCounter++; } else { agent [i].stagnationCounter = 0; } // Сбрасываем агента, если он находится в стагнации слишком долго if (agent [i].stagnationCounter > 5) { // Сброс только части агентов с вероятностью, зависящей от стагнации double resetProb = 0.2 * (1.0 + (double)agent [i].stagnationCounter / 10.0); if (u.RNDprobab () < resetProb) { ApplyMutation (i); agent [i].stagnationCounter = 0; resetCount++; } } } } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculateWeightedGradient" используется для оценки градиента ограничения для конкретного агента и координаты с учетом степени нарушения этих ограничений. Он помогает определить, в каком направлении и с какой силой следует скорректировать решение для устранения нарушения, взвешивая градиент по уровню нарушения.
Вначале проверяются индексы агента и координаты, чтобы убедиться, что они находятся в допустимых пределах. Если индексы некорректны, возвращается нулевое значение, что означает отсутствие направления для корректировки. Далее метод перебирает все координаты, связанные с текущим агентом, и вычисляет значение нарушения для каждого. На протяжении этого процесса он ищет максимальное нарушение среди них. Если нарушение для данной координаты больше порога "eps", считается, что есть смысл предпринимать корректирующие действия, иначе возвращается ноль — движение в этом направлении не имеет смысла или не требуется.
Если нарушение значимо, для координаты вычисляется градиент ограничения — мера направления и силы изменения ограничения относительно изменений в этой координате. Градиент умножается на вес, который определяется, как отношение нарушения текущей координаты к максимальному нарушению среди всех ограничений. Это обеспечивает, что большее нарушение оказывает более сильное влияние на направление корректировки. Итоговое значение — это взвешенный градиент ограничения, который указывает, насколько и в каком направлении нужно скорректировать решение, чтобы устранить нарушение в данной координате, пропорционально его степени.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateWeightedGradient (int agentIdx, int coordIdx) { // Вычисляем максимальное значение нарушения ограничений double maxViolation = eps; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); maxViolation = MathMax (maxViolation, violation); } // Нарушение для текущей координаты double violation = CalculateConstraintValue (agentIdx, coordIdx); // Если нет значительного нарушения, возвращаем 0 if (violation <= eps) return 0.0; // Вычисляем градиент double gradient = CalculateConstraintGradient (agentIdx, coordIdx); // Нормализуем влияние в зависимости от степени нарушения double weight = violation / maxViolation; return gradient * weight; } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculateConstraintValue" используется для оценки степени нарушения ограничений для определенной координаты определенного агента. Он определяет, насколько текущее значение координаты выходит за допустимые пределы (границы) и возвращает численное значение, отражающее величину этого нарушения.
Сначала метод проверяет индексы агента (agentIdx) и координаты (coordIdx) на корректность. Метод получает текущее значение координаты "x" из состояния агента, а также определяет минимальную (min) и максимальную (max) допустимые границы для этой координаты соответственно. Далее метод проверяет, находится ли значение "x" в пределах допустимого диапазона (min и max). В завершение, метод возвращает значение "violation", которое представляет собой суммарную величину нарушения ограничений для данной координаты данного агента.
Ключевые особенности:
- Метод возвращает положительное значение, если ограничение нарушено, и 0, если оно соблюдено.
- Величина нарушения пропорциональна тому, насколько значение координаты выходит за допустимые границы.
В итоге, метод "CalculateConstraintValue" предоставляет важную информацию о том, насколько каждый агент в популяции удовлетворяет ограничениям задачи. Он измеряет величину нарушения, что помогает алгоритму понять, насколько сильно нужно скорректировать положение агента.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintValue (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженная функция нарушения ограничений с плавным переходом на границе double violation = 0.0; // Проверка нижней границы if (x < min) { violation += min - x; } // Проверка верхней границы else if (x > max) { violation += x - max; } return violation; } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculateConstraintGradient" выполняет вычисления градиента ограничения для определенной координаты конкретного агента. Этот метод определяет, в каком направлении и с какой силой необходимо изменять значение координаты в связи с нарушением ограничений.
Сначала метод проверяет входные индексы агента (agentIdx) и координаты (coordIdx) для обеспечения их корректности. Если хотя бы один из индексов находится вне допустимого диапазона, метод возвращает 0.0, что указывает на невозможность вычисления градиента. Метод извлекает текущее значение координаты агента, а также минимальные и максимальные границы, установленные для этой координаты. Эти значения необходимы для дальнейших оценок. Далее, метод проверяет, находится ли текущее значение координаты "x" за пределами установленных границ.
Итоговое значение, которое возвращает метод, отражает направление и необходимость изменения текущего значения координаты агента с учетом заданных ограничений.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintGradient (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженный градиент для лучшей стабильности if (x < min) return -1.0; // Нужно увеличивать значение else if (x > max) return 1.0; // Нужно уменьшать значение return 0.0; } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculatePenaltyFunction" вычисляет значения целевой функции с учетом штрафа за нарушение ограничений для конкретного агента. Он комбинирует базовое значение целевой функции со штрафом, основанным на величине нарушений ограничений.
Метод начинает работу с проверки корректности индекса агента (agentIdx), и если индекс корректен, метод получает базовое (не оштрафованное) значение целевой функции этого агента (a [agentIdx].f) и сохраняет его в переменной "baseValue". Затем метод перебирает все координаты (coords) каждого агента. Для каждой координаты вычисляется величина нарушения ограничений. Если величина нарушения (violation) превышает заданную небольшую величину "eps", то квадрат величины нарушения добавляется к сумме штрафов "penaltySum".
Квадратичный штраф используется для более "мягкой" оценки при небольших нарушениях и более "жесткой" при больших. После того, как просуммированы все штрафы за нарушение ограничений, вычисляется общий штраф "penalty".
В заключение, метод вычисляет "оштрафованное" значение целевой функции путем вычитания штрафа "penalty" из базового значения целевой функции "baseValue". Возвращается оштрафованное значение целевой функции.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculatePenaltyFunction (int agentIdx) { // Базовое значение целевой функции double baseValue = a [agentIdx].f; // Штрафной терм double penaltySum = 0.0; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); // Квадратичный штраф для лучшего разрешения близких к границе решений if (violation > eps) { penaltySum += violation * violation; } } // Применяем динамический коэффициент штрафа double penalty = currentSigma * penaltySum; // Для задачи максимизации: f_penalty = f - penalty return baseValue - penalty; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" является основной управляющей процедурой для продвижения решения в процессе оптимизации. Он выполняет последовательные шаги, направленные на обновление текущего состояния системы, адаптацию параметров и управление фазами поиска.
Первым делом увеличивается счетчик текущей эпохи. Если это первый вызов метода, инициируется создание начальной популяции агентов, после чего, эта стадия завершает работу. Далее происходит динамическое обновление параметра штрафа (sigma), что помогает регулировать влияние штрафных функций в процессе поиска. Важной задачей является периодическая проверка и сброс агентов, которые застряли или не показывают прогресса, что способствует предотвращению застоя в локальных ловушках.
Затем определяется текущая фаза поиска по значению счетчика эпохи — на начальных этапах выполняется глобальный поиск, а затем, переходит к более узкому, локальному поиску. В зависимости от фазы вызываются соответствующие стратегии поиска, которые управляют движением агентов.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Moving () { epochNow++; if (!revision) { InitialPopulation (); revision = true; return; } // Динамическое обновление параметра штрафа UpdateSigma (); // Сброс агентов, находящихся в стагнации if (epochNow % 5 == 0) { ResetStagnatingAgents (); } // Определяем фазу поиска if (epochNow <= S1) { FirstCarrierWaveSearch (); } else if (epochNow <= S1 + S2) { SecondCarrierWaveSearch (); } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" отвечает за улучшение решений и адаптацию параметров поиска в ходе итерационного процесса оптимизации. Он выполняет повторную оценку текущего состояния популяции, обновляет лучшие решения и регулирует параметры поиска в зависимости от эффективности последних шагов.
Метод перебирает все решения в популяции, вычисляя их новую "штрафную" ценность с помощью функции штрафов, что позволяет учитывать нарушение ограничений. Проверяется корректность полученного значения, и, если оно допустимо, то оно сохраняется как текущее значение функции. Для каждого агента, у которого новое значение функции лучше предыдущего, происходит обновление его личных данных: сохраняется новое значение, а также копируются текущие координаты. Это обеспечивает запоминание лучшего локального решения для каждого агента. Если у агента обнаружено решение лучше текущего глобального, то обновляется глобальный лучший результат, а также запоминаются соответствующие координаты. Также обновляется история лучших решений.
После первого уровня итераций (epochNow > 1), происходит оценка успешности поиска — определяется доля улучшений среди всех агентов. На основе этой оценки адаптируются параметры, особенно "alpha" (область поиска для каждой координаты). В зависимости от текущей фазы поиска (глобальной или локальной), правила корректировки "alpha" могут различаться: в фазе глобального поиска при низком уровне улучшений область поиска увеличивается, чтобы расширить возможности, в фазе локального поиска и при недостатке улучшений, область поиска тоже увеличивается, а при существенных успехах область поиска уменьшается, что помогает локализовать оптимальное решение. При этом параметр "alpha" ограничивается максимальными и минимальными значениями, исходя из диапазона допустимых значений для координаты.
Этот подход позволяет динамически балансировать между исследованием новых решений и локализацией оптимальных, используя информацию о результативности прошлых итераций.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Revision () { int improvementCount = 0; double bestImprovement = 0.0; // Оценка всех решений for (int i = 0; i < popSize; i++) { double newValue = CalculatePenaltyFunction (i); // Проверка на валидность нового значения if (!MathIsValidNumber (newValue)) continue; // Сохраняем текущее значение для следующей итерации a [i].f = newValue; // Обновление личного лучшего решения (перед глобальным для эффективности) if (newValue > a [i].fB) { a [i].fB = newValue; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); improvementCount++; } // Обновление глобального лучшего решения if (newValue > fB) { double improvement = newValue - fB; fB = newValue; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); // Обновляем историю лучших значений UpdateBestHistory (fB); bestImprovement = MathMax (bestImprovement, improvement); improvementCount++; } } // Адаптация параметров поиска в зависимости от фазы и успешности if (epochNow > 1) { // Коэффициент успешности поиска (предотвращение деления на ноль) double successRate = (double)improvementCount / MathMax (1, 2 * popSize); // Адаптация параметра alpha for (int c = 0; c < coords; c++) { double oldAlpha = alpha [c]; if (epochNow <= S1) { // В фазе глобального поиска if (successRate < 0.1) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate < 0.3) { // Мало улучшений - слегка увеличиваем область alpha [c] *= 1.2; } else if (successRate > 0.7) { // Много улучшений - сужаем область alpha [c] *= 0.9; } } else { // В фазе локального поиска if (successRate < 0.05) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate > 0.2) { // Достаточно улучшений - сужаем область alpha [c] *= 0.8; } } // Ограничения на диапазон alpha с безопасной проверкой границ if (c < ArraySize (rangeMax) && c < ArraySize (rangeMin)) { double maxAlpha = 0.2 * (rangeMax [c] - rangeMin [c]); double minAlpha = 0.0001 * (rangeMax [c] - rangeMin [c]); if (alpha [c] > maxAlpha) { alpha [c] = maxAlpha; } else if (alpha [c] < minAlpha) { alpha [c] = minAlpha; } } } } } //——————————————————————————————————————————————————————————————————————————————
Теперь, когда все методы мы разобрали, можем перейти непосредственно к тестированию алгоритма.
Результаты тестов
Собственно, результат сам говорит за себя, были немного оптимизированы внешние параметры, внутренние остались без изменения и представлены так, как описаны ранее в методах.COA(CHAOS)|Chaos Optimization Algorithm|50.0|10.0|40.0|2.0|1.2|0.0001|
=============================
5 Hilly's; Func runs: 10000; result: 0.6083668756744218
25 Hilly's; Func runs: 10000; result: 0.4079413401686229
500 Hilly's; Func runs: 10000; result: 0.2678056430575926
=============================
5 Forest's; Func runs: 10000; result: 0.668343763134901
25 Forest's; Func runs: 10000; result: 0.38894787694645416
500 Forest's; Func runs: 10000; result: 0.2198998763835145
=============================
5 Megacity's; Func runs: 10000; result: 0.32307692307692304
25 Megacity's; Func runs: 10000; result: 0.1987692307692308
500 Megacity's; Func runs: 10000; result: 0.10598461538461638
=============================
All score: 3.18914 (35.43%)
Хотелось бы обратить внимание на визуализацию работы алгоритма: сочетание многообразия применяемых методов поиска дает необычный визуальный эффект.
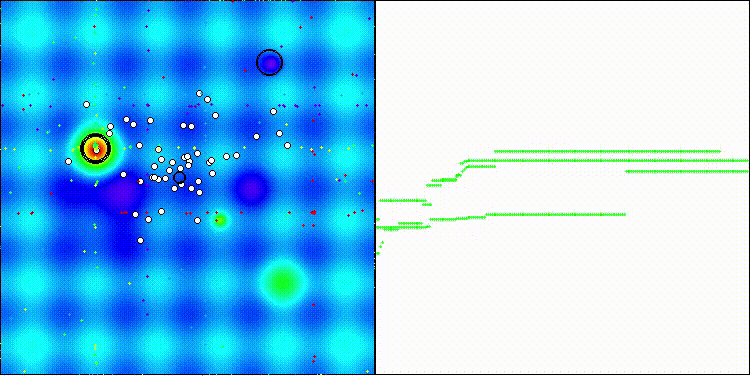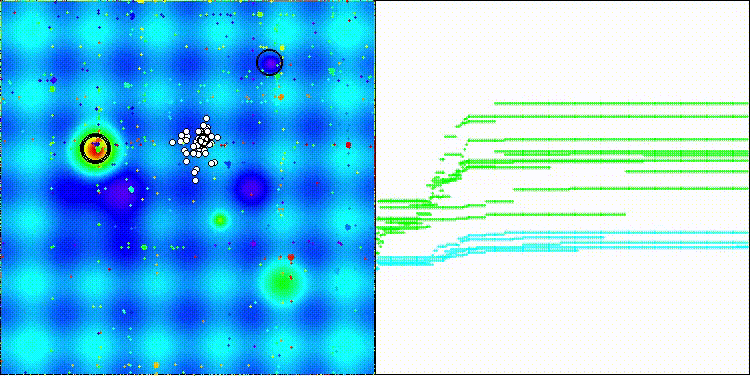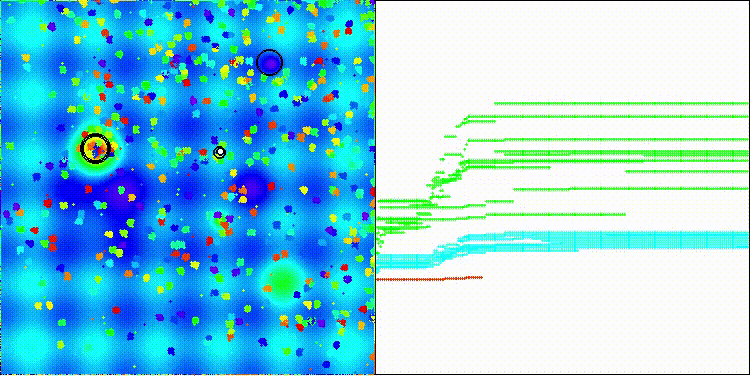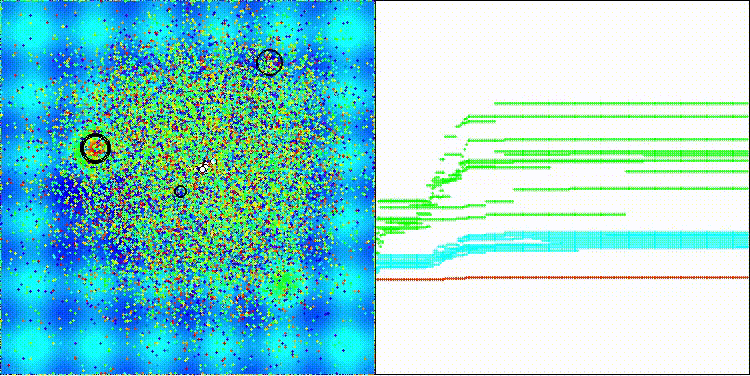
COA(CHAOS) на тестовой функции Hilly
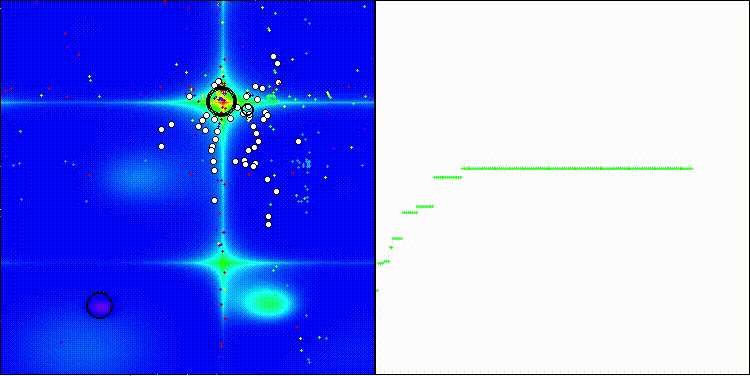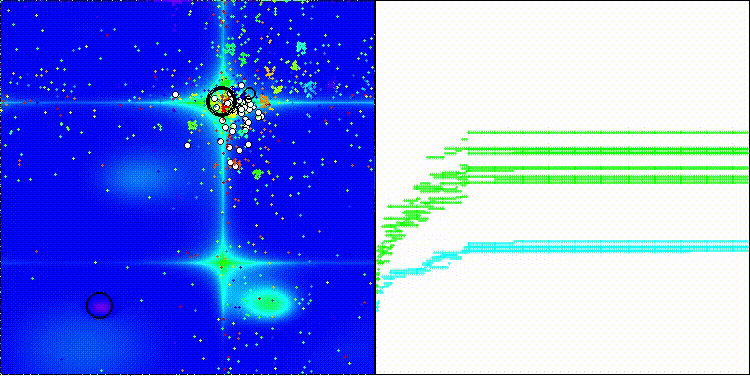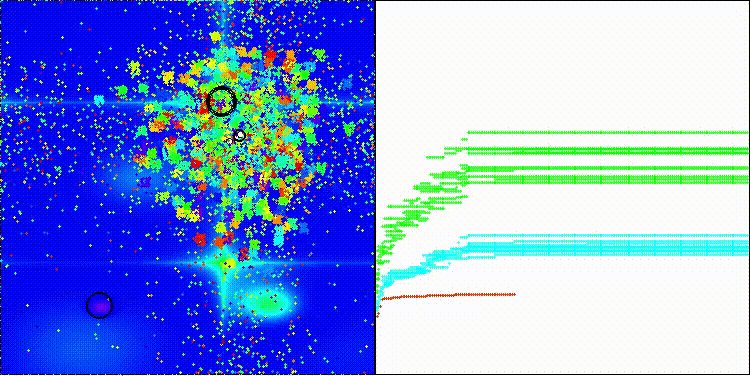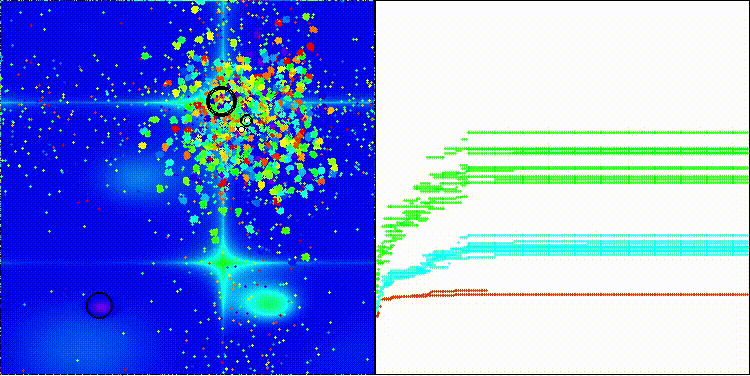
COA(CHAOS) на тестовой функции Forest
COA(CHAOS) на тестовой функции Megacity
По результатам тестирования алгоритм COA(CHAOS) представлен информационно в нашей рейтинговой таблице.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 43 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 44 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 45 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| CHAOS | chaos optimization algorithm | 0,60837 | 0,40794 | 0,26781 | 1,28412 | 0,66834 | 0,38895 | 0,21990 | 1,27719 | 0,32308 | 0,19877 | 0,10598 | 0,62783 | 3,189 | 35,43 | |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Результат в 35% после тестирования показывает неплохой потенциал алгоритма COA(CHAOS), особенно учитывая его сложность и количество настраиваемых внешних параметров, в том числе внутренних, которые не оптимизировались. Алгоритм просто не показал еще свою максимальную производительность.
Наиболее интересными и перспективными аспектами алгоритма представляются следующие: использование трех разных отображений (логистического, синусоидального и тент-отображения) для поисковых возможностей алгоритма; добавление инерции помогает алгоритму сохранять "импульс" движения с возможностью преодоления локальных ловушек; динамическое изменение параметров, в зависимости от успешности и фазы оптимизации, повышает его гибкость; отслеживание истории решений и сброс "застрявших" агентов дает возможность алгоритму не тратить вычислительные ресурсы на бесперспективные области. Кроме того, использование латинского гиперкуба и различных подходов к начальному размещению агентов обеспечивает хорошее покрытие пространства поиска с самого начала. Для дальнейшего улучшения алгоритма стоило бы провести более тщательную оптимизацию внутренних параметров.
Этот алгоритм представляет собой богатый источник идей для улучшения других оптимизационных методов, особенно его адаптивные механизмы и способы обработки стагнации могли бы быть успешно перенесены в другие алгоритмы машинного обучения и оптимизации для финансовых рынков.
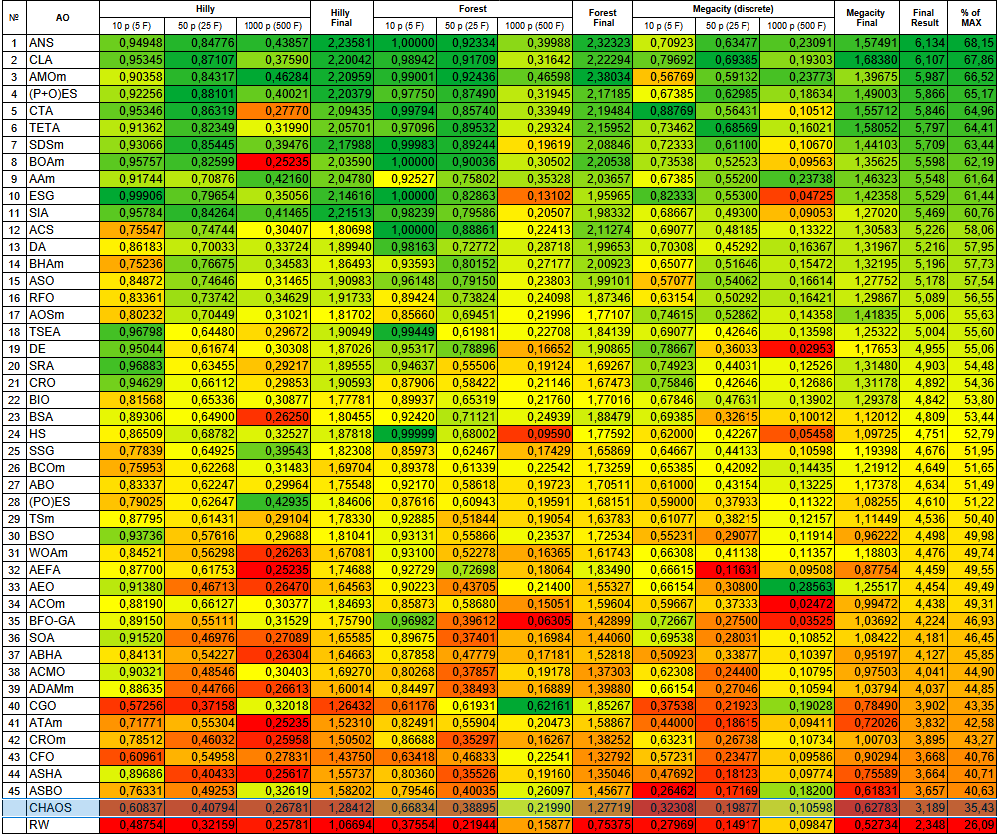
Рисунок 1. Цветовая градация алгоритмов по соответствующим тестам
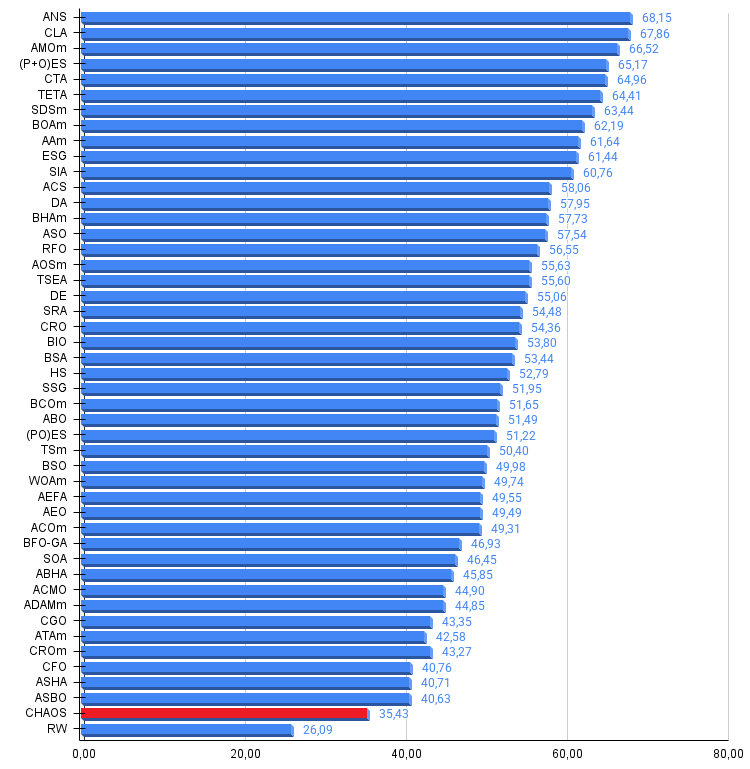
Рисунок 2. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма COA(CHAOS):
Плюсы:
- Разнообразие поисковых методов.
- Перспективная разработка.
- Стабильные результаты.
Минусы:
- Большое количество внешних параметров.
- Большое количество внутренних неоптимизируемых параметров.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_COA_chaos.mq5 | Скрипт | Испытательный стенд для COA(CHAOS) |
MQL5-советник, интегрированный в Telegram (Часть 7): Анализ команд для автоматизации индикаторов на графиках
Скальпинг по потоку ордеров (Order Flow Scalping) с MQL5
Компьютерное зрение для трейдинга (Часть 1): Создаем базовый простой функционал
Прогнозируем Ренко — бары при помощи ИИ CatBoost
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования