Anarchic Society Optimization (ASO) algorithm
1 499
0
Contents
1. Introduction
I have always been attracted to the topic of social relations and the possibility of constructing an algorithm in the concept of social connections, since this is the most interesting phenomenon in the development of society, and suggests a broad field of activity for the possibility of algorithmically describing the structure of the system of relationships and implementing an appropriate optimization algorithm.
In the previous articles, we have already considered algorithms of social behavior - evolution of social groups and artificial cooperative search. In this article, we will try to understand the concept of an anarchic society - a system of social interaction without a centralized power and hierarchical structures, where it is assumed that people can organize their lives and interact on the basis of voluntary agreements.
The anarchist society is based on the principles of autonomy and freedom, where each person can independently and autonomously make decisions concerning his life, without external interference, the principles of voluntary cooperation, at which people interact on the basis of the consent of all participants without coercion, equality of rights and opportunities, as well as the principles of solidarity, mutual assistance and cooperation. The idea is very interesting in terms of implementing it in the algorithm. The attempt has been made to implement such a social construction in the Anarchic Society Optimization (ASO) optimization algorithm. The algorithm was proposed by Ahmadi-Javid and published in 2011.
The main idea is the development of an optimization method inspired by the behavior of individuals in anarchic societies. Unlike existing swarm intelligence methods developed based on insect or animal swarms, such as PSO and ACO, developing an algorithm based on studying the construction of a standard human society can have only limited success, since a well-organized society does not have the ability to achieve its desires through individual decisions. Moreover, no member of society is truly independent and autonomous, and cannot radically improve his situation in a given period of time. This realization led the creator of the algorithm to the idea of borrowing the basic concept for development from a society based on an anomalous structure.
The core of the ASO is a group of individuals who are fickle, adventurous, do not like stability and often behave irrationally, moving to the worst positions they visited in the exploration phase. The level of anarchic behavior among members increases as the differences in their situations go up. Using these participants, ASO explores the solution space and tries to avoid falling into local optimum traps. Thus, the creator of ASO is trying to convey the idea that studying and applying principles based on anomalous community behavior can lead to the creation of efficient algorithms capable of solving complex optimization problems. We will consider a unified framework for ASO that can be easily used for both continuous and discrete problems.
2. Implementation of the algorithm
Before writing the code of the algorithm, we need to understand how it is structured and what basic mechanisms the author has put into it. The ASO algorithm is an optimization method that combines the advantages of the Particle Swarm Optimization (PSO) algorithm with new mechanisms characteristic of anarchic social behavior. The adaptive nature and ability to balance between different movement strategies is the main feature of the algorithm.
Let's start with a detailed description of the ASO algorithm:
1. Initialization:
- A population (popSize) is created from members of society.
- Each member is initialized to a random position in the search space.
- Each member retains his personal best and previous positions.
2. Basic optimization loop:
At each iteration, the algorithm performs the following steps for each member of society:
a) Calculation of indices:
- Fickleness Index (FI) — the index reflects the instability of a member of society and measures his dissatisfaction in comparison with other individuals.
- External Irregularity Index (EI) — the index evaluates the diversity of positions in society and shows the deviation from the global best solution.
- Internal Irregularity Index (II) — the index evaluates the changes in the individual's position during the iteration and reflects the deviation from the personal best solution.
b) Selecting movement policy:
Based on comparing FI, EI and II indices, one of three movement policies is selected:
- Current Movement Policy (CurrentMP) uses the PSO equation with inertia and acceleration ratios.
- Society Movement Policy (SocietyMP) applies a crossover with a randomly selected member of society.
- Past Movement Policy (PastMP) uses information about the individual's previous position.
c) Anarchic behavior: the individual's position can be completely randomized with anarchyprob probability.
d) Position update: The new position is checked against the search space constraints.
e) Update top positions:
- The pBest personal best position is updated if the current position is better.
- The gBest global best position is updated if a new better solution is found.
3. Adapting parameters:
- The anarchyProb probability of anarchic behavior gradually decreases.
- The alpha parameter for calculating FI gradually increases.
- The omega inertial weight gradually decreases.
4. Algorithm parameters:
- popSize — population size.
- omega, lambda1, lambda2 - parameters for calculating speed in CurrentMP (as in PSO).
- anarchyProb — probability of anarchic behavior.
- alpha, theta, delta — parameters for calculating FI, EI and II indices accordingly.
The algorithm is quite complex. I will try to describe its operation mechanism in a very clear and structured way for ease of understanding. The next step is to analyze the equations used in the algorithm.
The basic equation in the ASO algorithm is inherited from the PSO algorithm. It performs the calculation of the speed update: V_i (k+1) = ω * V_i (k) + λ1 * r1 * (P_i (k) - X_i (k)) + λ2 * r2 * (G (k) - X_i (k)), where:
- V_i (k) — i particle speed in k iteration.
- X_i (k) — i particle position in k iteration.
- P_i (k) — best position found by i particle before k iteration.
- G (k) — globally the best position found by all particles before k iteration.
- ω — inertial ratio.
- λ1, λ2 — acceleration ratios.
- r1, r2 — random numbers from the interval (0, 1).
The author points out that the PSO equation is a special case of the general ASO structure when the corresponding movement policies and combination rule are defined. In the original version, the agent previous speed was included in the calculations. I changed the approach by leaving only the current speed value, which resulted in a noticeable improvement in the algorithm performance.
Equations (1) and (2) define fickleness index and FI for i community member on k iteration in the ASO algorithm. These equations help assess the degree of dissatisfaction of an individual with his current position in comparison with other positions. Let's look at them in detail:
1. Equation (1) for calculating fickleness index: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (Xi (k*)) - f (Xi (k))).
This equation shows how much the current position of an i individual differs from his best personal position and his best global position weighted by the α (alpha) parameter.
2. Equation (2) for calculating the index of i individual fickleness on k iteration: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (G (k)) - f (Xi (k))).
This equation is similar to the first one, but is used for different purposes, where the current position, the best personal position, and the best global position are compared.
Both equations serve to assess the degree of dissatisfaction of society members, which allows them to make more informed decisions about how to change their positions in search of an optimal solution.
Equations (3) and (4) describe the external irregularity index and internal irregularity index for society members in the algorithm.
3. Equation (3) — external irregularity index of i individual on k iteration: (kEI)i = exp (-(θi) (f (G) - f (Xi (k)))).
4. Equation (4) — internal irregularity index of i individual on k iteration: (kEI)i = 1 - exp (-δi (kD)).
where;
- (kFI)i — fickleness index of i individual on k iteration.
- α — non-negative "alpha" number in the [0,1] interval.
- f (Xi (k)) — value of the objective function for i individual on k iteration.
- f (Pi (k)) — value of the objective function for the best position previously visited by the i individual.
- f (Xi (k)) — value of the objective function for the position of the best individual on k iteration.
- f (G (k)) — value of the objective function for the globally best position visited by the society before the k iteration.
- (kEI)i — index of external irregularity of the i individual on k iteration.
- θi — positive theta number.
- kD — suitable measure of diversity in society, for example, the ratio of variation of the individuals' objective function values.
- δi — positive delta number.
These equations show that if the diversity in a society increases (i.e., individuals have more different values of the objective function), individuals will be more likely to behave irregularly. The equations are used to evaluate the variability of the behavior of society members in the ASO algorithm, which allows them to make more diverse and adaptive decisions while searching for the optimal solution.
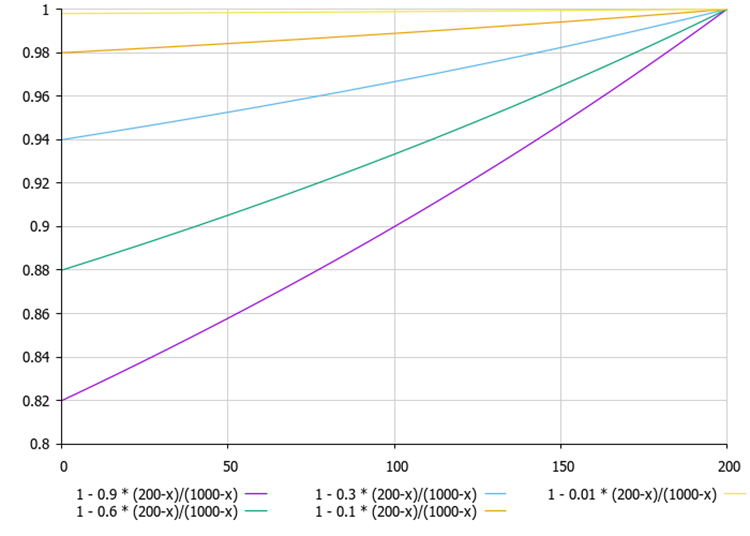
Figure 1. If the current best solution of the agent (200) is much smaller in value than the best solution for the population of agents (1000), then the line on the graph changes almost linearly
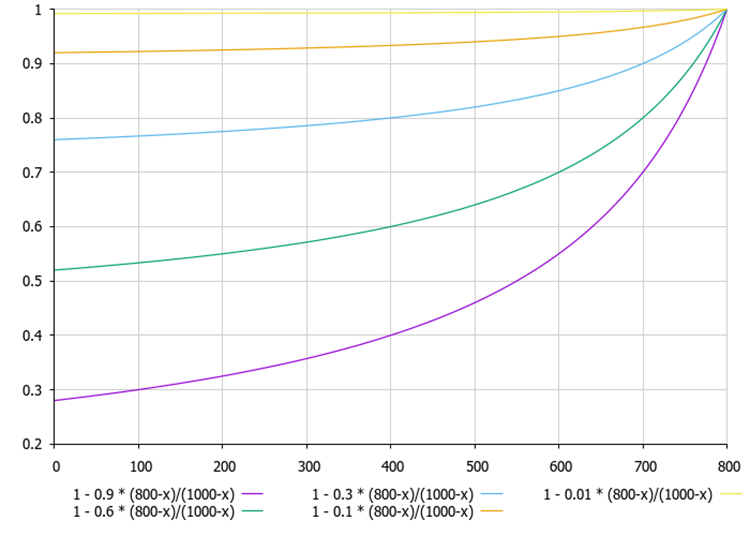
Figure 2. The smaller the difference between the agent's current best solution by the population of agents (1000), the more non-linear the line on the graph is
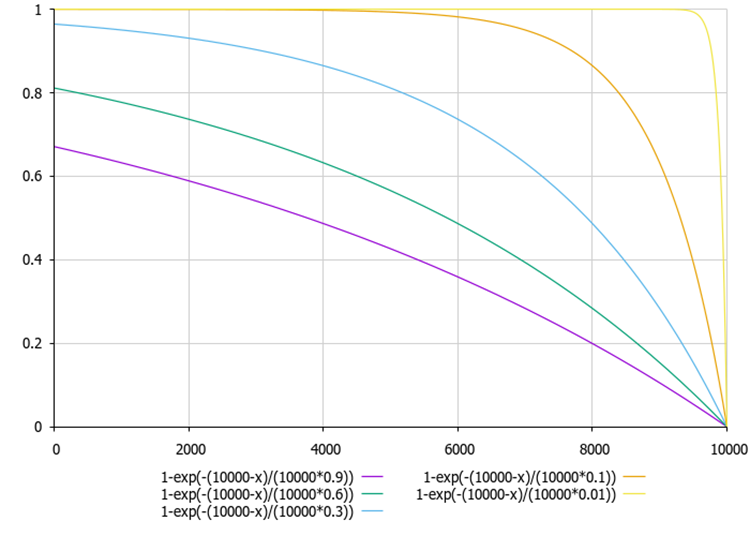
Figure 3. The graph of dependence of external indices and internal irregularities depending on the "theta" and "delta" ratios (using values from 0.01 to 0.9 as an example)
Thus, members of a society can use information about other members to make decisions about their movements, as well as how their behavior may vary depending on the level of diversity in the society.
Now we know a little more about the ASO algorithm and, based on the theory we have obtained, we can move on to the practical part. We will compose a pseudocode of the algorithm for its implementation in code. ASO algorithm pseudocode:
Initialization:
1. Set parameters: popSize, omega, lambda1, lambda2, anarchyProb, alpha, theta, delta, rangeMin [], rangeMax [], rangeStep []
2. Create a population of popSize members: for each i member from 0 to popSize-1: for each c coordinate from 0 to coords-1:
position [i].[c] = random number between rangeMin [c] and rangeMax [c]
pBest [i].[c] = position [i].[c]
prevPosition [i].[c] = position [i].[c]
pBestFitness [i] = -infinity
3. Set gBest = best position from initial population
4. Set gBestFitness = gBest fitness
Main loop:
5. Until the stopping criterion is reached: for each i member from 0 to popSize-1:
5.1 Calculate indices
FI = CalculateFI (i)
EI = CalculateEI (i)
II = CalculateII (i)
5.2 Select movement policy
If FI > EI and FI > II: newPosition = CurrentMP (i)
Otherwise, if EI > FI and EI > II: newPosition = SocietyMP (i)
Otherwise: newPosition = PastMP (i)
5.3 Apply anarchic behavior
If random number < anarchyProb: for each c coordinate from 0 to coords-1:
newPosition [c] = random number between rangeMin [c] and rangeMax [c]
5.4 Update position for each c coordinate from 0 to coords-1:
prevPosition [i].[c] = position [i].[c]
position [i].[c] = limit (newPosition [c], rangeMin [c], rangeMax [c], rangeStep [c])
5.5 Rate new 'fitness' position = rate_fitness (position [i])
5.6 Update personal 'best' if 'fitness' > pBestFitness [i]:
pBestFitness [i] = fitness
pBest [i] = position [i]
5.7 Update global 'best' if 'fitness' > gBestFitness:
gBestFitness = fitness
gBest = position [i]
5.8 Adapt the AdaptParameters () parameter
5.9 CalculateFI (i) function: return 1 - alpha * (fitness [i] - pBestFitness [i]) / (gBestFitness - fitness [i])
5.10 CalculateEI (i) function: return 1 - exp(-(gBestFitness - fitness [i]) / theta)
5.11 CalculateII (i) function: return 1 - exp(-(pBestFitness [i] - fitness [i]) / delta)
5.12 CurrentMP (i) function: for each c coordinate from 0 to coords-1:
r1 = random number between 0 and 1
r2 = random number between 0 and 1
velocity = omega * (position [i].[c] - pBest [i].[c]) + lambda1 * r1 * (pBest [i].[c] - position [i].[c]) + lambda2 * r2 * (gBest [c] - position [i].[c])
newPosition [c] = position [i].[c] + velocity
return newPosition
5.13 SocietyMP (i) function: j = random member of the population, not equal to i, for each c coordinate from 0 to coords - 1:
If random number < 0.5:
newPosition [c] = position [i].[c]
Otherwise: newPosition [c] = position [j].[c]
return newPosition
5.14 PastMP (i) function: for each c coordinate from 0 to coords - 1:
If random number < 0.5:
newPosition [c] = position [i].[c]
Otherwise: newPosition [c] = prevPosition [i].[c]
return newPosition
Now that we have the pseudocode, we can start writing the algorithm code based on it. Let's describe the S_ASO_Member structure used to represent a participant (agent) in the algorithm.
1. Structure fields:
- pPrev [] — array of previous positions of participants.
- pBest [] — array of the best known positions of the participants (personal best ones).
- pBestFitness — variable stores the fitness value (quality) of the best known position.
2. The Init method initializes the pPrev and pBest arrays setting their size according to the number of coordinates (or the dimensionality of the search space) passed as the coords parameter. ArrayResize(pBest, coords) and ArrayResize(pPrev, coords) — these calls resize arrays to the coords value. pBestFitness = -DBL_MAX — set the initial value for the best position fitness to ensure that any value found will be better than this one.
The S_ASO_Member structure is designed to store information about each participant in the optimization algorithm. It allows us to track both the current and best positions of the participant, as well as their fitness.
//—————————————————————————————————————————————————————————————————————————————— struct S_ASO_Member { double pPrev []; // Previous position double pBest []; // Personal best position double pBestFitness; // Personal best fitness void Init (int coords) { ArrayResize (pBest, coords); ArrayResize (pPrev, coords); pBestFitness = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Define the C_AO_ASO class inherited from the C_AO base class. Let's look at it in more detail:
1. Parameters are:
- popSize — population size (number of society members).
- anarchyProb — possibility of anarchic behavior, some participants may act independently of others.
- omega, lambda1, lambda2 — parameters related to inertia and acceleration used to control the behavior of participants.
- alpha, theta, delta — parameters used to calculate indicators (FI, EI, II).
2. params — array of parameters, where each element contains a name and a value.
3. SetParams () — the method updates the parameter values from the params array, which allows changing the parameters of the algorithm after its initialization.
4. Init () — the method initializes the algorithm with the given ranges and steps. It accepts the rangeMinP, rangeMaxP and rangeStepP arrays, as well as the epochsP number of epochs.
5. Moving() and Revision () — methods implement the basic logic of the movement of participants and their revision (update) in the optimization.
6. Class fields:
S_ASO_Member member [] — array of society members stores information about each participant in the algorithm.
7. Private methods:
- CalculateFI — the method for calculating the FI (Fitness Indicator) value for a specific participant.
- CalculateEI — the method for calculating the EI (Exploration Indicator).
- CalculateII — the method for calculating the value of II (Inertia Indicator).
- CurrentMP, SocietyMP, PastMP — the methods implement the logic of interaction of participants with their current, social and past positions.
The C_AO_ASO class is an implementation of the concept of an "anarchic society" where participants can act both jointly and independently of each other, and includes parameters that control the behavior of participants and methods for their initialization and updating.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASO () { } C_AO_ASO () { ao_name = "ASO"; ao_desc = "Anarchy Society Optimization"; ao_link = "https://www.mql5.com/en/articles/15511"; popSize = 50; // Population size anarchyProb = 0.1; // Probability of anarchic behavior omega = 0.7; // Inertia weight lambda1 = 1.5; // Acceleration coefficient for P-best lambda2 = 1.5; // Acceleration coefficient for G-best alpha = 0.5; // Parameter for FI calculation theta = 1.0; // Parameter for EI calculation delta = 1.0; // Parameter for II calculation ArrayResize (params, 8); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "anarchyProb"; params [1].val = anarchyProb; params [2].name = "omega"; params [2].val = omega; params [3].name = "lambda1"; params [3].val = lambda1; params [4].name = "lambda2"; params [4].val = lambda2; params [5].name = "alpha"; params [5].val = alpha; params [6].name = "theta"; params [6].val = theta; params [7].name = "delta"; params [7].val = delta; } void SetParams () { popSize = (int)params [0].val; anarchyProb = params [1].val; omega = params [2].val; lambda1 = params [3].val; lambda2 = params [4].val; alpha = params [5].val; theta = params [6].val; delta = params [7].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double anarchyProb; // Probability of anarchic behavior double omega; // Inertia weight double lambda1; // Acceleration coefficient for P-best double lambda2; // Acceleration coefficient for G-best double alpha; // Parameter for FI calculation double theta; // Parameter for EI calculation double delta; // Parameter for II calculation S_ASO_Member member []; // Vector of society members private: //------------------------------------------------------------------- double CalculateFI (int memberIndex); double CalculateEI (int memberIndex); double CalculateII (int memberIndex); void CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); void SocietyMP (S_AO_Agent &agent, int coordInd); void PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); }; //——————————————————————————————————————————————————————————————————————————————
Let's look at the following Init method of the C_AO_ASO class. Method logic:
- StandardInit — method is called to perform standard initialization using the passed ranges. If this method returns false, an error has occurred.
- ArrayResize — the method resizes the member array to popSize, which determines the number of participants (members of society) in the algorithm.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (member, popSize); for (int i = 0; i < popSize; i++) member [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Let's look at the Moving method code of the C_AO_ASO class. Method structure and logic:
1. First call check:
- If revision is false, the method initializes the a array with random values within specified ranges rangeMin and rangeMax.
- For each c coordinate of each i population member, the u.RNDfromCI method is called. It generates a random value, and then this value is normalized using u.SeInDiSp.
- The values are saved in member [i].pPrev [c] for further use.
- After that, revision is set to true, and the method completes execution.
2. Basic movement logic:
- For each i population member, three indices are calculated: fi, ei and ii. These are metrics that characterize the state of a population member.
- For each c coordinate, the following is executed:
- the current value is saved to member [i].pPrev [c].
- rnd random number is generated using u.RNDprobab ().
- if the random number is less than anarchyProb (which means the fulfillment of the probability of anarchy manifestation in behavior), the c coordinate for the i member will be initialized randomly from the range.
- otherwise, depending on the fi, ei and ii values, the CurrentMP, SocietyMP and PastMP methods are called.
- After all the changes, the value of each c coordinate is adjusted using u.SeInDiSp.
The Moving method implements the logic of moving members of the population in the solution space based on their current states and metrics.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); member [i].pPrev [c] = a [i].c [c]; } } revision = true; return; } //---------------------------------------------------------------------------- double fi = 0.0; //fickleness index double ei = 0.0; //external irregularity index double ii = 0.0; //internal irregularity index double rnd = 0.0; for (int i = 0; i < popSize; i++) { fi = CalculateFI (i); ei = CalculateEI (i); ii = CalculateII (i); for (int c = 0; c < coords; c++) { member [i].pPrev [c] = a [i].c [c]; rnd = u.RNDprobab (); if (u.RNDprobab () < anarchyProb) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); else { if (rnd > fi) CurrentMP (a [i], member [i], c); else { if (rnd < ei) SocietyMP (a [i], c); else { if (rnd < ii) PastMP (a [i], member [i], c); } } } } for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Let's move from Moving to Revision method. General structure and logic:
1. The ind variable is initialized with the value of -1. It will be used to store the index of the population member that has the best value of the f function.
2. The method runs through all members of the population from 0 to popSize - 1.
3. Finding the best function value: for each member of the population, a [i] is checked, namely whether its f function value is exceeded by the current best value of fB. If this is the case, fB is updated by a [i].f, while the ind index is set to i.
4. Update personal best value: the method also checks if the a [i].f function value is greater than the member [i].pBestFitness population member value. If yes, the value is updated and the current coordinates a[i].c are copied to member[i].pBest using the ArrayCopy function.
5. Copying the best solution: after the loop is complete, if the ind index (i.e. at least one member of the population had a function value greater than fB) is found, then the coordinates of this population member are copied to cB using ArrayCopy.
The Revision method is responsible for updating the best solution found in the population, as well as updating the personal best values for each member of the population. It uses simple logic to compare function values to determine, which solutions are the best, and stores them for later use.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > member [i].pBestFitness) { member [i].pBestFitness = a [i].f; ArrayCopy (member [i].pBest, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Next, the CalculateFI method of the C_AO_ASO class. Method description:
1. The method takes the index of the memberIndex population member tthe fitness is to be calculated for.
2. Getting fitness values:
- currentFitness — gets the current fitness value of a population member from the a array by the memberIndex index.
- personalBestFitness — get the personal best fitness value of this member from the member array.
- globalBestFitness — get the global best fitness value stored in the fB variable.
3. Fitness Index (FI) calculation - the method returns the value calculated using the equation.
The equation normalizes the difference between personal and current fitness by dividing it by the difference between global and current fitness. The CalculateFI method calculates a fitness index for a member of the population, which is used to evaluate its quality compared to its personal and global best fitness values.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateFI (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; double globalBestFitness = fB; //1 - 0.9 * (800-x)/(1000-x) return 1 - alpha * (personalBestFitness - currentFitness) / (globalBestFitness - currentFitness); } //——————————————————————————————————————————————————————————————————————————————
The CalculateEI method of the C_AO_ASO class comes next. The method does almost the same thing as the previous one, but uses the best global and personal current fitness to calculate it.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateEI (int memberIndex) { double currentFitness = a [memberIndex].f; double globalBestFitness = fB; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(globalBestFitness - currentFitness) / (globalBestFitness * theta)); } //——————————————————————————————————————————————————————————————————————————————
The CalculateII method of the C_AO_ASO class is completely similar to the previous one, but it uses the best and current own fitness.
The exponential function helps smooth out changes and provides a smooth transition between values. The CalculateII method calculates an improvement index for a member of the population that takes into account how well the current fitness state compares to personal achievements.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateII (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(personalBestFitness - currentFitness) / (personalBestFitness * delta)); } //——————————————————————————————————————————————————————————————————————————————
Let's move on to the CurrentMP method of the C_AO_ASO class. Description:
1. Random number generation:
- r1 = u.RNDprobab () — generate a random number r1 in the range [0, 1].
- r2 = u.RNDprobab () — generate a random number r2 in the range [0, 1].
2. Calculate velocity — the equation includes three components:
- omega * (agent.c [coordInd] - memb.pBest [coordInd]) — inertial component, the agent’s movement taking into account its previous position.
- lambda1 * r1 * (memb.pBest[coordInd] - agent.c[coordInd]) — direct the agent taking into account its personal best position
- lambda2 * r2 * (cB[coordInd] - agent.c[coordInd]) — direct the agent taking into account the best position of the population.
3. Updating the agent's position by adding the velocity to the current coordinate value.
The CurrentMP method implements the update of the agent's position in space based on its current position, personal best position, and the best position of the population.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { double r1 = u.RNDprobab (); double r2 = u.RNDprobab (); double velocity = omega * (agent.c [coordInd] - memb.pBest [coordInd]) + lambda1 * r1 * (memb.pBest [coordInd] - agent.c [coordInd]) + lambda2 * r2 * (cB [coordInd] - agent.c [coordInd]); agent.c [coordInd] += velocity; } //——————————————————————————————————————————————————————————————————————————————
The SocietyMP method of the C_AO_ASO class updates the agent's coordinates based on a random choice between group and personal information. This allows the agent to adapt to the state of both the entire population and an individual agent.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::SocietyMP (S_AO_Agent &agent, int coordInd) { int otherMember = u.RNDminusOne (popSize); agent.c [coordInd] = u.RNDprobab () < 0.5 ? cB [coordInd] : member [otherMember].pBest [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
The PastMP method of the C_AO_ASO class updates the agent's coordinate based on a random choice between the current best state of the population member and its previous state. This allows the agent to take into account both the current achievements of a population member and its past results. This approach improves the combinatorial properties of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { agent.c [coordInd] = u.RNDprobab () < 0.5 ? memb.pBest [coordInd] : memb.pPrev [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
3. Test results
ASO test stand results:
ASO|Anarchy Society Optimization|50.0|0.01|0.7|1.5|1.5|0.5|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8487202680440514
25 Hilly's; Func runs: 10000; result: 0.746458607174428
500 Hilly's; Func runs: 10000; result: 0.31465494017509904
=============================
5 Forest's; Func runs: 10000; result: 0.9614752193694915
25 Forest's; Func runs: 10000; result: 0.7915027321897546
500 Forest's; Func runs: 10000; result: 0.23802894131144553
=============================
5 Megacity's; Func runs: 10000; result: 0.5707692307692309
25 Megacity's; Func runs: 10000; result: 0.5406153846153848
500 Megacity's; Func runs: 10000; result: 0.16613846153846298
=============================
All score: 5.17836 (57.54%)
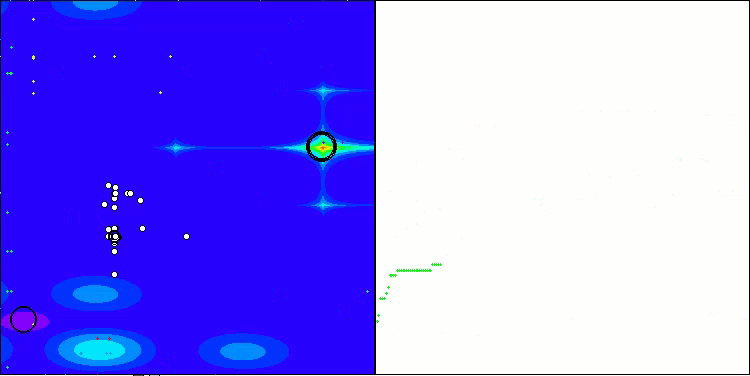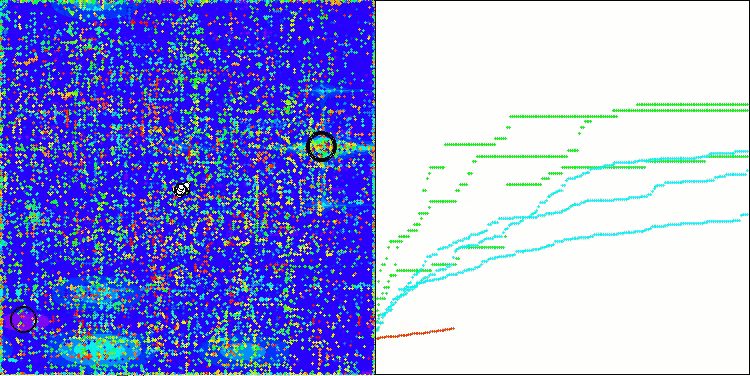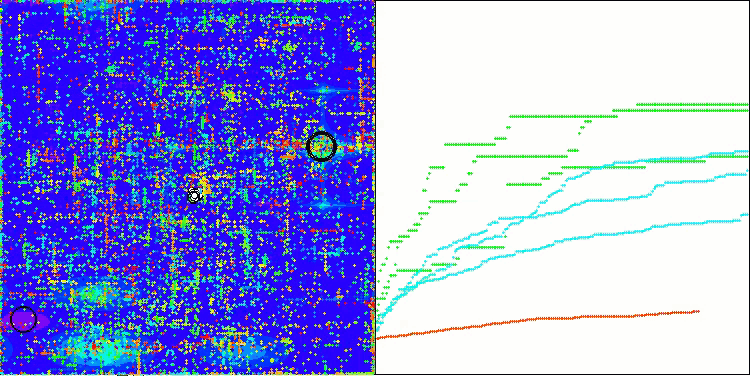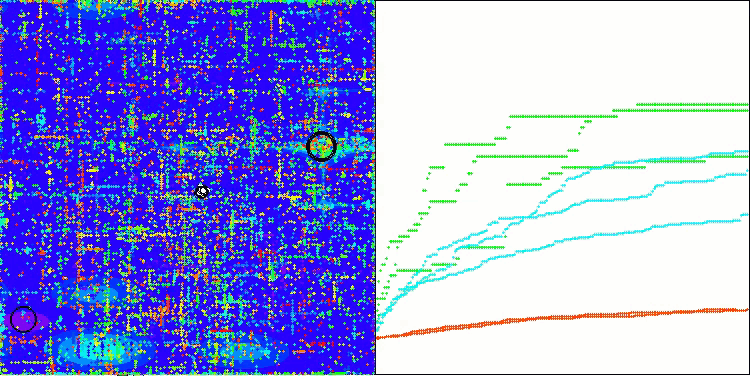
Looking at the visualization of the algorithm operation, we can draw some conclusions: there is a spread of results. However, the algorithm demonstrates good search capabilities when working with large-dimensional functions, which is also confirmed by its results.
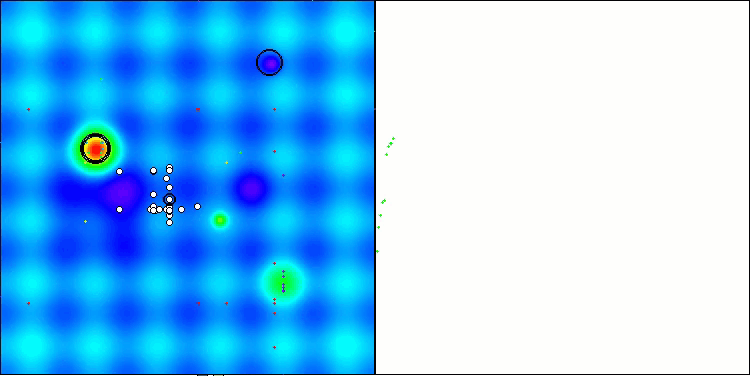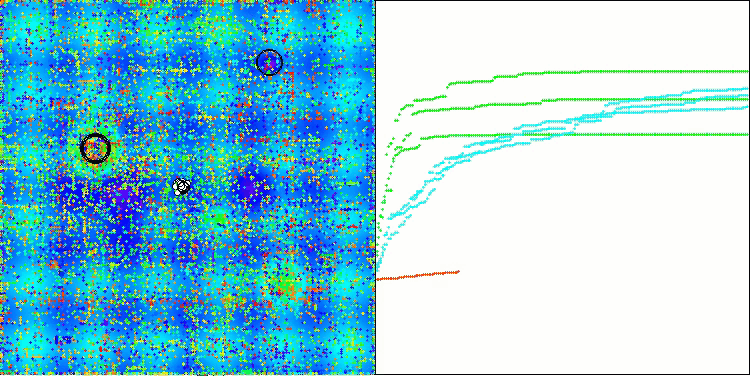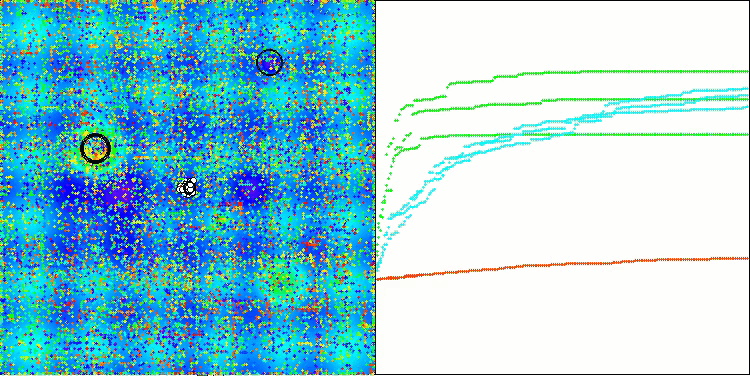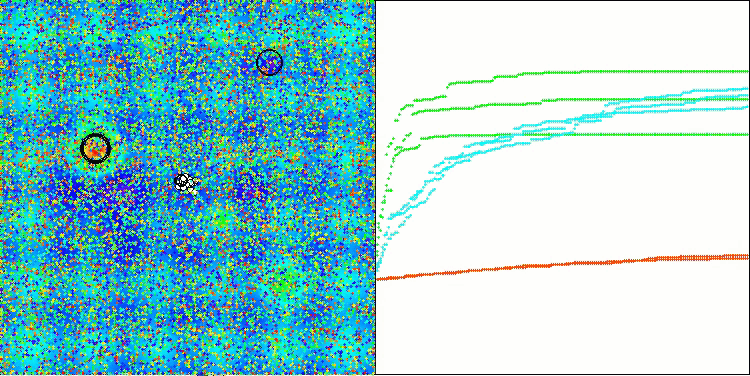
ASO on the Hilly function
ASO on the Forest function
ASO on the Megacity function
Population optimization algorithms rating table: ASO algorithm got into the top ten after the test and took 9 th place in the rating table.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | comet tail algorithm | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | evolution of social groups | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | simulated isotropic annealing | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 10 | TSEA | turtle shell evolution algorithm | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 20 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 21 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 22 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 23 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 24 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 25 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 26 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 27 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 28 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 29 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 30 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 31 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 32 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 33 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 34 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 35 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 36 | IWDm | intelligent water drops M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 37 | PSO | particle swarm optimisation | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 38 | Boids | boids algorithm | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 39 | MA | monkey algorithm | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 40 | SFL | shuffled frog-leaping | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 41 | FSS | fish school search | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 42 | RND | random | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 43 | GWO | grey wolf optimizer | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 44 | CSS | charged system search | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 45 | EM | electroMagnetism-like algorithm | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Summary
Based on the results of the algorithm operation on the test functions of different dimensions, the following conclusions can be made: ASO shows average results on the smooth Hilly function compared to its closest neighbors in the table, but very decent results on the "sharp" Forest and especially on the discrete Megacity. The overall final score is 5.17836 (57.54%). The algorithm demonstrates good search capabilities, especially when working with large-dimensional functions. In other words, it scales well. The algorithm can be recommended for solving discrete optimization problems, which is a priority for traders.
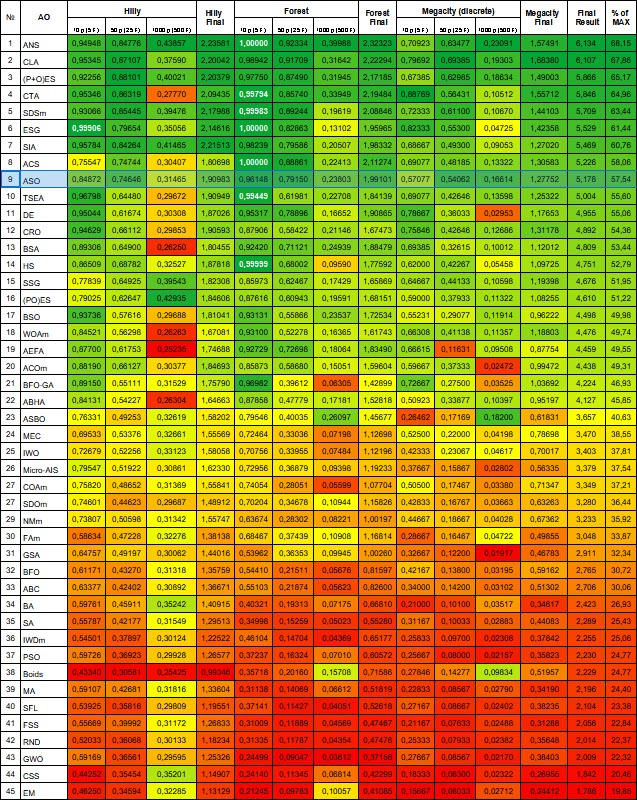
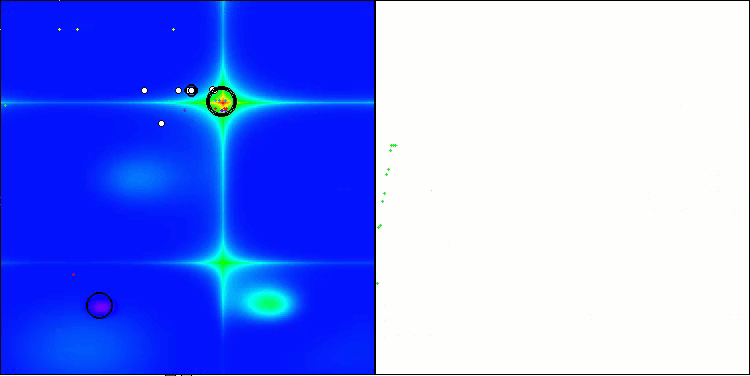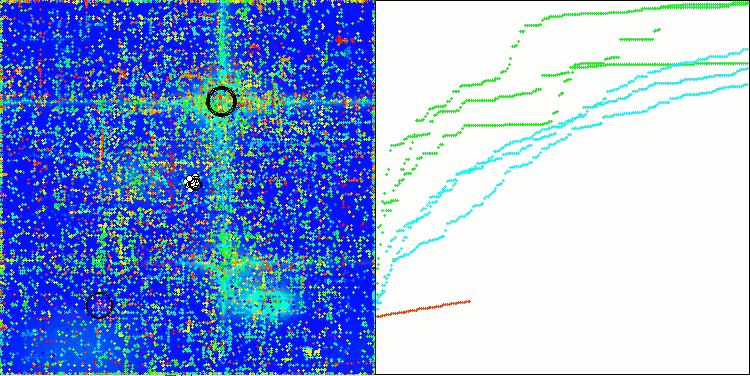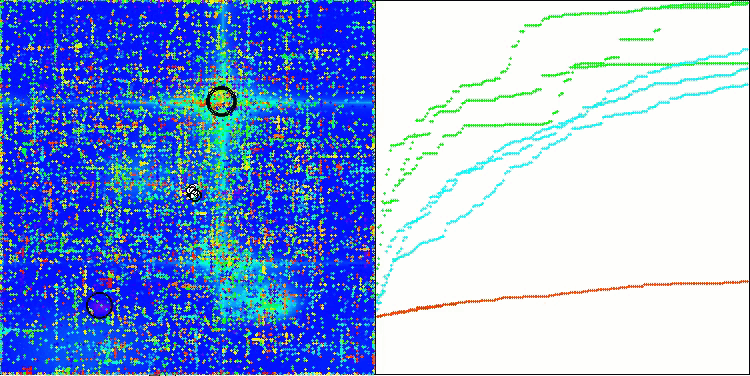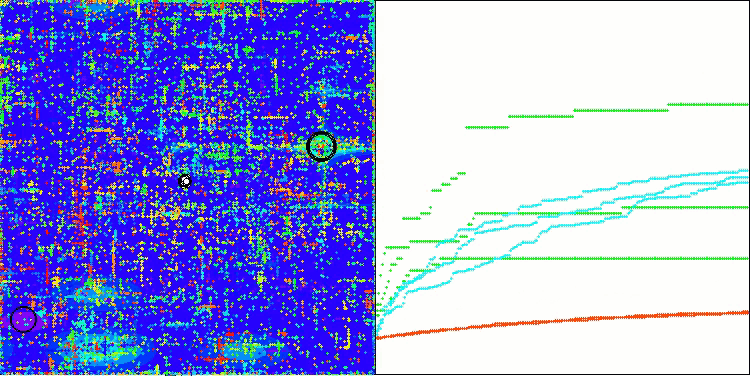
Figure 4. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
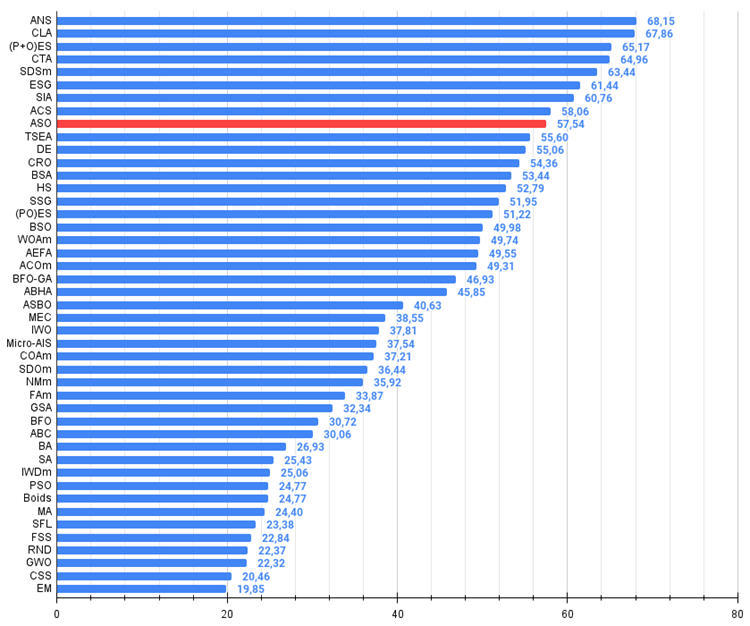
Figure 5. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
ASO algorithm pros and cons:
Advantages:
- Good convergence on various functions.
- Excellent results on discrete functions.
Disadvantages:
- Large number of parameters (very difficult to configure).
- Scatter of results on low-dimensional functions.
- Complex implementation.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/15511
Automating Trading Strategies in MQL5 (Part 9): Building an Expert Advisor for the Asian Breakout Strategy
MQL5 Wizard Techniques you should know (Part 55): SAC with Prioritized Experience Replay
Trading with the MQL5 Economic Calendar (Part 6): Automating Trade Entry with News Event Analysis and Countdown Timers
Automating Trading Strategies in MQL5 (Part 8): Building an Expert Advisor with Butterfly Harmonic Patterns
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use