Population ADAM (Adaptive Moment Estimation)
427
0
Contents
Introduction
In the world of machine learning, where data is rapidly growing and algorithms are becoming increasingly complex, optimization plays a key role in achieving high results. Among the many methods that attempt to tackle this problem, the ADAM (Adaptive Moment Estimation) algorithm stands out for its elegance and efficiency.
In 2014, two outstanding minds, D. P. Kingma and J. Ba proposed the ADAM algorithm, which combines the best features of its predecessors, such as AdaGrad and RMSProp. The algorithm was specifically designed to optimize the weights of neural networks using the gradients of the activation functions of neurons. It is based on adaptive first and second moment estimates, making it simple to implement and highly computationally efficient. The algorithm requires minimal memory resources and does not depend on diagonal rescaling of gradients, which makes it particularly suitable for problems with large amounts of data and parameters.
ADAM also performs well on non-stationary targets and situations where gradients may be noisy or sparse. The algorithm hyperparameters are easy to interpret and usually do not require complex tuning.
However, despite its efficiency in the field of neural networks, ADAM is limited to the use of analytical gradients, which narrows the range of its applications. In this article, we propose an innovative approach to modifying the ADAM algorithm by transforming it into a population-based optimization algorithm capable of handling numerical gradients. This modification not only extends the scope of ADAM beyond neural networks, but also opens up new possibilities for solving a wide range of optimization problems in general.
Our research aims to create a general-purpose optimizer that retains the benefits of the original ADAM but can operate effectively in settings where analytical gradients are not available. This will allow the modified ADAM to be applied in areas such as global optimization and multi-objective optimization, significantly expanding its potential and practical value.
Implementation of the algorithm
The ADAM algorithm is often classified as a stochastic gradient based optimization method. However, it is important to note that ADAM itself does not contain any internal stochastic elements in its core logic. The stochasticity associated with ADAM actually comes from the way the data is prepared and fed to the algorithm, not from its internal mechanics. It is important to distinguish between stochasticity in data preparation and the determinism of the optimization algorithm itself.
The ADAM algorithm itself is completely deterministic. Given the same input data and initial conditions, it will always produce identical results. The parameters in ADAM are updated based on clearly defined equations that do not include random elements.
This distinction between the deterministic nature of the ADAM algorithm and the stochastic nature of the data preparation for it is important for a proper understanding of its operation and potential for modification. Recognizing this fact opens up opportunities to adapt ADAM to problems where stochastic data preparation may not be applicable or desirable, while still retaining its powerful optimization properties.
Let's look at the pseudo code with the equations:
1. Initialization:
m₀ = 0 (initialization of the first moment)
v₀ = 0 (initialization of the second moment)
t = 0 (step counter)
2. At each t step:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (gradient calculation)
3. Updating first and second adjusted moments:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. Updating the parameters:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
where:
θₜ - model parameters at step t
f(θ) - target function
α - learning rate (usually α = 0.001)
β₁, β₂ - damping ratios for the moments (usually β₁ = 0.9, β₂ = 0.999)
ε - small constant to prevent division by zero (usually 10⁻⁸)
mₜ, vₜ - estimates of the first and second moments of the gradient
m̂ₜ, v̂ₜ - adjusted moment estimates
These equations capture the essence of the ADAM algorithm, showing how it adaptively adjusts the learning rate for each parameter based on estimates of the first and second moments of the gradients. As we can see, there is no stochasticity in the algorithm at all. As a rule, the ADAM algorithm in its numerous software implementations is firmly woven into the fabric of neural network architecture. However, in this article we will perform a little magic: we will not only make it an independent and self-sufficient entity, but also turn it into a population and truly stochastic method.
To begin with, we need to implement ADAM in a population format, preserving its original equations, while adding an element of randomness only at the stage of the initial initialization of the parameters to be optimized. But this is just the beginning! We will then introduce randomness into the dynamics of this gradient method's behavior and see what results this can lead to.
Let's define the S_Gradients structure, which will store gradients and two moment vectors (first and second). The Init (int coords) method sets the size of the arrays and initializes them to zero.
//—————————————————————————————————————————————————————————————————————————————— // Structure for storing gradients and moments struct S_Gradients { double g []; // Gradients double m []; // Vectors of the first moment double v []; // Vectors of the second moment // Method for initializing gradients void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Initialize gradients to zeros ArrayInitialize (m, 0.0); // Initialize the first moment with zeros ArrayInitialize (v, 0.0); // Initialize the second moment with zeros } }; //——————————————————————————————————————————————————————————————————————————————
The C_AO_ADAM class implements the ADAM optimization algorithm. Main functions of the class:
- Constructor initializes algorithm parameters such as population size, learning rates, and decay rates.
- SetParams () sets the values of parameters from the params array allowing them to be modified after initialization.
- Init () prepares the algorithm for work by accepting parameter ranges and the number of epochs.
- Moving () and Revision () are designed to perform optimization steps, update model parameters and check the state of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAM () { } // Class constructor C_AO_ADAM () { ao_name = "ADAM"; // Algorithm name ao_desc = "Adaptive Moment Estimation"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 50; // Population size alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 1e-8; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size alpha = params [1].val; // Set the learning ratio beta1 = params [2].val; // Set beta1 beta2 = params [3].val; // Set beta2 epsilon = params [4].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter }; //——————————————————————————————————————————————————————————————————————————————
The Init method of the C_AO_ADAM class performs the algorithm initialization:
- It calls StandardInit () for default parameter settings. If unsuccessful, it returns false.
- It rtesets the step and iteration t counters.
- It resizes the grad gradient array according to the popSize population size.
- It initializes gradients for each individual in the population using the coords coordinates.
If all operations are successful, the method returns true.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving method of the C_AO_ADAM class implements the optimization step in the ADAM algorithm:
1. Check step if step is less than 2:
- The previous value of the function and coordinates is saved for each individual in the population.
- New random coordinates are generated within the specified range and adjusted to acceptable values.
- The step counter is incremented and the method terminates.
2. Calculating gradients: if the step is 2 or more, the change in the value of the objective function and coordinates is calculated for each individual.
- To prevent division by zero, a small epsilon value is added. In addition, this value is an external parameter of the algorithm that influences the search properties.
- The gradient is calculated for each parameter.
3. Updating parameters for each individual:
- Previous values of the function and coordinates are preserved.
- The biased estimates of the first and second moments of the gradient are updated.
- Adjusted moment estimates are calculated and coordinates are updated using the ADAM equation.
- The coordinates are adjusted to ensure that they remain within acceptable limits.
4. The t iteration counter is incremented.
Thus, the method is responsible for updating the positions of individuals during the optimization using adaptive gradient moments. The first two steps of the algorithm are necessary to calculate the gradient of the change in the value of the fitness function, since the gradient is calculated numerically, without knowledge of the analytical equation of the optimization problem being solved. It requires at least two points to calculate, and the solutions obtained in the previous two steps can be used in subsequent steps.
The logic of the ADAM algorithm does not really suggest a specific way to calculate the gradient. The gradient can be calculated either analytically or numerically, and its calculation occurs outside the algorithm itself. Abstracting the algorithm from the ways in which it is used is really important for understanding the role of individual components in the overall machine learning project. This allows for a better assessment of the impact of each element on the final result and makes it easier to adapt the algorithm to different tasks.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
The Revision method of the C_AO_ADAM class performs the following actions:
- It initializes the index of the best ind individual as -1.
- It iterates through all individuals in the population and if the value of the current individual's function is greater than the best fB value found, it updates the best global solution and stores the index of the best individual.
- If a best individual was found, it copies its coordinates into the cB array.
Thus, the method finds and stores the coordinates of the best individual based on the values of the fitness function.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual } //——————————————————————————————————————————————————————————————————————————————
As we can see, the ADAM algorithm has now become population-based, and if we set the external population size parameter to 1, the algorithm will behave completely like a regular non-population ADAM. Now we can test the algorithm on our test functions. Let's look at the results:
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs: 10000; result: 0.3857584301959297
25 Hilly's; Func runs: 10000; result: 0.29733109680042824
500 Hilly's; Func runs: 10000; result: 0.25390478702062613
=============================
5 Forest's; Func runs: 10000; result: 0.30772687797850234
25 Forest's; Func runs: 10000; result: 0.1982664040653052
500 Forest's; Func runs: 10000; result: 0.15554626746207786
=============================
5 Megacity's; Func runs: 10000; result: 0.18153846153846154
25 Megacity's; Func runs: 10000; result: 0.12430769230769231
500 Megacity's; Func runs: 10000; result: 0.09503076923077
=============================
All score: 1.99941 (22.22%)
The results are unfortunately not the best, but this opens up opportunities for potential growth and gives us room to implement improvements, in particular introducing a true stochastic component into the algorithm.
In the above implementation of the ADAM population algorithm, each agent represents a separate "thread" of execution of the authors' original logic, like snakes crawling along the hills of the search space, distributed across the field due to the initial random initialization. These snakes do not interact with each other and do not exchange information about the best solutions. Since the algorithm is gradient-based, it is important for it to take into account changes in surface level at points located as close to each other as possible. By decreasing the numerical differentiation step, we may encounter slow convergence, while increasing the step leads to large jumps in space, making it difficult to obtain information about the surface between points.
To solve these problems, we will make part of the population hybrid individuals, which will consist of elements of the decisions of other agents. The idea is this: we sort the population by the fitness of the individuals, and at the end of the list (where the weakest individuals are located), we create hybrids. For such individuals, solutions will be generated by forming a new point in space based on elements of the solutions of more adapted individuals. The higher the fitness of an individual, the greater the likelihood that it will transmit information about its position to hybrids.
Thus, some individuals in the population will represent solutions according to the original logic of the algorithm, and the other part will be so-called hybrids, which are a combination of elements of solutions from the population. The resulting hybrid is not simply copied from parts of other individuals; each of these parts varies according to a power law probability distribution. We will call the degree of this law "hybrid stability": the higher the degree, the less changes the hybrid undergoes, and the more it resembles the elements of the best solutions in the population.
Now let's move on to the updated version of the algorithm. The C_AO_ADAMm class features several changes made to the C_AO_ADAM class, which, theoretically, can positively influence its functionality and behavior. Here are the main changes:
1. New parameters:
- hybridsPercentage - determine the percentage of hybrids in the population.
- hybridsResistance - regulate the resistance of hybrids to changes.
2. In the C_AO_ADAMm class constructor, we initialize new hybridsPercentage and hybridsResistance parameters. Their values are added to the params array.
3. SetParams features strings for setting new hybridsPercentage and hybridsResistance parameters allowing us to dynamically change their values.
Setting the hybrid percentage parameter to "1" will effectively disable the ADAM logic. Setting this value to "0" will result in the algorithm having no combinatorial properties. As a result, after some trials, I found the optimal value equal to "0.5", which turned out to be the best.
The second parameter is responsible for the resistance of hybrids to changes. When setting low values, hybrids after inheritance of traits change significantly and can cover the entire range of acceptable values of the optimized parameters. At the same time, if we set too high values, for example "20" or more, the variability of hybrids tends to "0", and they become only carriers of the best qualities of the parent individuals. The optimal value of "10" for this parameter was found on a trial basis as well.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAMm () { } // Class constructor C_AO_ADAMm () { ao_name = "ADAMm"; // Algorithm name ao_desc = "Adaptive Moment Estimation M"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 100; // Population size hybridsPercentage = 0.5; // Percentage of hybrids in the population hybridsResistance = 10; // Resistance of hybrids to changes alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 0.1; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size hybridsPercentage = params [1].val; // Set the percentage of hybrids in the population hybridsResistance = params [2].val; // Set hybrids' resistance to change alpha = params [3].val; // Set the learning ratio beta1 = params [4].val; // Set beta1 beta2 = params [5].val; // Set beta2 epsilon = params [6].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double hybridsPercentage; // Percentage of hybrids in the population double hybridsResistance; // Resistance of hybrids to changes double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter int hybridsNumber; // Number of hybrids in the population }; //——————————————————————————————————————————————————————————————————————————————
In the Init method of the C_AO_ADAMm class, the following changes have occurred compared to the similar method in the previous class:
- The number of hybrids in a population is calculated based on the hybridsPercentage percentage. This new value of hybridsNumber is used to control the composition of the population.
- Added a check to ensure that the number of hybrids does not exceed popSize. This prevents errors related to array out-of-bounds.
These changes make the Init more adaptive to the algorithm hybrid-related features and ensure correct management of the state and initialization of individuals in the population.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter hybridsNumber = int(popSize * hybridsPercentage); // Calculation of the number of hybrids in the population if (hybridsNumber > popSize) hybridsNumber = popSize; // Correction ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving method also features a few changes compared to the previous version of this method.
Updating parameters using the ADAM algorithm. Conditions for handling hybrids have been added to this block. If the i individual index exceeds or is equal to popSize - hybridsNumber, new coordinates are generated using a random distribution and the hybridsResistance parameter. This allows hybrids to have small deviations in inherited traits from their parent individuals (a kind of analogue of trait mutation). Otherwise, for individuals that are not hybrids, the biased first and second moment estimates are updated and then the adjusted estimates are calculated.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
The Revision method features the following changes compared to the previous version of this method.
Preparing an array for sorting: create a temporary array aT the size of the population and then call the u.Sorting () sorting method. A sorted population array allows for the inheritance of traits by hybrids with a higher probability from more adapted individuals. The temporary population array could have been moved to the class fields, but in this case it was done for greater clarity.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Test results
Let's look at the results of the modified version of the truly stochastic population ADAMm:
ADAMm|Adaptive Moment Estimation M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8863499654810468
25 Hilly's; Func runs: 10000; result: 0.4476644542595641
500 Hilly's; Func runs: 10000; result: 0.2661291031673467
=============================
5 Forest's; Func runs: 10000; result: 0.8449728914068644
25 Forest's; Func runs: 10000; result: 0.3849320103361983
500 Forest's; Func runs: 10000; result: 0.16889385703816007
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.2704615384615384
500 Megacity's; Func runs: 10000; result: 0.10593846153846247
=============================
All score: 4.03688 (44.85%)
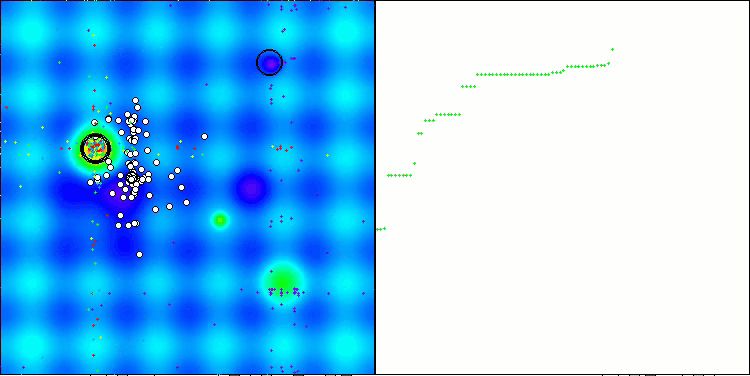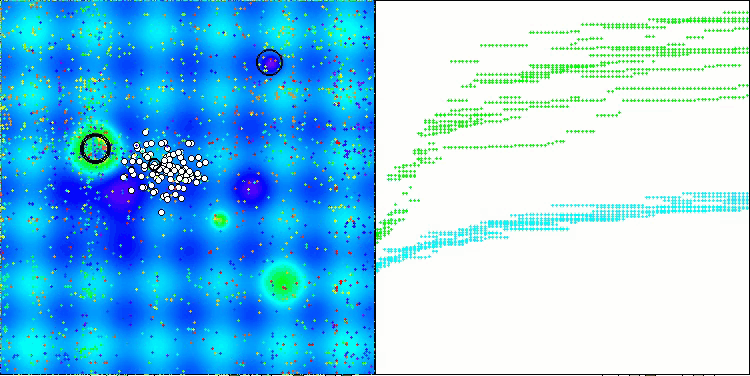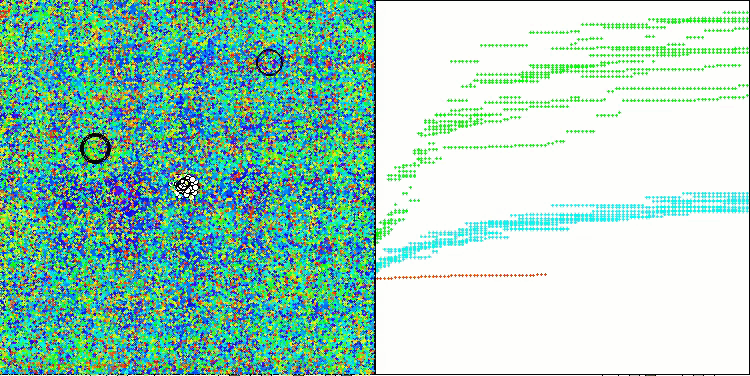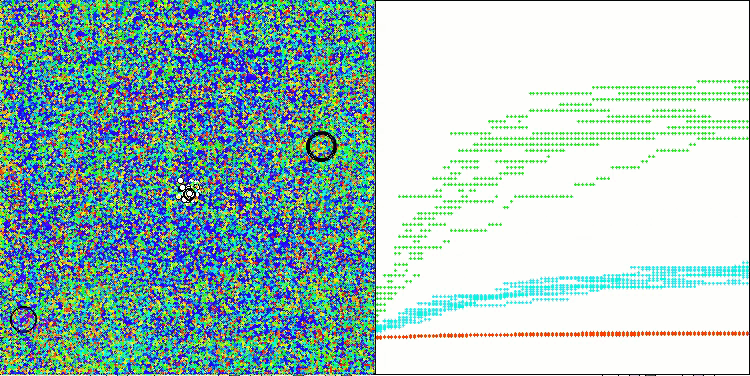
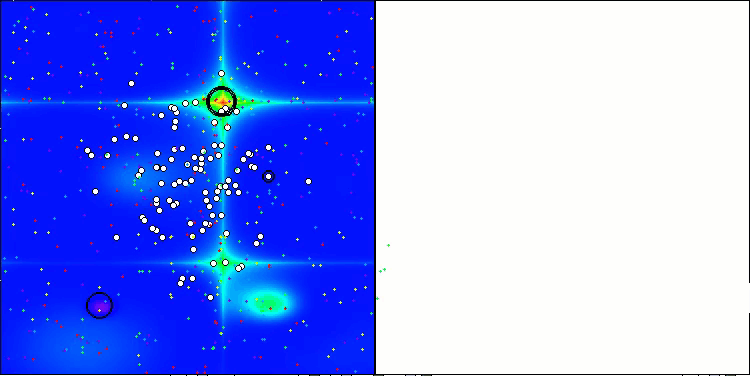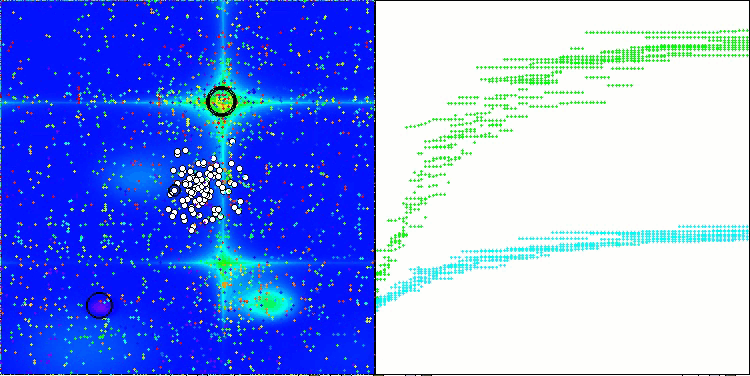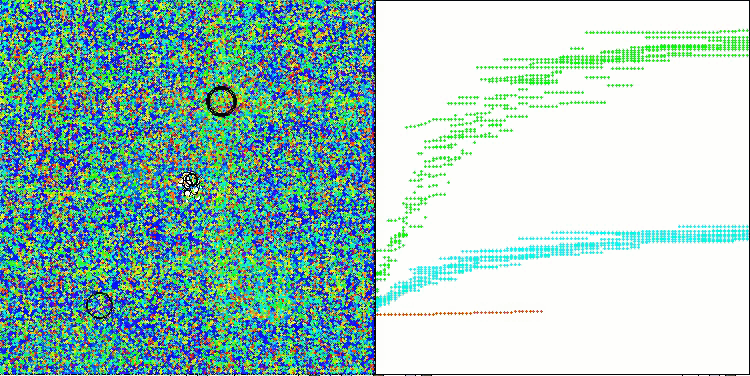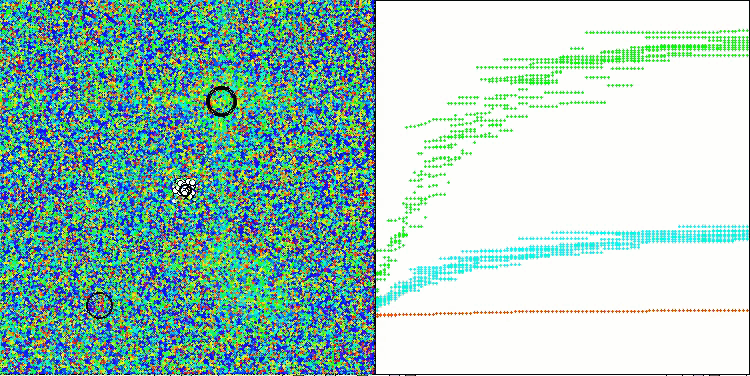
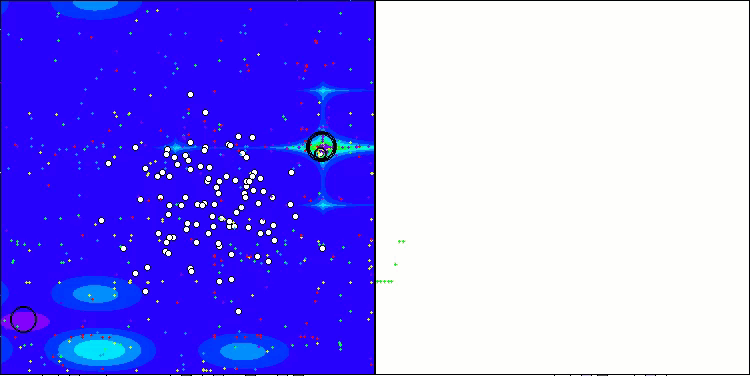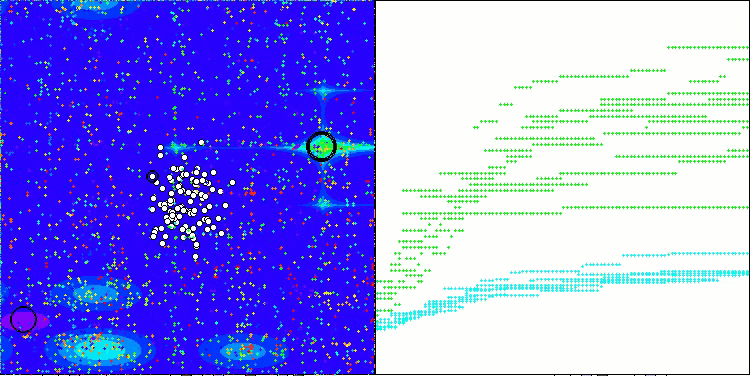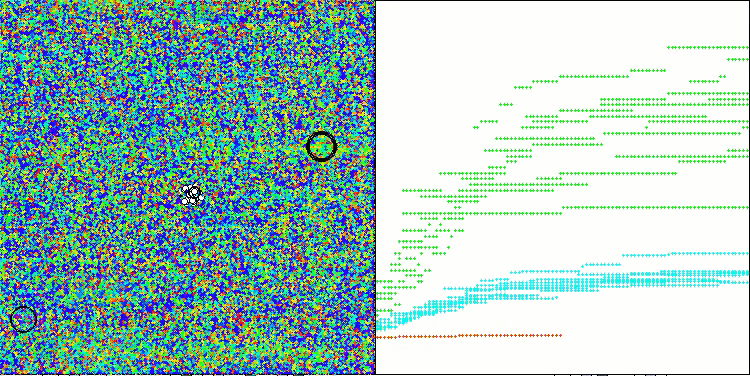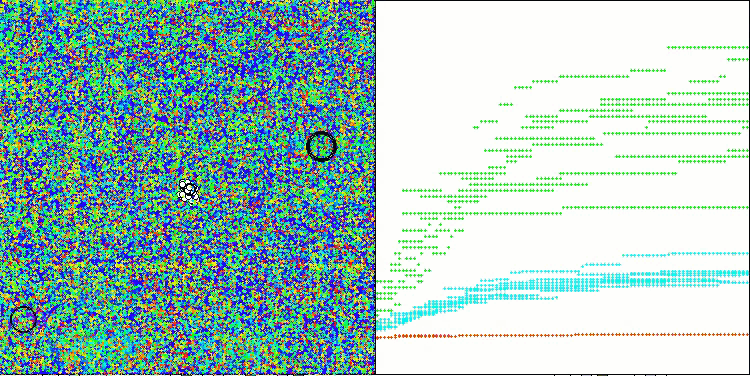
The results obtained have improved significantly. Below is a visualization of a simple ADAM population algorithm, showing the peculiar movement of individual "snakes" crawling in all directions as they explore the search space. Also presented are visualizations of stochastic population ADAMm, demonstrating more active movement of search agents towards the global optimum, but in this case the characteristic "snake" appearance is lost.
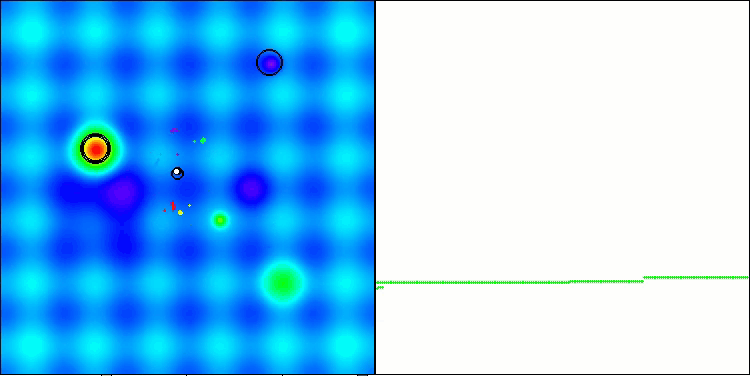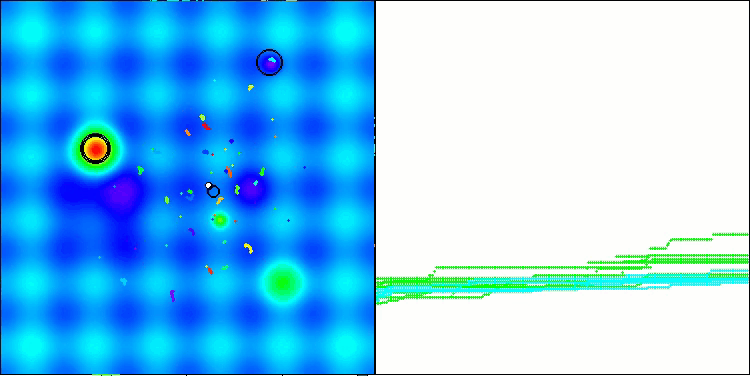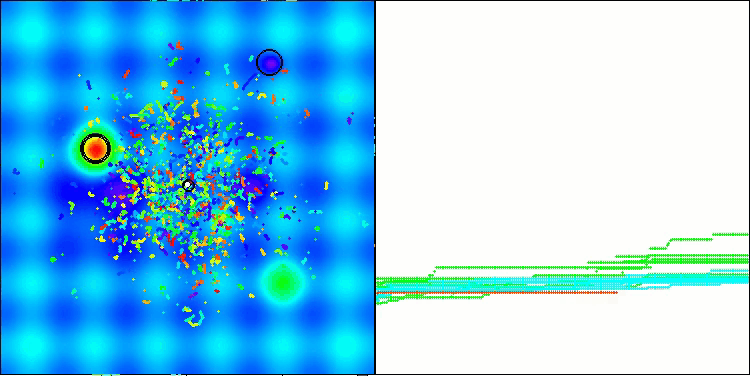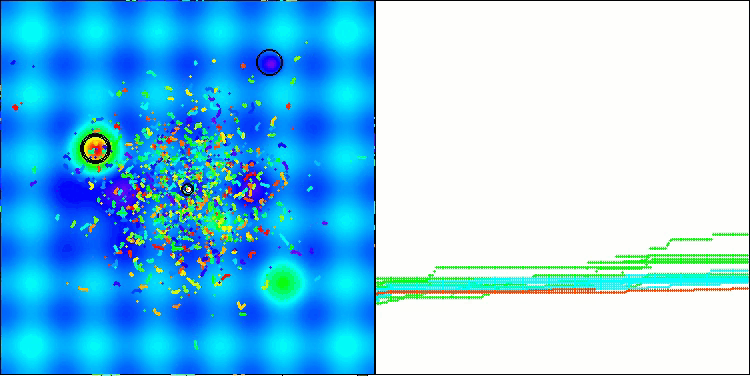
ADAM on the Hilly test function
ADAMm on the Hilly function
ADAMm on the Forest test function
ADAMm on the Megacity test function
Based on the test results, the stochastic population version of ADAM ranks 32nd in the ranking table, which is a fairly good result. The original version could not be included in the table due to its poor results.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 30 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 31 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 32 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 33 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 34 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 35 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 36 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 37 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 38 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 39 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 40 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 41 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 42 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 43 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 44 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 45 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
Summary
The article presents an attempt to adapt the well-known gradient method ADAM, traditionally used in neural networks, to solve optimization problems in general. This attempt was successful because the resulting truly stochastic population ADAMm is capable of competing with the most powerful algorithms for global optimization problems. The paper demonstrates that deterministic approaches to optimal solution search problems are often not as effective in multidimensional search spaces as stochastic methods, and only additional elements of randomness can expand the search capabilities of each optimization algorithm.
However, it should be noted that the use of network-integrated gradient methods, such as the conventional ADAM, still remains virtually unrivaled in training neural networks, since they use the exact gradient value in backpropagation. However, when training neural networks using more complex evaluation criteria than the error minimization function, gradient methods can encounter difficulties and get stuck in local optima, as noted by many authors of machine learning articles.
The approach presented here can be useful in the classical use of integrated methods in neural networks, maintaining excellent accuracy and convergence speed, using the analytical form of the activation function of neurons and greatly increasing the ability to resist jamming during training of neural networks. This will allow the use of classical methods in tasks with very complex metrics and criteria during training. I hope that this work will help researchers and practitioners look at optimization problems in general and machine learning methods in particular from a new perspective.
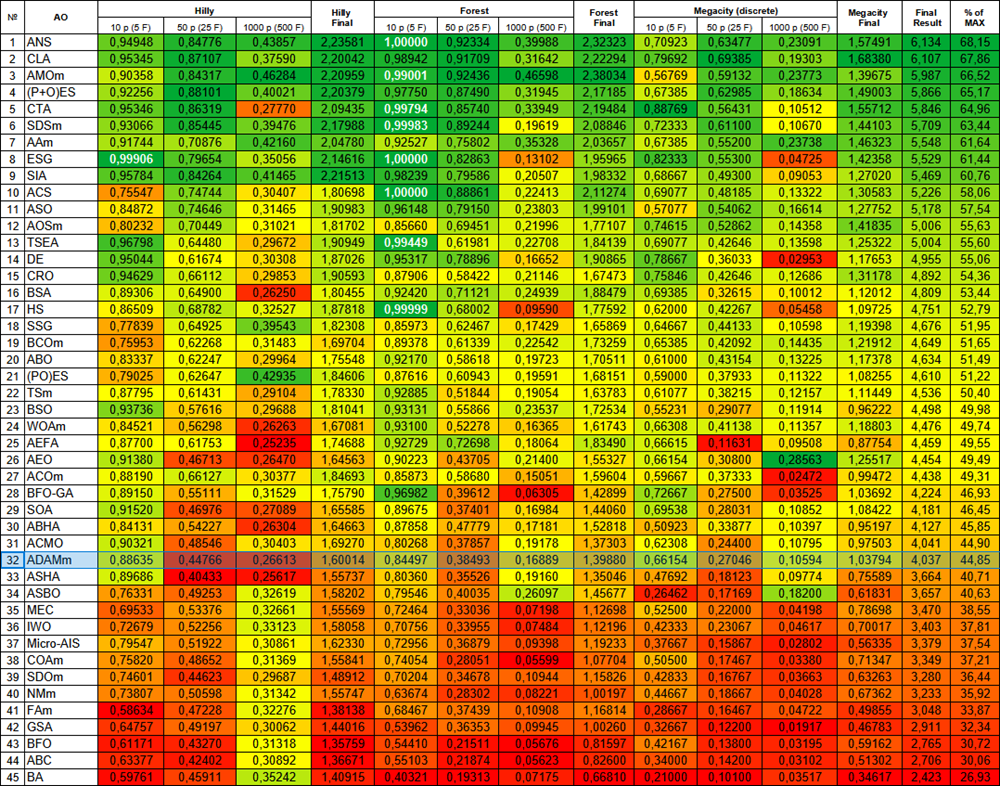
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
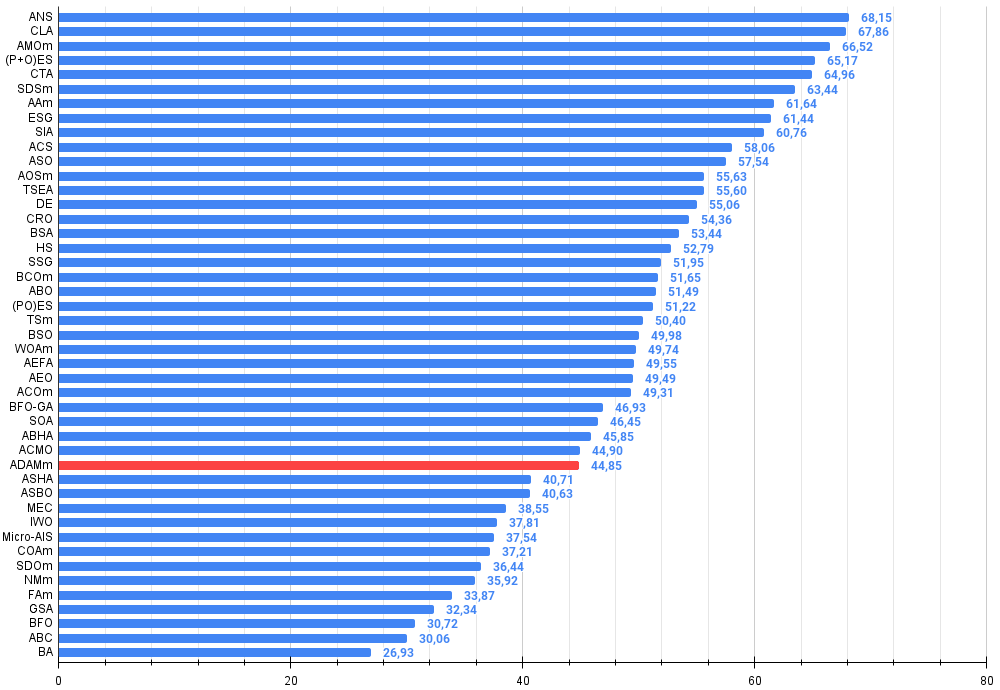
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
ADAMm pros and cons:
Pros:
- Good results on low-dimensional problems.
- Low scatter of results.
Cons:
- Many external parameters.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | Simple use of population optimization algorithms.mq5 | Script | A simple example of using population optimization algorithms without visualization |
| 9 | Test_AO_ADAM.mq5 | Script | ADAM and ADAMm test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16443
Features of Custom Indicators Creation
MQL5 Wizard Techniques you should know (Part 76): Using Patterns of Awesome Oscillator and the Envelope Channels with Supervised Learning
Features of Experts Advisors
Automating Trading Strategies in MQL5 (Part 24): London Session Breakout System with Risk Management and Trailing Stops
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use