Tabu Search (TS)

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

The Tabu Search algorithm, one of the first and best-known metaheuristic methods, was developed in the 1980s and was a real breakthrough in combinatorial optimization. This method was proposed by Fred Glover, and it immediately attracted the attention of researchers due to its innovative strategy of using memory to prohibit duplicate moves. There were other methods at the time, such as genetic algorithms, but Tabu Search stood out for its unique approach.

The algorithm starts with the selection of an initial solution and then explores neighboring options, where preference is given to those that improve the current result. To prevent a return to previously explored unsuccessful solutions, a tabu list is used - a structure that records "prohibited" movements. This allows us to avoid cyclic processes and explore the search space more efficiently. For example, in the knapsack problem, an algorithm might add or remove items one by one, seeking to maximize their value while avoiding returning to previously considered combinations.

The basis of Tabu Search is adaptive memory, which not only prevents returning to already found solutions, but also controls the search process, taking into account previous steps. Other researchers, such as Manuel Laguna and Rafael Marti, subsequently developed the algorithm, greatly expanding its application in areas ranging from production planning to financial analysis and telecommunications. Tabu Search still remains a relevant tool for solving complex combinatorial problems that require deep analysis and complex calculations.

Tabu Search is thus a great example of how innovative ideas can transform search optimization methods, opening up new possibilities in science and technology. Although the algorithm was originally developed to solve specific combinatorial problems, such as the traveling salesman problem and the knapsack problem, the article discusses a modification of the classical algorithm that allows it to solve more general optimization problems, including problems in a continuous search space.

Implementation of the algorithm

Let's consider the general equations and mechanisms used in the Tabu Search algorithm for solving combinatorial optimization problems (the conventional algorithm):

1. General formulation of the optimization problem:

• f (x) optimization - objective function.
• x ∈ X, where X is a set of constraints on the vector of x variables.

2. Neighborhood of solutions:

• N (x) is a set of solutions that can be reached from the current solution x using one "move".
• N* (x) is a modified neighborhood that takes into account the search history (short-term and long-term memory).

3. Short-term memory:

• Tracking attributes (characteristics of decisions) that have changed in the recent past.
• Prohibition of visiting solutions containing "tabu-active" attributes.

4. Long-term memory:

• Counting frequencies of attribute changes/presences in visited solutions.
• Using these frequencies to manage search diversification.

5. Intensification:

• Selecting the best move from a modified neighborhood N* (x).
• Returning to promising areas of the solution space.

6. Diversification: 

• Select moves that introduce new attributes not seen before.
• Search directions in an area different from those already explored.

7. Strategic fluctuations:

• Changing the rules for choosing moves when approaching a "critical level".
• Passing through the level and then returning.

8. Linking paths:

• Generating trajectories connecting high-quality support solutions.
• Selecting moves that bring the current solution as close as possible to the guiding solutions.

To solve the optimization problems, we will skip point 8 and focus on the main idea of the algorithm, trying to implement a modification of the Tabu Search, while keeping, if possible, points 1-7. The original algorithm works with discrete decisions, trying to find the shortest path between nodes. To adapt it to problems in a continuous search space, it is necessary to somehow discretize the feasible regions for each parameter being optimized. The problem is that we cannot label every possible solution, since the number of labels would be colossal, making the solution almost impossible.

Instead of a tabu list, we will introduce the concepts of a "white list" and "black list" for each parameter, dividing their ranges into sectors (a specified number of sectors for each optimized parameter). This way we can add a check mark to the white list when the solution is successful and make a mark to the black list if the solution is not improved compared to the previous step. Sectors with promising solutions will accumulate marks, which will allow for more thorough exploration of the area and refinement of the solution. However, a successful sector may also contain extremely unsuccessful decisions, in which case the sector will be blacklisted. This means that the same sector may contain both white list and black list marks.

The selection of sectors for generating the next solution should be done with a probability proportional to the number of labels in the white list. After generating a new solution, we check the corresponding sector against the blacklist and calculate the probability proportional to the black list marks as a fraction of the sum of the white list marks. If the probability is fulfilled, we choose another randomly selected sector.

Thus, taking into account the features of the surface of the function being optimized, the algorithm dynamically generates probabilities for exploring all available areas in the search space, without dwelling on any particular sector. Even if an algorithm ends up close to the global optimal solution, it will not be able to improve its results indefinitely. This, in turn, will lead to an increase in the blacklist marks for that sector, which will force the algorithm to change sectors and continue searching in other areas of hyperspace.

The idea is that this approach will ensure diversification of the refinement of the solutions found and a broad study of the problems. This should also minimize the number of external parameters of the algorithm, providing it with self-adaptive properties to the problem function being studied.

Let us highlight the main points of the idea of a modified implementation of the classic Tabu Search:

1. Discretization. Dividing the search space into sectors allows for more efficient exploration of areas.
2. White and black lists. Successful and unsuccessful decisions are recorded separately, providing dynamic tracking of the sector prospects.
3. Dynamic study. The algorithm generates probabilities for exploring all available areas, avoiding getting stuck in inefficient sectors.
4. Adaptability. The algorithm reacts to the accumulation of black list marks, which forces it to change the search direction and provide diversification.

Thus, our version of the algorithm combines elements of Tabu Search and evolutionary algorithms. It uses a memory mechanism in the form of black and white lists to direct the search to promising areas of the solution space and avoid areas that have led to a worse solution.

For clarity, we will schematically depict the white and black lists of sectors for each coordinate. For example, let's take three coordinates, each of which is divided into 4 sectors. White and black lists are set separately for each coordinate.

For example, the "0" coordinate of the "3)" sector in the white list features five "check marks", which is the largest number among all sectors of this coordinate. This means that the sector will be selected in the next iteration with the highest probability. On the other hand, this very sector features six "labels" in the black list, which will increase the likelihood of its replacement when generating a new solution, despite the fact that it is considered the most promising. Thus, a situation may arise where a sector with less potential will have a lower probability of being replaced by another sector when choosing sectors (this is not obvious at first glance).

As can be seen, there is a constant rebalancing of probabilities during the exploration of the search space, which allows taking into account the features of the surface. This direction seems to be very promising, since it depends little on the external parameters of the algorithm, which makes it truly self-adaptive.

 0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 

1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____|

2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____|



0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___|

1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______|

2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|

Now we can write a pseudocode for a modified version of the algorithm, which we will denote as TSm:

1. Initialization of the population:

    For each agent in the population:

      Set random coordinates within the specified range.

      Set the initial value of the previous fitness as the minimum possible one.

2. The main loop of the algorithm:

    Until the termination condition is reached, repeat:

     a) If this is the first iteration:

         Perform initial initialization of the population.

     b) Otherwise:

         Generate new coordinates for agents:

         For each agent and each coordinate:

             With a certain probability, copy the coordinate of the best known solution.

             Otherwise:

                 Select a sector from the agent's white list.

                 Generate a new coordinate in this sector.

             If the selected sector is on the black list, select a random sector and generate a coordinate in it.

             Check that the new coordinate does not go beyond the acceptable range.

     c) Evaluate the suitability of each agent with new coordinates.

     d) Update black and white lists:

         For each agent:

             Compare the current suitability with the previous one.

             If the suitability has improved, increase the counter in the white list for the corresponding sector.

             If it has got worse, increase the counter in the black list.

         Save the current fitness as the previous one for the next iteration.

     e) Update the best solution found if an agent with better fitness is found.

3. Upon the loop completion, return the best solution found.

Now let's start writing the code. Let's describe two structures: S_TSmSector and S_TSmAgent used to work with sectors and agents in the search strategy.

1. S_TSmSector - the structure contains an array of sector [] integers, which will store "check marks" for the corresponding sector (in fact, this is an array of counters).

2. S_TSmAgent - this structure is more complex. It describes the search agent in the algorithm and includes:

• blacklist [] - array of black lists by sectors for each coordinate.
• whitelist [] - array of white lists by sectors for each coordinate.
• fPrev - the value of the agent's previous fitness.

The Init method initializes the S_TSmAgent instance. Parameters:

• coords - number of coordinates.
• sectorsPerCord - number of sectors for each coordinate.

Logic:

1. Resizing the blacklist and whitelist arrays up to the number of coordinates.

2. Initialization of each sector in a loop for all coordinates:

• Resizing the sector array for the black list of the current coordinate.
• Same for the white list.
• Initialize all elements of the white and black lists to zeros (these are counters that will subsequently be incremented by one).
  

3. fPrev initialization - set the fPrev value to -DBL_MAX, which represents the minimum possible value. This is used to indicate that the agent has not yet acquired fitness.

The code creates an agent structure that can manage black lists and white lists for sectors of different dimensions of the search space, where it is necessary to keep track of allowed and forbidden sectors for agents to visit.

//——————————————————————————————————————————————————————————————————————————————
struct S_TSmSector
{
    int sector [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
struct S_TSmAgent
{
    S_TSmSector blacklist []; //black list by sectors of each coordinate
    S_TSmSector whitelist []; //white list by sectors of each coordinate

    double fPrev;             //previous fitness

    void Init (int coords, int sectorsPerCord)
    {
      ArrayResize (blacklist, coords);
      ArrayResize (whitelist, coords);

      for (int i = 0; i < coords; i++)
      {
        ArrayResize (blacklist [i].sector, sectorsPerCord);
        ArrayResize (whitelist [i].sector, sectorsPerCord);

        ArrayInitialize (blacklist [i].sector, 0);
        ArrayInitialize (whitelist [i].sector, 0);
      }

      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Describe the C_AO_TSm class inherited from the C_AO base class.

1. The constructor sets initial values for variables:

• popSize - population size is 50.
• sectorsPerCoord - number of sectors per coordinate is 100.
• bestProbab - probability of choosing the best solution is 0.8.
• It creates and initializes the params array with three parameters that correspond to the above variables.

2. The SetParams method sets the values of parameters from the params array back to the corresponding class variables.

3. The Init method initializes the algorithm with the specified ranges and search steps.

4. Moving () - the method is responsible for moving agents in the search space, while Revision () checks and updates current solutions using the Tabu Search logic.

5. Class members:

• S_Agent agents [] - array of agents represents solutions to the problem in the search process.

6. Private methods:

• InitializePopulation () - method for initializing a population of agents.
• UpdateLists () - method for updating black and white lists of sectors for agents.
• GenerateNewCoordinates () - method for generating new coordinates during the search.
• GetSectorIndex () - method for obtaining a sector index based on coordinate and dimension.
• ChooseSectorFromWhiteList () - method for selecting a sector from the white list for a given agent and dimension.
• GenerateCoordInSector () - method for generating a coordinate in a given sector.
• IsInBlackList () - method for testing the performance of the probability of selecting another sector with an impact on the selection of white and black lists.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_TSm : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_TSm ()
  {
    ao_name = "TSm";
    ao_desc = "Tabu Search M";
    ao_link = "https://www.mql5.com/en/articles/15654";

    popSize         = 50;
    sectorsPerCoord = 100;
    bestProbab      = 0.8;

    ArrayResize (params, 3);

    params [0].name = "popSize";         params [0].val = popSize;
    params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord;
    params [2].name = "bestProbab";      params [2].val = bestProbab;
  }

  void SetParams ()
  {
    popSize         = (int)params [0].val;
    sectorsPerCoord = (int)params [1].val;
    bestProbab      = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    sectorsPerCoord;
  double bestProbab;

  S_TSmAgent agents [];

  private: //-------------------------------------------------------------------
  void   InitializePopulation      ();
  void   UpdateLists               ();
  void   GenerateNewCoordinates    ();
  int    GetSectorIndex            (double coord, int dimension);
  int    ChooseSectorFromWhiteList (int agentIndex, int dimension);
  double GenerateCoordInSector     (int sectorIndex, int dimension);
  bool   IsInBlackList             (int agentIndex, int dimension, int sectorIndex);

};
//——————————————————————————————————————————————————————————————————————————————

It is time to consider the Init method of the C_AO_TSm class responsible for initializing the Tabu Search algorithm. Let's break it down piece by piece:

1. The method first calls StandardInit by passing the arrays of minimum and maximum values and steps to it. This is a standard initialization that sets up the algorithm parameters. Next, the agents array is resized based on popSize and the number of agents in the population is defined. Next is a loop that goes through each agent in the agents array. The Init method is called for each agent. The method initializes its parameters, including coordinates (coords) and the number of sectors per coordinate (sectorsPerCoord).

2. If all initialization steps are successful, the method returns true, indicating successful initialization of the algorithm.

The Init method is key to preparing the Tabu Search algorithm for work. It sets the search ranges, initializes the array of agents and prepares them for further solution searching. If an error occurs at any stage of initialization, the method terminates and returns false.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agents, popSize);

  for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Let's consider the Moving method of the C_AO_TSm class. Method logic:

• if (!revision) - here the revision logical variable is checked. If it is false (initialization has not yet been performed), the next code block is executed.
• InitializePopulation () - responsible for initializing the agent population.
  

On the second and subsequent iterations of the algorithm, the GenerateNewCoordinates () method is called. The method generating new coordinates (new solutions) for agents in the search process.

The Moving method manages moving agents in the Tabu Search algorithm. It first checks whether the population has been initialized. If not, it initializes the population, otherwise the method generates new coordinates for the agents.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    InitializePopulation ();
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  GenerateNewCoordinates ();
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method is responsible for updating the current best solution during the Tabu Search. It goes through all the solutions in the population, compares their scores with the current best value, and if it finds a better solution, updates the corresponding variables. At the end of the method, the white and black lists are updated, which is necessary for further execution of the algorithm.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }

  //----------------------------------------------------------------------------
  UpdateLists ();
}
//——————————————————————————————————————————————————————————————————————————————

The next method InitializePopulation is responsible for initializing the population of Tabu Search agents. It generates random values for each agent coordinate in given ranges, and also sets the initial value for each agent's previous score. This is necessary for further iterations of the algorithm, where the evaluation and updating of solutions will take place.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::InitializePopulation ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    agents [i].fPrev = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Next is the UpdateLists method of the C_AO_TSm class. Method logic:

• The outer loop goes through all agents in the population, where popSize is the population size.
• The inner loop goes through all the coordinates of each agent.
• For each c coordinate of the a [i] agent, the sector index is calculated using the GetSectorIndex method. This is necessary to classify the values into specific sectors for further analysis.
• If the agent's current score a [i].f exceeds its previous one agents [i].fPrev, this means the agent has improved its decision. In this case, the whitelist counter is increased for the relevant sector.
• If the current score is less than the previous one, it means that the agent has worsened its decision and the blacklist counter for the corresponding sector increases.
• After all coordinates have been handled, the agent's previous estimate is updated to the current one so that it can be compared with the new value in the next iteration.

The UpdateLists method is responsible for updating the lists (white and black) for each agent in the population based on their current and previous scores. This allows the Tabu Search algorithm to track which sectors were successful (white list) and which were not (black list). Thus, the method helps in further managing the search for solutions by avoiding re-visiting inefficient areas of the solution space.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::UpdateLists ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      int sectorIndex = GetSectorIndex (a [i].c [c], c);

      if (a [i].f > agents [i].fPrev)
      {
        agents [i].whitelist [c].sector [sectorIndex]++;
      }
      else
        if (a [i].f < agents [i].fPrev)
        {
          agents [i].blacklist [c].sector [sectorIndex]++;
        }
    }
    agents [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Now let's look at the GenerateNewCoordinates method of the C_AO_TSm class. Method logic:

• The outer loop goes through all agents in the population, where popSize is the population size.
• The inner loop goes through all the coordinates of each agent.
• First, the probability is checked using the RNDprobab method. If the probability is fulfilled, the agent receives a coordinate from the cB [c] best global solution.
• If the probability is not fulfilled, a sector is selected from the white list using the ChooseSectorFromWhiteList() method.
• Then a new coordinate is generated in this sector using the GenerateCoordInSector () method.
• If the selected sector is in the black list, a new sector is selected randomly using u.RNDminusOne () and a new coordinate is generated in it.
• Checks whether the new coordinate is within the given boundaries and with the required step.

The GenerateNewCoordinates method is responsible for generating new coordinates for each agent in the population. It uses a probabilistic approach to choose between the best known coordinates and random generation in sectors based on white and black lists. The method also ensures the validity of the coordinates by checking them for compliance with the specified boundaries.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::GenerateNewCoordinates ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < bestProbab)
      {
        a [i].c [c] = cB [c];
      }
      else
      {
        int sectorIndex = ChooseSectorFromWhiteList (i, c);
        double newCoord = GenerateCoordInSector (sectorIndex, c);

        if (IsInBlackList (i, c, sectorIndex))
        {
          sectorIndex = u.RNDminusOne (sectorsPerCoord);
          newCoord = GenerateCoordInSector (sectorIndex, c);
        }

        newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = newCoord;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Let's analyze the GetSectorIndex function code, which specifies the sector index for a given coordinate in the specified dimension. The function logic:

• If the maximum and minimum values of a range for a given dimension are equal, it means that the range has no length. In this case, the function immediately returns 0, since there is no way to divide the range into sectors.
• Next, the length of one sector sL is calculated by dividing the length of the range by the number of sectors sectorsPerCoord.
• The ind sector index is calculated using an equation that determines which sector a given coordinate falls into. First, the minimum value of the range is subtracted from the coordinate, then the result is divided by the length of the sector, and the resulting value is rounded down to the nearest integer.
• If the coordinate is equal to the maximum value of the range, the function returns the index of the last sector.
• Further checks ensure that the index does not go beyond the acceptable values. If the index is greater than or equal to the number of sectors, the last sector is returned. If the index is less than 0, return 0.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::GetSectorIndex (double coord, int dimension)
{
  if (rangeMax [dimension] == rangeMin [dimension]) return 0;

  double sL =  (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;

  int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL);

  // Special handling for max value
  if (coord == rangeMax [dimension]) return sectorsPerCoord - 1;

  if (ind >= sectorsPerCoord) return sectorsPerCoord - 1;
  if (ind < 0) return 0;

  return ind;
}
//——————————————————————————————————————————————————————————————————————————————

Let's move on to the ChooseSectorFromWhiteList method, which selects a sector from the "white list" of sectors for a given agent and dimension. The method returns the index of the selected sector. The method logic:

• The totalCount variable is initialized by zero. It is used to count the total number of "check marks" in white list sectors.
• If totalCount is equal to zero, this means that the sectors do not yet contain "check marks" and all sectors are equal. In this case, the method selects a random sector from all available sectors and returns it.
• Next, the number of "check marks" is cumulatively counted in the loop. If randomValue is less than or equal to the current cumulative value, the method returns the index of the current sector s. This allows selecting a sector proportionally to its weight in the white list.

The ChooseSectorFromWhiteList method allows selecting a sector from the white list for an agent based on a probability distribution simulating roulette selection.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension)
{
  int totalCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    totalCount += agents [agentIndex].whitelist [dimension].sector [s];
  }

  if (totalCount == 0)
  {
    int randomSector = u.RNDminusOne (sectorsPerCoord);
    return randomSector;
  }

  int randomValue = u.RNDminusOne (totalCount);
  int cumulativeCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s];

    if (randomValue <= cumulativeCount)
    {
      return s;
    }
  }

  return sectorsPerCoord - 1;
}
//——————————————————————————————————————————————————————————————————————————————

Let's analyze the GenerateCoordInSector method, which generates a random coordinate in a given sector for a given dimension. The method logic:

• The sector size for a given dimension is calculated.
• sectorStart is calculated as the minimum value of the range for a given dimension plus an offset equal to the sector index multiplied by the sector size. sectorEnd is defined as sectorStart plus sectorSize. This defines the sector boundaries.
• The RNDfromCI function is called next. The function generates a random value from sectorStart to sectorEnd. This value represents a coordinate generated within the specified sector.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension)
{
  double sectorSize  = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;
  double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize;
  double sectorEnd   = sectorStart + sectorSize;

  double newCoord = u.RNDfromCI (sectorStart, sectorEnd);

  return newCoord;
}
//——————————————————————————————————————————————————————————————————————————————

In conclusion, analyze the IsInBlackList method, which checks if the agent is in the "black list" for a given sector and dimension. Parameters:

• agentIndex - index of the agent the check is performed for.
• dimension - dimension index.
• sectorIndex - index of the sector being checked.

The method returns true if the agent is on the black list and the probability of changing the sector is met, taking into account the "achievements" of the sector according to the white list.

• blackCount and whiteCount get the number of entries in the black and white lists respectively for the specified agent, dimension and sector.
  
• Total number of entries totalCount is calculated as the sum of black and white entries.
• If the total number of records is zero, the method immediately returns false, which means that the agent cannot be blacklisted, since there are no black or white entries.
• Next, the probability that a given sector should be considered as being on the blacklist is calculated. This is done by dividing the number of black entries by the total number of entries.
• The RNDprobab () method generates a random number between 0 and 1. If this random number is less than the calculated blackProbability blacklist probability, the method returns true.
  

The IsInBlackList method takes into account both black and white entries to determine the probability that a sector is blacklisted and needs to be changed. The greater the number of entries in the black list compared to the entries in the white list, the higher the probability of changing the sector to another random one in the future.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex)
{
  int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex];
  int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex];
  int totalCount = blackCount + whiteCount;

  if (totalCount == 0) return false;

  double blackProbability = (double)blackCount / totalCount;
  return u.RNDprobab () < blackProbability;
}
//——————————————————————————————————————————————————————————————————————————————

Test results

TSm test stand results:

TSm|Tabu Search M|50.0|100.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8779456463913048
25 Hilly's; Func runs: 10000; result: 0.6143121517195806
500 Hilly's; Func runs: 10000; result: 0.2910412462428753
=============================
5 Forest's; Func runs: 10000; result: 0.9288481105123887
25 Forest's; Func runs: 10000; result: 0.5184350456698835
500 Forest's; Func runs: 10000; result: 0.19054478009120634
=============================
5 Megacity's; Func runs: 10000; result: 0.6107692307692308
25 Megacity's; Func runs: 10000; result: 0.3821538461538462
500 Megacity's; Func runs: 10000; result: 0.1215692307692319
=============================
All score: 4.53562 (50.40%)

As we can see, the algorithm works quite well. There are decent results both on the test functions and visualization. Of course, there is a spread on the functions with small dimensions, but as you have noticed, many algorithms are subject to this phenomenon. Note the good ability of the algorithm to highlight the majority of significant surface areas of the function under study.

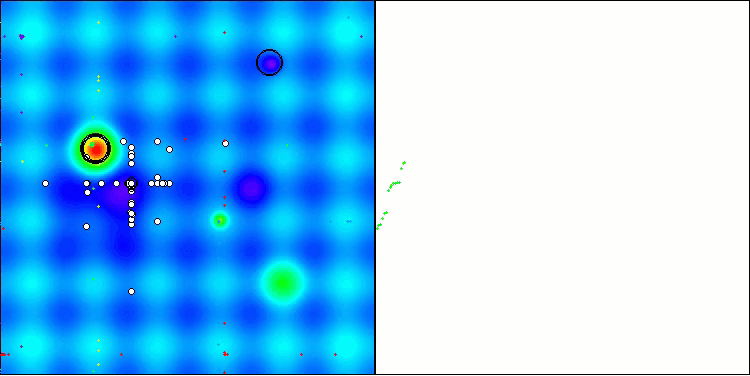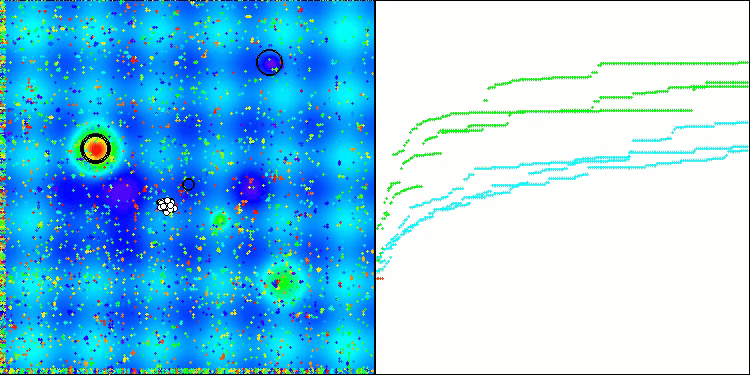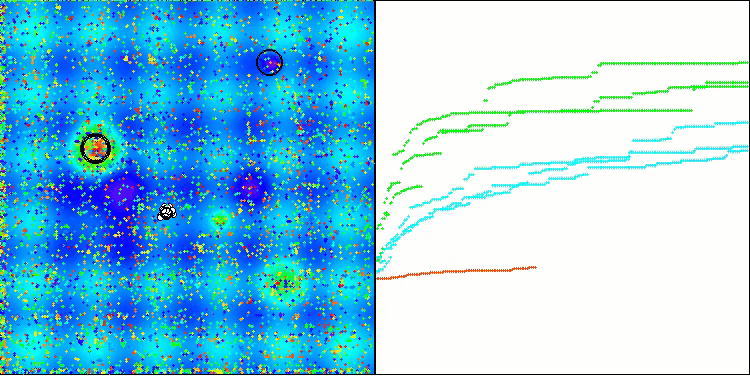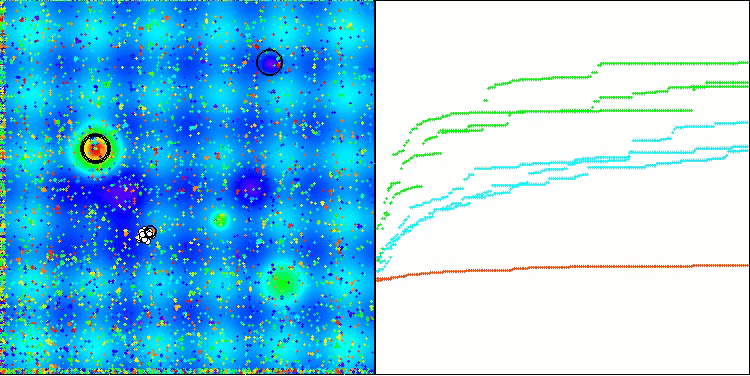
TSm on the Hilly test function

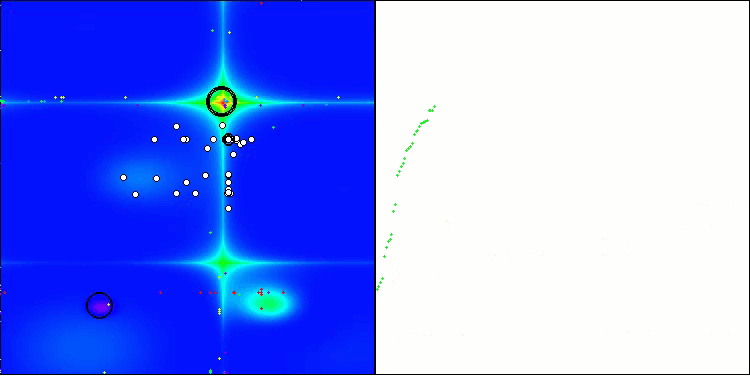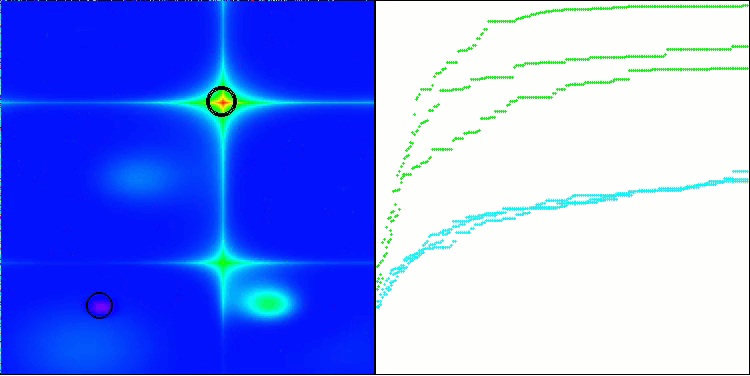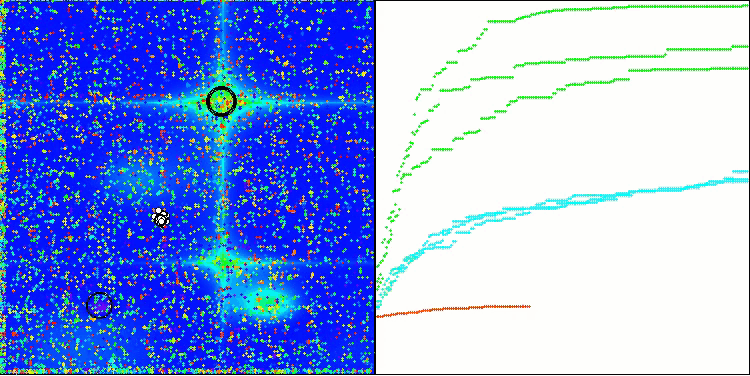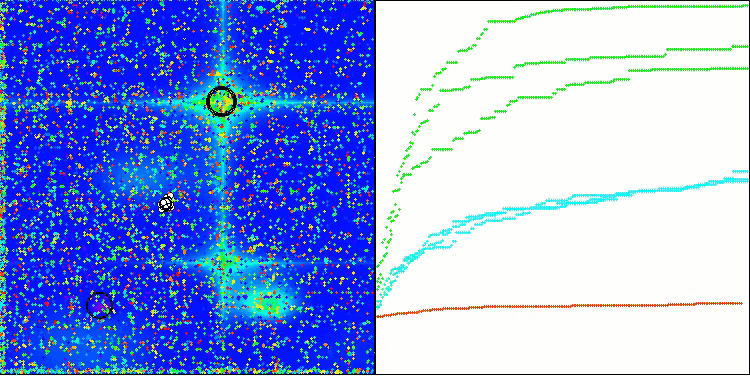
TSm on the Forest test function

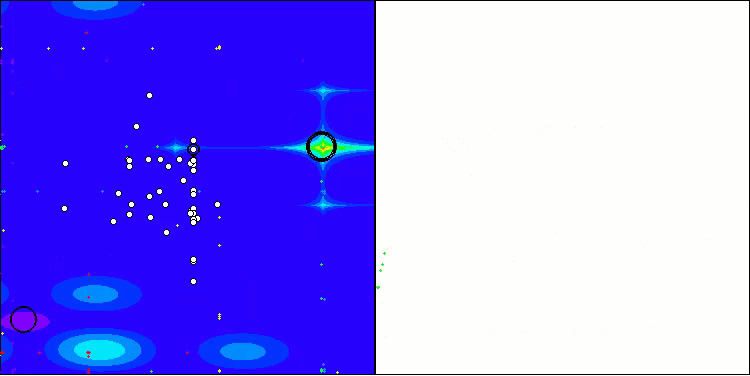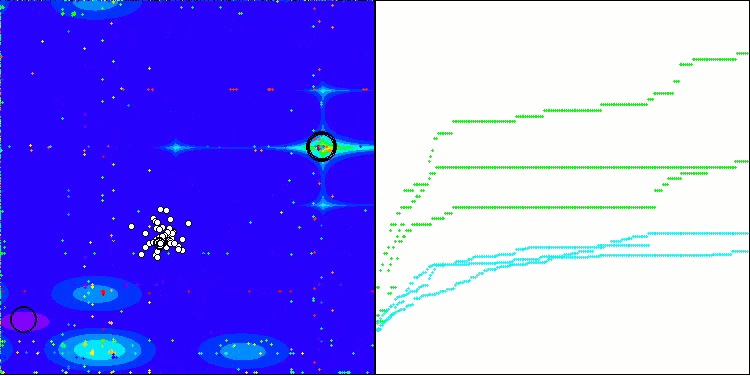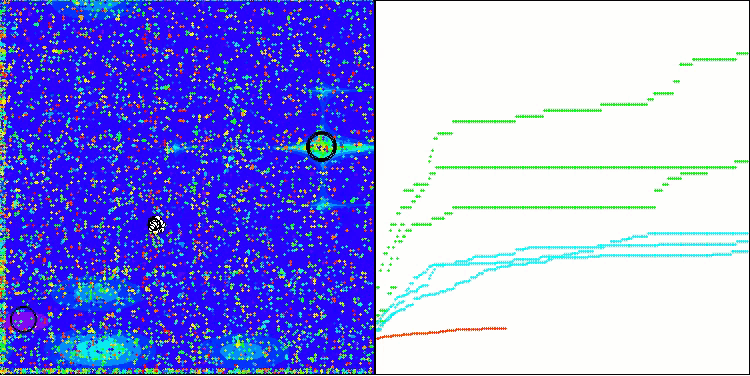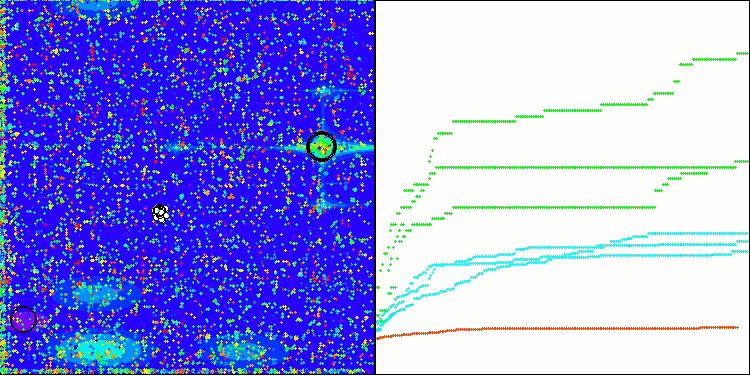
TSm on the Megacity test function

Based on the test results, the algorithm ranks 18 th in the rating table. This is an above average result.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	turtle shell evolution algorithm	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
19	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
20	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
21	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
22	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
23	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
24	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
25	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
26	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
27	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
28	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
29	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
30	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
31	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
32	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
33	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
34	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
35	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
36	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
37	AAA	algae adaptive algorithm	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
38	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
39	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
40	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
41	Boids	boids algorithm	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
42	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
43	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
44	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
45	RND	random	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37

Summary

Considering the results of the algorithm's work on test functions of different dimensions, it can be noted that the algorithm has a more difficult time coping with large-dimensional problems on the smooth Hilly function. In other tests, the algorithm demonstrates consistently good results.

The proposed modification of the well-known Tabu Search algorithm, unlike the original version, can be used in any general optimization problems in continuous search spaces, including both smooth and discrete problems. The algorithm can serve as a powerful basis for applying the underlying idea in other algorithms. To improve the accuracy of convergence, we can use the methods applied in the previously discussed algorithms, but at this stage I present the modification "as is".

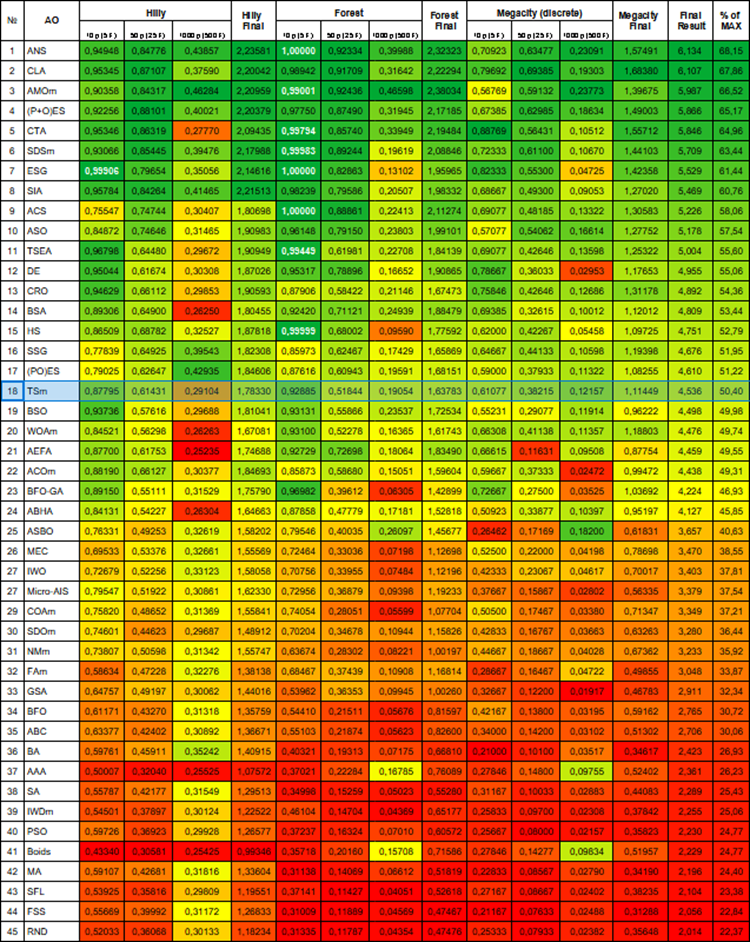
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

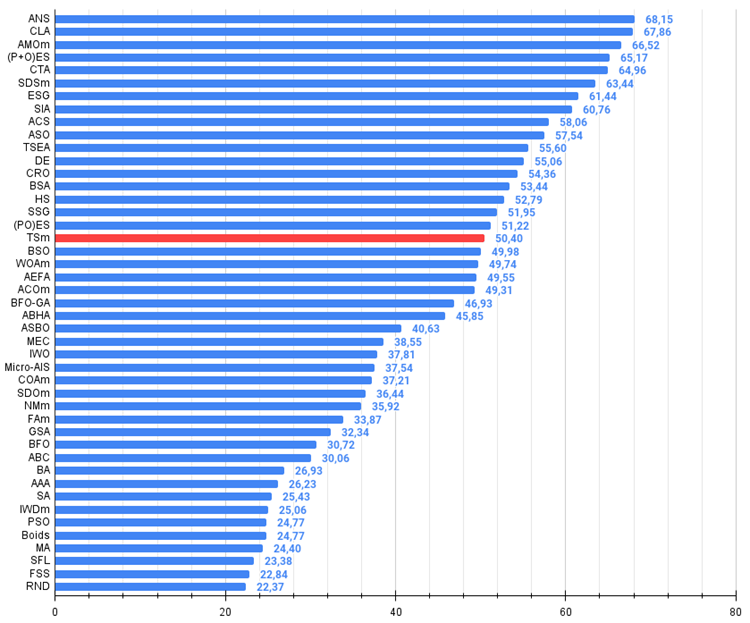
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

TSm pros and cons:

Advantages:

1. A promising idea for further improvement and use as a basis for new algorithms.
   
2. Good scalability.
3. A small number of intuitive parameters (only two, excluding the population size).
   

Disadvantages:

1. Convergence accuracy could have been better.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355