Population optimization algorithms: Harmony Search (HS)

Contents:

1. Introduction
2. Algorithm
3. Test results

1. Introduction

Musical composition consists of several components - rhythm, melody and harmony. While rhythm and melody form a single whole of a musical work, then harmony is what it is decorated with. A play or a song without harmony is like an uncolored picture in children's books - it is drawn, but there is no color, no brightness, no expressiveness. A properly selected harmony caresses the ears, ennobles the sound allowing us to fully enjoy the wonderful sounds of the piano, guitar or any other musical instrument. A melody can be sung, while a harmony can only be played. Musical harmony is a set of chords, without which not a single song or any piece of music will be full-fledged and full-sounding.

Harmony appears exactly at the moment when we connect two sounds - one after the other or in simultaneous flow. A more capacious synonym would be "combination". After one sound is connected with another, we get a combination, in which the hierarchy is already trying to line up in its own way. In music schools, colleges and conservatories there is a special discipline - harmony, where students study all the chords existing in music theory, learn to apply them in practice and even solve problems in harmony.

During a musical improvisation, musicians try to tune the pitch of their instruments to achieve pleasing harmony (best condition). In nature, harmony is determined by a special relationship between several sound waves that have different frequencies. The quality of the improvised harmony is determined by the aesthetic evaluation. In order to improve aesthetic appreciation and find the best harmony, musicians go through practice after practice. There is a similarity between improvising and optimization.

The Harmony Search (HS) method is an emerging metaheuristic optimization algorithm that has been used to solve numerous complex problems over the past decade. The Harmony Search algorithm (HS) was first proposed in 2001 by Z. W. Geem. The HS method is inspired by the founding principles of musical improvisation and the search for musical harmony. The combinations of perfect harmony of sounds are matched with the global extremum in the multidimensional optimization problem, while the musical improvisation process is matched with a search for the extremum.

During improvisation, each musician reproduces a sound at any measure of a piece of music (within the capabilities of their musical instrument), so that the sounds of all the musicians of the orchestra at this measure form one vector of harmony. Combinations of sounds that form "good" harmonies are memorized by each of the musicians and can be used by them to form even better harmonies in subsequent measures of the piece of music.

As a rule, during the improvisation, a musician fulfills one of the following three requirements: forming an absolutely random sound from the range of sounds available; playing any sound from the memory of harmonies; playing an adjacent harmony vector from the same memory. The main features of the HS algorithm are the possibility of using it to solve both continuous and discrete optimization problems.

The distinguishing features of HS are the simplicity of the algorithm and the efficiency of the search. Because of this, the algorithm attracts considerable attention of researchers and is rapidly developing both in theoretical and practical terms. HS is a metaheuristic technique that provides high stability between exploration and exploitation phases in the search process. HS is inspired by human creativity, and the method of finding the perfect solution to a given problem is similar to that used by a musician trying to find a pleasing harmony. The method used to obtain the value of the fitness function is similar to the method for obtaining a reference using the pitch of each musical instrument.

2. Algorithm

The work of HS logic is similar to the work of a musician in creating perfect harmony. The musician tries to change the various tones until the perfect harmony is found. After that, the collection of found harmonies is stored in memory. In an optimization problem, harmonies undergo various changes; if the results of the variation are favorable, then the memory is renewed by adding harmony to the memory and removing the undesirable elements... All this may sound pretty confusing. So what is harmony? What are tones? Let's try to understand the algorithm using our own terms.

What is a piece of music? Of course, I'm not a musician (which is a pity), but a programmer. But for the sake of the algorithm detection, it will be sufficient to apply the concept of "note". A piece of music is composed of notes (chords). Figure 1 schematically shows the "mechanism" for building a piece of music. The selection of notes corresponds to a piece of music, which is easily determined even without an ear for music or musical education. Those willing to guess may leave a comment below.

Optimizing the HS algorithm consists in moving the green bars with notes across the blue bar of the piece itself. The range of the green bar is an octave, which is made up of individual notes. The product (blue bar) corresponds to one of the optimization solutions. The notes on the green bar are the corresponding optimization parameters of the problem. The musician's memory stores several versions of the piece (several variants of blue bars), this is the algorithm population.

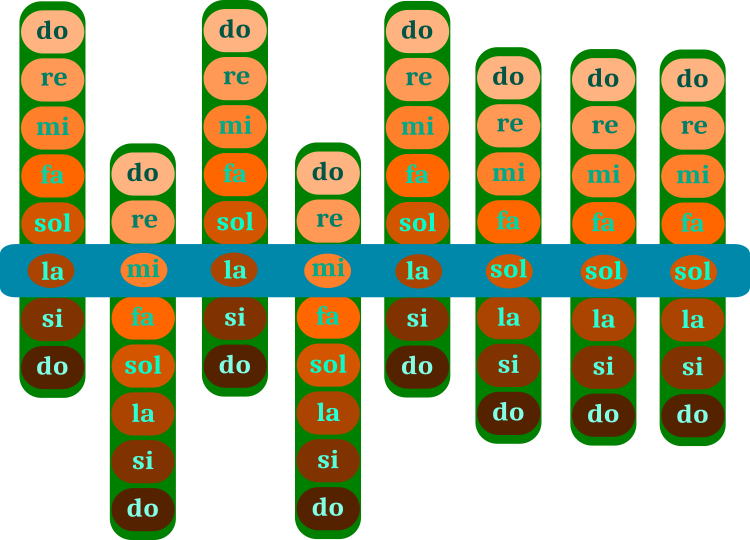
Figure 1. Selection of notes in a piece of music (search for harmony). The blue bar is a piece. The green bars are set of notes

The example in Figure 1 corresponds to the solution of a discrete problem, where there are eight steps in the parameter. The example is provided for ease of understanding the operation of the algorithm. However, in an arbitrary task, there can be any step of the optimized parameters and there are also intermediate notes - semitones. The correct parameters for solving the problem correspond to the correct notes in the piece.

So, the process of creating a piece of music begins with a random set of sounds of a musical instrument that lie in the range of reproducible frequencies of the instrument. It is necessary to create several variants of a piece to be able to combine individual sections of the variant notes. The next step is changing the notes in these variations. We can do this in three possible ways:

1. Randomly change one of the notes in the piece that is in the range of the musical instrument.
2. We can take a note with the corresponding serial number from other versions of the piece.
3. We can take a note from another version of the piece and slightly change it making it higher or lower in key.

Having thus obtained a new set of variants of a musical work, we evaluate each of the variants in terms of sound harmony and store the variants in their original position in memory provided that the new version is better than its previous version. The unique feature of the algorithm is that there is no need to sort the population, in our case the set of products. Each new best option will replace the old worst one in the same place. This process is a bit like the work of genetic algorithms that mimic evolution when the fittest individuals survive. In addition, similarities are also observed with the combination of genes in the chromosome.

Based on the foregoing, we can preliminarily compose the pseudocode of the HS algorithm:

1. Generation of random harmonies.
2. Measurement of the quality of harmonies (calculation of the fitness function).
3. Use the chord selection of a randomly selected harmony with the probability of Eh.
  3.1 Change the chord according to the equation if the chord is selected from some harmony with the probability of Ep.
    3.1.1 Leave the selected chord unchanged.
  3.2 New chord according to the equation.
4. Measurement of the quality of harmonies (calculation of the fitness function).
5. repeat from p.3 until the stop criterion is met.

So, let's move on to describing the input parameters of the algorithm, which are few and intuitive.

input int    Population_P = 50;    //Population size
input double Eh_P         = 0.9;   //random selection frequency
input double Ep_P         = 0.1;   //frequency of step-by-step adjustment
input double Range_P      = 0.2;   //range

• Population_P - the number of variants of a piece in the musician's memory (population size);
• Eh_P - how often a variant of a piece is selected from memory affects how often we will refer to other variant to borrow a note. A higher value means higher combinatorial properties of the algorithm;
• Ep_P - how often you need to slightly change the note, higher or lower in tone, if the note was selected from another version of the piece;
• Range_P - the range of the note in the edited version of the piece, if it was not taken from another version. For example, 0.2 would mean 20% of the musical instrument note range.
• 
  

The HS algorithm operates with harmonies (musical compositions), which can be described by the S_Harmony structure. Harmony consists of notes (chords), this is an array representing c[] parameters to be optimized. The best chords of the piece will be stored in the cB [] array. It is in this array that the successful composition will be sent to, and it is with these compositions (harmonies) that we will perform combinatorial permutations borrowing notes from them. The quality of the harmony is stored in the h variable, and the best harmony is stored in the hB variable.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

The array of harmony structures is used in the C_AO_HS class. The declarations in the method and member class are compact, because the algorithm is extremely concise and has low computational requirements. Here we will not see sorting used in many other optimization algorithms. We will need arrays to set the maximum, minimum and step of the parameters being optimized (they play the role of the range and step of the chords) and constant variables to transfer the external parameters of the algorithm to them. Let's move on to the description of the methods that contain the main logic of HS.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

The Init () public method initializes the algorithm. Here we set the size of the arrays. We initialize the quality indicator of the best found harmony with the minimum possible 'double' value. We will do the same with the corresponding variables of the array of harmony structures.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

The first public method Moving(), which is required to be executed at each iteration, has the 'iter' input - the current iteration. On the first iteration, when the 'revision' flag is 'false', it is necessary to initialize the harmonies with random values in the range of musical instruments, which is equivalent to randomly playing chords by a musician. To reduce repetitive operations, let's store the sound frequency range of the corresponding chords (optimized parameters) in the frequency[] array.

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

At the second and subsequent iterations, improvisation takes place, i.e. sequential change of chords and their combinations. There are several harmonies in memory, which we will change and combine. For each new harmony, we will sequentially sort through the chords. For each chord, there is a probability of being chosen randomly from the memory of the harmony, i.e. harmony will be chosen randomly (equiprobably for all harmonies). If the chord is taken from the memory of harmonies, then the probability of its change is also checked by the equation:

h [har].c [c] = h [har].c [c] + r * B * frequency [c];

where:

r - random number between -1 and 1
frequency - frequency range of the instrument
B - coefficient calculated by the formula:

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

where:

maxIterations - maximum number of iterations
iter - current iteration
maxB - maximum coefficient limit
minB - minimum coefficient limit

Figure 2 shows the dependence of the coefficient B on the tuning parameters of the algorithm and the current iteration.

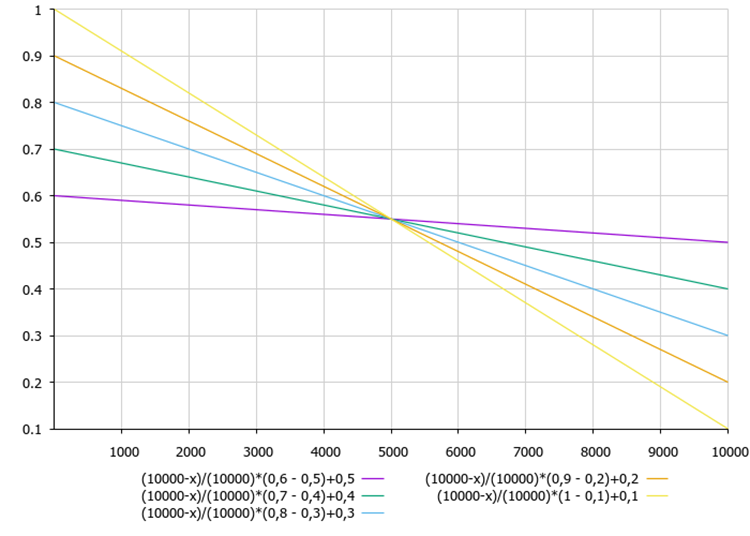
Figure 2. The dependence of the coefficient B on the tuning parameters of the maxB, minB algorithm and the current iteration

The B coefficient calculation equation shows that the B coefficient decreases with each iteration. Thus, the found extremums are refined by the end of the optimization.
If a chord has not been selected from the harmonies memory, the one that already exists at the moment will be changed. The difference in a chord change from the previous change is the fixed range of sound wave values.

After the process of changing the chord is completed, let's check the resulting chord for going beyond the allowable values of the musical instrument.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision () is the second public method called on each iteration after the fitness function has been calculated. Its purpose is to update the found global solution. In case the harmony is better than its best version h > hB, then update the best version of this harmony.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Having carefully studied the code, we see that there are no fundamentally new ideas in the harmony search algorithm. The Harmony Search algorithm borrows from previously used ideas of evolutionary algorithms, including global uniform recombination, uniform mutation, Gaussian mutation and replacement of the worst individual every generation. Some sources indicate the need to replace the worst harmony in memory with a new one. In our algorithm, harmony can only replace its best solution. This is slightly different from the classical version, because my studies indicate that it is this implementation of the algorithm that will be more productive.

The contribution of the harmony search algorithm lies in two areas: the combination of these ideas in this algorithm is novel; the musical motivation of the harmony search algorithm is new. Very few publications on harmony search discuss musical motifs or extensions of the harmony search algorithm. Most of the publications are devoted to the hybridization of the harmony search algorithm with other evolutionary algorithms, the adjustment of the harmony search parameters or the application of the harmony search algorithm to specific problems. If more musically conditioned extensions could be applied to the HS algorithm, then this would help to distinguish it as a separate evolutionary algorithm. Such research would require the study of music theory, the study of the process of musical composition and arrangement, the study of educational theories of music and the inventive application of these theories in the harmony search algorithm.

3. Test results

HS test stand results look as follows:

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Score: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's; Func runs 10000 result: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score: 0.05410

The high values of the test functions are striking, giving hope that the results in the overall test score will be outstanding. A characteristic feature of HS on visualization is that we do not see any structural formations in the form of groups of coordinates, as in the case of some of the previous algorithms. Visually there are no patterns in the movement of agents in the search space. This is similar to the behavior of the RND optimization algorithm, although the convergence graphs behave very confidently, progressively approaching the solution of the optimization problem. Getting stuck in local extrema is not typical for this algorithm.

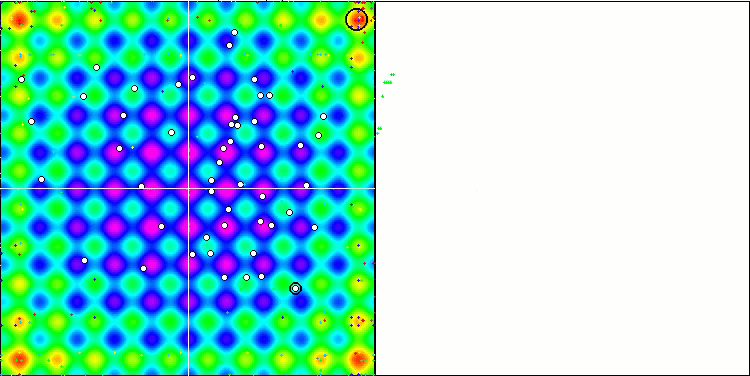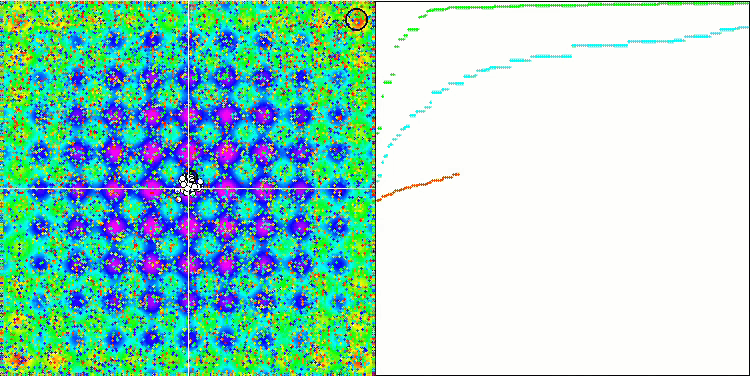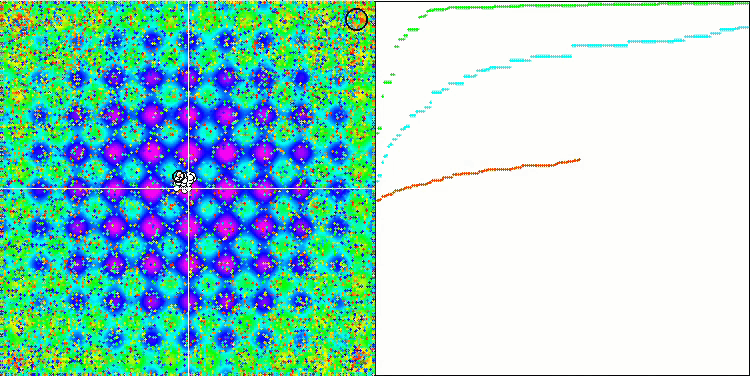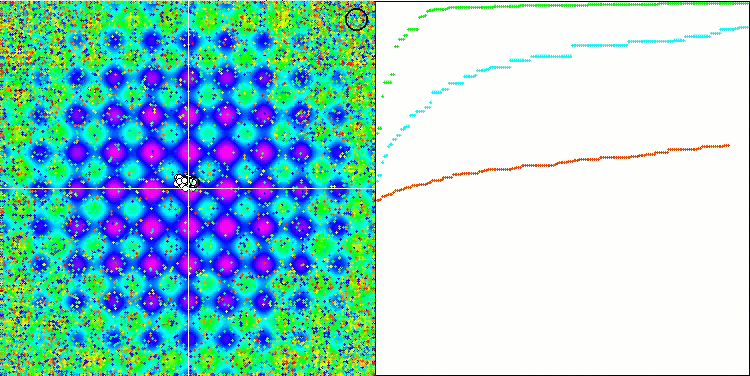
  HS on the Rastrigin test function

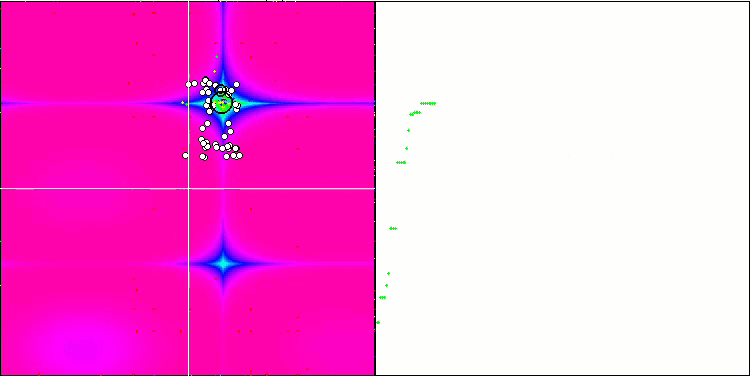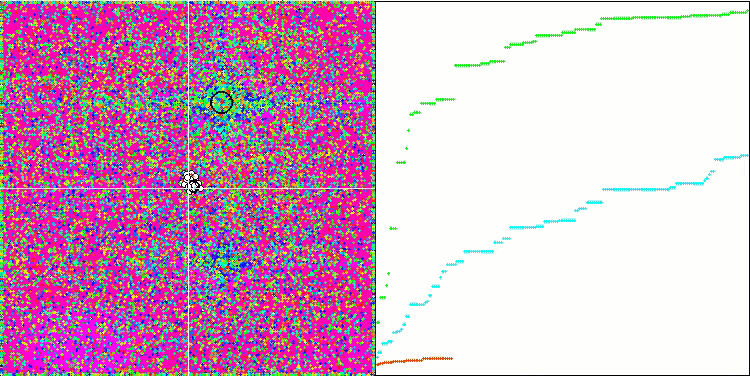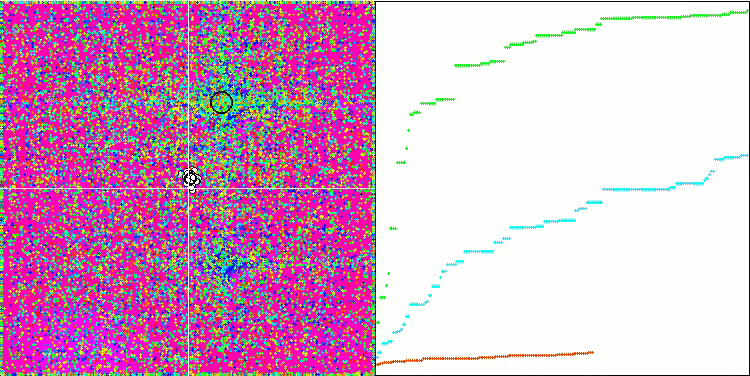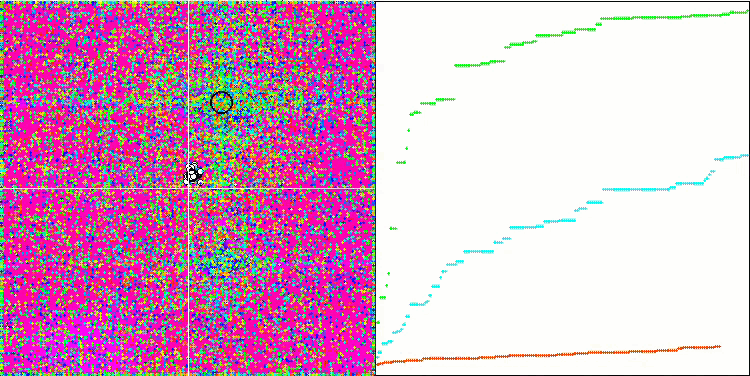
  HS on the Forest test function

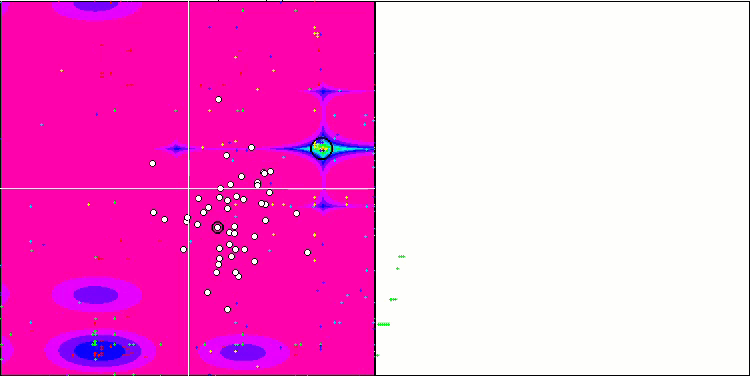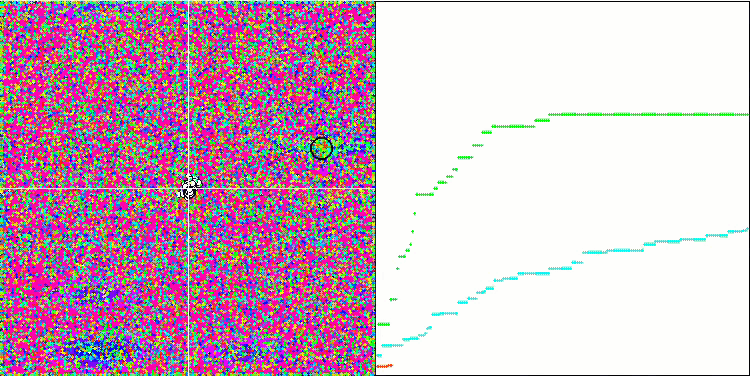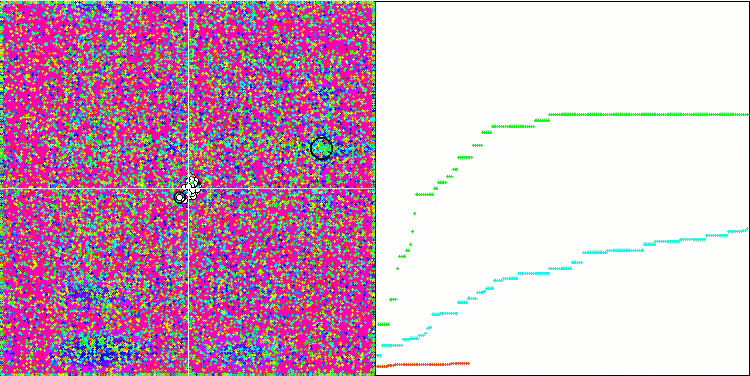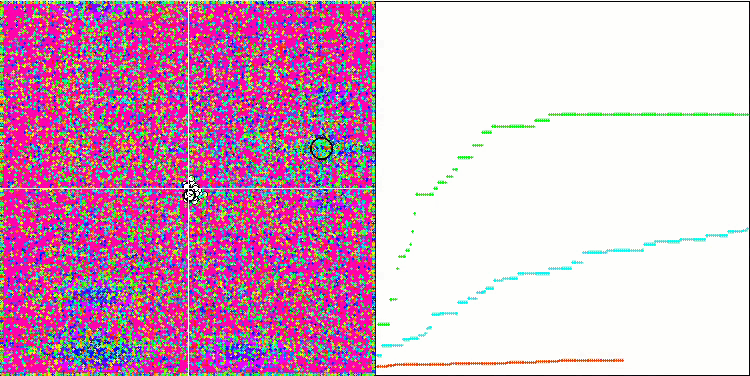
  HS on the Megacity test function

It is time to analyze the results in the table and answer the question set in the article title. In previous articles, I expressed doubt whether we can see an algorithm that would bypass the leader in the rating table on a discrete function. The algorithm, which visually looks like a random one, has been able to become a leader not only on a discrete function (best in three tests), but also on other test functions, eventually becoming the best in 6 out of 9 tests.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
HS	harmony search	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.00000
ACOm	ant colony optimization M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	invasive weed optimization	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	cuckoo optimization algorithm M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	firefly algorithm M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	bat algorithm	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	artificial bee colony	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	bacterial foraging optimization	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	gravitational search algorithm	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
FSS	fish school search	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	particle swarm optimisation	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	random	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	grey wolf optimizer	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Let's summarize. At the time of writing, the HS algorithm occupies a leading position on the histogram of test results with a huge lead in relation to other optimization algorithms, which indicates the strength and power of the algorithm and its potential in the field of optimizing the processes of solving problems of varying complexity.

In my opinion, a very important factor that allows demonstrating impressive results on various types of test functions, including very complex ones, is the inheritance of some methods (techniques) present in other optimization algorithms: HS does not have a solution pool sort, each solution updates only its local decision - this is typical of the cuckoo search optimization algorithm, where a new path for the development of a decision branch occurs only if the egg is better than the one in the nest. Also, HS methods are similar to the methods used in genetic algorithms - combinatorics of solution elements.

The powerful HS optimization algorithm, which has exceptionally high performance, can be safely recommended for solving a wide variety of complex problems with many variables, both for smooth scaling functions and for complex discrete combinatorial problems. The HS algorithm has already been successfully applied in many areas of engineering (optimization of the topology of structures and the optimal shape of parts), electronics and logistics.

The ease of implementation of the HS algorithm gives room for research allowing us to add and combine various optimization strategies. This suggests that the capabilities of the algorithm are far from being fully realized.

The histogram of the algorithm test results is provided below.

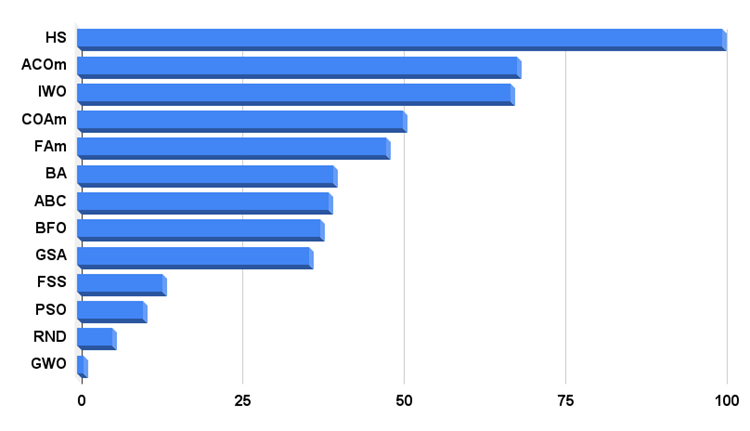
Figure 3. Histogram of the test results of the algorithms

Pros and cons of the HS harmonic search algorithm:

Pros:
1. Easy implementation.
2. Excellent convergence on all types of functions with no exception.
3. Impressive scalability.
4. Very fast.
5. Small number of external parameters.

Cons:
Not found.

Each article features an archive that contains updated current versions of the algorithm codes for all previous articles. The article is based on the accumulated experience of the author and represents his personal opinion. The conclusions and judgments are based on the experiments.